多項式の展開 
最近、整式という言葉が使われなくなりつつあり、「多項式」という言葉に取って代わられ
ようとしている。
以前は、単項式のいくつかを、「＋」や「−」で結びつけた式を多項式と呼んだが、今では
単項式も多項式の一つの場合に過ぎないという見方でとらえられている。
このページでは、（１＋ｘ）ｎ の展開について考える。
この多項式の展開については、当ＨＰの「パスカルの三角形」で既に述べられている。
そこでは、小さい ｎ の値については、パスカルの三角形を使うのが有効であるが、十分
大きい ｎ の値に対しては、２項定理を利用するという話であった。
２項定理（Ｂｉｎｏｍｉａｌ Ｔｈｅｏｒｙ）
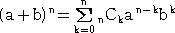
ここで、ｎＣｋ は、２項係数といわれ、異なる ｎ 個のものから、異なる ｋ
個のもの
をとる組合せの数である。
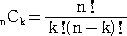
但し、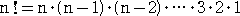
（ｎ の階乗）とする。
確かに、２項定理は、各項の係数を即座に計算できるという利点はあるが、十分大きい
ｎ の値に対しては、「計算が大変だ！」というのが本音だろう。
そこで、このページでは漸化式の考えを取り入れ、順次前の項の係数から次の項の係
数を求める公式を紹介したい。
例 （１＋ｘ）3 ＝ａ0＋ａ1ｘ＋ａ2ｘ2＋ａ3ｘ3 とおき、数列 ｛ ａｎ ｝ の漸化式を作ってみよう。
例えば、ｘ の項に注目すると、ａ1 は次のような考えで定まる数であった。
３つの １＋ｘ のうちの１つから、「ｘ」 を選択し、他の２つからは、「１」
を選択する。
このような場合の数は、３通りある。 よって、 ａ1 ＝ ３ となる。
すなわち、下表で、黄色の部分からは「ｘ」 を選択し、白色の部分からは「１」
を選
択する。
|
| １． |
１＋ｘ |
１＋ｘ |
１＋ｘ |
| ２． |
１＋ｘ |
１＋ｘ |
１＋ｘ |
| ３． |
１＋ｘ |
１＋ｘ |
１＋ｘ |
|
この３つのそれぞれの場合を起点として、ｘ2 の項を作るとき、その場合の数が、
ａ2 となる。
例えば、場合１．について、白色の部分から、もう一つ「ｘ」 を選択すればよい。
選ばれた部分を、赤色で表す。
|
|
|
 |
|
| Ａ． |
１＋ｘ |
１＋ｘ |
１＋ｘ |
| Ｂ． |
１＋ｘ |
１＋ｘ |
１＋ｘ |
|
同様にして、場合２．、場合３．についても次のようになる。
|
|
|
|
|
| Ｃ． |
１＋ｘ |
１＋ｘ |
１＋ｘ |
| Ｄ． |
１＋ｘ |
１＋ｘ |
１＋ｘ |
|
|
|
|
|
|
| Ｅ． |
１＋ｘ |
１＋ｘ |
１＋ｘ |
| Ｆ． |
１＋ｘ |
１＋ｘ |
１＋ｘ |
|
以上から、場合の数は、６通りありそうに思えるが、実は上記の場合には同じもの
が含まれている。（ＡとＣ、ＢとＥ、ＤとＦ）
したがって、２通りずつ同じものが含まれるので、求める場合の数は、３通りで、
ａ2 ＝ ３ となる。
このとき、 ａ2 と ａ1 の関係は、次のようになっている。
ａ2 ＝ ａ1 × ２ ÷ ２
このことから、 ａｋ＋１ ＝ ａｋ × （３−ｋ） ÷ （ｋ＋１） という漸化式が予想される。
上記の例を一般化して、漸化式を実際に求めてみよう。
（１＋ｘ）ｎ ＝ａ0＋ａ1ｘ＋・・・＋ａｋｘｋ＋ａｋ＋１ｘｋ＋１＋・・・＋ａｎｘｎ とおく。
ｎ 個の １＋ｘ のうち、ｋ 個の １＋ｘ から、「ｘ」 を選択し、残りの
ｎ−ｋ 個の １＋ｘ
から、「１」 を選択する。 このような場合の数が ａｋ となる。
各場合について、残りの ｎ−ｋ 個の １＋ｘ から、「ｘ」 を １
個選択する場合の数
は、ｎ−ｋ 通りある。
ところが、それらの場合には同じものが含まれる。 ｋ＋１ 個ずつ同じものがで
きるので、求める場合の数は、
ａｋ×（ｎ−ｋ）/（ｋ＋１） 通り
となる。この値は、ａｋ＋１ に等しい。
すなわち、
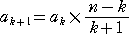
が成り立つ。
（別解） もちろん上記のような推論を経なくても、次の式変形から明らかだろう。
ａｋ+1＝ｎＣｋ+1＝ｎ！/（（ｋ＋１）！（ｎ−ｋ−１）！）
＝｛ｎ！/（ｋ！（ｎ−ｋ）！）｝・｛（ｎ−ｋ）/（ｋ＋１）｝
＝ｎＣｋ・｛（ｎ−ｋ）/（ｋ＋１）｝＝ａｋ×｛（ｎ−ｋ）/（ｋ＋１）｝ （終）
この漸化式を用いると、多項式の展開は容易である。
例 （１＋ｘ）5 を展開してみよう。
ａ0 ＝ １
ａ1 ＝ ａ0×（5−0）/（0＋1）＝５
ａ2 ＝ ａ1×（5−1）/（1＋1）＝１０
ａ3 ＝ ａ2×（5−2）/（2＋1）＝１０
ａ4 ＝ ａ3×（5−3）/（3＋1）＝５
ａ5 ＝ ａ4×（5−4）/（4＋1）＝１
よって、 （１＋ｘ）5 ＝ １＋５ｘ＋１０ｘ2＋１０ｘ3＋５ｘ4＋ｘ5 となる。
例 （１＋ｘ）10 ＝ １＋１・（10/1）ｘ＋１0・（9/2）ｘ2＋45・（8/3）ｘ3＋１20・（7/4）ｘ4＋・・・
＝１＋１０ｘ＋４５ｘ2＋１２０ｘ3＋２１０ｘ4＋・・・
（コメント） ２項係数の対称性を利用すれば、上記の計算は半分で済む。面倒な２項係数
の計算をしなくても上記の公式を用いれば、展開しながら次々に係数を暗算で求
めて展開できるわけで、何か「鮮やか！」と感じるのは私だけだろうか？
（参考文献：ア・マルクシェビィチ 著 鈴木竹夫 訳 級数 （東京図書））
（追記） 平成２２年１０月９日付け
当ＨＰがいつもお世話になっているＨＮ「攻略法」さんから、計算機における２項係数の効
率的な求め方について、ご教示いただいた。攻略法さんに感謝します。
ｎＣｒ＝ｎ（ｎ−１）（ｎ−２）・・・（ｎ−ｒ＋１）/ｒ（ｒ−１）（ｒ−２）・・・３・２・１
＝（ｎ/１）（（ｎ−１）/２）（（ｎ−３）/３）・・・（（ｎ−ｒ＋１）/ｒ） ←
漸化式表現
階乗をそのまま計算すると桁あふれを起こすが、このように求めると抑えることができる
そうである。
例 10Ｃ4＝（１０/１）（９/２）（８/３）（７/４）＝２１０