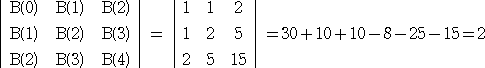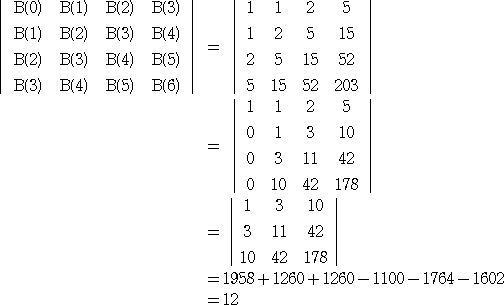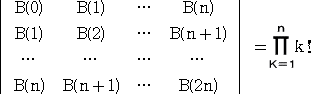ベル数 
最近、本を読んでいると、「ベル数」という言葉が目についてきた。もちろん、この言葉が
出てくるような分野の本を読んでいるからだろうが、時たま、「エッ!こんなところにもベル
数?」という出会いもあり、興味がわいてきたので、少しまとめてみようという気になった。
ベル数 B(n) とは、「 n 個のものを空でない、いくつかのまとまりに分けるときの場合の
数」のことである。
このベル数という概念は、Eric Temple Bell (1883〜1960)によって研究されたらしい。
例 n=1 のときは、明らかに、 B(1)=1
n=2 のときは、 1組に分ける場合(2個のまとまり)が、1通り
2組に分ける場合(1個ずつ)が、1通り で、 計 2通り
よって、 B(2)=2
n=3 のときは、 1組に分ける場合(3個のまとまり)が、1通り
2組に分ける場合(1個と2個)が、3通り
3組に分ける場合(1個ずつ)が、1通り で、 計 5通り
よって、 B(3)=5
n=4 のときは、 1組に分ける場合(4個のまとまり)が、1通り
2組に分ける場合
(1個と3個)が、4通り
(2個と2個)が、4C2÷2=3通り
3組に分ける場合(1個、1個、2個)が、4C2=6通り
4組に分ける場合(1個ずつ)が、1通りで、 計 15通り
よって、 B(4)=15
このように計算していくと、値 n のベル数を求める場合に何組に分けるのかが大切だと
気づく。
「 n 個のものを空でない、k 組のまとまりに分ける場合の数」のことを、第2種スターリン
グ数 nSk というようだ。
この記号を使うと、 B(n)=nS1+nS2+ ・・・ +nSn となる。
第2種スターリング数 nSk を下記のように並べてみた。
1S1=1
2S1=1 、 2S2=1
3S1=1 、 3S2=3 、 3S3=1
4S1=1 、 4S2=7 、 4S3=6 、 4S4=1
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
「ボーッ!」と眺めていても、パスカルの三角形のような美しい関係は見えてこない。
第2種スターリング数 nSk については次の漸化式が知られている。
(1) nS1=1 、 nSn=1
(2) nSk =n-1Sk-1 +k・n-1Sk (k=2、3、・・・、n−1)
この漸化式を眺めていると、上記の三角形の関係が多少は見えてくるように感じる。
例 3S2=3 、 3S3=1
4S3=6(=3+3×1)
(漸化式の証明)
(1)は、明らかとしていいだろう。
(2) n 個のりんごを、k 枚のお皿に盛ることを考える。1個もりんごがのっていないお皿は
ないものとする。 n 個のりんごのうち、特定の1個のりんご(A)の盛り方に注目する。
求める場合は、次の2つの場合の何れかである。
(イ) あるお皿に盛られているりんごが、Aのみの場合
このとき、残りの n−1個のりんごを、k−1枚のお皿に盛る方法の数は、n-1Sk-1 通り
(ロ) あるお皿に盛られているりんごが、A以外にもある場合
このとき、残りの n−1個のりんごを、k枚のお皿に盛る方法の数は、n-1Sk-1通りで、
そのうちの1通りに対して、Aをどれかのお皿に付け足す方法は、 k 通りなので、この場合
の数は、 k・n-1Sk 通り
したがって、 nSk =n-1Sk-1 + k・n-1Sk が成り立つ。 (証終)
この漸化式を用いると、第2種スターリング数 nSk の表を作ることは易しい。
したがって、ベル数 B(n) も順次求められる。
| n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
B(n) |
| 1 |
1 |
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・ |
|
1 |
| 2 |
1 |
1 |
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・ |
|
2 |
| 3 |
1 |
3 |
1 |
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・ |
|
5 |
| 4 |
1 |
7 |
6 |
1 |
・・・・・・・・・・・・・・・・・・・・・・・・・・・・ |
|
15 |
| 5 |
1 |
15 |
25 |
10 |
1 |
・・・・・・・・・・・・・・・・・・・・・・ |
|
52 |
| 6 |
1 |
31 |
90 |
65 |
15 |
1 |
・・・・・・・・・・・・・・・・ |
|
203 |
| 7 |
1 |
63 |
301 |
350 |
140 |
21 |
1 |
・・・・・・・・・・ |
|
877 |
| 8 |
1 |
127 |
966 |
1701 |
1050 |
266 |
28 |
1 |
・・・・ |
|
4140 |
| 9 |
1 |
255 |
3025 |
7770 |
6951 |
2646 |
462 |
36 |
1 |
|
21147 |
練習問題 5人を3つのグループに分ける方法の数を求めよ。
この問題に対して、これまでは、次のような解法しか思い浮かばなかった...。
(解) (35−3・25+3)/3!=(243−96+3)/6=150/6=25 (通り) (終)
この練習問題は、第2種スターリング数 5S3 を求めることに等しいので、漸化式を用いて、
5S3=4S2+3・4S3=3S1+2・3S2+3・(3S2+3・3S3)
=3S1+2・(2S1+2・2S2)+3・((2S1+2・2S2)+3・3S3)
=1+2・(1+2・1)+3・((1+2・1)+3・1)=1+6+3・6=25
(コメント) 上記のようには計算しないで、実際に表を作った方が速かったかな?
上記では、同一行の第2種スターリング数の総和という形でベル数を計算したが、ベル数
そのものを直接に計算する三角形も存在するようだ。
下記の三角形は、Aitken’s array(A011971)から得られる。
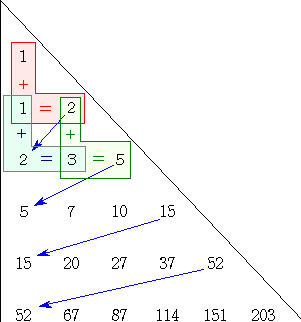 |
(左図の三角形の作り方)
1. まず、1を2つ縦に並べ、1+1を計算し
て、その答え2を下段の1の横に書く。
2. 答え2を下段の1の下にも書き入れ、
1+2を計算して、その答え3を2の横に
書く。
3. 上段にある2と、答え3を加えて、その
答え5を、3の横に書き入れる。
4. 上記のような操作を繰り返すと、左図
のような三角形が出来る。
このとき、各段の最右端の数がベル数
を与える。
|
上記の計算のからくりを第2種スターリング数nSk を用いて確認してみよう。
最初の B(1)=1 は、 B(1)=1S1=1 からでいいだろう。
次の B(2)=2 は、 下段の1を、2S1=1 と考え、1+1=2 は、1S1+2S1=2 と理
解する。
このとき、 1S1+2S1=2S1+2S2 なので、B(2)=2S1+2S2=2
となる。
次の B(3)=5 は、 (1+1)+(1+2)=2+3 において、 B(2)の計算では、
1+1=2 を 2S1+2S2=2 としたが、これは、 3S1+3S3=2 としてもよい。
また、 1+2=3 を、 2S2+(2S1+2S2)=3 と理解する。
このとき、
B(3)=(3S1+3S3)+{2S2+(2S1+2S2)}
=(3S1+3S3)+(2S1+2・2S2)=(3S1+3S3)+3S2=3S1+3S2+3S3 =5
となる。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
こんな風に考えていくと、上記の三角形の最右端にベル数 B(n)が表れる理由が分かる
ような気がする。
ベル数は、フィボナッチ数列のように単純な計算では求められず、上記の三角形で地道
に計算するしかない。
これに対して、HN「Harry」さんという方が面白い覚え方を考案されている。
人 に この 苺 コップ 触れさせ、 バナナ 良いようだ。
1 2 5 15 52 203 877 4140
私も「Harry」さんに触発されて、覚え方を考えてみた。
イッチ−ニーGo!囲碁のコツ は掴み、 歯並び 良いよ。
1 2 5 15 52 203 877 4140
(ちょっと、私のは駄作かな?)
次のようなベル数の並び:
B(1)=1、B(2)=2、B(3)=5、B(4)=15、B(5)=52、B(6)=203、
B(7)=877、B(8)=4140、・・・
の中に、法則性を発見された方もおられるようだ。
次のような合同式(Touchard’s congruence)が知られている。
B(p+k)≡B(k)+B(k+1) (mod p) ただし、p
は素数
実際に、 B(2+1)=B(3)=5
B(1)+B(2)=1+2=3 で、 5≡3 (mod 2) より、
B(2+1)=B(1)+B(2) (mod 2) が成り立つ。
さらに、 B(2+2)=B(4)=15
B(2)+B(3)=2+5=7 で、 15≡7 (mod 2) より、
B(2+2)=B(2)+B(3) (mod 2) が成り立つ。
B(3+4)=B(7)=877
B(4)+B(5)=15+52=67 で、 877≡67 (mod 3) より、
B(3+4)=B(4)+B(5) (mod 3) が成り立つ。
(コメント) う〜む!なるほど。 僅かしか計算していないが、美しい合同式ですね!
ベル数を直接計算する漸化式も知られている。
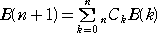
今まで、n=0 の場合、すなわち、B(0)の値を考えてこなかったが、合理的なB(0)の値
は一体何だろうか?
S.Plouffe により、ベル数 B(n) ; n=0 〜 3015 の 表 が与えられている。これ
は圧巻というほかはない。
この表によれば、 B(0)=1 となっている。
順列・組合せにおいて、 nC0=1 であるが、これは n 個のものから何もとらない場合が
1通りあると考えれば合点がいく。(もちろん計算で納得する方法もある!)
これと同様に考えて、B(n) は、「 n 個のものを空でない、いくつかのまとまりに分けると
きの場合の数」であるが、分けるものが何もない場合が1通りあると考えればいいのだろう。
漸化式を用いると、
B(0)=1 、B(1)=1 を利用して帰納的に順次 B(n) を求めることが出来る。
B(2)=1C0B(0)+1C1B(1)=1・1+1・1=1+1=2
B(3)=2C0B(0)+2C1B(1)+2C2B(2)=1・1+2・1+1・2=1+2+2=5
B(4)=3C0B(0)+3C1B(1)+3C2B(2)+3C3B(3)=1・1+3・1+3・2+1・5
=1+3+6+5=15
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
上記で赤字の数字は、パスカルの三角形から得られるものである。パスカルの三角形を
利用して簡便にベル数が求められることが分かった。
ところで、
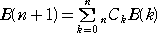
という漸化式には、どんな意味があるのだろうか?
B(3)=2C0B(0)+2C1B(1)+2C2B(2) が成り立つ意味を考えてみよう。
B(3)は、3個のものを空でない、いくつかのまとまりに分けるときの場合の数である。
この3個のうち、特定の1個に注目する。分けられ方には、次の3種類がある。
特定の1個が単独のとき、
残りの2個から2個を選んで分ける方法の数は、 2C2・B(2)通り
特定の1個が他の1個のみと一緒のとき、
残りの2個から特定の1個と一緒になる1個を選び、その選び方 1 通りに対して、
残り1個の分け方の数は、 2C1・B(1)通り
特定の1個が他の2個と一緒のとき、
残りの2個から0個を選んで分ける方法の数は、 2C0・B(0)通り
よって、 B(3)=2C0B(0)+2C1B(1)+2C2B(2) が成り立つ。
この考え方を一般化すれば、漸化式が成り立つことも明瞭に理解される。
もちろん、計算で確かめることもできる。
2C0B(0)+2C1B(1)+2C2B(2)=1+2・1S1+2S1+2S2
=1+(2S1+2・1S1)+2S2=3S1+(2S1+2・2S2)+3S3
=3S1+3S2+3S3=B(3)
(コメント) 計算で機械的に示しても感動はないですね!やはり、上記のように文章で説得
された方が分かりやすいかな?
また、ベル数の列:
B(0)=1、B(1)=1、B(2)=2、B(3)=5、B(4)=15、B(5)=52、B(6)=203、
B(7)=877、B(8)=4140、・・・
において、 B(0)×B(2)−B(1)×B(1)=1×2−1×1=1 であるが、これは、
行列式
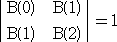
を計算したものである。 同様にして、
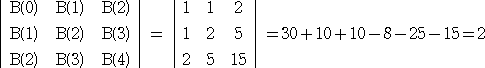
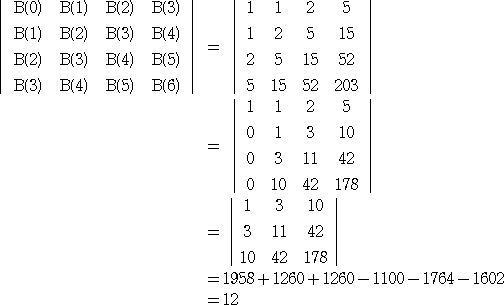
これらの計算に一見法則性がないように感じられるが、Lenard(1992)は次の定理を
見いだしている。
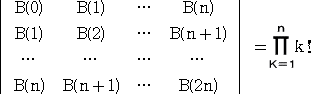
確かに、
n=1 のときは、 1!=1
n=2 のときは、 1!×2!=2
n=3 のときは、 1!×2!×3!=12
となって、上記の計算結果と一致している。
(コメント) 順列組合せの問題でよく用いられる階乗の記号がベル数とこんな風に関係して
いるとは驚きです!
ところで、第2種スターリング数は上記で求めたように、下表のようであった。
| n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 1 |
1 |
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・ |
| 2 |
1 |
1 |
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・ |
| 3 |
1 |
3 |
1 |
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・ |
| 4 |
1 |
7 |
6 |
1 |
・・・・・・・・・・・・・・・・・・・・・・・・・・・・ |
| 5 |
1 |
15 |
25 |
10 |
1 |
・・・・・・・・・・・・・・・・・・・・・・ |
| 6 |
1 |
31 |
90 |
65 |
15 |
1 |
・・・・・・・・・・・・・・・・ |
| 7 |
1 |
63 |
301 |
350 |
140 |
21 |
1 |
・・・・・・・・・・ |
| 8 |
1 |
127 |
966 |
1701 |
1050 |
266 |
28 |
1 |
・・・・ |
| 9 |
1 |
255 |
3025 |
7770 |
6951 |
2646 |
462 |
36 |
1 |
この第2種スターリング数が、次の関数
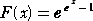
を微分しても得られる点は興味深い。(赤字の部分が、第2種スターリング数)
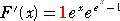
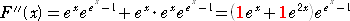
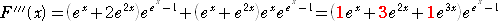
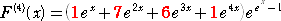
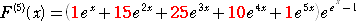
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
したがって、
F(0)=1、F’(0)=1、F”(0)=2、F”’(0)=5、F(4)(0)=15、F(5)(0)=52、・・・
と順次、ベル数 B(n) を得ることが出来る。 すなわち、
B(n) =F(n)(0) 但し、 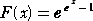
が成り立つ。
このことから、ベル数 B(n) は、自然対数の底 e と何らかの関係がありそうである。
自然対数の底 e は、次の式で定義される。
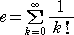
ここで、次のような級数の計算をしてみよう。
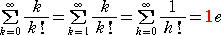
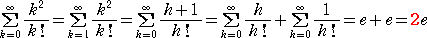
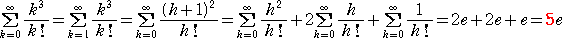
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
各級数の計算結果を見ると、自然対数の底 e の係数がベル数 B(n) になっている。
このことから一般的に、
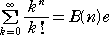
が成り立つことが伺える。
この式を証明するには、次のような議論が必要である。
まず、相異なる n 個のものから r 個取る順列の数 nPr=n×(n−1)×・・・×(n−k+1)
になぞらえて、x の関数 Pk(x) ( k は、自然数)を
Pk(x)=x(x−1)・・・(x−k+1)
と定義する。このとき、
Pk(n)=nPk
である。 特に、 Pn(n)=n! である。
ここで、 nP0=1 であるので、 P0(x)=1 と約束することは理にかなったものだろう。
例 P1(x)=x 、 P2(x)=x(x−1) 、 P3(x)=x(x−1)(x−2) 、
P4(x)=x(x−1)(x−2)(x−3) 、 ・・・・・・・・・・・・・・・・・・・・
この Pk(x) (k=1、2、3、・・・) を用いて多項式 (x+1)n を表すことを考えてみよう。
x+1=P1(x)+P0(x)=1・P0(x)+1・P1(x)
(x+1)2=(x+1)(x+1)=(x+1)(x−1+2)=x(x−1)+2x+x−1+2
=P2(x)+3P1(x)+P0(x)=1・P0(x)+3・P1(x)+1・P2(x)
(x+1)3=(x+1)(x+1)(x+1)=(x+1)(x−1+2)(x−2+3)
=x(x−1)(x−2)+3x(x−1)+2x(x−2)+6x+(x−1)(x−2)+3(x−1)+2(x−2)+6
=x(x−1)(x−2)+3x(x−1)+2x(x−1−1)+6x+x(x−1)−2(x−1)+3(x−1)+2(x−2)+6
=x(x−1)(x−2)+3x(x−1)+2x(x−1)−2x+6x+x(x−1)−2x+2+3x−3+2x−4+6
=x(x−1)(x−2)+6x(x−1)+7x+1
=P3(x)+6P2(x)+7P1(x)+P0(x)
=1・P0(x)+7・P1(x)+6・P2(x)+1・P3(x)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
上記の赤字の数がちょうど第2種スターリング数になっている点が興味深い。
さて、 (x+1)3=P3(x)+6P2(x)+7P1(x)+P0(x) という計算は少し拙く感じる。
もっと上手い計算はないものだろうか?
すぐ思いつく方法は次のようなものである。(こちらの方が普通だったりして...。)
(x+1)3=Ax(x−1)(x−2)+Bx(x−1)+Cx+D において、
x=0 を代入して、 D=1
x=1 を代入して、 C+1=8 より、 C=7
x=2 を代入して、 2B+14+1=27 より、 B=6
x=3 を代入して、 6A+36+21+1=64 より、 A=1
よって、 (x+1)3=P3(x)+6P2(x)+7P1(x)+P0(x) が成り立つ。
(厳密には、十分性を確認する必要があるだろう...。)
以下、工事中