
有限集合 A の要素の個数 n(A) に関する次の個数定理は、高校1年で学ぶ数学Aの中
でも最重要公式と呼べるものだろう。これらの公式をもとに、確率の加法定理が示される。
n(A∪B)=n(A)+n(B)−n(A∩B)
n(A∪B∪C)
=n(A)+n(B)+n(C)−n(A∩B)−n(B∩C)−n(C∩A)+n(A∩B∩C)
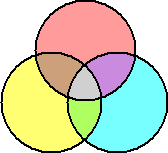
ベン図等を用いて、この等式は視覚的に容易に了解されることだろう。
個数定理 
有限集合 A の要素の個数 n(A) に関する次の個数定理は、高校1年で学ぶ数学Aの中
でも最重要公式と呼べるものだろう。これらの公式をもとに、確率の加法定理が示される。
n(A∪B)=n(A)+n(B)−n(A∩B)
n(A∪B∪C)
=n(A)+n(B)+n(C)−n(A∩B)−n(B∩C)−n(C∩A)+n(A∩B∩C)
ベン図等を用いて、この等式は視覚的に容易に了解されることだろう。
 |
 |
上式は、何れも A、B、・・・ の何れかの性質を持つものの個数を求める定理であるが、
問題によっては、これらの性質を全く持たないものの個数を求めたいという場合がある。
これについては、全体集合を U とすると、補集合の考えを用いて、
AでもBでもないものの個数は、
n(U)−n(A∪B)=n(U)−n(A)−n(B)+n(A∩B)
AでもBでもCでもないものの個数は、
n(U)−n(A∪B∪C)
= n(U)−n(A)−n(B)−n(C)+n(A∩B)+n(B∩C)+n(C∩A)−n(A∩B∩C)
と求められる。
k 個の集合 E1、E2、・・・、Ek に対して、性質 Em を持つ要素の個数を n(Em)=Nm
とし、 n(U)=N 、n(E1∩E2)=N12 、n(E1∩E2∩E3)=N123 、 ・・・・ 等とすれば、
上記の2式は次のように書き直すことができる。
性質 E1、E2 を全く持たないものの個数は、 N−N1−N2+N12
性質 E1、E2、E3 を全く持たないものの個数は、
N−N1−N2−N3+N12+N23+N31−N123
この等式を一般化すれば、次の定理が得られる。
定 理 性質 E1、E2、・・・、Ek を全く持たないものの個数は、
N−ΣNa+ΣNab−ΣNabc+・・・+(−1)kN123・・・k
この公式は、「包含と排除の原理(包除原理)」(Principle of Inclusion and Exclusion)
と呼ばれる。
性質 E1、E2、・・・、Ek を全く持たないものの個数を直接的に求めることは難しいが、い
ろいろな性質を持つ場合の数を計算した方が易しい場合がある。そんな状況に、この包除
原理が大活躍するわけである。
例 3人 a 、b、c を、2組 A、B に分けたい。何通りあるだろうか?
中学校レベルでは次のように場合を尽くして数え上げるのだろう。
|
左表より、 求める場合の数は、 6通り |
高校レベルでは、組合せの公式を用いて、場合の数を求めるのだろう。
3C2・1C1+3C1・2C2=3+3=6(通り)
また、重複順列の考えを用いても場合の数は求められる。
異なる2個のものから重複を許して3個取る順列の総数は、 23=8(通り)
この中には、3人全員がA、または、3人全員がB の場合が含まれる。
よって、求める場合の数は、 8−2=6(通り)
この重複順列の考えを一般化したものが包除原理を用いた解答となる。
3人を2つの部屋 1 と 2 に振り分ける。
そのときの振り分け方の総数は、 N=23=8(通り) である。
性質 E1 は部屋 1 が空室である場合、性質 E2 は部屋 2 が空室である場合とする。
このとき、求める場合の数は、包除原理より、 N−N1−N2+N12 で求められる。
ところで、 N1=1 、N2=1 、N12=0 なので、
求める場合の数は、 8−1−1+0=6(通り) となる。
例 4人 a 、b、c、d を、3組 A、B、C に分けたい。何通りあるだろうか?
4人を3つの部屋 1 と 2 と 3 に振り分ける。
そのときの振り分け方の総数は、 N=34=81(通り) である。
性質 Em (m=1、2、3)は部屋 m が空室である場合とする。
このとき、求める場合の数は、包除原理より、
N−N1−N2−N3+N12+N23+N31−N123
で求められる。ところで、
N1=N2=N3=24=16 、N12=N23=N31=1 、N123=0 なので、
求める場合の数は、 81−16×3+1×3−0=36(通り) となる。
(追記) 平成26年2月22日付け
今まで組み分けの問題というと、だいたい3組までが相場であったが、東京理科大学薬学
部(2014)の入試問題で、4組に分ける場合が出題された。いよいよ「包含と排除の原理
(包除原理)」が大学入試の基本テクニックになる日が近づいてきたのだろうか。
r は2以上9以下の自然数とする。nを r 以上の自然数として、次の条件を満たすn桁の自
然数を考える。
(イ)各位の数は1からrまでの数 1、2、・・・、r のどれかである。
(ロ)1、2、・・・、rのどの一つも必ずどこかの位に現れる。
このような自然数全体の集合を考え、この集合の要素の個数を rSn とおく。また、この集
合のすべての要素の和を fr(n)とおく。
(1) r=2とする。
(a) 2S2 、 2S3 を求めよ。また、2Sn を求めよ。
(b) f2(2)、f2(3)を求めよ。また、f2(n)を2Sn を用いて表せ。
(2) r=3とする。
(a) 3Sn を求めよ。
(b) f3(n)を3Sn を用いて表せ。
(3) r=4とする。
(a) 4Sn を求めよ。
(b) f4(n)を4Sn を用いて表せ。
(解)
(1) r=2のとき、(イ)(ロ)を満たすn桁(n≧2)の自然数の個数が 2Sn である。
(a) n=2 のとき、 12 、21 なので、 2S2=2
n=3 のとき、 112 、121 、211 、122 、212 、221 なので、 2S3=6
2Sn は、異なるn個のものをA、Bの2組(各組は1個以上)に分ける場合の数に等しいの
で、 2Sn=2n−2
(b) (a)より、 f2(2)=12+21=33
f2(3)=112+121+211+122+212+221=3(100+200)+3(10+20)+3(1+2)=999
一般に、f2(n)=(2Sn/2)(3+30+300+3000+・・・+300・・・00)
=(2Sn/2)・3(10n−1)/9=(1/6)(10n−1)2Sn
(2) r=3のとき、(イ)(ロ)を満たすn桁(n≧3)の自然数の個数が 3Sn である。
(a) 3Sn は、異なるn個のものをA、B、Cの3組(各組は1個以上)に分ける場合の数に等
しいので、3Sn=3n−{3(2n−2)+3}=3n−3・2n+3
(b) f3(n)=(3Sn/3)(6+60+600+6000+・・・+600・・・00)
=(3Sn/3)・6(10n−1)/9=(2/9)(10n−1)3Sn
(3) r=4のとき、(イ)(ロ)を満たすn桁(n≧4)の自然数の個数が 4Sn である。
(a) 4Sn は、異なるn個のものをA、B、C、Dの4組(各組は1個以上)に分ける場合の数
に等しいので、
4Sn=4n−{4C1・(3n−3・2n+3)+4C2・(2n−2)+4}
=4n−4・3n+12・2n−12−6・2n+12−4=4n−4・3n+6・2n−4
(b) f4(n)=(4Sn/4)(10+100+1000+10000+・・・+1000・・・00)
=(4Sn/4)・10(10n−1)/9=(5/18)(10n−1)4Sn
例 (出合いの問題または手紙と封筒の問題)・・・モンモール(1708年)
( → 参考 : 「自然対数の底 e の体感」 )
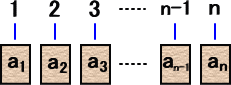 |
1 から n までの自然数の書かれたカードが n 枚 ある。今そのカードをよく切って、左図のように番号 順に置いていく。 もし、 ak=k |
となるような k が存在するとき、「出合い」が起こったといわれる。
このとき、「出合いが起こらない確率」はいくつになるであろうか?
この問題は、「自然対数の底 e の体感」においては、次のように解かれた。
出合いが起こらない場合の数を F(n) とおくと、F(n) について漸化式
F(n)=(n−1)(F(n−1)+F(n−2))
が成り立つ。 明らかに、F(1)=0、F(2)=1 である。
このとき、 F(n)−nF(n−1)=−(F(n−1)−(n−1)F(n−2))
=・・・=(−1)n から、
![]()
と変形できるので、
![]()
さらに、F(1)=0 なので、
![]()
となる。したがって、
![]()
上記では、かなり大変な計算をしてF(n) を求めているが、包除原理を用いるとごく自然に
上式が得られる。実際に求めてみよう。
1 から n までの自然数の書かれたカードをよく切って並べる場合の数の総数は、
N=n!(通り)
である。また、性質 Em (m=1、2、・・・、n)は、 am=m である場合とする。
このとき、 Nm個の要素=(n−m)!(通り) なので、包除原理より、
F(n)=N−ΣNa+ΣNab−ΣNabc+・・・+(−1)nN123・・・n
=n!−nC1・(n−1)!+nC2・(n−2)!−・・・+(−1)n
=n!−n!/1!+n!/2!−・・・+(−1)n
=n!(1−1/1!+1/2!−・・・+(−1)n/n!)
すなわち、
![]()
であることが示された。
(コメント) 今まで、「手紙と封筒の問題」というと、漸化式を解く場合しか知りませんでした
が、こんなに軽妙に求められることに驚きました。包除原理の偉大さがよ〜く分
かりました... f(^^;) 。
例 赤、青、黄の3色の球がそれぞれ大小1個ずつ合計6個ある。これらの球を一列
に並べるとき、同じ色の球が隣り合わないように並べたい。並べ方は全部で何通
りあるだろうか。
普通に考えれば、次のように求められる。
まず、大小の赤球を一列に並べる場合の数は、 2!=2(通り)
その1通り、例えば ×
● × ● × に対して、大小2個の青球を×印に入れる場合の
数は、 3P2=3×2=6(通り)
その1通り、例えば ×
● × ● × ● × ●× に対して、大小2個の黄球を×印に入
れる場合の数は、 5P2=5×4=20(通り)
したがって、求める場合の数は、 2×6×20=240(通り)
これに対して、包除原理を用いると、次のように求められる。
6個の球を一列に並べる場合の数は、 N=6!=720(通り) である。
また、 性質 Er
: 大小の赤球が隣り合っている
性質 Eb : 大小の青球が隣り合っている
性質 Ey :
大小の黄球が隣り合っている
とする。このとき、 Nr=Nb=Ny=2!×5!=240(通り)
Nrb=Nry=Nby=2!×2!×4!=96(通り)
Nrby=2!×2!×2!×3!=48(通り)
であるので、包除原理より、求める場合の数は、
720−3×240+3×96−48=240(通り) となる。
(コメント) 色数が少ないので、普通の解答の方が易しく感じるが、もっと色数が多い場合
は、包除原理の方が易しく感じられるだろう。
例 オイラー関数 φ(n)
自然数 n と互いに素な自然数の個数を表すオイラー関数も包除原理の適当な例になっ
ている。
自然数 n が素因数分解されて、 n=paqb・・・rc と書けるとき、
φ(n)=n(1−1/p)(1−1/q)・・・(1−1/r)
と書ける。
素数 p に対して、p と互いに素な自然数は、 1、2、・・・、p−1 の p−1個あるので、
φ(p)=p−1=p(1−1/p)
素数 p に対して、1 から pa までの自然数のうち、p の倍数になっているものは、
p・1 、 p・2 、 ・・・・ 、 p・pa-1
の pa-1 個あるので、pa と互いに素な自然数は、 φ(p)=pa−pa-1=pa(1−1/p) 個あ
る。このことから、上記の φ(n)の式が成り立つことは予想されよう。
証明は、包除原理を用いると容易だろう。
1 から n までの自然数の総数は、 N=n (個) である。
また、性質 Ep は、p の倍数になっている場合
性質 Eq は、q の倍数になっている場合
・・・・・・・・・・・・・・・・・・・・・・・・・・・・
性質 Er は、r の倍数になっている場合
とする。
このとき、 Np=n/p 、Nq=n/q 、・・・ 、Nr=n/r 、Npq=n/pq 、・・・・ なので、
包除原理より、
φ(n)=N−ΣNp+ΣNpq−・・・±Npq・・・r
=n−n(1/p+1/q+・・・+1/r)+n(1/pq+・・・)−・・・±n/pq・・・r
=n(1−1/p)(1−1/q)・・・(1−1/r)
であることが分かる。
たとえば、 φ(2)=2(1−1/2)=1
実際に、 2 と互いに素な自然数は、 1 の1個
φ(3)=3(1−1/3)=2
実際に、 3 と互いに素な自然数は、 1、2 の2個
φ(4)=4(1−1/2)=2
実際に、 4 と互いに素な自然数は、 1、3 の2個
φ(5)=5(1−1/5)=4
実際に、 5 と互いに素な自然数は、 1、2、3、4 の4個
φ(6)=6(1−1/2)(1−1/3)=2
実際に、 6 と互いに素な自然数は、 1、5 の2個
・・・・・・・・・・・・・・・・・・・・・・・
例 外見上全く区別のできない箱がいくつかあり、それぞれの箱の中には同様な確か
らしさで、k種類( k≦n )の図形のうちのどれか一つが入っているという。
この箱を n個( n≧k )用意するとき、k種類の図形が全種類揃う確率を求めよ。
まず、起こり得る全ての場合の数は、 N=kn (通り) である。
k 種類の図形の名前を、 1、2、3、・・・、k として、
性質 Em (m=1、2、3、・・・、k)は、図形 m が揃わない場合
とする。このとき、k 種類の図形が全種類揃う場合の数は、包除原理から、
kn−kC1(k−1)n+kC2(k−2)n+・・・+(−1)k-1kCk-11n
したがって、求める確率は、
1−kC1(1−1/k)n+kC2(1−2/k)n+・・・+(−1)k-1kCk-1(1/k)n
(コメント)
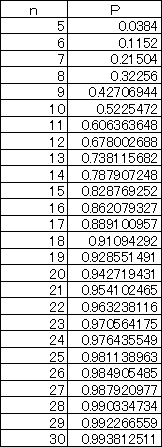 |
k=5 の場合を実験してみよう。 確率は、 1−5(4/5)n+10(3/5)n−10(2/5)n+5(1/5)n である。 Excel さんに、n=5、6、・・・、30 について確率の値を計算 してもらったのが左表である。 左図の計算結果によれば、n=30 のときの確率が 99.4% となり、かなり高い確率で全種類揃うことになる。 因みに、 n=60 のとき、確率は、99.999%で、これは ほぼ確実と言ってもいいかな? n=100 のときは、確率 99.9999999%である。 |
| この例について、当HPがいつもお世話になっているHN「zk43」さんより、アドバイスを頂 いた。(平成21年10月30日付け) |
|
少し視点を変えて、
「全 k 種類の図形を集めるための箱の個数の平均値はいくらか?」
という問題ではどうでしょうか?
m種類(0≦m≦k−1)の図形が初めて集まったという段階で、次に箱を1個用意したとき、
その中にまだ集めていない新しい種類の図形がある確率は、 1−m/k であるから、新し
い種類の図形を集めるまでに用意しなければならない箱の個数 X は、
パラメータ p=1−m/k の幾何分布 P(X= t )=p・(1−p)t-1 (t=1、2、3、・・・)
に従う。よって、 Σ(1−p)t=(1−p)/p より、 Σt・(1−p)t-1=1/p2 なので、
その期待値 E(X) は、 1/p=k/(k−m) である。
よって、求める箱の個数の期待値は、これらを加えて、
1+k/(k−1)+k/(k−2)+・・・+k/2+k/1
=k(1/k+1/(k−1)+1/(k−2)+・・・+1/2+1/1)
=k(1+1/2+1/3+・・・+1/k)
となる。
(コメント) 確かに、何箱か用意して全種類の図形が揃う確率を求めるよりも、全種類の図
形が揃うには大体何箱用意すればいいかを考える方が現実的で興味があります
ね!zk43 さんに感謝します。
因みに、 k=5 のとき、箱の個数の期待値は、
5(1+1/2+1/3+1/4+1/5)=137/12=11.4・・・
以上から、図形の種類が5種類であるとき、11〜12個の箱を用意すれば、目的が達せら
れることが期待できる。
(追記) 平成22年11月21日付け
11月20日付けで、上記の例に関して、H.Y.さんよりメールをいただいた。
上記の例の問題を見て、それまでわからなかった問題が解けました。もしよろしかったら、
「ガチャポンを全種類集めるには」
を読んでみて下さい。わからなかった問題というのは「コマ大数学科」という番組で出た
10種類のくじを全部引き当てるには何回くじを引けばよいか期待値を求めなさい
という問題で、上記の問題がヒントになりました。
(コメント) 問題解決に当HPが役立ったということで嬉しい限りです。「コマ大数学科」から
は以前問題使用依頼が来たことがあったのですが、もしかしてこの問題だったの
かな...?
ところで、上記のHPサイトによると、「コマ大数学科」では次のように解かれていたという。
(1) k−1種類まで集まった時点で、次に、k種類目が出る確率は、ak=1−(k−1)/10
(2) k種類目が出るまでには、平均して、1/ak 回かかる。
(→例えば、さいころを投げて1の目が出る確率は1/6なので、その逆数の6回投げれば1の目が
出ることが期待できる。)
(3) 従って、全種類出るまでには、平均して、Σ1/ak 回かかる。
このように考えると、上記の計算で得られた「求める箱の個数の期待値を表す式」
1+k/(k−1)+k/(k−2)+・・・+k/2+k/1
=1/(1−0/k)+1/(1−1/k)+1/(1−2/k)+・・・
+1/(1−(k−2)/k)+1/(1−(k−1)/k)
の意味が明瞭に浮き彫りになってきますね!H.Y.さんに感謝します。
以上のいくつかの例を見ても分かるように、包除原理は見た目よりも豊かな応用を持って
いることが分かる。
「包除原理はいろいろな場面に応用できそうで面白いですね。」と、zk43さん。私も同感
です! さて、先延ばしにしてきた包除原理の証明に取りかかろう。
2個の集合についての個数定理 n(A∪B)=n(A)+n(B)−n(A∩B) を出発点として、
3個の集合についての個数定理
n(A∪B∪C)=n(A)+n(B)+n(C)−n(A∩B)−n(B∩C)−n(C∩A)+n(A∩B∩C)
が成り立つことは容易に示される。同様にして、
n(A∪B∪C∪D)、n(A∪B∪C∪D∪E)、・・・・・・
も個別に地道に展開すれば、等式を作ることは容易である。ただ、この方法では包除原理
を一般的に示すことは難しい。
証明の準備として、次のような集合 A に付随する特性関数 A(x) を定義する。
x ∈ A のとき、 A(x)=1 、 x ∈ A でないとき、 A(x)=0
この特性関数を用いると、集合 A の要素の個数 n(A) は、
n(A)=ΣA(x) (ただし、 x ∈ U)
例 全体集合 U に対して、常に、 U(x)=1 である。
以下において、全体集合 U は有限集合であるものとする。
例 空集合 φ に対して、常に、 φ(x)=0 である。
この特性関数を用いると、集合 A の要素の個数 n(A) は、
n(A)=ΣA(x) (ただし、 x ∈ U)
で表される。
例えば、 n(U)=ΣU(x)=Σ1 (Uの要素の個数だけ1を加える)
n(φ)=Σφ(x)=Σ0=0
例 集合 A の補集合 Ac に対して、
x ∈ A のとき、 Ac(x)=0 、 x ∈ A でないとき、 Ac(x)=1
であるので、 Ac(x)=1−A(x) が成り立つ。
例 2つの集合 A 、B の共通部分 A∩B に付随する特性関数 A∩B(x)
について、
x ∈ A∩B のとき、 A∩B(x)=1 、 x ∈ A∩B でないとき、 A∩B(x)=0
であるが、一方、
x ∈ A∩B のとき、 A(x)B(x)=1 、 x ∈ A∩B でないとき、 A(x)B(x)=0
が成り立つ。よって、 A∩B(x)=A(x)B(x) が成り立つ。
例 2つの集合 A 、B の結び A∪B に付随する特性関数 A∪B(x) について、
x ∈ A∪B のとき、 A∪B(x)=1 、 x ∈ A∪B でないとき、 A∪B(x)=0
であるが、一方、
x ∈ A∪B のとき、 x ∈ Ac∩Bc でないので、 Ac(x)Bc(x)=0
すなわち、 {1−A(x)}{1−B(x)}=0 より、 A(x)+B(x)−A(x)B(x)=1
が成り立つ。同様にして、
x ∈ A∪B でないとき、 x ∈ Ac∩Bc なので、 Ac(x)Bc(x)=1
すなわち、 {1−A(x)}{1−B(x)}=1 より、 A(x)+B(x)−A(x)B(x)=0
が成り立つ。
以上から、 A∪B(x)=A(x)+B(x)−A(x)B(x) が成り立つ。
このように考えると、集合における演算(補集合、共通部分、結び)が、数における演算
(+−×)に翻訳できることが分かる。
また、 Ac∩Bc(x)=(A∪B)c(x)=1−A∪B(x) であるので、
Ac∩Bc(x)=1−A(x)−B(x)+A(x)B(x)={1−A(x)}{1−B(x)}
が成り立つ。
このことから、k 個の集合 E1、E2、・・・、Ek に対して、
E1c∩E2c∩・・・∩Ekc(x)={1−E1(x)}{1−E2(x)}・・・{1−Ek(x)}
=1−ΣEa(x)+ΣEa(x)Eb(x)−・・・+(−1)kE1(x)E2(x)・・・Ek(x)
が成り立つ。 ここで、集合 Em の要素の個数を n(Em)=Nm とし、
n(U)=N 、n(E1∩E2)=N12 、n(E1∩E2∩E3)=N123 、 ・・・・ 等とすれば、
上式は次のように書き直すことができる。
性質 E1、E2、・・・、Ek を全く持たないものの個数
= N−ΣNa+ΣNab−ΣNabc+・・・+(−1)kN123・・・k
(コメント) お世辞にも厳密な証明とはいかないが、包除原理を納得するには十分であろう。
当HPがいつもお世話になっているHN「GAI」さんより、包除原理を用いる確率の問題をい
ただいた。(平成23年3月22日付け)
問 題 52枚のトランプのカードからランダムに13枚を選びパケットを裏向きに持つ。
「13」と声に出してパケットのトップからカードを一枚表向きにしてテーブルへ出す。
号令とカードの数字が異なれば、次に「12」と発声して次のカードを重ねていく。
このように、最後まで「1」の発声とカードの数字が合わずに終わってしまう確率を
求めよ。
この問題に、当HPがいつもお世話になっているHN「at」さんが取り組まれた。
(平成23年3月22日付け)
(解) 52枚のトランプのカードを左から横一列に並べたとき、左から13枚のカードのすべて
が号令と一致しないような並べ方を数え上げればよい。
これら13枚のカードを並べる13箇所のうち、特定のk箇所(0≦k≦13)にあるカードが号
令と一致するような並べ方は、同一数字が4枚あることに注意して、
4k・(52−k)! 通り。
したがって、13箇所のうちの k 箇所にあるカードが号令と一致するような52枚のカードの
並べ方は、 13Ck・4k・(52−k)! 通り。
よって、左端から13枚のカードのすべてが号令と一致しないような並べ方は、包除原理より、
Σ[k=0〜13](−1)k・13Ck・4k・(52−k)! 通り。
これを、52!で割ったものが求める確率となる。
求める確率は、
9571721884148096/26816424180170625≒0.35693505665926537249298212905…
で、約 0.3569 となる。 (終)
at さんの解に対して、GAI さんからのコメントです。(平成23年3月23日付け)
計算有り難うございます。この一致しない13枚のパケットの山が4つ作れたら(52枚のす
べてのカード一致せずに終了する。)、その確率は、0.35694=0.016225・・・(約1%強)と
なるので、これは非常に珍しいことが起きたと思えるわけですね。
逆に言うと、52枚もの枚数で試行すれば、必ず号令と一致するカードを出すことができる
訳ですね。
at さんからのコメントです。(平成23年3月31日付け)
1組のトランプ52枚のカードをすべて使って、13枚ずつのパケットの山を4つ作り、この4
つの山のそれぞれに対して、「13、12、11、・・・」と号令を発しながら、カードのナンバー
を一枚ずつ調べていくのですね。
このとき、号令とカードのナンバーが全く一致しないような確率は、確かに0.016225ぐらい
になります。ただ、GAI さんの計算方法が、0.35694 となっているのが少々気になります。
52枚のトランプのカードからランダムに13枚を選び出し、この13枚に対し、号令とカード
のナンバーが全く一致しない確率を p1 とします。p1 の値は先に示したように、
p1 =(9571721884148096)/(26816424180170625)=0.3569…
です。
1組のトランプ52枚のカードをすべて使って13枚ずつのパケットの山を4つ作ったとき、
すべての山について、号令と13枚のカードのナンバーが全く一致しないような確率は p14
ではなく、正確な確率は p14 よりもごくわずかに大きい値になります。
たとえば、次の問題を考えてみます。
問題 同じ形をしたカードが全部で8枚あり、各々のカードには正整数が1つだけ記入され
ている。「1」が記入されたカードが4枚、「2」が記入されたカードが4枚あるものとする。
この8枚のカードを、2枚ずつのパケットの山4つに分ける。この4つの山のそれぞれに対
して次のような実験を行う。
[実験] 「2」と声に出してパケットのトップからカードを一枚表向きにしてテーブルへ出す。
号令とカードの数字が異なれば、次に「1」と声に出して次のカードを重ねる。
この実験において、どの山についても「1」を発声し、なおかつ号令とカードの数字が全く
一致しない確率はいくらか?
ひとつの山に注目するとき、その山について、「1」を発声し、なおかつ号令とカードの数字
が全く一致しない確率は、
{Σ[k=0〜2](−1)k・2Ck・4k・(8−k)!}/8!=2/7
です。山は全部で4つあるので、この問題の答えは、(2/7)4 と解答するのは誤りです。
題意を満たすためには、4つの山それぞれの一番上には「1」と記入されたカードがあり、
一番下には「2」と記入されたカードがあればよいので、それぞれの順列を考えることによ
り、この問題の正答は、 4!4!/8!=1/70 となります。
冒頭の52枚のトランプのカードの問題ですが、正確な確率 p2 を求める式は、次のように
なります。
p2=【Σ[k=0〜52](−1)k{[xk](Σ[j=0〜4]4Cj2・j・xj)13}・(52−k)!】/52!
(この式の、『[xk](Σ[j=0〜4]4Cj2・j・xj)13』の部分は、x の多項式(Σ[j=0〜4]4Cj2・j・xj)13 を
展開したときの xk の係数を表しています。)
この式を使って、p2 を計算すると、
p2=(4610507544750288132457667562311567997623087869)
/(284025438982318025793544200005777916187500000000)
なので、p14 との差は、 p2−p14=0.000001296145… となります。
GAI さんからの新たな疑問です。(平成23年3月23日付け)
一組のトランプから何枚のカードを取り出して、この実験(いくつから数え落とす。)を
したら、一致する確率が0.5を初めて超えるのだろうか?
GAI さんからの続報です。(平成23年3月30日付け)
52枚のトランプから、任意の n 枚のカードを取り出し、n からカウントダウンしていき、号
令とカードの数字が最後まで一致しないで終わる確率を、at さんの計算式を参考に計算を
実行したら、次のような結果を得ました。
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 確率 | 1.00000 | 0.92307 | 0.85218 | 0.78684 | 0.72661 | 0.67108 | 0.61987 | 0.57265 |
| n | 8 | 9 | 10 | 11 | 12 | 13 |
| 確率 | 0.52909 | 0.48891 | 0.45184 | 0.41763 | 0.38607 | 0.35693 |
これより9枚のカードをランダムに取り出し、「9からカウントダウン」していけば、号令とカ
ードの数字が一致してしまう確率が初めて0.5を超える現象を起こせると考えられる。
何度か実験してみましたが、割と一致することが少ない枚数にもかかわらず起こることが
実感できました。
at さんからのコメントです。(平成23年3月31日付け)
一組のトランプから n 枚(0≦n≦13)を取り出し、n からカウントダウンしていくとき、号令
とカードのナンバーが一致する確率を p(n) とすると、
p(n)=1−{Σ[k=0〜n](−1)k・nCk・4k・(52−k)!}/52!
この式を使って計算すると、 p(8)=0.470・・・ 、 p(9)=0.511・・・ となるので、
一致する確率が0.5を初めて超えるような最小枚数は確かに 9 ですね。
(追記) 平成24年10月11日付け
当HP読者のHN「はやふみ」さんからのコメントです。
上記の「52枚のトランプで、1〜13の号令と合うかどうか」の確率の問題なんですが...。
これら13枚のカードを並べる13箇所のうち、特定のk箇所(0≦k≦13)にあるカードが
号令と一致するような並べ方は、同一数字が4枚あることに注意して、
4k・(52−k)! 通り。
したがって、13箇所のうちの k 箇所にあるカードが号令と一致するような52枚のカード
の並べ方は、 13Ck・4k・(52−k)! 通り。
の部分で、例えば、1ヶ所合うとすると、k=1を代入して、
13C1・4・51!=13×4×51!=52!(通り)
になるということでしょうか?
(コメント) 計算は合っていますよ!たまたま結果の数字が52!になっただけです...。
(追記) 令和元年11月30日付け
ある部屋に3ヶ国語のうち少なくとも1ヶ国語を知っている何人かの人がいる。そのうち10
人は中国語を、8人は英語を、9人はフランス語を知っている。5人は中国語と英語を知って
いる。4人は英語とフランス語を知っている。3人はフランス語と中国語を知っている。2人は
3ヶ国語全部を知っている。部屋には何人いるか。そのうちで中国語だけを知っている人は
何人いるか。
(解) n(中)=10、n(英)=8、n(仏)=9、n(中&英)=5、n(英&仏)=4、
n(仏&中)=3、n(中&英&仏)=2
から、個数定理より、
n(中)+n(英)+n(仏)−n(中&英)−n(英&仏)ーn(仏&中)+n(中&英&仏)
=10+8+9−5−4−3+2
=17
中国語だけを知っている人は、
n(中)−n(中&英)−n(仏&中)+n(中&英&仏)=10−5−3+2=4 (終)
(コメント) 個数定理を用いた解法は上記の通りであるが、次のような考え方もあることを
最近知ることができた。
題意より、次の表を得る。
| 中国語 | 英語 | 仏語 | 中&英 | 英&仏 | 仏&中 | 中&英&仏 |
| 10 | 8 | 9 | 5 | 4 | 3 | 2 |
この状態から、中&英&仏を知っている人が退室すると、下表のようになる。
| 中国語 | 英語 | 仏語 | 中&英 | 英&仏 | 仏&中 | 中&英&仏 |
| 8 | 6 | 7 | 3 | 2 | 1 | 0 |
次に、中&英を知っている人が退室すると、下表のようになる。
| 中国語 | 英語 | 仏語 | 中&英 | 英&仏 | 仏&中 | 中&英&仏 |
| 5 | 3 | 7 | 0 | 2 | 1 | 0 |
同様にして、英&仏、仏&中を知っている人が退室すると、下表のようになる。
| 中国語 | 英語 | 仏語 | 中&英 | 英&仏 | 仏&中 | 中&英&仏 |
| 4 | 1 | 4 | 0 | 0 | 0 | 0 |
この表から、退室した人(2+3+2+1)+まだ残っている人(4+1+4)を求めると、部屋
には17人いたことが分かる。また、中国語だけを知っている人は、4人である。
#3つの場合の個数定理を知らなくても機械的な計算で求められますね!
(追記) 令和3年8月17日付け
「包含と排除の原理(包除原理)」を用いる問題を考えてみよう。
問題 5個の数字の並び ***** がある。*に入る数字は、0〜9の10種類ある。この並び
の中で、数字の並び「12」を含むものは何個あるだろうか?
(解) E1:12*** のタイプの並び、E2:*12** のタイプの並び、E3:**12* のタイプの並び、
E4:***12 のタイプの並び とすると、求める場合は、 E1∪E2∪E3∪E4 となる。
まず、 n(E1)=n(E2)=n(E3)=n(E4)=103
次に、 n(E1∩E2)=0、n(E1∩E3)=10、n(E1∩E4)=10、n(E2∩E3)=0、
n(E2∩E4)=10、n(E3∩E4)=0
また、相異なる i、j、k に対して、 n(Ei∩Ej∩Ek)=0 なので、求める場合の数は、
4・103−3・10=3970(個) (終)
(追記) 令和4年8月6日付け
個数定理や包除原理に関する問題が一橋大学(2021年)で出題された。
問題 1000以下の素数は、250個以下であることを示せ。
1000以下の数で、2の倍数だけで500個、2で割り切れない3の倍数は、167個あり、
これだけで、667個。あと残りは、333個なので、もう少しエラトステネスの篩をかければ、
なんとか250個までは減らせそうだ。この方針で、問題を解いてみよう。
(解) 1000以下の数で、2の倍数の個数は、500個、3の倍数の個数は、333個、5の
倍数の個数は、200個、7の倍数の個数は、142個、11の倍数の個数は、90個、・・・
そこで、1000以下の数で、2の倍数全体を集合A、3の倍数全体を集合B、5の倍数全体
を集合C、7の倍数全体を集合D、11の倍数全体を集合E、・・・ とおく。
集合Aの要素の個数をn(A)で表すと、 n(A)=500 となる。同様にして、
n(B)=333 、n(C)=200 、n(D)=142 、n(E)=90 、・・・
個数定理を考えれば、次の集合の要素の個数も調べなければならない。
n(A∩B)=166 、n(B∩C)=66 、n(C∩A)=100 、n(A∩B∩C)=33
ここで、
n(A∪B∪C)=n(A)+n(B)+n(C)−n(A∩B)−n(B∩C)−n(C∩A)+n(A∩B∩C)
=500+333+200−166−66−100+33=734
このとき、1000以下の素数は、 1000−734+3=269(個) 以下で、まだ不十分!
7の倍数までエラトステネスの篩を広げて、
n(A∪B∪C∪D)
=n(A)+n(B)+n(C)+n(D)−n(A∩B)−n(A∩C)−n(B∩C)−n(B∩D)
−n(C∩D)−n(D∩A)+n(A∩B∩C)+n(A∩B∩D)+n(A∩C∩D)+n(B∩C∩D)
−n(A∩B∩C∩D)
=500+333+200+142−166−100−66−47−28−71+33+23+14+9−4
=772
このとき、1000以下の素数は、 1000−772+4=232(個) 以下で、250個以下が
示せた。 (終)
(追記) 令和6年6月29日付け
個数定理に関する面白い問題が、東北大学(1977年)で出題されている。
第1問(文理共通) 1から250までの自然数で、2以上のある自然数mの2乗m2で割り
切れるもの全体の集合をAとする。
(1) 22で割り切れるAの要素の個数を求めよ。
(2) 22と32で同時に割り切れるAの要素の個数を求めよ。
(3) Aの要素の個数を求めよ。
(解)(1) 250÷4=62 ・・・ 2 より、22で割り切れるAの要素の個数は、62個
(2) 22と32で同時に割り切れる数は、62の倍数なので、250÷36=6 ・・・ 34 より、
62で割り切れるAの要素の個数は、6個
(3) m2≦250 で考えれば十分なので、mは、m≦15 の素数としてよい。
m=2、3、5、7、11、13 について、ベン図を描けば、下図の通りである。

よって、求める個数は、
53+6+20+1+7+2+1+4+2+1=97(個)
(追記) 令和6年10月11日付け
次の問題は、整数の性質を絡めた集合の問題である。
問題 ある学校の、それぞれ人数が等しい5クラスで、部活動(運動部、文化部)の加入状
況の調査を行った。全体の3/7が運動部に所属し、70人はどちらにも所属していなかっ
た。
5クラス全体の人数で、考えられる最少の人数はいくらか?
(解) 5クラス全体の人数をN人とすると、題意より、Nは5の倍数かつ7の倍数なので、35
の倍数となる。よって、N=35k (kは自然数) と書ける。
文化部のみに所属する人数を y 人とすると、題意より、 15k+y+70=35k
すなわち、 y=20k−70 で、y≧0 から、 k≧4 となる。
したがって、5クラス全体の人数で、考えられる最少の人数は、k=4のときで、
N=35・4=140(人) となる。 (終)
以下、工事中