
紀元前3、4世紀頃のギリシア数学においては、調和と均斉が重要なテーマであった。平
面図形では、円や正多角形、空間図形では、球や正多面体が興味を引く対象物であった。
正多面体とは、全ての面が合同な正多角形からなり、各頂点に集まる辺の数が全て等し
い多面体のことをいう。
例えば、正4面体は立派な正多面体であるが、正4面体2つを重ねてできる6面体は正多
面体とはみなされない。全ての面が合同な正三角形であるが、各頂点に集まる辺の数が全
て等しいとは言えないからだ。
ユークリッドの時代(紀元前3世紀)には、既に5種類の正多面体が知られていたという。
正4面体 正6面体 正8面体
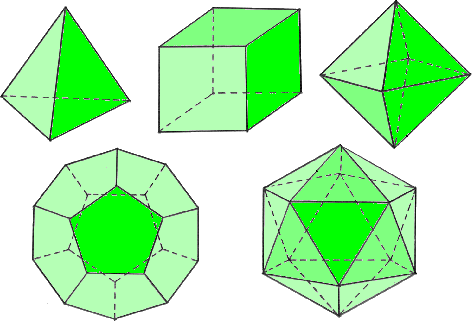
正12面体 正20面体
正多面体を構成する面の特徴から、辺の長さが同じ場合は、正12面体が最も大きいこと
が分かる。また、正十二面体の各面の中央に点を取り、隣り合う面の点同士を直線で結ん
で出来る立体は、正二十面体となる。
(参考文献) 根上生也、中本敦浩 著 基礎数学力トレーニング (日本評論社)
(追記) 令和3年4月28日付け
正多面体において、シュレーフリの表記法というものが知られている。
シュレーフリ(1814~1895)は、スイスの幾何学者である。
シュレーフリの表記法によれば、正多面体は、
{面の形状,頂点における面の数}
と表記される。
| 正4面体 | 正6面体 | 正8面体 | 正12面体 | 正20面体 | ||||
| {3,3} | {4,3} | {3,4} | {5,3} | {3,5} |
(追記) 令和3年5月12日付け
頂点、辺、面を数えやすくする方法として、次のようにグラフ的な作図法が知られている。
これは展開図と比べても、実際の立体に近いという点で優れていると思う。
| 正4面体 | 正6面体 | 正8面体 | ||
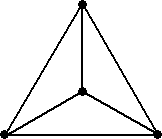 |
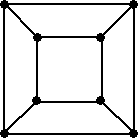 |
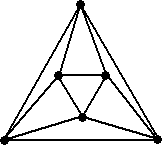 |
| 正12面体 | 正20面体 | |
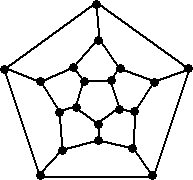 |
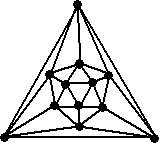 |
(追記) 令和3年5月13日付け
四色問題を意識して、上記のグラフの色分けを考えてみよう。
| 正4面体 | 正6面体 | 正8面体 | ||
 |
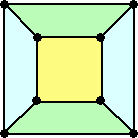 |
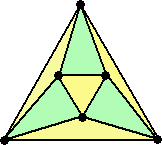 |
||
| 必ず4色が必要 円順列で2通りの塗り分け |
3色あれば十分 この1通りしかない |
2色あれば十分 この1通りしかない |
| 正12面体 | 正20面体 | |
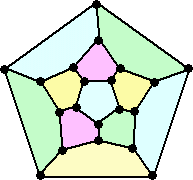 |
 |
|
| 必ず4色が必要 4通りの塗り分けがある |
3色あれば十分 144通りの塗り分けがある |
(追記) カルピスさんからのコメントです。(令和元年5月14日付け)
「正四面体」のトンガリ具合は、体のツボを押すのに心地良い角度だし、どう転がってもトン
ガリが上を向いてくれるので、いつも敷布団の上に適当に転がして置いておきます。
腰に当てたり、首に当てたりして寝ると気持ち良いですよ。仰向けに寝た時に背面のツボ
押しの為に、わざわざ購入しました。
(決して正四面体のルービックキューブを楽しむ為に購入した訳ではありません。)
スミマセン。数学に全く関係無いことでした。
(でも、こういうのを、数学を実生活に役立てていると言うのかなぁ~)
正多面体の展開図は次のようになる。
| 正4面体 | 正6面体 | 正8面体 | 正12面体 | 正20面体 | ||||
 |
 |
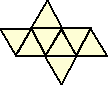 |
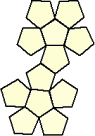 |
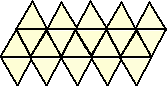 |
プラトンは、その著書「ティマイオス」の中で、これらを自然界の4元素(土・水・火・空気)に
関連づけて論じている。
正6面体 ・・・・・土 (面が正方形で最も安定性が強いので)
正20面体・・・・・水 (同じ大きさの正三角形を使って 正4面体・正8面体・正20面体を
作ると、正20面体が一番大きいので)
正4面体 ・・・・・火 (最も安定性が弱いので、四大元素の一つ「火」と名付けた。ギリシャ
人は正4面体をピュラミス(ピラミッドの語源)と呼んだ。ギリシャ語で
「火」は、ピュレと言われる)
正8面体 ・・・・・空気 (「火」の正4面体と「水」の正20面体の中間の存在と考え、四大元
素の「空気」と名付けた)
正12面体に対応するものがないので、プラトンもその処理に困ったらしく、宇宙を象徴す
るものという、分かったような分からないような表現でごまかしている。
以上のことから、正多面体のことを、プラトン図形またはプラトンの立体と呼ぶことがあ
る。
正多面体が5種類しかないことは、プラトンの友人の数学者テアイテトスやピタゴラスによ
り証明されていたらしい。
(追記) ピタゴラス教団は事実上の宗教団体で、数学上の発見を決して外部に漏らさない
という誓いをたてされていた。新しい正多面体(正12面体)の発見を公表してしまっ
た男の人は、誓いを破ったということで、溺死させられたという。
(参考文献:サイモン・シン著 青木 薫訳 「フェルマーの最終定理」 (新潮社))
その証明はいろいろ知られているが、次のオイラーの多面体定理を利用するものが一番
わかりやすい。
オイラーの多面体定理
1つの多面体の頂点(vertex)の個数を V、辺(稜(edge)または線)の個数を E、面(face)
の個数を F とすると、
V-E+F=2
が成り立つ。覚えるときは、E=V+F-2 (線は帳面に引け) と変形したほうがよい。
(正多面体に限らず、多面体の頂点と辺と面の個数の間には、ある定まった関係がある。
この関係は、18世紀を代表する数学者レオンハルト・オイラーによって発見された。)
各正多面体の頂点・辺・面の個数を書き上げてみると、次の表のようになる。
| V | E | F | V-E+F | |
| 正4面体 | 4 | 6 | 4 | 2 |
| 正6面体 | 8 | 12 | 6 | 2 |
| 正8面体 | 6 | 12 | 8 | 2 |
| 正12面体 | 20 | 30 | 12 | 2 |
| 正20面体 | 12 | 30 | 20 | 2 |
このオイラーの定理の覚え方として、杉浦光夫先生が講義中ボソッと、「この公式は、
『 線 は 帳 面 に引け 』
(辺) = (頂)+(面)-2
と覚えるといいですよ!」と仰ったのが、今でも耳に残っている。
(注)帳面というのは、もう死語かもしれない。今風に言えば、ノートのこと。でも、ノートでは
上手い語呂合わせを作るのは難しい。我々は、日本語に感謝しなければいけない。
(補足) 平成19年8月20日付け
オイラーの多面体定理の応用例を一つあげておこう。
サッカーボールは、正5角形と正6角形をそれぞれ何枚かずつ貼り合わせて作られ
ている。正5角形と正6角形の枚数は、それぞれ何枚だろうか?
正5角形、正6角形の枚数をそれぞれ、a 枚、b 枚とする。
上図はサッカーボールの一部分を展開したものであるが、どの頂点でも正5角形1枚と正
6角形2枚が集まっていることが分かる。
よって、頂点の個数に注目して 5×a=(6×b)/2
(正6角形の2つの頂点が重なって1つの正5角形の頂点を表す)
すなわち、 5a=3b が成り立つ。
サッカーボールを多面体と考え、頂点の個数を V、辺の個数を E、面の個数を F とす
ると、
V=(5a+6b)/3 ・・・ 1個の頂点が3回重複して数えられている
E=(5a+6b)/2 ・・・ 1個の辺が2回重複して数えられている
F=a+b ・・・・・・・・・・ 正5角形、正6角形の総数が面の個数になる
である。オイラーの多面体定理より、 E=V+F-2 なので、
(5a+6b)/2=(5a+6b)/3+(a+b)-2
よって、 15a+18b=10a+12b+6a+6b-12 より、 a=12
5a=3b より、 b=20
したがって、サッカーボールにおいて、
正5角形の枚数は、12枚 、 正6角形の枚数は、20枚
となる。(→ 今度、数えてみようっと...!)
(補足) 平成19年8月22日付け
20日付けで上記をアップしたところ、21日付けで、北海道の「ma-.」さんからメールを頂
いた。(一部表現を修正させていただきました!)
20日付けで更新のサッカーボールの話題に関するメールです。
サッカーボールは、正20面体のすべての頂点を切り取ることによって作ることができる。
実際に、正20面体は、1つの頂点に5つの正三角形が集まり、1つの頂点を切り取ること
により1つの正五角形が出来る。正20面体は12個の頂点を持っているので、正五角形は
合計で12個出来ることになる。元の正三角形は、すべての頂点が切り取られ正六角形が
出来ることになる。
以上から、サッカーボールは
・正20面体の12個の頂点から生まれた、12個の正五角形
・正20面体の20個の面(正三角形)から生まれた、20個の正六角形
からなる32面体と言える。
ところで、辺の本数は、新たに生まれた12個の正五角形の分だけ増えるので、
30+12×5=90(本)
となる。
頂点の個数は、元の12個の頂点がなくなり、その代わりに新たに生まれた12個の正五
角形の分だけ増えるので、
12-12+12×5=60(個)
となる。これらの関係は、
90=60+32-2 ( (辺) = (頂)+(面)-2 )
という等式を満たし、サッカーボールにおいても、オイラーの多面体定理が成り立つ。
(コメント) 私自身、この話題を授業で扱ったことはないが、「ma-.」さんにとっては結構好
きな内容とのことで、授業でも時折話されているそうである。この問題を文章表現の
みで球の中のサッカーボールを想像してみれば、かなり空間把握の訓練になるので
はないかとのこと。更に、空間把握が得意な生徒には正20面体から始めてサッカー
ボールを図に描かせてみると意外と自分なりの法則を見つけて描けるようになるの
ではないかとのこと。「ma-.」さんの貴重なご提案に感謝いたします。
「ma-.」さんの行った方法
多面体の角を切り落として新しい多面体を作る
は、かなり有名で、線形凸不等式における重要な手法となっている。
この話題については、ページを改めて起こしたいと考えている。
(→参考:凸図形の理論と応用)
(追記) 令和元年6月13日付け
単に、サッカーボールの正5角形、正6角形が何個ずつあるかは、オイラーの多面体定理
を用いて鮮やかに求められるが、どちらか一方の個数がわかっている場合はもっと簡単に
求められる。
問題 サッカーボールには12個の正5角形がある。正6角形は何個あるか?
(解) |
正6角形の個数を x 個とする。 正5角形にくっついている正6角形の辺の数は、 5×12=60(個) 正6角形にくっついている正5角形の辺の数は、3x で、 3x=60 より、 x=20(個) (終) |
オイラーの多面体定理の証明は数学の専門書に委ね、我々は先を急ごう。(→ 証明)
プラトンの多面体定理
正多面体は、
正4面体、正6面体、正8面体、正12面体、正20面体
の5種類しかない。
正多面体が存在するためには、
「1つの頂点に集まる面の個数は3以上」
かつ、
「頂点のまわりの頂角の合計は360°より小」
であることが必要である。このことから、面となる正多角形が限られてくる。
正n角形(nは3以上)の頂角の大きさは、(n-2)×180°÷n なので、
3×((n-2)×180°÷n)<360° が成り立つ。
これより、n<6 となり、n の値は、3、4、5 となる。
従って、面となる正多角形が正3角形、正4角形、正5角形の場合のみを考えればよい。
#以上から、すべての面が正六角形であるような多面体は存在しないということが分かる。
ここで、正F面体の1つの面である正n角形の1つの頂点に集まる辺の個数を k とすると、
k 回の重複を考慮して、V=n×F÷k、 2回の重複を考慮して、E=n×F÷2 が成り立
つことに注意する。
(イ) 面が正5角形のとき
正5角形の頂角は、108°だから、1つの頂点に集まる面の個数は3で、k=3 。
よって、V=5F÷3、E=5F÷2 だから、V-E+F=2 に代入して、F=12 。
(ロ) 面が正4角形のとき
1つの頂点に集まる面の個数は3で、k=3 。
よって、V=4F÷3、E=4F÷2 だから、V-E+F=2 に代入して、F=6 。
(ハ) 面が正3角形のとき
1つの頂点に集まる面の個数は3、4、5で、k=3、4、5 。
(ⅰ) k=3 のとき
V=3F÷3、E=3F÷2 だから、V-E+F=2 に代入して、F=4 。
(ⅱ) k=4 のとき
V=3F÷4、E=3F÷2 だから、V-E+F=2 に代入して、F=8 。
(ⅲ) k=5 のとき
V=3F÷5、E=3F÷2 だから、V-E+F=2 に代入して、F=20 。
以上で、プラトンの多面体定理は証明された。
ところで、正多面体には、正多面体が正多面体を生み出すという、面白い性質がある。
正6面体→正4面体→正8面体
↑ ↓
正12面体 ← 正20面体
正6面体ABCD-EFGHにおいて、A-CFHは正4面体になる。正4面体の各辺の中点を
結んでできる多面体は正8面体となる。
同様に、適切に頂点を選ぶことにより、正12面体から正6面体が作られる。
正8面体からは、黄金比などを活用して、正12面体が作られる。正12面体の各面の中心
を結んでいくと、正20面体になる。逆に、正20面体の各面の中心を結んでいくと、正12面
体になる。
(参考文献:山下純一 著 数学史物語(東京図書)
小林隆章 著 正多面体の不思議(数学探求講座)
横田一郎 著 やさしい位相幾何学の話(現代数学社))
(追記) 平成18年12月19日付け
冒頭で、
正多面体を構成する面の特徴から、辺の長さが同じ場合は、正12面体が最も大きいこと
が分かる。
(参考文献) 根上生也、中本敦浩 著 基礎数学力トレーニング (日本評論社)
ということを述べた。同様の話題が、朝日新聞夕刊の特集「ニッポン人脈記」の「数学する
ヒトビト」(12月18日付け)でも取り上げられている。
正12面体と正20面体を球に内接させるとき、その体積は、どちらがより球の体
積に近いか?
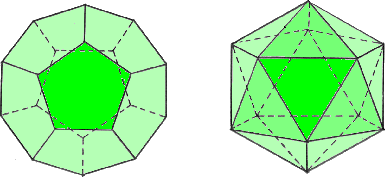
正12面体 正20面体
正12面体の頂点の個数は20個で、正20面体の頂点の個数は12個である。頂点の個
数が多い方がより球に近い図形ということで、正12面体の方が、より球の体積に近いこと
になる。字面からだと正20面体の方と答えがちだが、図形の形を知っている人は、多分間
違えることはないだろう。
(追記) 平成25年8月18日付け
当HP読者のHN「あにげら」さんより、次のようなご指摘を頂いた。
外接球を考えると正12面体の方が球に近いですが、内接球を考えると正20面体の方が
球に近いので、どちらが球に近いとは言えないのではないですか?
上記の問いかけがちょっと言葉足らずでした!(上記の文言は修正済み)確かに、球に内
接する場合は、正12面体が球に近いですが、球に外接する場合は、面の数がより多い正
20面体が球に近くなりますね。あにげらさん、ご指摘ありがとうございます。
当HPがいつもお世話になっているHN「らすかる」さんからのコメントです。
(平成25年8月20日付け)
正多面体が球にどれくらい近いかは、例えば、(外接球の半径)/(内接球の半径) で表
すことができると思います。この値は、
正4面体 : ![]() ・tan(π/3)=3
・tan(π/3)=3
正6面体 : ![]() ・tan(π/4)=
・tan(π/4)=![]() ≒1.73
≒1.73
正8面体 : ![]() ・tan(π/4)=
・tan(π/4)=![]() ≒1.73
≒1.73
正12面体 : ![]() ・tan(π/5)=√(15-6√5)≒1.26
・tan(π/5)=√(15-6√5)≒1.26
正20面体 : ![]() ・tan(π/5)=√(15-6√5)≒1.26
・tan(π/5)=√(15-6√5)≒1.26
ですので、最も円に近いのは、正12面体と正20面体の二つということになりますね。
# 値は外接球と内接球の半径を検索で見つけ、計算したものです。![]() ・tan(π/n) は、こ
・tan(π/n) は、こ
のように表すと綺麗に書けるということをたまたま発見しました。
(コメント) 「近い」という感覚はいろいろあるんですね!らすかるさんに感謝します。
(追記) カルピスさんからのコメントです。(令和3年7月16日付け)
正四面体の「内接球の半径」と「外接球の半径」を足すと「正四面体の高さ」になる。。。
らすかるさんからのコメントです。(令和3年7月16日付け)
頂点Aから底面に垂線AHを下すと、重心GはAH上にあり、
AG=外接球の半径 、GH=内接球の半径
なので、そうなりますね。
(コメント) 正四面体の内接球、外接球の中心は同一点で、丁度、正四面体の高さを3:1
に内分する点なので、
「内接球の半径」と「外接球の半径」を足すと「正四面体の高さ」になる
は、明らかだと思われます。
1辺の長さがaの正四面体に対して、具体的に計算してみると、
正四面体の高さ=(![]() /3)a
/3)a
内接球の半径=(![]() /12)a
/12)a
外接球の半径=(![]() /4)a
/4)a
となります。
GAI さんからのコメントです。(平成25年8月20日付け)
らすかるさんの投稿を見ていたら、この外接球半径/内接球半径の値があまりにも法則
的で表されていたのにびっくりして、つい次の事が思い出されてきました。
コペルニクスがプトレマイオス以来固く信じられてきた地球中心説を完全にぶち壊し、地
球を宇宙中心から追い出す考えを強く支持する理論をティコ・ブラーエの観測結果から導き
出したにもかかわらず、彼は神の存在を強く信じ、この地球の軌道位置に特別な意味をあ
たえるべく、プラトンの5つの正多面体の内接球と外接球を割り当て、
正八面体の内接球を水星の軌道、外接球を金星の軌道
正二十面体の内接球を金星の軌道、外接球を地球の軌道
正十二面体の内接球を地球の軌道、外接球を火星の軌道
正四面体の内接球を火星の軌道、外接球を木星の軌道
正六面体の内接球を木星の軌道、外接球を土星の軌道
を回っていると、当時知られていた6個の惑星を5つのプラトン正多角形(またこの5つしか
考えられない限定物であることも、神秘性を深める役目を負っていよう)に当て、妄想を膨ら
ましていったという。
さて、このモデルがどれ位実際の公転半径の数値と近似できているのか?何方か、天文
並びに数理的処理に詳しい方の情報をお願いしたいところです。
らすかるさんからのコメントです。(平成25年8月20日付け)
筑波大学大学院修士課程教育研究科 楊 彬 さんの授業資料によれば、
(土星の軌道半径)÷(木星の軌道半径)=1.8334
(木星の軌道半径)÷(火星の軌道半径)=3.4146
(火星の軌道半径)÷(地球の軌道半径)=1.5237
(地球の軌道半径)÷(金星の軌道半径)=1.3825
(金星の軌道半径)÷(水星の軌道半径)=1.8625
だそうです。近似…と言えるかどうか微妙なところですね。
GAI さんからのコメントです。(平成25年8月20日付け)
H(x)= 2.071914568234473011289824256・10-10・x16 -0.00000003541090352982553873840790546x15
+ 0.000002775214838302083450117135774x14 - 0.0001323053283485750710375576327x13
+ 0.004291952063830477787106427020x12 - 0.1004033868112229727355610085x11
+ 1.751265270336276947719200843x10 - 23.22268387022547953782758387x9
+ 236.5170063817017123672965756x8 - 1855.738664715399069933697331x7
+ 11177.18711897551629130916468x6 - 51127.43805634368500580149860x5
+ 174109.2821309472507446501843x4 - 426720.9554224005855970506116x3
+ 709938.2801033539717247443195x2 - 716499.3359289822018603359711x
+ 330571.6597211232403165347772
と定義しておけば、
正八面体 --> 金星軌道/水星軌道≒(外接球の半径/内接球の半径)×H(8)
正二十面体 --> 地球軌道/金星軌道≒(外接球の半径/内接球の半径)×H(20)
正十二面体 --> 火星軌道/地球軌道≒(外接球の半径/内接球の半径)×H(12)
正四面体 --> 木星軌道/火星軌道≒(外接球の半径/内接球の半径)×H(4)
正六面体 --> 土星軌道/木星軌道≒(外接球の半径/内接球の半径)×H(6)
が成立すると思う。
(追記) 平成19年3月17日付け
上記で、正多面体の体積を話題にしたが、他の正多面体についても、その図形固有の
量を一覧にしておこう。
| 正4面体 | 正6面体 | 正8面体 | 正12面体 | 正20面体 | |
| 頂点の数 | 4 | 8 | 6 | 20 | 12 |
| 辺の数 | 6 | 12 | 12 | 30 | 30 |
| 面の数 | 4 | 6 | 8 | 12 | 20 |
| 面の形状 | 正三角形 | 正方形 | 正三角形 | 正五角形 | 正三角形 |
| 表面積 | |||||
| 体積 |
ただし、正多面体の1辺の長さを、a とする。
この表では、1辺の長さを与えているが、a=1 としてもよい。後は相似比の性質を用いて
上記の公式は容易に作ることが出来る。( → 参考 : 相似比の真実)
(追記) 平成28年2月24日付け
今日ふとしたことがきっかけで「ギブズの相律」のことが話題になった。
「ギブズの相律(phase rule)」とは、2つ以上の相が共存して平衡している不均一系物質に
おける自由度を定める熱力学的法則のことである。自由度をF、相の数をP、独立成分の数
をNとすれば、F=N+2-Pで示される。これを、 N=P+F-2 と書き直せば、オイラーの
多面体定理 E=V+F-2 との類似性がうかがわれる。
ここで、自由度とは、平衡にある系の状態を決めるのに必要な独立の状態変数(圧力、温
度および成分物質の濃度)の数のことをいう。
例 一成分系(N=1)の場合、その系が一つの相(気相、液相、固相のうちどれか一つ、す
なわち、P=1)であれば、F=2となり、温度と圧力の2変数を自由に変えることができる。
一成分系で二つの相(たとえば液相と気相)が共存する系では、F=1となり、温度または
圧力のどちらか一つを決めるとほかはすべて決まる。
一成分系で三つの相が共存すれば、温度も圧力もその物質に特有な一定値となってしまう。
水の三重点はこの例になっている。
水は、一成分系であるので、共存できる最多の相数は、2+1=3となる。勿論これは、氷
の相、水の相、水蒸気の相の3相のことである。これらが共存する条件は、水の温度と蒸気
圧と化学ポテンシャルが、水に固有なある値を示すときのみである。これは水の三重点とよ
ばれ、この時の温度は、273.15℃で、これは温度基準として用いられる。
例 メタノール水溶液の場合、
成分の数 N=2 (メタノール と 水) 、相の数 P = 1 (均一な水層)
なので、自由度 F=N+2-P=2+2-1=3 となる。
(コメント) 相図を考えると、多面体っぽいですね!
(追記) 令和3年9月8日付け
上記で、オイラーの多面体定理の証明は数学の専門書に委ね、我々は先を急ごうとした
が、やはり自分で証明しないと気持ちが悪いということで、証明に挑戦してみた。
オイラーの多面体定理 とは、次の事実を言う。
1つの多面体の頂点(vertex)の個数を V、辺(稜(edge)または線)の個数を E、
面(face)の個数を F とすると、
V-E+F=2
が成り立つ。
証明は、数学的帰納法による。
(証明) n面体の頂点の個数をV(n)、辺の個数をE(n)、面の個数をF(n)とおく。
n=4 すなわち、四面体に対して、V(4)=4、E(4)=6、F(4)=4 なので、
V(4)-E(4)+F(4)=4-6+4=2 より、n=4のとき、等式は成り立つ。
n=k(k≧4)のとき、等式が成り立つと仮定する。すなわち、 V(k)-E(k)+F(k)=2
k面体の1つの頂点から出る全ての辺と交わる平面で、k面体を切り分けて、次のように
(k+1)面体を作る。
このとき、上図の頂点から出る辺の個数をNとすると、
V(k+1)=V(k)-1+N 、E(k+1)=E(k)+N 、F(k+1)=F(k)+1
より、 V(k+1)-E(k+1)+F(k+1)=V(k)-1+N-E(k)-N+F(k)+1
=V(k)-E(k)+F(k)=2
よって、等式は、n=k+1のときも成り立つ。
以上から、数学的帰納法により、4以上の全てのn面体に対して、
V(n)-E(n)+F(n)=2
が成り立つ。 (証終)
(追記) 令和3年9月24日付け
上記のオイラーの多面体定理の証明で、数学的帰納法というのは、堅実ではあるが、い
かにも生ぬるい感じがする。
球面三角形を用いた直接的な証明も存在する。
(証明) もとの多面体のn角形の数を cn とおき、多面体の内部に含まれる球面を考える。
球の中心をOとし、半径をRとする。多面体の各頂点と中心Oを結び、球面との交点により、
球面の多角形を作ることができる。もとの多面体のn角形は、球面のn角形となる。
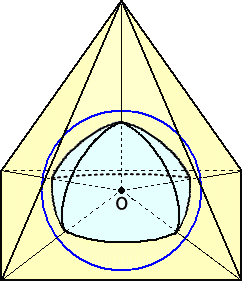
「球面の三角形」において、次の公式を得た。
半径Rの球面上にあり、内角の大きさがA、B、Cである三角形の面積は、
S=(A+B+C-π)R2
で与えられる。
n角形は、(n-2)個の三角形に分割され、球面の面積は、分割された球面の多角形の
面積の和であるので、
S/R2=(全ての内角の和)-Σ(n-2)πcn=4π
が成り立つ。
ここで、一つの頂点の周りの角度は、球面でも 2πなので、 (全ての内角の和)=2πV
また、各面ごとに辺の本数を数えると、 ∑ncn=2E で、∑cn=F である。
以上より、 S/R2=2πV-2πE+2πF=4π なので、
V-E+F=2 が成り立つ。 (証終)
(追記) 令和3年11月25日付け
オイラーの多面体定理の応用として、次の問題を考えてみよう。
問題 7個の稜(辺)を持つ多面体は存在しない。
(証明) 7個の稜(辺)を持つ多面体が存在すると仮定する。
多面体の頂点、稜、面の個数を v、e、f とおくと、オイラーの多面体定理より、
e=v+f-2 すなわち、 7=v+f-2 から、 v+f=9 が成り立つ。
ところが、多面体の各面は三角形以上で、一つの頂点に集まる面の数は3以上なので、
2e=14≧3f 、2e=14≧3v より、 f≧4 、v≧4 でなければならないので、
f=4 e=4 である。このとき、 v+f=8 となり、これは矛盾である。
よって、7個の稜(辺)を持つ多面体は存在しない。 (証終)
以下、工事中!