A:ピッツバーグ(米国ペンシルベニア州) 緯度:40.4398、経度:-79.9768
(北緯:40°26′23″、西経:79°58′36″)
B:ロンドン(英国) 緯度:51.5073、経度:-0.1277
(北緯:51°30′26″、西経:0°7′39″)
C:ブエノスアイレス(アルゼンチン) 緯度:-34.6036、経度:-58.3815
(南緯:34°36′13″、西経:58°22′54″)
を選ぶとき、球面三角形△ABCの面積をS(km2)とするとき、Sの数値を求めてみてください。
但し、地球は、半径R=6378(km)の球であるとして計算してください。
(コメント) 球面三角法について不慣れだったので、少し勉強してみた。
手元に、
辻 正次、平野智治 著 「新三角法」(共立全書)
がある。
それによれば、球面上の2点A、B間の距離とは、2点A、Bを通る大円上の円弧で、大き
くない方の部分(劣弧)の長さをいう。
また、点Cで交わる2つの大円の交角は、大円が定める2つの平面のなす角に等しい。
球の中心Oを頂点とする三面角O-ABCと球面との交わりは球面三角形ABCとなる。
球面三角形の3辺の長さを a、b、c とし、球面の半径を R とすると、a/R、b/R、c/R は、
三面角の3つの面角を与える。
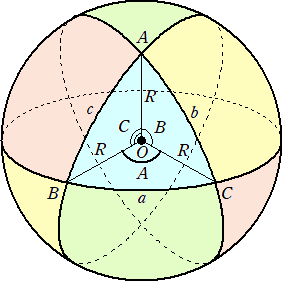
半径Rの球面上にあり、内角の大きさがA、B、Cである三角形の面積は、
S=(A+B+C−π)R2
で与えられる。
(証明) 半径Rの球面の表面積 4πR2は、大円により、2等分される。
球面三角形ABCを含む面角Aに対応する部分の表面積をSAとすると、
SA=2πR2×(A/π)=2AR2
同様にして、
SB=2πR2×(B/π)=2BR2
SC=2πR2×(C/π)=2CR2
このとき、 SA+SB+SC−2S の2倍が球面の表面積となるので、
(SA+SB+SC−2S)×2=4πR2
したがって、2AR2+2BR2+2CR2−2S=2πR2 より、
S=(A+B+C−π)R2 (証終)
# 上記の公式において、S>0から、A+B+C>π である。すなわち、球面上の三角形
の内角の和は、πより大きいことが分かる。
例 地点A(北緯0°東経0°)、地点B(北緯0°東経90°)、地点C(北緯90°東経0°)
の3点からなる球面三角形の面積は、A=B=C=π/2 より、
S=(A+B+C−π)R2=πR2/2
この面積は当然ながら、球面の表面積 4πR2 の1/8倍である。
問題は、一般の位置にある場合の計算である。

以下、工事中!
