
丂憡帡偺娭學偵偁傞恾宍娫偱丄懳墳偡傞晹暘偺挿偝偺斾偺偙偲傪丄憡帡斾偲偄偆丅憡帡偵
偮偄偰偼丄拞妛俁擭偱妛傇偑丄憡帡側恾宍偺柺愊斾丄懱愊斾偵偮偄偰偼丄崅峑侾擭偺乽悢
妛嘥乿傪懸偨側偗傟偽側傜側偄丅
丂幚嵺偵丄乽悢妛嘥乿傪侾擭娫挱傔偰傒偰丄嶰妏斾偺榖偑壚嫬偵擖偭偨偲偙傠乮惓尫掕棟傗
梋尫掕棟丄柺愊乯偱撍慠僊儎僠僃儞僕偟偨傛偆偵憡帡恾宍偺榖丄媴偺懱愊傗昞柺愊偺榖偵
堏傞偺偵偼彮偟堘榓姶傪妎偊偨丅
丂椺偊偽丄偦傟傑偱嶰妏宍偺曈偺挿偝傗妏偺戝偒偝偑梌偊傜傟偰丄偦偙傪婲揰偵嶰妏宍偺
柺愊傪媮傔偰偄偨傕偺偑撍慠憡帡斾偺惈幙傪巊偭偰嶰妏宍偺柺愊傪媮傔偝偣傜傟傞偐傜
偩丅
栤丂俀偮偺嶰妏宍 俹 偲 俻 偼憡帡偱丄憡帡斾偼 俀 丗 俁 偱偁傞丅俹 偺柺愊偑 係 偺偲偒丄俻 偺
丂丂柺愊偼偄偔偮偐丠
丂偙偺栤戣傪夝偔偵偼丄師偺婎杮揑側岞幃偑妶桇偡傞丅
丂俀偮偺恾宍 俹 偲 俻 偼憡帡偱丄憡帡斾偑 倣 丗 値 偱偁傞偲偒丄
丂丂丂俹 偲 俻 偺柺愊斾偼丄 倣2 丗 値2 偲側傞丅丂乮柺愊斾偼憡帡斾偺俀忔偵摍偟偄乯
摨條偵丄
丂俀偮偺恾宍 俹 偲 俻 偼憡帡偱丄憡帡斾偑 倣 丗 値 偱偁傞偲偒丄
丂丂丂俹 偲 俻 偺懱愊斾偼丄 倣3 丗 値3 偲側傞丅丂乮懱愊斾偼憡帡斾偺俁忔偵摍偟偄乯
丂偙偺傛偆側娭學偼埲慜偼拞妛偱壗偺堘榓姶傕側偔庢傝埖傢傟偰偒偨傕偺偩偑丄嶰妏斾偺
妛廗偺嵟屻偺曽偱撍慠尰傟偰偄傞偙偲偵堘榓姶傪妎偊傞偺偼壥偨偟偰巹偩偗偱偁傠偆偐丠
丂偝偰丄忋婰偺惈幙傪梡偄傞偲丄栤偼師偺傛偆偵夝偐傟傞丅
丂俹 丗 俻 亖 俀2 丗 俁2 亖 係 丗 俋 丂傛傝丄丂係俻亖俋俹亖俋亊係亖俁俇丂丂傛偭偰丄俻亖俋
丂夝摎偼旕忢偵僔儞僾儖偱偁傞偑丄怴偟偄敪憐偵寢峔惗搆偼屗榝偆傛偆偱偁傞丅
丂偙偺傛偆側憡帡斾偺惈幙偼丄悢妛偵偍偄偰偼偐側傝廳梫偲巚傢傟傞丅偙偺儁乕僕偱偼丄憡
帡斾偺惈幙偵拝栚偟丄偦偺慺惏傜偟偄墳梡傪挱傔偰偄偒偨偄偲巚偆丅
椺戣丂嵗昗暯柺忋偱丄俀揰俙乮侾丆侽乯丄俛乮侽丆俀乯傪捠傞捈慄 俀倶亄倷亅俀亖侽 偵丄揰俠乮俀丆俀乯傛
丂丂丂傝悅慄偺懌俫傪壓傠偡丅偙偺偲偒丄仮俙俠俫偺柺愊傪媮傔傛丅

丂乮夝乯丂捈慄俠俫偺曽掱幃偼丄
丂丂丂丂丂丂丂倷亖乮侾/俀乯倶亄侾
丂丂丂側偺偱丄捈慄俙俛偺曽掱幃偲楢棫偟偰丄
丂丂丂丂丂丂丂俫乮俀/俆 丆俇/俆乯
丂丂丂偑媮傔傜傟傞丅
丂丂丂丂偙偺偲偒丄丂俙俫亖俁/
丂丂丂側偺偱丄仮俙俠俫偺柺愊偼丄
丂丂丂丂乮侾/俀乯乮俁/
丂梌偊傜傟偨忦審偐傜帺慠偵忋婰偺傛偆偵寁嶼偼偱偒傞偑丄偁傑傝旤偟偝偼姶偠傜傟側偄丅
偙偺夝朄偵懳偟偰丄憡帡斾傪梡偄偨師偺傛偆側旤偟偄夝摎偑懚嵼偡傞丅
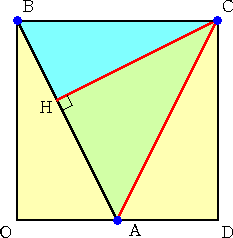
丂丂乮夝乯丂嵍恾偵偍偄偰丄仮俷俙俛佷仮俫俛俠丂偱憡帡斾
丂丂丂丂丂偼丄
丂丂丂丂丂丂丂仮俷俙俛 丗 仮俫俛俠 亖 俆 丗 係
丂丂丂丂丂傛偭偰丄丂仮俫俛俠亖乮係/俆乯亊侾亖係/俆
丂丂丂丂丂偟偨偑偭偰丄
丂丂丂丂丂丂仮俙俠俫亖係亅侾亊俀亅係/俆亖俇/俆丂丂乮廔乯
乮僐儊儞僩乯丂憡帡斾傪梡偄偨夝朄偺慺惏傜偟偝偼丄柺愊傪媮傔傞嵺偵摉奩恾宍偺忣曬偲偟偰
丂丂丂丂丂丂憡帡斾偑暘偐傟偽廫暘偲偄偆偙偲偩傠偆丅憡帡斾傪媮傔傞偵偼懳墳偡傞侾懳偺慄
丂丂丂丂丂丂暘偺斾偑暘偐傟偽傛偄偺偱丄柺愊寁嶼偱昁梫側彅乆偺彅寁嶼傪偟側偔偰傕嵪傓偲
丂丂丂丂丂丂偄偆棙揰偑偁傞丅
丂憡帡斾偵娭傢傞栤戣偼丄壗偲拞妛庴尡偱弌戣偝傟偰偄傞丅摿偵丄柺愊斾偑憡帡斾偺俀忔
偵斾椺偡傞偲偄偆惈幙傕栤傢傟偰偄傞偙偲偵偼嬃偒傪塀偣側偄丅岞棫偱恑媺偟偰偒偨惗搆偑
崅峑侾擭偱弶傔偰妛傇撪梕偑彫妛俇擭惗偵壽偝傟偰偄傞偐傜偩丅偨偩丄偙偺偙偲偱拞妛擖帋
傪斲掕偟傛偆偲偼巚傢側偄丅悢妛偵偍偗傞塱墦晛曊偺恀棟傪丄偄偮抦傞偐偲偄偆偺偼丄恖偦
傟偧傟帺桼偱偁傞傋偒偲巚偆偐傜偩丅
岞暥崙嵺妛墍拞摍晹乮俀侽侽係擭乯乮堦晹夵戣乯
丂惓曽宍俙俛俠俢偺曈俛俠傪壗摍暘偐偟丄俛偵傕偭偲傕嬤偄揰傪俹偲偡傞丅俛偐傜俙俹偵悅捈側
慄傪傂偒丄俙俹偲偺岎揰傪俫丄俙俹亖侾侽cm偲偡傞偲偒丆師偺栤偄偵摎偊傛丅
乮侾乯丂壓恾偺傛偆偵丄曈俛俠傪俁摍暘偡傞偲偒丄俛俫丗俫俹 傪傕偭偲傕娙扨側惍悢偺斾偱昞偣丅
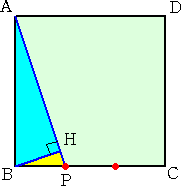
丂丂偙傟偼丄丂仮俛俫俹 佷 仮俙俛俹 傛傝丄
丂丂丂丂丂俛俫 丗 俫俹 亖 俙俛 丗 俛俹 亖 俁 丗 侾
丂偱偁傞偙偲偼柧傜偐偩傠偆丅
乮俀乯丂乮侾乯偲摨條偵丄曈俛俠傪俁摍暘偡傞偲偒丄惓曽宍俙俛俠俢偺柺愊傪媮傔傛丅
丂丂丂乮侾乯傛傝丄丂俛俹亖倶丂偲偍偔偲丄丂俙俛亖俁倶丂偱丄丂嶰暯曽偺掕棟傛傝丄
丂丂丂丂丂丂丂丂丂丂倶2亄俋倶2亖侾侽侽丂丂偡側傢偪丄丂侾侽倶2亖侾侽侽丂傛傝丂丂倶2亖侾侽
丂丂丂丂丂丂傛偭偰丄丂惓曽宍俙俛俠俢偺柺愊偼丄丂俋倶2亖俋侽丂乮cm2乯
乮僐儊儞僩乯丂僂乣儉両偙偺夝摎偱偼丄偳偆尒偰傕彫妛惗岦偒偱偼側偄偱偡偹丅
丂丂丂丂丂丂懡暘丄彫妛惗側傜師偺傛偆偵夝偔偺偩傠偆偐丠
丂丂丂丂丂乮侾乯傛傝丄丂俛俫 丗 俫俹 亖 俙俛 丗 俛俹 亖 俁 丗 侾
丂丂丂丂丂仮俙俫俛 佷 仮俛俫俹 傛傝丄丂俙俫 丗 俛俫 亖 俛俫 丗 俫俹 亖俁 丗 侾
丂丂丂丂丂丂傛偭偰丄丂俙俫 丗 俫俹 亖 俋 丗 侾丂偱丄丂俙俹亖侾侽丂傛傝丄丂俙俫亖俋丂丄丂俫俹亖侾
丂丂丂丂丂俛俫亖俁丂傛傝丄丂仮俙俫俛亖俁亊俋亐俀亖俀俈/俀
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂仮俛俫俹亖俁亊侾亐俀亖俁/俀
丂丂丂丂丂丂傛偭偰丄丂丂仮俙俛俹亖俀俈/俀亄俁/俀亖侾俆
丂丂丂丂丂偟偨偑偭偰丄丂惓曽宍俙俛俠俢偺柺愊偼丄丂侾俆亊俀亊俁亖俋侽丂乮cm2乯
乮俁乯丂俛俫丗俫俹亖俈丗侾 偺偲偒丄仮俙俛俹偺柺愊傪媮傔傛丅
丂丂丂丂丂俛俫 丗 俫俹 亖 俈 丗 侾丂傛傝丄丂俙俫 丗 俛俫 亖 俈 丗 侾
丂丂丂傛偭偰丄丂俙俫 丗 俫俹 亖 係俋 丗 侾丂偱丄丂俙俹亖侾侽丂傛傝丄丂俙俫亖係俋/俆丂丄丂俫俹亖侾/俆
丂丂丂丂丂俛俫亖俈/俆丂傛傝丄丂仮俙俛俹亖乮俈/俆乯亊侾侽亐俀亖俈丂乮cm2乯
乮係乯丂仮俙俛俫偺柺愊偑 侾俇 們m2 偱仮俛俹俫偺柺愊偑 係 們m2 偺偲偒丄惓曽宍俙俛俠俢偺柺愊
丂丂傪媮傔傛丅
丂丂丂丂仮俙俛俫 丗 仮俛俹俫 亖 侾俇 丗 係 亖 係2丗俀2丂傛傝丄
丂丂仮俙俛俫 偲 仮俛俹俫 偺憡帡斾偼丄丂俀 丗 侾 偱偁傞丅
丂丂丂傛偭偰丄丂俙俫 丗 俛俫 亖 俀 丗 侾丂丂傛傝丄丂俙俛 丗 俛俹 亖 俀丗 侾丂偱丄俹 偼丄曈俛俠偺拞揰丅
丂丂偟偨偑偭偰丄丂惓曽宍俙俛俠俢偺柺愊偼丄丂乮侾俇亄係乯亊俀亊俀亖俉侽丂乮cm2乯
乮僐儊儞僩乯丂乮係乯偼丄俹偑曈俛俠偺壗摍暘揰偐偑暘偐傜側偄偲偙傠偑儈僜偩傠偆偐丠
丂丂丂丂丂丂岻柇偵柺愊斾偺惈幙傪梡偄偰丄俹偑拞揰偱偁傞偙偲傪帵偟偰偄傞揰偑柺敀偄丅
丂忋婰偺夝摎偱偼丄柺愊斾偺惈幙傪梡偄偰偄傞偑丄師偺傛偆偵傕夝偗傞偩傠偆丅
丂丂丂丂丂仮俙俛俫 偲 仮俛俹俫丂偺崅偝偑嫟捠側偺偱丄柺愊斾偲掙曈偺斾偼摍偟偄丅
丂丂丂丂傛偭偰丄丂俙俫 丗 俫俹 亖 侾俇 丗 係丂亖 係 丗 侾丂偱丄丂
丂丂丂丂丂丂俙俹亖侾侽丂傛傝丄丂俙俫亖俉丂丄丂俫俹亖俀丂偱丄偙偺偲偒丄丂俛俫亖係丂偲側傞丅
丂丂丂丂傛偭偰丄丂俙俛 丗 俛俹 亖 俙俫 丗 俛俫 亖 俉 丗 係丂亖 俀 丗 侾丂偱丄俹 偼丄曈俛俠偺拞揰丅
丂丂丂丂偟偨偑偭偰丄丂惓曽宍俙俛俠俢偺柺愊偼丄丂乮侾俇亄係乯亊俀亊俀亖俉侽丂乮cm2乯
乮僐儊儞僩乯丂偙偺傛偆偵夝偄偨曽偑廫暘彫妛惗揑偐側丠
丂偙傟偐傜柺敀偄墳梡偵擖傞慜偵丄婎慴抦幆傪惍棟偟偰偍偙偆丅
 丂丂丂嵍恾偺傛偆側棫曽懱 俷俙俛俠-俢俤俥俧 偵偍
丂丂丂嵍恾偺傛偆側棫曽懱 俷俙俛俠-俢俤俥俧 偵偍丂丂偄偰丄俁捀揰 俤丄俛丄俧 傪寢傫偱弌棃傞嶰妏
丂丂宍偼丄惓嶰妏宍偱偁傞丅
丂丂丂偙偺偙偲偼丄嶰妏宍偺俁曈 俤俛丄俛俧丄俧俤
丂丂偺挿偝偑憡摍偟偄偙偲偐傜柧傜偐偩傠偆丅
丂丂丂偙偺応柺偼悢妛俛偱妛傇乽儀僋僩儖乿偱丄撪
丂丂愊偺寁嶼偵傛偔梡偄傜傟傞丅
丂丂丂棫曽懱偺侾曈偺挿偝傪 倎 偲偡傞偲丄偙偺偲
丂丂偒弌棃傞惓嶰妏宍偺柺愊偼丄
丂丂丂丂丂丂丂丂丂
丂傑偨丄忋恾偺傛偆偵惓嶰妏宍偲慄暘 俷俥 偲偺岎揰傪 俫 偲偡傞偲丄俫 偼惓嶰妏宍偺廳怱
偱偁傞丅
丂幚嵺偵丄丂俥俤亖倎丂丄俥俛亖倐丂丄俥俧亖們丂丂乮儀僋僩儖傪懢帤偺幬懱偱昞偡偙偲偵偡傞丅乯偲
偡傞偲丄暯柺 俤俛俧 偺曽掱幃偼丄丂倫亖倶倎亄倷倐亄倸們丂丂乮 倶亄倷亄倸亖侾 乯 偱昞偝傟傞丅
傑偨丄丂俥俫亖倠乮倎亄倐亄們乯丂乮倠 偼幚悢乯丂偲彂偗傞丅
丂揰 俫 偑暯柺 俤俛俧 忋偵偁傞偲偒丄丂丂俁倠亖侾丂丂偲側傝丄丂丂倠亖侾/俁
傛偭偰丄丂丂俥俫亖乮倎亄倐亄們乯/俁丂丂偲側傝丄偙傟偼丄揰 俫 偑嶰妏宍 俤俛俧 偺廳怱偱偁傞偙偲
傪帵偡丅
丂傑偨丄俁悅慄偺掕棟傛傝丄柧傜偐偵慄暘 俷俥 偼揰 俫 偵偍偄偰丄暯柺 俤俛俧 偲捈岎偡傞丅
丂崱搙偼丄俷 偲 俥 傪捠傜側偄曈偺拞揰傪寢傫偩恾宍傪峫偊傞丅
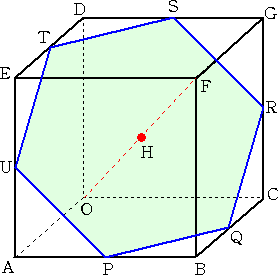 丂丂丂嵍恾偺傛偆側棫曽懱 俷俙俛俠-俢俤俥俧 偵偍
丂丂丂嵍恾偺傛偆側棫曽懱 俷俙俛俠-俢俤俥俧 偵偍丂丂偄偰丄俇揰 俹丄俻丄俼丄俽丄俿丄倀 傪寢傫偱弌棃
丂丂傞恾宍偼丄惓榋妏宍偱偁傞丅
丂丂丂偨偩丄偙偺応崌偼慜弎偺惓嶰妏宍偺応崌
丂丂偲堎側偭偰帺柧偲偡傞偙偲偵偼掞峈偑偁傞偩
丂丂傠偆丅
丂丂丂師偺俁揰傪妋偐傔傟偽廫暘偱偁傞丅
丂丂乮侾乯丂俇揰偑摨堦暯柺忋偵偁傞偙偲
丂丂乮俀乯丂俇曈偺挿偝偑慡偰摍偟偄偙偲
丂丂乮俁乯丂俇偮偺撪妏偑慡偰摍偟偄偙偲
丂丂丂偙偺偙偲傪埲壓偱傑偢帵偦偆丅
丂乮侾乯丂恾傛傝丄丂俥俿亖俷俿丂丄丂俥俻亖俷俻丂偱丄偐偮丄丂俥俿亖俥俻丂側偺偱丄
丂丂丂暯峴巐曈宍 俥俿俷俻 偼丄傂偟宍偱偁傞丅
丂丂丂丂傛偭偰丄丂懳妏慄 俷俥 偲 俻俿 偼丄慄暘 俷俥 偺拞揰 俫 偵偍偄偰丄捈岎偡傞丅
丂丂丂摨條偵偟偰丄丂慄暘 俷俥 偲 倀俼 丄慄暘 俷俥 偲 俹俽 偼揰 俫 偵偍偄偰丄捈岎偡傞丅
丂丂丂丂偟偨偑偭偰丄俇揰 俹丄俻丄俼丄俽丄俿丄倀 偼慄暘 俷俥 偲揰 俫 偵偍偄偰捈岎偡傞暯柺忋
丂丂丂偵偁傞丅
丂乮俀乯丂俇曈偺挿偝偑慡偰摍偟偄偙偲偼柧傜偐偩傠偆丅
丂乮俁乯丂乮侾乯傛傝丄丂俫俹亖俫俻亖俫俼亖俫俽亖俫俿亖俫倀丂側偺偱丄俇偮偺撪妏偑慡偰摍偟偄偙
丂丂丂偲傕柧傜偐偩傠偆丅
丂拞揰楢寢偺掕棟傪梡偄偰傕傛偄丅壓恾傪挱傔偰偄傞偲帺偢偐傜徹柧偑晜偐傃忋偑偭偰偔
傞偙偲偩傠偆丅
丂丂丂丂丂丂丂丂丂

丂偝偰丄偄傛偄傛杮榑偵擖傠偆丅
丂愭擔壗偲偼側偟偵俿倁傪尒偰偄偨傜乽妛峑傊峴偙偆両俵俙倃乿乮俀寧俀侽擔曻憲丂俿俛俽宯乯偲偄偆
斣慻偺拞偱乽揤嵥彮擭曞廤両両乿偲偄偆僞僀僩儖偱棫懱恾宍偺愗傝岥偺柺愊傪媮傔傞栤戣偑
弌戣偝傟偰偄偨丅捈偖偵愗傝岥偺僀儊乕僕偑巚偄晜偐偽偢丄嫽枴傪堷偄偨栤戣側偺偱峫偊偰
傒傞偙偲偵偟偨丅
丂揤嵥彮擭曞廤両両偺栤戣乮堦晹暥復昞尰夵戣乯
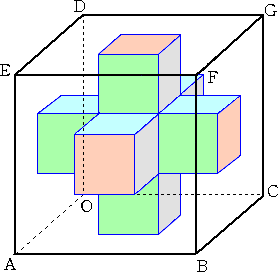 丂丂嵍恾偺傛偆側棫曽懱 俷俙俛俠-俢俤俥俧 偵偍偄
丂丂嵍恾偺傛偆側棫曽懱 俷俙俛俠-俢俤俥俧 偵偍偄丂
丂偰岦偐偄崌偭偨柺偐傜柺傑偱丄惓曽宍偺寠傪
丂
丂偮偒偸偗傞傛偆偵俁曽岦偵偁偗傞丅寠偺惓曽宍
丂
丂偺拞怱偲棫曽懱偺柺偺拞怱偼摨堦捈慄忋偵
丂
丂偁傞傕偺偲偟丄寠偺惓曽宍偺侾曈偺挿偝偼丄棫
丂
丂曽懱偺侾曈偺挿偝偺侾/俁偲偡傞丅
丂寠偺偁偄偨忋婰偺棫懱恾宍傪丄俷 偲 俥 傪捠傜側偄曈偺拞揰傪寢傫偩惓俇妏宍偺暯柺偱
愗傞偙偲傪峫偊傞丅
丂丂丂丂丂丂丂丂丂
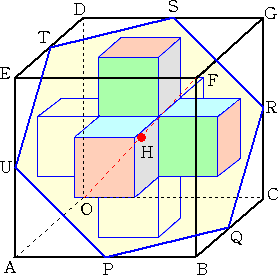
丂偄傑丄惓俇妏宍俹俻俼俽俿倀偺柺愊偑丄侾係係們倣2偱偁傞偲偒丄偦偺愗傝岥偺柺愊傪媮傔傛丅
乮夝乯丂忋恾傪徻偟偔夝愅偡傞偲丄媮傔傞柺愊偼丄壓恾偺恾宍 俿倄倃倅俽 偺柺愊偺俇攞偱偁傞丅
丂丂丂丂丂丂丂丂丂丂
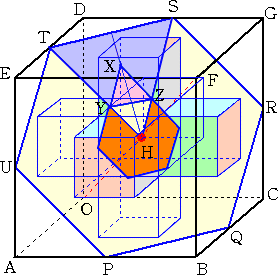
丂嶰妏宍 倃倄倅 偲嶰妏宍 俫倄倅 偼屳偄偵崌摨側惓嶰妏宍偱偁傞丅
戝偒偄惓俇妏宍偲彫偝偄惓俇妏宍偼憡帡偱丄憡帡斾偼丄俁 丗 侾 側偺偱丄柺愊斾偼丄俋 丗 侾 偱
偁傞丅傛偭偰丄戝偒偄惓俇妏宍偺柺愊偑丄侾係係們倣2偱偁傞偺偱丄彫偝偄惓俇妏宍偺柺愊偼丄
丂丂丂丂侾係係亊乮侾/俋乯亖侾俇 乮們倣2乯
偲側傞丅丂偟偨偑偭偰丄媮傔傞柺愊偼丄
丂丂丂丂侾係係亅侾俇亊俀亖侾侾俀 乮們倣2乯
偱偁傞丅
乮僐儊儞僩乯丂偙偺栤戣偑暘偐傞彫妛惗偼丄懡暘擔杮偺偳偙偐偵偼偄傞偺偩傠偆両
乮捛婰乯丂暯惉俀俉擭俀寧侾俉擔晅偗
丂俀偮偺恾宍 俹 偲 俻 偼憡帡偱丄憡帡斾偑 倣 丗 値 偱偁傞偲偒丄
丂丂丂俹 偲 俻 偺柺愊斾偼丄 倣2 丗 値2 偲側傞丅丂乮柺愊斾偼憡帡斾偺俀忔偵摍偟偄乯
偲偄偆帠幚偼丄嵟嬤傑偱乽悢妛嘥乿偱偺妛廗撪梕偱偁偭偨偑丄怴妛廗巜摫梫椞偱偼丄拞妛峑
偺巜摫撪梕偵栠偝傟偰偄傞丅堘榓姶偑偁偭偨偺偱帺慠側懳墳偩傠偆丅
丂暯惉俀俉擭俀寧侾俇擔偵峴傢傟偨恄撧愳導岞棫崅峑擖帋乮悢妛乯偱師偺傛偆側栤戣偑弌戣
偝傟偨丅
栤戣丂塃偺恾偺傛偆側暯峴巐曈宍ABCD偑偁傝丄曈CD偺拞揰傪E偲偡傞丅傑偨丄曈AD忋偵揰
丂丂丂F傪AF丗FD亖係丗俁 偲側傞傛偆偵偲傝丄曈BC忋偵揰G傪AB乤FG 偲側傞傛偆偵偲傞丅慄暘AE
丂丂丂偲慄暘FG偲偺岎揰傪H丄慄暘BE偲慄暘FG偲偺岎揰傪I偲偡傞丅
丂丂丂丂偙偺偲偒丄嶰妏宍BGI偲嶰妏宍EHI偺柺愊偺斾傪嵟傕娙扨側惍悢偺斾偱昞偟側偝偄丅
丂丂丂丂丂
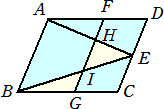
乮夝乯丂俥俢丗俙俢亖俁丗俈丂傛傝丄丂仮俤俫俬丗仮俤俙俛亖俁2丗俈2亖俋丗係俋丂側偺偱丄仮俤俫俬亖俋俽丂偲偍
丂偔偲丄仮俤俙俛亖係俋丂偱偁傞丅偙偺偲偒丄仮俛俠俤亖乮係俋/俀乯俽丂偲側傞丅
丂丂傛偭偰丄丂仮俛俧俬丗仮俛俠俤亖係2丗俈2亖侾俇丗係俋丂側偺偱丄
丂丂丂仮俛俧俬亖乮係俋/俀乯俽亊乮侾俇/係俋乯亖俉俽丂偲側傞丅
丂偟偨偑偭偰丄丂仮俛俧俬丗仮俤俫俬亖俉俽丗俋俽亖俉丗俋丂偱偁傞丅丂丂乮廔乯
乮捛婰乯丂暯惉俁侽擭俉寧係擔晅偗
丂杮擔悢妛偵娭偡傞夛崌偑偁傝丄偦偺惾偱挿壀椇夘愭惗偐傜崅峑悢妛偺埆偟偒姷廗偵偮偄
偰偺榖傪巉偭偨丅
丂憡帡斾偲尵偆偲丄壗偲側偔 倣 丗 値 偲抲偄偰偟傑偆偺偩偑丄偙傟偼屆戙僊儕僔儍帪戙偵丄斾偲
尵偊偽帺慠悢偺斾偩偭偨偙偲偺柤巆偩偲偄偆丅尰戙晽偩偲丄倲 丗 侾亅倲 偲抲偄偨曽偑傛偄偲偺
偙偲偱偁傞丅
丂妋偐偵丄倲 丗 侾亅倲 偲抲偄偨曽偑丄暘揰偺岞幃偱暘曣偑侾偲娙慺壔偝傟傞傢偗偱偁傞偑丄巹
揑偵偼丄斾偲偟偰丄倣 丗 値 偲抲偔偙偲偺椙偝傕偁傞傢偗偱丄椪婡墳曄偵巊偄暘偗偰偄偒偨偄偲
巚偆丅
丂丂埲壓丄岺帠拞