
�@�w�Z������w�����Ő��V�p�`�������邱�Ƃ́A�قƂ�ǂȂ����A���̐}�`�̒��ɔ�
�߂�ꂽ�����ɂ͂ƂĂ����������̂����邱�Ƃ��ŋߒm�����B
���V�p�`�̂��鐫���@ �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�w�Z������w�����Ő��V�p�`�������邱�Ƃ́A�قƂ�ǂȂ����A���̐}�`�̒��ɔ�
�߂�ꂽ�����ɂ͂ƂĂ����������̂����邱�Ƃ��ŋߒm�����B
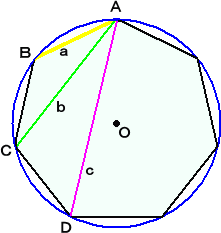 |
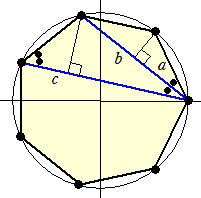
�@�@���}�͔��a �P�O�R �̉~�ɓ��ڂ��鐳�V�p�`�ł���B |
�@���̗\�z�͐������A���̂悤�ɏؖ������B�������A�~ �n �̔��a�� �P �Ƃ���B
�@�ڂa�`�b���Ɓi����/�V�j�Ƃ����ƁA�ڂ`�n�a���Q�ƁA�ڂ`�n�b���S�ƁA�ڂ`�n�c���U�Ɓ@�ł���B
���̂Ƃ��A�����Q�������ƁA�����Q�������Q�ƁA�����Q�������R�Ɓ@�ł���B
����āA
�@�����|�����{�������S�������Q�Ƃ������Ɓ|�S�������R�Ƃ������Q�Ɓ{�S�������R�Ƃ�������
���|�Q�i�������R�Ɓ|�������Ɓj�{�Q�i�������T�Ɓ|�������Ɓj�|�Q�i�������S�Ɓ|�������Q�Ɓj
���|�Q�i�������S�Ɓ{�������R�Ɓj�{�Q�i�������T�Ɓ{�������Q�Ɓj
���|�S������(7/2)�Ƃ�����(1/2)�Ɓ{�S������(7/2)�Ƃ�����(3/2)��
���S������(7/2)�Ɓi������(3/2)�Ɓ|������(1/2)�Ɓj
�@�����ŁA�P�S�Ɓ��R�U�O�����A(7/2)�Ɓ��X�O���Ȃ̂ŁA������(7/2)�Ɓ��O
���������āA�@�����|�����{�������O�@�@���Ȃ킿�@�@�P/�����P/���{�P/���@�@�����藧�B
�i�R�����g�j�@��L�̂悤�ɏؖ��͂ł����̂����A��͓I�Ȏ�@��p���Ă���̂ŁA�ؖ�����
�@�@�@�@�ɂ��܂���������������Ȃ��B���̓����́A������p���ďؖ��ł��Ȃ��̂���
�@�@�@�@�����H����́A�ǎ҂̂��߂̗��K���Ɏc���Ă������B
�@�����I�ؖ����ł������́A�����������Ƀ��[���ʼn������������B
�i�NjL�j�@��L�̏����I�ؖ��Ƃ��āA�v�g���}�C�I�X�̒藝��p����ƑN�₩�Ɏ������B
�@�@�@�@����ނ���A���܂�ɑN�₩�����āA�����𖡂키�]�T���Ȃ���������Ȃ��B
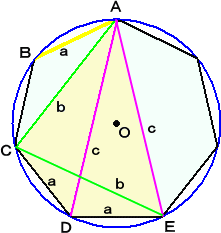 |
�i�ʏj�@���}�ɂ����āA�l�p�` �`�b�c�d �́A�~�ɓ��ڂ��� �@�@�@�@�l�p�`�Ȃ̂ŁA�v�g���}�C�I�X�̒藝���A �@�@�@�@�@�@�@�`�c�E�b�d���b�c�E�`�d�{�`�b�E�c�d �@�@�@����āA�@�@���� �� ���� �{ �����@�@�����藧���� �@�@�@�@�@�@�@�P/�����P/���{�P/�� �@�@�ł���B�@�i�ؖ��I�j |
�i�R�����g�j�@���̏����I�ؖ����݂�ƁA��͓I�ؖ����������v���Ă���B�܂��ɁA������
�@�@�@�@�@�@���̐ꖡ�ɁA���@�藝�����������ł���B�����Ƃ��A���@�藝���A�v�g���}�C�I�X
�@�@�@�@�@�@�̒藝���瓱����邱�Ƃ��l����ƁA��������R�̋A���ł��낤���I
�i�NjL�j�@�����P�V�N�T���U���t��
�@�s�D�h�D����Ƃ���������ʏؖ��Ղ����B���̎�|�����Ȃ��瑽���⑫�E�C�����s��
�����̂����L�̏ؖ��ł���B
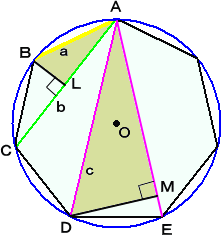 |
�@�@�@���}�ɂ����āA �_�a�A�_�c��肻�ꂼ������`�b�A �@�@�����`�d���������낵�A���̐����̑����k�A�l�� �@�@����B�@���̂Ƃ��A �@�@�@ �ڂa�`�k���ڂc�`�l�A�ڂa�k�`���ڂc�l�`���X�O�� �@�@�Ȃ̂ŁA �@�@�@�@�@�@�@�@�@���`�a�k �� ���`�c�l �@�@�ł���B �@�@�@���܁A�ڂa�`�b���Ɓ@�Ƃ����B �@ |
���`�a�b �ɂ����āA�]���藝���A�@�@��2����2�{��2�|�Q�����������Ɓ@�Ȃ̂ŁA�@�����Q����������
�@�@����āA�@������/(�Q��������)�@�����藧�B
�i���̎��́A�]���藝��p���Ȃ��Ă����߂邱�Ƃ��ł���B�����a�k�̒����ɒ��ڂ���A
�@���������Ɓ�(1/2)���������Ɓ�(1/2)����������/�������Ɓ@���A������/(�Q��������)�@�����藧�B�j
���l�ɁA���`�b�c �ɂ����āA�]���藝���A�@�@��2����2�{��2�|�Q������������
�@���`�c�d �ɂ����āA�]���藝���A�@��2����2�{��2�|�Q��2�������Ɓ@�Ȃ̂ŁA
�@��2���Q��2�i�P�|�������Ɓj
�@���̎����A�@��2����2�{��2�|�Q�����������Ɓ@�ɑ�����āA
�@�Q��2�i�P�|�������Ɓj����2�{��2�|�Q�����������Ɓ@�@���A�Q���i���|���j�������Ɓ���2�|��2
�@����āA�@�������@�Ȃ̂ŁA�@����(���{��)/(�Q��������)�@�����藧�B
�����ŁA�@���`�a�k �� ���`�c�l�@�Ȃ̂ŁA�@�`�a �F �`�c �� �a�k �F �c�l
���������āA�@�� �F �� �� ���E�������� �F ���E�������Ɓ@�ɂ����āA
�@��/(�Q��������) �F (���{��)/(�Q��������) �� ���E�������� �F ���E��������
����āA�@�@�����E��������/�Q �� ��(���{��)�E��������/�Q�@���A�@���� �� ��(���{��)�@�����藧�B
������A�@�@�P/�����P/���{�P/���@�@�ł��邱�Ƃ�������B
�i�R�����g�j�@�`���̏ؖ��ł́A�O�p���̘a�ς̌����A�Ϙa�̌��������p���Ă���̂ŁA��
�@�@�@�@�w�U�̃��x���̏ؖ��ƌ�����B����ɑ��āA���Ղ����ؖ��́A�]���藝�����p����
�@�@�@�@����̂ŁA���w�T�̃��x���̏ؖ��ƌ�����B�ʏؖ��������������s�D�h�D����Ɋ��ӂ���
�@�@�@�@���܂��B
�i�NjL�j�@��L�ŁA�u�s�D�h�D����̎�|�����Ȃ���v�s�����ؖ��̂���ł��������A�s�D�h�D
�@�@�@�@�@����Ɖ��x�����[�������Ƃ肵�āA�S���u�s�D�h�D����̎�|�v�����Ă��Ȃ����Ƃ�
�@�@�@�@�@�C�Â����ꂽ�B
�@��L�̏ؖ��ł͗]���藝��p���Ă��邪�A�ȒP�ȎO�p��̌v�Z�ŏؖ������悤�ł���B
�@�����ł́A�u�s�D�h�D����̎�|�v�𒍈Ӑ[�����炵�A�ēx�ؖ����L�q���悤�Ǝv���B��L�̏�
�������āA������������A�s�D�h�D����͕s���Ɏv��ꂽ��������Ȃ��B���l�ѐ\���グ�܂��B
 |
�@�@�@���}�ɂ����āA �_�a�A�_�c��肻�ꂼ������`�b�A �@�@�����`�d���������낵�A���̐����̑����k�A�l�� �@�@����B�@���̂Ƃ��A �@�@�@ �ڂa�`�k���ڂc�`�l�A�ڂa�k�`���ڂc�l�`���X�O�� �@�@�Ȃ̂ŁA �@�@�@�@�@�@�@�@�@���`�a�k �� ���`�c�l �@�@�ł���B �@�@�@���܁A�ڂa�`�b���Ɓ@�Ƃ����B �@ |
���p�O�p�`�`�a�k �ɂ����āA�@�������Ɓ�(�P/�Q)��/���@�@���A�@�@������/(�Q��������)�@�����藧�B
�܂��A�l�p�`�`�a�c�d �́A���r��`�Ȃ̂ŁA�@�@�`�l�����{(���|��)/�Q��(���{��)/�Q
����āA�@���p�O�p�`�`�c�l �ɂ����āA�@�������Ɓ�((���{��)/�Q)/���@�@���A
�@����(���{��)/(�Q��������)
�����藧�B
�����ŁA�@���`�a�k �� ���`�c�l�@�Ȃ̂ŁA�@�`�a �F �`�c �� �a�k �F �c�l
���������āA�@�� �F �� �� ���E�������� �F ���E�������Ɓ@�ɂ����āA
�@��/(�Q��������) �F (���{��)/(�Q��������) �� ���E�������� �F ���E��������
�@����āA�@�@�����E��������/�Q �� ��(���{��)�E��������/�Q�@���A�@����
�� ��(���{��)�@�����藧�B
������A�@�@�P/�����P/���{�P/���@�@�ł��邱�Ƃ�������B
�i�R�����g�j�@��r�I�����I�ŁA�X�b�L�������ؖ��ł��ˁI
�@����ɁA�s�D�h ����O�p���p���Ȃ��ŎO�����̒藝�ŏ\���Ƃ̂������������������B
���p�O�p�`�`�a�k �ɂ����āA�O�����̒藝���A
�@![]()
�܂��A�l�p�`�`�a�c�d �́A���r��`�Ȃ̂ŁA�@�@�`�l�����{(���|��)/�Q��(���{��)/�Q
���̂Ƃ��A���p�O�p�`�`�c�l �ɂ����āA�O�����̒藝���A
�@![]()
�����ŁA�@���`�a�k �� ���`�c�l�@�Ȃ̂ŁA�@�`�a �F �`�c �� �a�k �F �c�l
����āA
�@![]()
������A
�@![]()
�����藧�B
�@���������āA�@���� �� ��(���{��)�@�Ȃ̂ŁA�@�P/�����P/���{�P/���@�@�ł��邱�Ƃ�������B
�i�NjL�j�@�����P�V�N�P�P���P�R���t��
�@�s�D�r�D����u�O�p�����g��Ȃ�����ɏ����I�ȏؖ����v�������v�|�̃��[����
�����B
�@�����̐����݂̂�p����ؖ��ł���A�������������C�����Љ�����Ǝv���B
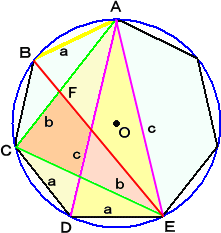 |
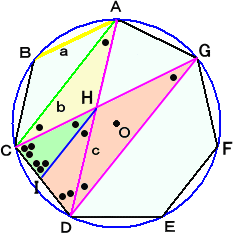
�i�j�@���}�ɂ����āA �����a�d�Ɛ����`�b�̌�_�� �e �@�@ �Ƃ����B �@�@�@���̂Ƃ��A�����d�e�́A�ڂ`�d�b�̂Q�������Ȃ̂ŁA �@�@�@�@�@�@�@�@�b�e �F �e�` �� �� �F �� �@�@����āA �@�@�@�@�@�@�@�@�b�e�����~�i��/�i���{���j�j����2/�i���{���j �@�@�܂��A���`�c�d �� ���d�b�e�@�Ȃ̂ŁA �@�@�@�@�@�@�@�@�`�c �F �c�d �� �d�b �F �b�e�@���A �@�@�@�@�� �F �� �� �� �F ��2/�i���{���j �� �i���{���j �F �� �@�@ �@�@����āA�@���� �� ��(���{��)�@���A�P/�����P/���{�P/�� �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�؏I�j |
�i�R�����g�j�@�ƂĂ��Ȗ��ȏؖ��Ŋ������܂����B�p�̂Q�����̐������I���Ɏg���Ă��Ė�
�@�@�@�@�@�@�����ł��ˁI�s�D�r ����Ɋ��ӂ������܂��B
�i�NjL�j�@�����P�X�N�U���R���t��
�@��ʌ��ݏZ�̑�w�� �g�D�r�D����u�����I�ȏؖ����v�������v�|�̃��[�������B
�@�ꕔ���������C�����Љ�����Ǝv���B�g�D�r�D����Ɋ��ӂ��܂��B
 |
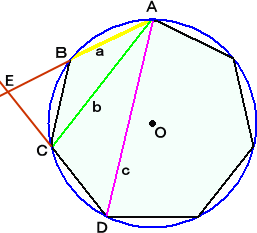
�i�j�@���}�ɂ����āA �����b�f�Ɛ����`�c�̌�_�� �g �@�@ �Ƃ��A�`�b//�f�c//�g�h�@�ƂȂ�_ �h ���Ƃ�B �@�@�@���̂Ƃ��A���b�c�g�A���g�b�h�@�͂Q���ӎO�p�`�Ȃ� �@�@�ŁA�g�h���g�b���b�c�����@�����藧�B �@�@�@�܂��A���g�`�b �� ���g�c�f�@��� �@�@�@�@�@�@�@�@�b�g �F �g�f �� �� �F �� �@�@����āA���b�g�h �� ���b�f�c�@�Ȃ̂ŁA �@�@�@�@ �@�@�@ �b�g �F �b�f �� �g�h �F �f�c �@�@���Ȃ킿�A �@�@�@�@�@�@�@�@�� �F ���{�� �� �� �F �� �@�@����āA�@���� �� ��(���{��)�@���A�P/�����P/���{�P/�� �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�؏I�j |
�i�R�����g�j�@���s���̍��p�⓯�ʊp�A�Q���ӎO�p�`�̐����A�����O�p�`�̐����ƁA�\����
�@�@�@�@�@�@���I�ȏؖ��ł��ˁI�����̊Ȗ��ȏؖ��Ɩ`���̏ؖ�����ׂ�ƁA������ƐԖ�
�@�@�@�@�@�@���Ă��܂��܂��ˁI
�i�NjL�j�@�����Q�Q�N�V���P�S���t��
�@�L���H�Ƒ�w�@��쌤�������A��L�̉���̏ؖ��Ƃ��قȂ�ʏ����邱�Ƃ����[����
�����������������B
�@�`�����@�����@�o�������������@�r������������
�@���̂g�o�ł́A�g�m�u�����������X�Q�v����ɂ�鎟�̂悤�ȏؖ��i�g�Q�Q�D�V�D�P�S�j���Љ��Ă���B
 |
�i�j�@���}�̂悤�ɁA�ӂ`�a�Ƃb�c�̉�����̌�_ �@�@�@���d�ƒu���ƁA�ڂ`�d�b���ڂ`�b�d���R��/�V�@�ŁA �@�@�@���`�d�b�́A�`�d���`�b�̂Q���ӎO�p�`�ł���B �@�@�@����āA�@��/�����`�a/�`�c���a�b/�`�c �@�@�@�܂��A�a�b�Ƃ`�c�͕��s�Ȃ̂ŁA �@�@�@�@�a�b/�`�c���a�d/�`�d���i���|���j/�� �@�@���������āA��/�����i���|���j/�����P�|��/���@���A �@�@�@�@�P/�����P/���{�P/���@�@�@�@�i�؏I�j |
�i�R�����g�j�@�ӊO�ȂƂ���ɂQ���ӎO�p�`�ł����ˁI�������ؖ��ł��B
�i�NjL�j�@�����Q�T�N�V���P�Q���t��
�@�s���̍��Q�̕�����A�����Q�T�N�V���P�O���t���ŁA�������ؖ����v�����ꂽ�Ƃ̃��[��
�����B�ꕔ���������C�������Ă��������܂����B���������������B
�i�ؖ��j�@���_���S�A���a�P�̏㔼�~����ɁA
�@�_�`���i�������i����/�V�j�C�������i����/�V�j�j�@�@�i�����O�A�P�A�Q�A�E�E�E�A�U�j
���Ƃ�B�����n�`�� �i�����Q�A�R�A�S�A�T�A�U�j�ƒ��������P�Ƃ̌�_�����ꂼ��@�o�A�p�A�q�A�r�A�s ��
��߂�B
�@���̂Ƃ��A�@�ڂs�n�p���ڂs�p�n���R��/�V�@���A�@�s�n���s�p�@�E�E�E�E�E�@�i�P�j
�@�܂��A�@�ڂn�q�p���ڂn�p�q���R��/�V�@���A�@�n�q���n�p�@�E�E�E�E�E�@�i�Q�j
�@���l�ɁA�@�ڂp�n�r���ڂp�r�n���Q��/�V�@���A�@�p�n���p�r�@�E�E�E�E�E�@�i�R�j
�@�ڂn�o�r���ڂn�r�o���Q��/�V�@���A�@�n�o���n�r�@�E�E�E�E�E�@�i�S�j
�@�ڂr�n�s���ڂr�s�n����/�V�@���A�@�r�n���r�s�@�E�E�E�E�E�@�i�T�j
�@�i�Q�j�i�R�j���A�@�n�q���p�r�@�ŁA�i�S�j�i�T�j���A�@�n�o���r�s
�@����āA�@�n�s���p�s���p�r�{�r�s���n�o�{�n�q�@�ƂȂ�B
�@�����ŁA�@�n�s�E�������i�U��/�V�j���n�o�E�������i�Q��/�V�j���n�q�E�������i�S��/�V�j���P
�@���V�p�`�̊O�ډ~�̔��a���q�Ƃ���ƁA�����藝���A
�@�����Q�q�������i��/�V�j���Q�q�������i�U��/�V�j
�@�����Q�q�������i�Q��/�V�j
�@�����Q�������i�R��/�V�j���Q�q�������i�S��/�V�j
�@���������āA
�@�P/�����P/�i�Q�q�������i�U��/�V�j�j���n�s/�Q�q
�@�P/���{�P/�����P/�i�Q�q�������i�Q��/�V�j�j�{�P/�i�Q�q�������i�S��/�V�j�j���n�o/�Q�q�{�n�q/�Q�q
�@�n�s���n�o�{�n�q�@���A�@�n�s/�Q�q���n�o/�Q�q�{�n�q/�Q�q
����āA�@�P/�����P/���{�P/���@�����藧�B�@�@�i�؏I�j
�i�R�����g�j�@�m���ɔ������ؖ��ł��ˁI�n�s���n�o�{�n�q�@�Ƃ����W�ɋ����܂����B�ؖ���
�@�@�@�@�@�@�e���������Ɋ��ӂ��܂��B
�i�NjL�j�@��t�������Z�R�N�̂j�D�x�D���烁�[�������B�i�����Q�T�N�P�O���P�U���t���j
�@�ȑO�A�������Z�̐搶�Ɛ��k���A�w���V�p�`�̂��鐫���x�Ƃ������ƂŔ��\���Ă����̂���
�܂����B���̒���ɏؖ���������ł����A�Z���������Ȃ����Ă��܂��܂����B������Еt���Ă�
��Q�N���炢�O�ɉ������ؖ������@���ꂽ�̂ŁA���̂����ɓ��e�������Ǝv���܂��B
�@�T�C�g�ł݂��ӎO�p�`�ł̏ؖ������ɏ����Ă��������ƂɎ����ł������ł��i�j�B
���ɂ��Ă͊m�����Z�̂Ƃ��Ɏg�������W�ɏ����Ă������̂ŁA�g������
�����Ǝv���܂����B
�@
�@��7�p�`�ɂ�����̏ؖ�
�@
�y���z�@���}�ɂ����āA�P/�����P/���{�P/���@�ł��邱�Ƃ��ؖ�����B
�@�@�@�@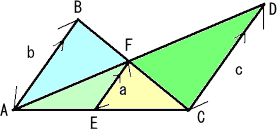
�i���̏ؖ��j�@��AEF�䁢ACD�@���A
�@AE �F AC = EF �F CD = a �F �� �@�́@ a�~AC=���~AE
���l�ɁA�@��CEF�䁢CAB�@���A
�@CE �F CA = EF �F AB = a �F �� �@�́@ a�~CA=���~CE
�ȏォ��A�@���~AE=���~CE�@ �� �@b �F c = AE �F CE
����āA�ĂсA��AEF�A��ACD�@�ɂ����āA
�@AE �F AC = EF �F CD �@�́@ b �F b+c = a �F c
�́@ ab+ac=bc �@�́@ 1/b+1/c=1/a �@�@�i�؏I�j
�i�ؖ��j�@���܁A��7�p�`�ɂ��āA���}�̂悤�ɕ⏕���������B
�@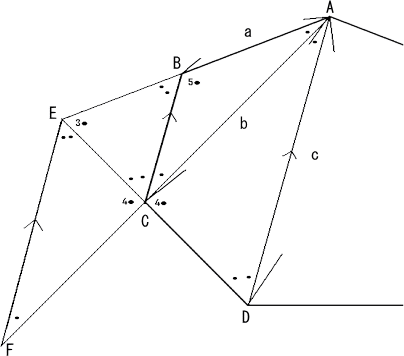
�@����ƁAAD // BC // EF�ł��邩��A���߂鎮��ɂ́AEF=b �ł����
�悢�B�����ŁA�O�p�`�̑����ɒ��ڂ��āA��ABC�䁢AEF�ł��邱�Ƃ���A
�@AB �F AE = BC�F: EF
�@�܂��A��ACE�͓ӎO�p�`�ł��邱�Ƃ��l�����A
�@AB �F AE = BC �F EF �� a �F b = a �F EF �@���A�@EF=b
�@���������āA��肩��A�@1/b+1/c=1/a�@�����藧�B�@�@�i�؏I�j
�i�R�����g�j�@�j�D�x�D����A�ؖ������肪�Ƃ��������܂��B
�i�NjL�j�@���Z�R�N�̂g�m�u���������v���烁�[���ŕʏ����B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�V�N�P�Q���P�X���t���j
| �i�ؖ��j�@�����P�@�Ƃ��Ă���ʐ�������Ȃ��B | |
 |
�@�@��/�V���ƂƂ��āA���A���́A �@�@�����Q�������Ɓ@�A�����������Q�Ɓ{���������Ɓ��S������2�Ɓ|�P �@���̂Ƃ��A�@�P�|�i�P/���{�P/���j �@�@���i�W������3�Ɓ|�S������2�Ɓ|�S�������Ɓ{�P�j/�i�����j �@�ƂȂ�B |
�@�����ŁA�@�V�Ɓ����A�@�R�Ɓ��|�S�Ɓ@����A�@�������R�Ɓ��������S��
�@�R�{�p�̌������A
�������R�Ɓ��R�������Ɓ|�S������3�Ɓ��R�������Ɓ|�S�������Ɓi�P�|������2�Ɓj���������Ɓi�S������2�Ɓ|�P�j
�܂��A�Q�{�p�̌������A
�������S�Ɓ��Q�������Q�Ƃ������Q�Ɓ��S�������Ƃ������Ɓi�Q������2�Ɓ|�P�j���S�������Ɓi�Q������3�Ɓ|�������Ɓj
�@����āA�@�������Ɓi�S������2�Ɓ|�P�j���S�������Ɓi�Q������3�Ɓ|�������Ɓj
�������Ɓ��O�@�Ȃ̂ŁA�@�S������2�Ɓ|�P���W������3�Ɓ|�S��������
�@���Ȃ킿�A�@�W������3�Ɓ|�S������2�Ɓ|�S�������Ɓ{�P���O�@�����藧�B
�@�ȏォ��A�@�P�|�i�P/���{�P/���j���O�@���Ȃ킿�A�@�P/�����P/���{�P/���@�����藧�B�@�i�؏I�j
�@������������̃R�����g�ł��B�i�����Q�V�N�P�Q���P�X���t���j
�@���̂悤�ɁA�ؖ��̓r���ɁA�u�������i��/�V�j�|�������i�Q��/�V�j�{�������i�R��/�V�j���P/�Q�v �̗L��
�Ȗ��Ƃ�����ł���Ȃ��Ɗ����܂����I
�Ɓ��R��/�V�@�̂Ƃ��A�@�������R�Ɓ��������i�X��/�V�j���|�������i�Q��/�V�j
�@�������S�Ɓ��������i�P�Q��/�V�j���|�������i�Q��/�V�j�@���A�@�������R�Ɓ��������S��
�Ɓ��T��/�V�@�̂Ƃ��A�@�������R�Ɓ��������i�P�T��/�V�j���������i��/�V�j
�@�������S�Ɓ��������i�Q�O��/�V�j���������i�Q��/�V�j�@���A�@�������R�Ɓ��������S��
����āA�������R�Ɓ��������S�Ɓ@���Ȃ킿�A�W������3�Ɓ|�S������2�Ɓ|�S�������Ɓ{�P���O�@�́A
�@�Ɓ���/�V�@�A�R��/�V�@�A�T��/�V
�Ő��藧�B�����ŁA�������i��/�V�j�A�������i�R��/�V�j�A�������i�T��/�V�j�͑��قȂ�����ŁA�R��������
�@�W��3�|�S��2�|�S���{�P���O
�̂R�������ƂȂ�B���̂Ƃ��A���ƌW���̊W���A
�@�������i��/�V�j�{�������i�R��/�V�j�{�������i�T��/�V�j���P/�Q
���Ȃ킿�A�@�������i��/�V�j�|�������i�Q��/�V�j�{�������i�R��/�V�j���P/�Q
�i�R�����g�j�@��@�I�ɂ́A�y�[�W�`���̎O�p���𗘗p������̂Ɠ����ł����A�L������
�@�������i��/�V�j�{�������i�R��/�V�j�{�������i�T��/�V�j���P/�Q
�����ގ��ό`�Ɋ������܂����B������������Ɋ��ӂ��܂��B
�@�f�`�h ����̃R�����g�ł��B�i�����R�P�N�R���P�R���t���j
�@��L�̃R�����g�����āA�L���Ƃ͒m�炸�C�ɂȂ�����ŐF�X���ׂ���A
cos(��/5) - cos(2��/5)=1/2
cos(��/7 )- cos(2��/7) + cos(3��/7)=1/2
cos(��/9) - cos(2��/9) + cos(3��/9) - cos(4��/9)=1/2
cos(��/11) - cos(2��/11) + cos(3��/11) - cos(4��/11) + cos(5��/11)=1/2
���������������������������
�ƁA��ʂɁA�@F(n)=��[i=1,n](-1)^(n+1)*cos(i*��/(2*n+1))�@�ɑ��A
�@�@F(n)==1/2 (for��n��N)
�������o�����ł��ˁB
�@���̕����̌�オ�C�ɂȂ����̂ŁA���ׂăv���X�̕����ɂ������ׂ̂���A
cos(��/5) + cos(2��/5)=1/2*(1/sin(��/10)-1)
cos(��/7) + cos(2��/7) + cos(3��/7)=1/2*(1/sin(��/14)-1)
cos(��/9) + cos(2��/9) + cos(3��/9) + cos(4��/9)=1/2*(1/sin(��/18)-1)
cos(��/11) + cos(2��/11) + cos(3��/11) + cos(4��/11) + cos(5��/11)=1/2*(1/sin(��/22)-1)
���������������������������
�@��ʂɁA�@G(n)=��[i=1,n]cos(i*��/(2*n+1))�@�ɑ��A
�@G(n)==1/2*(1/sin(4*n+2)-1) (for��n��N)
�ł���悤�ł��B
�i�R�����g�j�@cos(��/5) - cos(2��/5)=1/2 ���C�ɂȂ����̂Ō����Ă݂��B
�@cos(��/5) -cos(2��/5)
= cos(��/5) +cos(3��/5)
= 2cos(2��/5) cos(��/5)
= 2cos(��/5) sin(��/5) cos(2��/5) / sin(��/5)
= sin(2��/5) cos(2��/5) / sin(��/5)
= sin(4��/5) / 2sin(��/5)
= sin(��/5) / 2sin(��/5)
= 1/2
�@�Y��ɖł��܂����I
�i�R�����g�j�@cos(��/5) + cos(2��/5)=(1/sin(��/10)-1)/2 ���C�ɂȂ����̂Ō����Ă݂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����R�P�N�R���P�U���t���j
cos(��/5) + cos(2��/5)
=2cos(3��/10)cos(��/10)
=2cos(3��/10) sin(��/10) cos(��/10)/ sin(��/10)
=cos(3��/10) sin(��/5) / sin(��/10)
=(sin(��/2)-sin(��/10) / (2sin(��/10))
=(1/sin(��/10)-1)/2
�ƌv�Z���Ă݂͂����̂́Acos(��/5) + cos(2��/5)=��5/2�@�̕������������ȁH
�@���ۂɁA��=��/5�@�Ƃ����ƁA�@2��=��-3�Ɓ@�Ȃ̂ŁAcos2��=�|cos3��=-4cos3��+3cos��
�@2cos2��-1=�|cos3��=-4cos3��+3cos�Ɓ@����A 4cos3��+2cos2��-3cos��-1=0
�@�icos��+1�j�i4cos2��-2cos��-1�j=0
�@cos��+1��0�@�Ȃ̂ŁA�@4cos2��-2cos��-1=0
�@cos�Ɓ�0�@���A�@cos��=�i1+��5)/4�@�@���̂Ƃ��A�@cos2��=�i-1+��5)/4
�@�ȏォ��A�@cos(��/5) + cos(2��/5)=�i1+��5)/4+�i-1+��5)/4=��5/2
�@�f�`�h ����̃R�����g�ł��B�i�����R�P�N�R���Q�Q���t���j
�@���_��ς��āAsin(Pi/3)=��3/2�@�Acos(Pi/3)=1/2�@�͉��瓖�R�̔@���~�߂Ă��邪�A
sin(Pi/5)*sin(2*Pi/5)=��5/4�@�Acos(Pi/5)*cos(2*Pi/5)=1/4
sin(Pi/7)*sin(2*Pi/7)*sin(3*Pi/7)=��7/8�@�Acos(Pi/7)*cos(2*Pi/7)*cos(3*Pi/7)=1/8
sin(Pi/9)*sin(2*Pi/9)*sin(3*Pi/9)*sin(4*Pi/9=3/16
cos(Pi/9)*cos(2*Pi/9)*cos(3*Pi/9)*cos(4*Pi/11=1/16
sin(Pi/11)*sin(2*Pi/11)*sin(3*Pi/11)*sin(4*Pi/11)*sin(5*Pi/11)=��11/32
cos(Pi/11)*cos(2*Pi/11)*cos(3*Pi/11)*cos(4*Pi/11)*cos(5*Pi/11)=1/32
������������������������������
������������������������������
��ʂɁA
��[k=1,m]sin(k*Pi/(2*m+1))=��(2*m+1)/2^m�@�A��[k=1,m]cos(k*Pi/(2*m+1))=1/2^m
�̓�������������������Ǝv���ƍl���[�����̂�����B
�i�R�����g�j�@������(��/5)������(2��/5)=��5/4�@�Acos(��/5)cos(2��/5)=1/4�@���C�ɂȂ����̂Ō�
�@�@�@�@�@�@���Ă݂��B�i�����R�P�N�R���Q�R���t���j
�@��L�̌v�Z����A�@cos(��/5)=�i1+��5)/4�@�Acos(2��/5)=�i-1+��5)/4�@���Ȃ킿�A
�@������(��/5)=��i10-2��5)/4�@�A������(2��/5)=��i10+2��5)/4
�Ȃ̂ŁA������(��/5)������(2��/5)=��i10-2��5)��i10+2��5)/16=��5/4
�@cos(��/5)cos(2��/5)=�i1+��5)�i-1+��5)/16=1/4
�i�NjL�j�@�����R�P�N�R���Q�W���t��
����@���̘a�����߂�B�i���}�k�W�����j
�@3�ゃ����(2��/7)�{3�ゃ����(4��/7)�{3�ゃ����(8��/7)
�i���j�@3�ゃ����(2��/7)�����A3�ゃ����(4��/7)�����A3�ゃ����(8��/7)�����@�Ƃ����ƁA
�@��3��������(2��/7)�@�A��3��������(4��/7)�@�A��3��������(8��/7)
���̂Ƃ��A�@�Ɓ�2��/7�@�Ƃ����ƁA�@�V�Ɓ��Q�@���A�@�R�Ɓ��Q�|�S��
�@����āA�@�������R�Ɓ��������S�Ɓ@���A
�@�S������3�Ɓ|�R�������Ɓ��Q������2�Q�Ɓ|�P���Q�i�Q������2�Ɓ|�P�j2�|�P���W������4�Ɓ|�W������2�Ɓ{�P
����āA�@�W������4�Ɓ|�S������3�Ɓ|�W������2�Ɓ{�R�������Ɓ{�P���O
�@�i�������Ɓ|�P�j�i�W������3�Ɓ{�S������2�Ɓ|�S�������Ɓ|�P�j���O
�@���炩�ɁA�������Ɓ��P�@�Ȃ̂ŁA�@�W������3�Ɓ{�S������2�Ɓ|�S�������Ɓ|�P���O
�@�Ɓ�4��/7�@�A�Ɓ�8��/7�@�Ƃ����Ă����l�̎���������̂ŁA
�@������(2��/7)�@�A������(4��/7)�@�A������(8��/7)�@�́A�R���������@�W��3�{�S��2�|�S���|�P���O�@��
���قȂ�R�̉��ƂȂ�B���ƌW���̊W����A
�@��3�{��3�{��3���|�P/�Q
�@��3��3�{��3��3�{��3��3���|�P/�Q
�@��3��3��3���P/�W�@���A�@���������P/�Q
�@�����ŁA�@���{���{�������@�A�����{�����{���������@�Ƃ����ƁA
��3��3�{��3��3�{��3��3�|�R��2��2��2
���i�����{�����{�����j�i��2��2�{��2��2�{��2��2�|����2���|����2���|����2���j
���i�����{�����{�����j�i��2��2�{��2��2�{��2��2�|������(���{���{��)�j
�����i��2��2�{��2��2�{��2��2�|�i�P/�Q�j���j
�����ŁA
�@��2��2�{��2��2�{��2��2���i�����{�����{�����j2�|�Q������(���{���{��)����2�|��
�Ȃ̂ŁA
��3��3�{��3��3�{��3��3�|�R��2��2��2�����i��2�|���|�i�P/�Q�j���j����3�|�i�R/�Q�j����
���Ȃ킿�A�@�|�P/�Q�|�R/�S����3�|�i�R/�Q�j�����@���A�@��3�|�i�R/�Q�j�������|�T/�S
�@�܂��A
�@��3�{��3�{��3�|�R������
��(���{���{��)�i��2�{��2�{��2�|�i�����{�����{�����j�j
��(���{���{��)�i(���{���{��)2�|�R�i�����{�����{�����j�j����3�|�R����
���Ȃ킿�A�@�|�P/�Q�|�R/�Q ����3�|�R�����@���A�@��3�|�R�������|�Q
�@��3�|�i�R/�Q�j�������|�T/�S�@���A�@��3��3�|�i�R/�Q�j�����E��3���|�i�T/�S�j��3
�@�������i�P/�R�j�i��3�{�Q�j�@�������āA
�@�i�P/�R�j3�i��3�{�Q�j3�|�i�P/�Q�j�i��3�{�Q�j�E��3���|�i�T/�S�j��3
�@�i�P/�Q�V�j�i��9�{�U��6�{�P�Q��3�{�W�j�|�i�P/�Q�j��6�|��3���|�i�T/�S�j��3
�@�i�P/�Q�V�j��9�|�i�T/�P�W�j��6�{�i�Q�T/�R�U�j��3�{�W/�Q�V���O
���ӂ��Q�V�{���āA�@��9�|�i�P�T/�Q�j��6�{�i�V�T/�S�j��3�{�W���O
�@�i��3�|�T/�Q�j3�{�P�Q�T/�W�{�W���O
�@�i��3�|�T/�Q�j3���|�P�W�X/�W�@���A�@��3�|�T/�Q���|�i�R/�Q�j3��V
����āA�@��3���T/�Q�|�i�R/�Q�j3��V�@���A�@����3��i�T/�Q�|�i�R/�Q�j3��V�j
�i�R�����g�j�@��L�̌v�Z����A
�@������(2��/7)�{������(4��/7)�{������(8��/7)
���|������(��/7)�{������(2��/7)�|������(3��/7)���|�P/�Q�@�Ȃ̂ŁA
�@�f�`�h ����̎��@������(��/7)�|������(2��/7)�{������(3��/7)���P/�Q�@���������B
�i�NjL�j�@�g�m�u�܂����`�v����̏��ł��B�i�����Q�W�N�P�Q���Q�O���t���j
�@���R�������u�����₩�Ȑ��w�̌��@�����p�`���a����ȉ~�K�E�X�a���v�ɂ��Ɛ��Q�R
�p�`�ł����l�̂��Ƃ����藧�悤�ŁA����������̓K�E�X�a�ƂȂɂ��W������悤��
���B���̋L���� ���Ă��������������C�������ł����A���ɍ���͖̂l���g����
�����B�����A���������������Ǝv�����̂ŁA�Ƃ肠�������̈ꌏ�����ł��B���� ������
���Ă�K���ł��B
�@�f�`�h ����̃R�����g�ł��B�i�����R�P�N�R���P�U���t���j
�@���R�P�p�`�ł����l�̒��a������悤�ł��B
�@���R�P�p�`�ł́A���Ɉ����Ίp��(�ӂ̒������܂�15��ނł���B�j��Z��������
�@a1�Aa2�Aa3�A����Aa15�@(a1���ӂ̒����j
�Ƃ��Ă����ƁA
�@�@1/a2+1/a3+1/a4+1/a8+1/a10+1/a11+1/a13+1/a14+1/a15
�@=1/a1+1/a5+1/a6+1/a7+1/a9+1/a12
�̊W����������B
�@�f�`�h ����̃R�����g�ł��B�i�����R�P�N�R���P�V���t���j
�@�K�E�X�ŗL���Ȑ�17�p�`�ɂ����āA�ӂ��܂߂W��ނ̒��������Ίp����
�@�@�@a1��a2��a3��a4��a5��a6��a7��a8�@�@�i��a1���ӂ̒����j
�Ƃ���A�����̒����ɂ͂��܂�������Ƃ͌����Ȃ����A���̊W����������B
�@L(k)=2*R/��(4*R^2-ak^2)�@�ɑ��AL(2)+L(3)+L(4)+L(5)+L(7)+L(8)=L(1)+L(6)+4*��17
�ł���B�������AR�͐�17�p�`�̊O�ډ~�̔��a�Ƃ���B
�i�NjL�j�@�����Q�Q�N�X���P�U���t��
�@���g�o�����������b�ɂȂ��Ă���g�m�u�e�m�v������A���̘b��Ɋ֘A����V��������
�������B
�@���V�p�`�݂͌��ɑ���������A���A���A�� �̔�͌��܂�B���̂��߂ɂ́A
�@�P/�����P/���{�P/��
�Ƃ������P�ł͑���Ȃ��B�����ЂƂ̎��͂��낢�날�邾�낤���A��ԕ��ʂȂ̂́A
�@���{������2/���@�@�i�������A�������@�j
���낤�B������A�g���~�[�̒藝����e�Ղɏؖ��ł���B
�@���ۂɁA�l�p�` �`�a�b�c �́A�~�ɓ��ڂ���l�p�`�Ȃ̂ŁA
�@�`�b�E�a�c���`�a�E�b�c�{�a�b�E�`�c�@���Ȃ킿�A�@��2����2�{����
���������āA�@���{������2/���@�����藧�B�i�I�j
�@���V�p�`�̕ӂƑΊp���̒��� ���A���A�� �i�����������j �͂��̂Q�̎��œ����Â�����B
�@���A���A�� �̊Ԃɂ͂��낢��ȊW�����邾�낤���A�S�Ă��̂Q�����瓱�����͂��ł���B
�i��j�@�Ⴆ�A�@��2�������{��2�@�����藧�B
�@�����ŁA�@������/���@�A������/���@�Ƃ����ƁA��L�œ���ꂽ�W���́A
�@�@���������{���@�A�@��2�����{�P�@�A�@��2�������{�P
�Ƃ܂Ƃ߂���B�@������2�|�P�@���P���ɑ�����āA�� ���������R��������
�@��3�|��2�|�Q���{�P���O
��������B���l�ɂ��āA�� ���������R��������
�@��3�|�Q��2�|���{�P���O
��������B
�@�܂��A�� ���������L�����W���̕������ŁA��3�|��2�|�Q���{�P���O ���ŏ������ł��邱�Ƃ�
�ȒP�Ɏ������B
�@��3�|��2�|�Q���{�P�� ���|���@�i���͐����j�@�������Ɏ��Ɖ��肷��ƁA��3�|��2�|�Q���{�P���O
�@���̂Ƃ��A�@�P���|���i��2�|���|�Q�j�@���A
�@�@�����P�A��2�|���|�Q���|�P�@�܂��́A�@�����|�P�A��2�|���|�Q���P
�@�����̓��������������͑��݂��Ȃ��B
�@����āA�� ���������L�����W���̕������ŁA��3�|��2�|�Q���{�P���O ���ŏ������ł���B
���Ȃ킿�A�ڂa�`�b���ƂƂ����ƁA�����Q�������Ƃ̍ŏ����������A��3�|��2�|�Q���{�P���O �ƂȂ�B
�@���āA���K���ł���B
�@���V�p�`�̕ӂ̒����� �� �A�Ίp���̒����� ���A�� �i�����������j �Ƃ���Ƃ��A
�@�@�@�@��2/a2�{��2/��2�{��2/��2
�̒l�����߂�B
�@�Q������㐔�̖��Ƃ��ĉ����Ă��������A���V�p�`�̕ӂƑΊp���ł��邱�Ƃ���O�p��
���Ƃ����g���Ă����܂��܂���B
�@�e�m����̖������āA�����ʓ|�����Ǝv�����̂ŁA���l�v�Z�œ��������Z���Ă݂��B
�i���Z�j�@�`���̍�}���瓾��ꂽ���l�@�����X�O�@�A�����P�U�Q�@�A�����Q�O�R�@��������ƁA
�@��2/a2�{��2/��2�{��2/��2���T�D�O�O�U�V�W�S�S�E�E�E
�Ȃ̂ŁA���߂�l�́A�u�T�v���ȁH�i������āA�ד��ł���ˁD�D�D�B�j
�@�e�m����u�����I�v�ƌ����āA��L�̃A�o�E�g�Ȍv�Z�̋C�p������������A�����Ɛ^��
�ڂɌv�Z���悤�Ǝv���������B�i�����Q�Q�N�X���P�W���t���j
�i���j�@���V�p�`�̕ӂ̒����� �� �A�Ίp���̒����� ���A�� �i�����������j
�Ƃ���Ƃ��A
�@�@�@��L���A�@�P/�����P/���{�P/���@���Ȃ킿�A�@�����������{����
�@�@�@�@�@�@�@�@�@�@���{������2/���@���Ȃ킿�A�@��2����2�{����
�@�@�����藧�B
 |
�@���l�ɂ��āA�l�p�` �`�a�c�d �́A�~�ɓ��ڂ���l�p�` �Ȃ̂ŁA�@�`�c�E�a�d���`�a�E�c�d�{�a�c�E�`�d �@�@�@���Ȃ킿�A�@��2����2�{�����@�����藧�B �@�@�����̂R����p���āA �@�@�@�@�@��2/a2�{��2/��2�{��2/��2���T �@�����藧���Ƃ������B |
�@�܂��A�@��2����2�{�����@���A�@��2/a2���P�{��/��
�@����ɁA�@�P/�����P/���{�P/���@���A�@��/������/���{�P�@�Ȃ̂ŁA�@��2/a2���Q�{��/��
�@��2����2�{�����@���A�@��2/��2����2/��2�{��/��
�@��2����2�{�����@���A�@��2����2�|�����@�Ȃ̂ŁA�@��2/��2���P�|��/��
����āA
�@��2/a2�{��2/��2�{��2/��2
���Q�{��/���{��2/��2�{��/���{�P�|��/��
���R�{�Q��/���{��2/��2�|��/��
�@�����ŁA�@�P/�����P/���{�P/���@���A�@��/�����P�|��/���@�Ȃ̂ŁA
�@��2/a2�{��2/��2�{��2/��2
���R�{�Q��/���{�P�|�Q��/���{��2/��2�|��/��
���S�{�Q��/���|�Q��/���{��2/��2�|��/��
���S�{�Q��/���|�Q��/���{�P�|��/���|��/��
���T�{�Q�i��/���|��/���|��/���j
�@�����ŁA�@��2����2�{�����@�A��2����2�{�����@���A�@��2�|��2�������|�����@�Ȃ̂ŁA
�@��/���|��/���|��/�����i��2�|�����|��2�j/�������i�����|�����|�����j/�������O
�@���������āA�@��2/a2�{��2/��2�{��2/��2���T�@�����藧�B�@�i�I�j
�@���̖��ɁA���g�o�����������b�ɂȂ��Ă���g�m�u�炷����v��������킳�ꂽ�B
�i�����Q�Q�N�X���P�W���t���j
�i���j�@�P/�����P/���{�P/���@�E�E�E�@�i�P�j�@�A�@���{������2/���@�E�E�E�@�i�Q�j
�@�i�P�j����A�@��������/�i���|���j�@�@������A�i�Q�j�ɑ�����āA�@���{����/�i���|���j����2/��
���Ȃ킿�A�@���i���|���j�{��������2�i���|���j/���@���A�@�Q�����|a2����3/���|��2
�@���ӂ��A���� �Ŋ����āA�@�Q�|��/������2/a2�|��/��
�@����āA�@��2/a2����/���|��/���{�Q�@�E�E�E�@�i�R�j
�@���ӂ� ��/�� ���|���Đ�������ƁA�@��2/��2���Q��/���|��/���{�P�@�E�E�E�@�i�S�j
�@�i�P�j����A�@�P����/���{��/���@�Ȃ̂ŁA
�@��2/��2���i�P�|��/���j2���P�|�Q��/���{��2/��2���P�|�Q��/���{�Q��/���|��/���{�P���Q�|��/��
�@�i�Q�j����A�@��/���{��/������/���@�Ȃ̂ŁA
�@��2/��2���i��/���|��/���j2����2/a2�{��2/��2�|�Q
�@���i��/���|��/���{�Q�j�{�i�Q��/���|��/���{�P�j�|�Q���P�{��/��
���������āA�ȏォ��A
�@��2/a2�{��2/��2�{��2/��2���i��/���|��/���{�Q�j�{�i�P�{��/���j�{�i�Q�|��/���j���T
�ƂȂ�B�@�i�I�j
�i�R�����g�j�@�v�Z�̖{���I�ȃA�C�f�A�ŁA���Ƃ炷���邳��̉ł͋��ʂ��镔��������
�@�@�@�@�@�@�܂��ˁI�炷���邳��Ɋ��ӂ��܂��B
�i�NjL�j�@�����p�`�̂��鐫���Ƃ��āA��L�ł́A
�i�P�j�@�P/�����P/���{�P/��
�i�Q�j�@��2/��2�{��2/��2�{��2/��2���T
���ؖ��������A����ɁA���̂悤�Ȑ��������邱�Ƃg�o�����������b�ɂȂ��Ă���g�m
�u�r�i�g�j�v�����育�Љ���������B�i�����Q�W�N�X���P�Q���t���j
�i���@�Q�l�F�g�m�usintakenoko�v�����Web�T�C�g�u���w���ނ̕����v�́u�����p�`�̐����v�j
�i�R�j�@��/���|��/���{��/�����P
�i�S�j�@��2/��2�{��2/��2�{��2/��2���U
(�ؖ��j�i�R�j�@���{������2/���@����A�@��/���{��/������/��
�@����āA�@��/���|��/���{��/�����i��/���{��/���j�|��/���{��/��
�@�@�@�@�@����/���{��/�������i�P/���{�P/���j�����E�i�P/���j���P
�i�S�j�@�P/�����P/���{�P/���@���A�@��/�����P�|��/���@�A��/������/���|�P�@�A��/������/���{�P�@�Ȃ̂ŁA
��2/��2�{��2/��2�{��2/��2
���i�P�|��/���j2�{�i��/���|�P�j2�{�i��/���{�P�j2
����2/��2�{��2/��2�{��2/��2�{�Q�i�|��/���|��/���{��/���j�{�R���T�|�Q�{�R���U�@�@�i�؏I�j
�@�e�m����̖��Ɋ֘A���āA�U���@���֘A�����N���ꂽ�B
�i�����Q�Q�N�X���P�W���t���j
�֘A����@�@���̖₢�ɓ�����B
�i�P�j�@���a��1�̉~�ɓ��ڂ��鐳�V�p�`�̕ӂ̒����� �� �A�Ίp���̒����� ���A��
�i�����������j
�@�@�@�Ƃ���Ƃ��A�@��2�{��2�{��2���V�@�����藧���Ƃ������B
�i�Q�j�@�P�ʉ~�ɓ��ڂ��鐳���p�`�ɂ����āA�P�̒��_���瑼�̒��_������
���|�P �{�̐�
�@�@���i�ӂ܂��͑Ίp���j�̒����̐ς����߂�B
�@�@�@�i�����F�@n �@�i���@�F ���a�q�̉~�ɓ��ڂ���ꍇ�́A ���E�q��-1�j�j
�i�R�j�@�P�ʉ~�ɓ��ڂ��鐳���p�`�ɂ����āA�ӂ� �� �{�A�Ίp���́A���b2�|�������i���|�R�j/�Q
�@�@�{�ł���B���̂Ƃ��A���̖₢�ɓ�����B
�@�i�C�j�@�ӂ܂��͑Ίp���̂��ׂĂ̒����̕����a�����߂�B
�@�@�@�i�����F�@��2�@�i���@�F ���a�q�̉~�ɓ��ڂ���ꍇ�́A ��2�E�q2 �j�j
�@�i���j�@�ӂ܂��͑Ίp���̂��ׂĂ̑��قȂ钷���̕����a�����߂�B
�@�@�@�i�����F�@��� ���A������ ���{�Q�j
�@�@�@�@�@�@�@�i���@�F ���a�q�̉~�ɓ��ڂ���ꍇ�A��� ���q2�A������ �i���{�Q�j�q2 �j
�@�i�n�j�@�ӂ܂��͑Ίp���̂��ׂĂ̒����̘a�����߂�B
�@�@�@�i�����F�@�P�ӂ̒��������A�ŒZ�̑Ίp���̒��������Ƃ���ƁA��2�E��/(�Q���|��)
�@�e�m����i�Q�j�̉��܂����B�i�����Q�Q�N�X���P�W���t���j
�@��肪�T������܂��ˁB(�Q)�͂ł����Ǝv���܂��B
�i���j�@���f���ʂōl���āA�������P�@�̉����A�`(�P)�A�`(�Q)�A�E�E�E�A�`(���|�P)�A�`(��)���P�@�Ƃ���B
�@�����|�P��(���|�`(�P))(���|�`(�Q))�E�E�E(���|�`(���|�P))(���|�P)�@���A
�@�i�����|�P�j/�i���|�P�j��(���|�`(�P))(���|�`(�Q))�E�E�E(���|�`(���|�P))�@�Ȃ̂ŁA
�@����-1�{�E�E�E�{���{�P��(���|�`(�P))(���|�`(�Q))�E�E�E(���|�`(���|�P))
�@�����ŁA�@�����P�@�������Đ�Βl�����A
�@�b�P�|�`(�P)�b�b�P�|�`(�Q)�b�E�E�E�b�P�|�`(���|�P)�b�����@�i�I�j
�i���@�Q�l�F�u�~���̓����_�̐����v�j
�@�e�m����̃R�����g�ł��B�i�����Q�Q�N�X���P�X���t���j
�@�炷���邳��̉ŁA
�@�@��2/a2����/���|��/���{�Q�@�A��2/��2���Q�|��/���@�A��2/��2���P�{��/��
�ƁA�R�̕������A��/���Ƃ�/���̂P�����ŏ����Ă��ꂢ�ɏ�����Ƃ́D�D�D�B
�@�e�m����́A�u ��/���A�|��/���A��/�� �������R�������������v���Ƃ��玦���ꂽ�����ł���B
�@��@�̎w�j�������ꂽ�A�e�m����̉ɂ�����������̂ŁA�ސ����čl���Ă݂��B
�i���j�@�P/�����P/���{�P/���@�E�E�E�@�i�P�j�@�A�@���{������2/���@�E�E�E�@�i�Q�j
�@�@�@�i�P�j����A�@��������/�i���|���j�@�@������A�i�Q�j�ɑ�����āA�@���{����/�i���|���j����2/��
�@�@���Ȃ킿�A�@���i���|���j�{��������2�i���|���j/���@���A�@�Q�����|a2����3/���|��2
�@�@���ӂ��A���� �Ŋ����āA�@�Q�|��/������2/a2�|��/��
�@�@�@����āA�@��2/a2����/���|��/���{�Q�@�E�E�E�@�i�R�j
�@�@�����ŁA�@��/�������@�Ƃ����ƁA�@��2�����|�P/���{�Q�@���A�@��3�|��2�|�Q���{�P���O
�@�@�@����āA�@��/�������@�́A�R���������@��3�|��2�|�Q���{�P���O�@�̉��ł���B
�@�@�����O�@�Ȃ̂ŁA���ӂ� ��3 �Ŋ����āA�@�i�P/���j3�|�Q�i�P/���j2�|�i�P/���j�{�P���O
�@�@�܂��A�@�i�P�j���A�@��/�����P�|��/���@�Ȃ̂ŁA�@��/�������@�Ƃ����ƁA�@�P/�����P�|��
�@�@����������āA�@�i�P�|���j3�|�Q�i�P�|���j2�|�i�P�|���j�{�P���O�@���A
�@�@��3�|��2�|�Q���{�P���O
�@�����藧�B
�@���̂��Ƃ���A��/�������@�́A�R���������@��3�|��2�|�Q���{�P���O�@�̉��ł���B
�@�R���������̉��ƌW���̊W����A�c��̉��� �� �Ƃ���ƁA
�@��/���{��/���{�����P�@���A�@�����|��/���|��/���{�P
�Ƃ���ŁA�@�P�|��/������/���@�A��/������/���|��/���@�Ȃ̂ŁA
�@�����|��/���{��/�����|��/���{��/���|��/�����|��/��
�ȏォ��A������/���@�A������/���@�A�����|��/���@�́A�R���������@��3�|��2�|�Q���{�P���O
�̉��Ȃ̂ŁA���ƌW���̊W����A
�@���{���{�����P�@�A�@�����{�����{�������|�Q�@�A���������|�P
����āA���̂Ƃ��A
��2/a2�{��2/��2�{��2/��2����2�{��2�{��2
���i���{���{���j2�|�Q�i�����{�����{�����j���T�@�i�I�j
�i�R�����g�j�@�������ꂽ�A�G���K���g�ȉł��ˁI�������܂����B�e�m����Ɋ��ӂ��܂��B
�@�@�@�@�@�@��w�������ɂ��g�������ȃ��x���ł��ˁB
�@�����ŁA���g�o�́u���̏����v�œ���ꂽ���ʂ�p����ƁA
�@�R���������@��3�|��2�|�Q���{�P���O�@�ɑ��鏄��� �f�i���j�́A�f�i���j���Q�|��2�@�ŗ^����
���B
�@���������āA�@�f�i���j���Q�|��2���Q�|�i���|�P/���{�Q�j���P/���|�������@���A
�@�f�i���j�����@�A�@�f�i���j����
�����藧�B
�@�f�i���j�����@���A�@�Q�|��2�����@���Ȃ킿�A�@��2/��2���Q�|��/��
�ŁA�炷���邳��̑�Q�̎���������B
�܂��A�f�i���j�����@���A�Q�|��2�����@���Ȃ킿�A��2/��2���Q�|��/�����P�{�P�|��/�����P�{��/��
�ŁA�炷���邳��̑�R�̎���������B
�i�R�����g�j�@����ȂƂ���Łu���̏���v�̗��_������Ƃ͋����ł��I
�i�NjL�j�@�����R�O�N�W���V���t��
�@��L����A�R���������@��3�|��2�|�Q���{�P���O�@�̂R�̉��́A��/���A�|��/���A��/�� �ł���B
�@�����ŁA�~ �n �̔��a�P �A�Ɓ���/�V�Ƃ��āA�����Q�������ƁA�����Q�������Q�ƁA�����Q�������R�ƂȂ̂ŁA
�@������/�����Q�������Q��/�i�Q�������Ɓj���Q�������Ɓ��Q�������i��/�V�j
�@��/�����Q�������R��/�i�Q�������Ɓj���R�|�S������2�Ɓ��R�|�Q�i�P�|�������Q�Ɓj���Q�������Q�Ɓ{�P
�@����āA�@�����|��/�����P�|��/�����|�Q�������Q�Ɓ��|�Q�������i�Q��/�V�j���Q�������i�T��/�V�j
�@������/�����f�i���j���Q�|�S������2�i�Q��/�V�j
�@�@���Q�|�Q�i�P�{�������i�S��/�V�j�j���|�Q�������i�S��/�V�j���|�Q�������i�|�R��/�V�j���Q�������i�R��/�V�j
�@�ȏォ��A�R���������@��3�|��2�|�Q���{�P���O�@�̂R�̉��́A
�@�@�����Q�������i��/�V�j�@�A�����Q�������i�R��/�V�j�@�A�����Q�������i�T��/�V�j
�ŁA�����́A����� �f�i���j���Q�|��2�@�ɂ�菄��B
�@�����f�i���j���Q�|�S������2�i�R��/�V�j
�@���Q�|�Q�i�P�{�������i�U��/�V�j�j���|�Q�������i�U��/�V�j���|�Q�������i�|��/�V�j���Q�������i��/�V�j
�@�����f�i���j���Q�|�S������2�i��/�V�j
�@�@���Q�|�Q�i�P�{�������i�Q��/�V�j�j���|�Q�������i�Q��/�V�j���Q�������i�T��/�V�j
�@
�@�e�m�������U���@����̒�N���ꂽ���ɂ��čl�@���ꂽ�B�i�����Q�Q�N�X���P�X���t���j
�@�i�R�j�@�P�ʉ~�ɓ��ڂ��鐳���p�`�ɂ����āA���̖₢�ɓ�����B
�@�@�i�C�j�@�ӂ܂��͑Ίp���̂��ׂĂ̒����̕����a�����߂�B�i�����F�@��2 �j
�@�@�i���j�@�ӂ܂��͑Ίp���̂��ׂĂ̑��قȂ钷���̕����a�����߂�B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����F�@��͂��A������ ���{�Q�j
�@�@�i�n�j�@�ӂ܂��͑Ίp���̂��ׂĂ̒����̘a�����߂�B
�@�@�@�@�i�����F�@�P�ӂ̒��������A�ŒZ�̑Ίp���̒��������Ƃ���ƁA��2�E��/(�Q���|��)
�@���@�Ƃ��ẮA�Ƃ肠�����A�R�ʂ肮�炢�l������B
�@�@(��)�@���f���ʂōl����@�@(��)�@�O�p���ōl����@�@(��)�@�g���~�[�̒藝�ōl����
���ʂ́A(��)���Ǝv���܂����A(��)�ł��ł������ȋC�����܂��B(��)�͖����ł��傤���A����ł�
����Ζʔ����ł��B�C���[�W�́A(�C)�́A(��)�A(��)�́A(��)�̊����ł��B
�@(�C)��(��)�̊W�����Ă����܂��B(�C)�̉����r�A(��)�̉����s�Ƃ���B�\�����ȒP�ɂ��邽
�߁A�ӂ��Ίp���̂ЂƂƂ݂Ȃ��܂��B
�@�P�̒��_����������Ίp���̕����̘a�́A
�@�@�@�� ����̂Ƃ��́A���������̂��Q�{�����邩��A�Q�s
�@�@�@�� �������̂Ƃ��́A���a(�����Q)�ȊO�͂Q�{�����邩��A�Q(�s�|�S)�{�S���Q�s�|�S
�@�e�_����������Ίp���̕����̘a�͂����� �� �{�������̂����A�P�{�̑Ίp���ɂ��āA
�Q�����Ă��邩��A�Q�Ŋ�������B
�@�]���āA
�@�@�� ����̂Ƃ��A�r�����E�Q�s/�Q�����s
�@�@�� �������̂Ƃ��A�r�����E�i�Q�s�|�S�j/�Q�����i�s�|�Q�j
�����A
�@�@�� ����̂Ƃ��A�s���r/��
�@�@�� �������̂Ƃ��A�s���r/���{�Q
������A(�C)��������A(��)�������邵�t�������B
�@��L�̂e�m����̉�@�̎w�j���āA�i�R�j�́i�C�j���������Ƃɂ���B���̘b��́A���Ƃ�
�Ƃ́A�u�~���̓����_�̐����v�Ɍf�ڂ��悤�Ǝv���Ă������̂ł���B
�i���j�@�e�m���p����ꂽ�L�@��p���āA
�@���f���ʂōl���āA�������P�@�̉����A�`(�P)�A�`(�Q)�A�E�E�E�A�`(���|�P)�A�`(��)���P�@�Ƃ���B
�@�@���Ȃ킿�A�@�`(��)����2����/���@�i�����P�A�Q�A�E�E�E�A���j
�@�P�ʉ~����̔C�ӂ̓_�o�i���j�@�i �b���b���P �j�ɑ��āA
�@�@�o�`(�P)2�{�o�`(�Q)2�{�E�E�E�{�o�`(��)2
�@���b���|�`(�P)�b2�{�b���|�`(�Q)�b2�{�E�E�E�{�b���|�`(��)�b2
�@�����b���b2�|�i�`(�P)�{�`(�Q)�{�E�E�E�{�`(���j�j���f�|�i�`(�P)�f�{�`(�Q)�f�{�E�E�E�{�`(���j�f�j��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�{�i�b�`(�P)�b2�{�b�`(�Q)�b2�{�E�E�E�{�b�`(��)�b2�j
�@�i�����ŁA�� ����� �`(��)�@���f�������ꂼ�� ���f�@�A�`(��)�f�@�ŕ\�����̂Ƃ���B�j
�@�����ŁA�`(�P)�A�`(�Q)�A�E�E�E�A�`(���|�P)�A�`(��)�@�́A�������P�@�̉��Ȃ̂ŁA
�@�`(�P)�{�`(�Q)�{�E�E�E�{�`(���j���O
�܂��A�@�b�`(�P)�b2���b�`(�Q)�b2���E�E�E���b�`(��)�b2���P�@�Ȃ̂ŁA
�@�o�`(�P)2�{�o�`(�Q)2�{�E�E�E�{�o�`(��)2���Q���@�ƂȂ�B
�@���ɁA�o���`(��)�@�i�����P�A�Q�A�E�E�E�A���j�ƍl���A�Ίp���͂Q��d�����Đ�������̂ŁA
�@���߂�ӂ܂��͑Ίp���̂��ׂĂ̒����̕����a�́A�@�Q���~�����Q����2�@�ł���B�@�i�I�j
�@���̖��i�C�j�ɂ��āA�e�m��������܂����B�i�����Q�Q�N�X���P�X���t���j
�i���j�@���f���ʂōl����B�P�� �� �捪���A
�@���@�A��2�@�A��3�@�A�@�E�E�E�@�A����-1�@�A�������P�@�Ƃ���B
���̂Ƃ��A�@���� �̋��f���́A�@����-���@�ł���A
�b�����|�����b2���i�����|�����j�i����-���|����-���j���P�|����-���|����-���{�P���Q�|�i����-���{����-���j
�@���߂�a�́A������A1�������������@�������ׂĂ� ���A���@�ɂ��đ����悢�B
�@������� ���A�� �̌��́A���i��-�P�j/�Q�@�ł���B
�@�� ���Œ肵�āA�� �� �P ���� �� �܂ŁA�������A�� �������ē������ƁA����-�� �́A��0���P�ȊO
�� ���@�A��2�@�A��3�@�A�@�E�E�E�@�A����-1 ���B
�@�]���āA���̘a�́A�P�{���{��2�{��3�{�@�E�E�E�@�{����-1���O�@���A
�@���{��2�{��3�{�@�E�E�E�@�{����-1���|�P�@�ł���B�@����-�� �ɂ��Ă����l�ł���B
�ȏ���A���߂�a�́A�Q�~���i��-�P�j/�Q�|�i�|�P�|�P�j�~��/�Q����2�|���{������2�@�@�i�I�j
�@���̂��Ƃ���A�e�m����̌��ʂ�p���āA�i�R�j�́i���j�����̂悤�ɋ��߂���B
�i���j�@�ӂ܂��͑Ίp���̂��ׂĂ̑��قȂ钷���̕����a�́A
�@�@�@�� ����̂Ƃ��A�@��2/������
�@�@�@�� �������̂Ƃ��A�@��2/���{�Q�����{�Q�@�@�i�I�j
�@�����ŁA(�P)�́A(��)�ɂ����āA�����V�̏ꍇ�ł���B���Ȃ킿�A
�@�@���a��1�̉~�ɓ��ڂ��鐳�V�p�`�̕ӂ̒����� �� �A�Ίp���̒����� ���A��
�i�����������j
�@�Ƃ���Ƃ��A�@��2�{��2�{��2���V�@�����藧�B
�@�c��́i�n�j�ɂ��ẮA�e�m���O�p����p���ĉ������ꂽ�B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�Q�N�X���P�X���t���j
(��)�@�Ɓ���/n�Ƃ���ƁA�ӂ܂��͑Ίp���̂��ׂĂ̒����̘a�́A
�@���o�������Ɓ{�������Q�Ɓ{�������R�Ɓ{�E�E�E�{�������i���|�P�j�Ɓp
�ŗ^������B
�@�����ŁA�������Ɓ{�������Q�Ɓ{�������R�Ɓ{�E�E�E�{�������i���|�P�j�Ƃ̒l�����߂�B
�����������Ɓ{���E�������Ɓ@�Ƃ����B���̂Ƃ��A�P�{���{��2�{�E�E�E�{����-1��(�P�|����)/(�P�|��)
�ɂ����āA�@�������������i���Ɓj�{���E�������i���Ɓj���������{���E���������|�P�@���A
�@�E�Ӂ��Q/(�P�|�������Ɓ|���E��������)���P�{���E��������/�i�P�|�������Ɓj
�@���������āA���ӂ̋������r���āA
�@�������Ɓ{�������Q�Ɓ{�������R�Ɓ{�E�E�E�{�������i���|�P�j�Ɓ���������/�i�P�|�������Ɓj
�Ȃ̂ŁA���߂�a�́A�@���E��������/�i�P�|�������Ɓj�@�ƂȂ�B
�@�����ŁA�@�����Q�������Ɓ@�A�����Q�������Q�Ɓ��Q���E�������Ɓ@�Ȃ̂ŁA
�@���E��������/�i�P�|�������Ɓj�����E�i��/�Q�j/�i�P�|��/�i�Q���j�j����2�E��/(�Q���|��)�@�@�i�I�j
�i�R�����g�j�@��肪���ׂĉ������āA�X�b�L�����܂����I�e�m����Ɋ��ӂ��܂��B
�i�NjL�j�@��L�́i�n�j�̖��ɂ��āA�g�m�uaerile_re�v����ʉ������������܂����B
�@�@�@�@�@aerile_re����Ɋ��ӂ��܂��B�i�����R�P�N�R���P�O���t���j
�@��L�́i�n�j�̖����A�g���~�[�̒藝���g���Ăł��܂����̂ŕ��܂��B
�@�����ꂽ���_�����ԕӂ��邢�͑Ίp���� a[k] �Ƃ����B�i�X�I�ɁAa[0]=a[N]=0
���g���j
�@�g���~�[�̒藝���A�ȉ������藧�B
�@a[1]a[0] = a[2]a[1]-a[1]a[2]
�@a[1]a[1] = a[2]a[2]-a[1]a[3]�@�@�i���@�g���~�[�̒藝�I�ɂ́Aa[2]a[2]��a[1]a[3]�{a[1]a[1]�@�j
�@
�@a[1]a[2] = a[2]a[3]-a[1]a[4]�@�@�i���@�g���~�[�̒藝�I�ɂ́Aa[2]a[3]��a[1]a[4]�{a[1]a[2]�@�j
�@a[1]a[3] = a[2]a[4]-a[1]a[5]
�@�@�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E
�@a[1]a[N-2] = a[2]a[N-1]-a[1]a[N]
�@���������v����ƁA
�@a[1](a[0]+�E�E�E+a[N-2]) = a[2](a[1]+�E�E�E+a[N-1]) - a[1](a[2]+�E�E�E+a[N])
�@��a[k]��S �Ƃ����ƁA�ia[N-1]=a[1] �ł��邱�Ƃɒ��Ӂj
�@�@2*a[1](S-a[1]) = a[2]*S
�@�������āA�@S = 2*a[1]^2 / (2*a[1]-a[2])
�i�R�����g�j�@�����ׂ����́Aa[1]^2*�� / (2*a[1]-a[2])�@�����A�ǂ��C����������̂��낤�H
�@�炷���邳��̃R�����g�ł��B�i�����R�P�N�R���P�Q���t���j
�@��L��S�́A�u1���_���瑼�̂��ׂĂ̒��_�Ɉ����������̒����̘a�v�Ȃ̂ŁA��������{
���ĂQ�Ŋ�����
�@�@ a[1]^2*n / (2*a[1]-a[2])
���A�u���ׂĂ̕ӂƑΊp���̒����̘a�v�ɂȂ�܂��ˁB
�i�R�����g�j�@�Ȃ�قǁI�����ł��ˁB�������肵�܂����B�炷���邳��Ɋ��ӂ��܂��B
�@�U���@����̃R�����g�ł��B�i�����Q�Q�N�X���Q�O���t���j
�@���V�p�`�����a�q�̉~�ɓ��ڂ���ꍇ�ɂ����āA�R�i�n�j�̈�ʉ����l����B
�@�Ɓ���/�� �Ƃ���A�P�̒��_���瑼�̒��_������(���|�P)�{�̐����i�ӂ܂��͑Ίp���j
�̒����̘a�́A�@�Q�q�i�������Ɓ{�������Q�Ɓ{�������R�Ɓ{�E�E�E�{�������i���|�P�j�Ɓj�@�ł��邩��A�ӂ�
���͑Ίp���̑��a �k�� �́A�@�k���� ���q�i�������Ɓ{�������Q�Ɓ{�������R�Ɓ{�E�E�E�{�������i���|�P�j�Ɓj
�ŗ^������B�e���� �Q������(��/�Q) ���|���ĐϘa�����Acos(-��)=cos�Ƃ�K�p����ƁA
�@�Q�k���E������(��/�Q) �����q�i������(��/�Q) �| ������((���|�P/�Q)�Ɓj
�@�����ŁA�Ɓ���/n ���A�@(���|�P/�Q)�Ɓ��|��/�Q�@�Ȃ̂ŁA
�@�Q�k���E������(��/�Q) ���Q���q�E������(��/�Q)
�@���������āA�@�k�� �� ���q / ������(��/�Q) �� ���q / ������(��/�i�Q���j)
�@�e�m����̃R�����g�ł��B�i�����Q�Q�N�X���Q�O���t���j
�@�������Ɓ{�������Q�Ɓ{�������R�Ɓ{�E�E�E�{�������i���|�P�j�Ɓ@�̌v�Z�͊ȒP�ɂł���̂ł��ˁB
�Ƃ���/n�łȂ���ʂ̂Ƃ����A���l�ɂ��Čv�Z�ł��܂����B�㎮�́A�� ���|�P ���܂ł̘a��
�����A�Ɓ���/���@�̂Ƃ��́A�悎�����Asin(����)��sin��0�@�ƂȂ邩��ŁA��ʂ̏ꍇ�͓�
�R�A�� �� ���܂ł̘a�ŏ����ق��������ł��傤�B
�@�������Ɓ{�������Q�Ɓ{�E�E�E�{�������i���Ɓj��������((���{�P)��/�Q)�E������(����/�Q)/������(��/�Q)
�ؖ��́A������(��/�Q)�������āA�Ϙa�̌������g���đS�����l�ɂł��܂��B
�@�������@�ɂ��Ă����l�̎�������܂��B
�@�������Ɓ{�������Q�Ɓ{�E�E�E�{�������i���Ɓj��������((���{�P)��/�Q)�E������(����/�Q)/������(��/�Q)
�ؖ������l�ł��B������g���A�U���@�����(��)�̎O�p���ɂ��ؖ����ł��܂��B
�@�����Q���{�P�@�̂Ƃ��A���߂�a �r �́A
�@�@�r����(�Q�������i���Ɓj)2�@�i�������A���́A�����P���炍�܂ł̘a���Ƃ�B(�ȉ��̃�������)�j
�@�����ŁA�@�S(�������i���Ɓj)2���Q(�P�|�������i�Q���Ɓj)�@������A
�@�r���Q��(�P�|�������i�Q���Ɓj)���Q���|�Q������((���{�P)/�Q��Q��)�E������(��/�Q��Q��)/��������
���Q���|�i������(�Q���{�P)�Ɓ|��������)/�������Ɓ��Q���{�P����
�@�����Q���@�̂Ƃ������l�ɂ��Ăł���B
�@���ۂɁA�r���Q��(�P�|�������i�Q���Ɓj)
�@���Q���|�Q������((���{�P)/�Q��Q��)�E������(��/�Q��Q��)/��������
�@���Q���|�i������(�Q���{�P)�Ɓ|��������)/��������
�@���Q���|�i������(�{�Ɓj�|��������)/�������Ɓ����{�Q
�i�R�����g�j�@�Ȃ�قǁI�U���@����A�e�m����Ɋ��ӂ��܂��B
�@�j�r����̃R�����g�ł��B�i�����Q�V�N�P�Q���Q�Q���t���j
�@���V�p�`�̐����Ƃ��ẮA
�@��7���P �i�����P�j�̂Ƃ��A�@��/(�P�{z2)�{z2/(�P�{z4)�{z3/(�P�{z6)���|�Q
���A�ʔ����Ǝv���܂��B
�i�R�����g�j�@�㐔�I�ɏؖ����Ă݂܂����B�w�I�ɂ��ؖ��ł����ł��傤�ˁH
�@��7���P �i�����P�j���A�@�P�{���{z2�{z3�{z4�{z5�{z6���O�@�Ȃ̂ŁA
�^�����o��(�P�{z4)(�P�{z6)�{z2(�P�{z2)(�P�{z6)�{z3(�P�{z2)(�P�{z4)�p/(�P�{z2)(�P�{z4)(�P�{z6)
�����ŁA���q�����{�P�{z5�{z4�{z2�{���{z4�{z3�{z3�{�P�{z5�{z2
�@�@�@�@�@�@�@���Q�i�P�{���{z2�{z3�{z4�{z5�j���|�Qz6
�@���ꁁ�P�{z2�{z4�{z6�{z6�{���{z3�{z5��z6
�@�ȏォ��A�@�^�����|�Qz6/z6���|�Q
�i�NjL�j�@�����Q�X�N�U���Q�U���t��
 |
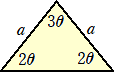
�@�@�`���ŁA���}�̂悤�Ȑ��V�p�`�ɂ����āA |
�@�V�Ɓ��P�W�O���Ƃ��āA
�@�@�@�@![]() �@�@�@�@
�@�@�@�@ �@�@�@�@
�@�@�@�@![]()
�@�����̂Q���ӎO�p�`�����v�X���p���āA���V�p�`�͎��̂悤�ɖ��ߐs�������B
�@�@�@�@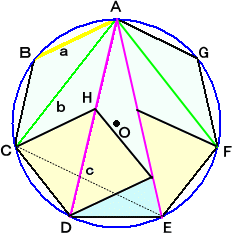
�@��}�ŁA���b�c�g�䁢�b�d�`�@���A�@�� �F �� �� ���|�� �F ���@�����藧�̂ŁA
�@�@�@�����������|�����@���A�@�����������{����
�@���ӂ��A������ �Ŋ���ƁA�@�P/�����P/���{�P/���@�̐��藧���Ƃ�������B
�i�R�����g�j�@�`���ł��A�O�p�`�̑����𗘗p�����ؖ��������������������A������L�肩
�@�@�@�@�@�@�ȂƎv����悤�ȏ����I�ؖ��ł��ˁB
�@�R��ނ̂Q���ӎO�p�`���������珇�Ɂ@�i�`�j�A�i�a�j�A�i�b�j �Ƃ����B
| �i�`�j | �i�a�j | �i�b�j | |||
| �@ | �@ |  |
�@ |
�@�����̂Q���ӎO�p�`�����v�X���i�i�`�j�F�P���A�i�a�j�F�R���A�i�b�j�F�T���j�p���āA���V�p�`��
���ߐs�����ꂽ���A���V�p�`�̕~���l�߂ɗv����Q���ӎO�p�`�̖����͂��ꂵ���Ȃ�����
���A���̂悤�Ȍv�Z�Ŋm���߂邱�Ƃ��o����B
�@�P�ӂ̒������P�i�����j�̐��V�p�`�̖ʐς��r�Ƃ����ƁA�Ɓ���/�V�Ƃ��āA�����Q�������ƂŁA
�@�O�ډ~�̔��a���A�P/�i�Q�������Ɓj�Ȃ̂ŁA
�@�@�r���i�P/�Q�j�o�P/�i�Q�������Ɓj�p2�������Q�Ɓ~�V���V��������/�i�S�������Ɓj���V��/�i�W�������Ɓj
�@�����ŁA�Q���ӎO�p�`�i�`�j�̖ʐς́A�i�P/�Q�j��������
�@�Q���ӎO�p�`�i�a�j�̖ʐς́A
�i�P/�Q�j�������R�Ɓ��i�P/�Q�j�i�R�������Ɓ|�S������3�Ɓj
���i�P/�Q�j�������Ɓi�S������2�Ɓ|�P�j���i�P/�Q�j�i��2�|�P�j��������
�@�Q���ӎO�p�`�i�b�j�̖ʐς́A�V�Ɓ����A
�i�P/�Q�j�������T�Ɓ��i�P/�Q�j�i�������i�|�Q�Ɓj
���i�P/�Q�j�������Q�Ɓ��������Ƃ������Ɓ��i�P/�Q�j����������
�@�Q���ӎO�p�`�i�`�j�A�i�a�j�A�i�b�j �̖��������ꂼ�� ���A���A�� ���Ƃ���ƁA
�@���E�i�P/�Q�j�������Ɓ{���E�i�P/�Q�j�i��2�|�P�j�������Ɓ{���E�i�P/�Q�j���������Ɓ��V��/�i�W�������Ɓj
�@���ӂ��W�������Ɣ{���āA�@�S������2�Ɓi���{���i��2�|�P�j�{�����j���V��
�@���Ȃ킿�A�@�i�S�|��2�j�i���{���i��2�|�P�j�{�����j���V���@����A
�@�@����4�{����3�{�i���|�T���j��2�{�i�V�|�S���j���|�S���{�S�����O�@�E�E�E(*)
�@�����������ŏ��������́A��3�|��2�|�Q���{�P���O�@�Ȃ̂ŁA(*)�̍��ӂ́A��3�|��2�|�Q���{�P
�Ŋ�����B
�@����āA�]�聁�i���|�Q���{���j��2�{�i�V�{���|�Q���j���|�S���{�R���|�����O�@����A
�@�@�@���|�Q���{�����O�@�E�E�E�i�P�j�@�A�V�{���|�Q�����O�@�E�E�E�i�Q�j�@�A�|�S���{�R���|�����O�@�E�E�E�i�R�j
�@�i�P�j�~�Q�{�i�Q�j�@���A�@�Q���|�R���{�V���O�@�E�E�E�i�S�j
�@�i�R�j�~�i�|�Q�j�{�i�Q�j�@���A�@�W���|�T���{�V���O�@�E�E�E�i�T�j
�@�i�S�j�~�S�|�i�T�j�@���A�@�|�V���{�Q�P���O�@���A�@�����R
�@�i�S�j�ɑ�����āA�@�����P�@�@���������āA�i�P�j���A�@�����T
�@�ȏォ��A�p������Q���ӎO�p�`�̌��́A�i�`�j�F�P���A�i�a�j�F�R���A�i�b�j�F�T���@�ł���B
�@�@�ȉ��A�H����