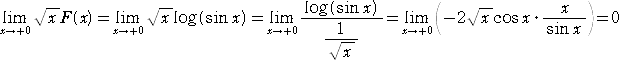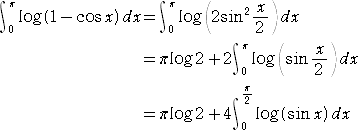墌廃偺摍暘揰偺惈幙丂丂丂 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂暯惉侾俋擭俋寧俁擔晅偗偱摉俫俹偺宖帵斅乽弌夛偄偺愹乿偵丄摉俫俹偑偄偮傕偍悽榖偵側偭
偰偄傞乽傜偡偐傞乿偝傫偐傜栤戣偑採婲偝傟偨丅
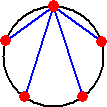
丂扨埵墌廃忋偵摍娫妘偵丄値 揰乮値亞俀乯傪偲傝丄偁傞揰偲懠偺 値亅侾 揰傪偦傟偧傟
寢傇偲丄偦傟傜 値亅侾 杮偺慄暘偺挿偝偺愊偼 値 偱偁傞
丂偙偺徹柧偼擄偟偄偩傠偆偐丠
丂丂丂乮曗懌乯丂倸倕倶倝倧 偝傫偵傛傟偽丄偙偺栤戣偼丄侾俋俋俋乣俀侽侽俀擭埵偵弌斉偝傟偨乽戝妛
丂丂丂丂丂丂丂傊偺悢妛乿偺廻戣偵偁偭偨偦偆偱偁傞丅
丂傜偡偐傞偝傫偺栤戣傪攓尒偟偰丄偦偺徹柧塢乆偺慜偵丄乽偦傫側惈幙傕偁傞偺偐両乿偲姶
摦偟偰偟傑偭偨丅乮巹偵偼丄弶尒偱偟偨両乯
丂偄偔偮偐庤寁嶼偱妋擣偟偰傒傛偆丅
 |
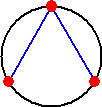
値亖俀丂偺偲偒偼丄
丂挿偝偺愊亖俀
側偺偱丄柦戣偼惉傝棫偮丅 |
丂 |
 |
値亖俁丂偺偲偒偼丄
丂挿偝偺愊亖 亊 亊
丂丂丂丂丂丂亖俁
側偺偱丄柦戣偼惉傝棫偮丅 |
| 丂 |
|
|
|
|
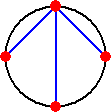 |
値亖係丂偺偲偒偼丄
丂挿偝偺愊亖 亊俀亊 亊俀亊
丂丂丂丂丂丂亖係丂
側偺偱丄柦戣偼惉傝棫偮丅
|
|
|
|
| 丂 |
|
|
|
|
 |
値亖俆丂偺偲偒偼丄埲壓偺傛偆側寁嶼傪峴偆丅
丂丂丂俴1亖俀倱倝値俁俇亱偱丄偝傜偵丄梋尫掕棟偵傛傝丄俴2亖俀倱倝値俈俀亱
偙偙偱丄丂兤亖俁俇亱偲偍偔偲丄丂俆兤亖侾俉侽亱傛傝丄丂俁兤亖侾俉侽亱亅俀兤
|
丂丂丂丂丂丂丂丂丂丂丂丂傛偭偰丄丂丂倱倝値俁兤亖倱倝値乮侾俉侽亱亅俀兤乯亖倱倝値俀兤丂偐傜丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂俁倱倝値兤亅係倱倝値3兤亖俀倱倝値兤們倧倱兤
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂倱倝値兤亗侽丂側偺偱丄丂丂俁亅係倱倝値2兤亖俀們倧倱兤
丂丂丂丂丂偡側傢偪丄俁亅係乮侾亅們倧倱2兤乯亖俀們倧倱兤丂傛傝丄丂係們倧倱2兤亅俀們倧倱兤亅侾亖侽
丂偙傟傛傝丄丂們倧倱兤亜侽丂偵拲堄偟偰丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂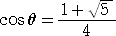
丂偙偺偲偒丄
丂丂丂丂 丂丂丂丂 丂丂丂丂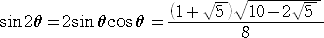
丂偟偨偑偭偰丄丂挿偝偺愊亖乮俀倱倝値兤丒俀倱倝値俀兤乯2亖俆丂偲側傞偺偱丄柦戣偼惉傝棫偮丅
|
| 丂 |
 |
丂丂値亖俇丂偺偲偒偼丄
丂丂丂丂挿偝偺愊亖侾亊 亊俀亊 亊俀亊 亊侾亖俇 亊侾亖俇
丂丂側偺偱丄柦戣偼惉傝棫偮丅
|
| 丂 |
|
|
|
|
 |
丂丂値亖俈丂偺偲偒丄丂侾俉侽亱/俈亖兤丂偲偍偔偲丄
丂丂丂丂丂俴1亖俀倱倝値兤
丂丂丂丂丂俴22亖侾亄侾亅俀們倧倱係兤亖係倱倝値2俀兤丂傛傝丄丂俴2亖俀倱倝値俀兤丂丂丂丂丂
|
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 俴32亖侾亄侾亅俀們倧倱俇兤亖係倱倝値2俁兤丂傛傝丄丂俴3亖俀倱倝値俁兤
偟偨偑偭偰丄挿偝偺愊亖乮俴1丒俴2丒俴3乯2亖俇係乮倱倝値兤丒倱倝値俀兤丒倱倝値俁兤乯2丂傪媮傔傟偽傛偄丅
丂偙偺偲偒丄幃丂倱倝値兤丒倱倝値俀兤丒倱倝値俁兤丂偵偮偄偰丄偁傞枺榝揑側岞幃偑抦傜傟偰偄傞丅 |
| 丂 |
 |
値亖俉丂偺偲偒
丂丂俴12亖侾亄侾亅俀們倧倱係俆亱亖俀亅
丂丂俴2亖俀倱倝値俋侽亱亖 丂傛傝丄丂俴22亖俀 丂傛傝丄丂俴22亖俀
|
丂丂丂俴32亖侾亄侾亅俀們倧倱侾俁俆亱亖俀亄
柧傜偐偵丄丂丂丂俴4亖俀
偟偨偑偭偰丄丂挿偝偺愊亖俴12丒俴22丒俴32丒俴4亖乮俀亅 乯丒俀丒乮俀亄 乯丒俀丒乮俀亄 乯丒俀亖俉丂偲側傞丅丂丂丂丂 乯丒俀亖俉丂偲側傞丅丂丂丂丂
|
丂偲偙傠偱丄値亖俈丂偺偲偒偺寁嶼偐傜丄偙偺栤戣偺杮幙偼師偺寁嶼偵偁傞偙偲偑嶡偣傜傟傞丅
 |
丂丂丂侾俉侽亱/値亖兤丂偲偍偔丅嵍恾偵偍偄偰丄梋尫掕棟傛傝丄
丂俙0俙倠2亖侾亄侾亅俀們倧倱俀倠兤亖俀乮侾亅們倧倱俀倠兤乯亖係倱倝値2倠兤
丂丂丂丂傛偭偰丄丂丂俙0俙倠亖俀倱倝値倠兤
|
丂丂偟偨偑偭偰丄媮傔傞挿偝偺愊偼丄
丂俙0俙1亊俙0俙2亊丒丒丒亊俙0俙値亅1亖俀倱倝値兤亊俀倱倝値俀兤亊俀倱倝値俁兤亊丒丒丒亊俀倱倝値乮値亅侾乯兤
亖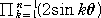
丂偙偙偱丄塃曈偺抣偑丄値 偵摍偟偄偙偲傪帵偡偵偼丄懡偔偺媄岻揑側弨旛偲彮偟偺桬婥偑偄
傞偑丄嵍曈偺抣偑丄値 偵摍偟偄偙偲傪帵偡偙偲偼堈偟偄傛偆偩丅
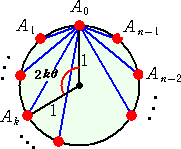
丂俙値倧値倷倣倧倳倱 偝傫偐傜偺忣曬偵傛傟偽丄師偺傛偆偵帵偡曽朄偑嵟傕娙柧偩傠偆丅
丂丂丂丂丂丂丂丂丂丂丂乮尒帠側徹柧偱丄姶摦偟傑偟偨両俙値倧値倷倣倧倳倱
偝傫偵姶幱偄偨偟傑偡丅乯
乮徹柧乯丂僈僂僗暯柺 俠 偵偍偄偰丄丂俙0乮侾乯 偲偟丄侾俉侽亱/値亖兤丂偲偡傞丅
丂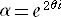
偲偍偔偲丄丂俙k乮兛k乯 偲彂偔偙偲偑偱偒傞丅
丂偙偺偲偒丄丂俙0乮侾乯 偺抲偒曽偐傜丄俀揰 俙k 偲 俙値亅k 偼幚幉偵娭偟偰慄懳徧偱丄
俀偮偺暋慺悢 兛k 偲 兛値亅k 偼屳偄偵嫟栶側暋慺悢偲側傞丅
偟偨偑偭偰丄丂 俀偮偺暋慺悢 侾亅兛k 偲 侾亅兛値亅k 傕屳偄偵嫟栶側暋慺悢偲側傞丅
偙偺偲偒丄丂偦偺愊偵偮偄偰丄
丂乮侾亅兛k乯乮侾亅兛値亅k乯亖乥侾亅兛k乥丒乥侾亅兛値亅k乥亖俙0俙倠亊俙0俙値亅倠
偑惉傝棫偮丅
丂埲忋偐傜丄丂
丂俙0俙1亊俙0俙2亊丒丒丒亊俙0俙値亅1亖乮侾亅兛乯乮侾亅兛2乯丒丒丒乮侾亅兛値亅2乯乮侾亅兛値亅1乯
偲側傞丅
丂偙偙偱丄丂俥乮倶乯亖乮倶亅兛乯乮倶亅兛2乯丒丒丒乮倶亅兛値亅2乯乮倶亅兛値亅1乯丂偲偍偔偲丄
兛 偼丄侾 偺 値 忔崻側偺偱丄丂曽掱幃 倶値亅侾亖侽丂偺夝偱偁傞丅
丂偙偺偲偒丄丂兛亗侾丂偱丄丂倶値亅侾亖乮倶亅侾乯俥乮倶乯丂偑惉傝棫偮丅
椉曈傪 倶 偱旝暘偟偰丄丂値倶値-1亖俥乮倶乯亄乮倶亅侾乯俥乫乮倶乯
忋幃偵丄倶亖侾 傪戙擖偟偰丄
丂値 亖 俥乮侾乯 亖 乮侾亅兛乯乮侾亅兛2乯丒丒丒乮侾亅兛値亅2乯乮侾亅兛値亅1乯
偟偨偑偭偰丄俙0俙1亊俙0俙2亊丒丒丒亊俙0俙値亅1 亖 値
偑惉傝棫偮丅丂丂乮徹廔乯
乮偙傟偑丄傜偡偐傞偝傫偺峫偊傜傟偨栤戣偱偁偭偨丅乯
丂傑偨丄偙偺寢壥偐傜丄師偺枺榝揑側岞幃傕徹柧偝傟傞丅
丂 兤亖侾俉侽亱/値丂偺偲偒丄丂丂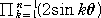 亖 値
亖 値
乮徹柧乯丂俙0俙1亊俙0俙2亊丒丒丒亊俙0俙値亅1亖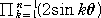 丂丂側偺偱丄忋婰偺寢壥傛傝丄
丂丂側偺偱丄忋婰偺寢壥傛傝丄
丂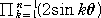 亖 値
亖 値
偑惉傝棫偮丅丂丂乮徹廔乯
乮僐儊儞僩乯丂偦傟偵偟偰傕丄旤偟偄寢壥偱偡偹両両
丂傜偡偐傞偝傫偑懠強偺俫俹偱彂偒崬傒偝傟偰偄傞偺傪攓尒偡傞偲丄偙偺栤戣偺偦傕偦傕偺
敪抂偼丄
丂倱倝値俁俇亱亊倱倝値俈俀亱亊倱倝値侾侽俉亱亊倱倝値侾係係亱
偲偄偆栤戣偩偲偺偙偲偱偁傞丅偙傟偼挌搙丄忋婰偺 値亖俆 偺応崌偺栤戣偱偁傞丅
乮捛婰乯丂暯惉俀俈擭俋寧侾係擔晅偗
丂師偼丄們倧倱(兾/俈)們倧倱(俀兾/俈)們倧倱(俁兾/俈)亖侾/俉丂偺徹柧偱偁傞丅敪憐偺巃怴偝偵扙朮偱
偡丅
 |
丂丂惓俈妏宍偺撪妏偺戝偒偝偼丄俆兾/俈丂偱丄佢俙俹俛亖兾/俈
丂丂丂倱倝値(兾/侾係)亖倎/俀們丂丄倱倝値(俁兾/侾係)亖們/俀倐丂丄
丂丂丂倱倝値(俆兾/侾係)亖倐/俀倎
丂丂偙傟傜偺幃傪曈乆妡偗偰丄
丂丂丂倱倝値(兾/侾係)倱倝値(俁兾/侾係)倱倝値(俆兾/侾係)亖侾/俉
偙偙偱丄倱倝値(兾/侾係)亖們倧倱乮兾/俀亅兾/侾係)亖們倧倱乮俁兾/俈乯
丂丂丂倱倝値(俁兾/侾係)亖們倧倱乮兾/俀亅俁兾/侾係)亖們倧倱乮俀兾/俈乯
丂丂丂倱倝値(俆兾/侾係)亖們倧倱乮兾/俀亅俆兾/侾係)亖們倧倱乮兾/俈乯 |
丂傛偭偰丄丂們倧倱(兾/俈)們倧倱(俀兾/俈)們倧倱(俁兾/俈)亖侾/俉丂偑惉傝棫偮丅
丂偲偙傠偱丄倫倛倎倧倱 偝傫偲偄偆曽乮埲慜偵傕摉俫俹偱偍悽榖偵側傝傑偟偨両乯偑丄侾俋俋俉擭偵
丂 兤亖侾俉侽亱/値丂偺偲偒丄丂丂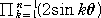 亖 値
亖 値
傪徹柧偝傟偰偄傞丅
丂傗偼傝嫟栶暋慺悢偺峫偊曽傪梡偄偨丄旕忢偵媄岻揑側徹柧偱丄偦偺娙柧偝偵偼嬃偐偝傟
傞丅懡彮暥尵傪廋惓偟偰丄側偧偭偰傒偨偄偲巚偆丅
乮徹柧乯丂丂乮倶値亅侾乯2亖乮倶値亅侾乯乮倶値亅侾乯
丂丂丂丂亖乮倶亅倕2兾倝乯乮倶亅倕亅2兾倝乯丂丂乮仼丂偙偺曄宍偵丄偟傃傟傑偟偨両乯
丂丂丂丂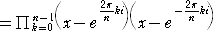
傛偭偰丄丂倶亗侾丂偲偟偰丄
丂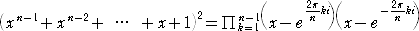
忋幃偵偍偄偰丄倶 偑尷傝側偔 侾 偵嬤偯偔偲偒偺嬌尷抣傪峫偊偰丄
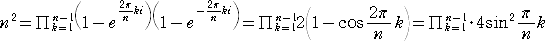
偡側傢偪丄丂兾/値亖兤丂偲偍偄偰丄丂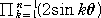 亖 値丂偑惉傝棫偮丅丂乮徹廔乯
亖 値丂偑惉傝棫偮丅丂乮徹廔乯
乮僐儊儞僩乯丂忋婰傪傑偲傔傞偵偁偨傝丄傜偡偐傞偝傫丄俙値倧値倷倣倧倳倱
偝傫傪巒傔丄倕倝倐倳偝傫傗
丂丂丂丂丂丂倠倧倠倧倳偝傫丄倸倕倶倝倧 偝傫偐傜偺忣曬偑戝偄偵栶棫偪傑偟偨丅偙偺応傪偐傝偰姶幱
丂丂丂丂丂丂偄偨偟傑偡丅
乮捛婰乯丂暯惉侾俋擭俋寧侾俁擔晅偗
丂俙値倧値倷倣倧倳倱丂偝傫偺偛恠椡偵傛傝丄傜偡偐傞偝傫偺栤戣偺尨揟偑尒偄偩偝傟偨丅
丂俬倖 俠1俠2俠3丒丒丒俠n 倝倱 倎 倰倕倗倳倢倎倰 値-倗倧値 倝値倱們倰倝倐倕倓 倝値 倎 們倝倰們倢倕 倧倖 倳値倝倲 倰倎倓倝倳倱
們倕値倲倕倰倕倓 倎倲 俷 丆倎値倓 俹 倝倱 倲倛倕 倫倧倝値倲 倧値 俷俠1 倎倲 倎 倓倝倱倲倎値們倕 倶 倖倰倧倣 俷 丆
倲倛倕値丂倶値亅侾亖俹俠1丒俹俠2丒丒丒俹俠n 丏
丂乮尨揰拞怱偺扨埵墌偵撪愙偡傞惓 値 妏宍 俠1俠2俠3丒丒丒俠n 偵偍偄偰丄俷俠1忋偵揰 俹 傪
丂 俷俹 亖 倶 偱偁傞傛偆偵偲傞丅偙偺偲偒丄 倶値亅侾亖俹俠1丒俹俠2丒丒丒俹俠n丂偑惉傝棫偮丅乯
丂丂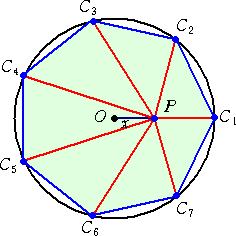
丂俙値倧値倷倣倧倳倱丂偝傫偵傛傟偽丄偙偺掕棟偺敪尒幰偼僐乕僣乮俼倧倗倕倰丂俠倧倲倕倱丂1682乣1716乯
偲偺偙偲丅僯儏乕僩儞偺偍掜巕偝傫偱丄僾儕儞僉僺傾戞俀斉偺曇廤傪峴偭偨曽丅僯儏乕僩儞偼憗
偡偓傞斵偺巰傪搲傫偱丄
丂俬倖丂倛倕丂倛倎倓丂倢倝倴倕倓丂倵倕丂倣倝倗倛倲丂倛倎倴倕丂倠値倧倵値丂倱倧倣倕倲倛倝値倗丏
偲尵偭偨偦偆偱偁傞丅
丂堄栿傪偡傟偽丄
丂斵偑巰傫偱偟傑偭偰丄変乆偵枹抦偺晹暘偑巆偭偰偟傑偭偨両
偲偱傕側傞偺偐側丠
丂偲偙傠偱丄丂倶亖侽丂偺偲偒丄丂俹俠1丒俹俠2丒丒丒俹俠n亖亅侾丂偵側傞偑丄俹俠1丄俹俠2丄丒丒丒偵壗傜
偐偺堄枴偯偗偑昁梫偩傠偆丅
丂僈僂僗暯柺偵偍偄偰丄丂俹丄俠1丄俠2丄丒丒丒丄俠n丂傪暋慺悢偲偟丄椺偊偽丄丂俹俠1亖俹亅俠1丂偲
峫偊傟偽丄柕弬偑婲偒側偄傛偆偵巚偆丅
丂偡側傢偪丄丂乥俹俠1乥丒乥俹俠2乥丒丒丒乥俹俠n乥亖亅俹俠1丒俹俠2丒丒丒俹俠n亖侾丂偲側傞丅
丂傑偨丄偙偺傛偆偵棟夝偡傟偽掕棟偺幃偼崱擔偱尵偆偲偙傠偺暋慺悢偺斖埻偱偺場悢暘夝
丂倶値亅侾亖乮倶亅俠1乯乮倶亅俠2乯丒丒丒乮倶亅俠n乯
偲摨媊偱偁傝丄忋婰偱弎傋偨徹柧偱丄暋慺悢偑巊傢傟傞尨揟偵傕側偭偰偄傞傛偆偩丅
乮僐儊儞僩乯丂崱偐傜俁侽侽擭傎偳慜偐傜抦傜傟偰偄偨栤戣偲偄偆偙偲偱姶摦偟傑偟偨丅
丂丂丂丂丂丂俙値倧値倷倣倧倳倱丂偝傫偺偛恠椡偵姶幱偄偨偟傑偡丅
乮捛婰乯丂暯惉俀侽擭俁寧侾俉擔晅偗
丂嶰妏斾偺抣偱丄丂倲倎値乮兾/俇乯亖侾/ 丂丄丂倲倎値乮兾/俁乯亖
丂丄丂倲倎値乮兾/俁乯亖 丂偲偄偆偙偲傪棟夝偟偰傕丄
丂偲偄偆偙偲傪棟夝偟偰傕丄
丂丂倲倎値乮兾/俇乯亊倲倎値乮兾/俁乯亖侾
偲偄偆帠幚偵婥偑偮偔崅峑侾擭惗偼彮側偄偐傕偟傟側偄丅
乮仺傕偪傠傫丄崅峑侾擭惗偼丄屖搙朄偱偼側偔偰丄搙悢朄偱偡偑丏丏丏両乯
丂師偺抣丂倲倎値乮兾/俉乯亊倲倎値乮兾/係乯亊倲倎値乮俁兾/俉乯丂偼偄偔偮偵側傞偩傠偆偐丠
丂傕偪傠傫丄丂倲倎値乮兾/係乯亖侾丂側偺偱丄丂倲倎値乮兾/俉乯亊倲倎値乮俁兾/俉乯丂偺抣傪媮傔傟偽傛偄
偺偩偑丏丏丏丅
丂悢妛嘦偱妛傇敿妏偺岞幃傪梡偄傟偽丄
丂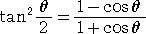
側偺偱丄丂倲倎値2乮兾/俉乯亖乮 亅侾乯2丂傛傝丄丂倲倎値乮兾/俉乯亖
亅侾乯2丂傛傝丄丂倲倎値乮兾/俉乯亖 亅侾
亅侾
丂倲倎値2乮俁兾/俉乯亖乮 亄侾乯2丂傛傝丄丂倲倎値乮兾/俉乯亖
亄侾乯2丂傛傝丄丂倲倎値乮兾/俉乯亖 亄侾
亄侾
丂偟偨偑偭偰丄丂倲倎値乮兾/俉乯亊倲倎値乮兾/係乯亊倲倎値乮俁兾/俉乯亖乮 亅侾乯丒侾丒乮
亅侾乯丒侾丒乮 亄侾乯亖侾
亄侾乯亖侾
丂埲忋偺偙偲偼丄壓恾偲嵘傔偭偙偡傟偽婔壗妛揑偵擺摼偱偒傞偙偲偩傠偆丅
丂丂丂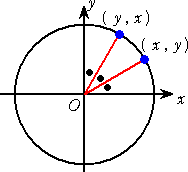 丂丂丂丂
丂丂丂丂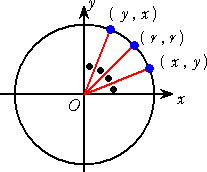
丂偙偺栤戣偺摿挜偼丄兾/俀 傪丄値 摍暘偟丄偦傟傜偺妏偺惓愙傪偡傋偰妡偗崌傢偣偰偄傞
揰偩傠偆丅
丂偙偺偲偒丄
丂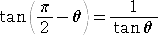
偲偄偆岞幃偑惉傝棫偮偺偱丄忋婰偺偙偲偐傜丄堦斒偵
丂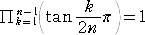
偑惉傝棫偮偙偲偼丄傎傏帺柧偲尵偊傞丅
丂偡偖擺摼偝傟側偄曽偺偨傔偵丄師偺傛偆側徹柧偑抦傜傟偰偄傞偺偱徯夘偟傛偆丅
乮徹柧乯丂
丂丂丂丂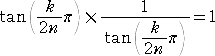
傛傝丄
丂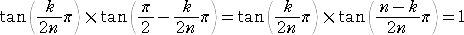
傛偭偰丄
丂
丂偟偨偑偭偰丄
丂丂丂丂丂丂丂丂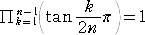 丂丂乮徹廔乯
丂丂乮徹廔乯
丂偙偺摍幃傪梡偄傞偲丄
丂丂丂丂丂丂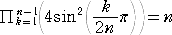 丂丂丂丂丂
丂丂丂丂丂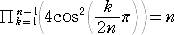
偑惉傝棫偮偙偲偑娙扨偵帵偝傟傞丅
丂幚嵺偵丄
丂丂丂丂丂丂丂
側偺偱丄
丂丂丂丂丂丂丂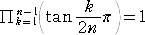
傪妡偗偨傝丄妱偭偨傝偡傟偽傛偄丅
丂暯惉俀侽擭俁寧侾俉擔晅偗偱丄摉俫俹偺宖帵斅乽弌夛偄偺愹乿偵丄倸倠係俁偝傫偺彂偒崬傒偑
偁偭偨丅
丂掕愊暘偺寁嶼
丂
偵丄偙偺儁乕僕偱峴偭偨庤朄偑惗偐偣傞偲偄偆傕偺偱偁傞丅
丂捠忢丄忋婰偺掕愊暘偼師偺傛偆側抲姺愊暘朄偵傛傝媮傔傜傟傞丅
 丂丂丂傑偢丄嵍曈偼摿堎揰傪帩偮娭悢偺掕愊暘側偺偱丄
丂丂丂傑偢丄嵍曈偼摿堎揰傪帩偮娭悢偺掕愊暘側偺偱丄
丂丂壜愊暘偱偁傞偙偲傪帵偦偆丅
丂丂丂偙偺応崌丄師偺掕棟偑梡偄傜傟傞丅
丂丂丂娭悢 俥乮倶乯 偑嬫娫 [ 倎 丆 倐 ] 偵偍偄偰丄倎 傪摿
丂丂堎揰偲偡傞偲偒丄侽亙兛亙侾 側傞偁傞 兛 偵偮偄偰丄
丂丂丂倶 仺 倎亄侽丂偺偲偒丄 乮倶亅倎乯兛俥乮倶乯偑桳尷妋掕
丂丂抣偵廂懇偡傟偽丄娭悢 俥乮倶乯 偼嬫娫 [ 倎 丆 倐 ]
丂丂偵偍偄偰壜愊暘偲側傞
丂丂丂徹柧偼丄乮倶亅倎乯兛俥乮倶乯 偺桳奅惈偐傜柧傜偐偩傠偆丅
丂忋婰偺掕棟傪梡偄偰丄
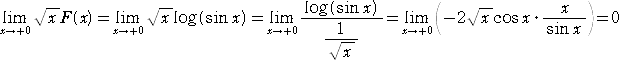
偐傜丄壜愊暘偲側傞丅丂偝偰丄
丂丂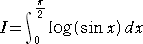
| 偲偍偒丄丂倶丂仺丂兾/俀亅倶丂偲抲姺偡傞偲丄 |
丂丂丂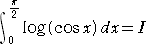 |
| 偱偁傞丅傑偨丄丂倶丂仺丂兾亅倶丂偲抲姺偡傞偲丄 |
丂丂丂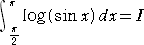 |
偱偁傞丅丂偙偺偲偒丄
丂丂
丂偦偙偱丄
丂
側偺偱丄
丂丂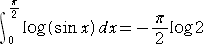
偑惉傝棫偮丅
乮僐儊儞僩乯丂搑拞偺幃曄宍偱丄乽偙偙傑偱偡傞両乿偲偄偆姶摦傕偁傞偑丄柍枴姡憞側幃曄宍偱
丂丂丂丂丂丂偁傞偙偲偵曄傢傝偼側偄丅
丂偙偺榖戣偵偮偄偰丄倸倠係俁偝傫偼師偺傛偆偵峫偊傜傟偨丅
丂偙偺儁乕僕偺朻摢偺寢壥偐傜丄
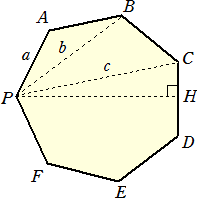
丂敿宎 侾 偺墌偵撪愙偡傞惓 値 妏宍偑偁傝丄堦偮偺捀揰偲懠偺 値亅侾 屄偺捀揰傪
寢傇慄暘 値亅侾 杮傪嶌傞偲丄偙傟傜 値亅侾 杮偺慄暘偺挿偝偺愊偼丄値
偱偁偭偨丅
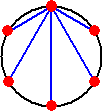
丂偦偙偱丄崱搙偼敿宎 侾 偺墌偵撪愙偡傞惓 俀値 妏宍俙0俙1俙2丒丒丒俙2値亅1傪峫偊丄偦偺堦偮
偺捀揰傪僈僂僗暯柺 俠 偵偍偄偰丄丂俙0乮侾乯 偲偟丄兾/(俀値)亖兤丂偲偡傞丅
丂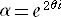
偲偍偔偲丄丂俙k乮兛k乯 偲彂偔偙偲偑偱偒傞丅
丂偙偺偲偒丄丂俙0乮侾乯 偺抲偒曽偐傜丄俀揰 俙k 偲 俙2値亅k 偼幚幉偵娭偟偰慄懳徧偱丄
俀偮偺暋慺悢 兛k 偲 兛2値亅k 偼屳偄偵嫟栶側暋慺悢偲側傞丅
偟偨偑偭偰丄丂 俀偮偺暋慺悢 侾亅兛k 偲 侾亅兛2値亅k 傕屳偄偵嫟栶側暋慺悢偲側傞丅
偙偺偲偒丄丂偦偺愊偵偮偄偰丄
丂丂 乮侾亅兛k乯乮侾亅兛2値亅k乯亖乥侾亅兛k乥丒乥侾亅兛2値亅k乥亖俙0俙倠亊俙0俙2値亅倠
偑惉傝棫偮丅丂埲忋偐傜丄
丂丂俙0俙1亊俙0俙2亊丒丒丒亊俙0俙2値亅1
亖乮俙0俙1亊俙0俙2値亅1乯亊乮俙0俙2亊俙0俙2値亅2乯亊丒丒丒亊乮俙0俙値亅1亊俙0俙値亄1乯亊俙0俙値
亖俀乮侾亅們倧倱乮兾/値乯乯丒俀乮侾亅們倧倱乮俀兾/値乯乯丒丒丒俀乮侾亅們倧倱乮乮値亅侾乯兾/値乯乯丒乮侾亅們倧倱乮値兾/値乯乯
偲側傞丅偡側傢偪丄
丂丂丂乮侾亅們倧倱乮兾/値乯乯乮侾亅們倧倱乮俀兾/値乯乯丒丒丒乮侾亅們倧倱乮値兾/値乯乯亖俀値/俀値亅1亖値/俀値亅2
丂傛偭偰丄
丂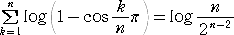
側偺偱丄
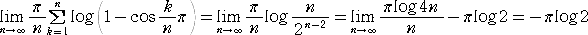
偲側傞丅丂偟偨偑偭偰丄嬫暘媮愊朄偵傛傝丄
丂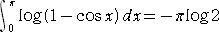
偙偙偱丄
丂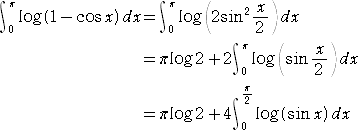
側偺偱丄
丂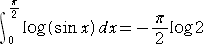
偑惉傝棫偮丅
乮僐儊儞僩乯丂側傞傎偳両侾俈悽婭偵偍偗傞墌廃偺摍暘揰偺惈幙偐傜侾俉悽婭偺僆僀儔乕偺掕
丂丂丂丂丂丂愊暘偑摫偗傞傢偗偱丄悢妛偺楌巎偑楢柸偲懕偄偰偄傞偲偄偆堦偮偺徹嵍偱偡偐
丂丂丂丂丂丂偹丠偙傫側宱尡傪偝偣偰偄偨偩偄偨倸倠係俁偝傫偵姶幱偄偨偟傑偡丅
丂墌廃偺摍暘揰偺惈幙偲偟偰丄師偺惈幙傕嫽枴怺偄丅
丂扨埵墌廃忋偺擟堄偺揰俹偵懳偟偰丄俹俙(侾)2亄俹俙(俀)2亄丒丒丒亄俹俙(値)2亖俀値
乮徹柧乯丂暋慺暯柺偱峫偊偰丄倶値亖侾丂偺夝傪丄俙(侾)丄俙(俀)丄丒丒丒丄俙(値亅侾)丄俙(値)亖侾丂偲偡傞丅
丂丂偡側傢偪丄丂俙(倠)亖倕2兾倠倝/値丂乮倠亖侾丄俀丄丒丒丒丄値乯
丂扨埵墌廃忋偺擟堄偺揰俹乮倸乯丂乮 乥倸乥亖侾 乯偵懳偟偰丄
丂丂俹俙(侾)2亄俹俙(俀)2亄丒丒丒亄俹俙(値)2
丂亖乥倸亅俙(侾)乥2亄乥倸亅俙(俀)乥2亄丒丒丒亄乥倸亅俙(値)乥2
丂亖値乥倸乥2亅乮俙(侾)亄俙(俀)亄丒丒丒亄俙(値乯乯倸乫亅乮俙(侾)乫亄俙(俀)乫亄丒丒丒亄俙(値乯乫乯倸
丂丂丂亄乮乥俙(侾)乥2亄乥俙(俀)乥2亄丒丒丒亄乥俙(値)乥2乯
丂偙偙偱丄俙(侾)丄俙(俀)丄丒丒丒丄俙(値亅侾)丄俙(値)丂偼丄倶値亖侾丂偺夝側偺偱丄
丂俙(侾)亄俙(俀)亄丒丒丒亄俙(値乯亖侽
丂傑偨丄丂乥俙(侾)乥2亖乥俙(俀)乥2亖丒丒丒亖乥俙(値)乥2亖侾丂側偺偱丄
丂丂俹俙(侾)2亄俹俙(俀)2亄丒丒丒亄俹俙(値)2亖俀値丂偲側傞丅丂乮徹廔乯
乮僐儊儞僩乯丂偙偺掕棟偼丄師偺儁乕僕乽惓俈妏宍偺偁傞惈幙乿偱妶桇偡傞丅
丂摉俫俹撉幰偺俫俶乽傜偄乿偝傫偐傜偺幙栤偱偡丅乮暯惉俀俁擭侾侾寧侾俋擔晅偗乯
丂桭払偐傜慜偵傕傜偭偨栤戣偱丄
丂敿宎侾偺墌偵撪愙偡傞惓値妏宍偺1捀揰偐傜懠偺奺捀揰偵堷偄偨慄暘偺挿偝偺愊
偑値偵側傞偙偲傪徹柧偣傛
偲偄偆栤戣側偺偱偡偑丄暋慺悢傪巊偆埲奜偺徹柧偼偱偒傑偡偐丠
丂摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞俫俶乽俥俶乿偝傫偐傜偺僐儊儞僩偱偡丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮暯惉俀俁擭侾侾寧侾俋擔晅偗乯
丂忋婰偺俙値倧値倷倣倧倳倱 偝傫偺徹柧偺傛偆偵丄暋慺悢傪巊偆偺偑帺慠偱偐側傝偒傟偄偵徹柧
偱偒傑偡偐傜丄偦傟埲奜偺曽朄偼丄偁傑傝峫偊傞婥偑偟側偄偱偡偹丅嶰妏娭悢偱夝偔偺偼壜
擻偱偟傚偆偑丄暋慺悢傛傝偆傑偔偄偔偲偼巚偊傑偣傫丅弶摍婔壗偱偱偒傟偽柺敀偄偱偡偑丄擄
偟偦偆偱偡丅弶摍婔壗側傜僩儗儈乕偺掕棟偑庡栶偱偟傚偆偑丏丏丏丅
丂傜偄偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俁擭侾侾寧侾俋擔晅偗乯
丂壗偐旤偟偄婔壗妛揑側夝偒曽偑偁傟偽丄柺敀偄偐偲巚偭偨偺偱偡偑丏丏丏丅
乮捛婰乯丂俫俶乽moonlight乿偝傫偐傜偛搳峞偄偨偩偒傑偟偨丅乮暯惉俀俉擭侾俀寧俀俋擔晅偗乯
丂嶐栭丄Twitter乮偦偙偱偼丄倱倝値2 偺媡悢偺榓偱偟偨乯偱丄
丂丂儼k=1乣値-1 們倧倲2乮倠兾/値乯亖乮値亅俀乯乮値亅侾乯/俁
偲偄偆旤偟偄幃傪尒偐偗傑偟偨丅彮偟峫偊偰偼傒偨偺偱偡偑丄椺偵傛偭偰丄偳偆偟偰側偺偐暘
偐傝傑偣傫偱偟偨丅彆偗偰壓偝偄丅桳柤側摍幃側偺偱偟傚偆偐丏丏丏丅
丂俫俶乽傑偡偨乣乿偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俉擭侾俀寧俀俋擔晅偗乯
丂倂倕倐僒僀僩丗乽崅峑悢妛偺旤偟偄暔岅乿偺乽僶乕僛儖栤戣偺弶摍揑側徹柧乿傗乽搶嫗岺嬈
戝妛丂屻婜乮侾俋俋侽擭乯乿偑嶲峫偵側傞傫偠傖側偄偐偲丏丏丏丅
乮僐儊儞僩乯丂倶亖倠兾/値丂偲偍偔偲丄丂値倶亖倠兾丂側偺偱丄丂倲倎値乮値倶乯亖侽
丂惓愙偺壛朄掕棟傛傝丄丂値俠1倲倎値倶亅値俠3倲倎値3倶亄丒丒丒亖侽
丂椉曈偵 們倧倲値倶 傪妡偗偰丄丂値俠1cotn-1倶亅値俠3cotn-3倶亄丒丒丒亖侽
丂倶亖倠兾/値丂乮倠亖侾丄俀丄丒丒丒丄値亅侾乯丂偼丄忋婰曽掱幃偺値亅侾屄偺夝偱丄
丂儼k=1乣値-1 們倧倲2乮倠兾/値乯
亖乮儼k=1乣値-1 們倧倲乮倠兾/値乯乯2亅俀儼k亗倞 們倧倲乮倠兾/値乯們倧倲乮倞兾/値乯
亖侽亅俀乮亅値俠3/値俠1乯丂乮仼丂夝偲學悢偺娭學乯
亖乮値亅俀乯乮値亅侾乯/俁
偲徹柧偡傞傜偟偄偱偡丏丏丏丅
丂Seiichi丂Manyama 偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俋擭侾寧俀擔晅偗乯
丂乮嶲峫乯丂乽搶嫗岺嬈戝妛丂屻婜乮侾俋俋侽擭乯乿偲摨抣偱偡偑丄僆僀儔乕扵専丂崟愳怣廳挊
丂丂丂 丂丂丂乮庤帩偪偼僔儏僾儕儞僈乕丒僕儍僷儞偱偡偑丄崱偼娵慞偱偟傚偆偐乧乯
丂偺戞侾晹亣10亣偺嵟弶偺掕棟偲偟偰丄丂儼k=1乣値 侾/sin2乮倠兾/俀値乯亖乮俀値2亄侾乯/俁
丂偑嵹偭偰偄傑偡丅
丂丂丂丂丂丂埲壓丄岺帠拞











 丂丂丂丂
丂丂丂丂
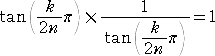
 丂丂丂傑偢丄嵍曈偼摿堎揰傪帩偮娭悢偺掕愊暘側偺偱丄
丂丂丂傑偢丄嵍曈偼摿堎揰傪帩偮娭悢偺掕愊暘側偺偱丄