カタラン数 
数学セミナー(2009 8月号)の特集で、寺尾宏明氏(北大・理)がカタラン数のことを取
り上げておられる。2006オープンキャンパスで高校生や一般の方を対象に話されたもの
ということで興味深く読ませていただいた。
その中で、実は当HPで既に、「三角形分割」や「最短経路問題」で、「カタラン数」のことに
触れているということに気づかされた。
何でも、「カタラン数」の解釈の仕方にはいろいろあって、2009年4月3日現在、170通
りもあるそうである。
「カタラン数」という名は、ベルギーの数学者 E.C.Catalan(1814~1894) の名に由来す
るという。
n 番目のカタラン数は、「Cn」と記される。
カタラン数の解釈として、私的には「トーナメント(勝ち抜き戦)表の場合の数」が一番分か
りやすいような気がする。
例 題 m チームがトーナメント戦を行う。各試合に引き分けはないものとすると、
優勝チームが決まるまで全部で m-1 試合が必要であることは自明だろう。
それではその試合のやり方は何通りあるのだろうか。ただし、m≧2 とする。
いま、 Cn : n+1 チームによるトーナメント表の場合の数 とする。
(イ) m=2 のとき、
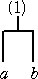
で、1種類しかない。 このとき、 C1=1 となる。
(ロ) m=3 のとき、
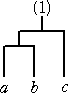
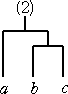
で、2種類しかない。 このとき、 C2=2 となる。
(ハ) m=4 のとき、
で、5種類しかない。 このとき、 C3=5 となる。
ところで、上図の(イ)(ロ)(ハ)を眺めていると、演算の結合法則が関係していそうな雰囲
気が漂ってくる!実のところ、カタランの当初の考え方と聞く。
すなわち、(イ)の(1)は、「 a に b を掛ける」とも理解される。(もちろん「足す」と考えてもよい。)
このことを、「(ab)」 と書くことにすると、
(ロ)の(1)は、((ab)c) だし、 (ロ)の(2)は、(a(bc)) という意味になる。
また、(ハ)の(1)は、(((ab)c)d) だし、(ハ)の(2)は、((a(bc))d) となり、
(ハ)の(3)は、((ab)(cd)) で、(ハ)の(4)は、(a((bc)d)) となり、
(ハ)の(5)は、(a(b(cd))) であるものと解釈できる。
この解釈は、さらに次のように考えると、道順の問題に翻訳される。
すなわち、「 (ab) 」は、「 a に b を掛ける」ということなので、「 ab× 」と書くことにする。
このとき、 ((ab)c) は、 ab×c× 、(a(bc)) は、 abc×× と書ける。
また、(((ab)c)d) は、 ab×c×d× 、((a(bc))d) は、 abc××d× 、
((ab)(cd)) は、 ab×cd×× 、(a((bc)d)) は、 abc×d×× 、
(a(b(cd))) は、 abcd××× と書ける。
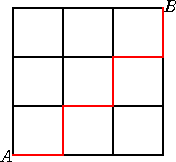
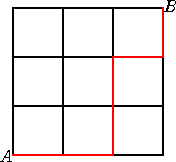
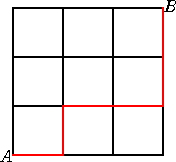
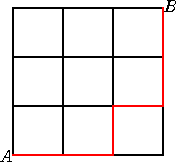
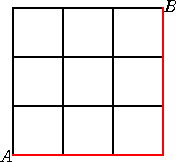
以下では、(ハ)の場合について、道順の場合の数との対応を考えよう。
そこで、次のような3×3の格子状の道を準備する。

点Aを出発し、点Bに至る道を考える。ただし、
ab×c×d×などの順列の2番目以降において、
文字(b、c、d)ならば、「-」(横に移動)、 掛け算「×」ならば、「|」(縦に移動)
するものとする。このとき、
| ab×c×d× |
|
abc××d× |
|
ab×cd×× |
 |
|
 |
|
 |
| |
|
|
|
|
| abc×d×× |
|
abcd××× |
|
|
 |
|
 |
|
|
 |
上記の道順の方法は、ちょうど左図のような街路の最短
経路の場合の数に等しい。
その場合の数は、「最短経路問題」によれば、
4C2-1=5(通り)
で、上記の結果と一致する。 |
一般に、n+1 チームによるトーナメント表を考え、それを道順の問題に翻訳すると、下図
の街路の点Aから点Bまでの最短経路の場合の数が、カタラン数 Cn となる。
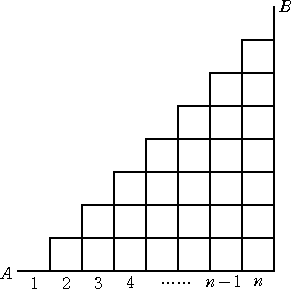
このとき、下図のような補助の街路を考えることにより、Cn が求められる。
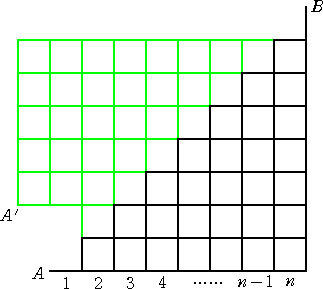 |
左図より、
Cn=2n-2Cn-1-2n-2Cn-3
で、上式の右辺をさらに計算すると、
2(2n-1)!/{(n+1)!(n-1)!}
すなわち、
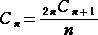
という公式が得られる。 |
この公式により、カタラン数を全て求めることが出来る。
| n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
・・・ |
| Cn |
1 |
2 |
5 |
14 |
42 |
132 |
429 |
1430 |
4862 |
16796 |
・・・ |
ところで、カタラン数と組合せの式の関係と言えば、巷間では、

が広く知れ渡っているようである。これは、下図のような補助街路を用いて、最短経路を求
めることにより得られる。
 |
左図より、
Cn=2nCn-2nCn-1
で、何れも、

となるので等しいのは当然だが、素朴
な疑問で、どちらの方が覚えやすいの
かな? |
上記では、最短経路問題として、 Cn=2nCn-2nCn-1 を導いたが、別な視点で、こ
の公式の意味づけを考えてみよう。
例 500円硬貨を持つ人が n 人、千円札を持つ人が n 人の計 2n 人が一列に並ぶ。
各自より、500円を集金するとき、集金する人がおつりを用意しなくても済むような並び
方は何通りあるか。
この問題で、例えば、n=3 とし、500円硬貨を持つ人を○、千円札を持つ人を●で表し、
実際に並び方を書いてみよう。
まず、おつりのことを考えずに、並び方の全てを書きだしてみると、
| ○○○●●● |
|
○○●○●● |
|
○○●●○● |
|
○○●●●○ |
|
○●○○●● |
|
|
|
|
|
|
|
|
|
| ○●○●○● |
|
○●○●●○ |
|
○●●○○● |
|
○●●○●○ |
|
○●●●○○ |
|
|
|
|
|
|
|
|
|
| ●○○○●● |
|
●○○●○● |
|
●○○●●○ |
|
●○●○○● |
|
●○●○●○ |
|
|
|
|
|
|
|
|
|
| ●○●●○○ |
|
●●○○○● |
|
●●○○●○ |
|
●●○●○○ |
|
●●●○○○ |
の 6C3=20 通りある。このうち、おつりを用意せずに済む並び方は、次の5通りである。
(上記の表の内の青色部分)
| ○○○●●● |
|
○○●○●● |
|
○○●●○● |
|
○●○○●● |
|
○●○●○● |
問題は、おつりが不足する場合の数の数え方である。次の15通りが該当する。
| ○○●●●○ |
|
○●○●●○ |
|
○●●○○● |
|
○●●○●○ |
|
○●●●○○ |
|
|
|
|
|
|
|
|
|
| ●○○○●● |
|
●○○●○● |
|
●○○●●○ |
|
●○●○○● |
|
●○●○●○ |
|
|
|
|
|
|
|
|
|
| ●○●●○○ |
|
●●○○○● |
|
●●○○●○ |
|
●●○●○○ |
|
●●●○○○ |
上記の15通りの内、おつり不足が最初に発生する位置は、それぞれ赤色の部分である。
この場合の数を数えるために、●までの○と●を入れかえる。
この操作により、●の直前までは、○と●は同数なので、必ず、○が1個増え、●が1個
減る。
| ●●○○○○ |
|
●○●○○○ |
|
●○○○○● |
|
●○○○●○ |
|
●○○●○○ |
|
|
|
|
|
|
|
|
|
| ○○○○●● |
|
○○○●○● |
|
○○○●●○ |
|
○○●○○● |
|
○○●○●○ |
|
|
|
|
|
|
|
|
|
| ○○●●○○ |
|
○●○○○● |
|
○●○○●○ |
|
○●○●○○ |
|
○●●○○○ |
このとき、上記の場合の数は、○4個と●2個の順列の総数に等しいので、
6C2=15 通りである。
よって、求める場合の数は、 6C3-6C2=5 (通り) である。
上記の考え方を一般化すると、
まず、500円硬貨を持つ人が n 人、千円札を持つ人が n 人の計 2n 人が一列に並ぶ
場合の数は、 2nCn 通りある。このとき、あるところでおつり不足が発生する場合の数は、
500円硬貨を持つ人が n+1 人、千円札を持つ人が n-1 人の計 2n 人が一列に並ぶ
場合の数に等しいので、 2nCn-1 通りある。
よって、求める場合の数は、 2nCn-2nCn-1 通りある。
(コメント) 背景に最短経路問題を意識したので、ちょっとスッキリしないような意味づけで
した。読者の方で、「これは!」という意味づけをお持ちの方は是非ご教示下さい。
平成21年8月11日付けで、HN「凡人」さんよりカタラン数の漸化式の話題をいただいた。
トーナメント戦の考え方において、次のように考えると、カタラン数についての漸化式が得
られる。
「n+1 チームによるトーナメント戦の決勝の相手は、
n チームによるトーナメント戦の優勝チームと、残り 1 チーム
n-1 チームによるトーナメント戦の優勝チームと、
残り 2 チームによるトーナメント戦の優勝チーム
n-2 チームによるトーナメント戦の優勝チームと、
残り 3 チームによるトーナメント戦の優勝チーム
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
2 チームによるトーナメント戦の優勝チームと、
残り n-1 チームによるトーナメント戦の優勝チーム
1 チームと、残り n チームによるトーナメント戦の優勝チーム
の各場合が考えられるので、 C0=1 として、
Cn=Cn-1・C0+Cn-2・C1+Cn-3・C2+・・・+C0・Cn-1
が成り立つ。
(コメント) 凡人さん、ありがとうございます。とても分かりやすい導き方ですね!でも、この
漸化式を解くことは可能なのでしょうか?解はもう分かっているので、漸化式とい
うよりも、一つの性質ととらえておけばいいのかな?
カタラン数 Cn はまた、凸 (n+2)角形の三角形分割の個数としてもとらえられる。
次のように考えればよい。( → 参考:「三角形分割」)
左辺以外の辺に時計回りに、a、b、c、・・・ と文字を割り当て、三角形の第3の辺に、他
の2辺の積を割り当てる。
例 三角形の場合
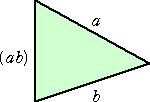 この場合、 C1=1 となる。
この場合、 C1=1 となる。
例 四角形の場合

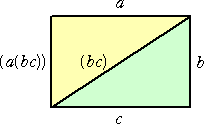
となり、演算結果 ((ab)c) 、(a(bc)) と三角形分割の方法とが関連づけられる。
この場合、 C2=2 となる。
「三角形分割」において、次のことを示した。
凸 n 角形( n≧3 )において、三角形分割の方法の数が、F(n) 通りあるものとする。
明らかに、F(3)=1 である。 いま、n≧4 とする。 3<k<n において、凸 n 角形は、
3つの部分に分割される。
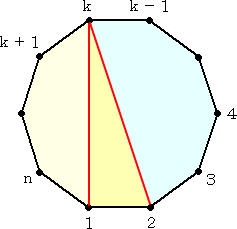 |
F(n) の定義より、
F(n) =1・F(n-1)+F(3)・F(n-2)+・・・
+ F(k-1)・F(n-k+2) +・・・
+ F(n-2)・F(3) +F(n-1)・1
が成り立つ。 |
この公式を用いて、カタラン数 Cn を計算してみよう。
C1=F(3)=1
C2=F(4)=1・F(3)+F(3)・1=2
C3=F(5)=1・F(4)+F(3)・F(3)+F(4)・1=2+1+2=5
C4=F(6)=1・F(5)+F(3)・F(4)+ F(4)・F(3) +F(5)・1=5+2+2+5=14
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
ここで、 C0=1 とすれば、例えば、C4 は、
C4=C0・C3+C1・C2+ C2・C1 +C3・C0
と書き直せるように、一般のカタラン数 Cn に関する漸化式
Cn=Cn-1・C0+Cn-2・C1+Cn-3・C2+・・・+C0・Cn-1
の成り立つことが、F(n) に関する漸化式より分かる。
「三角形分割」において、F(n) に関する漸化式の一般項
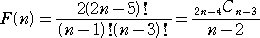
を求めることができた。 Cn = F(n+2) という関係から、Cn の一般項
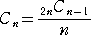
が直ちに得られる。この式と最短経路の問題で得られた Cn の式
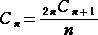
は、当然同じ値になる。(すなわち、 2nCn-1=2nCn+1 より明らか!)
(コメント) 上記の話で、HN「凡人」さんの疑問に答えられたでしょうか...?
平成21年8月17日付けで、「凡人」さんがカタラン数の漸化式の解釈に取り組まれた。
(一部文言等を修正させていただきました!)
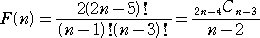
より、F(n+2)=2nCn-1/n=Cn
一方、F(n+3)=2n+2Cn/(n+1) なので、
F(n+3)/F(n+2)=n・2n+2Cn/{(n+1)・2nCn-1}=2(2n+1)/(n+2)
よって、 Cn = F(n+2) より、
(n+2)・Cn+1=2(2n+1)・Cn
が成り立つ。この式は、三角形分割の個数 F(n) から得られたが、最初から、
(n+2)・Cn+1=2(2n+1)・Cn
という漸化式が導けないかというのが「凡人」さんの意図するところであろう。
例 4・C3=10・C2 の解釈を考えてみよう。
C2=2 は、次の2通りであった。


このうちの1通り、例えば、

に、新しい1チームを加えるために新しい試合を追加する方法を考える。
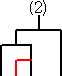

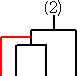

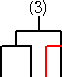
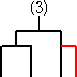

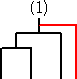
上記の通り、10通りある。同様にして、

に、新しい1チームを加えるために新しい試合を追加する方法を考えると、
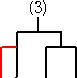
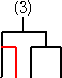
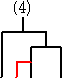
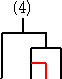
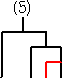

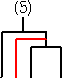
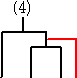
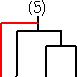
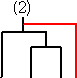
で、これも10通りある。これらを、C3=5 の場合
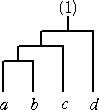
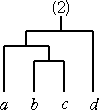
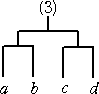

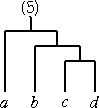
と比較すると、上記の20通りの中には、4通りずつ同じものが出現していることが分かる。
(トーナメント表の番号が同じものは、同じトーナメント表!)
以上から、漸化式 4・C3=10・C2 の成り立つことが分かる。
上記のことを一般化して、「凡人」さんは軽妙に次のように考えられた。
1.(n+1)チームによるトーナメント表の縦線の本数は「試合数×2+1」本であるが、試
合数は、n であるので、2n+1(本)の縦線がある。
このトーナメント表に新たに 1チームを加えるには、2n+1(本)の縦線のうちの
1 本
から横に線を出して張り出しのような形で 1 チーム分の試合を追加する。
2.横線は左右どちらにも出す事ができて、それらは区別されるので、計 2(2n+1)通り
の増やし方がある。
3.(n+1)チームでの全てのトーナメント表で同じことを行うと、2(2n+1)・Cn 通りにな
る。
4.ところで、(n+2)チームのトーナメント表で、新しく加えられた 1
チームの入る場所を
区別して考えると、(n+2)・Cn+1 通りのトーナメント表が得られる。
5.上述の 3.と4.のトーナメント表の数は一致するので、漸化式
(n+2)・Cn+1=2(2n+1)・Cn
が得られる。
(コメント) 「凡人」さんの非凡さに感動しました! このような経験をさせていただいた「凡
人」さんに感謝します。この考え方をすれば、何も三角形分割を持ち出すことなく、
漸化式が作れますね。
漸化式 (n+2)・Cn+1=2(2n+1)・Cn より、
(n+1)・Cn=2(2n-1)・Cn-1
n・Cn-1=2(2n-3)・Cn-2
(n-1)・Cn-2=2(2n-5)・Cn-3
・・・・・・・・・・・・・・・・・・・・・
4・C3=10・C2
3・C2=6・C1
これらを辺々かけて、
(n+1)!・Cn/2=2n-1・(2n-1)!/{2n-1・(n-1)!}=(2n-1)!/(n-1)!
よって、Cn=2(2n-1)!/{(n+1)!(n-1)!}
すなわち、
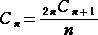
が得られる。
上記で、三角形分割と演算の順番の関係を見たが、円周上の互いに交差しない弦の引
き方にも関係することを以下に見てみよう。
円周上に 2n 個の点があるものとする。
例 n=1 のとき
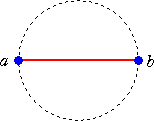 |
これは、 (ab) に相当し、括弧のつけ方に注目すれば、
( )
で、その場合の数は、カタラン数 C1=1 と一致する。
|
例 n=2 のとき
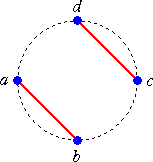
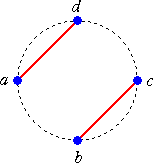
これらは、a を省いて考えると、 (b(cd)) や ((bc)d) となり、3文字 A、B、C の場
合の演算の結合の仕方: (A(BC)) や ((AB)C) の場合の数に一致するので、カタラ
ン数 C2=2 となる。
例 n=3 のとき
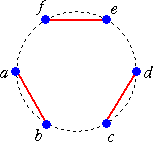
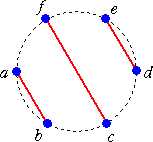
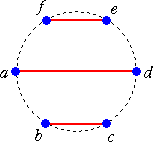

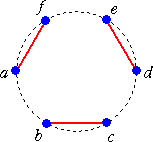
これらは、a を省いて考えると、
(b(cd)(ef)) 、(b(c(de)f)) 、((bc)d(ef)) 、 ((b(cd)e)f) 、 ((bc)(de)f)
となり、さらに、b を省いて、括弧のつけ方を考慮すると、4文字 A、B、C、D の場合の演
算の結合の仕方
((AB)(CD)) 、((A(BC))D) 、(A(B(CD))) 、(((AB)C)D) 、(A((BC)D))
の場合にそれぞれ対応するので、カタラン数 C3=5 と一致する。
これらのことを一般化して、次の事実が成り立つ。
円周上の 2n 個の点を互いに交差しない弦で結ぶ方法の数は、カタラン数 Cn
(証明)
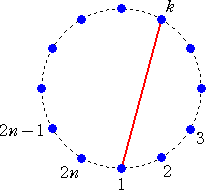 |
円周上の 2n 個の点を互いに交差しない弦で結ぶ方
法の数を F(n)とおく。
点 1 と点 k を結ぶ弦で、円周上の 2n 個の点を2つ
のグループに分ける。点 k は、点 1 と同じグループに
入るものとする。
このとき、題意より、k の値が奇数になることはない。
k=2、4、6、・・・、2n-2、2n と場合分けして考える。 |
k=2 のとき、 円周上 2n-2 個の点を互いに交差しない弦で結ぶ方法の数は、
F(n-1)通りで、その1通りに対して、残りの2点の弦の引き方は、1通り。
よって、この場合の数は、 1・F(n-1) 通り
k=4 のとき、 円周上 2n-4 個の点を互いに交差しない弦で結ぶ方法の数は、
F(n-2)通りで、その1通りに対して、点 1 と点 4 を除いた残りの2点の弦の引き方は、
F(1)通り。
よって、この場合の数は、 F(1)・F(n-2) 通り
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
k=2n-2 のとき、 点 1 と点 2n-2 を除いた残りの2点の弦の引き方は、F(1)通り
で、その1通りに対して、円周上 2n-4 個の点を互いに交差しない弦で結ぶ方法の数は、
F(n-2)通り。
よって、この場合の数は、 F(n-2)・F(1) 通り。
k=2n のとき、 点 1 と点 2n の弦の引き方は、1通りで、その1通りに対して、円
周上、2n-2 個の点を互いに交差しない弦で結ぶ方法の数は、F(n-1)通り。
よって、この場合の数は、 F(n-1)・1 通り
以上から、求める場合の数 F(n)は、
F(n) =1・F(n-1)+F(1)・F(n-2)+・・・+ F(n-2)・F(1) +F(n-1)・1
となる。これは、カタラン数 Cn の漸化式
Cn=1・Cn-1+C1・Cn-2・+・・・+C1・Cn-2・+Cn-1・C0
に一致するので、F(n)は、カタラン数 Cn に一致する。 (証終)
当HPがいつもお世話になっているS(H)さんが、平成21年3月21日付けで、数学的帰納
法の練習問題として、次のような問題を提起された。
集金問題 ある劇場の入場料は、5千円とする。5千円札しかもっていない n(≧ 1)人と、
1万円札しかもっていない n 人の合計 2n 人が劇場前の広場で勝手に円形の
輪を作って開場を待っているとする。
このとき、劇場の入口の受付人は、ある適当な人から時計回りに集金すれば、釣り銭に不
足することがないようにできることを示せ。
(この集金問題が必ず可能であることは、カタラン数 Cn≧1 から明らかだろう。
→ 参考:「集金問題」)
命題 P : 全ての自然数 n に対して、劇場の入口の受付人は、ある適当な人から時計回
りに集金すれば、釣り銭に不足することがないようにできる
(証明) 数学的帰納法による。
n=1 のとき、 5千円札しかもっていない人と、1万円札しかもっていない人の合計 2人
が劇場前の広場で待っているので、5千円札しかもっていない人から、5千円札を受け取り、
次に、1万円札しかもっていない人から1万円札を受け取り、5千円札を渡せばよい。
よって、n=1 のとき成り立つ。
n=k(k≧1)のとき、命題 P が成り立つと仮定する。
すなわち、5千円札しかもっていない k(≧ 1)人と、1万円札しかもっていない k 人の合計
2k 人が劇場前の広場で勝手に円形の輪を作って開場を待っていて、劇場の入口の受付
人は、ある適当な人から時計回りに集金すれば、釣り銭に不足することがないようにできる。
今、5千円札しかもっていない k+1人と1万円札しかもっていない k+1人の合計2k+2
人が劇場前の広場で勝手に円形の輪を作って開場を待っているものとする。
この中には、5千円札しかもっていない人がいて、しかも、時計回りで隣の人が、1万円札
しかもっていない人である組合わせが必ず存在する。
この2人を除くと、残りは、5千円札しかもっていない k(≧ 1)人と、1万円札しかもっていな
い k 人の合計 2k 人が劇場前の広場で勝手に円形の輪を作って開場を待っていて、劇場
の入口の受付人は、ある適当な人から時計回りに集金すれば、釣り銭に不足することがな
いようにできる。途中で、最初に見つけた2人からは、5千円札しかもっていない人から、5
千円札を受け取り、次に、1万円札しかもっていない人から1万円札を受け取り、5千円札
を渡せばよい。
よって、 n=k+1 のときも、命題 P は成り立つ。
以上から、全ての自然数 n に対して、劇場の入口の受付人は、ある適当な人から時計
回りに集金すれば、釣り銭に不足することがないようにできることが示された。 (証終)
さて、次は、カタラン数の生成関数の話題に移ろう。
カタラン数については、上記の計算で、
| n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
・・・ |
| Cn |
1 |
2 |
5 |
14 |
42 |
132 |
429 |
1430 |
4862 |
16796 |
・・・ |
であることを見た。そこでは、カタラン数そのものは、バラバラな感じであったが、これら全て
のカタラン数を係数とする1つの多項式を考え、カタラン数の持つ性質を追究しようというの
が、生成関数の考え方である。
生成関数には、カタラン数に関する情報が全て含まれると言っても過言ではないだろう。
カタラン数 Cn の生成関数とは、 C0=1 として、
F(x)=C0+C1・x+C2・x2+C3・x3+・・・+Cn・xn+・・・
と書けるものを言う。
具体的には、 F(x)=1+x+2x2+5x3+14x4+・・・ という多項式である。
ここで、 Cn=Cn-1・C0+Cn-2・C1+Cn-3・C2+・・・+C0・Cn-1 から、
F(x)2=C02+(C1・C0+C0・C1)x+(C2・C0+C1・C1+C0・C2)x2+・・・
=C1+C2x+C3x2+・・・
なので、 1+x・F(x)2=C0+C1・x+C2・x2+C3・x3+・・・=F(x) であると言える。
すなわち、 F(x)は、等式 x・F(x)2-F(x)+1=0 を満たす。
これを、F(x)に関する2次方程式と考えれば、その解は、
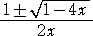
となるが、F(0)=1 なので、
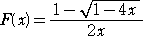
と書ける。これが、カタラン数 Cn の生成関数となる。
ここで、Taylor 展開のことを考えれば、Cn=F(n)(0)/n! が成り立つ。
例
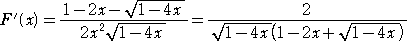
なので、 F’(0)=1 より、 C1=F’(0)/1!=1 となる。
2項定理というと、(a+b)n の展開公式だが、実は、n の値は自然数に限らず任意の実
数においても成り立つことが知られている。
( → 参考「超越数を手計算で求める」における二項級数の項)
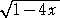 を二項級数に展開して、xn+1 の項を求めると、
を二項級数に展開して、xn+1 の項を求めると、
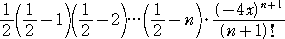
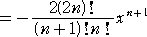
となる。したがって、
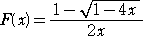
を二項級数に展開したときの xn の項は、
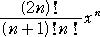
となる。よって、カタラン数 Cn の値は、

すなわち、

となる。
(追記) 平成25年5月18日付け
私の代数学の恩師 土井先生が勤められていた立命館大学の文学部・産業社会学部
A方式(2013年)でカタラン数を題材とする問題が出題された。
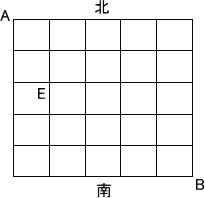 |
|
 |
【図1】 |
|
【図2】 |
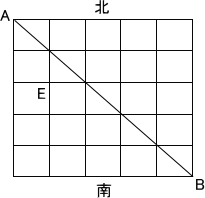
上図で東西、南北それぞれ6本の線分は道であるが、対角線ABは道ではないとする。
(1) 【図1】において、AからEを通ってBへ行く最短経路は何通りあるか。(105通り)
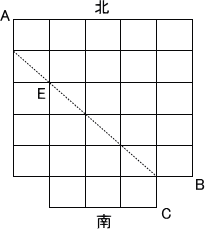 |
(2) 左図は、(1)の経路において、EからBへ行く経路
を、図の点線を軸に対称移動させたものであり、Bは
Cに移る。この図において、AからEを通ってCへ行く
最短経路は何通りあるか。(105通り) |
(3) 【図2】において、対角線ABより南側を通らないで、AからBへ行く最短経路は何通り
あるかを考える。
(イ) (2)の図のような考え方を用いて、AからBへ行く最短経路のうち、対角線ABより
南側を通る最短経路は何通りあるか。(210通り)
(ロ) 対角線ABより南側を通らないで、AからBへ行く最短経路は何通りあるか。(42通り)
(4) 東西、南北それぞれn+1本の線分を道とし、対角線ABは道ではないとする。このとき、
対角線ABより南側を通らないで、AからBへ行く最短経路は何通りあるか。
((2n)!/(n!(n+1)!)通り)
(コメント) 上記では、紙面の都合で説明を大幅に省略してあるが、実際の本文では、経路
を数える手順が図を用いて丁寧に導かれている。ただ、説明が長すぎて、受験生
が試験時間内に対応できたかはちょっと不明...。
(4)はまさに、カタラン数 Cn である。
(追記) 「カタラン数から派生した疑問」と題して、当HPがいつもお世話になっているHN
「moonlight」さんからご投稿いただきました。(令和4年1月15日付け)
先日ネタが切れて、そういえばと、「カタラン数」知らんかもと紹介を兼ねて、こんな問題を
投げてみました。
下図のように円周上に10個の点があり、10個の点を2点ずつの組にして線分で結ぶ。
但し、線分は交差しないものとする。全部で、何通りの結び方があるか。
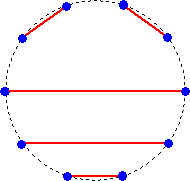
ごく平凡なカタラン数の問題なのですが、その後で、ついつい、「10個の点は等間隔だから
回したり裏返して同じパターンになるものが沢山あるよなぁ」と...。
そこで、「回転させたり裏返したりして同じ結び方になる(見える)ものは1通りと数えると全
部で何通りあるか」と訊いてみようとして... えっと、どう説明できるか... と思い止まってしまし
ました。若い頃なら勢いで訊いていたところでしょう。歳をとってしまいました。
で、何通りあるかはどのように考えれば要領が良いでしょうか。もちろん点の数が、2nの
場合であれば、とても有難いのですが... (いつも質問ばかりで申し訳ない)。
らすかるさんからのコメントです。(令和4年1月15日付け)
回答ではないのですが、もしかして、「A006082」の数列ですか?違ったらごめんなさい。
# 要領のよい数え方は今のところわかっていません。
moonlight さんからのコメントです。(令和4年1月15日付け)
どうでしょうか。ちょっと眺めただけではよく分かりません。集中力が欠けてきたのかも...。
Rubyでプログラムを書いて、確認してみました。10項までは合致したので、同じものかもしれ
ません。
らすかるさんからのコメントです。(令和4年1月16日付け)
私も確認しました。手作業では、「1,2,3,6,12,27」までで音を上げてしまったので、特定
できませんでしたが、プログラムを作って、次の「65」まで確認すると、「1,2,3,6,12,27,65」
を含む数列は、この一つしかないですね。
ということで、やはりこの数列で正しそうです。
(プログラムでは490まで確認しました)
このページに非常に複雑な計算式がありますが、もし要領よく数えられるとしたら、その要
領に従って計算式ももう少し簡単になっても良さそうなものですので、要領よく数えるうまい
方法はなさそうな気がします。
(コメント) monlight さんの問題設定は、「カタラン数」の問題設定と微妙に違うんですね!
回転や裏返しで重なるものは同一視するというのは、「カタラン数」の計算にはない
設定です。
らすかるさんが手作業で「1,2,3,6,12,27」までを確認された由、私もらすかるさんに倣っ
て挑戦しようと思い立ちましたが、n=5までで心が折れ力尽きました。大変な計算ですね。
n=1のとき、 1通り
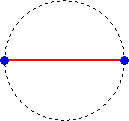
n=2のとき、 1通り
n=3のとき、 2通り
n=4のとき、 3通り
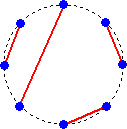

n=5のとき、 6通り
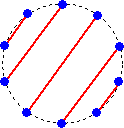
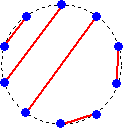
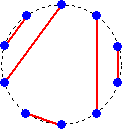
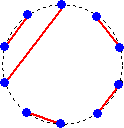
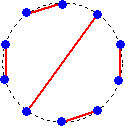
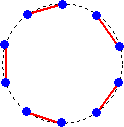
GAI さんからのコメントです。(令和4年1月18日付け)
# 要領のよい数え方は今のところわかっていません。
サイト「A006082」でのリングを頼りにプログラム化(PARI/GP)したら、
gp > p(n)=binomial(2*n,n)/(n+1)+sumdiv(n,d,eulerphi(n/d)*binomial(2*d,d))
-binomial(2*n,n)+n*binomial(n,floor(n/2))
gp > q(n)=binomial(2*n,n)/(n+1)+binomial(n+1,(n+1)/2)
+sumdiv(n,d,eulerphi(n/d)*binomial(2*d,d))-binomial(2*n,n)+n*binomial(n,floor(n/2))
と組んで、nの奇遇に分けて使い分けるといいようです。
gp > for(n=1,30,if(n%2==0,print1(p(n)/(4*n)","),print1(q(n)/(4*n)",")))
1,1,2,3,6,12,27,65,175,490,1473,4588,14782,48678,163414,555885,1913334,6646728,23278989,
82100014,291361744,1039758962,3729276257,13437206032,48620868106,
176611864312,643834562075,2354902813742,8640039835974,31791594259244,
一方、「A006082」(ただし、n=1,2,3,・・・)
1, 1, 2, 3, 6, 12, 27, 65, 175, 490, 1473, 4588, 14782, 48678, 163414,
555885, 1913334,
6646728, 23278989, 82100014,291361744, 1039758962, 3729276257, 13437206032,
48620868106, 176611864312, 643834562075, 2354902813742, 8640039835974,
31791594259244
らすかるさんからのコメントです。(令和4年1月18日付け)
プログラムの高速化をあれこれ考えているうちに、「要領のよい数え方」がわかってきまし
た。
結ぶ点を A、B、C、… として、最短:(A,B) (AとBを結ぶという意味)・・・これを「1」とします。
AとDを結ぶ場合は、BとCを結ぶ必要があります。
つまり、(A,D)(B,C)・・・このAとDのように、3つ離れた点を結ぶものを「2」とします。
AとFを結ぶ場合は、B~Eは、(A,F)(B,E)(C,D) または、(A,F)(B,C)(D,E) の2通りがあります。
・・・このAとFのように、5つ離れた点を結ぶものを「3」とします。
点が10個のとき、最も離れていて「3」です。
「1」「2」「3」で足して5になる順列を考えます。ただし、回転は同一視しますので、3+2と2+3
は同じです。
3+2:「3」が2通り、「2」が1通りなので2×1=2通り
3+1+1:同様に、2通り
ただし、3+2と3+1+1で一つ重複が発生(このように対角を結ぶ場合は重複に注意が必要)
2+2+1:1×1×1=1通り
2+1+1+1:同様に1通り
1+1+1+1+1:同様に1通り
従って、n=10 の場合は、2+2-1+1+1+1=6(通り) となります。
n=12の場合は、合計6を考えます。
3+3:一つ目の「3」と二つ目の「3」で異なるパターンにする場合が重複しますので、
2×2-1=3通りです。
3+2+1:2×1×1=2通り
3+1+1+1:2×1×1×1=2通り
2+2+2:1×1×1=1通り
2+2+1+1:1通り
2+1+2+1:1通り
2+1+1+1+1:1通り
1+1+1+1+1+1:1通り 以上、合計12通り
nが14以上になると、「4」が必要になりますが、「4」は非対称の形が出現しますので少し
面倒になります。
moonlight さんからのコメントです。(令和4年1月18日付け)
らすかるさんの、このアイデアは面白いです。なるほど!そう数える手があったかと。
当HP読者のHN「Copyソル」さんからのコメントです。(令和5年6月2日付け)
Cn をn番目のカタラン数としたとき、
Cn=Σ[k=1,floor((n+1)/2)] (-1)^(k-1)*Cn-k*n+1-kCk
(floor(x)は床関数で、nCk は二項係数)
の等号が成立することを、証明することは可能でしょうか?
一応、コンピュータで、n=100 まで成り立つことは検証済みです。偶然、上記の成立しそう
な関係を見つけたのですが、証明する手立ても実力もなく、軽く調べた限り、このような総和
で記した文献が見当たらなかったため、質問した次第です。(→ 参照:「Catalan Number」)
(コメント) いくつか試算してみた。 C1=1、C2=2、C3=5、・・・ に注意して、
C2=C1・2C1=1・2=2 、C3=C2・3C1-C1・2C2=2・3-1・1=6-1=5 、・・・
なるほど...!
GAI さんからのコメントです。(令和5年6月2日付け)
カタラン数Cnの再帰的漸化式として、(ただし、C0=1 とする)
Cn=∑[k=0,n-1] Ck*Cn-1-k
Cn=∑[k=0,n-1] n-1C2k*2^(n-1-2*k)*Ck
Cn=∑[k=1,floor((n+1)/2)] (-1)^(k-1)*Cn-k*n+1-kCk
などがあるようです。(→ 参考:「A000108」のFORMULAの部分)
(→ 第3式の at さんによる証明)
DD++ さんからのコメントです。(令和5年6月3日付け)
「A000108」に掲載されているということは正しいということなんでしょうけど、OEIS には証明
までは載っていませんね。
カタラン数が関係するなら組み合わせで証明したいところですが、(-1)^k が入った式で、そ
れやるの、難しいんですよねえ。
式の意味を無視して式変形でやるなら、カタラン数も二項係数も階乗に直す方針になるん
でしょうか?まだやってみていませんけど...。
GAI さんからのコメントです。(令和5年6月6日付け)
カタラン数C(n)に関して、一般には、n×n の格子路に対して、(0,0)から(n,n)までを(0,0)、(n,n)
を結ぶ対角線より上方へははみ出さない部分で行ける経路の数を与えるものと紹介される例
をよく見る。
そこで、正方形の格子路を改め、n×mでの長方形の格子路を考え、x 軸方向へは、n、y
軸方向へは、mとし、(0,0)、(n,m)を結ぶ対角線を引き、この直線より上方へは立ち入らずに
(0,0)から格子点を通過しながら(n,m)地点に辿り着けるカタラン路が何通りあるかを考えるこ
とにする。
この求めたい総数を、C(n,m) と記して、式を構成しようと頑張ってみたのだが、意外とnに
よって構造が異なってしまうので、まだ、一つの式で表すものに辿り着けていません。
どなたか、関心を寄せられましたら是非、C(3,m)とC(4,m)に対して、どんな式(もしくはプロ
グラムで算出できるコード等)を発見されるのか、お示し願えれば有難いです。
らすかるさんからのコメントです。(令和5年6月6日付け)
私の解釈が間違っていなければ、
C(3,m)は、m=0~100に対して、
1,1,2,5,5,7,12,12,15,22,22,26,35,35,40,51,51,57,70,70,77,92,92,100,117,117,126,145,145,155,176,
176,187,210,210,222,247,247,260,287,287,301,330,330,345,376,376,392,425,425,442,477,477,
495,532,532,551,590,590,610,651,651,672,715,715,737,782,782,805,852,852,876,925,925,950,
1001,1001,1027,1080,1080,1107,1162,1162,1190,1247,1247,1276,1335,1335,1365,1426,1426,
1457,1520,1520,1552,1617,1617,1650,1717,1717
C(4,m)は、m=0~100に対して、
1,1,3,5,14,14,23,30,55,55,76,91,140,140,178,204,285,285,345,385,506,506,593,650,819,819,938,
1015,1240,1240,1396,1496,1785,1785,1983,2109,2470,2470,2715,2870,3311,3311,3608,3795,
4324,4324,4678,4900,5525,5525,5941,6201,6930,6930,7413,7714,8555,8555,9110,9455,10416,
10416,11048,11440,12529,12529,13243,13685,14910,14910,15711,16206,17575,17575,18468,
19019,20540,20540,21530,22140,23821,23821,24913,25585,27434,27434,28633,29370,31395,
31395,32706,33511,35720,35720,37148,38024,40425,40425,41975,42925,45526
のようになり、この値から式を作ると、
C(3,m)=[(m+3)/3]^2+[(m+1)/3][(m+4)/3]/2
C(4,m)=[(m+4)/4](4[(m+4)/4]^2-1)/3+[(m+1)/4][(m+5)/4]^2/2+[(m+2)/4][(m+6)/4](5[(m+2)/4]+1)/6
という式で表されそうです。
GAI さんからのコメントです。(令和5年6月6日付け)
自分では、この求めるべき経路数を一つずつ作図しながら求めていたものですから、mが
100までのデータは考えられもしませんでした。
nが3の時の数の並びの変化の状態から、k=m\3 (mを3で割ったときの商をk)、L=3*k+1
として置けば、通常の3×mの格子路での全経路数S=(3+m)!/(3!*m!)に対する比率が、m%3
の値に依存していることが起こりそうだと思われた。
つまり、
m%3==0 ==>C(3,m)=S/L
m%3==1 ==>C(3,m)=S/(L+3)
m%3==2 ==>C(3,m)=S/(L+4)
これに従い、プログラムを組んで並べて行き、m=20 位までぐらいを確認していました。
(なにせ手作業で図を描いてやっと経路数を見つけていたものですから)
これで上手く行きそうだと思ってしまったので、n=4も、k=m\4 (mを4で割ったときの商をk)
L=4*k+1 として置けば、通常の4×mの格子路での全経路数S=(4+m)!/(4!*m!)に対する比
率がm%4の値に依存していることが起こりそうだと思われた。
つまり、
m%4==0 ==>C(4,m)=S/L
m%4==1 ==>C(4,m)=S/(L+4)
m%4==2 ==>C(4,m)=S/(L+5)
m%4==3 ==>C(4,m)=S/(L+6)
ところがどっこい、実際に起こる経路数が、m%4==2 の場合、分数の値を返してきて反映
してくれない。
何とかSの値は利用したかったので、実際に起こる経路数と一致させるための調整が
m%4==2 ==>C(4,m)=(S-k*(k+1)*(4*k+5)/6)/(L+4)
へ辿り着きました。
Sから除くパターンの部分が、なぜか「A016061」に繋がっているのが不思議でした。
これを元にプログラムを組んで、やはり m=20 辺り位までしか確認していませんでした。
それでらすかるさんの値と比較し、m=98==2(mod 4) でも一致できていたので安心しました。
しかしこれを一つの式で表せられるなんて思ってもいませんでした。感じとしては、nが素数
である時は、例の規則で行けそうですが、nが合成数になると、途端に厄介になりそうです。
今、n=6に挑戦していますが、図を描いて正解数を求めるしか手がないので、らすかるさん、
前もってその配列数をm=100までを教えて貰えませんか?
らすかるさんからのコメントです。(令和5年6月6日付け)
C(6,m) なら、m=0~100 に対して、
1,1,4,12,23,42,132,132,227,377,525,728,1428,1428,2010,2803,3504,4389,7084,7084,9097,11654,
13793,16380,23751,23751,28931,35246,40356,46376,62832,62832,73950,87143,97584,109668,
141778,141778,162883,187453,206591,228459,285384,285384,322046,364124,396510,433160,
527085,527085,586638,654240,705789,763686,910252,910252,1002037,1105317,1183487,
1270752,1489488,1489488,1625096,1776599,1890570,2017169,2331924,2331924,2525439,
2740354,2901207,3079140,3518515,3518515,3786757,4083170,4304066,4547556,5145336,
5145336,5508104,5907251,6203610,6529292,7324878,7324878,7805193,8331713,8721393,
9148503,10187344,10187344,10811692,11493880,11997356,12547920,13881945,13881945,
14680520,15550580,16191123
のようになると思います。
(追記) Webサイト:「道順の場合の数を求めるテクニック」の「書き込み方式」に従って、
プログラミングすると簡単ですよ。
対角線を越える点をカウントしないようにするだけですから、
・(幅+1)×(長さ以上)の配列を作る(幅は3,4,6など、100まで出すなら「長さ以上」は101以上)
・配列全体を0にして(0,0)要素だけ1にする
・y=0~(長さ)まで以下の処理を行う
・x=0~(幅)まで以下の処理を行う(ただしy=0のときのみx=1から)
・(長さ)×x>(幅)×yのときxのループを抜ける(対角線を越える格子点)
・配列の(x-1,y)要素と(x,y-1)要素の和を(x,y)要素の値とする(ただしx-1やy-1が負のとき0)
これで最終的に(幅,長さ)要素に格納された値が答えです。
GAI さんからのコメントです。(令和5年6月6日付け)
ヒントをもらったので、PARIのソフトで挑戦してみました。配列がmatrixの道具しかなく、成分
は[1,1]から取ってあるので、微妙に取り方をずらしながら組んでみました。
F(n,m)={M=matrix(n+1,m+1,i,j,if(j==1,1,i==1&&j>1,0))};\
for(x=2,n+1,for(y=2,m+1,if(m*(x-1)<n*(y-1),next,\
M[x,y]=M[x-1,y]+M[x,y-1])));M
これより
gp > F(6,10)
%813 =
[1 0 0 0 0 0 0 0 0 0 0]
[1 1 0 0 0 0 0 0 0 0 0]
[1 2 2 2 0 0 0 0 0 0 0]
[1 3 5 7 7 7 0 0 0 0 0]
[1 4 9 16 23 30 30 0 0 0 0]
[1 5 14 30 53 83 113 113 113 0 0]
[1 6 20 50 103 186 299 412 525 525 525]
gp > F(6,18)
%818 =
[1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[1 2 3 4 4 4 4 0 0 0 0 0 0 0 0 0 0 0 0]
[1 3 6 10 14 18 22 22 22 22 0 0 0 0 0 0 0 0 0]
[1 4 10 20 34 52 74 96 118 140 140 140 140 0 0 0 0 0 0]
[1 5 15 35 69 121 195 291 409 549 689 829 969 969 969 969 0 0 0]
[1 6 21 56 125 246 441 732 1141 1690 2379 3208 4177 5146 6115 7084 7084 7084 7084]
あの手作業が夢のようです。
また、nが素数の場合は予想が当たるか確認してみた。n=7でやってみると、
F7(m)={k=m\7;L=7*k+1;S=(7+m)!/(m!*7!);}\
if(m%7==0,print(m";"S/L),m%7==1,print(m";"S/(L+7)),\
m%7==2,print(m";"S/(L+8)),m%7==3,print(m";"S/(L+9)),\
m%7==4,print(m";"S/(L+10)),m%7==5,print(m";"S/(L+11)),\
m%7==6,print(m";"S/(L+12)))
と組んで走らせると、
gp > for(m=1,50,F7(m))
1;1
2;4
3;12
4;30
5;66
6;132
7;429
8;429
9;715
10;1144
11;1768
12;2652
13;3876
14;7752
15;7752
16;10659
17;14421
18;19228
19;25300
20;32890 |
|
21;53820
22;53820
23;67860
24;84825
25;105183
26;129456
27;158224
28;231880
29;231880
30;278256
31;332112
32;394383
33;466089
34;548340
35;749398
36;749398
37;870922
38;1008436
39;1163580
40;1338117 |
|
41;1533939
42;1997688
43;1997688
44;2270100
45;2572780
46;2908360
47;3279640
48;3689595
49;4638348
50;4638348 |
一方、
G(n,m)={M=matrix(n+1,m+1,i,j,if(j==1,1,i==1&&j>1,0))};\
for(x=2,n+1,for(y=2,m+1,if(m*(x-1)<n*(y-1),next,\
M[x,y]=M[x-1,y]+M[x,y-1])));M[n+1,m+1]
から、
gp > for(m=1,50,print(m";"G(7,m)))
1;1
2;4
3;12
4;30
5;66
6;132
7;429
8;429
9;715
10;1144
11;1768
12;2652
13;3876
14;7752
15;7752
16;10659
17;14421
18;19228
19;25300
20;32890 |
|
21;53820
22;53820
23;67860
24;84825
25;105183
26;129456
27;158224
28;231880
29;231880
30;278256
31;332112
32;394383
33;466089
34;548340
35;749398
36;749398
37;870922
38;1008436
39;1163580
40;1338117 |
|
41;1533939
42;1997688
43;1997688
44;2270100
45;2572780
46;2908360
47;3279640
48;3689595
49;4638348
50;4638348 |
予想大当たり!!!
しかし、n=6の場合は、S=(6+m)!/(6!*m!) の数値から導くのは困難でした。
(未だに解決できずです。)
at さんが、
Cn=∑[k=1,floor((n+1)/2)] (-1)^(k-1)*Cn-k*n+1-kCk
の証明に取り組まれました。(令和5年6月7日付け)
∑[k=0,floor((n+1)/2)] (-1)^(k-1)*Cn-k*n+1-kCk=0
を示せばよいですね。
t の関数 f(t) をべき級数展開したときの t^n の係数を [t^n]f(t) と書くことにします。
Σ[k=0,floor((n+1)/2)] (-1)^(k-1)*Cn-k*n+1-kCk
=Σ[p=n-floor((n+1)/2),n] (-1)^(n-p-1)*Cp*p+1Cn-p
=Σ[p=0,∞] (-1)^(n-p-1)*Cp*p+1Cn-p
=Σ[p=0,∞] (-1)^(n-p-1)*Cp*[t^n]( (1+t)*(t*(1+t))^p)
=(-1)^(n-1)*[t^n]( (1+t)*Σ[p=0,∞] Cp*(-t*(1+t))^p)
=(-1)^(n-1)*[t^n]( (1+t)*(1-sqrt(1-4*(-t*(1+t))))/(2*(-t*(1+t))) )
=(-1)^(n-1)*[t^n]( (1-sqrt((1+2*t)^2))/(2*(-t)) )
=(-1)^(n-1)*[t^n](1)
=(-1)^(n-1)*0
=0.
DD++ さんからのコメントです。(令和5年6月7日付け)
なるほど、カタラン数は母関数で扱う方針がありましたか。
(コメント) 素晴らしいです!at さんに感謝します。DD++ さんには証明を若干修正していた
だきました。DD++ さんに感謝します。
at さんからのコメントです。(令和5年6月8日付け)
DD++ さん、ご指摘ありがとうございます。Σ[p=ceil((n-1)/2)~n] と書かなければいけない
ところを、間違って、Σ[p=floor((n-1)/2)~n] と書いてしまっていましたね。失礼しました。
以下、工事中







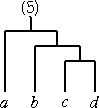







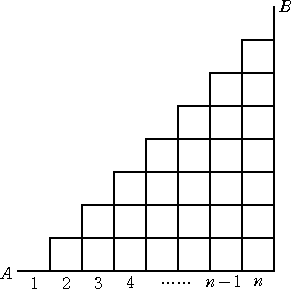


 この場合、 C1=1 となる。
この場合、 C1=1 となる。















































