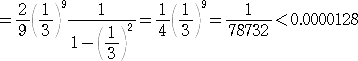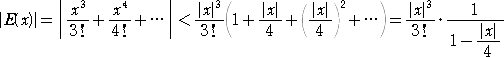超越数を手計算で求める 
いろいろな数を手計算で求めることは、その数のおおよその値の把握に有効なことはも
ちろん、その数に対して親近感が増すという意味でも、常々意識しなければいけないことだ
と思う。
当HPでは、平方根や立方根を手計算で求める方法について整理している。
(参考) 平方根・立方根を筆算で求める方法について
方程式による開平
また、「手計算が面白い」には、種々の数を手計算で求める方法がまとめられている。
平方根や立方根などの代数的数は、その定義方程式があるので、比較的手計算で求め
やすく、方法も、種々考えられる。
複素数 α が代数的数とは、有理数を係数とする代数方程式
aXn + bXn-1 + ・・・ + c = 0 ( n≧1 、 a≠0 )
の根になっている場合をいう。(→参考 「根と解の違い」)
(上記では、方程式の係数として、有理数体を考えているが、もちろん、一般の体
F上
の代数的数も定義される。このページでは、F として、有理数体に限定して、話を進
めることにする。)
代数的数 α に対して、上記のような性質を持つ方程式のことを、定義方程式という。
定義方程式は無数に存在するが、特に、左辺の多項式において、a = 1 で次数
n が最
小な多項式はただ一つに定まる。この多項式のことを、代数的数 α の最小多項式という。
最小多項式は、必ず、既約である。(すなわち、これ以上因数分解できない。)
例 虚数単位 i は、X2+1=0 を満たす。したがって、虚数単位 i は、代数的数である。
X2+1 は、虚数単位 i の最小多項式である。
代数的数について、次のことが知られている。
定理 2つの代数的数の 和・差・積・商 も代数的数である。
(もちろん、商の場合は、分母は、0以外とする。)
例 上記の定理から、 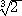 +
+ 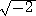 は代数的数である。その最小多項式は、
は代数的数である。その最小多項式は、
X6 + 6 X4 − 4 X3 + 12 X2 + 24 X + 8
である。 (参考 「方程式の生成」)
代数的数にならない複素数を、超越数という。
例 超越数としては、円周率 π や自然対数の底 e などが有名である。
1900年、ヒルベルトは、数学の将来の問題として「23の問題」を提出した。これらの問
題がどれほど解けたかが、数学の進歩を測る指標にもなっている。その中の7番目の問
題が、超越数に関するものである。(タイトルは、「種々の数の無理性と超越性」)
『 0 または 1 でない代数的数を α 、有理数でない代数的数を β とするとき、
数 α β は、超越数であるか? 』
上記の問題は、1934年 ゲルフォント、シュナイダーによって独立に肯定的に解決され
た。
したがって、eπ が超越数になることはもちろん、2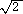 のような代数的数同士の組合せ
のような代数的数同士の組合せ
ですら、 が有理数でないということから、超越数となる。
が有理数でないということから、超越数となる。
円周率のおおよその値を手計算で求めることは、大変興味あることである。
(→ 参考 「大学入試問題001」 、 「円周率を近似する分数」)
ただ、円周率の場合、手計算よりむしろ、最近では、スーパーコンピュータの性能検査に、
円周率の計算が使われたりする。(→ 参考 「 π の歴史」)
自然対数の底 e の値も興味ある数であるが、手計算で求めることは、少し大変である。
1.01100 を計算した位では、2.7 位しか求まらず、2.718 という数にたどり着くには、
1.000110000 程度まで計算する必要がある。自然対数の底 e の値を実験で体感する
方法もある。(→ 参考 「自然対数の底 e の体感」)
このように、超越数を手計算で求めることは、代数的数の場合と違って、すんなりとはい
かない。
超越数 2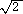 の場合はどうであろうか。
の場合はどうであろうか。
表計算ソフト Excel を用いて計算してみると、その値は、およそ 2.665144143・・・
となる。せめて小数点以下第3位ぐらいまでは、手計算で求めてみたいという希望はある
ものの、その方法はあるのだろうか?
 <1.5 なので、(21.5)2=8<9 より、2
<1.5 なので、(21.5)2=8<9 より、2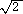 <3 であることは、直ちに分かる。
<3 であることは、直ちに分かる。
さらに、 1.4< なので、 (21.4)15=221=2097152>1889568=185
なので、 (21.4)15=221=2097152>1889568=185
よって、 (21.4)3>18 で、 2.63=17.576 より、 2.6 < 21.4 < 2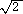
 <1.5 という評価が少し甘すぎたので、試しに、
<1.5 という評価が少し甘すぎたので、試しに、  <1.45 としてみる。
<1.45 としてみる。
このとき、(21.45)10=214.5=214 <214×1.4142<23170.253
<214×1.4142<23170.253
ところで、29619.677<2.810 なので、(21.45)10<2.810
したがって、 2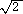 <2.8 となり、 2.6<2
<2.8 となり、 2.6<2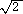 <2.8 が成り立つ。
<2.8 が成り立つ。
このように、上記のような評価のみに頼った計算では、小数第1位すら確定することが
出来ない。
この数を小数第3位まで手計算で求める方法について、北海道大学の中村先生より解
答をお寄せいただいた。お忙しい中、お考えいただいた中村先生に感謝しつつ、その方策
を展望したいと思う。
まず、予備知識を確認しておこう。高校で学習する二項定理を一般化して、次の定理が
成り立つ。
定理(二項級数) α は任意の実数とするとき、−1<X<1 において、
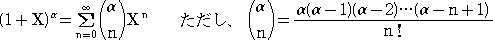
が成り立つ。
| いま、 |
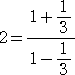 |
であることに注意すれば、 |
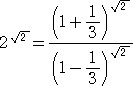 |
となる。 |
よって、(1+a)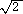 (ただし、a=1/3 または、-1/3)の近似値をある程度詳しく求めれ
(ただし、a=1/3 または、-1/3)の近似値をある程度詳しく求めれ
ば、2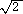 の値もある程度詳しく知ることができる。
の値もある程度詳しく知ることができる。
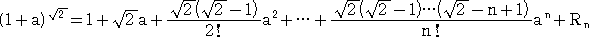
において、
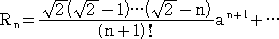
とする。
このとき、
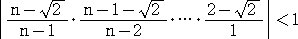
であることに注意して、

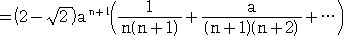
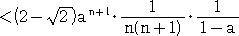
次に、  ≒ 1.414214 として、|Rn|<0.00001 となるような n の値を定める。
≒ 1.414214 として、|Rn|<0.00001 となるような n の値を定める。
不等式を変形すれば、 n(n+1)・3n >29289.3 である。
n = 6 のとき、n(n+1)・3n =30618 なので、|Rn|<0.00001 となるためには、
n = 6 で十分である。
a=1/3 のとき、 (1+a)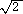 =A+R6 (ここで、|R6|<0.00001) とおく。
=A+R6 (ここで、|R6|<0.00001) とおく。
同様に、
a=1/3 のとき、 (1−a)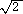 =B+R’6 (ここで、|R’6|<0.00001) とおく。
=B+R’6 (ここで、|R’6|<0.00001) とおく。
このとき、二項級数の式に、 ≒ 1.414214 を代入して計算すれば、
≒ 1.414214 を代入して計算すれば、
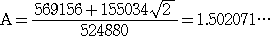
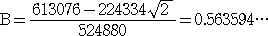
(実は、この A 、 B の計算が最もハードでした。手計算でやれないほどではありませ
んが、時間短縮のため、電卓を用いたことを正直に告白しておきます...f(^_^) )
したがって、
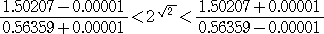
これより、
2.665117<2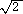 <2.665247
<2.665247
であることが分かった。
よって、2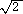 を小数第3位まで正しく求めれば、 2.665 となる。
を小数第3位まで正しく求めれば、 2.665 となる。
(コメント) 多少の忍耐があれば、同様な方法で、小数点以下もっと詳しい値を求めること
ができると思う。しかし、上記の計算量からも分かるように、「手計算で求める」と
いう趣旨からすれば、小数第3位までの計算がギリギリの境界線というところでし
ょうか?
(追記) 備忘録として、超越数の証明の歴史をまとめておこう。
e ・・・ 無理数性の証明は、オイラー(1737)
超越性の証明は、エルミート(1873)
π ・・・ 無理数性の証明は、ランベルト(1761)
超越性の証明は、リンデマン(1881)
2 ・・・ 超越性の証明は、ゲルフォント(1934)
・・・ 超越性の証明は、ゲルフォント(1934)
eπ ・・・ 超越性の証明は、ゲルフォント(1934)
(追々記) 平成18年2月20日付けで当HPの掲示板「出会いの泉」に、ハルさんという方
が、2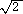 を手計算で求める別解を示された。ここでは、その方法を、私なりの解
を手計算で求める別解を示された。ここでは、その方法を、私なりの解
釈を加えながら整理したいと思う。
ハルさんも、上記で用いられた式変形
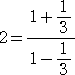
を活用されている。上記では、この式から、
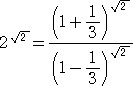
の分母・分子を2項展開して、近似値を求めたが、ハルさんの方法は、両辺の対数をとって、
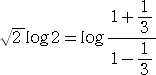
の右辺の近似値を求めるものである。
上記の右辺について、次のような展開公式が知られている。
|x|<1 のとき、
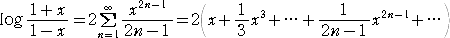
が成り立つ。
| (証明) |
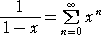 |
を項別積分して、 |
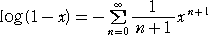 |
| 同様に、 |
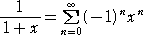 |
を項別積分して、 |
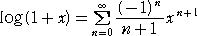 |
なので、よって、
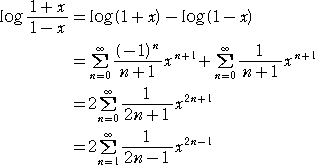 が成り立つ。(証終)
が成り立つ。(証終)
ここで、
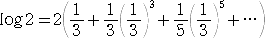
2(0.3333333+0.0123456+0.000823+0.0000653)<
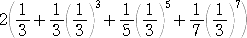
<2(0.3333334+0.0123457+0.000824+0.0000654)
| 0.6931344< |
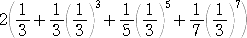 |
<0.693137 |
また、
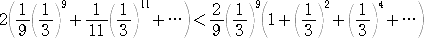
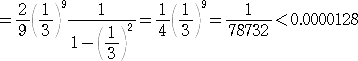
なので、 0.6931344 < log 2 < 0.6931498
また、 1.4142135< <1.4142136 より、
<1.4142136 より、
0.9802400257944< log 2<0.98026187399729
log 2<0.98026187399729
両辺より 1 を引いて、
−0.0197599742056< log 2−1<−0.01973812600271
log 2−1<−0.01973812600271
よって、 −0.01976< log 2−1<−0.01973 である。
log 2−1<−0.01973 である。
ところで、
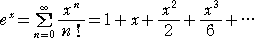
より、 ex の値を、−0.02<x<−0.01 において、
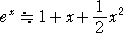
により近似すると、その誤差 E(x)は、x <0 に注意して、
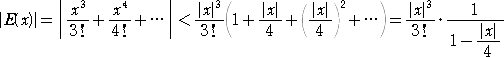
よって、 e-0.01976 ≒ 1−0.01976+(0.01976)2/2=0.9804352288・・・ で、
誤差は、|E(−0.01976)|<0.00000129228・・・ なので、
0.980433<e-0.01976 <0.980437
同様にして、
e-0.01973 ≒ 1−0.01973+(0.01973)2/2=0.98046463645・・・ で、
誤差は、|E(−0.01973)|<0.0000012864・・・ なので、
0.980463<e-0.01973 <0.980466
以上から、 0.980433<e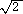 log 2−1<0.980466 であると言える。
log 2−1<0.980466 であると言える。
ここで、 2.718281<e<2.718282 なので、
2.66509239567<e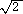 log 2<2.66518307941
log 2<2.66518307941
よって、 e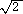 log 2=2
log 2=2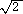 なので、
なので、
2.66509239567<2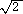 <2.66518307941
<2.66518307941
表計算ソフト Excel に、2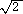 を計算させると、およそ 2.66514414269・・・ なので、
を計算させると、およそ 2.66514414269・・・ なので、
2.665までは正しく計算されている。
(コメント) 小数計算がたくさんあるので、手計算とはいかず電卓を用いました。誤差に注
意して計算したつもりですが、いろいろなタイプの誤差が錯綜している感じで、計
算にはあまり自信がありません。
ハルさんによれば、log2 の級数をもう1項増やし、途中の数値の精度をもう1
桁ずつ増やして計算すると、
2.665135< 2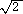 <2.665154
<2.665154
が出るそうです。
新たな手計算の方法をお教えいただいたハルさんに感謝いたします。

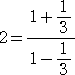
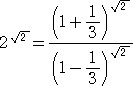
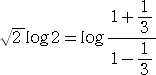
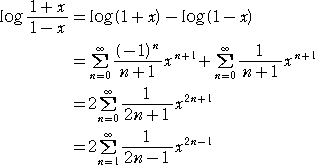 が成り立つ。(証終)
が成り立つ。(証終)