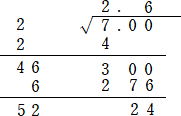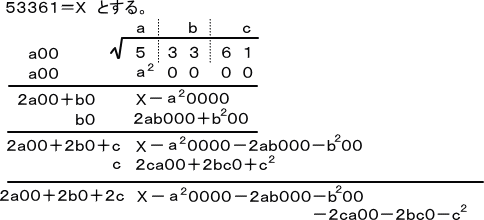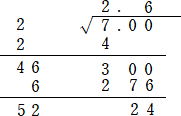平方根・立方根を筆算で求める方法 
近所の図書館では毎年古本市を開いている。在庫があるとか、貸出利用がないとかで
不要になった書籍を無料で開放している。隣町では、一人２０冊までとかの冊数制限を設
けているが、我が街の図書館は冊数無制限である。そんな太っ腹な所が好きで、毎年足
を運んでいる。朝１０時開館前から並ぶ人も多く、会場は超満員であった。
今年も、３０冊近く本をGETすることができた。その中で気になる本が１冊あった。
昭和９年初版発行、昭和１７年９月１３日に１３版発行（２０００部）と記された
問谷 力・森本清吾著 袖珍 数学公式要覧（山海堂出版部）
という本である。（出版社は、現存する「山海堂」のことだと思うが、詳細は不明。）
公式集としては、高校生向けの『科学新興社モノグラフ２４．公式集』が有名であるが、
上記の公式集は、小学校から大学初年級位までの、数学のありとあらゆる公式が網羅
され読むものを圧倒する迫力が感じられた。多分もう絶版だと思うが、惜しい限りである。
学習指導要領も改訂の度ごとに内容が削減され、数学教育に携わる者として寂しい思
いをしていた。ただ、今度の新学習指導要領では、それまでの上限という認識から、下限
という認識に立って教えていいことになったので、生徒の興味のおもむくまま、これまでは
躊躇していたいろいろなことを紹介していきたいと思う。その材料を上記の本に見つける
ことが出来たのである。
私が高校生のころ、教科書のコラムに「開平法」というのがあり、そこで、筆算で平方根
を計算する方法を学んだ。同年代の人に聞くと、「やったね！」という声が返ってきたので、
多分日本全国で、開平法というものが高校生の目に触れる機会はあったのだと思う。でも、
今はどの教科書をみてもその記述はないようである。上記の本では、その開平法はもちろ
んのこと、私が知らなかった開立法というものも紹介されていた。因みに、開立法について
は、我々より一世代前の方はご存知のようである。
九去法とあわせ、それらをこのホームページで紹介し、先人たちが学んだことを、少しで
も我々が受け継ぎ、それらを後世に残していきたいと思う。
（開平法の原理については、こちらを参照）
○ 開平法
例 ８５２４８２８９ の平方根を求めよ。
 |
（手順）
１．右より２位ずつ区切る。
２．平方して８５より小さくなる最大の数９を
求める。
３．副運算の方で９＋９を計算して１８を求
め、主運算の方で９と９を掛け合わせて
８１を求め、８５より引き、４を出す。
４．その４の横に上の２４を下ろし、４２４を
つくる。 |
５．副運算の１８*に*を掛けて主運算の４２４より小さくなる最大の*を求めて２を得る。これ
が平方根の次位となり、主運算で９の横に入る。副運算の１８２に２を掛けて３６４とし、こ
れを上の数から引いて６０を得る。
６．副運算で１８２と２との和を求める。この１８４は、副運算で９２＋９２を計算していること
に相当する。
７．上記のような操作を続ける。開ききれないときは、０を右側に２つずつ添えていき、操作
を続ける。
上記の計算から、８５２４８２８９ の平方根は、９２３３ となる。
（コメント） 計算機に頼らず、手計算で平方根が求められることに感動しました！
○ 開立九九
平方根を求めるために数の平方が使われたように、立方根を求めるために次の計算は
使われる。
１3＝１、２3＝８、３3＝２７、４3＝６４、５3＝１２５、６3＝２１６、７3＝３４３、８3＝５１２、９3＝７２９
○ 開立法
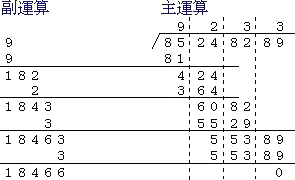
例 ９５１９３５９３４９６ の立方根を求めよ。
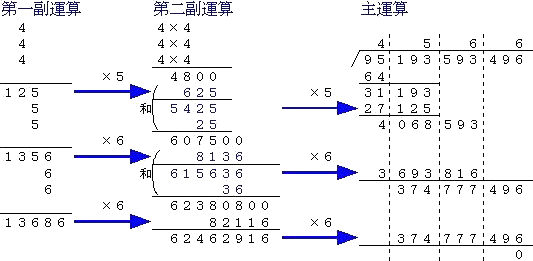
（手順）
１．右より３位ずつに区切る。
２．開立九九を用いて、９５より小さい数で最大のものを探し、立方根の首位４を求める。
３．４3＝６４を９５より引き、３１を出す。３１の横に上の１９３を下ろし、３１１９３を作る。
４．求めた数４の３倍１２と４2＝１６の３倍４８を作り、これを第一及び第二副運算の数とする。
第二副運算の横に０を２つ並べる。
５．第一副運算で１２*に*を掛けて、第二副運算の４８００を加えたものにさらに*を掛けて出
来る数のうち、主運算の３１１９３より小さくなる最大の*を求めて、５を得る。
６．第一副運算で１２にこの５を添えて１２５とし、第二副運算では、これに更に５を掛けた数
６２５と４８００との和５４２５を求める。これに更に５を掛けて２７１２５とし、これを主運算の
３１１９３より引き、その値４０６８に上から下ろした５９３を添えて４０６８５９３とする。
７．第一副運算で１２５に５を２つ加えて１３５を作る。これは、４５の３倍を計算していることに
相当する。第二副運算では先ほどの数５４２５に更に６２５と５2＝２５を加え６０７５を得る。
これは、４５2＝２０２５の３倍を計算していることに相等する。
８．上記のような操作を続ける。
○ 九去法
電卓の普及により四則計算は容易になったが、計算の結果が正しいだろうかと疑問に思
ったとき、実は面白い検算法がある。それは九去法というものである。この方法については
和田秀男 著 数の世界 整数論への未知（岩波書店） ｐ．２〜ｐ．５
に詳しく述べられている。その原理は、
Ａ×Ｂ＝Ｃ という計算で、Ａ、Ｂを９で割った余りの積を更に９で割った余りは、
Ｃを９で割った余りに等しい
というものである。Ａ＋Ｂ＝Ｃについても同様である。
ある数を９で割った余りを求めるには、その数の各位の数字の和を求め、その和の各位
の数字の和を求め、これを繰り返して、一位の数字を求めればよい。
これらのことを用いて、四則の検算をすることが出来る。
例 ２５７８１３×２４８１＝６３９６３４０５３ は正しいか？
２５７８１３ → ２＋５＋７＋８＋１＋３＝２６ → ２＋６＝８
２４８１ → ２＋４＋８＋１＝１５ → １＋５＝６
よって、 ８×６＝４８ → ４＋８＝１２ → １＋２＝３ より、左辺を９で割った余りは、３
６３９６３４０５３ → ６＋３＋９＋６＋３＋４＋０＋５＋３＝３９→３＋９＝１２→１＋２＝３
よって、右辺も９で割った余りは、３
以上から、この計算は正しいだろうと判断される。
（注意） もちろん、両辺を９で割った余りが一致するからと言って、計算が実は間違ってい
るということもあり得る。ただその可能性は、上記の計算をする前の九分の一に減っ
たという意味で、九去法の意義があるのである。
九去法を使えば、次のような数当てゲームが出来ると、和田秀男 著 「数の世界」 には
書かれている。面白いゲームなので紹介したい。
（遊び方）
１．一つの数を紙に書く。
２．各位の数字の和を求める。
３．もとの数から２．で求めた数を引く。
４．３．で得られた数の各位の数字の順番をめちゃめちゃにして、新しい数を作る。
５．その数に８１を加える。
６．５．で出来た数の各位の数字のうち、一つの数字を消す。
７．各位の数字の和を求める。
８．９から（７．で得られた数を９で割った余り）を引いて得られる数が、６．で消された数字と
なる。
開平法の原理
開平法については、私自身高校生のころ学んだわけであるが、その原理について深く考
えようとしたことは、恥ずかしながら、今まで一度もなかった。大学受験ということもあるが、
「解ければＯ．Ｋ．」という考えが先に立ち、立ち止まってじっくり取り組むという時間もなかっ
た。全てが効率主義であったと、今大いに反省しているところである。ただ、「突っ走って先
を急ぐ」ということも数学の学習では大切であると思う。一つの高い山に登る場合、山道を寄
り道しながら進むよりも、一気に山頂に登りつめ、山頂から今登ってきた道を振り返る方が、
はるかに見通しよく山を語ることができる。数学の学習でもその方法は有効で、深入りしす
ぎて迷路に迷い込むこともなくなる。ある程度直感的に正しいと思うことは、深く考えずどん
どん先に進むという方が精神衛生上にもいいのかもしれない。数学のノーベル賞といわれる
フィールズ賞を受賞された広中平祐氏も、細く、先を急ぐという学習をされていたと聞く。（特
異点解消理論によりフィールズ賞を受賞された後、文化勲章を受章され、日本に一時帰国
されたときのNHKでの対談より）
このページでは開平法の原理について、具体例を通して眺めてみたい。
例 (２３１)２＝５３３６１ なので、５３３６１の平方根は ２３１ である。
ここでは、５３３６１を与えて、その平方根２３１が求まる原理を調べようと思う。
(２３１)２＝５３３６１の両辺を、10進法展開すれば、
（２×１００＋３×１０＋１）２＝５×１００００＋３×１０００＋３×１００＋６×１０＋１
となる。従って、ａ、ｂ、ｃを、０〜９の整数として（ただし、ａは０でない）、
５×１００００＋３×１０００＋３×１００＋６×１０＋１＝（ａ×１００＋ｂ×１０＋ｃ）２
を満たすａ、ｂ、ｃ を合理的に見つける手順を探せばよい。
ところで、ａ×１００ を ａ００ などと表すことにすると、
（ａ００＋ｂ０＋ｃ）２＝ａ２００００＋ｂ２００＋ｃ２＋２ａｂ０００＋２ｃａ００＋２ｂｃ０
＝ａ００２＋（２ａ００＋ｂ０）×ｂ０＋（２ａ００＋２ｂ０＋ｃ）×ｃ
と変形される。
この式を見ると、副運算で、なぜ、あのような計算を行う必要があったのか、鮮やかにそ
のからくりが見えてくる。
５００００＋３０００＋３００＋６０＋１＝（ａ００＋ｂ０＋ｃ）２ において、まず、左辺の５００００
に関係するのは、右辺ではａ００ のみである。
（ａ００）２が一番５００００ に近くなる、即ち、ａ２が一番５に近くなる数を探す。
このことにより、ａ＝２ が定まる。次に、
（ａ００＋ｂ０＋ｃ）２− （ａ００）２を求めて、この値に一番近い値（２ａ００＋ｂ０）×ｂ０ を与え
る ｂ を見つけなければならない。そのために、副運算の方で、２ａ００ を求めておくのであ
る。c についても以下同様である。開平法のからくりの図式を次にまとめてみた。
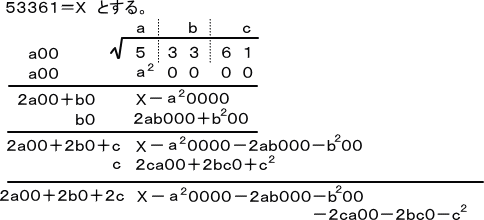
特に、Ｘ−ａ２００００−２ａｂ０００−ｂ２００−２ｃａ００−２ｂｃ０−ｃ２＝０ のとき、
Ｘ＝ａ２００００＋２ａｂ０００＋ｂ２００＋２ｃａ００＋２ｂｃ０＋ｃ２
＝（ａ００＋ｂ０＋ｃ）２
が成り立つ。
（追記） 令和２年１月２６日付け
上記で説明されている「開平法のからくり」を、別な視点で、もっと分かりやすく説明したい
と思う。
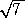を例にとる。近似値を覚えている方は、 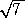＝２．６４５７５・・・（菜に虫いない） と言
えると思うが、ここでは、
２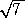＜＜３ から、 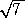＝２．ａ・・・＝２＋（ａ/１０）＋・・・ （ａは、０≦ａ≦９の整数）
として、ａの値を求める手順を考える。
１辺の長さが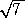の正方形を考えると、上式は、１辺の長さが２の正方形に少しずつ図形
を継ぎ足して、１辺の長さが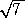の正方形に近づけるものと考えられる。
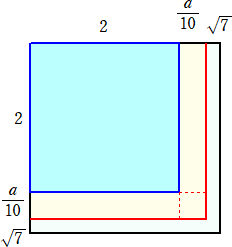
このとき、 ２×２＋２×（ａ/１０）＋２×（ａ/１０）＋（ａ/１０）2＋・・・＝７ なので、
２×（ａ/１０）＋２×（ａ/１０）＋（ａ/１０）2≦７−２×２＝３ から、
すなわち、 ｛（２＋２）×１０＋ａ｝×ａ≦３００ を満たす最大数ａを求めればよい。
このように考えていくと、小数点を境になぜ２桁ずつ区切るのかとか、なぜ「２＋２」を計算
するのか等、その理由が明確に分かり、次の計算図が理解されることと思う。
