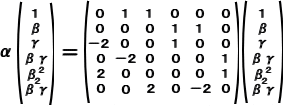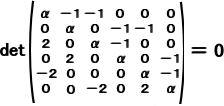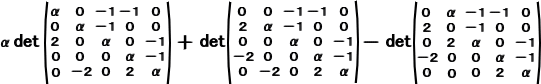方程式の生成 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　数の拡張は、方程式に依存している。自然数のみの世界で生きる者にとっては、方程式
　Ｘ＋１＝０　の解は存在しえないが、整数のみの世界で生きている者にとっては、解は存
在して、−１　と答えられる。しかし、方程式　２Ｘ＋１＝０　の解は考えられない。

　今、α 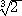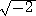＝ ＋ という数を考える。我々は、この数が、ある方程式の解と認識でき
る世界に生きているものとする。

　数 α の満たす方程式とは、どんなものだろうか？

　普通に計算すれば、次のようにするのだろう。

　　（ α − 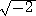）³＝（ ）³　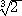　より　、　α³ − ３ 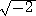α² − ６ α 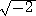＋ ２ ＝ ２

よって、　　α³ − ６ α − ２ ＝ （３ α² − ２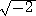） 　の両辺を平方して、

　　　　α⁶ ＋ ３６ α² ＋ ４ − １２ α⁴ ＋ ２４ α − ４ α³ ＝ （９ α⁴ − １２ α² ＋ ４）・（−２）

整理して、　　α⁶ ＋ ６ α⁴ − ４ α³ ＋ １２ α² ＋ ２４ α ＋ １２ ＝ ０　となる。

　以上から、数 α の満たす方程式は、

　　　　　　　　Ｘ⁶ ＋ ６ Ｘ⁴ − ４ Ｘ³ ＋ １２ Ｘ² ＋ ２４ Ｘ ＋ １２ ＝ ０

となる。（逆に、この方程式を解いて、数 α が解になるというのは想像もつきませんね！）

　上記のような解法が一般的と思われるが、次のような解法もあることを最近知った。

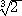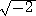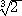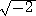　数 α ＝ ＋ において、β ＝ 　、γ ＝ とおく。

このとき、　α ＝ β ＋ γ　、　β³ ＝ ２ 　、　γ² ＝ −２　　である。

（ １ ， β ， β² ） と （ １ ， γ ） の組合せ

から、　　１　、　β　、　γ　、β γ　、　β²　、　β² γ　の ６ 個の数を考える。

このとき、　　α・１ ＝ １・β ＋ １・γ
　　　　　　　　　　　＝０・１＋１・β＋１・γ＋０・β γ＋０・β²＋０・β² γ

　　　　　　　　α・β ＝ １・β² ＋ １・βγ
　　　　　　　　　　　＝０・１＋０・β＋０・γ＋１・β γ＋１・β²＋０・β² γ

　　　　　　　　α・γ ＝ １・β γ＋ １・γ² ＝ −２・１＋ １・β γ
　　　　　　　　　　　＝−２・１＋０・β＋０・γ＋１・β γ＋０・β²＋０・β² γ

　　　　　　　　α・βγ ＝ １・β² γ＋ １・β γ² ＝ −２・β＋ １・β² γ
　　　　　　　　　　　＝０・１＋（−２）・β＋０・γ＋０・β γ＋０・β²＋１・β² γ

　　　　　　　　α・β² ＝ １・β³＋ １・β² γ ＝ ２・１＋ １・β² γ
　　　　　　　　　　　＝２・１＋０・β＋０・γ＋０・β γ＋０・β²＋１・β² γ

　　　　　　　α・β² γ＝ １・β³ γ＋ １・β² γ² ＝ ２・γ＋ （−２）・β²
　　　　　　　　　　　＝０・１＋０・β＋２・γ＋０・β γ＋（−２）・β²＋０・β² γ

から、次のような行列の式で表される。

　　　　　　　　

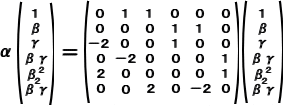
　上記の列ベクトルは、零ベクトルでないから、行列の理論を用いて、

　　　　　　　　

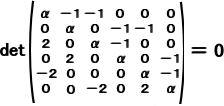
が成り立つ。行列式の計算公式から、左辺は、

　　　

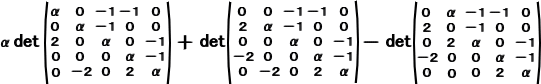
と分解される。　同様な分解を続ければ、左辺は、

　　　　　　　　α⁶ ＋ ６ α⁴ − ４ α³ ＋ １２ α² ＋ ２４ α ＋ １２

となる。（ここの計算は、少し大変でした！）

　以上から、数 α の満たす方程式は、

　　　　　　　　Ｘ⁶ ＋ ６ Ｘ⁴ − ４ Ｘ³ ＋ １２ Ｘ² ＋ ２４ Ｘ ＋ １２ ＝ ０

となる。

（コメント）
　このような解法は、裏技とは呼べない代物かもしれないが、発想がとても斬新であり、感
動を引き起こす。

（参考文献：山本芳彦　著　数論入門２　（岩波書店））

（追記）　平成１８年５月９日　当ＨＰの読者の方（ＨＮ：Ｕ　様）より、方程式の定数項に誤り
　　　　　がある旨のご指摘をいただいた。再計算したところ、確かに誤りであることが確認
　　　　　された。お詫びして訂正いたします。（上記は既に修正済み）