| 円周率を近似する分数 | を作る繁分数 | |
円周率の連分数展開
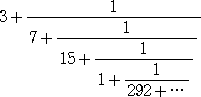
において、
分母を 292+・・・ とする分数は十分 0 に近い
として、
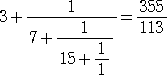
が得られる。
円周率の連分数展開に関して、次の書籍: 高木貞治 著 初等整数論講義(共立出版)
が詳しい。
円周率を、3.1415926535 として、ひたすら割り算を実行することにより、上記の連
分数展開が得られる。
(追記) 平成18年5月3日付け
円周率を近似する分数として有名な分数(450年頃、中国の祖冲之によるもの)
![]()
の小数表示(もちろん循環小数になる)は次の通りである。
3.1415 9292 0353 9823 0088 4955 7522 1238 9380 5309
7345 1327 4336 2831 8584 0707 9646 0176 9911 5044
2477 8761 0619 4690 2654 8672 5663 7168
(赤字の 1 と 8 の間が循環節である)
因みに、πの近似値
3.1415 9265 3589 7932 3846 2643 3832 7950 2884 1971
6939 9375 1058 2097 4944 5923 0781 6406 2862 0899
8628 0348 2534 2117 0679 8214 8086 5132 8230 6647
0938 4460 9550 5822 3172 5359 0812 8481 1174 5028
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
と比較してみると、 「3.141592」までは正しい。昔の人の偉大さが実感できる!
(追記) 円周率を近似する分数の小数表示について、HN「画楽」さんより、一部数値が
欠落してある旨のご指摘をいただきました。(平成23年11月16日付け)
確認したところ、ご指摘の通りで、早速修正させていただきました。上記は、修正
済みのものです。多倍長演算ルーチンを作成していて、たまたま発見されたとのこ
とで、画楽さんに感謝いたします。(→ 画楽のS研究所)
FNさんも検証されました。(平成23年11月17日付け)
エクセルで確認してみました。A1セルに113、B1セルに355を書く。
A2セルに=INT(B1/A$1)、B2セルに=(B1-A2*A$1)*10を書く。
A2、B2を下へ100個強コピーする。A2以下に結果が出ます。
確かに画楽さんの書かれてる通りになっています。
p、qが自然数で、pとqが互いに素であるとき、q/pを小数で表せば、循環節の長
さがp-1以下の循環小数になることはすぐにわかりますが、pが素数であれば循環
節の長さは、p-1の約数になるようです。
113は素数だから、355/113の循環節の長さは、112の約数であり、107になる可
能性はないので、計算しなくても間違いがあることはわかります。画楽さんはこのこ
とから間違いがあるはずだとして計算されたのかもしれません。
問題 pは素数、qは、0<q<pを満たす自然数とする。このとき、q/pを小数で表
したときの循環節の長さは、p-1の約数であることを証明せよ。
循環節の長さは、10n≡1 (mod p) を満たす自然数 n で定まる。フェルマ
ーの小定理より、pが2または5の倍数でないとして、10p-1≡1 (mod p)が成
り立つ。したがって、巡回群の位数を考えれば、10n≡1 (mod p) を満たす
自然数 n は、p-1 の約数であることが分かる。
FNさんからのコメントです。(平成23年11月18日付け)
上記の解答を見ると、わりと簡単なようです。と言ってもフェルマーの小定理を
使うので、そんなに簡単でないとも言えます。フェルマーの小定理を使うぐらいだ
から、「巡回群の位数を考えれば」以下の部分は証明不要なのでしょうが、多少
気になります。p は5でない奇素数とすべきでした。
p が素数でない場合も、オイラーのφ関数を使って似たような結果が成り立
つでしょうが、次の形で成り立つでしょうか。
p、q は互いに素な自然数で、p は2、5と互いに素、かつ、p≠1 とする。q/p
を小数で表せば、循環節の長さがφ(p)の約数である循環小数になる。
Seiichi Manyamaさんからのコメントです。(平成28年3月20日付け)
繁分数の話ではないのですが、円周率の近似に関する面白い記事がありました。(記事名
を見て侮ることなかれ?)
GAI さんからのコメントです。(平成28年10月13日付け)
円周率の近似分数として有名なものとして、「22/7」と「355/113」がある。これを、より憶え
やすくと工夫してみた。
22/7=(22*720)/(7*720)=(2*11*10*9*8)/(7*6!)
これより、 π/2≒(11・10・9・8)/(7・6・5・4・3・2・1)
また、
355/113
=5*(7+8^2)/(7^2+8^2) (∵113がmod(113,4)≡1 型の素数なので)
=(35+5*8^2)/(7^2+8^2)
=(6^2-1+(4+1)*8^2)/(7^2+8^2)
=(6^2+8^2+4*8^2-1)/(7^2+8^2)
=(6^2+8^2+255)/(7^2+8^2)
=(6^2+8^2+5^2+230)/(7^2+8^2)
=(6^2+8^2+5^2+7^2+181)/(7^2+8^2)
=(6^2+8^2+5^2+7^2+9^2+10^2)/(7^2+8^2)
より、なんと、 π≒(52+62+72+82+92+102)/(72+82)
らすかるさんからのコメントです。(平成28年10月14日付け)
π≒(11・10・9・8)/(7・6・5・4・3)
としてもいいですね。
(コメント)
![]()
これは美しいですね!