��v�Z���ʔ����@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�������̌v�Z���ł���d�삪�A�قڃ^�_���R�Ŏ�ɓ��鐢�̒��ɂ����āA���낢��Ȑ�
�w�I�l�������ł��Ȃ��l����������B
�@ �̒l���c������Ă��Ȃ����̂�����A��ӁA���ӂ̒������A�P �� �Q �̒��p�O�p�`��
�̒l���c������Ă��Ȃ����̂�����A��ӁA���ӂ̒������A�P �� �Q �̒��p�O�p�`��
�����ƁA�Εӂ̒����́A�����l�����ɁA �Ǝ��M���X�ɓ�����B�����ɁA�Q�F�P�F
�Ǝ��M���X�ɓ�����B�����ɁA�Q�F�P�F �@�̔�
�@�̔�
�����O�p�`�̎����ɂ͂܂��Ă���Ƃ��������ł���B
�@ �́A�Q ��菬�������Ȃ̂ŁA���̂R�ӂ̑g�����ł́A�����ĎΕӂ̒����Ƃ͂Ȃ蓾�Ȃ��B
�́A�Q ��菬�������Ȃ̂ŁA���̂R�ӂ̑g�����ł́A�����ĎΕӂ̒����Ƃ͂Ȃ蓾�Ȃ��B
���w�E���w�E���Z�ɂ����āA���̒l��c������P���̕K�v����Ɋ�����B
�@�Ⴆ�A���w�R�N�Ŋw�K����u����̗L�����v�́A���̒l��c�����邽�߂̌v�Z�Ȃ̂ł�
��A�����u����ɖ�����������Ɣ������Ȃ�����v�Ƃ������R�ŗL��������킯�ł͂Ȃ��̂�
����B�����Əڂ������y����A�p�i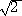 �j���p�m
�j���p�m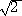 �n���^�̈Ӗ�����Ƃ���ł��邪�D�D�D�B
�n���^�̈Ӗ�����Ƃ���ł��邪�D�D�D�B
�@������ӂ̔F�������݂̒��w�E���Z���ɂ͂Ȃ��悤�Ɋ�������B������A����ɖ�����
���c�����܂܂ł悢�Ƃ����ƁA��l�ɐ��k�͌˘f�����o����悤���B���܂܂ŁA�@�B�I�ɕ���
�̗L�������s���Ă����c�P���낤�B
�@�݂Ȃ���́A���̖�ɂ��������邱�Ƃ��ł��邾�낤���H
��@ ���P�D�V�R�Q�@�ł��邱�Ƃ�p���āA���̐��͂����悻������ʂ��H
���P�D�V�R�Q�@�ł��邱�Ƃ�p���āA���̐��͂����悻������ʂ��H
| �@�i�P�j |
�@�@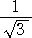 |
�@�@�@�@�@�@�@�@�@�i�Q�j |
�@�@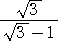 |
�i���j�@�i�P�j�@�O�D�T�V�V�@�@�i�Q�j�@�Q�D�R�U�U
�@��v�Z�ŕ������A���������v�Z������@���m���Ă���̂ŁA���������������ꂽ�琥
��A���킵�ė~�����Ǝv���B
�@���̃y�[�W�ł́A���낢��Ȓl����v�Z�ŋ��߂���@�ɂ��Ă܂Ƃ߂Ă݂����B
��@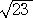 �̒l��������P�ʂ܂Ő��������߂�B
�̒l��������P�ʂ܂Ő��������߂�B
�i���j�@�S2���Q�R���T2�@�ŁA�S��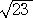 ���T�@���A�@
���T�@���A�@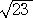 ���S�{���@�i�O�������P�j�@�Ƃ�����B
���S�{���@�i�O�������P�j�@�Ƃ�����B
���ӂ����Ď�������ƁA�@��2�{�W���|�V���O �@�Ƃ����Q����������������B
���̂Ƃ��A�P�O�� �i���̂P�O�{���l���邱�Ƃɂ��A���̏�����P�ʂ����߂�I�j�� �w �Ƃ����B
�����w/�P�O ���A�����قǂ̂Q���������ɑ�����Ď�������ƁA
 |
�@�@�@�@�@�w2�{�W�O�w�|�V�O�O���O
�@�e�i�w)���w2�{�W�O�w�|�V�O�O�@�Ƃ����ƁA
�@�@�@�@�@�e(�V)���|�X�P���O�A�e(�W)���S���O
�@���������āA���}���A�P�O�����w���V�D�E�E�E�@�ƂȂ�̂ŁA
�@�@�����O�D�V�E�E�E�@�ł��邱�Ƃ�������B
�@ |
�@�ȏォ��A�@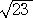 �� �S�D�V�E�E�E�@�ƂȂ�B�@�@�i�I�j
�� �S�D�V�E�E�E�@�ƂȂ�B�@�@�i�I�j
�@���̕��@������������A�������̒l�ɂ��߂�������������B
�i���݂ɁA�d���p����A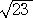 �� �S�D�V�X�T�W�R�E�E�E�@�ł���B�j
�� �S�D�V�X�T�W�R�E�E�E�@�ł���B�j
��@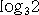 �̒l��������P�ʂ܂Ő��������߂�B
�̒l��������P�ʂ܂Ő��������߂�B
�@���̒l�́A���d���p����A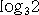 ���O�D�U�R�O�X�Q�X�V�S�U�E�E�E �ł���B���d�삪�Ȃ�
���O�D�U�R�O�X�Q�X�V�S�U�E�E�E �ł���B���d�삪�Ȃ�
�Ă��A������P�ʂ��炢�܂ł͎�v�Z�ŁA�������܂�悤�ɂ��Ă����������̂��B
�i���j�@�Q6���R4�@���A�Q���R0.666�E�E�E�@������A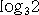 ���O�D�U�U�U�E�E�E
���O�D�U�U�U�E�E�E
�@�܂��A�R5���Q8�@���A�R0.625���Q�@������A�O�D�U�Q�T��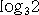
���������āA�O�D�U�Q�T��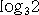 ���O�D�U�U�U�E�E�E �ƂȂ�A
���O�D�U�U�U�E�E�E �ƂȂ�A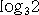 ���O�D�U�E�E�E�@�ł��邱�Ƃ�������B
���O�D�U�E�E�E�@�ł��邱�Ƃ�������B
�@���̎�v�Z�ŁA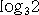 �̏�����Q�ʂ����肷�邱�Ƃ͓���B
�̏�����Q�ʂ����肷�邱�Ƃ͓���B
�@�Q20���P�O�S�W�T�V�U�A�R13 ���P�T�X�S�R�Q�R�@�ŁA�Q20���R13�@���A�Q���R0.65�@������A
�@�O�D�U�Q�T��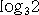 ���O�D�U�T�@�����߂�̂�����t�ł���B
���O�D�U�T�@�����߂�̂�����t�ł���B
�i�NjL�j�@�����Q�T�N�W���R�O���t��
�@���g�o�ǎ҂̂g�m�u�����������̕��v�����育���e�����܂����B
�@��L�̌v�Z�ŁA�w�����P�����������āA�Q19���T�Q�S�Q�W�W�A�R12���T�R�P�S�S�P�ŁA
�@�Q19���R12 ���A�Q���R0.63158�@������A�@�O�D�U�Q�T��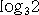 ���O�D�U�R�Q�@�Ƌ��܂�B
���O�D�U�R�Q�@�Ƌ��܂�B
������A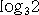 �̏�����Q�ʂ́A�Q�܂��͂R�Ƃ������Ƃ�������B����ɑ����āA
�̏�����Q�ʂ́A�Q�܂��͂R�Ƃ������Ƃ�������B����ɑ����āA
�@�Q46���V�O�R�U�W�V�S�S�P�V�V�U�U�S�A�R29���U�W�U�R�O�R�V�V�R�U�S�W�W�R�@�ŁA�Q46���R29�@���A
�@�Q���R0.6304�@������A�@�O�D�U�R�O�S��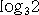 ���O�D�U�R�Q�@�Ƌ��܂�B
���O�D�U�R�Q�@�Ƌ��܂�B
�@������A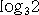 �̏�����Q�ʂ́A�R�Ƃ������Ƃ�������B
�̏�����Q�ʂ́A�R�Ƃ������Ƃ�������B
�i�R�����g�j�@�Q46�ƂR29�̌v�Z�͑�ςł����A��v�Z�ł���Ă��Ȃ����Ƃ͂Ȃ��ł��ˁI
�@�@�@�����A���̂Q���̑g��T�����������Ƒ�ς����D�D�D�B�����������̕�����Ɋ��ӂ��܂��B
�i�NjL�j�@DD++ ���炲���e���������܂����B�i�����Q�X�N�P���Q�T���t���j
�@log3 �Q ���i��v�Z�Łj���߂�A�Ƃ������ɂ��āA�Q���Rx �̉����t�@���C����I�ɗL����
�ߎ����Ă��������̂ł͂Ȃ����Ƃ������Ƃ��v�����܂����B
�@�܂��A��Ɛ^���̂�������������1��Ƒ傫������0����r���܂��B
(2= ) 2^1 > 3^0 ( =1) �c�c (1)
�@���ɁA����������1��Ƒ傫������1����r���܂��B
(2= ) 2^1 < 3^1 ( =3) �c�c (2)
�ȉ��A�Ō�ɏo�Ă������ӂ��傫�����ƁA�Ō�ɏo�Ă����E�ӂ��傫�����ŕӁX�ς��Ƃ�A
�召�肵�܂��B
(1)(2) �̕ӁX�Őς��Ƃ��Ĕ�r�@�@(4= ) 2^2 > 3^1 ( =3) �c�c (3)
(3)(2) �̕ӁX�Őς��Ƃ��Ĕ�r�@�@(8= ) 2^3 < 3^2 ( =9) �c�c (4)
(3)(4) �̕ӁX�Őς��Ƃ��Ĕ�r�@�@(32= ) 2^5 > 3^3 ( =27) �c�c (5)
(5)(4) �̕ӁX�Őς��Ƃ��Ĕ�r�@�@(256= ) 2^8 > 3^5 ( =243) �c�c (6)
(6)(4) �̕ӁX�Őς��Ƃ��Ĕ�r�@�@(2048= ) 2^11 < 3^7 ( =2187) �c�c (7)
(6)(7) �̕ӁX�Őς��Ƃ��Ĕ�r�@�@(524288= ) 2^19 < 3^12 ( =531441) �c�c (8)
(6)(8) �̕ӁX�Őς��Ƃ��Ĕ�r�@�@(134217728= ) 2^27 > 3^17 ( =129140163) �c�c (9)
(9)(8) �̕ӁX�Őς��Ƃ��Ĕ�r�@�@(70368744177664= ) 2^46 > 3^29 ( =68630377364883)
�ŁA 3^(29/46) < 2 < 3^(12/19) �������A�@0.6304 < 29/46 <log3 �Q< 12/19 < 0.6316 ����
�o�����Ƃ��ł��܂��B
�@���̕��@�̉������������Ƃ����A�|���Z��2�邲�ƂɁA����܂ł��ǂ��s�������K
����ɓ���_�B���������v�Z�����̂ɓ��Ă��O��ăK�b�J���Ƃ������Ƃ������܂���B
�@�^�����s�������������ɘA������Ɓi�܂�log�̒l���ȒP�ȕ���̗L�����ɋ߂��Ɓj����
�����ɂ������Ƃ������_�͂���܂����B
�r������K�v�Ȍ������̗L�������ɂ��Ă����v�Ǝv���܂��B
10^0 < 2^1 ( =2)
10^1 > 2^1 ( =2)
10^1 > 2^2 ( =4) ---> log[10]2 < 1/2 = 0.5
10^1 > 2^3 ( =8) ---> log[10]2 < 1/3 < 0.334
10^1 < 2^4 ( =16) ---> log[10]2 > 1/4 = 0.25
10^2 < 2^7 ( =128) ---> log[10]2 > 2/7 > 0.285
10^3 < 2^10 ( =1024) ---> log[10]2 > 3/10 = 0.3
10^4 > 2^13 ( =8192) ---> log[10]2 < 4/13 < 0.30770
10^7 > 2^23 ( =0.8389�~10^7) ---> log[10]2 < 7/23 < 0.30435
10^10 > 2^33 ( =0.8590�~10^10) ---> log[10]2 < 10/33 < 0.30304
10^13 > 2^43 ( =0.8796�~10^13) ---> log[10]2 < 13/43 < 0.30233
10^16 > 2^53 ( =0.9007�~10^16) ---> log[10]2 < 16/53 < 0.30189
10^19 > 2^63 ( =0.9223�~10^19) ---> log[10]2 < 19/63 < 0.30159
10^22 > 2^73 ( =0.9444�~10^22) ---> log[10]2 < 22/73 < 0.30137
10^25 > 2^83 ( =0.9671�~10^25) ---> log[10]2 < 25/83 < 0.30121
10^28 > 2^93 ( =0.9903�~10^28) ---> log[10]2 < 28/93 < 0.301075
10^31 < 2^103 ( =1.0141�~10^31) ---> log[10]2 > 31/103 > 0.300971
10^59 < 2^196 ( =1.0043�~10^59) ---> log[10]2 > 59/196 > 0.301020
10^87 > 2^289 ( =0.9946�~10^87) ---> log[10]2 < 87/289 < 0.3010381
10^146 > 2^485 ( =0.9989�~10^146) ---> log[10]2 < 146/485 < 0.30103092
10^205 < 2^681 ( =1.0032�~10^205) ---> log[10]2 > 205/681 > 0.30102790
10^351 < 2^1166 ( =1.0021�~10^351) ---> log[10]2 > 351/1166 > 0.30102915
10^497 < 2^1651 ( =1.0010�~10^497) ---> log[10]2 > 497/1651 > 0.30102967
10^643 ? 2^2136 ( =0.9999�~10^643) ---> log[10]2 ? 643/2136 = 0.30102996�c�c
�i����̗L���������ƍŌ�̑召�͔��ɂ��₵���̂ŕs�̗p�j
�ŁA 0.30102967 < 497/1651 < log10 �Q< 146/485 < 0.30103092 �܂����B
�@���ɁA�Ō�� 643/2136 �́A����������������1�ɋ߂Â����̂ŁA�召�͕s���ł�������
��悢�ߎ������ɂȂ��Ă���̂ł͂Ȃ����ƍl�����܂��B
�@�E�̌v�Z�͎������x�̎Q�l�ɂ���������ŁA���ۂ͕K�v�ȍs�������Ώ\���ł��B����
�Ȃ��v�Z�ł��Ȃ�Ƃ��Ȃ�̂ł͂Ȃ��ł��傤���B
�@3/10 �ɒl���߂������ŁA3���ڂ̌���ɂ����������Ȃ��ƂƁA���̌�͈�C�ɐi�s����
���Ƃ����Ď��܂��ˁBlog10 �R �͂����Ƒ������܂�Ǝv���܂��B
�@�炷���邳��̃R�����g�ł��B�i�����Q�X�N�P���Q�T���t���j
�@log �̎�v�Z�͈ȑO�l�������Ƃ�����܂����A�ȉ��̌������g���ƌ����ǂ����x���グ��
��܂��B(�ȉ��A��̂Ȃ��ΐ��͎��R�ΐ��ł�)
�@y = (x-1)/(x+1) �Ƃ���ƁA�@logx = log((1+y)/(1-y)) = 2(y + y^3/3 + y^5/5 + �c)�@�Ȃ̂ŁA
x=(t+1)/t �Ƃ���ƁA y=1/(2t+1) �ƂȂ�A
�@log((t+1)/t) = 2(1/(2t+1) + 1/((2t+1)^3�E3) + 1/((2t+1)^5�E5) + �c)
�@������g���āAlog3 �Q�����߂܂��Bt ���傫���قǐ��x���ǂ��̂ŁA������ t ���g���̂�
�����A�܂��A
�@log(7/6)��2{1/13+1/(13^3�E3)}��0.154150
�@log(8/7)��2{1/15+1/(15^3�E3)}��0.133531
�@log(9/8)��2{1/17+1/(17^3�E3)}��0.117783
��3�����߂�ƁA
�@log2=2{log(7/6)+log(8/7)}+log(9/8)��0.693145
�@log3=3{log(7/6)+log(8/7)}+2log(9/8)��1.098609
���Alog3 �Q=log2/log3��0.693145/1.098609��0.630930�@�̂悤�ɋ��܂�܂��B
�@2/(13^5�E5)��10^(-6) �Ȃ̂ŁA��L�̂悤�ɋ���2����6���߂��̐��x������܂��B������1
�����₷�Ɛ��x��2���ȏ�オ��܂��B����1�Alog(10/9)�����߂Ă����A
�@log2=2{log(7/6)+log(8/7)}+log(9/8)
�@log3=3{log(7/6)+log(8/7)}+2log(9/8)
�@log4=2log2
�@log5=log4+log(9/8)+log(10/9)
�@log6=log2+log3
�@log7=log6+log(7/6)
�@log8=3log2
�@log9=2log3
�@log10=log2+log5
�̂悤�ɁAlog2�`log10 �܂ŋ��߂��܂��̂ŁAlog10 �Q�`log10 �X���Z�o�ł��邱�ƂɂȂ�܂��B
�@�܂����`����̃R�����g�ł��B�i�����Q�X�N�P���Q�U���t���j
�@�܂��ɃI�C���[�̗p�������@�ł��ˁB����͎��s����ŋC�t�������̂Ȃ̂ł��傤���H��
��Ƃ������������Ɖ�������̕��@�ł��炩���߉����Ă����̂ł��傤���H�����̑������v
�Z���邱�ƂȂ��͂�����@�����邩�ȑO�ӂƎv�������Ƃ������ċC�ɂȂ�܂����B�����悯��
�������������B
�@�炷���邳��̃R�����g�ł��B�i�����Q�X�N�P���Q7���t���j
�@�I�C���[�̗p�������@�������̂ł����A����͑����܂���ł����B��L�͎��s����ŋC�t
���܂����B�ő��2��������������d��v���O���������̂ɁA���낢��Ȍv�Z�Ŏ����𑬂�
����K�v������Alog�Ɍ��炸�������낢��l���܂����B
�@�܂����`����̃R�����g�ł��B�i�����Q�X�N�P���Q�W���t���j
�@�Ȃ�قǃv���O���������@�������̂ł��ˁB���肪�Ƃ��������܂����B
��@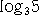 �̒l��������P�ʂ܂Ő��������߂�B
�̒l��������P�ʂ܂Ő��������߂�B
�i���j�@�T2���R3�A�R7���T5�@���A�P�D�S��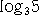 ���P�D�T�@������A
���P�D�T�@������A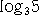 ���P�D�S�E�E�E�@�@�i�I�j
���P�D�S�E�E�E�@�@�i�I�j
��@ �A
�A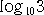 �̂����悻�̒l�����߂�B
�̂����悻�̒l�����߂�B
�i���j�@�Q3���W���P�O�@������A�R �� �P�@�@�@����āA
�� �P�@�@�@����āA �� �O�D�R�E�E�E
�� �O�D�R�E�E�E
�@�Q3���R2���P�O�@������A�R ���Q
���Q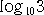 ���P
���P
����āA�O�D�S�T�E�E�E��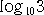 ���O�D�T�@�͈̔͂̐��ł��邱�Ƃ�������B�@�@�i�I�j
���O�D�T�@�͈̔͂̐��ł��邱�Ƃ�������B�@�@�i�I�j
�i�NjL�j�@�����Q�T�N�P�O���Q�U���t��
�@��L�̗Ⴉ���������悤�ɁA���̂����悻�̒l�����߂�ꍇ�A�s�����ɂ��]������
�ł͉�����E������B
�@�ŋ߁ANiklaus Wirth ����̂g�o�T�C�g�uProgramming in Oberon�v�̂P�S�łɁA�ΐ������߂�
�v���O�������ڂ��Ă��邱�Ƃ��A�s���[�썂�Z�̉����@�ꂳ��ɂ����������������B
�@���̂悤�Ȏ菇�ŋ��߂�炵���B
�i�P�j�@������10�����i1/2�j������10��2
�i�Q�j�@��2���P�O�@�Ȃ�A�@������10��2���P�{������10�i��2/�P�O�j
�@�ȍ~�A�i�P�j�i�Q�j���J��Ԃ��B
��@���ۂɁA���̃A���S���Y���Ōv�Z���Ă݂�ƁA
�@ ���P/�Q2�{�P/�Q5�{�P/�Q6�{�P/�Q8�{�P/�Q12�{�E�E�E
���P/�Q2�{�P/�Q5�{�P/�Q6�{�P/�Q8�{�P/�Q12�{�E�E�E
�@���O�D�Q�T�{�O�D�O�R�P�Q�T�{�O�D�O�P�T�U�Q�T�{�O�D�O�O�R�X�O�U�Q�{�O�D�O�O�O�Q�S�S�P�{�E�E�E
�@���O�D�R�O�P�O�Q�T�R�E�E�E�E
��L�̌v�Z����A������R�ʂ܂ł͐������l�ł�����̂Ɛ��@�����B
�i�Q�l�j�@ �� �O�D�R�O�P�O �Q�X�X�X �T�U�U�R �X�W�P�P �X�T�Q�P �R�V�R�W �W�X�S�V �Q�S�S�X �E�E�E
�� �O�D�R�O�P�O �Q�X�X�X �T�U�U�R �X�W�P�P �X�T�Q�P �R�V�R�W �W�X�S�V �Q�S�S�X �E�E�E
�i�R�����g�j�@��L�̌v�Z����v�Z�ōs���̂͏�������������܂����A���ʂ̓d��ŏ\���v�Z
�@�@�@�@�@�\�ł��ˁI
�@���l�ɂ��āA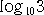 ���v�Z���Ă݂��B
���v�Z���Ă݂��B
������10�R��(1/2)������10�X��(1/4)������1081��1/4�{(1/4)������108�D1
�@��1/4�{(1/8)������1065�D61��1/4�{1/8�{(1/8)������106�D561
�@��1/4�{1/8�{(1/16)������1043�D046721
�@��1/4�{1/8�{1/16�{(1/16)������104�D3046721
�@��1/4�{1/8�{1/16�{(1/32)������1018�D530201
�@��1/4�{1/8�{1/16�{1/32�{(1/32)������101�D8530201
�@��1/4�{1/8�{1/16�{1/32�{(1/64)������103�D4336834
�@��1/4�{1/8�{1/16�{1/32�{(1/128)������1011�D790181
�@��1/4�{1/8�{1/16�{1/32�{1/128�{(1/128)������101�D1790181
�@��1/4�{1/8�{1/16�{1/32�{1/128�{(1/2048)������1013�D942072
�@��1/4�{1/8�{1/16�{1/32�{1/128�{1/2048�{(1/2048)������101�D3942072
�@��0�D25�{0�D125�{0�D0625�{0�D03125�{0�D0078125�{0�D0004882�{�E�E�E
�@���O�D�S�V�V�O�T�O�V�E�E�E
�@��L�̌v�Z����A������R�ʂ܂ł͐������l�ł�����̂Ɛ��@�����B
�i�Q�l�j�@������10�R �� �O�D�S�V�V�P �Q�P�Q�T �S�V�P�X �U�U�Q�S �R�V�Q�X �T�O�Q�V �X�O�R�Q �T�T�P�Q �E�E�E
�i�R�����g�j�@�A���S���Y���͗����ł������A�Ƃ��Ă��������x���悤�ȁD�D�D����ȕ��͋C�B
��@�Q20 �͉����̐��ŁA���̎�ʂ̐��͉����H�������A ���O�D�R�O�P�O�B
���O�D�R�O�P�O�B
�i���j�@ �� �O�D�R�O�P�O�@ ������A�Q�O
�� �O�D�R�O�P�O�@ ������A�Q�O ���U�D�O�Q
���U�D�O�Q
�@����āA�P�O6���Q20���P�O7�@�ƂȂ�A�V���̐��ł��邱�Ƃ�������B
�@�܂��A�O���O�D�O�Q���O�D�R�O�P�O�@���A�U���U�D�O�Q���U�{
�@���������āA�P�O6���Q20���Q�E�P�O6�@������A�Q20�@�̎�ʂ̐��́A�P �ł���B
�i���݂ɁA�Q20 ���P�O�S�W�T�V�U�@�ł���B�j
��@�i�P/�Q�j20 �͏����扽�ʂɏ��߂ĂO�łȂ�����������邩�H�܂��A���̐�����
�@�����H�@�������A ���O�D�R�O�P�O �A
���O�D�R�O�P�O �A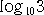 ���O�D�S�V�V�P�@�Ƃ���B
���O�D�S�V�V�P�@�Ƃ���B
�i���j�@�|�Q�O �� �|�U�D�O�Q�@�Ȃ̂ŁA�P�O-7���i�P/�Q�j20���P�O-6
�� �|�U�D�O�Q�@�Ȃ̂ŁA�P�O-7���i�P/�Q�j20���P�O-6
����āA������V�ʂɏ��߂ĂO�łȂ������������B
�܂��A�|�U�D�O�Q���|�V�{�O�D�X�W�@�ŁA�Q�~�O�D�S�V�V�P���O�D�X�W���P�@������A
�@�|�V�{�Q�~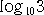 ���|�U�D�O�Q ���|�U�@���Ȃ킿�A�X�E�P�O-7���i�P/�Q�j20���P�O-6
���|�U�D�O�Q ���|�U�@���Ȃ킿�A�X�E�P�O-7���i�P/�Q�j20���P�O-6
���������āA���߂鐔�́A�X �ł���B
�i���݂ɁA�i�P/�Q�j20 ���O�D�O�O�O�O�O�O�X�T�R�U�V�E�E�E �ł���B�j
��@(�O�D�X�X)10�@�̒l��������Q�ʂ܂Ő��������߂�B
�i���j�@�Q���藝�@(���{��)���������{������-1���{��(��-1)/2����-2��2�{�E�E�E�{���� ��p���āA
�@(�O�D�X�X)10��(�P�|0�D01)10
�@���P�|�P�O�E0�D01�{�S�T�E0�D0001�|�P�Q�O�E0�D000001�{�E�E�E
�@���O�D�X�O�E�E�E�@�@�@�i��R����45�E0�D0001�ȉ��}���ɏ������Ȃ�I�j
��@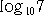 �̒l��������R�ʂ܂Ő��������߂�B
�̒l��������R�ʂ܂Ő��������߂�B
�@�������A ���O�D�R�O�P�O �A
���O�D�R�O�P�O �A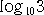 ���O�D�S�V�V�P�@�Ƃ���B
���O�D�S�V�V�P�@�Ƃ���B
�@���̖��́A���k��w�@���n�@����i�Q�O�O�W�j�̓������̈ꕔ�ł���B
�i���j�@�S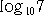 ��������10�Q�S�O�P�@�ł���̂ɑ��āA���̋߂��̒l�Ƃ���
��������10�Q�S�O�P�@�ł���̂ɑ��āA���̋߂��̒l�Ƃ���
������10�Q�S�O�O��������10�Q�S�~�P�O�O
�@��������10�R�{�R������10�Q�{�Q
�@���O�D�S�V�V�P�{�R�~�O�D�R�O�P�O�{�Q���R�D�R�W�O�P�@�@�ł��邱�Ƃɒ��ڂ���B
�@�����ŁA�@������10�Q�S�O�P�|������10�Q�S�O�O��������10�i�P�{�P/�Q�S�O�O�j
�Ƃ���ŁA�@�����O�@�̂Ƃ��A�@�������i�P�{���j�����@�����藧�B
�@���ۂɁA�@�e�i���j �� ���|�������i�P�{���j�@�Ƃ����ƁA�e�f�i���j �� �P�|�P/�i�P�{���j �� ��/�i�P�{���j ���O
�ł���̂ŁA�@�e�i���j �͒P���ɑ�������B�@�܂��A�@�e�i�O�j �� �O�@�ł���̂ŁA
�@�����O�@�̂Ƃ��A�@�e�i���j �� �O�@�ƂȂ�A�@�������i�P�{���j �� ���@�ƂȂ�B
���̂��Ƃ���A
�@������10�Q�S�O�P�|������10�Q�S�O�O
�@��������10�i�P�{�P/�Q�S�O�O�j
�@���������i�P�{�P/�Q�S�O�O�j���P/�Q�S�O�O���O�D�O�O�O�S�P�U�U�E�E�E
���A�@������10�Q�S�O�P��������10�Q�S�O�O�{�O�D�O�O�O�S�P�U�U�E�E�E���R�D�R�W�O�T�P�U�U�E�E�E
���Ȃ킿�A�@�R�D�R�W�O�P���S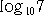 ���R�D�R�W�O�T�Q�@���A�O�D�W�S�T�O�Q�T��
���R�D�R�W�O�T�Q�@���A�O�D�W�S�T�O�Q�T��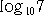 ���O�D�W�S�T�P�R
���O�D�W�S�T�P�R
�Ȃ̂ŁA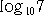 �̒l��������R�ʂ܂Ő��������߂�A�@�O�D�W�S�T�@�ƂȂ�B�@�@�i�I�j
�̒l��������R�ʂ܂Ő��������߂�A�@�O�D�W�S�T�@�ƂȂ�B�@�@�i�I�j
�i�NjL�j�@�����R�O�N�V���P�P���t��
�@�����ʐMNo�D�X�P�i�����o�Łj�ŁA��ʌ����L�����Z�̌���`���搶���A����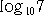 ��
��
�l�ɂ��čl�@����Ă���B�����[���q�ǂ����Ă����������B
�@�P���̏�p�ΐ��́A���ׂ�  �A
�A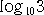 �̒l��p���ċ��߂���B
�̒l��p���ċ��߂���B
�@���ۂɁA
������10�S���Q
������10�T���P�|
������10�U�� �{
�{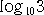
������10�W���R
������10�X���Q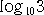
�@���āA���́A������10�V �ł���B��L�̂悤��  ��
�� 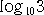 ��p���������ŕ\�����Ƃ�
��p���������ŕ\�����Ƃ�
���߂�K�v�����肻�������A�s�����ŕ]������Ƃ����Z���L���ł���B
�@������10�V �̒l��������Q�ʂ܂ŋ��߂����ꍇ
�@�s�����@�S ���V���T
���V���T �@�ɂ����āA
�@�ɂ����āA
�@������10�S ���Q
���Q �{�i�P/�Q�j
�{�i�P/�Q�j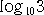
�@�@ ���O�D�R�O�P�O�A
���O�D�R�O�P�O�A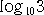 ���O�D�S�V�V�P�@�Ƃ��āA������10�S
���O�D�S�V�V�P�@�Ƃ��āA������10�S ���O�D�W�S�O�T�T
���O�D�W�S�O�T�T
�@���l�ɂ��āA
�@������10�T ���P�|
���P�| �{�i�P/�Q�j
�{�i�P/�Q�j ���P�|�i�P/�Q�j
���P�|�i�P/�Q�j ���O�D�W�S�X�T
���O�D�W�S�X�T
�@����āA�@�O�D�W�S�O�T�T��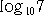 ���O�D�W�S�X�T�@����A�@
���O�D�W�S�X�T�@����A�@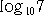 ���O�D�W�S�E�E�E�@�ƌ�����B
���O�D�W�S�E�E�E�@�ƌ�����B
�@������10�V �̒l��������R�ʂ܂ŋ��߂����ꍇ
�@��L�̓��k��w�̖��̂悤�ɉ����Ă������邪�A���̂悤�ȕʉ���������Ă���B
�@�@�S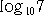 ��������10�Q�S�O�P��������10�Q�S�O�O�@�ł��邱�Ƃɒ��ڂ��āA
��������10�Q�S�O�P��������10�Q�S�O�O�@�ł��邱�Ƃɒ��ڂ��āA
�@�@������10�Q�S�O�O��������10�Q�S�~�P�O�O��������10�R�{�R������10�Q�{�Q���R�D�R�W�O�P
�@�@����āA�@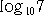 ���O�D�W�S�T�O�Q�T
���O�D�W�S�T�O�Q�T
�@�܂��A�@�Q4�E�R�~�Q10���S�W�~�P�O�Q�S���S�X�P�T�Q���S�X�O�O�O���V2�~�P�O3�@�ɒ��ڂ��āA
�@������10�Q4�E�R�~�Q10��������10�V2�~�P�O3
�@���Ȃ킿�A�@�P�S �{
�{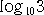 ���Q
���Q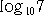 �{�R�@���A
�{�R�@���A
�@�@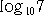 ���i�P�S
���i�P�S �{
�{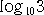 �|�R�j/�Q���O�D�W�S�T�T�T
�|�R�j/�Q���O�D�W�S�T�T�T
�@����āA�@�O�D�W�S�T�O�Q�T��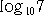 ���O�D�W�S�T�T�T�@����A�@
���O�D�W�S�T�T�T�@����A�@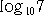 ���O�D�W�S�T�E�E�E�@�ƌ�����B
���O�D�W�S�T�E�E�E�@�ƌ�����B
�i�R�����g�j�@�s�����̕]���ɂ��A���Ƃ�������R�ʂ܂ł͐��������߂�ꂽ���A����ɁA��
�@�@�@�@�@�@����S�ʂ܂Ő������E�E�E�Ɩ����ƁA���Ȃ����D�D�D�B
�i�NjL�j�@�����Q�O�N�V���R�O���t��
�@���g�o�̌f���u�o��̐�v�ɂg�m�u�܂�����[�ȁv�����d��ɂ��ď������݂�
���ꂽ�B
�@���d�삪�A�v������������ �ɕW���ŕt���Ă���Ƃ������Ƃ��f���āA���낢��V��ł݂��B
�i�莝���̃J�V�I�̊��d����v���Ԃ�Ɉ�������o���Ďg���Ă݂���A�t��������������ł��ĂЂ�
���K�b�J�������I���̂��C�ɓ��肾�����̂ɁD�D�D�B�j
�@���ʂ̓d������d����Ƃ��ɂR�Q���̕\���ŁA���Ȃ荂���\�ł���B���ꂾ�ƁA������
�d���ʓr�w������K�v�͑S���Ȃ��ł��ˁI
�@��p�ΐ��͒ʏ�S�����炢�����o���Ă��炸�A���̐悪�ǂ��Ȃ��Ă��邩��������������
�Ōv�Z�����Ă݂��B
�@������10�Q �� �O�D�R�O�P�O �Q�X�X�X �T�U�U�R �X�W�P�P �X�T�Q�P �R�V�R�W �W�X�S�V
�Q�S�S�X �E�E�E
�@������10�R �� �O�D�S�V�V�P �Q�P�Q�T �S�V�P�X �U�U�Q�S �R�V�Q�X �T�O�Q�V �X�O�R�Q
�T�T�P�Q �E�E�E
�@�f���ŁA�u�܂�����[�ȁv����́A���̖����N���ꂽ�B
�@�R�̂P�O�O�O�����p�ΐ��\���g���āA�ߎ��l�����߂���
�@���w�U�Ŋw�Ԏ�@�ł́A���̂悤�ɉ������B
�@������10�R1000���P�O�O�O�~������10�R
�ʏ�́A������10�R �� �O�D�S�V�V�P�@���A�@������10�R1000 ���@�S�V�V�D�P�@�ƂȂ�̂ŁA
�@������10 �� ���O�D�P�@�ƂȂ鐔 �� ���Ƃ�A�� �͂������� �P�D�Q�U�`�P�D�T�W �̊Ԃ̐��ŁA
�@�R1000 �� �� �~ �P�O477
�Ə����邱�ƂɂȂ�B
�@���̂��Ƃ���A�R1000 �́A�S�V�W���̐����ŁA��ʂ̐��́A�P �ŁA���ʂ̐��� �P �ƂȂ�B
������ӂ��A��p�ΐ��\�ŋ��߂�����E�ł���B
�@�v������������ �ɕW���ł��Ă�����d��ɏo��܂ł́A��L�̉Ŗ������Ă���
���A�u�܂�����[�ȁv����ɋ����Ă������������d����g���Ƃ���ɏڂ������ׂ���B
�@������10�R �� �O�D�S�V�V�P �Q�P�Q�T �S�V�P�X �U�U�Q�S �R�V�Q�X �T�O�Q�V �X�O�R�Q
�T�T�P�Q �E�E�E
�Ȃ̂ŁA
�@������10�R1000���P�O�O�O�~������10�R
���S�V�V�D�P�Q�P�Q�@�T�S�V�P�@�X�U�U�Q�@�S�R�V�Q�@�X�T�O�Q�@�V�X�O�R�@�Q�T�T�P�@�Q �E�E�E
�@����āA�@������10 �� ���O�D�P�Q�P�Q�@�T�S�V�P�@�X�U�U�Q�@�S�R�V�Q�@�X�T�O�Q�@�V�X�O�R�@�Q�T�T�P�@�Q
�E�E�E
�ƂȂ� �� �̒l���ڂ������߂�A�R1000 �Ɋւ�������ڂ����Ȃ�B
�@���d���p����ƁA
�@�@�� �� �P�D�R�Q�Q�O �V�O�W�P �X�S�W�O �W�O�U�U �R�U�W�X �O�S�T�T �Q�T�X�V �U�U�S �E�E�E
�ƊȒP�ɋ��߂���B�i�u�h�����v�Ɓu�������v�����p����悢�I�j
�@���̂��Ƃ���A�|�낵���傫�����@�R1000�@�̂��������̗l�q��������B
�@�R1000 �� �P�R�Q�Q �O�V�O�W �P�X�S�W �O�W�O�U �U�R�U�W �X�O�S�T �T�Q�T�X �V�U�U�S
�E�E�E�E �E�E�E�P
�@����́A������Ɗ������̂ł��ˁD�D�D�I
�@����Ȗʓ|�Ȃ��Ƃ��������d����g���A
�@�R1000 �� �P�R�Q�Q �O�V�O�W �P�X�S�W �O�W�O�U �U�R�U�W �X�O�S�T �T�Q�T�X �V�T�Q�P
�E�E�E�E �E�E�E�P
�Əo��B
�@�擪����R�O�Ԗڈȍ~�̐��ɈႢ������̂ŁA������ӂ���덷�������Ă���̂��낤�B
������ƁA�C�ɂȂ�܂��ˁD�D�D�H
�i�R�����g�j�@���d��́A���㎄�Ƃ��F�B�ɂȂꂻ���ł��B���d��̂��Ƃ������Ă�����
�@�@�@�@�@�@�����u�܂�����[�ȁv����Ɋ��ӂ������܂��B
�i�NjL�j�@�����Q�W�N�P�Q���U���t��
�@�ŋ߁A����w�O�����n�i�����P�Q�N�x�j�̓������ɁA��L�̘b��Ɋ֘A�����肪
�o�肳��Ă��邱�ƂɋC�Â����ꂽ�B
����@�W�O���W�P����тQ�S�R���Q�T�O�ł��邱�Ƃɒ��ӂ��āA
�@�@�@�R/�P�O��������10�Q���Q�R/�V�T�A�P�X/�S�O��������10�R���P�Q/�Q�T
�ł��邱�Ƃ������B
�i���j�@�Q10���P�O3�@���A�@�P�O������10�Q���R�@�Ȃ̂ŁA�@�R/�P�O��������10�Q�@��������B
�@����ɁA�@�W�O���W�P�@���A�@�R������10�Q�{�P���S������10�R
�@�Q�S�R���Q�T�O�@���A�@�T������10�R���R�|�Q������10�Q�@�Ȃ̂ŁA�S������10�R���P�Q/�T�|�i�W/�T�j������10�Q
�@����āA�@�R������10�Q�{�P���P�Q/�T�|�i�W/�T�j������10�Q�@���A
�@�@�@�i�Q�R/�T�j������10�Q���P�Q/�T�|�P���V/�T�@�Ȃ̂ŁA�@������10�Q���V/�Q�R
�@�V/�Q�R�|�Q�R/�V�T���i�T�Q�T�|�T�Q�X�j/�i�Q�R�E�V�T�j���O�@�Ȃ̂ŁA�@�V/�Q�R���Q�R/�V�T
�@����āA�@�R/�P�O��������10�Q���V/�Q�R���Q�R/�V�T
�@�R������10�Q�{�P���S������10�R�@���A�@�R�i�R/�P�O�j�{�P���S������10�R�@�Ȃ̂ŁA�@�P�X/�S�O��������10�R
�@�܂��A�@�T������10�R���R�|�Q������10�Q���R�|�Q�i�R/�P�O�j���P�Q/�T�@���A�@������10�R���P�Q/�Q�T
�@����āA�@�P�X/�S�O��������10�R���P�Q/�Q�T
�i�R�����g�j�@�Q�R/�V�T���O�D�R�O�U�U�U�E�E�E�@�ɑ��āA�@�V/�Q�R���O�D�R�O�S�R�S�V�W�E�E�E�@�Ȃ̂ŁA
�@��蕶�̕]�����@�R/�P�O��������10�Q���Q�R/�V�T�@�����A�R/�P�O��������10�Q���V/�Q�R�@�̕���
�@��茵�����]���ƂȂ�B�܂��A�V/�Q�R���Q�R/�V�T�@����A������10�Q���Q�R/�V�T�@�����������A����
�Ɏ������Ƃ��\�ł���B
�@�@�R������10�Q�{�P���S������10�R�@�Ɓ@������10�R���P�Q/�Q�T�@����A�@�R������10�Q�{�P���S�W/�Q�T
�@����āA�@������10�Q���i�S�W/�Q�T�|�P�j/�R���Q�R/�V�T
�@��L�̌v�Z����A�m���Ɍ����邱�Ƃ́A�@������10�Q���O�D�R�O�E�E�E�@�ł��邱�ƂƁA
�P�X/�S�O���O�D�S�V�V�T�E�E�E�@�A�P�Q/�Q�T���O�D�S�W�@����A�@������10�R���O�D�S�E�E�E�@�ł���B
�i�NjL�j�@���̓��{��w�i�P�X�X�V�j�̖�����v�Z�̖��͂�Nj��������ł���B
�@�@�@�@�i�����Q�X�N�P���Q�T���t���j
����@�P�O�P100�̉��W���́H
�i���j�@�Q���藝���A
101�O100= (100+1)�O100
= 1�O100 + 100�b1�E100 + 100�b2�E100�O2 + 100�b3�E100^3 + 100�b4�E100�O4 + �E�E�E
�@���߂�͉̂��ʂW���Ȃ̂ŁA��̎�����
�@1�O100 + 100�b1�E100 + 100�b2�E100�O2 + 100�b3�E100^3
�̒l�����߂�Ώ\���ł���B�i100�O4�͂X���̐��j
�@����āA
�@1�O100 + 100�b1�E100 + 100�b2�E100�O2 + 100�b3�E100^3
= 1 + 100�E10^2 + 4950�E10�O4 + 161700�E10^6
= 161749510001
���A���߂鉺�W���́A�u49510001�v�ł���B
�i�NjL�j�@�ߘa�U�N�P���Q�X���t��
�@�d���p����ƁA�@ ���R�D�U�O�T�T�T�P�Q�V�T�E�E�E�@�ł���B
���R�D�U�O�T�T�T�P�Q�V�T�E�E�E�@�ł���B
�@���� �́u���������A������P�ʁA������Q�ʂ����߂�v�Ƃ�����肪�A
�́u���������A������P�ʁA������Q�ʂ����߂�v�Ƃ�����肪�A
�ߘa�U�N�P���P�S���ɍs��ꂽ��w���w���ʃe�X�g�@���w �h�{�` ����P��m�P�n�ŏo�肳�ꂽ�B
�@�v�Z�̕��@�́A�Q �̏���������]�������@�����ꂽ�B
�̏���������]�������@�����ꂽ�B
�@�Q �̏��������� �� �Ƃ����A�����P/�� �̎�蓾��l�͈̔͂����߂āA
�̏��������� �� �Ƃ����A�����P/�� �̎�蓾��l�͈̔͂����߂āA �̋ߎ��l��
�̋ߎ��l��
���߂���B
�@���ۂɁA�V���Q ���W�@����A�Q
���W�@����A�Q �̐��������́A�V�@�Ȃ̂ŁA�������� �� �́A
�̐��������́A�V�@�Ȃ̂ŁA�������� �� �́A
�����Q �|�V�@�ƂȂ�B���̂Ƃ��A�����P/�����P/�i�Q
�|�V�@�ƂȂ�B���̂Ƃ��A�����P/�����P/�i�Q �|�V�j���i�Q
�|�V�j���i�Q �{�V�j/�R�@�ɂ����āA
�{�V�j/�R�@�ɂ����āA
�V���Q ���W�@����A�P�S/�R�������T�@�ƂȂ�B����āA�@�P/�T�������R/�P�S�@�ƂȂ�B
���W�@����A�P�S/�R�������T�@�ƂȂ�B����āA�@�P/�T�������R/�P�S�@�ƂȂ�B
�@�P/�T���Q �|�V���R/�P�S�@�Ȃ̂ŁA�@�P�W/�T��
�|�V���R/�P�S�@�Ȃ̂ŁA�@�P�W/�T�� ���P�O�P/�Q�W
���P�O�P/�Q�W
�@�����ŁA�P�W/�T���R�D�U�@�A�P�O�P/�Q�W���R�D�U�O�V�E�E�E�@�Ȃ̂ŁA
 �̐��������͂R�ŁA������P�ʂ̐����͂U�A������Q�ʂ̐����͂O�ł��邱�Ƃ�������B
�̐��������͂R�ŁA������P�ʂ̐����͂U�A������Q�ʂ̐����͂O�ł��邱�Ƃ�������B
�@�u�Q �v�ł́A������Q�ʂ܂ł����������v�Z����Ȃ��B��ʂ́u��
�v�ł́A������Q�ʂ܂ł����������v�Z����Ȃ��B��ʂ́u�� �v�ɁA���̎�@��p
�v�ɁA���̎�@��p
���āA �̋ߎ��l��Nj����邱�Ƃɂ��悤�B
�̋ߎ��l��Nj����邱�Ƃɂ��悤�B
�@�u�T �v�ł́A�P�W���T
�v�ł́A�P�W���T ���P�X�@�Ȃ̂ŁA�����T
���P�X�@�Ȃ̂ŁA�����T �|�P�W�@�Ƃ����A�P/�� �����߂�B
�|�P�W�@�Ƃ����A�P/�� �����߂�B
�P/�����T �{�P�W�@���A�@�R�U���P/�����R�V�@�Ȃ̂ŁA�@�P/�R�V�������P/�R�U
�{�P�W�@���A�@�R�U���P/�����R�V�@�Ȃ̂ŁA�@�P/�R�V�������P/�R�U
���Ȃ킿�A�@�i�P�W�{�P/�R�V�j/�T�� ���i�P�W�{�P/�R�U�j/�T�@���A
���i�P�W�{�P/�R�U�j/�T�@���A
�@�R�D�U�O�T�S�E�E�E�� ���R�D�U�O�T�T�E�E�E
���R�D�U�O�T�T�E�E�E
�@����āA �̏�����R�ʂ��T�ł��邱�Ƃ��m���߂�ꂽ�B
�̏�����R�ʂ��T�ł��邱�Ƃ��m���߂�ꂽ�B
�@��L�̌v�Z���番����悤�ɁA������S�ʂ��܂����m��ł���B���������v�Z�𑱂��悤�B
�@�u�P�T �v�ł́A�T�S���P�T
�v�ł́A�T�S���P�T ���T�T�@�Ȃ̂ŁA�����P�T
���T�T�@�Ȃ̂ŁA�����P�T �|�T�S�@�Ƃ����A�P/�� �����߂�B
�|�T�S�@�Ƃ����A�P/�� �����߂�B
�P/�����i�P�T �{�T�S�j/�X�@���A�@�P�Q���P/�����P�O�X/�X�@�Ȃ̂ŁA�@�X/�P�O�X�������P/�P�Q
�{�T�S�j/�X�@���A�@�P�Q���P/�����P�O�X/�X�@�Ȃ̂ŁA�@�X/�P�O�X�������P/�P�Q
���Ȃ킿�A�@�i�T�S�{�X/�P�O�X�j/�P�T�� ���i�T�S�{�P/�P�Q�j/�P�T�@���A
���i�T�S�{�P/�P�Q�j/�P�T�@���A
�@�R�D�U�O�T�T�O�E�E�E�� ���R�D�U�O�T�T�T�E�E�E
���R�D�U�O�T�T�T�E�E�E
�@����āA �̏�����S�ʂ��T�ł��邱�Ƃ��m���߂�ꂽ�B
�̏�����S�ʂ��T�ł��邱�Ƃ��m���߂�ꂽ�B
�� �̏�����S�ʂ����߂�̂ɁA�u�P�T
�̏�����S�ʂ����߂�̂ɁA�u�P�T �v�̌v�Z���K�v�ł������B����قǔ\���̂�
�v�̌v�Z���K�v�ł������B����قǔ\���̂�
�@�����@�ł͂Ȃ��̂�������Ȃ��B
�@DD++ ����̃R�����g�ł��B�i�ߘa�U�N�Q���P���t���j
�@ �ɂ��āA����ɂ��̐��Nj��������Ǝv���܂��B
�ɂ��āA����ɂ��̐��Nj��������Ǝv���܂��B
�@(�T )^2�|�P�W^2���P �ƉE�ӂ� 1 �i�܂��� -1�j�ɂȂ���̂����_�ŁA���Ƃ́A
)^2�|�P�W^2���P �ƉE�ӂ� 1 �i�܂��� -1�j�ɂȂ���̂����_�ŁA���Ƃ́A
(�T �|�P�W) (�T
�|�P�W) (�T �{�P�W)���P �̗��ӂ� n �悷�邾���ŊȒP�ɐ��x�����߂��܂��B
�{�P�W)���P �̗��ӂ� n �悷�邾���ŊȒP�ɐ��x�����߂��܂��B
�E�Q��̏ꍇ
(649�|180 ) (649�{180
) (649�{180 )�� 1 �� 1298 �� 649+180
)�� 1 �� 1298 �� 649+180 �� 1299 ���A
�� 1299 ���A
(649�|1/1298)/180 �� �� (649�|1/1299)/180�@���Ȃ킿�A
�� (649�|1/1299)/180�@���Ȃ킿�A
3�D60555127546�c�c �� �� 3�D60555127876�c�c�@�ŁA�����_�ȉ� 8 ���܂Ő������B
�� 3�D60555127876�c�c�@�ŁA�����_�ȉ� 8 ���܂Ő������B
�E�R ��̏ꍇ
(6485 �|23382) (6485
�|23382) (6485 �{23382)�� 1 �� 46764 �� 6485
�{23382)�� 1 �� 46764 �� 6485 �{23382 �� 46765
�{23382 �� 46765
���A�@(23382�{1/46765)/6485 �� ��(23382�{1/46764)/6485�@���Ȃ킿�A
��(23382�{1/46764)/6485�@���Ȃ킿�A
3�D6055512754639187�c�c �� �� 3�D6055512754639892�@�ŁA
�� 3�D6055512754639892�@�ŁA
�����_�ȉ� 13 ���܂Ő������B
�@ �� 3�D6055512754639892931�c�c �Ɣ�r����킩��悤�ɁA������ł͉������A��
�� 3�D6055512754639892931�c�c �Ɣ�r����킩��悤�ɁA������ł͉������A��
����ł͏�������Ȃ萸�x�̂����ߎ��ɂȂ�܂��B
�i1��̎������͏�����͂��Ȃ萸�x���悢�j
�i�R�����g�j�@DD++ ����A����Ȃ�Nj������肪�Ƃ��������܂��B
�@�炷���邳��̃R�����g�ł��B�i�ߘa�U�N�Q���P���t���j
�@�A�����̑ł���Ƃ̊W
 ��[3;1,1,1,1,6,1,1,1,1,6,1,1,1,1,6,�c]�@�ɂ����āA
��[3;1,1,1,1,6,1,1,1,1,6,1,1,1,1,6,�c]�@�ɂ����āA
�@[3;1,1,1,1] = 18/5
�@[3;1,1,1,1,6,1,1,1,1] = 649/180 = (18+1/36)/5
�@[3;1,1,1,1,6,1,1,1,1,6,1,1,1,1] = 23382/6485
�@[3;1,1,1,1,6,1,1,1,1,6,1,1,1,1,6,1,1,1,1] = 842401/233640 = (649-1/1298)/180
�@[3;1,1,1,1,6,1,1,1,1,6,1,1,1,1,6,1,1,1,1,6,1,1,1,1] = 30349818/8417525
�@[3;1,1,1,1,6,1,1,1,1,6,1,1,1,1,6,1,1,1,1,6,1,1,1,1,6,1,1,1,1] = 1093435849/303264540
= (23382+1/46764)/6485
�@�Ȃ��A��Əd�����܂����A
(649-1/1298)/180 = 3�D60555127546�c = [3;1,1,1,1,6,1,1,1,1,6,1,1,1,1,6,1,1,1,1]
(649-1/1299)/180=3�D60555127876�c = [3;1,1,1,1,6,1,1,1,1,6,1,1,1,1,3]
(23382+1/46765)/6485=3�D60555127546391878�c = [3;1,1,1,1,6,1,1,1,1,6,1,1,1,1,6,1,1,1,1,6,2,2,3,3,3]
(23382+1/46764)/6485=3�D60555127546398929�c = [3;1,1,1,1,6,1,1,1,1,6,1,1,1,1,6,1,1,1,1,6,1,1,1,1,6,1,1,1,1]
����A
�@(649�|1/1298)/180 �� �� (649�|1/1299)/180
�� (649�|1/1299)/180
�@(23382�{1/46765)/6485 �� ��(23382�{1/46764)/6485
��(23382�{1/46764)/6485
�@���ꂩ��A��̗��������ƁA
18/5 = 3.6
(18+1/(18*2))/5 = 649/180 = 3�D60555�c
(649-1/(649*2))/180 = 842401/233640 = 3�D60555127546�c
(842401-1/(842401*2))/233640 = 1419278889601/393637139280 = 3�D60555127546398929311922�c
(1419278889601-1/(1419278889601*2))/393637139280
= 4028705132934095091878401/1117361763886065161254560
= 3�D605551275463989293119221267470495946251296573845�c�i������ �ƈ�v���錅�̂݁j
�ƈ�v���錅�̂݁j
�̂悤�Ɍv�Z���邱�ƂŐ��x��{�X�ɂ��邱�Ƃ��ł��܂��ˁB
�@DD++ ����̃R�����g�ł��B�i�ߘa�U�N�Q���P���t���j
�@�y���������̉��̍\�����璅�z�Ă���̂ŁA�A�����W�J�ƊW������̂́A�܂���
���̒ʂ�ł��B�炷���邳��̕��@�ŋ^��Ȃ�ł����A�{���x�ň�v���Ă����ۏ͂ǂ���
����̂ł��傤�H
�@�炷���邳��̃R�����g�ł��B�i�ߘa�U�N�Q���P���t���j
�@DD++ ����́u�Q��̏ꍇ�v�̌v�Z���猾���Ă���悤�ȋC�����܂����A�Ⴂ�܂����ˁH
�@(a-b )(a+b
)(a+b ) = 1 �̂Ƃ��A(a-b
) = 1 �̂Ƃ��A(a-b )^2 = a^2+13b^2-2ab
)^2 = a^2+13b^2-2ab = 2a^2-1-2ab
= 2a^2-1-2ab
�@(2a^2-1)/(2ab) = (a-1/(2a))/b�@�ƂȂ�A����́Aa/b �Ɣ�r���Đ��x���Q�{
�@������ƎG�����������m��܂���̂ŕ⑫���܂��B
�@(a-b )(a+b
)(a+b ) = 1 �̂Ƃ��A
) = 1 �̂Ƃ��A
�@a-b = 1/(a+b
= 1/(a+b ) ���Aa/b-
) ���Aa/b- = 1/{b(a+b
= 1/{b(a+b )}
)}
�ŏ��̎����Q�悷��ƁA
�@(a-b )^2(a+b
)^2(a+b )^2 = 1 ���A2a^2-1-2ab
)^2 = 1 ���A2a^2-1-2ab = 1/(a+b
= 1/(a+b )^2
)^2
(2a^2-1)/2ab- = 1/{2ab(a+b
= 1/{2ab(a+b )^2}��1/{b(a+b
)^2}��1/{b(a+b )}^2 = (a/b-
)}^2 = (a/b- )^2
)^2
�@����āA�@(a-1/(2a))/b- ��(a/b-
��(a/b- )^2
)^2
������⑫�B
�@(a-b )(a+b
)(a+b ) = -1 �̏ꍇ�i5
) = -1 �̏ꍇ�i5 -18 = 1 �̂悤�ȏꍇ�j�́A13b^2 = a^2-1 �łȂ��A
-18 = 1 �̂悤�ȏꍇ�j�́A13b^2 = a^2-1 �łȂ��A
13b^2 = a^2+1 �ƂȂ�܂��̂ŁA�@(a-b )^2 = a^2+13b^2-2ab
)^2 = a^2+13b^2-2ab = 2a^2+1-2ab
= 2a^2+1-2ab
���A(2a^2+1)/(2ab) = (a+1/(2a))/b�@�̂悤�ɁA�P�ӏ��������ς��܂����A���͓����ł��B
�@��x�Q�悵����́Aa-b = 1 �̌`�ɂȂ�܂��̂ŁA(a+1/(2a))/b �̂悤�Ƀv���X�ɂȂ�
= 1 �̌`�ɂȂ�܂��̂ŁA(a+1/(2a))/b �̂悤�Ƀv���X�ɂȂ�
�\��������̂͏����ł��B
�@DD++ ����̃R�����g�ł��B�i�ߘa�U�N�Q���Q���t���j
�@���̂́A3�D60555127546�c�c �� �� 3�D60555127876�c�c �Ə㉺���狲��ł�̂ŁA
�� 3�D60555127876�c�c �Ə㉺���狲��ł�̂ŁA
�E3�D60555127 �܂ł͊m��
�E������ 546 ���炢�܂ł����Ă����i�\�z�j
�Ƃ����悤�ɏؖ��Ɨ\�z����ʂ��ďo���Ă��܂��B
�@�炷���邳��̃R�����g�ł��B�i�ߘa�U�N�Q���Q���t���j
�@DD++��������Ă���]���Ƃ��Ă͂��̒ʂ�ł��ˁB�������A�v�Z��2�悵�Ă��邱�Ƃ�
��A�i���������G�ł����j �Ƃ̌덷���Q�悳��Ă��āA���x���Q�{�ɂȂ��Ă��邱�Ƃ���
�Ƃ̌덷���Q�悳��Ă��āA���x���Q�{�ɂȂ��Ă��邱�Ƃ���
�ĂƂ�܂��ˁB
�@������������̌v�Z������ƁA���ۂɂ͂Q���肳��ɏ������Ȃ��Ă���i�Q��̖�0.14�{�j
���Ƃ��킩��܂��B
�@���ہA��L�ŏ������v�Z�ł��A�����������_�ȉ��̌������A2���A5���A11���A23���A48��
�̂悤�ɂQ�{�ȏ�ɂȂ��Ă��܂��ˁB
�@���̌v�Z���@�́A �ȊO�ɂ��g���āA���ۂɂ������v�Z���Ă݂܂������A
�ȊO�ɂ��g���āA���ۂɂ������v�Z���Ă݂܂������A
 �́A7/5 = 1�D4 ����n�߂āA5 ��̌v�Z�ŁA72 ��
�́A7/5 = 1�D4 ����n�߂āA5 ��̌v�Z�ŁA72 ��
 �́A7/4 = 1�D75 ����n�߂āA5 ��̌v�Z�ŁA71 ��
�́A7/4 = 1�D75 ����n�߂āA5 ��̌v�Z�ŁA71 ��
 �́A9/4 = 2�D25 ����n�߂āA5 ��̌v�Z�ŁA78 ��
�́A9/4 = 2�D25 ����n�߂āA5 ��̌v�Z�ŁA78 ��
 �́A5/2 = 2�D5 ����n�߂āA5 ��̌v�Z�ŁA62 ��
�́A5/2 = 2�D5 ����n�߂āA5 ��̌v�Z�ŁA62 ��
�i������������͐^�l�ƈ�v���Ă��鏬���_�ȉ��̌����j
�̂悤�ɂȂ��Ă��܂����B���������v�Z�����̂ŁA���ۂ̌v�Z�������Ă����܂��傤�B
�E
7^2-(5 )^2 = -1�i�����}1�ł��邱�Ƃ͏d�v�j
)^2 = -1�i�����}1�ł��邱�Ƃ͏d�v�j
7/5 = 1�D4
(7+1/(7*2))/5 = 99/70�@�i7-5 ��0 �Ȃ̂ŁA���������u�{�v�j
��0 �Ȃ̂ŁA���������u�{�v�j
(99-1/(99*2))/70 = 19601/13860
(19601-1/(19601*2))/13860 = 768398401/543339720
(768398401-1/(768398401*2))/543339720 = 1180872205318713601/835002744095575440
(1180872205318713601-1/(1180872205318713601*2))/835002744095575440
= 2788918330588564181308597538924774401/1972063063734639263984455073299118880
= 1�D414213562373095048801688724209698078569671875376948073176679737990732478�c
�E
7^2-(4 )^2 = 1
)^2 = 1
7/4 = 1�D75
(7-1/(7*2))/4 = 97/56�@�i7-4 ��0 �Ȃ̂ŁA����́u�|�v�A�ȉ��A
��0 �Ȃ̂ŁA����́u�|�v�A�ȉ��A ��
�� �������j
�������j
(97-1/(97*2))/56 = 18817/10864
(18817-1/(18817*2))/10864 = 708158977/408855776
(708158977-1/(708158977*2))/408855776 = 1002978273411373057/579069776145402304
(1002978273411373057-1/(1002978273411373057*2))/579069776145402304
= 2011930833870518011412817828051050497/1161588808526051807570761628582646656
= 1�D73205080756887729352744634150587236694280525381038062805580697945193301�c
�E
9^2-(4 )^2 = 1
)^2 = 1
9/4 = 2�D25
(9-1/(9*2))/4 = 161/72
(161-1/(161*2))/72 = 51841/23184
(51841-1/(51841*2))/23184 = 5374978561/2403763488
(5374978561-1/(5374978561*2))/2403763488 = 57780789062419261441/25840354427429161536
(57780789062419261441-1/(57780789062419261441*2))/25840354427429161536
= 6677239169351578707225356193679818792961/2986152136938872067784669198846010266752
= 2�D236067977499789696409173668731276235440618359611525724270897245410520925637804�c
�E
5^2-(2 )^2 = 1
)^2 = 1
5/2 = 2.5
(5-1/(5*2))/2 = 49/20
(49-1/(49*2))/20 = 4801/1960
(4801-1/(4801*2))/1960 = 46099201/18819920
(46099201-1/(46099201*2))/18819920 = 4250272665676801/1735166549767840
(4250272665676801-1/(4250272665676801*2))/1735166549767840
= 36129635465198759610694779187201/14749861913749949808286047759680
= 2�D44948974278317809819728407470589139196594748065667012843269256�c
�@DD++ ����̃R�����g�ł��B�i�ߘa�U�N�Q���Q���t���j
�@�����A���́A���̋��ʃe�X�g�̖��͂����ɂȂ��Ă܂����ˁH���̖��͂ǂꂾ���߂��L
���������邩�ł͂Ȃ��A�^�l���킩��Ȃ���ԂŁA�ォ�� n �����m�肵�����Ƃ����Ӑ}��
���ł��B�Ȃ̂ŁA�u���ۂ̐^�l������Əォ�� n �������Ă���v�����Ȃ̂́A����قlj��l
�͂Ȃ��̂ł���B
�@�炷���邳��̃R�����g�ł��B�i�ߘa�U�N�Q���Q���t���j
�@�������A�q�����Ă��܂���B�ŏ�����A�u���̂悤�Ɍv�Z����Ɛ��x�̍����l�邱�Ƃ�
�o���܂��ˁv�Ƃ����A���̖��Ƃ͊W�Ȃ��i���́j����������v�Z�������������̂����
���B���̖�肩��b������Ă͂����Ȃ������̂ł�����A���߂�Ȃ����B
�@DD++ ����̃R�����g�ł��B�i�ߘa�U�N�Q���Q���t���j
�@���Ă����Ȃ����Ƃ͂Ȃ��ł����A�ʂ̘b���ƒf������Ă���n�߂Ȃ��ƁA�������Ӗ�
�ɏ�����������邾�����Ǝv���܂��B
�@�����āA�߂��L�������������Ȃ̂ł���A
(5 -18)^16 = 4028705132934095091878401 - 1117361763886065161254560
-18)^16 = 4028705132934095091878401 - 1117361763886065161254560
���E�E�E�i���j
�ŁA�킴�킴�{�X�v�Z��H��Ȃ��Ă� 1 �s�̎��� 48 �����킹���܂���B
�i�NjL�j�@DD++ ���炲���e���������܂����B�i�ߘa�U�N�X���P�T���t���j
�@��p�ΐ��l�̎�v�Z�̘b��ł��B
�@����A���͂ӂ� 4374��2�E37 �� 4375��54�E7 ���ǂ���� 1 ���̑f�������������Ȃ����Ƃ�
�C�Â��܂����B�����āA224��25�E7 �� 225��32�E52�A2400��25�E3�E52 �� 2401��74 �����l��
���������ƒm���Ă������́A�ȉ��̂悤�Ȍv�Z�܂����Blog �͑S�ď�p�ΐ��ł��B
�@224 �� 225 ���A�@5 log 2 + log 7 �� 2 log 3 + 2 log 5
�@2400 �� 2401 ���A�@5 log 2 + log 3 + 2 log 5 �� 4 log 7
�@4374 �� 4375 ���A�@log 2 + 7 log 3 �� 4 log 5 + log 7
�����āA�@log 2 + log 5 = 1
�@������A������ 4 �� 1 ���������Ǝv���ĉ����ƁA������6�ʎl�̌ܓ��ŁA
log 2 �� 72/239 �� 0.30126 �i�^�l 0.30103�j
log 3 �� 114/239 �� 0.47699 �i�^�l 0.47712�j
log 5 �� 167/239 �� 0.69874 �i�^�l 0.69897�j
log 7 �� 202/239 �� 0.84519 �i�^�l 0.84510�j
�������Ĕ�r�I�ȒP�ɂ悢�ߎ��l��������悤�ł��B
�@��������ċ^�₪�������D�D�D�B
(1)�@���� 239 �Ƃ����̂͂ǂ̂��炢�̗D�G���Ȃ�ł��傤���H�����A4 �̑ΐ��ꂪ��
�ʂȗL�����ŋߎ�����ꍇ�A���ꁃ1000 ���炢�ʼn��Ԗڂ��炢�ɗD�G�ȋߎ��l����
����Ȃ�ł��傤���H
�i��Ό덷�̘a�ŕ]�����邩���Ό덷�̘a�ŕ]�����邩�ł��ς��Ǝv���܂����j
(2)�@4 ���ō��� 1 �ł�����̂����A7���ȏ�ō��� 11 �� 13 ���邢�͂������܂� 2 ����
�炢�̍������ł�����̂�p�����������x���悭�Ȃ肻���ȋC�����܂��c�c�{���ł��傤���H
�{�����Ƃ��āA��̓I�ɂǂ̂��炢���x���グ����ł��傤�H
�i���� 1 ���̑f�������������Ȃ����̂́AABC�\�z�̏ؖ���M����Ȃ� 44100 ����ɂ�
���݂��Ȃ��͂��j
(3)�@�� �ł͂Ȃ��A�s�����ł̕]���͓��l�̕��@�ʼn\�ł��傤���H
(4)�@�g���f���� 11 ���܂߂� 5 �� 1 ���ɂ���A�g���f���� 13 �܂Ŋ܂߂� 6 �� 1 ���ɂ���A
�ȂǂŐ��x�̌���͉\�ł��傤���H
���ɁA (1) (2) (4) �͎��Ƃł͖��d�ɂ��قǂ�����̂ŁA�R���s���[�^�n�̉��R�����肢���܂��B
�i�R�����g�j�@�u4 �� 1 ���������Ǝv���ĉ����v�Ƃ����̂́A�V�������z�ł��ˁI
�@�炷���邳��̃R�����g�ł��B�i�ߘa�U�N�X���P�T���t���j
�@�Ƃ肠����(1)�����F���� 239 �Ƃ����̂͂ǂ̂��炢�̗D�G���Ȃ�ł��傤���H
�@���ꁃ1000�ł�(���Ό덷�̍��v��)70�ԖڂɗD�G�ł����B
�@239�ő��Ό덷�̍��v��0.001457�c�ł��B
�@1�ʂ�568�ŁA���Ό덷�̍��v��0.0001758�c�ł��B
�@2�ʈȉ��́A897�A960�A807�A794�A�c�@�Ƒ����܂����A���ꂪ�傫����Α��Ό덷��������
�͓̂��R�ŁA���������Ӗ��ł�69�Ԗڂ܂łɕ��ꂪ239�����̂��̂͂���܂���̂ŁA239��
���\�D�G�ƌ�����Ǝv���܂��B
�@����̑傫�����l�����āA�u���Ό덷�̍��v�~����v�Ń����L���O�����ƁA
1�ʂ�568�A2�ʂ�897�͕ς��܂��A3�ʂ�329�A������4�ʂ�239�ƂȂ�܂��B
�@���Ό덷�̍��v�~����̋�̒l(5�ʂ܂�)�́A
568 0.099882607730
897 0.222871229356
329 0.285662258393
239 0.348293385746
103 0.383956736568
�̂悤�ɂȂ��Ă��āA��������Ă� 568 �����ˏo���Ă��銴���ł��B���Ȃ݂ɁA���ꂪ568��
�ꍇ�̑ΐ��̋ߎ��l�́A
log2 �� 171/568 �� 0.30106
log3 �� 271/568 �� 0.47711
log5 �� 397/568 �� 0.69894
log7 �� 480/568 �� 0.84507
�Ȃ̂ŁA���Ȃ�ǂ��ߎ��ɂȂ��Ă��܂��ˁB
�@���ꂪ568�ɂȂ�悤�ȑg������K���ɒT���Ă݂�ƁA
�@(2400,2401)�@�A(4374,4375)�@�A(250000,250047)
���玮�𗧂Ă�Ώ�L�̒l�ɂȂ�悤�ł��B(���Z���Ă��܂���B)
�@DD++ ����̃R�����g�ł��B�i�ߘa�U�N�X���P�T���t���j
�@�����[�A568 �D�G�ł��ˁB�������A250047 �͐l�͂��ᗬ�ɂ�����Əo�Ă��Ȃ��c�c�B
�@����ς茅���������� 2 ���̍������������Ă��C�ɂȂ�Ȃ��Ȃ��Ă����̂Ő��x�オ���
�ۂ��ł��ˁB
�@�炷���邳��̃R�����g�ł��B�i�ߘa�U�N�X���P�U���t���j
�@(3)�ɂ��āA
5log2 + log7 �� 2log3 + 2log5
5log2 + log3 + 2log5 �� 4log7
log2 + 7log3 �� 4log5 + log7
��
5log2 + log7 + a = 2log3 + 2log5
5log2 + log3 + 2log5 + b = 4log7
log2 + 7log3 + c = 4log5 + log7
�ia�Ab�Ac��0�j
�Ƃ��Čv�Z����ƁA
log2 = (72 - 27a - 5b - 7c) / 239
log3 = (114 + 17a + 12b - 31c) / 239
log5 = (167 + 27a + 5b + 7c) / 239
log7 = (202 - 16a + 59b - 13c) / 239
�ƂȂ�܂��B���̎�����A
�@log2 �� 72/239�@�Alog5 �� 167/239
�͂������ɂ킩��܂����Alog3 �� 114/239 �̑召�W�́A17a + 12b - 31c �̕�����
�Ȃ��Ƃ킩��܂���B�������A17a + 12b - 31c �̕����ׂ邽�߂Ɍv�Z����ƁA
�@17a + 12b - 31c = 239log3 - 114log10
�ƂȂ��āA3^239 �� 10^114 �̑召�W�ׂ邱�ƂɂȂ�A�{���]�|�ł��B
����āA���l�̕��@�ŕs�����ŏ㉺���炨�����邽�߂ɂ́A�ߎ����𑽐��p�ӂ��Ă��܂���
�召�W���킩�邱�ƂɊ��҂��邮�炢�����v�����܂��A�lj��̋ߎ�����p�ӂ��悤
�Ƃ���ƌ����������āA��v�Z�ɕs�����ɂȂ��Ă��܂��̂ŁA�Ƃ肠����
�@�u���̕��@�ł̕s�����ł̕]���͓���v
�ƌ����Ă悢���Ǝv���܂��B
�@DD++ ����̃R�����g�ł��B�i�ߘa�U�N�X���P�U���t���j
�@17a + 12b - 31c �̕����ׂȂ��Ƃ킩��܂���B
�@�Ȃ�قǁA������萔�����Ă��܂��悩�����̂ł��ˁB�A����������������Ԃ͂�������
�����Ă��܂��܂�����ǂ��B��ł��Ȃ�t�s��p�ӂ��ĉ����̂���ԑ������ȁH
�@{1/n - 1/(2*n^2)} log e < log{1+(1/n)} < {1/n} log e
���g���Alog e �͊���o���ĕ��u�ł����̂ŁAa, b, c �̐��^�����̐����]���͂Ȃ�Ƃ���
��P�[�X���������Ɏv���܂��B
�@(224, 225)�A(2400, 2401)�A(4374, 4375) �̃P�[�X�͎��ۂ���łȂ�Ƃ��Ȃ�݂����ł��B
�@�炷���邳��̃R�����g�ł��B�i�ߘa�U�N�X���P�U���t���j
�@(2)�ɂ��āA
�@�f�� 2�A3�A5�A7 �A10���ȉ���(2400,2401)���덷�������������̂́A�ȉ���6��������
�܂���ł����B���[�͌덷��(�傫�����̒l�����������̒l�|1)�ł��B
0.000040616 78121827 78125000
0.000066758 645657712 645700815
0.000107377 3954653486 3955078125
0.000188000 250000 250047
0.000228624 4374 4375
0.000295397 184473632 184528125
0.000416667 2400 2401
78121827 = 3^13 * 7^2, 78125000 = 2^3 * 5^10, �� = 3173 = 19 * 167
645657712 = 2^4 * 7^9, 645700815 = 3^17 * 5, �� = 43103 (�f��)
3954653486 = 2 * 7^11, 3955078125 = 3^4 * 5^11, �� = 424639 (�f��)
�@������g���āA
13log3 + 2log7 = 3log2 + 10log5 (78121827, 78125000)
4log2 + 9log7 = 17log3 + log5 (645657712, 645700815)
log2 + 11log7 = 4log3 + 11log5 (3954653486, 3955078125)
log2 + log5 = 1
�������ƁA�ꎟ�]���ʼn����܂���ł����B���炽�߂āA
78121827 = 3^13 * 7^2, 78125000 = 2^3 * 5^10, �� = 3173 = 19 * 167
645657712 = 2^4 * 7^9, 645700815 = 3^17 * 5, �� = 43103 (�f��)
250000 = 2^4 * 5^6, 250047 = 3^6 * 7^3, �� = 47 (�f��)
�@������g���āA
13log3 + 2log7 = 3log2 + 10log5 (78121827, 78125000)
4log2 + 9log7 = 17log3 + log5 (645657712, 645700815)
4log2 + 6log5 = 6log3 + 3log7 (250000, 250047)
log2 + log5 = 1
�������ƁA�@log2 = 171/568�@�Alog3 = 271/568�@�Alog5 = 397/568�@�Alog7 = 480/568
�E�E�E����͌��o��������܂��ˁB
�@�������A���̒l�́A(2400,2401)�A(4374,4375)�A(250000,250047)�����������̂ł͂Ȃ�
���Ǝv���āA��Łu���Z���Ă��܂���v�Ə������̂����炽�߂Č��Z���Ă݂�ƁA�Ȃ��
5log2 + log3 + 2log5 = 4log7 (2400, 2401)
log2 + 7log3 = 4log5 + log7 (4374, 4375)
4log2 + 6log5 = 6log3 + 3log7 (250000, 250047)
log2 + log5 = 1
�͈ꎟ�]���ʼn����܂���ł����B���\�����Ȃ��ꍇ���o�Ă���̂ł��ˁB
�@����ł́A���낢��g������ς��Ď������Ƃɂ��܂��B
13log3 + 2log7 = 3log2 + 10log5 (78121827, 78125000)
log2 + 11log7 = 4log3 + 11log5 (3954653486, 3955078125)
4log2 + 6log5 = 6log3 + 3log7 (250000, 250047)
log2 + log5 = 1
�� log2 = 171/568�@�Alog3 = 271/568�@�Alog5 = 397/568�@�Alog7 = 480/568
4log2 + 9log7 = 17log3 + log5 (645657712, 645700815)
log2 + 11log7 = 4log3 + 11log5 (3954653486, 3955078125)
4log2 + 6log5 = 6log3 + 3log7 (250000, 250047)
log2 + log5 = 1
�� log2 = 171/568�@�Alog3 = 271/568�@�Alog5 = 397/568�@�Alog7 = 480/568
13log3 + 2log7 = 3log2 + 10log5 (78121827, 78125000)
4log2 + 9log7 = 17log3 + log5 (645657712, 645700815)
log2 + 7log3 = 4log5 + log7 (4374, 4375)
log2 + log5 = 1
�� log2 = 171/568�@�Alog3 = 271/568�@�Alog5 = 397/568�@�Alog7 = 480/568
13log3 + 2log7 = 3log2 + 10log5 (78121827, 78125000)
log2 + 11log7 = 4log3 + 11log5 (3954653486, 3955078125)
log2 + 7log3 = 4log5 + log7 (4374, 4375)
log2 + log5 = 1
�� log2 = 171/568�@�Alog3 = 271/568�@�Alog5 = 397/568�@�Alog7 = 480/568
13log3 + 2log7 = 3log2 + 10log5 (78121827, 78125000)
4log2 + 6log5 = 6log3 + 3log7 (250000, 250047)
log2 + 7log3 = 4log5 + log7 (4374, 4375)
log2 + log5 = 1
�� �ꎟ�]��
4log2 + 9log7 = 17log3 + log5 (645657712, 645700815)
4log2 + 6log5 = 6log3 + 3log7 (250000, 250047)
log2 + 7log3 = 4log5 + log7 (4374, 4375)
log2 + log5 = 1
�� log2 = 171/568�@�Alog3 = 271/568�@�Alog5 = 397/568�@�Alog7 = 480/568
13log3 + 2log7 = 3log2 + 10log5 (78121827, 78125000)
log2 + 7log3 = 4log5 + log7 (4374, 4375)
5log2 + log3 + 2log5 = 4log7 (2400, 2401)
log2 + log5 = 1
�� �ꎟ�]��
�@���������Ă��������̂���ł����B������Ɛ��x���ǂ����炢���ƁA���܂�ς��Ȃ���
���ł��B
�@�ł́A����ɐ��x���ǂ����̂������Ď����܂��B
�@�������A�u10���ȉ��v��11���ȉ��A12���ȉ��A�E�E�E�Ƒ��₵�Ă��Ȃ��Ȃ�������܂���B
�u15���ȉ��v�܂ő��₵�āA�����
0.000026141 205885750000000 205891132094649
0.000033563 281474976710656 281484423828125
�̓��������܂����̂ŁA�����(78121827, 78125000)�Ŏ����܂��B
205885750000000 = 2^7 * 5^9 * 7^7, 205891132094649 = 3^30,
�� = 5382094649 = 3673 * 1465313
281474976710656 = 2^48, 281484423828125 = 5^11 * 7^8,
�� = 9447117469 (�f��)
7log2 + 9log5 + 7log7 = 30log3 (205885750000000, 205891132094649)
48log2 = 11log5 + 8log7 (281474976710656, 281484423828125)
13log3 + 2log7 = 3log2 + 10log5 (78121827, 78125000)
log2 + log5 = 1
��
log2 = 3125/10381 = 0.30103073 (�^�l 0.30103000)
log3 = 4953/10381 = 0.47712166 (�^�l 0.47712125)
log5 = 7256/10381 = 0.69896927 (�^�l 0.69897000)
log7 = 8773/10381 = 0.84510163 (�^�l 0.84509804)
�悤�₭�������x���オ��܂����B
�@���Ȃ݂ɂ����ꌅ���
0.000007053 2251783932057135 2251799813685248
2251783932057135 = 3^13 * 5 * 7^10, 2251799813685248 = 2^51,
�� = 15881628113 = 13 * 71 * 17206531
���g���āA
13log3 + log5 + 10log7 = 51log2 (2251783932057135, 2251799813685248)
7log2 + 9log5 + 7log7 = 30log3 (205885750000000, 205891132094649)
48log2 = 11log5 + 8log7 (281474976710656, 281484423828125)
log2 + log5 = 1
�Ƃ��Ă��A��Ɠ�������10381�̒l�ɂȂ�܂����B
�@�Ƃ����킯�ŁA�g�������̌��������Ȃ葝�₵�Ă����ʂ̐��x�����܂�オ��Ȃ��炵��
�Ƃ������Ƃ��킩��܂����B
�@DD++ ����̃R�����g�ł��B�i�ߘa�U�N�X���P�U���t���j
�@�g���������オ���Ă��A2�A3�A5�A7 �ō��鍇�����̊��������邱�Ƃőł�������Ă��܂��A
�덷�����Ȃ��Ȃ��������Ȃ�Ȃ���ł��ˁB�����Ȃ�ƁA11��13�̎g�p����������������x
�グ�ɂ͏d�v�Ȃ̂��ȁH
�@�炷���邳��̃R�����g�ł��B�i�ߘa�U�N�X���P�U���t���j
�@����œ����̉ۑ�͂Ƃ肠���������B
�@(4)�ɂ��āA
�y11��lj������ꍇ�z
(1���܂�)
0.000102041 9800 9801
0.000228624 4374 4375
0.000330688 3024 3025
0.000416667 2400 2401
0.001244444 5625 5632
9800 = 2^3 * 5^2 * 7^2, 9801 = 3^4 * 11^2
4374 = 2 * 3^7, 4375 = 5^4 * 7
3024 = 2^4 * 3^3 * 7, 3025 = 5^2 * 11^2
2400 = 2^5 * 3 * 5^2, 2401 = 7^4
3log2 + 2log5 + 2log7 = 4log3 + 2log11 (9800, 9801)
log2 + 7log3 = 4log5 + log7 (4374, 4375)
4log2 + 3log3 + log7 = 2log5 + 2log11 (3024, 3025)
5log2 + log3 + 2log5 = 4log7 (2400, 2401)
log2 + log5 = 1
�� �ꎟ�]��
5625 = 3^2 * 5^4, 5632 = 2^9 * 11, �� = 7
3log2 + 2log5 + 2log7 = 4log3 + 2log11 (9800, 9801)
log2 + 7log3 = 4log5 + log7 (4374, 4375)
5log2 + log3 + 2log5 = 4log7 (2400, 2401)
2log3 + 4log5 = 9log2 + log11 (5625, 5632)
log2 + log5 = 1
��
log2 = 270/897 = 0.301003 (�^�l 0.301030)
log3 = 428/897 = 0.477146 (�^�l 0.477121)
log5 = 627/897 = 0.698997 (�^�l 0.698970)
log7 = 758/897 = 0.845039 (�^�l 0.845098)
log11 = 934/897 = 1.041249 (�^�l 1.041393)
897�͏�̕���568�Ɏ����Ő��x�̗ǂ�����ł��B
(1���܂�)
0.000016089 3294172 3294225
0.000022158 67108864 67110351
0.000040616 78121827 78125000
0.000050668 14348180 14348907
3294172 = 2^2 * 7^7, 3294225 = 3^2 * 5^2 * 11^4, �� = 53 (�f��)
67108864 = 2^26, 67110351 = 3 * 7^5 * 11^3, �� = 1487 (�f��)
78121827 = 3^13 * 7^2, 78125000 = 2^3 * 5^10, �� = 3173 = 19 * 167
14348180 = 2^2 * 5 * 7^2 * 11^4, 14348907 = 3^15, �� = 727 (�f��)
2log2 + 7log7 = 2log3 + 2log5 + 4log11 (3294172, 3294225)
26log2 = log3 + 5log7 + 3log11 (67108864, 67110351)
13log3 + 2log7 = 3log2 + 10log5 (78121827, 78125000)
2log2 + log5 + 2log7 + 4log11 = 15log3 (14348180, 14348907)
log2 + log5 = 1
��
log2 = 6421/21330 = 0.3010314 (�^�l 0.3010300)
log3 = 10177/21330 = 0.4771214 (�^�l 0.4771213)
log5 = 14909/21330 = 0.6989686 (�^�l 0.6989700)
log7 = 18026/21330 = 0.8451008 (�^�l 0.8450980)
log11 = 22213/21330 = 1,0413971 (�^�l 1.0413927)
�@���\���x���オ��܂����B
�y13���lj������ꍇ�z
(1���܂�)
0.000102041 9800 9801
0.000150263 6655 6656
0.000228624 4374 4375
0.000236742 4224 4225
0.000244200 4095 4096
0.000330688 3024 3025
0.000416667 2400 2401
9800 = 2^3 * 5^2 * 7^2, 9801 = 3^4 * 11^2
6655 = 5 * 11^3, 6656 = 2^9 * 13
4374 = 2 * 3^7, 4375 = 5^4 * 7
4224 = 2^7 * 3 * 11, 4225 = 5^2 * 13^2
4095 = 3^2 * 5 * 7 * 13, 4096 = 2^12
3024 = 2^4 * 3^3 * 7, 3025 = 5^2 * 11^2
2400 = 2^5 * 3 * 5^2, 2401 = 7^4
3log2 + 2log5 + 2log7 = 4log3 + 2log11 (9800, 9801)
log5 + 3log11 = 9log2 + log13 (6655, 6656)
log2 + 7log3 = 4log5 + log7 (4374, 4375)
7log2 + log3 + log11 = 2log5 + 2log13 (4224, 4225)
2log3 + log5 + log7 + log13 = 12log2 (4095, 4096)
log2 + log5 = 1
�� �ꎟ�]��
3log2 + 2log5 + 2log7 = 4log3 + 2log11 (9800, 9801)
log5 + 3log11 = 9log2 + log13 (6655, 6656)
log2 + 7log3 = 4log5 + log7 (4374, 4375)
7log2 + log3 + log11 = 2log5 + 2log13 (4224, 4225)
2log3 + log5 + log7 + log13 = 12log2 (4095, 4096)
4log2 + 3log3 + log7 = 2log5 + 2log11 (3024, 3025)
log2 + log5 = 1
�� �ꎟ�]�� (����������Ă��Ȃ��ꎟ�]���Ȃ̂ő��̎����K�v)
3log2 + 2log5 + 2log7 = 4log3 + 2log11 (9800, 9801)
log5 + 3log11 = 9log2 + log13 (6655, 6656)
log2 + 7log3 = 4log5 + log7 (4374, 4375)
7log2 + log3 + log11 = 2log5 + 2log13 (4224, 4225)
5log2 + log3 + 2log5 = 4log7 (2400, 2401)
log2 + log5 = 1
��
log2 = 270/897 = 0.301003 (�^�l 0.301030)
log3 = 428/897 = 0.477146 (�^�l 0.477121)
log5 = 627/897 = 0.698997 (�^�l 0.698970)
log7 = 758/897 = 0.845039 (�^�l 0.845098)
log11 = 934/897 = 1.041249 (�^�l 1.041393)
log13 = 999/897 = 1.113712 (�^�l 1.113943)
11�����lj������Ƃ��Ɠ������x�ł��B
(1���܂�)
0.000007456 5767125 5767168
0.000008117 123200 123201
0.000013783 72772425 72773428
0.000015573 1990625 1990656
0.000016089 3294172 3294225
0.000018861 19140264 19140625
0.000022158 67108864 67110351
5767125 = 3 * 5^3 * 7 * 13^3, 5767168 = 2^19 * 11, �� = 43 (�f��)
123200 = 2^6 * 5^2 * 7 * 11, 123201 = 3^6 * 13^2
72772425 = 3^7 * 5^2 * 11^3, 72773428 = 2^2 * 7^2 * 13^5, �� = 1003 = 17 * 59
1990625 = 5^5 * 7^2 * 13, 1990656 = 2^13 * 3^5, �� = 31 (�f��)
3294172 = 2^2 * 7^7, 3294225 = 3^2 * 5^2 * 11^4, �� = 53 (�f��)
19140264 = 2^3 * 3^2 * 11^2 * 13^3, 19140625 = 5^8 * 7^2, �� = 361 = 19^2
67108864 = 2^26, 67110351 = 3 * 7^5 * 11^3, �� = 1487 (�f��)
log3 + 3log5 + log7 + 3log13 = 19log2 + log11 (5767125, 5767168)
6log2 + 2log5 + log7 + log11 = 6log3 + 2log13 (123200, 123201)
7log3 + 2log5 + 3log11 = 2log2 + 2log7 + 5log13 (72772425, 72773428)
5log5 + 2log7 + log13 = 13log2 + 5log3 (1990625, 1990656)
2log2 + 7log7 = 2log3 + 2log5 + 4log11 (3294172, 3294225)
log2 + log5 = 1
�� �ꎟ�]��
log3 + 3log5 + log7 + 3log13 = 19log2 + log11 (5767125, 5767168)
6log2 + 2log5 + log7 + log11 = 6log3 + 2log13 (123200, 123201)
7log3 + 2log5 + 3log11 = 2log2 + 2log7 + 5log13 (72772425, 72773428)
2log2 + 7log7 = 2log3 + 2log5 + 4log11 (3294172, 3294225)
3log2 + 2log3 + 2log11 + 3log13 = 8log5 + 2log7 (19140264, 19140625)
log2 + log5 = 1
��
log2 = 6079/20194 = 0.3010300089 (�^�l 0.3010299957)
log3 = 9635/20194 = 0.4771219174 (�^�l 0.4771212547)
log5 = 14115/20194 = 0.6989699911 (�^�l 0.6989700043)
log7 = 17066/20194 = 0.8451025057 (�^�l 0.8450980400)
log11 = 21030/20194 = 1.0413984352 (�^�l 1.0413926852)
log13 = 22495/20194 = 1.1139447361 (�^�l 1.1139433523)
�@���x��11�����lj��̂Ƃ��Ɠ����x�ł��B
�ilog2��log5�͐��x�������ł����A���͂����܂ŗǂ�����܂���j
�y29�܂Œlj������ꍇ�i�f��10�j�z
(1���܂�)
0.000000010 96059600 96059601
0.000000055 18085704 18085705
0.000000075 26578123 26578125
0.000000084 11859210 11859211
0.000000095 10556000 10556001
0.000000121 8268799 8268800
0.000000155 12901779 12901781
0.000000169 5909760 5909761
0.000000194 5142500 5142501
0.000000244 4096575 4096576
0.000000244 4090624 4090625
0.000000250 4004000 4004001
0.000000315 22194425 22194432
0.000000365 13697019 13697024
0.000000365 90312467 90312500
0.000000371 2697695 2697696
0.000000485 8254125 8254129
0.000000489 88012332 88012375
0.000000494 2023424 2023425
0.000000520 90312453 90312500
0.000000540 1852200 1852201
0.000000560 67874587 67874625
0.000000569 75557027 75557070
0.000000587 46000759 46000786
96059600 = 2^4 * 5^2 * 7^2 * 13^2 * 29, 96059601 = 3^8 * 11^4
18085704 = 2^3 * 3 * 7^3 * 13^3, 18085705 = 5 * 11 * 17 * 23 * 29^2
26578123 = 11 * 13^2 * 17 * 29^2, 26578125 = 3^5 * 5^6 * 7
11859210 = 2 * 3^4 * 5 * 11^4, 11859211 = 7 * 13 * 19^4
10556000 = 2^5 * 5^3 * 7 * 13 * 29, 10556001 = 3^4 * 19^4
8268799 = 7^2 * 11 * 23^2 * 29, 8268800 = 2^10 * 5^2 * 17 * 19
12901779 = 3^2 * 11 * 19^4, 12901781 = 23^2 * 29^3
5909760 = 2^8 * 3^5 * 5 * 19, 5909761 = 11^2 * 13^2 * 17^2
5142500 = 2^2 * 5^4 * 11^2 * 17, 5142501 = 3^3 * 7^2 * 13^2 * 23
4096575 = 3^4 * 5^2 * 7 * 17^2, 4096576 = 2^6 * 11^2 * 23^2
4090624 = 2^8 * 19 * 29^2, 4090625 = 5^5 * 7 * 11 * 17
4004000 = 2^5 * 5^3 * 7 * 11 * 13, 4004001 = 3^2 * 23^2 * 29^2
22194425 = 5^2 * 11^3 * 23 * 29, 22194432 = 2^8 * 3^3 * 13^2 * 19
13697019 = 3^4 * 7^3 * 17 * 29, 13697024 = 2^16 * 11 * 19
90312467 = 7 * 23^2 * 29^3, 90312500 = 2^2 * 5^7 * 17^2
2697695 = 5 * 7^3 * 11^2 * 13, 2697696 = 2^5 * 3^2 * 17 * 19 * 29
8254125 = 3^2 * 5^3 * 11 * 23 * 29, 8254129 = 13^4 * 17^2
88012332 = 2^2 * 3^4 * 17 * 19 * 29^2, 88012375 = 5^3 * 11^3 * 23^2
2023424 = 2^13 * 13 * 19, 2023425 = 3^2 * 5^2 * 17 * 23^2
90312453 = 3^2 * 7 * 11 * 19^4, 90312500 = 2^2 * 5^7 * 17^2
1852200 = 2^3 * 3^3 * 5^2 * 7^3, 1852201 = 13 * 17^3 * 29
67874587 = 11^2 * 23 * 29^3, 67874625 = 3^3 * 5^3 * 7 * 13^2 * 17
75557027 = 7 * 13^3 * 17^3, 75557070 = 2 * 3^3 * 5 * 23^4
46000759 = 7^6 * 17 * 23, 46000786 = 2 * 13^3 * 19^2 * 29
4log2 + 2log5 + 2log7 + 2log13 + log29 = 8log3 + 4log11 (96059600, 96059601)
3log2 + log3 + 3log7 + 3log13 = log5 + log11 + log17 + log23 + 2log29 (18085704, 18085705)
log11 + 2log13 + log17 + 2log29 = 5log3 + 6log5 + log7 (26578123, 26578125)
log2 + 4log3 + log5 + 4log11 = log7 + log13 + 4log19 (11859210, 11859211)
2log7 + log11 + 2log23 + log29 = 10log2 + 2log5 + log17 + log19 (8268799, 8268800)
2log3 + log11 + 4log19 = 2log23 + 3log29 (12901779, 12901781)
8log2 + 5log3 + log5 + log19 = 2log11 + 2log13 + 2log17 (5909760, 5909761)
4log3 + 2log5 + log7 + 2log17 = 6log2 + 2log11 + 2log23 (4096575, 4096576)
6log7 + log17 + log23 = log2 + 3log13 + 2log19 + log29 (46000759, 46000786)
log2 + log5 = 1
��
log2 = 360565/1197771 = 0.3010299966 (�^�l 0.3010299957)
log3 = 571482/1197771 = 0.4771212527 (�^�l 0.4771212547)
log5 = 837206/1197771 = 0.6989700034 (�^�l 0.6989700043)
log7 = 1012234/1197771 = 0.8450981031 (�^�l 0.8450980400)
log11 = 1247350/1197771 = 1.0413927203 (�^�l 1.0413926852)
log13 = 1334249/1197771 = 1.1139433164 (�^�l 1.1139433523)
log17 = 1473796/1197771 = 1.2304488922 (�^�l 1.2304489214)
log19 = 1531654/1197771 = 1.2787536182 (�^�l 1.2787536010)
log23 = 1631038/1197771 = 1.3617277426 (�^�l 1.3617278360)
log29 = 1751618/1197771 = 1.4623980711 (�^�l 1.4623979979)
�@�����1197771��10000000�܂łōł��덷�����Ȃ��Ȃ�l�ł��B
# �덷�̏��Ȃ����ɁA9��+(log2+log5=1)���ƈꎟ�]���ɂȂ�܂��B��������1���lj�����
�����Ă����炭�ꎟ�]���̂܂܂ŁA24�ڂ�(46000759,46000786)�̎���lj����Ă悤�₭��
���Ɨ��ɂȂ�܂��B�����Ă�������t���ɏ�����s�������Ă�����10�s�Ɍ��炵���̂��A���
���������ł��B
�@���_�Ƃ��āA�f���� 2�A3�A5�A7 �Ɍ��肵�Ă��܂��ƁA����Ȑ��ɂ��Ă����܂萸�x�����サ��
���A�f���̌��𑝂₵�Ă����A�����I�Ȓl�i�Ƃ����Ă���v�Z�͖����j�Ő��x����
�����邱�Ƃ��킩��܂����B
�@DD++ ����̃R�����g�ł��B�i�ߘa�U�N�X���P�V���t���j
�@���ɐ[���������Ă�������A���肪�Ƃ��������܂����B����ƕ��������ꎟ�]���ɂȂ���
���܂���肪���G�ɂȂ��Ă����͎̂v�������܂���ł����B��v�Z�ł���ς��Ɠ������
�̂̃o�����X�I�ɂ́A�ŏ��̂���v�����ȏ�ɗD�G��������ł��˂��c�c�B
�@�f�`�h ����̃R�����g�ł��B�i�ߘa�U�N�X���P�W���t���j
�@�炷���邳��̂��d���ŁA���ꂾ���̑f���ɑ����p�ΐ��l�����ʕ����
log2 = 360565/1197771 = 0.3010299966 (�^�l 0.3010299957)
log3 = 571482/1197771 = 0.4771212527 (�^�l 0.4771212547)
log5 = 837206/1197771 = 0.6989700034 (�^�l 0.6989700043)
log7 = 1012234/1197771 = 0.8450981031 (�^�l 0.8450980400)
log11 = 1247350/1197771 = 1.0413927203 (�^�l 1.0413926852)
log13 = 1334249/1197771 = 1.1139433164 (�^�l 1.1139433523)
log17 = 1473796/1197771 = 1.2304488922 (�^�l 1.2304489214)
log19 = 1531654/1197771 = 1.2787536182 (�^�l 1.2787536010)
log23 = 1631038/1197771 = 1.3617277426 (�^�l 1.3617278360)
log29 = 1751618/1197771 = 1.4623980711 (�^�l 1.4623979979)
�i�����1197771�́A10000000�܂łōł��덷�����Ȃ��Ȃ�l�j
�̗l�ɍ\���\�ł��邱�Ƃɋ����܂������A�ӂƕ���𑵂��Ȃ��Ƃ�����͂��̂ɂ���ĕω�
�����Ă��悢�Ȃ�ǂ��Ȃ�̂��C�ɂȂ��Ē��ׂĂ݂܂����B
�@�R���قǂ̕����ł̋ߎ��́A����𑵂��邱�ƂɍS��Ȃ��Ȃ�
gp > abs(146/485-log(2)/log(10))
%469 = 9.3217107035117801368259509460209827810 E-7
gp > abs(73/153-log(3)/log(10))
%470 = 2.9282868735104173903973984794620415878 E-6
gp > abs(339/485-log(5)/log(10))
%471 = 9.3217107035117801368259509460209517576 E-7
gp > abs(431/510-log(7)/log(10))
%472 = 7.9857055620241233702400874249978544429 E-10
gp > abs(478/459-log(11)/log(10))
%473 = 1.6503537575300559002466218995055742675 E-6
gp > abs(743/667-log(13)/log(10))
%474 = 3.2382107964776722479812223847580763836 E-7
gp > abs(299/243-log(17)/log(10))
%475 = 3.7535188454130236161139021156448952272 E-6
gp > abs(656/513-log(19)/log(10))
%476 = 1.1643056554722575810391097558286690920 E-6
gp > abs(1103/810-log(23)/log(10))
%477 = 5.5904413551619395128281053884536869710 E-7
gp > abs(525/359-log(29)/log(10))
%478 = 2.4547234686221517882671475279717504814 E-6
�̗l�ȕ����ł��Ȃ�̐��x���グ�ꂻ���ł��B
�@�炷���邳��̃R�����g�ł��B�i�ߘa�U�N�X���P�W���t���j
�@�ߎ������Ɋւ��Ă͈ȑO���������������Ƃ�����܂��B
�i�����̏����Ő��x���ɕ����������@���l���܂���(���\���ł�OK)�B�j
�@������Ă��镪���́A���ׂĘA������ł����ē����镪���ł��ˁB�������A�����
�u3���ȉ��ōł��ǂ��v������������Ƃ͌���܂���B
�@�Ⴆ�Alog17�́A299/243���881/716�̕����ǂ��ߎ��ɂȂ�܂��B
�@���l�ɁAlog29���A525/359���914/625�̕������������ǂ��ߎ��ɂȂ�܂��B
�@log23�́A3���ȉ��ŘA�����ł���œ����镪���ł�64/47���ő�ŁA���x���o�Ȃ���
�߂ɁA���q4�������e�������̂Ǝv���܂����A975/716�ł����������̐��x�͏o�܂��B
�@�唼�̒l�́A�����_�ȉ��̐��x��(����̌����~2)�����x�ɂȂ�܂����A���܂��ܘA����
�ł��蒼��̒l���傫���ꍇ�͐��x���ǂ��Ȃ�܂��ˁB
�@log7�́A[0;1,5,2,5,6,1,4813,1,1,�c]��4813�̑O�őł����Ă��邽�߁A���ꂾ�����ʂɐ��x
���ǂ��Ȃ��Ă��܂��B
�@�~������355/113�����l�ł��ˁB
�@DD++ ����̃R�����g�ł��B�i�ߘa�U�N�X���P�W���t���j
�@�P�� 1 �̑ΐ��l���@�B�v�Z�������Ď��R�ɗL�����ߎ����邾���ł�����A
�@���w������b > �ݏ�̏� 4 ��
���A���̃T�C�g�̉��������œ����c�_���J��Ԃ��s���Ă��܂��ˁB
�@kuiperbelt ����̃R�����g�ł��B�i�ߘa�U�N�X���Q�Q���t���j
�@29�܂ł̑f���ŁA��p�ΐ��̘A�����W�J�����߂Ă݂܂������Alog_{10}(7)�̂Ƃ���4813��
�悤�ȑ傫�Ȑ��͌���܂���ł����B�Ȃ��Alog_{10}(5)=1-log_{10}(2)�Ȃ̂ŏȗ����Ă��܂��B
log_{10}(2)=[0;3,3,9,2,2,4,6,2,1,1,3,1,18,...]
[0;3,3,9,2,2,4,6,2,1,1,3,1]=97879/325147=0.301029995663499893894146339963
log_{10}(3)=[0,2,10,2,2,1,13,1,7,18,...]
[0,2,10,2,2,1,13,1,7]=34367/33001=0.477121254550546065527863343601
log_{10}(11)=[1;24,6,3,2,1,1,3,1,1,1,9,...]
[1;24,6,3,2,1,1,3,1,1,1]=22014/21139=1.04139268507014938941244204721
log_{10}(13)=[1;1,8,1,3,2,7,1,6,16,...]
[1;1,8,1,3,2,7,1,6]=5113/4590=1.11394335511982570806100217865
log_{10}(17)=[1,4,2,1,17,1,13,1,1,3,3,26,...]
[1;4,2,1,17,1,13,1,1,3,3]=99797/81106=1.23045150790323773826843883313
log_{10}(19)=[1;3,1,1,2,2,1,3,2,2,1,4,1,1,1,6,1,3,1,3,1,47,...]
[1;3,1,1,2,2,1,3,2,2,1,4,1,1,1,6,1,3,1,3,1]=6497723/5081294=1.27875360095282815755199364571
log_{10}(23)=[1;2,1,3,4,17,2,1,2,66,...]
[1;2,1,3,4,17,2,1,2]=9016/6621=1.36172783567436943059960731007
log_{10}(29)=[[1;2,6,6,1,2,1,2,2,2,1,1,1,1,1,5,1,2,3,37,...]
[1;2,6,6,1,2,1,2,2,2,1,1,1,1,1,5,1,2,3]=5243915/3585833=1.46239799789895402267757589380
�@�炷���邳��̃R�����g�ł��B�i�ߘa�U�N�X���Q�Q���t���j
�@log[10]7�ŘA������8�Ԗڂ̒l��4813�ł����A
log[10]2�́A137�Ԗڂ�5393
log[10]3�́A562�Ԗڂ�2788
log[10]11�́A2179�Ԗڂ�3864
log[10]13�́A133�Ԗڂ�1378
log[10]17�́A710�Ԗڂ�3301
log[10]19�́A1341�Ԗڂ�2249
log[10]23�́A921�Ԗڂ�2695
log[10]29�́A352�Ԗڂ�1901
�̂悤�ɂ����Ɛ�܂Ō���Α傫�Ȑ��͂�����o�Ă��܂��Blog[10]7�͊�ՓI�ɑO�̕���
�������Ƃ������Ƃł��ˁB
�@�@�ȉ��A�H�����I

