丒俀係擭搙戝妛擖妛嫟捠僥僗僩丂 丂 丂 丂 丂 丂 丂 丂 俽丏俫 巵
丂係夞栚偺戝妛擖妛嫟捠僥僗僩偑椷榓俇擭侾寧侾俁擔丒侾係擔偺椉擔峴傢傟偨丅弶傔偰庴尡惗
偑俆侽枩恖傪妱偭偨戝妛擖妛嫟捠僥僗僩偼丄俇嫵壢俁侽壢栚偱偺幚巤偼崱擭偑嵟屻偱丄棃擭
偐傜偼丄嫵壢乽忣曬乿傪娷傓俈嫵壢俀侾壢栚偵嵞曇偝傟丄怴偟偄楌巎偑巒傑傞丅
丂杮斣捈慜偺抧恔偺塭嬁偱丄杒棨抧曽傪拞怱偵尩偟偄帋楙偲側偭偨偑丄惀旕幚椡傪堚姸側偔
敪婗偝傟偰婃挘偭偰傎偟偄傕偺偩丅
丂侾俈擔敪昞偺暯嬒揰拞娫廤寁偵傛傟偽丄悢妛俬丒俙偺暯嬒揰偼丄俆係丏俁俆揰乮嶐擭搙偼丄
俆俆丏俇俆揰乯丄悢妛俬俬丒俛偼丄俇侾丏侽俁揰乮俇侾丏係俉揰乯偱丄嶐擭搙暲偺擄堈搙偲側偭偨丅
丂俀寧俆擔偵丄妋掕暯嬒揰偺敪昞偑偁偭偨丅悢妛俬丒俙偺暯嬒揰偼丄俆侾丏俁俉揰乮嶐擭搙偼丄
俆俆丏俇俆揰乯丄悢妛俬俬丒俛偼丄俆俈丏俈係揰乮俇侾丏係俉揰乯偱丄拞娫敪昞傛傝俁揰傎偳壓偑傞寢壥偲
側偭偨丅
丂僇儖僺僗偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭侾寧侾俋擔晅偗乯
丂戝妛擖妛嫟捠僥僗僩悢妛偺暯嬒偼丄偩偄偨偄俆侽揰戜偩偗偳丄側傫偱偦傫側偵擄偟偔偡傞昁
梫偑偁傞偺偩傠偆丠
丂帺暘偑悢妛偺帋尡傪庴偗偰敿暘埵偟偐弌棃側偐偭偨傜丄棊偪偨偐側偲巚偭偰偟傑偆偗偳丅
惛恄揑偵棊偪崬傓丒丒丒丅
丂DD++ 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭侾寧侾俋擔晅偗乯
丂壖偵暯嬒揰偑80揰偺帋尡偩偭偨傜丄暯嬒埲忋偵悢妛偑偱偒傞恖偺娫偱嵟戝20揰偟偐嵎偑
偮偐側偄偐傜偱偟傚偆偹丅揰悢傪慡偰曃嵎抣壔偟偰崌斲傪寛傔傞曽恓偩偭偨傜丄暯嬒揰偑懡
彮忋壓偟偰傕栤戣側偄偲巚偄傑偡偑丄扨弮偵摼揰傪崌寁偡傞埲忋丄暯嬒揰傛傝忋偵廫暘側
暆偑側偔偰偼偄偗傑偣傫丅
丂傑偨丄偦傕偦傕戝妛擖帋偺僔僗僥儉偑乽壗揰埲忋偱崌奿乿偱偼側偔乽壗埵埲忋偑崌奿乿偱偁
傞埲忋丄擄偟偄偙偲偩偗偑棟桼偱棊偪傞偲偄偆偙偲偼傎偲傫偳側偄偼偢偱偡丅
丂僇儖僺僗偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭侾寧俀侽擔晅偗乯
丂DD++ 偝傫丄桳擄偆偛偞偄傑偡丅帺暘偺乽栘傪尒偰怷傪尒偢乿偺惈奿偩偲丄弌棃側偐偭偨偲偄
偆峫偊偩偗偑晜偐傃僱僈僥傿僽偵側偭偰偟傑偄傑偡丅
丂尦乆丄摢偺椙偄恖偭偰丄峫偊曽偑億僕僥傿僽側傫偱偡傛偹丅乽帺暘偵弌棃側偄栤戣偼丄傒傫
側傕弌棃側偄偺偩偐傜乿偲偐乽暿偵丄慡晹弌棃傞昁梫側傫偰側偄丄帺暘偵弌棃傞強偩偗傪傗
傟偽椙偄乿側偳丄婥帩偪偵梋桾偑偁傝傑偡偹丅
丂戝愄丄嫟捠堦師帋尡偑偁偭偨帪丄柾媅帋尡栤戣傪尒偨搑抂偵僥儞僔儑儞偑丄偖乕傫偲壓偑
傝丄乽傕偆懯栚偩乕乿偱摢偺拞偑偄偭傁偄偵側傝丄掹傔儌乕僪偱偩傜偩傜偲夝偄偨婰壇偑偁傝傑
偡丅
丂嵟弶偐傜丄暯嬒揰偑俆侽揰埵傪憐掕偟偰嶌偭偰偄傞栤戣偩偲暘偐偭偰偄偰挧傓偺偲丄慡偔抦
傜側偄偱挧傓偺偱偼惛恄揑側傕偺偑慡慠堘偭偰偒傑偡偹丅
丂嵟嬤丄戝妛擖妛嫟捠僥僗僩偑榖戣偵側偭偰丄夁嫀偺埫偄僩儞僱儖帪戙傪巚偄弌偟偰偟傑偄
傑偟偨丅幐楃抳偟傑偟偨丅
丂崱擭傕柺敀偦偆側栤戣傪偄偔偮偐庢傝忋偘丄挧愴偟偨偄偲巚偆丅栤戣暥偼堦晹夵戣偱偡丅
亂 悢妛俬丒俙 亃
戞俆栤丂壓恾偺惎宍偺恾宍傪峫偊傞丅
丂丂
丂偨偩偟丄俙俹 丗 俹俻 丗 俻俠亖俀 丗 俁 丗 俁丂丄俙俿 丗 俿俽 丗 俽俢亖侾 丗 侾 丗 俁丂偲偡傞丅
乮侾乯丂俻俼 丗 俼俢丂丄俻俛 丗 俛俢丂丄俛俻 丗 俻俼 丗 俼俢丂傪媮傔傛丅
乮夝乯丂仮俙俻俢偲捈慄俠俤偵娭偟偰丄儊僱儔僂僗偺掕棟傛傝丄
丂乮俻俼/俼俢乯乮俢俽/俽俙乯乮俙俠/俠俻乯亖侾丂側偺偱丄丂乮俻俼/俼俢乯乮俁/俀乯乮俉/俁乯亖侾
丂傛偭偰丄丂俻俼/俼俢亖侾/係丂傛傝丄丂俻俼 丗 俼俢亖侾 丗 係
摨條偵丄仮俙俻俢偲捈慄俛俤偵娭偟偰丄儊僱儔僂僗偺掕棟傛傝丄
丂乮俻俛/俛俢乯乮俢俿/俿俙乯乮俙俹/俹俻乯亖侾丂側偺偱丄丂乮俻俛/俛俢乯乮係/侾乯乮俀/俁乯亖侾
丂傛偭偰丄丂俻俛/俛俢亖俁/俉丂傛傝丄丂俻俛 丗 俛俢亖俁 丗 俉丂側偺偱丄丂俛俻 丗 俻俢亖俁 丗 俆
丂偟偨偑偭偰丄丂俛俻 丗 俻俼 丗 俼俢亖俁 丗 侾 丗 係丂偲側傞丅丂丂乮廔乯
乮俀乯丂俆揰俹丄俻丄俼丄俽丄俿偑摨堦墌廃忋偵偁傞偲偟丄俙俠亖俉丂偲偡傞丅
丂丂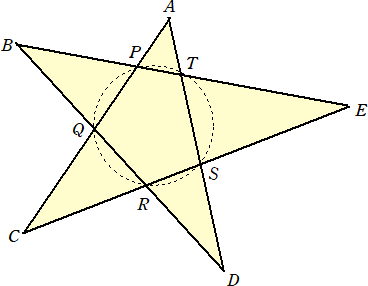
丂偙偺偲偒丄師偺栤偄偵摎偊傛丅
乮鶣乯丂俙俿丂丄俢俼丂偺抣傪媮傔傛丅
乮鶤乯丂俙俻丒俠俻丂偲丂俛俻丒俢俻丂偺戝彫傪挷傋傛丅
乮鶥乯丂俁揰俙丄俛丄俠傪捠傞墌偲捈慄俛俢偲偺岎揰偺偆偪丄俛偲堎側傞揰傪倃偲偡傞丅偙偺偲偒丄
丂丂俙俻丒俠俻丂偲丂俛俻丒倃俻丂偺戝彫傪挷傋傛丅
乮鶦乯丂揰俢偼俁揰俙丄俛丄俠傪捠傞墌偺奜晹偵偁傞偙偲傪帵偣丅
乮鶧乯丂偙偺惎宍偺恾宍偵偍偄偰丄俠俼丄俼俽丄俽俤丂偺抣傪媮傔傛丅
乮鶨乯丂揰俙丄俛偼丄俁揰俠丄俢丄俤傪捠傞墌偺奜晹偵偁傞偙偲傪帵偣丅
乮夝乯乮鶣乯丂俙俹亖俀丂丄俹俻亖俁丂丄俙俿亖俿俽亖倣丂偲偍偔偲丄曽傋偒偺掕棟傛傝丄
丂俀丒俆亖倣丒俀倣丂偐傜丄丂倣2亖俆丂側偺偱丄丂倣亖俙俿亖 丂偱偁傞丅
丂偱偁傞丅
偙偺偲偒丄丂俿俽亖 丂丄俽俢亖俁
丂丄俽俢亖俁 丂偱丄乮侾乯傛傝丄俻俼 丗 俼俢亖侾 丗 係丂側偺偱丄
丂偱丄乮侾乯傛傝丄俻俼 丗 俼俢亖侾 丗 係丂側偺偱丄
丂俻俼亖値丂丄俼俢亖係値丂偲偍偔偲丄曽傋偒偺掕棟傛傝丄
丂係値丒俆値亖俁 丒係
丒係 亖俇侽
亖俇侽
丂傛偭偰丄値2亖俁丂傛傝丄丂値亖 丂側偺偱丄丂俢俼亖係
丂側偺偱丄丂俢俼亖係
乮鶤乯丂俙俻丒俠俻亖俆丒俁亖侾俆丂偱丄乮侾乯傛傝丄俛俻 丗 俻俼 丗 俼俢亖俁 丗 侾 丗 係丂側偺偱丄
丂俛俻亖俁 丂丄俢俻亖俆
丂丄俢俻亖俆 丂傛傝丄丂俛俻丒俢俻亖係俆
丂傛傝丄丂俛俻丒俢俻亖係俆
丂傛偭偰丄丂俙俻丒俠俻亙俛俻丒俢俻丂偱偁傞丅
乮鶥乯丂曽傋偒偺掕棟傛傝丄丂俙俻丒俠俻亖俛俻丒倃俻丂偱偁傞丅
乮鶦乯丂俛俻丒倃俻亙俛俻丒俢俻丂傛傝丄丂倃俻亙俢俻丂側偺偱丄揰俢偼俁揰俙丄俛丄俠傪捠傞墌偺奜晹
丂丂偵偁傞偙偲偑暘偐傞丅
乮鶧乯丂仮俙俠俽偲捈慄俛俤偵娭偟偰丄儊僱儔僂僗偺掕棟傛傝丄
丂乮俙俹/俹俠乯乮俠俤/俽俤乯乮俽俿/俿俙乯亖侾丂側偺偱丄丂乮俀/俇乯乮俠俤/俽俤乯乮侾/侾乯亖侾丂傛傝丄
丂俠俤/俽俤亖俁丂側偺偱丄丂俠俤亖俁丒俽俤
摨條偵丄仮俙俠俽偲捈慄俛俢偵娭偟偰丄儊僱儔僂僗偺掕棟傛傝丄
丂乮俙俻/俻俠乯乮俠俼/俼俽乯乮俽俢/俢俙乯亖侾丂側偺偱丄丂乮俆/俁乯乮俠俼/俼俽乯乮俁/俆乯亖侾丂傛傝丄
丂俠俼/俼俽亖侾丂側偺偱丄丂俠俼亖俼俽丂偱偁傞丅
丂偙偙偱丄丂俠俽亖俀俽俤丂偐傜丄丂俠俼亖俼俽亖俽俤丂偑惉傝棫偮丅
丂曽傋偒偺掕棟傛傝丄丂俠俻丒俠俹亖俠俼丒俠俽丂側偺偱丄丂俁丒俇亖俽俤丒俀俽俤丂傛傝丄丂俽俤亖俁
丂埲忋偐傜丄丂俠俼亖俼俽亖俽俤亖俁丂偑惉傝棫偮丅
仈偙偺乮鶧乯偼杮暥偵柍忦審偱婰嵹偝傟偰偄傞丅帪娫抁弅偺偨傔偵妱垽偝傟偨偺偩傠偆丅
乮鶨乯丂俁揰俠丄俢丄俤傪捠傞墌偲捈慄俙俢偲偺岎揰偺偆偪丄俢偲堎側傞揰傪倄偲偡傞偲丄
丂俢俽丒俽倄亖俠俽丒俽俤亖俇丒俁亖侾俉丂偱丄堦曽丄俢俽丒俽俙亖俁 丒俀
丒俀 亖俁侽丂傛傝丄
亖俁侽丂傛傝丄
丂俢俽丒俽倄亙俢俽丒俽俙丂偐傜丄丂俽倄亙俽俙丂側偺偱丄揰俙偼丄俁揰俠丄俢丄俤傪捠傞墌偺奜晹偵偁
傞偙偲偑暘偐傞丅
丂俁揰俠丄俢丄俤傪捠傞墌偲捈慄俛俢偲偺岎揰偺偆偪丄俢偲堎側傞揰傪倅偲偡傞偲丄
丂俢俼丒俼倅亖俠俼丒俼俤亖俁丒俇亖侾俉丂偱丄堦曽丄俢俼丒俼俛亖係 丒係
丒係 亖係俉丂傛傝丄
亖係俉丂傛傝丄
丂俢俼丒俼倅亙俢俼丒俼俛丂偐傜丄丂俼倅亙俼俛丂側偺偱丄揰俛偼丄俁揰俠丄俢丄俤傪捠傞墌偺奜晹偵偁
傞偙偲偑暘偐傞丅丂丂乮廔乯
乮僐儊儞僩乯丂慺捈偵桿摫偵廬偊偽丄堈偟偄栤戣偩偭偨偱偟傚偆丅
戞係栤丂T3丄T4丄T6 傪師偺傛偆側僞僀儅乕偲偡傞丅丂
T3 丗 3恑悢傪3寘昞帵偡傞僞僀儅乕
T4 丗 4恑悢傪3寘昞帵偡傞僞僀儅乕
T6 丗 6恑悢傪3寘昞帵偡傞僞僀儅乕
側偍丄値恑悢偲偼値恑朄偱昞偝傟偨悢偺偙偲偱偁傞丅
丂偙傟傜偺僞僀儅乕偼丄偡傋偰師偺昞帵曽朄偵廬偆傕偺偲偡傞丅
亙昞帵曽朄亜
(a) 僗僞乕僩偟偨帪揰偱僞僀儅乕偼 000 偲昞帵偝傟偰偄傞丅
(b) 僞僀儅乕偼丄僗僞乕僩偟偨屻丄昞帵偝傟傞悢偑1昩偛偲偵1偢偮憹偊偰偄偒丄3寘偱昞帵偱偒
丂傞嵟戝偺悢偑昞帵偝傟偨1昩屻偵丄昞帵偑 000 偵栠傞丅
(們) 僞僀儅乕偼昞帵偑 000 偵栠偭偨屻傕丄(b)偲摨條偵丄昞帵偝傟傞悢偑1昩偛偲偵1偢偮憹偊
丂偰偄偒丄3寘偱昞帵偱偒傞嵟戝偺悢偑昞帵偝傟偨1昩屻偵丄昞帵偑 000 偵栠傞偲偄偆摦嶌傪
丂孞傝曉偡丅
(1)乮鶣乯丂T6偼丄僗僞乕僩偟偰偐傜10恑悢偱40昩屻偵昞帵偝傟傞悢傪媮傔傛丅
丂乮鶤乯丂T4偼丄僗僞乕僩偟偰偐傜2恑悢偱 10011(2) 昩屻偵昞帵偝傟傞悢傪媮傔傛丅
乮夝乯乮鶣乯丂係侽亖侾丒俇2亄係丂側偺偱丄40昩屻偺T6偺昞帵偼丄侾侽係 偱偁傞丅
丂乮鶤乯丂侾侽侽侾侾(2)亖侾丒俀4亄侾丒俀亄侾亖侾丒係2亄俁丂側偺偱丄10011(2)昩屻偺T4偺昞帵偼丄
丂丂丂侾侽俁丂偱偁傞丅丂丂乮廔乯
(2)乮鶣乯丂T4傪僗僞乕僩偝偣偨屻丄弶傔偰昞帵偑 000 偵栠傞偺偼丄僗僞乕僩偟偰偐傜 10恑悢偱
丂丂丂丂壗昩屻偱偁傞偐丅
丂乮鶤乯丂摨條偺峫嶡傪T6偵懳偟偰傕峴偆偙偲偵傛傝丄T4偲T6傪摨帪偵僗僞乕僩偝偣偨屻丄弶傔
丂丂丂丂偰椉曽偺昞帵偑摨帪偵 000 偵栠傞偺偼丄僗僞乕僩偟偰偐傜10恑悢偱丄壗昩屻偱偁傞偐丅
乮夝乯乮鶣乯丂俁丒係2亄俁丒係亄俁亄侾亖俇係丂側偺偱丄T4偺昞帵偑 000 偵栠傞偺偼丄僗僞乕僩偟偰
丂丂丂丂偐傜 10恑悢偱丄俇係昩屻偱偁傞丅
丂乮鶤乯丂俆丒俇2亄俆丒俇亄俆亄侾亖俀侾俇丂側偺偱丄T6偺昞帵偑 000 偵栠傞偺偼丄僗僞乕僩偟偰偐
丂丂丂傜 10恑悢偱丄俀侾俇昩屻偱偁傞丅T4偲T6傪摨帪偵僗僞乕僩偝偣偨屻丄弶傔偰椉曽偺昞帵偑
丂丂丂摨帪偵 000 偵栠傞傑偱偺帪娫傪偦傟偧傟 倶丄倷 昩屻偲偡傞偲丄
丂丂丂丂俇係倶亖俀侾俇倷丂偡側傢偪丄丂俉倶亖俀俈倷
丂俉偲俀俈偼屳偄偵慺側偺偱丄嵟彫偺帺慠悢夝偼丄丂倶亖俀俈丄倷亖俉
丂傛偭偰丄椉曽偺昞帵偑摨帪偵 000 偵栠傞偺偼丄僗僞乕僩偟偰偐傜10恑悢偱丄
丂丂俀侾俇亊俉亖侾俈俀俉乮昩屻乯丂偱偁傞丅丂丂乮廔乯
(3)乮鶣乯丂0埲忋偺惍悢俴偵懳偟偰丄T4傪僗僞乕僩偝偣偨俴昩屻偵T4偑 012 偲昞帵偝傟傞偙偲偲
丂丂丂丂摨抣側偙偲傪弎傋傛丅偨偩偟丄昞婰偼侾侽恑朄偱昞偡傕偺偲偡傞丅
丂乮鶤乯丂T 3偵偮偄偰傕摨條偺峫嶡傪峴偆丅T3偲T4傪摨帪偵僗僞乕僩偝偣偰偐傜丄弶傔偰椉曽
丂丂丂丂偑摨帪偵 012 偲昞帵偝傟傞傑偱偺帪娫傪倣昩偲偡傞偲偒丄倣傪10恑朄偱昞偣丅
丂乮鶥乯傑偨丄T4偲T6偺昞帵偵娭偡傞婰弎偲偟偰丄師偺婰弎偺偆偪丄惓偟偄傕偺傪媮傔傛丅
乮僀乯 T4偲T6傪摨帪偵僗僞乕僩偝偣偰偐傜丄倣昩屻傛傝慜偵弶傔偰椉曽偑摨帪偵 012 偲昞帵
丂丂偝傟傞丅
乮儘乯 T4偲T6傪摨帪偵僗僞乕僩偝偣偰偐傜丄偪傚偆偳倣昩屻偵弶傔偰椉曽偑摨帪偵 012 偲昞
丂丂帵偝傟傞丅
乮僴乯 T4偲T6傪摨帪偵僗僞乕僩偝偣偰偐傜丄倣昩屻傛傝屻偵弶傔偰椉曽偑摨帪偵 012 偲昞帵
丂丂偝傟傞丅
乮僯乯 T4偲T6傪摨帪偵僗僞乕僩偝偣偰偐傜丄椉曽偑摨帪偵 012 偲昞帵偝傟傞偙偲偼側偄丅
乮夝乯乮鶣乯丂T4偺昞帵偑 000 偵栠傞偺偼丄10恑悢偱丄俇係昩枅偱偁傞偺偱丄T4偺昞帵偑 012
丂丂丂丂偵側傞偺偼丄丂俇丄俈侽丄侾俁係丄丒丒丒丂側偺偱丄T4傪僗僞乕僩偝偣偨俴昩屻偵T4偑 012 偲
丂丂丂丂昞帵偝傟傞偙偲偼丄俴傪俇係偱妱偭偨梋傝偑俇偱偁傞偙偲偲摨抣偱偁傞丅
丂丂丂丂
丂乮鶤乯丂T 3偺昞帵偑 000 偵栠傞偺偼丄10恑悢偱丄俀俈昩枅偱偁傞偺偱丄T3偺昞帵偑 012
丂丂丂丂偵側傞偺偼丄丂俆丄俁俀丄俆俋丄丒丒丒丂側偺偱丄T3傪僗僞乕僩偝偣偨倣昩屻偵T3偑 012 偲
丂丂丂丂昞帵偝傟傞偙偲偼丄倣傪俀俈偱妱偭偨梋傝偑俆偱偁傞偙偲偲摨抣偱偁傞丅
丂丂丂摨條偵丄T4傪僗僞乕僩偝偣偨倣昩屻偵T4偑 012 偲昞帵偝傟傞偙偲偼丄倣傪俇係偱妱偭偨
丂丂丂梋傝偑俇偱偁傞偙偲偲摨抣偱偁傞丅
丂埲忋偐傜丄丂乮倣亅俆乯/俀俈亖倶丂丄乮倣亅俇乯/俇係亖倷丂偲偍偔偲丄倶丄倷偼帺慠悢偱丄
丂俀俈倶亄俆亖俇係倷亄俇丂偡側傢偪丄丂俀俈倶亅俇係倷亖侾
丂俀俈丒侾俋亅俇係丒俉亖侾丂側偺偱丄曈乆堷偄偰丄丂俀俈乮倶亅侾俋乯亖俇係乮倷亅俉乯
丂俀俈偲俇係偼屳偄偵慺側偺偱丄丂倶亖侾俋亄俇係値丂丄倷亖俉亄俀俈値丂乮値偼侽埲忋偺惍悢乯
丂弶傔偰椉曽偑摨帪偵 012 偲昞帵偝傟傞傑偱偺帪娫倣偼丄
丂倣亖俀俈倶亄俆亖俀俈丒侾俋亄俆亖俆侾俉乮昩乯
丂乮鶥乯丂T4偼俇係昩枅偵儕僙僢僩丄T6偼俀侾俇昩枅偵儕僙僢僩側偺偱丄T4偲T6傪摨帪偵僗僞乕僩偝
丂丂丂偣偰偐傜丄012 偲昞帵偝傟傞帪娫偼丄
丂T4丗丂俇丄俈侽丄侾俁係丄侾俋俉丄俀俇俀丄俁俀俇丄俁俋侽丄係俆係丄俆侾俉丄丒丒丒
丂T6丗丂俉丄俀俀係丄係係侽丄俇俆俇丄丒丒丒
丂偟偨偑偭偰丄
乮僀乯 T4偲T6傪摨帪偵僗僞乕僩偝偣偰偐傜丄俆侾俉昩屻傛傝慜偵弶傔偰椉曽偑摨帪偵 012 偲昞
丂丂帵偝傟傞丅
偼岆傝偱偁傞丅
乮儘乯 T4偲T6傪摨帪偵僗僞乕僩偝偣偰偐傜丄偪傚偆偳俆侾俉昩屻偵弶傔偰椉曽偑摨帪偵 012 偲昞
丂丂帵偝傟傞丅
偼丄岆傝偱偁傞丅
丂俇係倲亄俇亖俀侾俇倱亄俉丂偵偍偄偰丄俁俀倲亅侾侽俉倱亖侾丂傛傝丄嵍曈偼嬼悢偱丄塃曈偼婏悢偐傜
偙偺曽掱幃傪枮偨偡帺慠悢夝偼懚嵼偟側偄丅
偟偨偑偭偰丄
乮僴乯 T4偲T6傪摨帪偵僗僞乕僩偝偣偰偐傜丄俆侾俉昩屻傛傝屻偵弶傔偰椉曽偑摨帪偵 012 偲昞帵
丂丂偝傟傞丅
偼岆傝偱偁傞丅
乮僯乯 T4偲T6傪摨帪偵僗僞乕僩偝偣偰偐傜丄椉曽偑摨帪偵 012 偲昞帵偝傟傞偙偲偼側偄丅
偼惓偟偄偙偲偵側傞丅丂丂乮廔乯
戞俁栤丂敔偺拞偵僇乕僪偑俀枃埲忋擖偭偰偍傝丄偦傟偧傟偺僇乕僪偵偼傾儖僼傽儀僢僩偑侾暥帤
丂丂丂丂偩偗彂偐傟偰偄傞丅偙偺敔偺拞偐傜僇乕僪傪侾枃庢傝弌偟丄彂偐傟偰偄傞傾儖僼傽儀僢僩
丂丂丂丂傪妋擣偟偰偐傜傕偲偵栠偡偲偄偆帋峴傪孞傝曉偟峴偆丅
乮侾乯丂敔偺拞偵俙丄俛偺僇乕僪偑侾枃偢偮慡晹偱俀枃擖偭偰偄傞応崌傪峫偊傞丅
丂埲壓偱偼丄俀埲忋偺帺慠悢値偵懳偟丄値夞偺帋峴偱A丄B偑偦傠偭偰偄傞偲偼丄値夞偺帋峴偱
丂俙丄俛偺偦傟偧傟偑彮側偔偲傕侾夞偼庢傝弌偝傟傞偙偲傪堄枴偡傞丅
乮鶣乯丂俀夞偺帋峴偱A丄B偑偦傠偭偰偄傞妋棪傪媮傔傛丅
乮鶤乯丂俁夞偺帋峴偱A丄B偑偦傠偭偰偄傞庢傝弌偟曽傪峫偊丄俁夞偺帋峴偱A丄B偑偦傠偭偰偄
丂丂傞妋棪傪媮傔傛丅
乮鶥乯丂係夞偺帋峴偱A丄B偑偦傠偭偰偄傞庢傝弌偟曽傪峫偊丄係夞偺帋峴偱A丄B偑偦傠偭偰偄
丂丂傞妋棪傪媮傔傛丅
乮夝乯乮鶣乯丂俀夞偺帋峴偱婲偙傝偆傞偡傋偰偺応崌偺悢偼丄俀2亖係乮捠傝乯丂偦偺偆偪丄A丄B偑偦
丂丂丂丂丂傠偆応崌偺悢偼丄俙俛丄俛俙偺俀捠傝側偺偱丄媮傔傞妋棪偼丄俀/係亖侾/俀
乮鶤乯丂俁夞偺帋峴偱婲偙傝偆傞偡傋偰偺応崌偺悢偼丄俀3亖俉乮捠傝乯丂偦偺偆偪丄A丄B偑偦傠偆
丂丂庢傝弌偟曽偼丄俀3亅俀亖俇乮捠傝乯側偺偱丄媮傔傞妋棪偼丄俇/俉亖俁/係
乮鶥乯丂係夞偺帋峴偱婲偙傝偆傞偡傋偰偺応崌偺悢偼丄俀4亖侾俇乮捠傝乯丂偦偺偆偪丄A丄B偑偦傠
丂丂偆庢傝弌偟曽偼丄俀4亅俀亖侾係乮捠傝乯側偺偱丄媮傔傞妋棪偼丄侾係/侾俇亖俈/俉丂丂乮廔乯
乮俀乯丂敔偺拞偵俙丄俛丄俠偺僇乕僪偑侾枃偢偮慡晹偱俁枃擖偭偰偄傞応崌傪峫偊傞丅埲壓偱偼丄
丂丂俁埲忋偺帺慠悢値偵懳偟丄値夞栚偺帋峴偱弶傔偰A丄B丄C偑偦傠偆偲偼丄値夞偺帋峴偱俙丄
丂丂俛丄俠偺偦傟偧傟偑彮側偔偲傕侾夞偼庢傝弌偝傟丄偐偮俙丄俛丄俠偺偆偪偄偢傟偐侾枃偑値夞
丂丂栚偺帋峴偱弶傔偰庢傝弌偝傟傞偙偲傪堄枴偡傞丅丂
乮鶣乯丂俁夞栚偺帋峴偱弶傔偰A丄B丄C偑偦傠偆庢傝弌偟曽傪峫偊丄俁夞栚偺帋峴偱弶傔偰俙丄
丂丂俛丄俠偑偦傠偆妋棪傪媮傔傛丅
乮鶤乯丂係夞栚偺帋峴偱弶傔偰A, B. C偑偦傠偆庢傝弌偟曽傪峫偊丄係夞栚偺帋峴偱弶傔偰A丄
丂丂B丄C偑偦傠偆妋棪傪媮傔傛丅
乮鶥乯丂俆夞栚偺帋峴偱弶傔偰A, B, C偑偦傠偆庢傝弌偟曽傪峫偊丄俆夞栚偺帋峴偱弶傔偰A丄
丂丂B丄C偑偦傠偆妋棪傪媮傔傛丅
乮夝乯乮鶣乯丂俁夞偺帋峴偱婲偙傝偆傞偡傋偰偺応崌偺悢偼丄俁3亖俀俈乮捠傝乯丂偦偺偆偪丄弶傔偰
丂丂丂丂丂A丄B丄C偑偦傠偆応崌偺悢偼丄
丂丂丂丂俁夞栚偑俙偺偲偒丄丂俀2亅俀亖俀乮捠傝乯
丂丂丂丂俁夞栚偑俛偺偲偒丄丂俀2亅俀亖俀乮捠傝乯
丂丂丂丂俁夞栚偑俠偺偲偒丄丂俀2亅俀亖俀乮捠傝乯
丂丂側偺偱丄崌傢偣偰丄俀亊俁亖俇捠傝偁傞丅傛偭偰丄媮傔傞妋棪偼丄丂俇/俀俈亖俀/俋
乮鶤乯丂係夞偺帋峴偱婲偙傝偆傞偡傋偰偺応崌偺悢偼丄俁4亖俉侾乮捠傝乯丂偦偺偆偪丄弶傔偰
丂丂丂丂丂A丄B丄C偑偦傠偆応崌偺悢偼丄
丂丂丂丂係夞栚偑俙偺偲偒丄丂俀3亅俀亖俇乮捠傝乯
丂丂丂丂係夞栚偑俛偺偲偒丄丂俀3亅俀亖俇乮捠傝乯
丂丂丂丂係夞栚偑俠偺偲偒丄丂俀3亅俀亖俇乮捠傝乯
丂丂側偺偱丄崌傢偣偰丄俇亊俁亖侾俉捠傝偁傞丅傛偭偰丄媮傔傞妋棪偼丄丂侾俉/俉侾亖俀/俋
乮鶥乯丂俆夞偺帋峴偱婲偙傝偆傞偡傋偰偺応崌偺悢偼丄俁5亖俀係俁乮捠傝乯丂偦偺偆偪丄弶傔偰
丂丂丂丂丂A丄B丄C偑偦傠偆応崌偺悢偼丄
丂丂丂丂俆夞栚偑俙偺偲偒丄丂俀4亅俀亖侾係乮捠傝乯
丂丂丂丂俆夞栚偑俛偺偲偒丄丂俀4亅俀亖侾係乮捠傝乯
丂丂丂丂俆夞栚偑俠偺偲偒丄丂俀4亅俀亖侾係乮捠傝乯
丂丂側偺偱丄崌傢偣偰丄侾係亊俁亖係俀捠傝偁傞丅
丂丂傛偭偰丄媮傔傞妋棪偼丄丂係俀/俀係俁亖侾係/俉侾丂丂乮廔乯
乮俁乯丂敔偺拞偵俙丄俛丄俠丄俢偺僇乕僪偑侾枃偢偮慡晹偱係枃擖偭偰偄傞応崌傪峫偊傞丅埲壓偱
丂丂偼丄俇夞栚偺帋峴偱弶傔偰A丄B丄C丄D偑偦傠偆偲偼丄俇夞偺帋峴偱俙丄俛丄俠丄俢偺偦傟偧傟
丂丂偑彮側偔偲傕侾夞偼庢傝弌偝傟丄偐偮俙丄俛丄俠丄俢偺偆偪偄偢傟偐侾枃偑俇夞栚偺帋峴偱弶
丂丂傔偰庢傝弌偝傟傞偙偲傪堄枴偡傞丅
丂傑偨丄俁埲忋俆埲壓偺帺慠悢値偵懳偟丄俇夞偺帋峴偺偆偪値夞栚偺帋峴偱弶傔偰A丄B丄C偩
偗偑偦傠偆偲偼丄俇夞偺帋峴偺偆偪侾夞栚偐傜値夞栚偺帋峴偱丄俙丄俛丄俠偺偦傟偧傟偑彮側偔
偲傕侾夞偼庢傝弌偝傟丄俢偼侾夞傕庢傝弌偝傟偢丄偐偮俙丄俛丄俠偺偆偪偄偢傟偐侾枃偑値夞栚偺
帋峴偱弶傔偰庢傝弌偝傟傞偙偲傪堄枴偡傞丅俇夞偺帋峴偺偆偪値夞栚偺帋峴偱弶傔偰B丄C丄D
偩偗偑偦傠偆側偳傕摨條偵掕傔傞丅
丂懢榊偝傫偲壴巕偝傫偼丄俇夞栚偺帋峴偱弶傔偰A丄B丄C丄D偑偦傠偆妋棪偵偮偄偰峫偊偰偄
傞丅
懢榊丗椺偊偽丄俆夞栚傑偱偵俙丄俛丄俠偺偦傟偧傟偑彮側偔偲傕侾夞偼庢傝弌偝傟丄偐偮俇夞栚
丂丂丂偵弶傔偰俢偑庢傝弌偝傟傞応崌傪峫偊偨傜寁嶼偱偒偦偆偩偹丅
壴巕丗偦傟側傜丄弶傔偰A丄B丄C偩偗偑偦傠偆偺偑丄俁夞栚偺偲偒丄係夞栚偺偲偒丄俆夞栚偺偲
丂丂丂偒偱暘偗偰峫偊偰傒偰偼偳偆偐側丅
乮鶣乯丂俇夞偺帋峴偺偆偪俁夞栚偺帋峴偱弶傔偰A丄B丄C偩偗偑偦傠偆庢傝弌偟曽傪峫偊丄
丂丂乽俇夞偺帋峴偺偆偪俁夞栚偺帋峴偱弶傔偰A丄B丄C偩偗偑偦傠偄丄偐偮俇夞栚偺帋峴偱弶
丂丂傔偰俢偑庢傝弌偝傟傞乿庢傝弌偟曽偺悢傪媮傔傛丅
乮鶤乯丂乽俇夞偺帋峴偺偆偪係夞栚偺帋峴偱弶傔偰A丄B丄C偩偗偑偦傠偄丄偐偮俇夞栚偺帋峴
丂丂偱弶傔偰俢偑庢傝弌偝傟傞乿庢傝弌偟曽偺悢傪媮傔傛丅
乮鶥乯丂俇夞栚偺帋峴偱弶傔偰A丄B丄C丄D偑偦傠偆妋棪傪媮傔傛丅
乮夝乯乮鶣乯丂俇夞偺帋峴偺偆偪俁夞栚偺帋峴偱弶傔偰A丄B丄C偩偗偑偦傠偆庢傝弌偟曽偼丄
丂丂丂丂俇捠傝偁傝丄俇夞栚偺帋峴偱弶傔偰俢偑庢傝弌偝傟傞庢傝弌偟曽偺悢偼丄
丂丂丂丂俇亊俁2亖俆係乮捠傝乯
乮鶤乯丂俇夞偺帋峴偺偆偪係夞栚偺帋峴偱弶傔偰A丄B丄C偩偗偑偦傠偆庢傝弌偟曽偼丄
丂丂係夞栚偑俙偺偲偒丄丂俀3亅俀亖俇乮捠傝乯
丂丂係夞栚偑俛偺偲偒丄丂俀3亅俀亖俇乮捠傝乯
丂丂係夞栚偑俠偺偲偒丄丂俀3亅俀亖俇乮捠傝乯
丂側偺偱丄崌傢偣偰丄俇亊俁亖侾俉捠傝偁傞偐傜丄俇夞栚偺帋峴偱弶傔偰俢偑庢傝弌偝傟傞庢傝
丂弌偟曽偺悢偼丄丂侾俉亊俁亖俆係乮捠傝乯
乮鶥乯丂俇夞偺帋峴偺偆偪俆夞栚偺帋峴偱弶傔偰A丄B丄C偩偗偑偦傠偆庢傝弌偟曽偼丄
丂丂俆夞栚偑俙偺偲偒丄丂俀4亅俀亖侾係乮捠傝乯
丂丂俆夞栚偑俛偺偲偒丄丂俀4亅俀亖侾係乮捠傝乯
丂丂俆夞栚偑俠偺偲偒丄丂俀4亅俀亖侾係乮捠傝乯
丂側偺偱丄崌傢偣偰丄侾係亊俁亖係俀捠傝偁傞偐傜丄俇夞栚偺帋峴偱弶傔偰俢偑庢傝弌偝傟傞庢
丂傝弌偟曽偺悢偼丄丂係俀捠傝
丂俇夞偺帋峴偱婲偙傝偆傞偡傋偰偺応崌偺悢偼丄係6亖係侽俋俇乮捠傝乯丂偦偺偆偪弶傔偰A丄B丄C丄
D偑偦傠偆応崌偺悢偼丄丂乮俆係亄俆係亄係俀乯亊係亖俇侽侽乮捠傝乯丂側偺偱丄
媮傔傞妋棪偼丄丂俇侽侽/俈俀俋亖俈俆/俆侾俀丂丂乮廔乯
乮僐儊儞僩乯丂寛偟偰擄偟偄栤戣偱偼偁傝傑偣傫偑丄栤戣暥偺忕挿偝偲桿摫偵晅偄偰偄偔偺偵
丂丂丂丂丂旀傟傑偟偨両撪梕揑偵偼丄嫟捠堦師帋尡偩偲侾暸偵廂傑傞栤戣偱偡傛偹丅
戞俀栤丂[侾]丂嵗昗暯柺忋偵係揰俷(0丆0)丄A(6丆0)丄B(4丆6)丄C(0丆6)傪捀揰偲偡傞戜宍OABC
丂丂丂丂丂丂偑偁傞丅傑偨丄偙偺嵗昗暯柺忋偱丄揰P丄Q偼師偺婯懃偵廬偭偰堏摦偡傞丅
亙婯懃亜
丒P偼丄俷偐傜弌敪偟偰枅昩侾偺堦掕偺懍偝偱 倶 幉忋傪惓偺岦偒偵A傑偱堏摦偟丄A偵摓払偟
丂偨帪揰偱堏摦傪廔椆偡傞丅
丒Q偼丄C偐傜弌敪偟偰 y 幉忋傪晧偺岦偒偵俷傑偱堏摦偟丄俷偵摓払偟偨屻偼 倷 幉忋傪惓偺
丂岦偒偵C傑偱堏摦偡傞丅偦偟偰丄C偵摓払偟偨帪揰偱堏摦傪廔椆偡傞丅偨偩偟丄Q偼枅昩俀偺
丂堦掕偺懍偝偱堏摦偡傞丅
丒P丄Q偼摨帪崗偵堏摦傪奐巒偡傞丅
丂偙偺婯懃偵廬偭偰丄P丄Q偑堏摦偡傞偲偒丄P丄Q偼偦傟偧傟 A丄C 偵摨帪崗偵摓払偟丄堏摦
傪廔椆偡傞丅
丂埲壓偵偍偄偰丄P丄Q偑堏摦傪奐巒偡傞帪崗傪奐巒帪崗丄堏摦傪廔椆偡傞帪崗傪廔椆帪崗
偲偡傞丅
丂丂
乮侾乯丂奐巒帪崗偐傜侾昩屻偺仮PBQ偺柺愊傪媮傔傛丅
乮夝乯丂俛乮4丆6乯丄俹乮1丆0乯丄俻乮0丆4乯 偐傜丄仮PBQ亖乮1/2乯乥乮亅3乯乮亅2乯亅24乥亖9丂丂乮廔乯
乮俀乯丂奐巒帪崗偐傜俁昩娫偺仮PBQ偺柺愊偵偮偄偰丄柺愊偺嵟彫抣偲嵟戝抣傪媮傔傛丅
乮夝乯丂俛乮4丆6乯丄俹乮t丆0乯丄俻乮0丆6亅2t乯 偐傜丄
丂仮PBQ亖乮1/2乯乥乮t亅4乯乮亅2t乯亅24乥亖乥t2亅4t亄12乥亖乮t亅2乯2亄8
丂0亝t亝3丂偵偍偄偰丄t亖2丂偺偲偒丄嵟彫偱丄嵟彫抣偼丄8
丂t亖0丂偺偲偒丄嵟戝偱丄嵟戝抣偼丄12丂丂乮廔乯
乮俁乯丂奐巒帪崗偐傜廔椆帪崗傑偱偺仮俹俛俻偺柺愊偵偮偄偰丄柺愊偺嵟彫抣偲嵟戝抣傪媮
丂丂傔傛丅
乮夝乯丂3亝倲亝6丂偺偲偒丄俛乮4丆6乯丄俹乮t丆0乯丄俻乮0丆2t亅6乯 偐傜丄
丂仮PBQ亖乮1/2乯乥乮t亅4乯乮2t亅12乯亅24乥亖乥t2亅10t亄12乥亖亅乮t亅5乯2亄13
丂3亝倲亝6丂偵偍偄偰丄t亖5丂偺偲偒丄嵟戝偱丄嵟戝抣偼丄13
丂t亖3丂偺偲偒丄嵟彫偱丄嵟彫抣偼丄9
埲忋偐傜丄0亝倲亝6丂偵偍偄偰丄t亖5丂偺偲偒丄嵟戝偱丄嵟戝抣偼丄13
丂t亖2丂偺偲偒丄嵟彫偱丄嵟彫抣偼丄8丂丂乮廔乯
乮係乯丂奐巒帪崗偐傜廔椆帪崗傑偱偺仮俹俛俻偺柺愊偵偮偄偰丄柺愊偑侾侽埲壓偲側傞帪娫
丂丂傪媮傔傛丅
乮夝乯丂0亝t亝3丂偵偍偄偰丄乮t亅2乯2亄8亖10丂偺夝偼丄丂t亖2亅
丂3亝倲亝6丂偵偍偄偰丄亅乮t亅5乯2亄13亖10丂偺夝偼丄丂t亖5亅
丂傛偭偰丄媮傔傞帪娫偼丄丂5亅 亅乮2亅
亅乮2亅 乯亖3亅
乯亖3亅 亄
亄 丂乮昩娫乯丂丂乮廔乯
丂乮昩娫乯丂丂乮廔乯
乮僐儊儞僩乯丂仮PBQ偺柺愊偼丄丂乮戜宍偺柺愊乯亅乮俀偮偺嶰妏宍偺柺愊偺榓乯丂偱傕媮傔傜傟
丂丂丂丂丂傑偡偹丅
乵俀乶丂崅峑偺棨忋晹偱挿嫍棧嫞媄偺慖庤偲偟偰妶桇偡傞懢榊偝傫偼丄挿嫍棧嫞媄偺岞擣婰
丂丂榐偑宖嵹偝傟偰偄傞Web儁乕僕傪尒偮偗偨丅偙偺Web儁乕僕偱偼丄奺慖庤偵偍偗傞岞擣
丂丂婰榐偺偆偪嵟傕懍偄傕偺偑宖嵹偝傟偰偄傞丅
丂偦偺Web儁乕僕偵宖嵹偝傟偰偄傞丄偁傞慖庤偺偁傞挿嫍棧嫞媄偱偺岞擣婰榐傪丄偦偺慖庤
偺偦偺嫞媄偱偺儀僗僩僞僀儉偲偄偆偙偲偵偡傞丅
乮侾乯丂懢榊偝傫偼丄抝巕儅儔僜儞偺擔杮恖慖庤偺2022擭枛帪揰偱偺儀僗僩僞僀儉傪挷傋偨丅
丂偦偺拞偱丄2018擭傛傝慜偵儀僗僩僞僀儉傪弌偟偨慖庤偲2018擭埲崀偵儁僗僩僞僀儉傪弌偟偨
丂慖庤偵暘偗丄偦傟偧傟偵偍偄偰懍偄曽偐傜50恖偺慖庤偺儀僗僩僞僀儉傪僨乕僞A丄僨乕僞B
丂偲偟偨丅
丂偙偙偱偼丄儅儔僜儞偺儀僗僩僞僀儉偼丄幚嵺偺儀僗僩僞僀儉偐傜2帪栤傪堷偄偨帪娫傪昩扨埵
偱昞偟偨傕偺偲偡傞丅椺偊偽丄2帪娫5暘30昩偱偁傟偽丄60亊5亄30亖330(昩)丂偲側傞丅
乮鶣乯丂恾1偲恾2偼偦傟偧傟丄奒媺偺暆傪30昩偲偟偨A偲B偺僸僗僩僌儔儉偱偁傞丅側偍丄僸僗僩
丂僌儔儉偺奺奒媺偺嬫栤偼丄嵍懁偺悢抣傪娷傒丄塃懁偺悢抣傪娷傑側偄丅
丂丂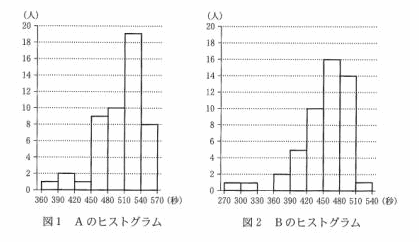
丂恾1偱丄A偺嵟昿抣偑娷傑傟傞奒媺傪媮傔傛丅傑偨丄恾2偱丄B偺拞墰抣偑娷傑傟傞奒媺傪
媮傔傛丅
乮夝乯丂A偺嵟昿抣偑娷傑傟傞奒媺偼丄俆侾侽埲忋俆係侽枹枮丅傑偨丄B偺拞墰抣偑娷傑傟傞奒
丂丂媺偼丄俀俆斣栚丄俀俇斣栚偑娷傑傟傞奒媺側偺偱丄係俆侽埲忋係俉侽枹枮丅丂丂乮廔乯
乮鶤乯丂恾3偼丄A丄B偦傟偧傟偺敔傂偘恾傪暲傋偨傕偺偱偁傞丅偨偩偟丄拞墰抣傪帵偡慄偼徣
丂偄偰偄傞丅
丂丂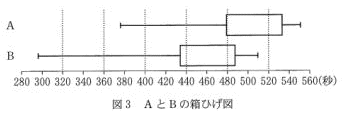
丂恾3傛傝師偺偙偲偑撉傒庢傟傞丅偨偩偟丄A丄B偦傟偧傟偵偍偗傞丄懍偄曽偐傜13斣栚偺慖庤
偼丄堦恖偢偮偲偡傞丅
丒B偺懍偄曽偐傜13斣栚偺慖庤偺儀僗僩僞僀儉偲丄A偺懍偄曽偐傜13斣栚偺慖庤偺儀僗僩僞僀
儉偺嵎偼偍傛偦壗昩偐丅
丒A偺巐暘埵斖埻偐傜B偺巐暘埵斖埻傪堷偄偨嵎偺愨懳抣偺庢傝摼傞斖埻傪媮傔傛丅
乮夝乯丂俆侽亐係亖侾俀丏俆丂偐傜丄A偺懍偄曽偐傜13斣栚偺慖庤偺儀僗僩僞僀儉偼丄係俉侽昩偱丄
丂B偺懍偄曽偐傜13斣栚偺慖庤偺儀僗僩僞僀儉偼丄係俁俆昩偱偁傞丅傛偭偰丄偦偺嵎偼丄係俆昩
丂A偺巐暘埵斖埻偼丄俆俁侽亅係俉侽亖俆侽乮昩乯丄B偺巐暘埵斖埻偼丄係俉俆亅係俁俆亖俆侽乮昩乯
丂傛偭偰丄椉幰偺嵎偺愨懳抣偺庢傝摼傞斖埻偼丄侽埲忋俀侽枹枮偲尵偊傞丅丂丂乮廔乯
乮鶥乯丂懢榊偝傫偼丄A偺偁傞慖庤偲B偺偁傞慖庤偺儀僗僩僞僀儉偺斾妑偵偍偄偰丄偦偺擇恖偺
丂慖庤偺儀僗僩僞僀儉偑懍偄偐抶偄偐偲偼暿偺娤揰偱傕峫偊傞偨傔偵丄師偺幃傪枮偨偡z偺
丂抣傪梡偄偰敾抐偡傞偙偲偵偟偨丅
丂幃丂丗丂(偁傞僨乕僞偺偁傞慖庤偺儀僗僩僞僀儉)
丂丂丂丂亖(偦偺僨乕僞偺暯嬒抣)亄倸亊(偦偺僨乕僞偺昗弨曃嵎)
丂擇恖偺慖庤偦傟偧傟偺儀僗僩僞僀儉偵懳偡傞倸偺抣傪斾妑偟丄偦偺抣偺彫偝偄慖庤偺曽偑
桪傟偰偄傞偲敾抐偡傞丅
丂壓昞偼丄A丄B偦傟偧傟偵偍偗傞丄懍偄曽偐傜1斣栚偺慖庤(埲壓丄1埵偺慖庤)偺儀僗僩僞僀
儉偲丄僨乕僞偺暯嬒抣偲昗弨曃嵎傪傑偲傔偨傕偺偱偁傞丅
丂昞丂1埵偺慖庤偺儀僗僩僞僀儉丄暯嬒抣丄昗弨曃嵎
| 僨乕僞 |
1埵偺慖庤偺儀僗僩僞僀儉 |
暯嬒抣 |
昗弨曃嵎 |
| A |
376 |
504 |
40 |
| B |
296 |
454 |
45 |
丂幃偲忋昞傪梡偄偰丄B偺1埵偺慖庤偺儀僗僩僞僀儉偵懳偡傞 z 偺抣傪媮傔傛丅
A丄B偦傟偧傟偵偍偗傞丄1埵偺慖庤偵偮偄偰偳傫側偙偲偑尵偊傞偐丅
乮夝乯丂B偺1埵偺慖庤偺儀僗僩僞僀儉偵懳偡傞 z 偺抣偼丄
丂俀俋俇亖係俆係亄係俆倸丂傛傝丄倸亖亅俁丏俆侾
丂偙偺偙偲偐傜丄B偺1埵偺慖庤偺儀僗僩僞僀儉偼丄暯嬒抣傛傝昗弨曃嵎偺偍傛偦俁丏俆侾攞偩
偗彫偝偄偙偲偑傢偐傞丅
丂摨條偵丄A偺1埵偺慖庤偺儀僗僩僞僀儉偵懳偡傞 z 偺抣偼丄
丂俁俈俇亖俆侽係亄係侽倸丂傛傝丄倸亖亅俁丏俀
丂偙偺偙偲偐傜丄A偺1埵偺慖庤偺儀僗僩僞僀儉偼丄暯嬒抣傛傝昗弨曃嵎偺偍傛偦俁丏俀攞偩
偗彫偝偄偙偲偑傢偐傞丅
丂埲忋偐傜丄儀僗僩僞僀儉偱斾妑偡傞偲丄B偺侾埵偺慖庤偺曽偑懍偔丄倸 偺抣偱斾妑偡傞偲丄俛
偺侾埵偺慖庤偺曽偑桪傟偰偄傞丅丂丂乮廔乯
乮俀乯丂懢榊偝傫偼丄儅儔僜儞丄10000m丄5000 m偺儀僗僩僞僀儉偵娭楢偑側偄偐傪挷傋傞偙偲偵
丂丂偟偨丅偦偺偨傔偵丄2022擭枛帪揰偱偺偙傟傜3庬栚偺儀僗僩僞僀儉傪偡傋偰妋擣偱偒偨擔
丂丂杮恖抝巕慖庤偺偆偪丄儅儔僜儞偺儀僗僩僞僀儉偑懍偄曽偐傜50恖傪慖傫偩丅
丂恾4偲恾5偼偦傟偧傟丄慖傫偩50恖偵偮偄偰偺儅儔僜儞偲10000 m偺傋僗僩僞僀儉丄5000 m偲
10000 m偺儀僗僩僞僀儉偺嶶晍恾偱偁傞丅偨偩偟丄5000 m偲10000 m偺儀僗僩僞僀儉偼昩扨埵
偱昞偟丄儅儔僜儞偺儀僗僩僞僀儉偼乮侾乯偺応崌偲摨條丄幚嵺偺儀僗僩僞僀儉偐傜2帪娫傪堷偄偨
帪娫傪昩扨埵偱昞偟偨傕偺偲偡傞丅側偍丄偙傟傜偺嶶晍恾偵偼丄姰慡偵廳側偭偰偄傞揰偼側偄丅
丂丂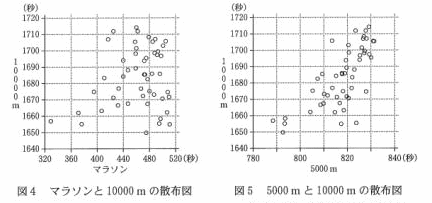
丂師偺(a)丄(b)偼丄恾4偲恾5偵娭偡傞婰弎偱偁傞丅
(a) 儅儔僜儞偺傋僗僩僞僀儉偺懍偄曽偐傜3斣栚傑偱偺慖庤偺10000 m偺儀僗僩僞僀儉偼丄3慖
丂庤偲傕1670昩枹枮偱偁傞丅
(b) 儅儔僜儞偲10000 m偺娫偺憡娭偼丄5000 m偲10000 m偺娫偺憡娭傛傝嫮偄丅
丂(a)丄(b)偺惓岆傪摎偊傛丅
乮夝乯丂儔僜儞偺傋僗僩僞僀儉偺懍偄曽偐傜3斣栚傑偱偺慖庤偺10000 m偺儀僗僩僞僀儉偼丄3慖
丂庤偲傕1670昩枹枮側偺偱丄乮倎乯偼惓偟偄丅
丂恾係偲恾俆偺嶶晍恾傪斾妑偟偰丄恾俆偺曽偑枾廤偟偰偄傞丅傛偭偰丄5000 m偲10000 m偺娫
偺憡娭偺曽偑丄儅儔僜儞偲10000 m偺娫偺憡娭傛傝嫮偄偲尵偊傞丅
丂傛偭偰丄乮倐乯偼岆傝偱偁傞丅丂丂乮廔乯
乮僐儊儞僩乯丂偙偺愝栤傕堎條偵暥復検偑懡偄丅偦偺妱傝偵愝栤儗儀儖偼嫵壢彂偺栤偄儗儀
丂丂丂丂丂儖偱丄擡懴椡偝偊偁傟偽崅摼揰偑婜懸偱偒傞偩傠偆丅
戞侾栤丂[侾]乮鶣乯丂晄摍幃丂値亙俀 亙値亄侾丂丒丒丒丂嘆丂傪枮偨偡惍悢値傪媮傔傛丅
亙値亄侾丂丒丒丒丂嘆丂傪枮偨偡惍悢値傪媮傔傛丅
丂丂乮鶤乯丂俀 偺彫悢晹暘傪倎偲偍偒丄倐亖侾/倎偲偍偔丅偙偺偲偒丄倐傪媮傔傛丅丂丒丒丒丂嘇
偺彫悢晹暘傪倎偲偍偒丄倐亖侾/倎偲偍偔丅偙偺偲偒丄倐傪媮傔傛丅丂丒丒丒丂嘇
丂丂乮鶥乯丂倎2亅俋倐2傪媮傔傛丅
丂丂乮鶦乯丂嘆嘇偐傜丄倐偺庢傝摼傞抣偺斖埻傪媮傔傛丅
丂丂乮鶧乯丂 偺彫悢戞侾埵偺悢帤丄彫悢戞俀埵偺悢帤傪媮傔傛丅
偺彫悢戞侾埵偺悢帤丄彫悢戞俀埵偺悢帤傪媮傔傛丅
乮夝乯乮鶣乯丂係俋亙俆俀亙俇係丂傛傝丄丂俈亙俀 亙俉丂側偺偱丄戣堄傪枮偨偡惍悢値偼丄値亖俈
亙俉丂側偺偱丄戣堄傪枮偨偡惍悢値偼丄値亖俈
乮鶤乯丂戣堄傛傝丄倎亖俀 亅俈丂偱丄倐亖侾/乮俀
亅俈丂偱丄倐亖侾/乮俀 亅俈乯亖乮俀
亅俈乯亖乮俀 亄俈乯/俁
亄俈乯/俁
乮鶥乯丂倎2亅俋倐2亖乮倎亄俁倐乯乮倎亅俁倐乯亖係 丒乮亅侾係乯亖亅俆俇
丒乮亅侾係乯亖亅俆俇
乮鶦乯丂乮鶣乯傛傝丄丂俈亙俀 亙俉丂側偺偱丄丂侾係亙俀
亙俉丂側偺偱丄丂侾係亙俀 亄俈亙侾俆丂傛傝丄
亄俈亙侾俆丂傛傝丄
丂丂侾係/俁亙倐亙俆丂偲側傞丅傛偭偰丄丂侾/俆亙倎亙俁/侾係丂偲側傞丅
乮鶧乯丂乮鶣乯傛傝丄丂俈/俀亙 亙係丂側偺偱丄
亙係丂側偺偱丄 偺惍悢晹暘偼丄俁丂偱丄乮鶦乯傛傝丄
偺惍悢晹暘偼丄俁丂偱丄乮鶦乯傛傝丄
丂侾/俆亙俀 亅俈亙俁/侾係丂側偺偱丄丂侾俉/俆亙
亅俈亙俁/侾係丂側偺偱丄丂侾俉/俆亙 亙侾侽侾/俀俉
亙侾侽侾/俀俉
丂偙偙偱丄侾俉/俆亖俁丏俇丂丄侾侽侾/俀俉亖俁丏俇侽俈丒丒丒丂側偺偱丄
丂 偺彫悢戞侾埵偺悢帤偼俇偱丄彫悢戞俀埵偺悢帤偼侽偱偁傞丅丂丂乮廔乯
偺彫悢戞侾埵偺悢帤偼俇偱丄彫悢戞俀埵偺悢帤偼侽偱偁傞丅丂丂乮廔乯
[俀]丂悈暯側抧柺(埲壓丄抧柺)偵悅捈偵棫偭偰偄傞揹拰偺崅偝傪丄偦偺塭偺挿偝偲懢梲崅搙
丂丂傪棙梡偟偰媮傔傛偆丅
丂丂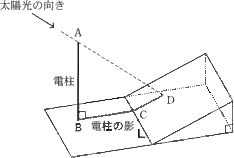
丂忋恾偺傛偆偵丄揹拰偺塭偺愭抂偼嶁偺幬柺(埲壓丄嶁)偵偁傞偲偡傞丅傑偨丄嶁偵偼孹幬傪
昞偡摴楬昗幆偑愝抲偝傟偰偄偰丄偦偙偵偼7亾偲昞帵偝傟偰偄傞偲偡傞丅
揹拰偺懢偝偲塭偺暆偼柍帇偟偰峫偊傞傕偺偲偡傞丅傑偨丄抧柺偲嶁偼暯柺偱偁傞偲偟丄抧柺
偲嶁偑岎傢偭偰偱偒傞捈慄傪俴偲偡傞丅
揹拰偺愭抂傪揰A偲偟丄崻傕偲傪揰B偲偡傞丅揹拰偺塭偵偮偄偰丄抧柺偵偁傞晹暘傪慄暘BC
偲偟丄嶁偵偁傞晹暘傪慄暘CD偲偡傞丅慄暘BC丄CD偑偦傟偧傟俴偲悅捈偱偁傞偲偒丄揹拰偺塭
偼嶁偵岦偐偭偰傑偭偡偖偵偺傃偰偄傞偲偄偆偙偲偵偡傞丅
丂揹拰偺塭偑嶁偵岦偐偭偰傑偭偡偖偵偺傃偰偄傞偲偡傞丅偙偺偲偒丄係揰A丄B丄C丄D傪捠傞
暯柺偼俴偲悅捈偱偁傞丅偦偺暯柺偵偍偄偰丄壓恾偺傛偆偵丄捈慄AD偲捈慄BC偺岎揰傪P偲
偡傞偲丄懢梲崅搙偲偼佢APB偺戝偒偝偺偙偲偱偁傞丅
丂丂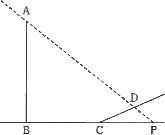
丂摴楬昗幆偺俈亾偲偄偆昞帵偼丄偙偺嶁傪偺傏偭偨偲偒丄侾侽侽倣偺悈暯嫍棧偵懳偟偰俈倣偺
妱崌偱崅偔側傞偙偲傪帵偟偰偄傞丅
乮鶣乯丂値傪侾埲忋俋埲壓偺惍悢偲偡傞偲偒丄嶁偺撢幬妏佢DCP偺戝偒偝偵偮偄偰
丂値亱亙佢DCP亙値亱亄侾亱傪枮偨偡値偺抣傪媮傔傛丅
丂埲壓偱偼丄佢DCP偺戝偒偝偼丄偪傚偆偳乮鶣乯偱媮傔偨抣偲偡傞丅
乮鶤乯丂偁傞擔丄揹拰偺塭偑嶁偵岦偐偭偰傑偭偡偖偵偺傃偰偄偨偲偒丄塭偺挿偝傪挷傋偨偲偙
丂丂傠丄BC亖俈倣丄CD亖係倣偱偁傝丄懢梲崅搙偼佢APB亖係俆亱偱偁偭偨丅揰D偐傜捈慄AB
丂丂偵悅捈側捈慄傪堷偒丄捈慄AB偲偺岎揰傪俤偲偡傞偲偒丄俛俤丄俢俤傪媮傔丄揹拰偺崅偝傪丄
丂丂彫悢戞俀埵偱巐幪屲擖偟偰媮傔傛丅
乮鶥乯丂暿偺擔丄揹拰偺塭偑嶁偵岦偐偭偰傑偭偡偖偵偺傃偰偄偨偲偒偺懢梲崅搙偼
丂丂佢APB亖係俀亱偱偁偭偨丅揹拰偺崅偝偑傢偐偭偨偺偱丄慜夞挷傋偨擔偐傜偺塭偺挿偝偺
丂丂曄壔傪抦傞偙偲偑偱偒傞丅揹拰偺塭偵偮偄偰丄嶁偵偁傞晹暘偺挿偝俠俢傪媮傔傛丅
乮夝乯乮鶣乯丂倲倎値佢俢俠俹亖俈/侾侽侽亖侽丏侽俈丂傛傝丄丂係亱亙佢俢俠俹亙俆亱丂側偺偱丄値亖係
丂埲壓偱丄佢俢俠俹亖係亱偲偡傞丅
乮鶤乯丂俛俤亖係丒倱倝値佢俢俠俹丂丄俢俤亖俈亄係丒們倧倱佢俢俠俹丂側偺偱丄
丂俙俛亖係丒倱倝値係亱亄乮俈亄係丒們倧倱係亱乯倲倎値係俆亱亖俈亄係乮倱倝値係亱們倧倱係亱乯
丂傛偭偰丄丂俙俛亖俈亄係乮侽丏侽俇俋俉亄侽丏俋俋俈俇乯亖侾侾丏俀俇俋俇
丂彫悢戞俀埵傪巐幪屲擖偟偰丄丂俙俛亖侾侾丏俁乮倣乯
乮鶥乯丂仮俙俛俹佷仮俢俫俹丂側偺偱丄
丂俈亄俠俢丒們倧倱佢俢俠俹亄乮俠俢丒倱倝値佢俢俠俹乯/倲倎値係俀亱丗 乮俠俢丒倱倝値佢俢俠俹乯/倲倎値係俀亱
亖俙俛 丗 俠俢丒倱倝値佢俢俠俹
傛偭偰丄
俙俛丒乮俠俢丒倱倝値佢俢俠俹乯/倲倎値係俀亱
亖乮俈亄俠俢丒們倧倱佢俢俠俹亄乮俠俢丒倱倝値佢俢俠俹乯/倲倎値係俀亱乯丒俠俢丒倱倝値佢俢俠俹
偡側傢偪丄
俙俛亖俈丒倲倎値係俀亱亄俠俢丒們倧倱佢俢俠俹丒倲倎値係俀亱亄俠俢丒倱倝値佢俢俠俹丂傛傝丄
俠俢乮倱倝値佢俢俠俹亄們倧倱佢俢俠俹丒倲倎値係俀亱乯亖俙俛亅俈丒倲倎値係俀亱
偟偨偑偭偰丄丂俠俢亖乮俙俛亅俈丒倲倎値係俀亱乯/乮倱倝値佢俢俠俹亄們倧倱佢俢俠俹丒倲倎値係俀亱乯
偙偙偱丄丂俙俛亖侾侾丏俁乮倣乯丂丄佢俢俠俹亖係亱傪戙擖偟偰丄
丂俠俢亖乮侾侾丏俁亅俈丒侽丏俋侽侽係乯/乮侽丏侽俇俋俉亄侽丏俋俋俈俇丒侽丏俋侽侽係乯
丂丂亖係丏俋俋俈俀/侽丏俋俇俉侽亖俆丏侾俇俀係
偟偨偑偭偰丄慜夞挷傋偨係倣傛傝丄栺侾丏侾俇俀係倣偩偗挿偄偙偲偑暘偐傞丅丂丂乮廔乯
亂 悢妛嘦丒俛 亃
戞俆栤丂揰俷傪尨揰偲偡傞嵗昗嬻娫偵係揰A(俀丆俈丆亅侾)丄B(俁丆俇丆侽)丄C(亅俉丆侾侽丆亅俁)丄
丂丂丂丂D(亅俋丆俉丆亅係)偑偁傞丅A丄B傪捠傞捈慄傪俴1偲偟丄C丄D傪捠傞捈慄傪俴2偲偡傞丅
乮侾乯丂俙俛丄俙俛丒俠俢傪媮傔傛丅
乮夝乯丂俙俛亖(侾丆亅侾丆侾)丂偱丄俠俢亖(亅侾丆亅俀丆亅侾)丂傛傝丄
丂俙俛丒俠俢亖亅侾亄俀亅侾亖侽丂丂乮廔乯
乮俀乯丂壴巕偝傫偲懢榊偝傫偼丄揰P偑俴1忋傪摦偔偲偒丄|俷俹|偑嵟彫偲側傞P偺埵抲偵偮偄偰峫
丂丂偊偰偄傞丅
丂P偑俴1忋偵偁傞偺偱丄AP亖sAB 傪枮偨偡幚悢 s 偑偁傝丄俷俹亖侽俙亄sAB偑惉傝棫偮丅
|俷俹|偑嵟彫偲側傞 s 偺抣傪媮傔傟偽俹偺埵抲偑媮傑傞丅偙偺偙偲偵偮偄偰丄壴巕偝傫偲懢榊
偝傫偑榖傪偟偰偄傞丅
壴巕丗|俷俹|2偑嵟彫偲側傞 倱 偺抣傪媮傔傟偽傛偄偹丅
懢榊丗|俷俹|偑嵟彫偲側傞偲偒偺捈慄OP偲俴1偺娭學偵拝栚偟偰傕傛偝偦偆偩傛丅
乮鶣乯丂|俷俹|2傪媮傔丄壴巕偝傫偺峫偊曽偱丄|俷俹|偑嵟彫偲側傞 s 偺抣傪媮傔傛丅
乮鶤乯丂|俷俹|偑嵟彫偲側傞偲偒丄捈慄俷俹偲俴1偺娭學偵拝栚偡傞偲丄俷俹丒俙俛亖侽偑惉傝棫偮
丂丂偙偲偑傢偐傞丅懢榊偝傫偺峫偊曽偱丄|俷俹|偑嵟彫偲側傞 s 偺抣傪媮傔傛丅
乮夝乯乮鶣乯丂俷俹亖(俀亄倱丆俈亅倱丆亅侾亄倱)丂側偺偱丄
丂|俷俹|2亖乮俀亄倱乯2亄乮俈亅倱乯2亄乮亅侾亄倱乯2亖俁倱2亅侾俀倱亄俆係亖俁乮倱亅俀乯2亄係俀
傛傝丄倱亖俀偺偲偒丄|俷俹|2偑嵟彫偲側傞丅
乮鶤乯丂俷俹丒俙俛亖俀亄倱亅乮俈亅倱乯亅侾亄倱亖俁倱亅俇亖侽丂傛傝丄倱亖俀
丂傛偭偰丄倱亖俀偺偲偒丄|俷俹|偑嵟彫偲側傞丅
乮俁乯丂揰P偑俴1忋傪摦偒丄揰Q偑俴2忋傪摦偔偲偡傞丅偙偺偲偒丄慄暘PQ偺挿偝偑嵟彫偵側傞偲
丂丂偒偺P丄俻偺嵗昗傪媮傔傛丅
乮夝乯丂俴1忋偺揰俹偵偮偄偰丄俷俹亖(俀亄倱丆俈亅倱丆亅侾亄倱)
丂俴2忋偺揰俻偵偮偄偰丄俷俻亖(亅俉亅倲丆侾侽亅俀倲丆亅俁亅倲)
偙偺偲偒丄丂俹俻亖(亅侾侽亅倲亅倱丆俁亅俀倲亄倱丆亅俀亅倲亅倱)丂偱丄
丂俹俻丒俙俛亖侽丂丄俹俻丒俠俢亖侽丂傛傝丄
丂亅侾侽亅倲亅倱亅乮俁亅俀倲亄倱乯亅俀亅倲亅倱亖亅侾俆亅俁倱亖侽丂傛偭偰丄丂倱亖亅俆
丂亅乮亅侾侽亅倲亅倱乯亅俀乮俁亅俀倲亄倱乯亅乮亅俀亅倲亅倱乯亖俇倲亄俇亖侽丂傛偭偰丄丂倲亖亅侾
丂偟偨偑偭偰丄俹(亅俁丆侾俀丆亅俇)丂丄俻(亅俈丆侾俀丆亅俀)丂偱偁傞丅丂丂乮廔乯
戞係栤乮侾乯丂悢楍乷倎値乸偑丂倎n+1亅倎n亖侾係丂乮値亖侾丄俀丄俁丄丒丒丒乯丂傪枮偨偡偲偡傞丅
乮鶣乯丂倎1亖侾侽 偺偲偒丄倎2丄倎3 傪媮傔傛丅
乮鶤乯丂悢楍乷倎値乸偺堦斒崁傪丄弶崁倎1 傪梡偄偰昞偣丅
乮夝乯乮鶣乯丂倎2亖倎1亄侾係亖俀係丂丄倎3亖倎2亄侾係亖俁俉
丂乮鶤乯丂摍嵎悢楍偺堦斒崁偺岞幃傛傝丄丂倎n亖倎1亄侾係乮値亅侾乯丂丂乮廔乯
乮俀乯丂悢楍乷倐値乸偑丂俀倐n+1亅倐n亄俁亖侽丂乮値亖侾丄俀丄俁丄丒丒丒乯丂傪枮偨偡偲偡傞丅
丂偙偺偲偒丄悢楍乷倐値乸偺堦斒崁傪丄弶崁倐1 傪梡偄偰昞偣丅
乮夝乯丂倐n+1亄俁亖乮侾/俀乯乮倐n亄俁乯丂傛傝丄丂倐n亄俁亖乮倐1亄俁乯(侾/俀)n-1 側偺偱丄
丂丂倐n亖乮倐1亄俁乯(侾/俀)n-1亅俁丂丂乮廔乯
乮俁乯丂懢榊偝傫偼丄(c値亄俁)(俀們n+1亅們値亄俁)亖侽丂乮値亖侾丄俀丄俁丄丒丒丒乯丂丒丒丒丂嘆丂傪枮偨偡
丂丂悢楍乷們値乸偵偮偄偰挷傋傞偙偲偵偟偨丅
乮鶣乯
丂丒悢楍乷們値乸偑嘆傪枮偨偟丄們1亖俆 偺偲偒丄們2 傪媮傔傛丅
丂丒悢楍乷們値乸偑嘆傪枮偨偟丄們3亖亅俁 偺偲偒丄們2 丄們1 傪媮傔傛丅
乮夝乯乮鶣乯丂們1亖俆 偺偲偒丄丂俉乮俀們2亅俆亄俁乯亖侽丂傛傝丄丂們2亖侾
丂們3亖亅俁 偺偲偒丄丂(c2亄俁)(俀們3亅們2亄俁)亖侽 傛傝丄丂(c2亄俁)2亖侽 丂傛偭偰丄c2亖亅俁
丂(c1亄俁)(俀們2亅們1亄俁)亖侽 傛傝丄丂(c1亄俁)2亖侽 丂傛偭偰丄c1亖亅俁丂丂乮廔乯
(鶤)丂懢榊偝傫偼丄悢楍乷們値乸偑嘆傪枮偨偟丄們3亖亅俁 偲側傞応崌偵偮偄偰峫偊偰偄傞丅
丂丂們3亖亅俁 偺偲偒丄們4 偑偳偺傛偆側抣偱傕丂(c3亄俁)(俀們4亅們3亄俁)亖侽 偑惉傝棫偮丅
丂丒悢楍乷們値乸偑嘆傪枮偨偟丄們3亖亅俁 丄們4亖俆 偺偲偒丄們5 傪媮傔傛丅
丂丒悢楍乷們値乸偑嘆傪枮偨偟丄們3亖亅俁 丄們4亖俉俁 偺偲偒丄們5 傪媮傔傛丅
乮夝乯丂們4亖俆 偺偲偒丄(c4亄俁)(俀們5亅們4亄俁)亖侽 傛傝丄俉(俀們5亅俀)亖侽 傛偭偰丄c5亖侾
丂們4亖俉俁 偺偲偒丄(c4亄俁)(俀們5亅們4亄俁)亖侽 傛傝丄俉俇(俀們5亅俉侽)亖侽
丂傛偭偰丄c5亖係侽丂丂乮廔乯
乮鶥乯丂懢榊偝傫偼乮鶣乯偲乮鶤乯偐傜丄們値亖亅俁 偲側傞偙偲偑偁傞偐偳偆偐偵拝栚偟丄師偺柦戣A
丂丂偑惉傝棫偮偺偱偼側偄偐偲峫偊偨丅
柦戣A丂悢楍乷們値乸偑嘆傪枮偨偟丄們1亗亅俁 偱偁傞偲偡傞丅偙偺偲偒丄偡傋偰偺帺慠悢値偵偮
丂丂丂丂偄偰丄們値亗亅俁 偱偁傞丅
丂柦戣A偑恀偱偁傞偙偲傪徹柧偣傛丅
乮夝乯丂悢妛揑婣擺朄偵傛傞丅
丂値亖侾丂偺偲偒丄忦審傛傝丄們1亗亅俁 側偺偱丄丂値亖侾偺偲偒丄柦戣俙偼惉傝棫偮丅
丂値亖倠偺偲偒丄柦戣俙偼惉傝棫偮偲壖掕偡傞丅偡側傢偪丄ck亗亅俁
丂偙偺偲偒丄丂(ck亄俁)(俀們k+1亅們k亄俁)亖侽 傛傝丄丂們k+1亖乮們k亅俁乯/俀丂偵偍偄偰丄
丂們k+1亖亅俁丂偲壖掕偡傞偲丄丂乮們k亅俁乯/俀亖亅俁丂傛傝丄丂們k亖亅俁
丂偟偐傞偵丄偙傟偼丄婣擺朄偺壖掕丂ck亗亅俁丂偵柕弬偡傞丅
丂傛偭偰丄們k+1亗亅俁丂偲側傝丄柦戣俙偼丄値亖倠亄侾偺偲偒傕惉傝棫偮偙偲傪帵偡丅
埲忋偐傜丄偡傋偰偺帺慠悢値偵偮偄偰丄們値亗亅俁 偱偁傞丅丂丂乮廔乯
仈帪娫抁弅偺偨傔偐丄偙偺徹柧偼丄杮暥偱偼惉傝棫偮傕偺偲偝傟妱垽偝傟偰偄傞丅
乮鶦乯丂師偺(嘥)丄(嘦)丄(嘨)偼丄悢楍乷們値乸偵娭偡傞柦戣偱偁傞丅偦傟偧傟偺恀婾傪挷傋傛丅
(嘥)丂們1亖俁 偐偮 們100亖亅俁 偱偁傝丄偐偮嘆傪枮偨偡悢楍乷們値乸偑偁傞丅
(嘦)丂們1亖亅俁 偐偮 們100亖亅俁 偱偁傝丄偐偮嘆傪枮偨偡悢楍乷們値乸偑偁傞丅
(嘨)丂們1亖亅俁 偐偮 們100亖俁 偱偁傝丄偐偮嘆傪枮偨偡悢楍乷們値乸偑偁傞丅
乮夝乯(嘥)丂們1亖俁亗亅俁丂側偺偱丄柦戣俙偐傜丄們100亗亅俁 側偺偱丄偙偺傛偆側悢楍乷們値乸偼
丂丂懚嵼偟側偄丅傛偭偰丄婾偱偁傞丅
(嘦)丂們1亖亅俁丂偺偲偒丄們2 偼擟堄偱偁傞丅偦偙偱丄們1亖們2亖丒丒丒亖們100亖亅俁 偱偁傞悢楍
丂偑懚嵼偟偆傞丅傛偭偰丄恀偱偁傞丅
(嘨)丂們1亖亅俁丂偺偲偒丄們2 偼擟堄偱偁傞丅偦偙偱丄們1亖們2亖丒丒丒亖們99亖亅俁丂偱丄
丂們100亖俁 偱偁傞悢楍偑懚嵼偟偆傞丅傛偭偰丄恀偱偁傞丅丂丂乮廔乯
戞俁栤丂埲壓偱偺乽惏傟乿偺掕媊偵偮偄偰偼丄婥徾挕偺揤婥奣嫷偺乽夣惏乿傑偨偼乽惏乿偲偡傞丅
乮侾乯丂懢榊偝傫偼丄帺暘偑廧傫偱偄傞抧堟偵偍偄偰丄擔梛擔偵惏傟偲側傞妋棪傪峫偊偰偄傞丅
丂丂惏傟偺応崌偼乽侾乿丄惏傟埲奜偺応崌偼乽侽乿偺抣傪偲傞妋棪曄悢傪X偲掕媊偡傞丅傑偨丄
丂丂X亖侾偱偁傞妋棪傪倫偲偡傞丅
乮鶣乯丂偙偺妋棪曄悢X偺暯嬒(婜懸抣)倣傪媮傔傛丅
乮鶤乯丂懢榊偝傫偼丄偁傞婜娫偵偍偗傞楢懕偟偨値廡偺擔梛擔偺揤婥傪丄忋婰偺妋棪暘晍傪
丂丂傕偮曣廤抍偐傜柍嶌堊偵拪弌偟偨戝偒偝値偺昗杮偲傒側偟丄偦傟傜偺X傪妋棪曄悢
丂丂X1丄X2丄丒丒丒丄Xn 偱昞偡偙偲偵偟偨丅偦偟偰丄偦偺昗杮暯嬒 傪棙梡偟偰丄曣暯嬒倣傪
傪棙梡偟偰丄曣暯嬒倣傪
丂丂悇掕偟傛偆偲峫偊偨丅幚嵺偵丄値亖俁侽侽偲偟偰惏傟偺擔悢傪挷傋偨偲偙傠丄壓昞偺傛偆偵
丂側偭偨丅
| 揤婥 |
惏傟 |
惏傟埲奜 |
寁 |
| 擔悢 |
俈俆 |
俀俀俆 |
俁侽侽 |
丂曣昗弨曃嵎傪冃偲偡傞偲丄値亖俁侽侽偼廫暘偵戝偒偄偺偱丄昗杮暯嬒 偼嬤帡揑偵惓婯暘
偼嬤帡揑偵惓婯暘
晍俶乮倣丆冃2/値乯偵廬偆丅
丂堦斒偵丄曣昗弨曃嵎冃偑傢偐傜側偄偲偒丄昗杮偺戝偒偝値偑戝偒偗傟偽丄冃偺戙傢傝偵昗
杮偺昗弨曃嵎俽傪梡偄偰傕傛偄偙偲偑抦傜傟偰偄傞丅俽偼丄
俽亖併乷乮乮X1亅 乯2亄乮X2亅
乯2亄乮X2亅 乯2亄丒丒丒亄乮Xn亅
乯2亄丒丒丒亄乮Xn亅 乯2乯/値乸
乯2乯/値乸
亖併乷乮X12亄X22亄丒丒丒亄Xn2乯/値亅 2乸
2乸
偱寁嶼偱偒傞丅偙偙偱丄X12亖X1丄X22亖X2丄丒丒丒丄Xn2亖Xn偱偁傞偙偲偵拝栚偟丄塃曈傪惍棟
偡傞偲丄俽亖併乷 乮侾亅
乮侾亅 乯乸偲昞偝傟傞偙偲偑傢偐傞丅
乯乸偲昞偝傟傞偙偲偑傢偐傞丅
丂昞傛傝丄戝偒偝値亖俁侽侽偺昗杮偐傜媮傔傜傟傞曣暯嬒倣偵懳偡傞怣棅搙俋俆亾偺怣棅嬫娫
傪媮傔傛丅乮仺丂嶲峫丗乽暯嬒偺悇掕乿乯
乮夝乯乮鶣乯丂倣亖侽丒乮侾-倫乯亄侾丒倫亖倫
乮鶤乯丂倫亖俈俆/俁侽侽亖侾/係丂傛傝丄 亖侾丒乮侾/係乯亖侾/係亖侽丏俀俆
亖侾丒乮侾/係乯亖侾/係亖侽丏俀俆
丂偙偺偲偒丄俽亖併乷乮侾/係乯乮俁/係乯乸亖 /係丂偲側傞偺偱丄怣棅搙俋俆亾偺怣棅嬫娫偼丄
/係丂偲側傞偺偱丄怣棅搙俋俆亾偺怣棅嬫娫偼丄
丂 亅侾丏俋俇丒俽/併俁侽侽亝倣亝
亅侾丏俋俇丒俽/併俁侽侽亝倣亝 亄侾丏俋俇丒俽/併俁侽侽
亄侾丏俋俇丒俽/併俁侽侽
傛傝丄丂侽丏俀俆亅侾丏俋俇/係侽亝倣亝侽丏俀俆亄侾丏俋俇/係侽丂側偺偱丄寁嶼偟偰丄
丂侽丏俀侽侾亝倣亝侽丏俀俋俋丂偲側傞丅
乮俀乯丂偁傞婜娫偵偍偄偰丄乽偪傚偆偳俁廡懕偗偰擔梛擔偺揤婥偑惏傟偵側傞偙偲乿偑偳偺偔傜偄
丂偺昿搙偱婲偙傝摼傞偺偐傪峫嶡偟傛偆丅埲壓偱偼丄楢懕偡傞倠廡偺擔梛擔偺揤婥偵偮偄偰丄
丂乮侾乯偺懢榊偝傫偑峫偊偨妋棪曄悢偺偆偪 X1丄X2丄丒丒丒丄Xk 傪梡偄偰挷傋傞丅偨偩偟丄倠偼
丂俁埲忋俁侽侽埲壓偺帺慠悢偲偡傞丅
X1丄X2丄丒丒丒丄Xk 偺抣傪弴偵暲傋偨偲偒偺侽偲侾偐傜側傞楍偵偍偄偰丄乽偪傚偆偳嶰偮懕偗偰侾
偑尰傟傞晹暘乿傪A偲偟丄A偺屄悢傪妋棪曄悢U倠偱昞偡丅
椺偊偽丄倠亖俀侽偲偟丄X1丄X2丄丒丒丒丄X20 偺抣傪弴偵暲傋偨偲偒
丂丂丂1,1,1,1, 0,1,1,1,0,0,1,1,1,1,1,0, 0,1,1,1
偱偁偭偨偲偡傞丅偙偺椺偱偼丄愒帤晹暘偼A傪帵偟偰偍傝丄侾偑巐偮埲忋懕偔晹暘偼A偲偼傒側
偝側偄偺偱丄U20亖俀 偲側傞丅
丂倠亖係 偺偲偒丄X1丄X2丄X3丄X4 偺偲傝摼傞抣偲丄偦傟偵懳墳偟偨U4偺抣傪彂偒弌偡偲丄壓
昞偺傛偆偵側傞丅
| X1 |
X2 |
X3 |
X4 |
U4 |
| 0 |
0 |
0 |
0 |
0 |
| 1 |
0 |
0 |
0 |
0 |
| 0 |
1 |
0 |
0 |
0 |
| 0 |
0 |
1 |
0 |
0 |
| 0 |
0 |
0 |
1 |
0 |
| 1 |
1 |
0 |
0 |
0 |
| 1 |
0 |
1 |
0 |
0 |
| 1 |
0 |
0 |
1 |
0 |
| 0 |
1 |
1 |
00 |
0 |
| 0 |
1 |
0 |
1 |
0 |
| 0 |
0 |
1 |
1 |
0 |
| 1 |
1 |
1 |
0 |
1 |
| 1 |
1 |
0 |
1 |
0 |
| 1 |
0 |
1 |
1 |
0 |
| 0 |
1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
0 |
丂偙偙偱丄U4偺婜懸抣傪媮傔偰傒傛偆丅乮侾乯偵偍偗傞倫偺抣傪倫亖侾/係偲偡傞丅
乮鶣乯丂倠亖係偺偲偒丄U4偺婜懸抣傪媮傔傛丅
乮鶤乯丂倠亖俆偺偲偒丄U5偺婜懸抣傪媮傔傛丅
乮鶥乯丂係埲忋偺倠偵偮偄偰丄倠偲俤乮U倠乯偺娭學傪徻偟偔挷傋傞偲丄嵗昗暯柺忋偺揰(係丆俤乮U4乯)丄
丂(俆丆俤乮U5乯)丄丒丒丒丄(俁侽侽丆俤乮U300乯)偼堦偮偺捈慄忋偵偁傞偙偲偑傢偐傞丅
丂偙偺帠幚偵傛偭偰丄俤乮U300乯偺抣傪媮傔傛丅
乮夝乯乮鶣乯丂U4偺抣偑侾偲側傞妋棪偼丄侾侾侾侽丄侽侾侾侾丂偐傜丄丂俀丒乮侾/係乯3乮俁/係乯亖俁/侾俀俉
丂側偺偱丄丂俤乮U4乯亖侾丒乮俁/侾俀俉乯亖俁/侾俀俉
乮鶤乯丂U5偺抣偑侾偲側傞妋棪偼丄侾侾侾侽侽丄侽侾侾侾侽丄侽侽侾侾侾丄侾侾侾侽侾丄侾侽侾侾侾丂偐傜丄
丂俁丒乮侾/係乯3乮俁/係乯2亄俀丒乮侾/係乯4乮俁/係乯亖俁俁/侾侽俀係
丂側偺偱丄丂俤乮U5乯亖侾丒乮俁俁/侾侽俀係乯亖俁俁/侾侽俀係
乮鶥乯丂捈慄偺孹偒偼丄丂乮俤乮U5乯亅俤乮U4乯)/乮俆亅係乯亖俁俁/侾侽俀係亅俁/侾俀俉亖俋/侾侽俀係
丂戣堄傛傝丄丂乮俤乮U300乯亅俤乮U4乯)/乮俁侽侽亅係乯亖俋/侾侽俀係丂側偺偱丄
俤乮U300乯亖俤乮U4乯亄俀俋俇丒乮俋/侾侽俀係乯亖俁/侾俀俉亄俁俁俁/侾俀俉亖俁俁俇/侾俀俉亖俀侾/俉丂丂乮廔乯
乮僐儊儞僩乯丂偙偺栤戣傕暥復偺挿偝偵鐒堈偟傑偟偨丅岞幃偲偟偰摉慠抦偭偰偄側偗傟偽偄偗側
丂丂丂丂丂偄偙偲傑偱僋僪僋僪偲婰弎偝傟偰偄偰旀傟傑偟偨両暥復検偺妱傝偵寁嶼検偼嬌抂偵
丂丂丂丂丂彮側偄偱偡丅
戞俀栤丂倣傪倣亜侾傪枮偨偡掕悢偲偟丄俥乮倶乯亖俁(x亅侾乯乮倶亅倣乯偲偡傞丅傑偨丄
俽乮倶乯亖佺0x 俥乮倲乯倓倲 偲偡傞丅娭悢 倷亖俥乮倶乯 偲 倷亖俽乮倶乯 偺僌儔僼偺娭學偵偮偄偰峫偊偰傒
傛偆丅
乮侾乯倣亖俀偺偲偒丄偡側傢偪丄俥乮倶乯亖俁(x亅侾乯乮倶亅俀乯偺偲偒傪峫偊傞丅
乮鶣乯丂俥乫乮倶乯亖侽 偲側傞 倶 偺抣傪媮傔傛丅
乮鶤乯丂俽乮倶乯傪寁嶼偟丄俽乮倶乯偺嬌戝抣丄嬌彫抣偍傛傃偦偺偲偒偺 倶 偺抣傪媮傔傛丅
乮鶥乯丂俥乮俁乯偺婔壗妛揑堄枴傪摎偊傛丅
乮夝乯乮鶣乯丂俥乫乮倶乯亖俁(x亅侾亄倶亅俀乯亖俁乮俀倶亅俁乯亖侽丂傛傝丄丂倶亖俁/俀
乮鶤乯丂俽乮倶乯亖佺0x 俁(倲亅侾乯乮倲亅俀乯倓倲亖俁佺0x 乷(倲亅侾乯2亅乮倲亅侾乯乸倓倲
丂丂亖俁乵(倲亅侾乯3/俁亅乮倲亅侾乯2/俀乶0x
丂丂亖俁乮(倶亅侾乯3/俁亅乮倶亅侾乯2/俀亄俆/俇乯亖倶3亅乮俋/俀乯倶2亄俇倶
丂俽乫乮倶乯亖俁倶2亅俋倶亄俇亖俁乮倶亅侾乯乮倶亅俀乯亖侽丂傛傝丄倶亖侾丄俀
丂偙偺偲偒丄倶亖侾偱俽乮倶乯偼嬌戝偱丄嬌戝抣俽乮侾乯亖俆/俀
丂倃亖俀偱俽乮倶乯偼嬌彫偱丄嬌彫抣俽乮俀乯亖俀
乮鶥乯丂俥乮俁乯亖俇丂偱丄俽乫乮俁乯亖俇丂側偺偱丄俥乮俁乯偺抣偲堦抳偡傞偺偼丄娭悢 倷亖俽乮倶乯 偺僌
丂儔僼忋偺揰(俁丆俽乮俁乯)偵偍偗傞愙慄偺孹偒偵摍偟偄丅丂丂乮廔乯
乮俀乯丂侽亝倶亝侾偺斖埻偱丄娭悢 倷亖俥乮倶乯偺僌儔僼偲 倶 幉偍傛傄 倷 幉偱埻傑傟偨恾宍偺柺愊
丂傪俽1丄侾亝倶亝倣 偺斖埻偱丄娭悢 倷亖俥乮倶乯 偺僌儔僼偲 倶 幉偱埻傑傟偨恾宍偺柺愊傪 俽2
丂偲偡傞丅
乮鶣乯丂俽1丄俽2 傪幃偱昞偟丄俽1亖俽2 傪娙扨偵偣傛丅
乮鶤乯丂俽1亖俽2 偑惉傝棫偮傛偆側俥乮倶乯偵懳偡傞娭悢 倷亖俽乮倶乯 偺僌儔僼偺奣宍傪媮傔傛丅
乮鶥乯丂俽1亜俽2 偑惉傝棫偮傛偆側俥乮倶乯偵懳偡傞娭悢 倷亖俽乮倶乯 偺僌儔僼偺奣宍傪媮傔傛丅
乮夝乯乮鶣乯丂俽1亖佺01 俥乮倶乯倓倶丄俽2亖亅佺1m 俥乮倶乯倓倶丂傛傝丄佺01 俥乮倶乯倓倶亖亅佺1m 俥乮倶乯倓倶
丂側偺偱丄丂佺0m 俥乮倶乯倓倶亖侽
乮鶤乯丂俽1亖俽2 偑惉傝棫偮偲偒丄丂俽乮倣乯亖侽丂偱丄偐偮丄丂俽乮侽乯亖侽
丂傛偭偰丄俽乮侽乯亖侽偱丄侽亝倶亝侾偱俽乮倶乯偼憹壛偟丄侾亝倶亝倣偱俽乮倶乯偼尭彮偟丄俽乮倣乯亖侽
丂偲側傝丄倣亝倶偱俽乮倶乯偼憹壛偡傞丅
乮鶥乯丂俽1亜俽2 偑惉傝棫偮偲偒丄侽亙倶丂偵偍偄偰丄俽乮倶乯亜侽丂偱偁傞偺偱丄
丂俽乮侽乯亖侽偱丄侽亝倶亝侾偱俽乮倶乯偼憹壛偟丄侾亝倶亝倣偱俽乮倶乯偼尭彮偟丄倣亝倶偱俽乮倶乯偼憹壛
偡傞丅丂丂乮廔乯
乮俁乯丂娭悢 倷亖俥乮倶乯 偺僌儔僼偺摿挜偐傜娭悢 倷亖俽乮倶乯 偺僌儔僼偺摿挜傪峫偊偰傒傛偆丅
乮鶣乯丂娭悢 倷亖俥乮倶乯 偺僌儔僼偼丄偁傞捈慄 倶亖倠 偵娭偟偰懳徧偱偁傞丅倠偺抣傪媮傔傛丅
乮鶤乯丂偡傋偰偺惓偺幚悢倫偵懳偟偰丄佺1-p1 俥乮倶乯倓倶 亖佺倣値 俥乮倶乯倓倶 偑惉傝棫偮傛偆側 値
丂丂偺抣傪媮傔傛丅
乮鶥乯丂俵亖倠偲偍偔偲丄侽亙倯亝俵亅侾 偱偁傞偡傋偰偺幚悢 倯 偵懳偟偰丄
丂丂丂佺M-倯M乮亅俥乮倶乯乯倓倶 亖佺MN 乮亅俥乮倶乯乯倓倶 偑惉傝棫偮傛偆側俶偺抣傪媮傔傛丅
乮鶦乯丂乮鶤乯丄乮鶥乯傪寁嶼偟丄摍幃傪嶌傟丅
乮鶧乯丂乮鶦乯偐傜丄偡傋偰偺惓偺幚悢倫偵懳偟偰丄俀揰乮侾亅倫丆俽乮侾亅倫乯乯丄乮倣亄倫丆俽乮倣亄倫乯乯
丂丂傪寢傉慄暘偺拞揰偵偮偄偰尵偊傞偙偲傪婰弎偣傛丅
乮夝乯乮鶣乯丂倠亖乮倣亄侾乯/俀
乮鶤乯丂値亖倣亄倫
乮鶥乯丂俶亖俵亄倯
乮鶦乯丂佺1-p1 俥乮倶乯倓倶 亖佺倣倣亄倫 俥乮倶乯倓倶丂丄佺M-倯M乮亅俥乮倶乯乯倓倶 亖佺M俵+q 乮亅俥乮倶乯乯倓倶
丂傛傝丄
丂俽乮侾乯亅俽乮侾亅倫乯亖俽乮倣亄倫乯亅俽乮倣乯丂丄俽乮俵亅倯乯亅俽乮俵乯亖俽乮俵乯亅俽乮俵亄倯乯
偡側傢偪丄丂俽乮侾亅倫乯亄俽乮倣亄倫乯亖俽乮侾乯亄俽乮倣乯
丂俀俽乮俵乯亖俽乮俵亅倯乯亄俽乮俵亄倯乯
丂偙偙偱丄倯亖俵亅侾丂偲偍偔偲丄丂俀俽乮俵乯亖俽乮侾乯亄俽乮俀俵亅侾乯亖俽乮侾乯亄俽乮倣乯丂偱偁傞丅
乮鶧乯丂偡傋偰偺惓偺幚悢倫偵懳偟偰丄俀揰乮侾亅倫丆俽乮侾亅倫乯乯丄乮倣亄倫丆俽乮倣亄倫乯乯傪寢傉
丂慄暘偺拞揰乮乮倣亄侾乯/俀丆乮俽乮侾亅倫乯亄俽乮倣亄倫乯乯/俀乯偵偮偄偰丄
乮乮倣亄侾乯/俀丆乮俽乮侾乯亄俽乮倣乯乯/俀乯亖乮俵丆俽乮俵乯乯丂偲側傞偙偲偐傜丄拞揰偼倫偺抣偵傛傜偢
堦偮偵掕傑傝丄娭悢 倷亖俽乮倶乯 偺僌儔僼忋偵偁傞偙偲偑暘偐傞丅丂丂乮廔乯
戞侾栤丂[侾]乮侾乯丂倠亜侽丄倠亗侾偲偡傞丅娭悢 倷亖倢倧倗倠倶 偲 倷亖倢倧倗2倠倶 偺僌儔僼偵偮偄偰峫偊
丂丂丂丂傛偆丅
乮鶣乯丂倷亖倢倧倗3倶 偵偮偄偰丄倶亖俀俈 偺偲偒偺倷偺抣傪媮傔傛丅
丂丂傑偨丄倷亖倢倧倗2乮倶/俆乯 偵偮偄偰丄倷亖侾 偺偲偒偺 倶 偺抣傪媮傔傛丅
乮鶤乯丂倷亖倢倧倗倠倶 偺僌儔僼偼丄倠偺抣偵傛傜偢偁傞掕揰傪捠傞丅掕揰偺嵗昗傪媮傔傛丅
乮鶥乯丂倠亖俀丄俁丄係 偺偲偒丄倷亖倢倧倗倠倶 偲 倷亖倢倧倗2倠倶 偺僌儔僼偺奣宍傪弎傋傛丅
乮夝乯乮鶣乯丂倷亖倢倧倗3俀俈亖倢倧倗3俁3亖俁倢倧倗3俁亖俁
丂倢倧倗2乮倶/俆乯亖侾丂傛傝丄丂倶/俆亖俀丂側偺偱丄丂倶亖侾侽
乮鶤乯丂侽亖倢倧倗倠侾 傛傝丄倠偺抣偵傛傜偢丄掕揰乮侾丆侽乯傪捠傞丅
乮鶥乯丂倷亖倢倧倗倠倶 偺僌儔僼偼丄倠亖俀丄俁丄係 偺偲偒丄倶亜侽 偵偍偄偰扨挷偵憹壛偟丄掕揰乮侾丆侽乯
丂傪捠傝丄偝傜偵丄
丂倠亖俀 偺偲偒丄乮俀丆侾乯傪捠傞丅
丂倠亖俁 偺偲偒丄乮俁丆侾乯傪捠傞丅
丂倠亖係 偺偲偒丄乮係丆侾乯傪捠傞丅
丂倷亖倢倧倗2倠倶 偺僌儔僼偼丄倠亖俀丄俁丄係 偺偲偒丄倶亜侽 偵偍偄偰扨挷偵憹壛偟丄偝傜偵丄
丂倠亖俀 偺偲偒丄乮侾/俀丆侽乯丄乮侾丆侾乯傪捠傞丅
丂倠亖俁 偺偲偒丄乮侾/俁丆侽乯丄乮俀/俁丆侾乯傪捠傞丅
丂倠亖係 偺偲偒丄乮侾/係丆侽乯丄乮侾/俀丆侾乯傪捠傞丅丂丂乮廔乯
乮俀乯丂倶亜侽丄倶亗侾丄倷亜侽丂偲偡傞丅倢倧倗倶倷 偵偮偄偰峫偊傛偆丅
乮鶣乯丂嵗昗暯柺偵偍偄偰丄曽掱幃 logx倷亖俀 偺昞偡恾宍偺奣宍傪弎傋傛丅
乮鶤乯丂嵗昗暯柺偵偍偄偰丄晄摍幃 侽亙logx倷亙侾 偺昞偡椞堟偵偮偄偰弎傋傛丅
丂丂偨偩偟丄嫬奅(嫬奅慄)偼娷傑側偄傕偺偲偡傞丅
乮夝乯乮鶣乯丂logx倷亖俀 傛傝丄丂倷亖倶2丂偱丄倶亜侽丄倶亗侾偺晹暘
乮鶤乯丂侽亙logx倷亙侾 傛傝丄丂logx侾亙logx倷亙logx倶
丂傛偭偰丄丂侽亙倶亙侾丂偺偲偒丄丂侾亜倷亜倶丂偱丄倶亜侾丂偺偲偒丄丂侾亙倷亙倶丂丂乮廔乯
[俀]丂S乮倶乯傪倶偺俀師幃偲偡傞丅倶偺惍幃P乮倶乯傪S乮倶乯偱妱偭偨偲偒偺彜傪俿乮倶乯丄梋傝傪倀乮倶乯偲
丂偡傞丅偨偩偟丄S乮倶乯偲俹乮倶乯偺學悢偼幚悢偱偁傞偲偡傞丅
乮侾乯丂P乮倶乯亖俀倶3亄俈倶2亄侾侽倶亄俆丄S乮倶乯亖倶2亄係倶亄俈 偺応崌傪峫偊傞丅曽掱幃S乮倶乯亖侽
丂丂偺夝傪媮傔傛丅傑偨丄俿乮倶乯丄倀乮倶乯傪媮傔傛丅
乮夝乯丂S乮倶乯亖侽丂傛傝丄丂倶亖亅俀亇併乮係亅俈乯亖亅俀亇 倝
倝
丂幚嵺偵妱傝嶼傪偟偰丄丂俿乮倶乯亖俀倶亅侾丂丄倀乮倶乯亖侾俀丂丂乮廔乯
乮俀乯丂曽掱幃S乮倶乯亖侽 偼堎側傞擇偮偺夝兛丄兝傪傕偮偲偡傞丅偙偺偲偒丄
丂丂乽P乮倶乯傪S(x)偱妱偭偨梋傝偑掕悢偵側傞乿偙偲偲摨抣側忦審傪峫偊傞丅
乮鶣乯丂梋傝偑掕悢偵側傞偲偒傪峫偊偰傒傛偆丅壖掕偐傜丄掕悢倠傪梡偄偰丄U(x)亖倠 偲偍偗傞丅
丂丂偙偺偲偒丄偳傫側偙偲偑尵偊傞偐弎傋傛丅
乮鶤乯丂媡偵丄乮鶣乯偑惉傝棫偮偲偒丄梋傝偑掕悢偵側傞偐傪挷傋傛偆丅
丂S(x)偑俀師幃偱偁傞偐傜丄倣丄値傪掕悢偲偟偰丄U(x)亖倣倶亄値 偲偍偗傞丅
丂P乮倶乯傪S乮倶乯丄T乮倶乯丄倣丄値傪梡偄偰昞偡偲偒丄P乮倶乯傪媮傔傛丅
偙偺偲偒丄梋傝偑掕悢偵側傞偙偲傪帵偣丅丂
丂乮鶣乯丄乮鶤乯偺峫嶡偐傜丄曽掱幃 S(x)亖侽 偑堎側傞擇偮偺夝兛丄兝傪傕偮偲偒丄P乮倶乯傪S乮倶乯
偱妱偭偨梋傝偑掕悢偵側傞偙偲偲乮鶣乯偼摨抣偱偁傞丅
乮夝乯乮鶣乯丂戣堄傛傝丄丂P乮倶乯亖S(x)俿乮倶乯亄倠丂偵偍偄偰丄S乮兛乯亖S乮兝乯亖侽丂傛傝丄
丂俹乮兛乯亖俹乮兝乯亖倠丂側偺偱丄
丂P乮倶乯傪S(x)偱妱偭偨梋傝偑梋傝偑掕悢偵側傞偲偒丄俹乮兛乯亖俹乮兝乯偑惉傝棫偮丅
乮鶤乯丂媡偵丄俹乮兛乯亖俹乮兝乯偑惉傝棫偮偲偡傞丅
丂偙偺偲偒丄P乮倶乯亖S(x)俿乮倶乯亄倣倶亄値丂偵偍偄偰丄
P乮兛乯亖倣兛亄値丂丄P乮兝乯亖倣兝亄値丂偐傜丄倣兛亄値亖倣兝亄値丂懄偪丄丂倣乮兛亅兝乯亖侽
丂兛丄兝偼丄曽掱幃S乮倶乯亖侽 偺堎側傞擇偮偺夝側偺偱丄丂倣亖侽丂偲側傞丅
丂傛偭偰丄俹乮兛乯亖俹乮兝乯偑惉傝棫偮偲偒丄P乮倶乯傪S(x)偱妱偭偨梋傝偑掕悢偵側傞丅丂丂乮廔乯
乮俁乯丂倫 傪掕悢偲偟丄P乮倶乯亖倶10亅俀倶9亅倫倶2亅俆倶丄S乮倶乯亖倶2亅倶亅俀 偺応崌傪峫偊傞丅
丂丂P乮倶乯傪S乮倶乯偱妱偭偨梋傝偑掕悢偵側傞偲偒丄倫偺抣丄偍傛傃丄偦偺偲偒偺梋傝傪媮傔傛丅
乮夝乯丂S乮倶乯亖倶2亅倶亅俀亖乮倶亅俀乯乮倶亄侾乯亖侽丂偲偍偔偲丄丂倶亖俀丄亅侾
丂乮俀乯偺寢壥偐傜丄P乮倶乯傪S乮倶乯偱妱偭偨梋傝偑掕悢偵側傞偲偒丄P乮俀乯亖P乮亅侾乯
丂傛偭偰丄丂亅係倫亅侾侽亖亅倫亄俉丂傛傝丄丂倫亖亅俇
丂梋傝偼丄P乮亅侾乯亖亅乮亅俇乯亄俉亖侾係丂丂乮廔乯
丂丂埲壓丄岺帠拞両
丂丂丂丂丂丂丂丂丂丂丂丂丂丂








