第４章 母集団と標本の関係 
考えようとする資料全体を母集団という。母集団から一つ一つ抜き出してきたものの集合を
標本といい、その抜き出してきた標本の要素の個数を標本の大きさという。標本を抜き出すこ
とを標本の抽出という。
標本の分布から全体を推定しようというのが標本調査である。これに対して、もれなく資料を
集めて調べることを全数調査という。
抽出法には無作為抽出（母集団の縮図となるように乱数表などを利用）と有意抽出がある。
（問） 乱数表を利用して、５０名から無作為に５名抽出せよ。
今、母集団（ｘｋ が ｆｋ 個（１≦ｋ≦ｎ）ある）を考える。Ｎ＝Σｋ=1〜ｎ ｆｋ とする。
この母集団から１個抜き出して、そのときの値を確率変数Ｘとすると、Ｘの確率分布は、
|
このとき、この分布を母集団分布という。また、Ｅ（Ｘ）を母平均、σ（Ｘ）を母標準偏差という。
母集団から毎回元に戻しながら資料を１個ずつ取り出すことを復元抽出といい、元に戻さ
ずに１個ずつ取り出すことを非復元抽出という。
定理 母集団に属する資料の個数Ｎが大きく、かつ抽出された無作為標本の大きさがＮ
に比べて小さいときは、すべて復元抽出と見なしてよい。
大きさ ｎ の無作為標本を Ｘ1、Ｘ2、・・・、Ｘｎ とする。これらは全て独立な確率変数である。
＝（Ｘ1＋Ｘ2＋・・・＋Ｘｎ）/ｎ を標本平均という。 も１つの確率変数である。
≪公式≫ 母集団の平均をｍ、標準偏差をσとすると、標本平均 について、
Ｅ（）＝ｍ 、σ（）＝σ/√ｎ
が成り立つ。
（問） 箱の中に製品が多数入っていて、その中の不良品の割合が１/６である。この箱の中
から無作為に３０個の製品を抽出する。このとき、ｋ番目に抽出された製品が不良品な
ら１、良品なら０の値を対応させる確率変数をＸｋとする。標本中の不良品の割合を表す
ことになる標本平均の期待値と標準偏差を求めよ。
（問） 上の（問）で、標本平均の標準偏差が０．０５以下とするためには、箱の中から抽出さ
れる標本の大きさ ｎ は少なくともどれくらい必要か。
第５章 平均の推定
一般に次のことが知られている。
母平均 ｍ、母標準偏差 σ の母集団から抽出された大きさ ｎ の無作為標本の標本平均
は、ｎ が十分大きいとき、正規分布Ｎ（ｍ，σ2/ｎ）に従うものと見なせる。
母平均の推定
母標準偏差が既知のとき、 Ｐ（ｍ−２σ/√ｎ≦≦ｍ＋２σ/√ｎ）＝０．９５
すなわち、 Ｐ（−２σ/√ｎ≦ｍ≦＋２σ/√ｎ）＝０．９５ から、
ｍが、区間[−２σ/√ｎ，＋２σ/√ｎ]に入ることは９５％の確からしさで起こるから、
区間[−２σ/√ｎ，＋２σ/√ｎ] を信頼度９５％の信頼区間という。
同様に、区間[−３σ/√ｎ，＋３σ/√ｎ] を信頼度９９％の信頼区間という。
（注意） 母標準偏差は未知の場合が多い。その場合は標本の標準偏差を代用する。
（例） ある店に入荷してある砂糖の袋の中から、１００個を無作為に抽出して重さを量った
ところ、平均が２９７．４ｇであった。重さの母標準偏差を７．５ｇとして、この店に入荷し
てある砂糖の１袋あたりの重さを、信頼度９５％で推定してみよう。
ｎ＝１００、＝２９７．４、σ＝７．５ より、 ２σ/√ｎ＝１．５ なので、信頼度９５％
の信頼区間は、[２９５．９，２９８．９]となる。
（問） 上記の（例）について、信頼度９９％で推定
練習問題
１．１８歳の男子４００人の身長を測って、平均１６８．８ｃｍ、標準偏差６．５ｃｍを得た。この
結果より、日本全体の１８歳男子の平均身長を９５％の信頼度で推定せよ。
２．胸囲の標準偏差が４．６ｃｍのとき、胸囲の平均を±０．４ｃｍの誤差の範囲で求めるに
は、何人について調査を行うとよいか。９５％の信頼度で考えよ。
３．ある清涼飲料水入りの瓶４０本について、Ａ成分の含有量を調査したところ、平均値が
３２．５ｍｇ、標準偏差が３．１ｍｇとなった。この清涼飲料水１瓶当たりのＡ成分の含有量
を９５％の信頼度で推定せよ。
４．期末テストで、あるクラス５０名から無作為に９名抽出してみたら、平均点が４０点、標準
偏差が３点であった。この結果から、クラスの平均点を９９％の信頼度で推定せよ。
第６章 検定
母集団の特性を表すある数値について、１つの仮説が立てられているとき、標本から得ら
れた数値によって、その仮説を棄てるべきかどうかを判断することを検定という。
例えば、今１個のさいころを７２０回投げたとき、１の目が６０回しか出なかった。このさい
ころは正しいさいころと言えるだろうか。ただし、正しいさいころとは、どの目の出る確率も
１/６であるものをいう。
常識的に考えて、このさいころは正しくないと思われる。このことを数学的に示すのが検
定の問題である。この検定の手法は、真実でないことを立証する反証の論理である。
ところで、正しい、正しくないの判断を下すには、ある基準を設定しておかなければならな
い。それを棄却域という。上記の例について検定の手順を示す。
（手順１） 仮説の設定、すなわち、次の命題を真とする。
Ｈ ： このさいころは正しいさいころである。
すると、１の目が出る確率は、１/６ となり、１の目の出る回数をＸとすると、Ｘは
２項分布Ｂ（７２０，１/６）に従うことになる。さらに、近似的に、正規分布Ｎ（１２０，１００）
に従うものと見なせる。
よって、 Ｚ＝（Ｘ−１２０）/１０ とおくと、Ｚは標準正規分布Ｎ（０，１）に従う。
（手順２） 棄却域の設定
確率Ｐ（｜Ｚ｜＞ｋ）≦０．０５ となるとき、｜Ｚ｜＞ｋ を危険率５％の棄却域という。
正規分布表より、Ｐ（１．９６）＝０．４７５ なので、危険率５％の棄却域は、｜Ｚ｜＞１．９６
（手順３） 検定
Ｘ＝６０ より、 ｜Ｚ｜＝６＞１．９６
よって、Ｘ＝６０は棄却域を満たすので、仮説Ｈは棄てられる。
従って、このさいころは、危険率５％で正しくないと判断される。
すなわち、「さいころは正しい」という仮説のもとで、Ｘ＝６０となる確率は非常に小さく０．０５
以下である。従って、その仮説の下では、非常に起こりにくいことが起こったということで、仮
説は間違いと判断し棄てるのである。そのときの判断基準が棄却域である。しかし、もしかし
たらその仮説は正しいかもしれない。仮説を棄てる危険率が５％ということである。
（注意） 危険率のことを有意水準ともいう。
（追記） 当ＨＰがいつもお世話になっているＨＮ「よおすけ」さんから、上記の類題をご紹介
頂きました。（平成２６年７月１９日付け）
一つのさいころを１２０回投げたところ、１の目が２８回出た。このさいころは異常であると
言えるか。有意水準５%で検定せよ。（出典：数学ワンポイント36 平均値の統計 ｐ．１１２）
書籍では「１の目が２７回」とありましたが、ここでは２８回としました。以下、略解です。
両側検定を行う。
正常なさいころであれば、１の目が出る確率は、１/６ 、母比率 ｐ0＝１/６ であり、標本
調査 ｔ ：
ｔ＝{(x/ｎ)−ｐ0}/{(√(ｐ0(１−ｐ0))/ｎ} ※ ｎ：標本の大きさ、ｘ：回数
の値を計算すると、
|t|＝{(28/120)−(1/6)}/{(√(1/6)(1-1/6))/120}＝４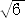
/５＝1．959591･･＜1．96
したがって、異常であるとは認められない。
計算前は「このさいころは異常だろう」と思って標本調査 t の値を計算したら、「異常では
ない」という結果になって、がっかりしたのを覚えています。淡い期待でした！
（コメント） 私も、よおすけさんのさいころを検定してみた。
「仮説 Ｈ ： このさいころは正しいさいころである。」とする。
１の目の出る回数をＸとすると、Ｘは、２項分布Ｂ（１２０，１/６）に従うことになる。さらに、近
似的に、正規分布Ｎ（２０，５０/３）に従うものと見なせる。
よって、 Ｚ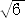＝（Ｘ−２０）/１０ とおくと、Ｚは標準正規分布Ｎ（０，１）に従う。
正規分布表より、Ｐ（１．９６）＝０．４７５ なので、危険率５％の棄却域は、｜Ｚ｜＞１．９６
である。ここで、 Ｘ＝２８ より、 ｜Ｚ｜＝４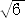/５＝１．９５９５９２・・・＜１．９６
よって、Ｘ＝２８は棄却域を満たさないので、仮説Ｈは棄てられない。すなわち、
有意水準９５％で、よおすけさんのさいころは正しいと判断される。
検定の数値から、仮説を棄てる、棄てないのぎりぎりの判断になるんですね！よおすけさん
が期待するのも理解できます。
練習問題
１．７月の期末テストで、３年生全体の平均点は、５６．３点であった。ところで、あるクラスの
生徒から２０名を抽出すると、その平均点は、５８．６点、標準偏差は、１２．５点であった。
この場合、このクラスの平均点は３年全体のうちで高い方であると判断してよいか。危険率
５％で検定せよ。
２．全国模試で、ある高校の数学の受験生は８８名で、平均点は５５．１点であった。全国平
均は、４９．８点、標準偏差は、２２．７点であったとすれば、この高校の成績は全国平均に
比べて特に差があると言えるか。危険率５％で検定せよ。