| �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ |
||||||
| �O�O�P | �����P�T�N�x�O�� | ������w | ���Ȍn | �E�E�E | �O�p���i���w�U�j | ���� |
�@�~���� �� �́A�R�D�O�T ���傫�����Ƃ��ؖ�����B
���̖��́A�������̈ӕ\��˂������ł͂Ȃ��������낤���H���A�J�Ԃł��b��
�ɂȂ��Ă���B�V�w�K�w���v�̂ł́A�~�����́A�R�@�Ƃ��Čv�Z���Ă��悢�Ƃ���Ă��邪�A
�u�~�����́A����ς�@�R�@���傫����ˁI�v�Ƃ������傩��̃��b�Z�[�W�ł͂Ȃ����Ƃ�
���������������ł���B
�@�~���� �� ���R�D�P�S�P�T�X�E�E�E�@�Ƃ����m�������Ȃ��ꍇ�́A�S���̂���グ��Ԃ�������
���Ɛ��@�����B�́A�c��`�m��w�ŁA�ΐ��̒�`��₤��肪�o�肳�ꂽ���A���ȏ���
�x���̓��e�ɂ��ւ�炸�A�s�ӂ����ꂽ���͌˘f�����炵���B
�i�⑫�j�@�您�����l����̏��ɂ��ƁA���w���i1963�N�j���o��Ƃ̂��ƁB�����҂͑S�̂�23���������Ƃ��B
�@�@���N�ɁA�ȉ��̖����o�肳��Ă���Ƃ̂��ƁB
�@�@A��0�AB��0�Aa��1�Aa��0�@�̂Ƃ��A�@logaAB��logaA�{logaB���ؖ�����B
�@����������҂͑S�̂�40���������Ƃ̂��ƁB�i�����Q�O�N�V���Q�P���NjL�j
�@����̖��ɂ��Ă��A�͍��m���u����v�Ɩ�背�x����]�����Ă���悤�ɁA��
�ɂƂ��Ă͑g������ł��������Ƃ͊ԈႢ�Ȃ��B�T�����{�ɂ����������Â���w��
����荧�k����������y���݂ł���B
�@���������~���� �� �Ƃ́A�@�i�~���j�� �� �~ �i���a�j�@���Ӗ�����B
�@���������āA�~���Ƃ����Ȑ��̒������A�������琳���p�`�̎��i�����̒����j�ŋߎ�����
�Ƃ������z�������ׂA���̖��́A�قƂ�Ǐo�������̂Ǝv���Ă悢�B
�@���Ƃ��A���a �P �̉~�����������A���Z�p�`�̎��ŋߎ�����A
�@�Q�~�� �U�~�P�@���Ȃ킿�A�@�� �R
�ƂȂ�B�i���̂��Ƃ�����A�~���� �� �� �R �Ƃ���̂ɂ́A����������I�j
�@���ł́A�����茵�����A�� �R�D�O�T�@�������A�Ƃ������Ƃł���B
�i�S��������ɔ����ȁA�R�D�O�T�@�ł���I�j
�@���Z�p�`�ł́A�ߎ����Â��̂ŁA�����p�`�A���\�p�`�A���\��p�`�A�E�E�E�@�ƁA�ӂ̐���
���₵�āA���̒������A�~���� �� �ɁA�ǂ�ǂ�߂Â��悤�ɂ���悢�B
�@�����p�`���ƁA��d�����̌v�Z���ς킵���̂ŁA�p�X�I
�@���\�p�`���ƁA�������R�U���̌v�Z���ς킵���̂ŁA�p�X�I
�@���\��p�`���ƁA�������R�O���̌v�Z�Ɠ�d�����̌v�Z�̗���������ł����������A�g��
�₷�����Ȃ̂ŁA���\��p�`�̏ꍇ�ɂ��āA�� �R�D�O�T�@���������B
�i�͍��m�̉���ł��A���\��p�`�̏ꍇ�ׂĂ��邪�A�l���������]���������ŁA����́A�����
�R�D�O�T �Ƃ������r���[�Ȑ��̓����������������Ă��Ȃ��B�����ł́A�R�D�O�T�@�̓����������������
����B�j
�i���̉��j
�@���a �P �̉~���ɁA���\��p�`�����ڂ��Ă�����̂Ƃ���B���\��p�`�̈�ӂ̒�����
�w �Ƃ���ƁA�]���藝�ɂ��A �w2���P2�{�P2�|�Q�E�P�E�P�E�������R�O���� ![]()
�@![]() �@�Ȃ̂ŁA
�@�Ȃ̂ŁA![]() �� �O�D�Q�U
�� �O�D�Q�U
����āA�i�Q�j2���i�P�Q�~�j2�@���A
�@��2 �� �R�U�E�~2�@�� �R�U�E�O�D�Q�U���X�D�R�U ���i�R�D�O�T�j2���X�D�R�O�Q�T
���������āA�� �� �R�D�O�T�@�������ꂽ�B
�i���j�@���̎����͈͂Ƃ��āA�`���ł͐��w�U�ƂȂ��Ă��邪�A��L�̂悤�ɉ�����̂ŁA
�@�@�@���w�T�͈̔͂Ƃ��Ă��悢�B
(���j�@���̖��ɑ��āA�e�\���Z�̉͂��ꂼ��ł��邪�A��{�I���j�͓����ł���B
�@��X�[�~�i�[���ł́A��̉Ɠ��l�ł��邪�A�����p�`��p���Ă���_���ʔ����B
�@�����A�����_�ȉ��R���̕����̌v�Z�����Ȃ���Ȃ炸�A���́A���̌v�Z��������B
�@�܂��A���i�n�C�X�N�[���ł́A���P�Q�p�`��p���āA��������@�R�D�O�T�@�ƂȂ�悤�ɏ�肭
�@�ߎ����Ă���_���f���炵���B
�@�~�������A���w�I�ɂ�����Ǝ�舵���A �� �� �R�D�P�S �Ƃ����F�����������̂́A�Ñ�M��
�V���̃A���L���f�X�iB.C.287?�`212�j�ł���B�i�ڂ����́A���������Q�Ɓj
�@��L�̂悤�ɁA�����p�`�̎��̒�����p���ĉ~���̒������ߎ�������@�́A�A���L���f
�X�̍l�������̂��̂ł���B
�@���w�Z�~�i�[�i�f�X�R�N�S�����A�T�����j�ɂ����āA���s��w�����̏�쌒��
�����A�A�ڂ�
�u�~���� �� ���߂����āv�Ƒ肵�Ċ�e���Ă���B
�i���搶�Ƃ́A�@������ɂP����ȂȂ������Ƃ�����B���̍��A���낢����搶����A�����Ƃ��b��
�@�f���Ă����悩�����Ȃƌ�����Ă��܂��B�j
�@���w�Z�~�i�[�ɂ́A�~���� �� �̋��ߕ������낢��ڂ��Ă���A������������A��������
��₵�����́A���̐��w�Z�~�i�[�̋L�����Q�l�ɂ����̂�������Ȃ��B
�@�����A���w�Z�~�i�[�i�T�����j�ɂ́A�������낢���ߕ����ڂ��Ă���̂ŁA�Љ�����B
| �I�C���[�ɂ��A�������� | �@�͎������A���̘a�́A | �@�ł���B���Ȃ킿�A | ||
| �@ |
||||
| ���������āA | ||||
| �@ |
||||
| ���̂��Ƃ���A |
||||
| ���Ȃ킿�A�@�@�� �� �R�D�O�T | ||||
�i���j�@��L�̖����������������邱�Ƃ͊ȒP�Ɏ�����邪�A���̘a�����߂邱�Ƃ͓���B
�@�@�a�����߂邽�߂ɁA�P�V���I����P�W���I�����܂Ő��w�҂�Y�܂��������B�I�C���[���A
�@�@�悤�₭�A���̘a�����߂��̂́A�P�V�R�T�N�̂��Ƃł���B
| �@�����������������邱�ƁF | ||
| �@�@�@�@�@�@�@�@�@�悎�����a�� | �Ƃ����ƁA | |
| �@�@�@�@�@�@ |
||
| �@�@���������āA�������� �@�@����āA��������B |
||
| �@���������̘a�����߂邱�ƁF | |||
| �@�@�@�@�@�@�@�@�@�@�����ρ@ | �@�ƁA | ||
| �@�@�@�@�@�@ �e�C���[�W�J�@ | �@�ɂ����āA�w�̌W�����r���āA | ||
| �@�@�@�@�@�@�@ |
|||
| �@�@����āA | |||
| �@�@�@�@�@�@�@ |
|||
�i�Q�l�����F�u��_��@���@�Ɍ��̐[�݁i��g���X�j�j
�i�NjL�j�@
�@�����P�T�N�@��T�Q��@��w�������k��@�i���{���w����w��@��Áj
�@�@�i�����P�T�N�T���Q�T���i���j�j
 |
�@�@�@�@�w�K�@��w�S���N�L�O��� �@�@�@���N���܂��A�������k��̋G�߂� �@�@����Ă����B�S�n�悢�V�̒��A�w �@�@�K�@��w�ɓ��{�e�n���瑽���̕��� �@�@�W�܂�A����̒��A���N�x�̑�w�� �@�@�����ɂ��āA���낢��Ȃ��b�� �@�@�����������Ƃ��ł����B �@�@�@�o�ȑ�w�́A���̒ʂ�ł���B �@�@�@�@�@�w�K�@��w �@�@�@�@�@���k��w �@�@�@�@�@�c���`�m��w �@�@�@�@�@�������ȑ�w �@�@�@�@�@���s��w �@�@�@�@�@������w �@�@�@�@�@����c��w |
�@�e�u�t�̐搶������̂��b��v�āA���ɁA���̓_����������Ă����B
�@��w�������ɂ���āA��w�ɓ����Ă���K�v�ƂȂ鐔�w�����ł��邩��������
�@�����̓��ōl���A���͓lj�͂Ƙ_�ؗ́A�����āA�_�����ƌv�Z�͂�b���A�w�I
�C���[�W������
�@���Z����W�҂ɂƂ��ẮA�w���̉��P���K�v�Ƃ����Ƃ���ł���B
�@����̍��k��ł̒��ڂ́A��͂�u������w�@���ȁv�̖��U �ł��낤�B
�@���̖��́A�V���ɂ����グ���A���Ԉ�ʂ̒��ڂ𗁂т��B
�@�o��̈Ӑ}�́A�u�t�̌l�I�ȍl���Ƃ��āA���̂悤�Ȃ��̂ł��낤�Ƙb���ꂽ�B
�@�����������ł��镽�����́A�ߎ��l������A���̊m�����������Ŋm�F�ł��邪�A�~
�����̏ꍇ�͂����ȒP�ɂ͏o���Ȃ��B�����ŁA��������p���ĉ~������]������Ƃ����l��
���������肾�낤�Ǝv���B
�@���̂悤�Ȗ��̏ꍇ�A�́i�~�ɓ��ڂ��鐳���p�`��p���遨��������]������j��
�ł��W���I���낤�Ǝv����B��ꂩ��A�u�~�����́A�~�̖ʐς�������߂���̂ł́H�v
�Ǝ��₳�ꂽ���A�u�~���������߂Ċw�ԏ��w�Z�ł́A�^�C�����P��]�����Ăǂ��܂œ]���邩�A
�Ƃ����̌��̉��ɉ~�����Ƃ������̂𗝉����Ă���̂ŁA�~�������a�̉~�����{�ŋ��߂��
��Ƃ������Ƃ͋��ʔF�����Ǝv���B�v�ƁA�b���ꂽ�B�������A�~�̖ʐς���ߎ��l���v�Z���邱
�Ƃ����肦�邾�낤�Ǝv���Ƃ��b���ꂽ�B�܂��A�u�~�����́A�R�D�P�S�P�T�X�@�Ȃ̂ŁA���藧�B�v��
���邱�Ƃ��l�����邪�A����ɂ��āA�i�u�t�̈ӌ��Ƃ��Ắj�_�O���Ǝv���Ɗ��z���q
�ׂ�ꂽ�B
�@�܂��A���g�o�̉A�e�\���Z�̑����̉ł͐����p�`��p���Čv�Z���Ă��邪�A����
�p�`��p���Ȃ��ꍇ�Ƃ��āA���̂悤�ȕʉ����l������Ƃ̂��Ƃł���B
�i�ʉ��j�@���}�̂悤�Ȕ��a �T �̎l���~���l����B�R�ӂ̒����� �R�A�S�A�T �̒��p�O�p�`��
�@�@�@�@���}�̂悤�ɔz�u����B���̂Ƃ��A�ʂ̒����́A ![]() ���傫���B
���傫���B
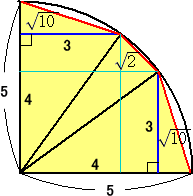 |
�@�@�@�Ƃ���ŁA �@�@�@�@�@�@�@�@�@ �@�@����āA �Q�~�~�T�~�P/�S���V�D�V�P�@���A �@�@�@�@�~���� �� ���V�D�V�P�~�O�D�S���R�D�O�W�S���R�D�O�T �@�@�����藧�B�@�i�I�j |
�@���ړI�Ɋm���߂��Ȃ����̂��A�����I�ɔc���ł�����̂�p���ĕ]������Ƃ������w��
��{��������ꂽ�悤�ȋC������B�ƂĂ������b�����Ƃ��ł��A�[�����������߂������Ƃ�
�o�����B
�i�ĒNjL�j�@�u�� �R�D�O�T�v�ł��邱�Ƃ��A��L�ł́A�����p�`�̕ӂ̒����Ɖ~���̒����̊W
�@�@�@�@����ؖ��������A�������A�����p�`�̖ʐςƉ~�̖ʐς̊W������������Ƃ��ł���B
�@�ӂ̒����ɒ��ڂ����ꍇ�́A�����p�`��\��p�`�Ȃǔ�r�I�g�߂ȑ��p�`�ŏ\������
���̂ɑ��āA�ʐςɒ��ڂ����ꍇ�́A���\��p�`�ł͏ؖ��Ɏ��s����悤�ł���B
�@�����ł́A����\�l�p�`��p���ďؖ�����B
���a���P�̉~�̖ʐς́A�� �ŁA���̉~�ɓ��ڂ��鐳��\�l�p�`�̖ʐς́A
�@�Q�S�~(�P/�Q)�������P�T�����P�Q�������P�T���ŗ^������B
���̂Ƃ��A�@�@�@���P�Q�������P�T���@�@�ł���B
�@�O�p���ɂ�������@�藝��p���āA
�@�������P�T����������(�S�T���|�R�O��) ���������S�T���������R�O���|�������S�T���������R�O���@����A
�@![]()
�����ŁA�@![]() ���P�D�V�R�Q�~�P�D�S�P�S���Q�D�S�S�X�O�S�W���Q�D�S�S�@�A
���P�D�V�R�Q�~�P�D�S�P�S���Q�D�S�S�X�O�S�W���Q�D�S�S�@�A![]() ���P�D�S�Q�@�Ȃ̂ŁA
���P�D�S�Q�@�Ȃ̂ŁA
�@���P�Q�~(�Q�D�S�S�|�P�D�S�Q)/�S���R�~�P�D�O�Q���R�D�O�U���R�D�O�T
�����藧�B
�i�Q�l�����F���c�@���@���@�������w�`���̗ǖ�P�O�O�@�i�u�k�Ёj�j
�i�NjL�j�@�����Q�O�N�P�O���P�T���t��
�@���g�o�̌f���u�o��̐�v�ɁA�P�S���t���ŁA�g�m�u�J�Y�v�����̂悤�ɏ������܂ꂽ�B
�i�������������C�������Ă��������܂����B�j
�@����A��1�̖������ʂ��m��2�N��������ŁA��L�̓���������̂��Ƃ����B�O�p
���̊�{���������ŏؖ����āA���ɋ����Ă�낤�Ƃ̑z���ŁA���ȗ��ŏؖ������Ă݂��B
�i�ؖ����@�j
(1)�@���a�� 1 �̉~�`�ɓ��ڂ��鐳�\��p�`��12�������ꂽ1�́��`�a�b���l����B���̂�
�@���A�~�ʂa�b����/6�ŁA���U�~�a�b�@�����藧�B
(2)�@���ɁA�a�b�~1/2���������P�T�����A�a�b���Q�~�������P�T���ƂȂ�̂ŁA(1)���A
�@���P�Q�~�������P�T���ƂȂ�B
(3)�@���̂Ƃ��A�������P�T�����O�D�Q�T�W�W ����
�@���P�Q�~�������P�T�����P�Q�~�O�D�Q�T�W�W���R�D�P�O�T�U���R�D�O�T�@�ƂȂ�B
(4)�@���������āA�~���� �� �́A�R�D�O�T ���傫���B
�@���̏ؖ����@�́A�u�]���藝�v�E�u���@�藝�v�����g�p���Ă��Ȃ����ƁA�������P�T���̋ߎ��l
��p�������Ƃɂ��A�v�Z���P���ŁA���ɗ������₷���Ǝv���B
�i�R�����g�j�@��L�́u�J�Y�v����̏ؖ��́A��{�I�ɍĒNjL�ŏq�ׂ��ʐϗ��p�̏ؖ��ƈ�v
�@�@����B
�@�������P�T���̒l���i�ĒNjL�j�ł͉��@�藝��p���ċ��߂����A���̐}�`��������߂���B
�@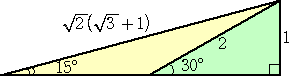
�@��}�̎Εӂ̌v�Z�ɂ́A��d�������O���v�Z�i���ȏ��ł͔��W���x���j���K�{�ł���B
���̓_�����O����A�u�J�Y�v����̏ؖ��͏\�����Z�P�N���x���ƌ�����B
�ؖ������u�J�Y�v����Ɋ��ӂ��܂��B
�i�NjL�j�@�����Q�O�N�P�P���R���t��
�@��}��p���āA�������P�T���̒l���v�Z����ꍇ�A��d�����̌v�Z�͔������Ȃ����A���}
��p����ƁA��d�����̌v�Z������ł��āA�������P�T���̒l�����߂��邱�Ƃ��A�J�Y����
�炲���������������B
�@�a���R�O���A�b���X�O���̒��p�O�p�`�`�a�b�ɂ����āA�ӂa�b��ɁA�ڂ`�c�b���S�T���ƂȂ�_�c
���Ƃ�A�_�c���ӂ`�a�ɐ����`�g�������B���̂Ƃ��A�ڂc�`�g���P�T���ł���B
�@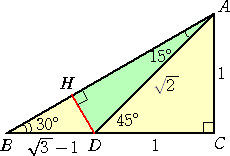
�@��}�ɂ����āA�@�c�g���i![]() �|�P�j/�Q�@�Ȃ̂ŁA�������P�T�����i
�|�P�j/�Q�@�Ȃ̂ŁA�������P�T�����i![]() �|�P�j/�Q
�|�P�j/�Q![]() ���i
���i![]() �|
�|![]() �j/�S
�j/�S
�Ƌ��߂���B
�i�R�����g�j�@�Ȗ��ɋ��߂���}�Ɋ������܂����B�J�Y����Ɋ��ӂ������܂��B
�@�܂��A�ʉ��Ƃ��āA���g�o�̌f���u�o��̐�v�ɁA�����Q�O�N�P�O���R�O���t���ŁA�g�m�u��
��v�l��蒸�������̂��Љ�����B
�@���@�藝�̏ؖ��ɗ��p�����}��p������@
�@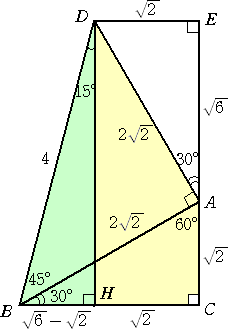
�@��}����́A�������V�T�����e�Ղɋ��߂邱�Ƃ��ł���B
�i�R�����g�j�@���̐}���ƕ���̗L�������Ȃ��̂Ōv�Z����܂ł��Ȃ��ł��ˁI �������P�T���̌v
�@�@�Z�̉��̐[�����v���m�炳��܂����I����l�Ɋ��ӂ������܂��B
�@���āA���܂ŏ����I�ȏؖ��Ƃ��ẮA������w�� �s �搶�ɂ��
�@
�Ƃ����}�`��p�����ؖ����f���炵���ƍl���Ă������A���g�o�����������b�ɂȂ��Ă���A
�炷���邳�O�p�����g��Ȃ������I�ȏؖ����l����ꂽ�̂ŏЉ�����Ǝv���B
�i�������������C�������Ă��������܂����B�j
�@�u�J�Y�v���ؖ��ɗp�������\��p�`��12�������ꂽ1�́��`�a�b���ɓ_�c��
�c�a���c�b�@�A�ڂa�c�b���X�O���ł���悤�ɂƂ�B
�@
���̂Ƃ��A�b�c���i![]() /�Q�j�a�b�@�ŁA����ɁA�ڂd�b�c���ڂa�`�b���R�O���Ȃ̂�
/�Q�j�a�b�@�ŁA����ɁA�ڂd�b�c���ڂa�`�b���R�O���Ȃ̂�
�@�b�d���i�Q/![]() �j�b�c���i
�j�b�c���i![]() /
/![]() �j�a�b���i
�j�a�b���i![]() /�R�j�a�b�@�A�c�d���i�P/�Q�j�b�d���i
/�R�j�a�b�@�A�c�d���i�P/�Q�j�b�d���i![]() /�U�j�a�b
/�U�j�a�b
�ƂȂ�B
�܂��A�@�`�d���a�d�@�ŁA�@�`�d���a�c�{�c�d���i![]() /�Q�{
/�Q�{![]() /�U�j�a�b�@���A
/�U�j�a�b�@���A
�@�`�b���`�d�{�b�d���i![]() /�Q�{
/�Q�{![]() /�U�j�a�b�{�i
/�U�j�a�b�{�i![]() /�R�j�a�b���i
/�R�j�a�b���i![]() /�Q�{
/�Q�{![]() /�Q�j�a�b
/�Q�j�a�b
�����ŁA�@�`�b���P�@�Ȃ̂ŁA�@�a�b��![]() /�Q�|
/�Q�|![]() /�Q
/�Q
�@�܂��A�@![]() ���Q�D�S�S�@�A�@
���Q�D�S�S�@�A�@![]() ���P�D�S�Q�@�Ȃ̂ŁA�@�a�b���O�D�T�P
���P�D�S�Q�@�Ȃ̂ŁA�@�a�b���O�D�T�P
���������āA�@���U�~�a�b���R�D�O�U���R�D�O�T�@�@�i�I�j
�i�R�����g�j�@���@�藝��p�����ɁA�a�b�̑傫�����]���ł���Ƃ͋����ł��I
�@�@�@�_�c�̊��p�͐��Ɂu�_�̎�v�ł��ˁB�炷���邳��Ɋ��ӂ��܂��B
�i�NjL�j�@�`�@�����P�T�i�Q�O�O�R�j�N�P�Q���Q�S���t�������V�������@�`
�@�Q�R���t������A�u�ς������@�]�@�̋���v�Ƒ肵�ē��W���n�܂����B�Q�S���t���́A����
���̐V���ȗ���Ƃ��āA�w�v�l�͂��d������X���ɂ���x���Ƃ���ɘ_�����A���̊i�D��
���Ƃ��āA���t�̓�����w�������u�~�����́A�R�D�O�T���傫�����Ƃ��ؖ�����B�v����
��グ���Ă���B
�@�����A���̋L���ɂ͌�肪����̂ŁA�����ŕ⑫���Ă��������B�����V���Ɍ����w�E����
���[���𑗂��Ă���������邱�Ƃ͂܂��Ȃ��i�ߋ��Ɍo������I�j�̂ŁA�g�o��œǎ҂̕���
�݂̂��m�点���鎟��ł���B
�@����ł́A��������u���a �P �̉~�ɓ��ڂ��鐳���p�`�������āA���̖ʐς��R�D�O�T
���傫�����Ƃ��������B�\���Z�Ŋm���߂���A�������ƌ���ꂽ�B�v�Ƃ��邪�A����́A��
�ɕs�\�Ȃ��Ƃł���B
�@�i���F�@��L�̐����p�`�̖ʐς́A�Q![]() �ŁA���悻 �Q�D�W�Q �ł���I�j
�ŁA���悻 �Q�D�W�Q �ł���I�j
�@��L�ł����������ʂ�A�ʐς�p�����ؖ��́A����\�l�p�`�ʼn\�ŁA�����p�`��\
��p�`�Ȃǂł͎��s����B
�@���̂��Ƃ́A����̏o����ł��b��ɂȂ�A�u�����p�`�ł͎�����Ȃ���ˁ`�v�ƐV���L��
�ɋ^��̐����W�������B
�@�����p�`�̕ӂ̒����ɒ��ڂ���A�ؖ��͉\�ł���B�i�Q�l�F��X�[�~�i�[������j
�@��L���̕��́A������w�ɍ��i���ꂽ�Ƃ������ƂȂ̂ŁA�P�Ȃ銨�Ⴂ�Ƃ͎v�����A
������ނ��ꂽ�����A�L���������i�K�ŁA�ӂ̒�����ʐςƌ�����ꂽ�̂ł͂Ȃ����Ɛ�
�@�����B�i�P�ʃg�b�v�L���Ȃ̂ɁA�����V���͍Z�������Ă��Ȃ��̂��낤���H�j
�@�܂�����ł́A�O�R�N�x������S���������鋳���̂��b�Ƃ��āA�u�������́A��w����
�M����ő�̃��b�Z�[�W���v�Ƃ��邪�A�����������Ɓi�H�j�ł���B���̃y�[�W�������ɂ�����
���{���w����w������̕��ɂ��낢�남���b�ɂȂ������A���̂Ƃ��̌o���Ƃ��āA�u��
�����đ�w���ǂ������S���҂𖾂炩�ɂ��邱�Ƃ͂���̂��낤���H�v�Ƃ����^��ł���B
�@�����V���̋L���ɂ��ẮA���낢��^�₪�c�邪�A���L�ɁA�����p�`�̕ӂ̒�����p
�����ؖ����L���Ă����B
�@���a �P �̉~�ɓ��ڂ��鐳���p�`�� �P �ӂ̒����� �w �Ƃ����ƁA�]���藝����A
�@�w2 �� �Q�|![]() �@
�@
�����藧�B���������āA (�W�w)2 �� �P�Q�W�|�U�S![]() �@�ł���B
�@�ł���B
�@�����ŁA�@![]() ���P�D�S�P�T�@�����藧�B
���P�D�S�P�T�@�����藧�B
���ۂɁA�@�P�D�S�P�T2 ���Q�D�O�O�Q�Q�Q�T �� �Q�@���A![]() ���P�D�S�P�T
���P�D�S�P�T
���������āA
�@(�W�w)2 �� �P�Q�W�|�U�S![]() ���P�Q�W�|�U�S�~�P�D�S�P�T���P�Q�W�|�X�O�D�T�U���R�V�D�S�S
���P�Q�W�|�U�S�~�P�D�S�P�T���P�Q�W�|�X�O�D�T�U���R�V�D�S�S
�@�����ŁA�R�V�D�S�S���R�V�D�Q�P���i�U�D�P�j2�@�Ȃ̂ŁA�@�W�w �� �U�D�P�@�ƂȂ�B
���a �P �̉~���̒����́A�~������ �� �Ƃ��āA�Q�� �ŁA���炩�ɁA�Q�� ��
�W�w
���������āA�@�Q�� �� �U�D�P�@���A�@�� �� �R�D�O�T�@�����藧�B�i�؏I�j
�i�NjL�j�@�����P�T�i�Q�O�O�R�j�N�P�Q���Q�T���t�������V�������ŁA��L�̌��Łu�����v���o�Ă����B
�@��͂�A���́A�����p�`�ł͌v�Z���Ă��Ȃ������B���g�o�ɂ�����̂Ɠ��l�ɐ���\�l
�p�`�̖ʐς�p���Ď������Ƃ����B���{�l��������̐\�����ꂪ�������̂��낤�B
�i�NjL�j�@�����Q�Q�N�Q���U���t��
�@�Q���S���t���ŁA�s�D�j�D����A��L�ł�����ꂽ����̏ؖ��ł��Ȃ��A���A���ȒP
�ȏؖ��Ƃ������̌��o���ꂽ�Ƃ������ƂŁA���[���������������̂ŏЉ�����B
�@�ȉ��̏ؖ��@���g���A���w�R�N���̒m���i�O�����̒藝�ƕ������j�ŏؖ��ł���Ƃ�
���Ƃł���B�i�ꕔ���������C�������Ă��������܂����I�j
�i�ؖ��j
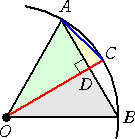 |
�@�@�~�n�̔��a�� �� �Ƃ��A���SO��ʂ�A�~���Ƃ`�A�a�Őڂ��鐳�O�p�` �@��`���B �@�@���̂Ƃ��A�����`�a�͉~�ɓ��ڂ��鐳�U�p�`�̂P�ӂł���B����ɁA �@�`�a�̒��_�ƁAO��ʂ钼���������A�~�Ƃ̌�_���b�Ƃ���B �@�@�`�b�͉~�ɓ��ڂ��鐳�P�Q�p�`�̂P�ӂł���B ���̒��������Ƃ���B |
�@���m�̉~�������ƒu�����Ƃ��A�~���̒����́A�Q�� �ł���B�܂��A���P�Q�p�`�̊O���́A
�P�Q���ł��邪�A���炩�ɁA�P�Q�����Q���@���A�U��/�����@�Ȃ̂ŁA
�@�R�D�O�T���U��/���@���ؖ�����悢�B
�@�`�a�Ƃn�b�̌�_���c�Ƃ���B���`�n�c�͒��p�O�p�`�ł���AAO�����@�A�`�c����/�Q�@�Ȃ̂ŁA
�n�c��![]() ��/�Q�@�ł���B�@����āA�@�b�c���i�Q�|
��/�Q�@�ł���B�@����āA�@�b�c���i�Q�|![]() �j��/�Q�@�ł���B
�j��/�Q�@�ł���B
�@���`�b�c���܂����p�O�p�`�ŁAAD����/�Q�@���A�@��2���`�b2���i�Q�|![]() �j��2�@�ƂȂ�B
�j��2�@�ƂȂ�B
������A�@�i�U��/���j2���R�U�i�Q�|![]() �j�@�ƂȂ�̂ŁA�@�i�R�D�O�T�j2���R�U�i�Q�|
�j�@�ƂȂ�̂ŁA�@�i�R�D�O�T�j2���R�U�i�Q�|![]() �j�@��������
�j�@��������
�悢���ƂɂȂ�B
�@�P�D�V�R�Q��![]() ���P�D�V�R�R�@�Ȃ̂ŁA�@�O�D�Q�U�V���Q�|
���P�D�V�R�R�@�Ȃ̂ŁA�@�O�D�Q�U�V���Q�|![]() ���O�D�Q�U�W
���O�D�Q�U�W
�����ŁA�@�i�O�D�T�P�j2���O�D�Q�U�O�P�@�A�@�i�O�D�T�Q�j2���O�D�Q�V�O�S�@�Ȃ̂ŁA
�@�@�i�O�D�T�P�j2���Q�|![]() ���i�O�D�T�Q�j2
���i�O�D�T�Q�j2
�@���Ȃ킿�A�@�U�~�O�D�T�P���U��/�����U�~�O�D�T�Q�@���A�@�R�D�O�U���U��/�����R�D�P�Q
�@�ȏォ��A�@�R�D�O�T���U��/���@���A�@�R�D�O�T���@�������ꂽ�B�@�i�؏I�j
�i�R�����g�j�@�s�D�j�D����A�����I�ŊȖ��ȏؖ������肪�Ƃ��������܂��B�ؖ��̕������͖`��
�@�@�@�@�ɂ����i���̉j�Ɠ�������ł��ˁB
�@�s�D�j�D����ɂ��A�u���̖��̓A���L���f�X�����X�U�p�`����~�������ߎ������j����
�m���Ă���A���z�ł�����̂Ǝv����v�Ƃ̂��ƂŁA��@���̂��̂͒P���ō��Z���w�Ȃ�
�K�v�Ȃ���w�����Ƃ��Ă͂ӂ��킵���Ȃ��悤�Ɏv���邪�A���҂́A�w���ɁA���w�̔\��
�����łȂ��A���w�j�ɂ��Ă��m���Ă��ė~�����ƍl�����̂ł͂Ȃ����Ƒz�����Ă���Ƃ̂��ƁB
�@�e�m���A��L�Ɋ֘A��������o�肳��܂����B�i�����Q�S�N�P���R���t���j
�@�~�������Ƃ���Ƃ��A���̕s�������ؖ�����B
| (A0)�@���R | �@ | (B0)�@���S |
| (A1)�@���R�D�O�P | (B1)�@���R�D�T | |
| (A2)�@���R�D�O�T | (B2)�@���R�D�Q | |
| (A3)�@���R�D�P | (B3)�@���R�D�P�T | |
| (A4)�@���R�D�P�S | (B4)�@���R�D�P�S�R |
�@�g���Ă����̂́A�̒�`�A�������a�P�̉~�̉~�����Q�ł��邱�ƂƔ��a�P�̉~�̖ʐ�
���ł��邱�Ƃ����Ƃ��܂��B(�ł���̒�`�����ɂ�����������͉\�ł��傤���H)
�@(A)�̕��́A�~�ɓ��ڂ��鑽�p�`(���ʂ͐����p�`)���l���āA���̎��̒������Q��菬
�������Ƃ���ؖ�����̂����ʂł��傤�B(B)�̕��́A�~�ɊO�ڂ��鑽�p�`���l���Ă��̖�
�ς����傫�����Ƃ���ؖ�����Ǝv���܂��B(�O�ڑ��p�`�̎��̒������~����蒷����
�Ƃ̏ؖ����ł���Ύ��̒����ł���)
�@�ǂ̂悤�ȓ��ڑ��p�`�A�O�ڑ��p�`���Ƃ��Ă��邩�Ƃ������ƂƁA���̎��̒����A���邢��
�ʐς��ǂ̂悤�ɕ]�����邩�Ƃ������ƂɂȂ�܂��B�ア�s�����ɂ��Ă͊ȒP�ȕ��@�ŁA
�����s�����ɂ��Ă͂�萸���ȕ��@�Ŏ������ƂɂȂ�܂��B
�@(A0)�͓��ڐ��Z�p�`�ŁA(B0)�͊O�ڐ����`�łł��܂�����A���w���̃��x���ł��B��v
�Z�łȂ��ƈӖ����Ȃ��ł����A(A4)(B4)����v�Z�ł��͓̂���̂ł͂Ȃ����Ǝv����
���B
�@(A2)�́A�`���̖��ł�����A����͂��������Ƃ��܂��B(A1)(A3)(B1)(B2)(B3)�ɂ��čl
���Ă݂Ă��������B
�@�Ⴆ�A(B1)�̉��Ƃ��ẮA(B1)�͏ؖ��ł��邪�A(B2)�͏ؖ��ł��Ȃ����x�̂��̂��]��
�����ł��B
�@�Ƃ���ŁA���傪�u�R�D�O�T�v�Ƃ��ďo�肵�����Ƃɂ��čl���Ă݂܂��B���ʂȂ�u�R�D�P�v��
�o�肵�����Ȃ��̂ł��B��������ƕ��@�����肳��邱�Ƃ��甽���������̂ł��傤�B���l
�Ȕ��z�ɂ��A���낢��ȉ��~���������Ƃ������Ƃł��傤���B
�@����Ȃ�A�u�R�D�O�P�v��u�R�D�O�Q�v���ł��悩�����͂��ł��B���̕����̕��͍L�����
���B�u�R�D�O�P�v����u�R�D�P�v�܂ł��낢�댟�����������ŁA�����ڂ��l���ɓ���āu�R�D�O�T�v��
�Ȃ����Ƃ������Ƃł��傤�B
�i�R�����g�j�@�ŋ߁A���̘b��ɐG���@�����܂����B�^�\���Z�ł́A
�@�~�����́A�R�D�P�P���傫�����Ƃ��ؖ�����B
�Ƃ����`�ʼn��K���Ă��邻���ł��B���̖��́A�e�m����̕��ށF�`�n��ɑ�������ł��ˁI
�i���j�@���a�P�̉~�ɓ��ڂ��鐳�Q�S�p�`���l����B���̎��̒������k�Ƃ���ƁA
�@�k���Q�S�~�Q������(��/�Q�S)���S�W������(��/�Q�S)
�����ŁA�@�Q������2(��/�Q�S)���P�|������(��/�P�Q)�@�ŁA����ɁA
�@�Q������2(��/�P�Q)���P�{������(��/�U)���i�Q�{![]() �j/�Q���i
�j/�Q���i![]() �{�P�j2/�S�@���A
�{�P�j2/�S�@���A
�@������(��/�P�Q)���i![]() �{�P�j/�Q
�{�P�j/�Q![]() ���i
���i![]() �{
�{![]() �j/�S
�j/�S
����āA�@�W������2(��/�Q�S)���S�|![]() �|
�|![]() �@���A
�@���A
�@�k2���S�W2������2(��/�Q�S)���Q�W�W�i�S�|![]() �|
�|![]() �j
�j
![]() ���P�D�S�P�S�R�@�A
���P�D�S�P�S�R�@�A![]() ���P�D�V�R�Q�P�@�Ȃ̂ŁA
���P�D�V�R�Q�P�@�Ȃ̂ŁA![]() ���Q�D�S�S�X�W�@�ł���B
���Q�D�S�S�X�W�@�ł���B
�@���̂Ƃ��A�@�k2���Q�W�W�~�O�D�P�R�T�X���R�X�D�P�R�X�Q
�@�����ŁA�@�i�Q�~�R�D�P�P�j2���R�W�D�U�W�W�S�@�Ȃ̂ŁA�@�k2���i�Q�~�R�D�P�P�j2�@����A
�@�k���Q�~�R�D�P�P�@�ŁA�@�Q���k�@����A�@���R�D�P�P�@�@�i�I�j
�i�R�����g�j�@��L�ł́A���a�P�̉~�ɓ��ڂ��鐳�Q�S�p�`�̎��̒�����]���������A���a��
�@�@�@�P�̉~�ɓ��ڂ��鐳�Q�S�p�`�̖ʐςɒ��ڂ����ꍇ�̕]�����́A
�@���R�i![]() �|
�|![]() �j
�j
�ł���B���̏ꍇ�A![]() �A
�A![]() �̏����_�ȉ����S�����x�̕]���ł́A�u���R�D�P�P�v����������
�̏����_�ȉ����S�����x�̕]���ł́A�u���R�D�P�P�v����������
�͍���Ȃ悤�ł���B�ړI��B�����邽�߂ɂ́A�A![]() �A
�A![]() �ɂ��āA��茵�����]�����K�v
�ɂ��āA��茵�����]�����K�v
�ł���B
�@�e�m����̃R�����g�ł��B�i�����Q�S�N�P���S���t���j
�@�����p�`�łȂ����p�`���l���邱�Ƃ́A(1)���x��������@(2)����(or�ʐ�)�𐳑��p�`��
��1�ł����̂ɕ��ʂ�2�ȏ�v�Z���Ȃ���Ȃ�Ȃ����Ƃ��烁���b�g�͂Ȃ��Ǝv���܂��B
���܂�Ӗ��͂Ȃ��Ǝv���܂����A�ア�s�����Ȃ�ؖ��ł��Ȃ����Ƃ��Ȃ��̂ŁA(A1)(B1)��
�����p�`�łȂ����p�`�ł���Ă݂܂����B
�@�i�ʉ��j�ɂ���悤�ɁA���a�T�̎l���~���l���āA���̎���ɂQ�_(3�C4)�A(4�C3)������Ă�
��̂��A1�_(3�C4)�������Ƃ�B�i�ʉ��j�́A���łȂ�12�p�`���l���Ă���̂����A����ł�
(A2)���ؖ��ł��Ă��܂��̂ŁA�キ���邽�߂ɐ��łȂ�8�p�`���l����Ƃ������Ƃł���B����
�Ƃ��Q�{�̌��̒����́A��10+2��5�ł���B����̂Q�{���A�u�R�D�O�P�v���傫�����Ƃ�������
�悢�B��10���R�D�P�A��5���Q�D�Q �ł͏ؖ��ł��Ȃ�((A0)�����łȂ�)���A��10���R�D�P�T
���炢
�ɂ��Ă����ł���B
�@(B1)�����a�T�̎l���~ ��2+��2=25�@(����0�A����0)���l���A����̂Q�_(3�C4)�A(4�C3)�������
�����ł̐ڐ����l���Ăł��邩�Ǝv������c�O�Ȃ��炿����Ƒʖڂł����B���R�D�U�Ȃ�o
�܂��B���傤���Ȃ�����A��2+��2=169 ���l���āA����̂Q�_(5�C12)�A(12�C5)������āA������
�̐ڐ����l������ł��܂����B���łȂ����p�`���l����̂͂��܂�Ӗ����Ȃ��Ǝv���܂��B
�@���a1�̉~�ɓ��ڂ��鐳n�p�`�̎��̒����́A2nsin(��/n)
�@���a1�̉~�ɓ��ڂ��鐳2n�p�`�̖ʐς́Ansin(��/n)
�@���a1�̉~�ɊO�ڂ��鐳n�p�`�̎��̒����́A2ntan(��/n)
�@���a1�̉~�ɊO�ڂ��鐳n�p�`�̖ʐς́Antan(��/n)
�]���āA�@nsin(��/n)����ntan(��/n)
(����́A0��x����/2�̂Ƃ��Asin �� �� �� ��tan �� �� �� �ɁA��/n �������āA���{��������)
�@�����p�`�ōl����Ƃ������Ƃ́A����K���ɂƂ��āAnsin(��/n)��ntan(��/n)��K���ɕ]��
���悤�Ƃ������Ƃł���B���Ƃ��ẮA�Q�̗ݏ悩����ɂR�����������̂����l���Ȃ����낤�B
�@4�A8�A16�A32�A64�A����@�܂��́@6�A12�A24�A48�A96�A���
�@�����Ȃ獪�����J�����Ƃ��ł���Η��_��v�Z�\�ł���B���_��Ȃ�A�T�p�`��P�V�p
�`�������������ŋ��߂邱�Ƃ��ł��邪�������Ȃ��Ƃ͂���͂����Ȃ��B
�@�ؖ��͎�v�Z�łȂ��ƈӖ��Ȃ����A������ƃJ���j���O������ nsin(��/n) ��
ntan(��/n) ��
�l���G�N�Z���Ƃ��Œ��ׂĂ����Ƃ����ł��傤�B
| �� | nsin(��/n) | ntan(��/n) |
| �S | 2.828427125 | 4 |
| �U | 3 | 3.464101615 |
| �W | 3.061467459 | 3.313708499 |
| �P�Q | 3.105828541 | 3.215390309 |
| �P�U | 3.121445152 | 3.182597878 |
| �Q�S | 3.132628613 | 3.159659942 |
| �R�Q | 3.136548491 | 3.151724907 |
| �S�W | 3.139350203 | 3.146086215 |
| �U�S | 3.140331157 | 3.144118385 |
| �X�U | 3.141031951 | 3.1427146 |
�@���������A�ؖ��̕��j��������x���܂�܂��B�������A�K������ �� ���������قnjv�Z
���₷���Ƃ͌���܂���B�Ⴆ�Asin(��/8)�́A2�d���������ǁAsin(��/12)�́A2�d�����ł�
�Ȃ����B
�@�u���R�D�P�P�v�̏ؖ��ŁAn=16�ł͂Ȃ���n=24���g���Ă��܂��Bn=16�Ȃ�3�d�����An=24�Ȃ�
2�d����������Ƃ������ƂƂ��킹�āA3.1326���>3.11�̕����A3.1214���>3.11���y�Ȃ͂���
�Ƃ������Ƃ���Ó��ȂƂ���ł��傤�B
�@�U���@���A(A2) ���R�D�O�T�@���ؖ�����܂����B�i�����Q�S�N�P���T���t���j
�i���@���̂P�j�@���P�O�p�`�A���Ȃ킿�A��=10�@���l����B
�@���̂Ƃ��A�@2�E������(18��)=(![]() -1)/2=1/�Ӂ@�i�ӂ͉�����j�ł���B
-1)/2=1/�Ӂ@�i�ӂ͉�����j�ł���B
�@�t�B�{�i�b�`����@0�C1�C1�C2�C3�C5�C8�C13�C21�C34�C55�C89�C144�C�c�@�̂Q���̔� Fn/Fn+1
�́A
�@0/1��1/2��3/5��8/13��21/34���c
1/�� �c��34/55��13/21��5/8��2/3��1/1
�ƂȂ�B
�@����āA�s�����@ ���E������(��/n)�������E������(��/n)�@�Ɓ@2������(18��)=1/�Ӂ�8/13�@���A
�@��10������(180��/10)��5�E(8/13)=3.07�c��3.05�@�@�i�I�j
���@�J���̏ꍇ�A![]() ��2.23�@�Ƃ��āAsin(18��)=(��5-1)/4��(2.23-1)/4=1.23/4=0.3075
��2.23�@�Ƃ��āAsin(18��)=(��5-1)/4��(2.23-1)/4=1.23/4=0.3075
�@�Ȃ̂ŁA�@��10������(18��)��3.075��3.05�@�@�i�I�j
�@�U���@����̃R�����g�ł��B�i�����Q�S�N�P���U���t���j
�@���̖��́Asin�ƁAtan�Ƃ̒l�����߂���Ƃ�������̂ł͂Ȃ��ł��傤���B
���Ƃ��A�@������(��/30)=(-1-![]() +
+ ![]() ��(5-
��(5-![]() ))/8=(-1-��5 + ��(30-6
))/8=(-1-��5 + ��(30-6![]() ))/8
))/8
�@���ۂɁA�R�{�p�̌������A�@3������(��/30)-4������3(��/30)=������(��/10)=(-1+![]() )/4
)/4
����āA��=������(��/30)�@�Ƃ��āA4��3 - 3�� + (-1+��5)/4 = 0�@�������悢�B
�i���������\�t�g���g�����܂�ł��傤�B�j
�Ƃ���ŁA2010�N�Z���^�[�����@���w�U�E���wB�@���
�@0���Ɓ���/2�@�Ƃ��āA�@sin(��/10)=(-1+![]() )/4
)/4
�ɂ��āA�܂��A
�@������4��=�������Ɓ@�����Ƃ����߂�B�E�ӂ�ό`���āA������4��=������(��/2-��)
�@�@0���Ɓ���/2�@�ɂ����āA0����������=������(��/2-��)��1�@���A�@0��������4�Ɓ�1
�@���̂Ƃ��A�@�Ƃ́A4��=��/2-�Ɓ@�܂��́@4��=��-(��/2-��)=��/2+�Ɓ@�����B
�@����āA�@��=��/6�@�܂��́@��=��/10
������A�@������4��=cos�Ɓ@�������A������(��/10)�@��������B
�@2������2�Ƃ�����2��=cos�Ɓ@����A2(2�������Ƃ�������)(1-2������2��)=��������
���ӂ� �������Ɓ�0�@�Ŋ���ƁA�@4��������(1-2������2��)=1
�@����āA�@8������3��-4��������+1=0
�@�����������āA�i��̃Ƃ̉���/6���Q�l�ɂ���j�@(2��������-1)(4������2��+2��������-1)=0
�Q���������̉��̌������A�@��������=(-1�}![]() )/4
)/4
�@�������Ɓ�0�@���A�@��������=(-1+![]() )/4
)/4
�i�R�����g�j�@�U���@����A���肪�Ƃ��������܂��B
�@�e�m����̃R�����g�ł��B�i�����Q�S�N�P���U���t���j
�@�u���̖��́A�������ƁA�������Ƃ����߂���I�H�v�ɂ��āA�u���߂�v�Ƃ����̂͋��������
���Ȃ��ア�悤�Ȋ����ł��B��͂�A�u�]������v�Ƃ������������ł��傤�B�������g���ĕ\��
��(�����A���ꂪ���߂�H)�����]������ꍇ�������Ƃ͎v���܂��B
�@���̖��𗣂�āA������(��/n)�����������g���ĕ\���͖̂ʔ�����肾�Ǝv���܂��B
�@�Ƃ���ŁA������(��/30)�́A�R�d�����ł͂Ȃ��̂ł��ˁB������(��/30)�́A�R�d�����̂悤�ł��B
���������\�t�g���g�����̂ł͖ʔ�������܂���B
�i���@���̂Q�j�@�@�R�ӂ� 5�A12�A13 �̒��p�O�p�`�A1�ӂ�12�̐����`�A���a17��4���~��
 |
�@�@�@���}�̂悤�ɔz�u����B�����`�̑Ίp���́A �@�@�@�@12 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����悻���W�p�`�j �@�@�@�}���A4���~�̌ʁ����p�O�p�`�̎ΕӁ~2�@�Ȃ̂ŁA �@�@�@�@2�~17/4��13�~2 �@�@�@����āA��13�~4/17=3.058�c��3.05�@�@�i�I�j |
�@�e�m����̃R�����g�ł��B�i�����Q�S�N�P���T���t���j
�@�i���@���̂P�j�̐�10�p�`�͂܂��l���Ȃ��Ƃ͎v���܂����A�ł��Ȃ����Ƃ͂Ȃ��ł��ˁB
�i�e�m����̒NjL�j�@�����Q�S�N�P���U���t��
�@�I�C���[�̃ӊ��ɂ��āA��(8)=��(10)=��(12)=4�@������A��/8�A��/10�A��/12�@�̂���
��ɂ��Ă��A���������߂�ɂ͂Q���������Q��(�������J���̂��Q��j�����痝�_�I�ɂ͓�
���ł��ˁB���ۂ̌v�Z�ɂ��Ắu12�v���L���Ƃ͎v���܂����A��10�p�`�����肤��Ǝv����
���ɂȂ�܂����B
�@��(��)=8 �ƂȂ� �� �A�����A�������J���̂��R��łł���̂́An=16�A20�A24�̑��ɁAn=15�A30
������܂��B���̖��𗣂�āA������(��/30)=������12���Ƃ������߂Ă݂�̂��ʔ������ł��B
�����A�R�d�����ł��傤���D�D�D�B
�@��(n)=16(�������J���̂��S��)�́An=32�A40�A48�A60 �̑��ɁAn=17 ������܂��B��17�p�`
�ɂ��ẮA�����Ă���Ԃ�1��͍l���Ă݂����Ǝv���܂��B
�@�i���@���̂Q�j�̕��͓��ڂ��炵�Ȃ�(�قړ��ڂ�����)���łȂ��W�p�`(�قڐ�������)�ŏo
���Ă��܂��̂��������ł��B
�@�}�l���A�u���n�Ƃ������Ő�III�̐ϕ����g������@�v��������܂����B
�i�����Q�S�N�P���U���t���j
�@f(��)=4/(��2+1)�@�ƒu���ƁAf�f(��)=-8��/(��2+1)2��0�@�Af�h(��)=8(��2-1)/(��2+1)3�@���A
�@0������1�@�ɂ����āAf(��)�́A��ɓʂȒP���������ł���B
�@�]���āA��01f(��)����=���o(f(0)+f(1))/2+��k=1�`n-1f(��/��)�p/�� = �o3+��k=1�`n-1f(��/��)�p/��
�@���E�ӂ́Af(��)=4/(��2+1)�A�� ���A�� ���A��=1 �ň͂܂��}�`�̖ʐς��`�ŋߎ������l
������A�e���̒l�Ōv�Z����ƁA
�@��=�P�@�̂Ƃ��A�@��3
�@��=2�@�̂Ƃ��A�@���i3+16/5�j/2=31/10=3.1
�@��=3�@�̂Ƃ��A�@���i3+36/10+36/13�j/3=203/65>3.123
�@��=4�@�̂Ƃ��A�@��5323/1700��3.131
�ƂȂ�u���R�D�P�R�v�܂ł͎�v�Z�ŏؖ��ł��܂��B����5 �̂Ƃ��́A�������Ɏ�v�Z�����
�Ȃ̂ŁAPC�ɂ��肢����ƁA�u���R�D�P�S�v�������ɂ́A��=11�܂Ōv�Z����K�v������܂��B
�ォ��̕]�������܂��s�����@���l�����ł��B
�@�e�m����̃R�����g�ł��B�i�����Q�S�N�P���U���t���j
�@����̖��̎�|���炢���A���Z�ł�������Ƃ͎g���Ă�������A���̂�肩��������
�ł��ˁBn=2 �͂����ȒP�Ɍv�Z�ł��āA����ŁA��3.1 ���łĂ��܂��̂��������ł��B����
�����ł̉����������������͂����̂ł��傤�Bn=4 �ŁA��3.13 ���o�Ă��܂����
���ˁB
�@���ʂ̂�肩���́A��(1-��2) �� 0 ���� 1 �܂ł̐ϕ��������̑�`�̖ʐςŕ]������
����Ƃ�������킯�ŁA�����l����Ȃ�A��������蕪�����̕������������o�Ă��Ȃ�
���A�͂邩�ɂ������ƂɂȂ�܂��B�����ϕ��Ƃ������x�Ȃ��Ƃ��g���Ă���킯�ł͂����
�����D�D�D�B
�@�U���@����̃R�����g�ł��B�i�����Q�S�N�P���U���t���j
�@��{1/(1+��2)}�����@�ɂ���
�@0��x��1�ɂ����āA�s���� 1/(1+��2)=1-��2+��4/(1+��2)��1-��2+��4/2�@���A
��01{1/(1+��2)}����=��/4����01{1-��2+��4/2}����=[��-��3/3+��5/10]01
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@=1-1/3+1/10=(30-10+3)/30=23/30
�@�@�ȏォ��A�@��46/15=3.06�c��3.05
�@���l�ɁA�@0��x��1�ɂ����āA�s���� 1/(1+��2)=1-��2+��4/(1+��2)��1-��2�@���A
��01/![]() {1/(1+��2)}����=��/6����01/
{1/(1+��2)}����=��/6����01/![]() {1-��2}����=[��-��3/3]01/
{1-��2}����=[��-��3/3]01/![]() =1/
=1/![]() -1/9
-1/9![]() =8
=8![]() /27
/27
�@�@�ȏォ��A�@��16��3/9=3.07�c��3.05
�@�e�m����̃R�����g�ł��B�i�����Q�S�N�P���U���t���j
�@��L�v�Z�̐^�������āA�t�����̕s�������o���Ă݂܂����B
�@�@1/(1+��2)=1-��2+��4/(1+��2)��1-��2+��4�@���A
��01{1/(1+��2)}����=��/4�� ��01{1-��2+��4}����=1-1/3+1/5=13/15
�@�@�ȏォ��A�@��52/15=3.46���<3.5
�@�Ƃ���ŁA�� �������Ƃ��āA
�@�@�@1/(1+��2)=1-��2+��4-��6+���+��2n/(1+��2)��1-��2+��4-��6+���+��2n
���g���Čv�Z����ƁA��/4��1-1/3+1/5-����+1/(2n+1)�@�������܂����A�������x������
�ŗL���ȋ���������A�������ʂ�̂͑�ςł��傤�B
�@�U���@����̃R�����g�ł��B�i�����Q�S�N�P���V���t���j
�@���C�v�j�b�c�̎� ��/4=ArcTan(1)=1-1/3+1/5-1/7+1/9- �c�@���́A�}�`���̎�
�@�@�@��/4=4ArcTan(1/5)-ArcTan(1/239)
���g���̂����p�I�ł��ˁB
�@�~���̒����̕]�����ł́A�u�~�ʂ̒����v�ɂ������X�l���̕s����
�@�@�O���Ɓ���/�Q�@�̂Ƃ��A
�@![]()
�ɂ����āA��=��/�U�@�̂Ƃ��A�@��������=1/2�A��������=![]() /2�A��������=
/2�A��������=![]() /3�@�Ȃ̂ŁA
/3�@�Ȃ̂ŁA
�@3�E(1/2)/(2+![]() /2)���Ɓ�(2�E(1/2)+
/2)���Ɓ�(2�E(1/2)+![]() /3)/3�@���A�@3(4-
/3)/3�@���A�@3(4-![]() )/13���Ɓ�(3+
)/13���Ɓ�(3+![]() )/9
)/9
����āA�@18(4-![]() )/13����2(3+
)/13����2(3+![]() )/3
)/3
�@![]() ��1.74�@�Ƃ��āA�@18(4-1.74)/13=3.12����2(3+1.74)/3=3.16�@�ł��傤�B
��1.74�@�Ƃ��āA�@18(4-1.74)/13=3.12����2(3+1.74)/3=3.16�@�ł��傤�B
�i�R�����g�j�@�ߎ��̐��x�͒u���Ƃ��āA�X�l���̕s�����͗L�p�ł��ˁI
�@�e�m����̃R�����g�ł��B�i�����Q�S�N�P���V���t���j
�@�}�`���̎��͈ꉞ�m���Ă��܂������A�X�l���̎��͒m��܂���ł����B�X�l���̎����ؖ�
�����āA������g���ă̕]����v������Ƃ������͑�w�������Ƃ��Ď荠�Ȋ����ł��B
�@�������Ɓ��Ɓ��������Ɓ@���A�P���ߎ��œ����ɂȂ�̂ɑ��āA�X�l���̎��́A�R���ߎ��œ�
���ɂȂ�悤�ł��B
�@�R���ߎ��ōl����ƁA�@3��������/(2+��������)��3(��-��3/6)/(3-��2/2)����
�@(2��������+��������)/3��(2��-��3/3+��+��3/3)/3����
������A���x�ɂ��Ȃ�̍����o��͔̂[���ł��܂��B
�@�U���@���A�u������(��/n)�����������g���ĕ\���͖̂ʔ�����肾�Ǝv���܂��B�v����
�āA��X�̎O�p���̒l�ׂ��܂����B�i�����Q�S�N�P���W���t���j
�� 60���i=��/3�j�A45���i=��/4�j�A30���i=��/6�j
�@sin(60��)=sin(��/3)=![]() /2�@�Acos(60��)=cos(��/3)=1/2
/2�@�Acos(60��)=cos(��/3)=1/2
�@sin(45��)=sin(��/4)=![]() /2�@�Acos(45��)=cos(��/4)=
/2�@�Acos(45��)=cos(��/4)=![]() /2
/2
�@sin(30��)=sin(��/6)=1/2�@�Acos(30��)=cos(��/6)=![]() /2
/2
�� 36���i=��/5�j
�@��=��/5�@���A2��+3��=�@�Ȃ̂ŁAsin(3��)=sin(��-2��)=sin(2��)
�{�p�A3�{�p�̌������g���āA4cos2��-2cos��-1=0
2���������̉��̌������Acos�Ɓ�0�ɒ��ӂ��āA
�@cos��=(1+![]() )/4=(1/2)�Ӂ@(������)
)/4=(1/2)�Ӂ@(������)
�@sin2��=1-cos2��=1-(1+![]() )/4)2=(10-2
)/4)2=(10-2![]() )/16
)/16
�@sin�Ɓ�0�@���A�@sin��=��(10-2![]() )/4
)/4
�i�ʉ��j�@��A=36���AAB=AC=���@�ABC=1�@�̓ӎO�p�`ABC���l����B
�@�@�_B����A��B=72���̓������Ђ��A��AC�Ƃ̌�_��D�Ƃ���B
�@�@��BCD�́ABC=BD=1�@�̓ӎO�p�`�A��DAB�́ADA=DB=1�@�̓ӎO�p�`�ƂȂ�B
�@�@��ABC�䁢BCD���AAB �F BC = BC �F CD�@�Ȃ̂ŁA�@�� �F 1 = 1 �F ��-1
�@�@����āA�@��(�� - 1) = 1�@���A�@��2 - �� - 1 = 0�@ �]���āA�� = (1 + ![]() )/2 = �Ӂ@(������)
)/2 = �Ӂ@(������)
�@���ɁA�_D�����AB�։��낵�������̑���K�Ƃ���B��DAK�߁�DBK�@�Ȃ̂ŁA��DAK��
�@�����āAcos(36��)=AK/AD=��/2=(1+![]() )/4
)/4
�� 22.5���i=��/8�j
�@��=��/8�@�Ƃ���ƁA2��=��/4
�@�]���̔{�p�̌��� cos(2��)=2cos2��-1 ���A�@![]() /2=2cos2��-1
/2=2cos2��-1
�@cos�Ɓ�0�ɒ��ӂ��āA�@cos��=��(![]() +2)/2
+2)/2
�@sin2��=1-cos2��=(2-![]() )/4�@�ŁAsin�Ɓ�0�@���Asin��=��(2-
)/4�@�ŁAsin�Ɓ�0�@���Asin��=��(2-![]() )/2
)/2
�i�ʉ��j�@��A=45���AAB=AC=![]() �@�̓ӎO�p�`ABC���l����B�_B����A��AC�։��낵
�@�̓ӎO�p�`ABC���l����B�_B����A��AC�։��낵
�������̑���D�Ƃ���B��BDA�́ABD=AD=1�@�̒��p�O�p�`�ƂȂ�B��BDC�̒��p�O�p�`
�ɂ����āA�@BC2=BD2+DC2=12+(![]() -1)2=4-2
-1)2=4-2![]()
�@�_A�����BC�։��낵�������̑���H�Ƃ���B
�@��ABH�ɂ����āAsin(22.5��)=BH/AB={��(4-2![]() )/2}/��2=��(2-
)/2}/��2=��(2-![]() )/2
)/2
�� 18���i=��/10�j
�@��=��/10�Ƃ���ƁA5��=��/2�@�ŁA2��+3��=��/2�@�Ȃ̂ŁA
�@�@sin3��=sin(��/2-2��)=cos2��
�@�{�p�A3�{�p�̌������g���Đ�������ƁA�@4sin3��-2sin2��-3sin��+1=0
�@�����������āA�@(sin��-1)(4sin2��+2sin��-1)=0
�@2���������̉��̌������Asin�Ɓ�0�ɒ��ӂ��āAsin��=(-1+![]() )/4
)/4
�@cos2��=1-sin2��=(10+2��5)/16�@�ŁAcos�Ɓ�0�@���Acos��=��(10+2![]() )/4
)/4
�i�ʉ��j�@��A=36���AAB=AC=���ABC=1�@�̓ӎO�p�`ABC���l����B�_B����A��B=72��
�̓������Ђ��B��AC�Ƃ̌�_��D�Ƃ���B��BCD�́ABC=BD=1�̓ӎO�p�`�A
��DAB��DB=DA=1�̓ӎO�p�`�ƂȂ�B��ABC�䁢BCD���AAB �F BC = BC �F CD
�Ȃ̂ŁA�@�� �F 1 = 1 �F ��-1�@���A�@��(��-1)=1�@�@����āA�@��2-��-1=0
�ȏォ��A�@��=(1+![]() )/2=�Ӂ@(������)
)/2=�Ӂ@(������)
���ɁA�_A�����BC�։��낵�������̑���H�Ƃ���B��BAH=18���Ȃ̂ŁA
sin(18��)=BH/AB=(1/2)/((1+��5)/2)=(-1+![]() )/4=(1/2)(1/��)
)/4=(1/2)(1/��)
�� 15���i=��/12�j
�@sin(��/12)=sin(��/3-��/4)
=sin(��/3)cos(��/4)-cos(��/3)sin(��/4)=(![]() /2)(
/2)(![]() /2)-(1/2)(
/2)-(1/2)(![]() /2)=(
/2)=(![]() -
-![]() )/4
)/4
�@cos(��/12)=cos(��/3-��/4)
=cos(��/3)cos(��/4)+sin(��/3)sin(��/4)=(1/2)(![]() /2)+(
/2)+(![]() /2)(
/2)(![]() /2)=(
/2)=(![]() +
+![]() )/4
)/4
�i�ʉ��j�@sin(��/12)=sin(��/4-��/6)
�@�@=sin(��/4)cos(��/6)-cos(��/4)sin(��/6)=(![]() /2)(
/2)(![]() /2)-(
/2)-(![]() /2)(1/2)=(
/2)(1/2)=(![]() -
-![]() )/4
)/4
�@cos(��/12)=cos(��/4-��/6)
=cos(��/4)cos(��/6)+sin(��/4)sin(��/6)=(![]() /2)(
/2)(![]() /2)+(
/2)+(![]() /2)(1/2)=(
/2)(1/2)=(![]() +
+![]() )/4
)/4
�i�ʉ��j�@��ADC�́AAC=1�A��ADC=30���A��C�����p�̒��p�O�p�`�ŁACD�̉�����B���Ƃ�A
�@��ABD�́AAD=BD=2�A��ABC=��BAD=15���̓ӎO�p�`�Ƃ���B
�@��ABC�ɂ����āAAB2=BC2+CA2�Ȃ̂ŁAAB2=(2+![]() )2+12=8+4
)2+12=8+4![]()
�@���̂Ƃ��AAB=![]() +
+![]()
�� 12���i=��/15�j
�@��/15=��/6-��/10�@�Ȃ̂ŁA���@�藝���A
�@sin(��/15)=sin(��/6-��/10)=sin(��/6)cos(��/10)-cos(��/6)sin(��/10)
=(1/2){��(10+2![]() )/4}-(
)/4}-(![]() /2){(-1+
/2){(-1+![]() )/4}=( ��(10+2)+
)/4}=( ��(10+2)+![]() -��15) ) /8
-��15) ) /8
�@cos(��/15)=cos(��/6-��/10)=cos(��/6)cos(��/10)+sin(��/6)sin(��/10)
=(![]() /2){��(10+2
/2){��(10+2![]() )/4}+(1/2){(-1+
)/4}+(1/2){(-1+![]() )/4}=( ��(30+6
)/4}=( ��(30+6![]() )+
)+![]() -1 )/8
-1 )/8
�� 9���i=��/20�j
�@��/20=��/4-��/5�@�Ȃ̂ŁA���@�藝���A
�@sin(��/20)=sin(��/4-��/5)=sin(��/4)cos(��/5)-cos(��/4)sin(��/5)
=(![]() /2){(1+
/2){(1+![]() )/4}-(
)/4}-(![]() /2){��(10-2
/2){��(10-2![]() )/4}=( ��10+
)/4}=( ��10+![]() -2��(5-
-2��(5-![]() ) )/8
) )/8
�@cos(��/20)=cos(��/4-��/5)=cos(��/4)cos(��/5)+sin(��/4)sin(��/5)
=(![]() /2){(
/2){(![]() +1)/4}+(
+1)/4}+(![]() /2){��(10-2
/2){��(10-2![]() )/4}=( ��10+
)/4}=( ��10+![]() +2��(5-
+2��(5-![]() ) )/8
) )/8
�� 7.5���i=��/24�j
�@��/24=��/6-��/8�@�Ȃ̂ŁA���@�藝���A
�@sin(��/24)=sin(��/6-��/8)=sin(��/6)cos(��/8)-cos(��/6)sin(��/8)
=(1/2){��(![]() +2)/2}-{
+2)/2}-{![]() /2}{��(2-
/2}{��(2-![]() )/2}=( ��(
)/2}=( ��(![]() +2)-��(6-3
+2)-��(6-3![]() ) )/4
) )/4
�@cos(��/24)=cos(��/6-��/8)=cos(��/6)cos(��/8)+sin(��/6)sin(��/8)
={![]() /2}{��(
/2}{��(![]() +2)/2}+(1/2){��(2-
+2)/2}+(1/2){��(2-![]() )/2}=( ��(6+3
)/2}=( ��(6+3![]() )+��(2-
)+��(2-![]() ) )/4
) )/4
�� 6���i=��/30�j
�@��/30=��/5-��/6�@�Ȃ̂ŁA���@�藝���A
�@sin(��/30)=sin(��/5-��/6)=sin(��/5)cos(��/6)-cos(��/5)sin(��/6)
�@�@�@�@�@�@�@={��(10-2![]() )/4}(
)/4}(![]() /2)-{(1+
/2)-{(1+![]() )/4}(1/2)=( ��(30-6
)/4}(1/2)=( ��(30-6![]() ) -1-
) -1-![]() )/8
)/8
�@cos(��/30)=cos(��/5-��/6)=cos(��/5)cos(��/6)+sin(��/5)sin(��/6)
�@�@�@�@�@�@�@ ={(1+![]() )/4}(
)/4}(![]() /2)+{��(10-2
/2)+{��(10-2![]() )/4}(1/2)=(
)/4}(1/2)=( ![]() +��15 +��(10-2
+��15 +��(10-2![]() ) )/8
) )/8
�� 4.5���i=��/40�j
�@��/40=��/8-��/10�@�Ȃ̂ŁA���@�藝���A
�@sin(��/40)
=sin(��/8-��/10)=sin(��/8)cos(��/10)-cos(��/8)sin(��/10)
={��(2-![]() )/2}{��(10+2
)/2}{��(10+2![]() )/4}-{��(2+
)/4}-{��(2+![]() )/2}{(-1+
)/2}{(-1+![]() )/4}
)/4}
=( ��(20-10![]() +4
+4![]() -2��10) +��(2+
-2��10) +��(2+![]() )-��(10+5
)-��(10+5![]() ) )/8
) )/8
=( ��(10+��10)-��(10-3��10) +��(2+![]() )-��(10+5
)-��(10+5![]() ) )/8
) )/8
�@cos(��/40)
=cos(��/8-��/10)=cos(��/8)cos(��/10)+sin(��/8)sin(��/10)
={��(2+![]() )/2}{��(10+2
)/2}{��(10+2![]() )/4}+{��(2-
)/4}+{��(2-![]() )/2}{(-1+
)/2}{(-1+![]() )/4}
)/4}
=( ��(20+10![]() +4
+4![]() +2��10) -��(2-
+2��10) -��(2-![]() )+��(10-5
)+��(10-5![]() ) ) /8
) ) /8
=( ��(10-��10)+��(10+3��10) -��(2-![]() )+��(10-5
)+��(10-5![]() ) ) /8
) ) /8
�� 3���i=��/60�j
�@��/60=��/10-��/12�@�Ȃ̂ŁA���@�藝���A
�@sin(��/60)
=sin(��/10-��/12)=sin(��/10)cos(��/12)-cos(��/10)sin(��/12)
={(![]() -1)/4}{(
-1)/4}{(![]() +
+![]() )/4}-{��(10+2
)/4}-{��(10+2![]() )/4}{(
)/4}{(![]() -
-![]() )/4}
)/4}
=( ��30+��10-![]() -
-![]() -��(60+12
-��(60+12![]() )+��(20+4
)+��(20+4![]() ) )/16
) )/16
�@cos(��/60)
=cos(��/10-��/12)=cos(��/10)cos(��/12)+sin(��/10)sin(��/12)
={��(10+2![]() )/4}{(
)/4}{(![]() +
+![]() )/4}+{(
)/4}+{(![]() -1)/4}{(
-1)/4}{(![]() -
-![]() )/4}
)/4}
=( ��30-��10-![]() +
+![]() +��(60+12
+��(60+12![]() )+��(20+4
)+��(20+4![]() ) )/16
) )/16
�@�炷���邳��̃R�����g�ł��B�i�����Q�S�N�P���W���t���j
�@�������킹�́A�������łǂ����B
�@�e�m����̃R�����g�ł��B�i�����Q�S�N�P���P�Q���t���j
�@��/3�A��/4�A��/6 �͗e�ՂƂ��āA��/5�A��/8�A��/10 ���v�Z���Ă����A���Ƃ͉��@�藝
�ŏo��Ƃ������Ƃł��ˁB���@�藝�ł́A�V���ɂQ�d�ɍ�����������͂��Ȃ�����A��/5�A
��/8�A��/10 �łQ�d���������肤�邾���ŁAk��/60 �ł́A�R�d�����͌���Ȃ��Ƃ������Ƃ�
���ˁB�ʔ��������Ƃ͎v���Ȃ��玩���ł͂���Ă܂���B��������Ă݂܂��B
�@�炷���邳��́A��/120��1�D5�����݂ŁA���ׂẲs�p�̎O�p����o���Ă�����̂�
���ˁB���ۂɂ���Ă݂��Ƃ��̓������킹�Ɏg�킹�Ē����܂��B1�D5���ł��R�d��������
��Ȃ��͈̂ӊO�Ɋ����܂��B
�@��/90��2�����/180��1���ɂ��ẮA��(90)=24�A��(180)=48 �ƂȂ��āA�f�����R����
�ނ��痧���������̂ł��傤�B�����A�����̊p�̐����������߂�̂͂ƂĂ�����̂�
���傤�B
�i�NjL�j�@�����Q�T�N�S���U���t��
�@������w�̉~�����̕]�����ɐG�����ꂽ�悤�ɁA���N�x���~�����𓌑�ȏ�Ɍ�����
�]�������肪����w�ŏo�肳�ꂽ�B
�@����w�@���n�i�Q�O�P�R�j�@�E�E�E�g�Q�T�N�x���V�݂��ꂽ����g�������
�@�@�R�D�P�S�P�����R�D�P�S�Q�@�������B
�@��L�̖��̑O�ɔ��ϕ��̖�肪�o�肳��A�����p���ĉ����炵�����A���̗U�����
����ʂɂ͌��J����Ă��Ȃ��B
�@��L��Excel����̕\
| �� | nsin(��/n) | ntan(��/n) |
| �S | 2.828427125 | 4 |
| �U | 3 | 3.464101615 |
| �W | 3.061467459 | 3.313708499 |
| �P�Q | 3.105828541 | 3.215390309 |
| �P�U | 3.121445152 | 3.182597878 |
| �Q�S | 3.132628613 | 3.159659942 |
| �R�Q | 3.136548491 | 3.151724907 |
| �S�W | 3.139350203 | 3.146086215 |
| �U�S | 3.140331157 | 3.144118385 |
| �X�U | 3.141031951 | 3.1427146 |
����s�������������߂ɂ́A�����X�U�ȏ�̕]�����K�v�ł���B������āA��v�Z�ʼn\��
�̂��낤���H����w�̗U����肪�傢�ɋC�ɂ�����I
�i�NjL�j�@���g�o�����������b�ɂȂ��Ă���g�m�u�您�����v����̏��ł��B
�@�@�i�ߘa�V�N�R���V���t���j
�@��L�̑���w�̖��ł����A������܂߂������������̂ŁA�����܂��B
�@�~�������Ƃ���B���̐������ɑ��A
�@![]() �@�A
�@�A![]()
�Ƃ����B
�i�P�j�@������������ ������������������ ��������/�P�Q�@���ؖ�����B
�i�Q�j�@�R�D�P�S�P�����R�D�P�S�Q�@���ؖ�����B
�@�������A�P�D�V�R�Q�O�T�O�W��![]() ���P�D�V�R�Q�O�T�O�X�@�ł���B
���P�D�V�R�Q�O�T�O�X�@�ł���B
�i�R�����g�j�@�您��������A�����肪�Ƃ��������܂��B�����A�v�Z����ς����ł��ˁI
�i�NjL�j�@�f�`�h ����A�b��̒ł��B�i�����Q�T�N�V���R�P���t���j
�@�A���L���f�X�l�Ă̔��a�P�̉~�ɓ��ڂƊO�ڂ��鐳���p�`���v�Z���邱�Ƃɂ��A�~����
�i��3.141592�E�E�E�j�̒l��������U�ʂ̐��x�܂Ŋm�肳���邽�߂ɂ́A�����p�`�܂ł�
�}�`���l�@���˂Ȃ�Ȃ��ł��傤���H
�@�����ŋ��߂����_���m���߂����̂ŁA�ǂȂ�������肢�܂��B
�@��M����̃R�����g�ł��B�i�����Q�T�N�V���R�P���t���j
�@Maxima �ɂ��ƁA�u5463�v�ł����B
�@�@f(n):=n*sin(%pi/n);
�@�@g(n):=n*tan(%pi/n);
�@�@/* [wxMaxima: input start ] */
�@�@float(f(5463));
�@�@float(g(5463));
�@�@float(g(5462));
�@�@/* [wxMaxima: input end ] */
�@�@> 3.141592480434425
�@�@> 3.141592999900581
�@�@> 3.1415930000274
�@�f�`�h ����̃R�����g�ł��B�i�����Q�T�N�V���R�P���t���j
�@�@f(n):=n*1/2*1^2*sin(%2*pi/n)=n/2*sin(%pi/(n/2))
�ɂȂ�܂��H���͐��T�U�Q�S�p�`�̌��_�ƂȂ�܂����B
�@�炷���邳��̃R�����g�ł��B�i�����Q�T�N�V���R�P���t���j
�@���ڂ��p�`�����̓ӎO�p�`�ɕ��������A���p�́A2��/�� �Ȃ̂ŁA��ӂ̒����́A
�@2sin(2��/n��2)=2sin(��/n)
����āA���̒����́A2nsin(��/n)�@�Ȃ̂ŁA�����i�p�x�j�ł́Ansin(��/n)�@�ƂȂ�܂��B
�i�Q�l�j�@���ڑ��p�`�ƊO�ڑ��p�`�ł́A�@sin�Ɓ��Ɓ�tan�Ɓ@�Ƃ��������g�p���܂����A
�@�@�@����̑���ɁA
�@sin�Ɓ��Ɓ�(sin��+tan��)/2
�i�܂�A�~���̒����͓��ڑ��p�`�ƊO�ڑ��p�`�̎��̕��ς�菬�����j
���g�p����An=2812�ŁA��=3.141592�c�@���m�肵�܂��ˁB�܂��A�Ƃ��������Ƃ�
�@�Ɓ�(2sin��+tan��)/3�ł��邱�Ƃ��g���ƁA�Ⴆ�An=5463 �̂Ƃ��A
�@��=3.14159265358981�c
�ƁA�����_�ȉ�12���܂Ő��m�ɋ��܂�܂��B�i�A���A���ꂾ���ł͉����܂Ő��m��������܂���B�j
�@�f�`�h ����̃R�����g�ł��B�i�����Q�T�N�V���R�P���t���j
�@���͎��̒����ł͂Ȃ��A�ʐςŋ���ł��܂����B�����ł���ˁA���̒����ŋ��ނׂ��ł���
�E�E�E�B�ł��A�ʐςōl���Ă͂����Ȃ��̂��ȁH
�@�炷���邳��̃R�����g�ł��B�i�����Q�T�N�V���R�P���t���j
�@���X�̖ړI�́A(�~��)��(���a)�̒l�����߂邱�Ƃ��Ǝv���܂��̂ŁA���̒����ōl�����
�����R���Ǝv���܂��B�������A(���a)=1 �̂Ƃ��A(�~��)��(���a)=(�ʐ�)�����m�Ƃ��ėǂ�
�̂ł���A�ʐςōl���Ă��ʂɍ\��Ȃ��Ǝv���܂����A���ʓI��n���傫���Ȃ�̂ő���
���ˁB
�@��M����̃R�����g�ł��B�i�����Q�T�N�W���P���t���j
�@�A���L���f�X�̕��@�Ə����Ă������̂ŁA�i�A���L���f�X�̕��@�͎��ƋL�����Ă����̂Łj
���ł��܂����B���ł�鎞�́A�u�O�ڑ��p�`�̎������~����蒷�����Ɓv���A���͎�����
�͂Ȃ����Ƃ�F�����Ă����K�v�����ɂ���Ǝv���܂��B�i���@�Q�l�F�u�~�̖ʐ��v�j
�@�f�`�h ����̃R�����g�ł��B�i�����Q�T�N�W���P���t���j
�@���a�P�̉~��`���B���̉~�����ډ~�ƂȂ鐳�O�p�`�����B����ɁA���̐��O�p�`�̊O��
�~��`���B���ܕ`�����~����ډ~�ƂȂ�悤�ɁA�O���ɐ��S�p�`�����B���̐��S�p�`�̊e
���_��ʂ�~��`���B���̉~�����ډ~�ƂȂ�悤�A�O���ɐ��T�p�`������A����ɂ��̐��T
�p�`�̊e���_��ʂ�~��`���B���̂悤�ɁA���X�Ɛ����p�`��ς��Ȃ���~���\�����Ă���
�Ƃ��A�����p�`�͌���Ȃ��~�ɋ߂Â��Ă����̂ŁA�O�ڂ���~�͂���傫���ȏ�ɂ͖c���
�Ȃ��B�����ŁA�������č\���ł���~�̋Ɍ��̔��a���m�肽���B�ǂ��܂Ŗc��܂������
���H
�@�炷���邳��̃R�����g�ł��B�i�����Q�T�N�W���P���t���j
�@�u�O�ڂ���~�͂���傫���ȏ�ɂ͖c��܂Ȃ��v�Ƃ͌���Ȃ��Ǝv���܂��B
1/2+1/3+1/4+�c �����U����̂Ɠ��l�ɁA�����ɐ����p�`��lj�����A�~�������ɑ傫
���Ȃ�\��������܂��B�ł��A�v�Z������A��������悤�ł��ˁB1/��[k=3�`��]cos(��/k)
�ɂȂ�Ǝv���܂����A����uWolframAlpha�v�Ōv�Z������A�u8.7000366252�c�v�Ƃ����l�ɂȂ�
�܂����B���̒l�́A�uA051762�v�ɂ���܂����B
�@��M����̃R�����g�ł��B�i�����Q�T�N�W���P���t���j
�@���O�p�`�̊O�ډ~�̔��a�͍ŏ��̉~�� 1/cos(��/3)�{�A���̉~�̔��a�͂����
1/cos(��/4)�{�A�E�E�E�Ƃ����킯�ŁAA = ��1/cos(��/n) �Ƃ����Ɍ��ł����A8.70 ���炢������
�ł��B
�@�������邱�Ƃ𗝋��Ŋm�F����ړI�ŕ]�������݂܂����B
�@�ΐ�������� logA = �� log(1/cos(��/n)) ���l���āA�@cos(��/x)��1-(��/x)2/ 2 �@���A
�@�@1/cos(��/x)��2x2/(2x2-��2)�@�Ȃ̂ŁAlog(1/cos(��/x))�� log(2x2/(2x2-��2))�@�E�E�E�i*�j
�@�����ŁA�i*�j���Ax=2���灇�܂Őϕ�����Ə�E��^����E�E�E�Ǝv������i*�j�̉E�ӂ�x����
�Œ�`����Ȃ��̂ŁA
�@A = 2*![]() *��(n=5�ȍ~) 1/cos(��/n)
*��(n=5�ȍ~) 1/cos(��/n)
�Ƃ��Ă����āA�i*�j���Ax=4���灇�܂Őϕ����ď�E��^���Ă݂�ƁA
�@A �� 2*![]() *(42/(42-��2/2))4
*(42/(42-��2/2))4
�@�E�ӂ𐔒l�v�Z������ƁA�u12.36483... �v�ƂȂ�A�u8.70�v���啝�ɑ傫���ł����A�i*�j�̕]
�����w���̌��Ƃ��Ĕ��f�����̂��߂ɑ������ꂽ�ƍl�����܂��B
�@���� ����̃R�����g�ł��B�i�����Q�T�N�W���Q���t���j
�@A = ��1/cos(��/n) ���������邱�Ƃ����������ł�����A���̂悤�ɂ���Ă������ł��ˁB
�@cos(��/k)��1-(��/k)2/2=(k2-(��/![]() )2)/k2 �Ȃ̂ŁAk��4�̂Ƃ��A
)2)/k2 �Ȃ̂ŁAk��4�̂Ƃ��A
�@�@1/cos(��/k)��k2/(k2-(��/![]() )2)��k2/(k2-32)
)2)��k2/(k2-32)
�����藧���܂��B���������āA��k=4�`n 1/cos(��/k)����k=4�`n k2/(k2-32)
�@�����ŁA��k=4�`n k2/(k2-32)=(��k=4�`n k/(k-3))*(��k=4�`n k/(k+3))
�@=(4/1)*(5/2)*(6/3)*�c*((n-2)/(n-5))*((n-1)/(n-4))*(n/(n-3))
�@*(4/7)*(5/8)*(6/9)*�c*((n-2)/(n+1))*((n-1)/(n+2))*(n/(n+3))
�@=(4*5*6*(n-2)*(n-1)*n)/(1*2*3*(n+1)*(n+2)*(n+3))��(4*5*6)/(1*2*3)=20
�@A(n)=��k=3�`n 1/cos(��/k) �Ƃ����ƁAA(n)=(1/cos(��/3))*��k=4�`n 1/cos(��/k)��2�E20=40
�@����āAA(n)�͒P�������ł����ď�ɗL�E�Ȃ̂ŁA��n=3�`�� 1/cos(��/n) �͎����B
�@�@�@�ȉ��A�H����