墌偺柺愊丂丂丂丂丂丂丂丂丂 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂墌偺柺愊偼丄乽墌廃棪亊敿宎亊敿宎乿偵傛傝梌偊傜傟傞丅擔杮偺彫妛峑偱偼丄彫妛係擭偱丄
柺愊偺奣擮傪妛廗偟偰惓曽宍傗挿曽宍偺柺愊傪媮傔丄彫妛俆擭偱丄傛偆傗偔丄暯峴巐曈宍
偺柺愊傪妛傫偩偁偲丄偦偺墑挿慄忋偱丄墌偺柺愊偑嫵偊傜傟傞丅
丂傕偭偲傕丄彫妛峑偱偼丄乽敿宎亊敿宎亊俁丏侾係乿乮幚嵺偵寁嶼偡傞応崌偼丄敿宎亊敿宎亊俁
偲奣悢寁嶼傪偟偰媮傔傞応崌偑偁傞偐傕偟傟側偄乯偱偁傞偑丄墌廃棪偲偟偰丄兾 傪梡偄傞偺
偼丄拞妛侾擭偵側偭偰偐傜偱偁傞丅
丂彫妛峑偱丄旝暘愊暘傪傗傞傢偗偵偼偄偐側偄偺偱丄壗偲側偔暤埻婥偱愢摼偝傟偰丄墌偺柺
愊偺岞幃傪擺摼偟偰偄傞偲偄偆偺偑尰忬偱偁傞丅
丂墌偺柺愊偼丄尩枾偵偼旝暘愊暘偵傛偭偰徹柧偝傟傞偑丄偦偺偙偲傪妛廗偡傞偺偼丄捠忢丄
崅峑俁擭偺廐乣搤偵妛廗偡傞乽悢妛III乿偵偍偄偰偱偁傞丅
乮堦晹偺庴尡恑妛峑偱偼丄俀擭偺搤乣俁擭弔崰偐傕偟傟側偄丅乯
丂偟偨偑偭偰丄墌偺柺愊偺岞幃傪彫妛峑俆擭偱妛傫偱埲棃丄崅峑俁擭偺廔傢傝嬤偔傑偱拞搑
敿抂側棫応偵丄墌偺柺愊偺岞幃偼娒傫偠偰偄傞傢偗偱偁傞丅乮壗偰寬婥側傫偩傠偆両乯
丂偟偐偟側偑傜丄乽悢妛III乿傪妛廗偡傞崅峑惗偼丄偦傟傎偳懡偔偼側偄丅偦偆偡傞偲丄擔杮偺崅
峑惗偺戝懡悢偼丄墌偺柺愊偺岞幃偵偮偄偰帺屓姰寢偟側偄傑傑悢妛偺妛廗傪廔椆偟偰偟
傑偭偰偄傞傢偗偱丄乽悢妛偼丄岞幃傪妎偊偰丄巊偊傟偽偄偄偺偝乿偲偄偆棳傟偵側偭偰偄傞丅
丂巹屄恖揑偵偼丄乽捈姶揑偵棟夝偱偒傟偽丄徹柧側偳側偔偰傕偄偄偐側乣乿偲偄偆棫応乮偙傟
偼丄傕偟偐偟偰丄僌儘僞儞僨傿僄僢僋棳偐側丠乯偩偑丄恖傪愢摼偟偨傝丄捈姶揑偵棟夝偱偒側偄
応崌偼丄傗偼傝丄撪揑丒奜揑偵愢摼偡傞摴嬶偲偟偰丄徹柧偼昁梫偩傠偆偲巚偆丅傑偨丄徹柧傪
捠偟偰丄岞幃偺杮幙揑側棟夝偑摼傜傟傞応崌偑偁傞偐傕偟傟側偄丅
丂崅峑俁擭偱妛廗偡傞嶰妏娭悢偺旝暘愊暘偑丄墌偺柺愊偺岞幃傪徹柧偡傞摴嬶偱偁傞丅
嶰妏娭悢偺旝暘愊暘偺婎慴偼丄
丂丂
偲偄偆岞幃偱偁傞丅
丂偙偺岞幃偺徹柧偼丄嫵壢彂偱偼丄嶰妏宍偲愵宍偺柺愊傪昡壙偡傞晄摍幃傪梡偄偰側偝傟
傞偺偑捠忢偱偁傞丅
丂廬棃偐傜丄偦偺傛偆側徹柧曽朄偼丄弞娐榑朄偱偁傞偲偄偆巜揈偼偁偭偨偑丄埶慠偲偟偰丄
嫵壢彂偺婰弎偑捈傜側偄偺偼丄崅峑悢妛偺幍晄巚媍偺堦偮偱偁傞丅
乮捛婰乯丂DD++偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俇擭俈寧俇擔晅偗乯
丂崅峑悢妛III偼弞娐榑朄偵側偭偰偄傞偲偄偆岆偭偨庡挘偼傛偔尒偐偗傑偡偑丄幚嵺偵丄嫵壢
彂傪尒傞偲丄崅峑悢妛偺斖埻撪偱偼偪傖傫偲惍崌惈偼庢傟偰偄傑偡丅偮傑傝丄乽柺愊偼愊暘
偵傛偭偰掕媊偝傟傞乿偲偄偆偺偼偁偔傑偱尰戙偺夝愅妛偱偺峫偊曽偱偁偭偰丄崅峑悢妛偼乽柺
愊傪媮傔傞曽朄偺1偮偵愊暘偲偄偆庤朄偑偁傞乿棫応偱偡丅偮傑傝丄崅峑悢妛偱偼乽愊暘側傫
偐偟側偔偰傕墌偺柺愊偼兾r2乿偑擣傔傜傟偰偄傑偡丅偦傟傪擣傔側偄悢妛傪傗傝偨偄恖偼丄
sin傗兾偺掕媊傕摨偠尰戙夝愅妛偺悽奅偱偺掕媊傪巊偊偽偄偄偼偢側偺偱偡偑丄側偤偐崅
峑悢妛棳偺sin傗兾偺掕媊偲尰戙夝愅妛偱偺柺愊偺掕媊傪慻傒崌傢偣丄俀偮偺岞棟宯偺摨
帪嵦梡偲偄偆悢妛揑嬛婖傪斊偟偰偍偐偟側悇榑傪偟丄戝敪尒傪偟偨偐偺傛偆偵"廋惓"埬傪敪
昞偡傞恖偺懡偄偙偲丏丏丏丅
丂偙偺偙偲偵偮偄偰丄弞娐榑朄偵側傜側偄宍偱丄忋婰偺嬌尷偺幃傪徹柧偟丄偦偺寢壥傪梡偄
偰丄墌偺柺愊偺岞幃傪徹柧丄嵟廔揑偵愵宍偺柺愊傪徹柧偡傞偲偄偆曽朄傪HP偲偟偰傑偲傔
傜傟偨曽偑偄傜傟傞偙偲傪丄嵟嬤抦偭偨丅
丂傎偦傗傫偺儂乕儉儁乕僕丂丗丂乽嶰妏娭悢偺嬌尷偲墌偺柺愊乿
丂偙偺儁乕僕偱偼丄忋婰俫俹傪嶲峫偵偝偣偰偄偨偩偒側偑傜丄墌廃棪偲墌廃偺挿偝偺娭學偐
傜巒傑偭偰丄墌偺柺愊偺岞幃傪摫偔傑偱傪惍棟偟偨偄偲巚偆丅
墌廃棪偺掕媊
丂偄傠偄傠側捈宎傪傕偮墌摏傪巻忋偱揮偑偟丄偦偺挿偝傪應傞丅偦偟偰丄幚尡寢壥偐傜丄捈
宎偲墌廃偺挿偝偺場壥娭學傪峫偊偝偣傞丅懡暘丄偙傟偑彫妛峑偱偺墌廃棪摫擖偺棳傟偱
偁傠偆丅
 |
丂丂丂傛偭偰丄彫妛峑俆擭偱丄
丂丂丂墌廃偺挿偝亖捈宎亊俁丏侾係
丂丂丂乮懄偪丄墌廃偺挿偝亖捈宎亊墌廃棪乯
丂丂丂偲偄偆岞幃傪丄懱姶偟偰妛廗偡傞丅 |
丂偦偺屻丄墌傪暯峴巐曈宍偺宍偵嬤帡揑偵摍愊曄宍偟丄墌偺柺愊偺岞幃傪妛廗偡傞丅偦
偺嵺丄乽墌廃偺挿偝亖捈宎亊俁丏侾係乿偺岞幃偑巊傢傟丄
丂墌偺柺愊亖敿宎亊敿宎亊俁丏侾係丂乮懄偪丄墌偺柺愊亖敿宎亊敿宎亊墌廃棪乯
偱偁傞偙偲傪抦傞丅
丂拞妛峑偵擖偭偰丄彫妛峑俆擭偱妛傫偩墌廃棪偲偄偆梡岅偵懳偟偰丄怴偟偔婰崋乽 兾 乿傪梡
偄傞偙偲傪妛廗偡傞偩偗偱丄媮愊栤戣偵廔巒偟丄怴偟偄恑揥偼堦愗側偄丅
丂墌偵娭偟偰寑揑偵曄壔偡傞偺偼丄崅峑偵擖偭偰偐傜偱偁傞丅
墌偺曽掱幃偺摫擖
丂拞妛峑偱偼丄墌偺埖偄偼恾宍偺榖偵巭傑偭偰偄偨偑丄崅峑偱偼丄乽悢妛 II 乿偵偍偄偰丄墌
傪夝愅婔壗揑偵庢傝埖偆偲偄偆怴偟偄帇揰傪妛廗偡傞丅
偡側傢偪丄拞怱偺嵗昗 乮 倎 丆 倐 乯 丄敿宎 倰 偺墌偺曽掱幃偼丄
丂(倃亅倎)2亄(倄亅倐)2亖倰2
偱梌偊傜傟傞偙偲傪抦傞丅
丂偦偺寢壥丄崱傑偱丄乽倃2亄倄2亖侾乿偲偄偆幃傪栤戣暥偺拞偵尒偰傕丄壗傕姶偠側偐偭偨傕偺
偑丄乽偙傟偼丄尨揰拞怱丄敿宎侾偺墌廃忋偺揰(倃丆倄)偑枮偨偡幃偩偹乿偲偄偆峫偊偑夎惗偊丄
悢妛偺栤戣傪丄拪徾揑側戙悢揑帇揰偐傜丄偁傞堄枴偱嬶懱揑側婔壗妛揑帇揰偵抲偒姺偊
傞偙偲傪壜擻偵偟偰偔傟傞丅
屖搙朄偺摫擖
丂屖搙朄偵偮偄偰偼丄乽悢妛 II 乿乮媽妛廗巜摫梫椞偱偼丄乽悢妛III乿乯偵偍偄偰丄妛廗偡傞丅偙傟偼
妏偺戝偒偝傪昞偡曽朄偱丄拞妛峑傑偱偼丄係俆搙偲偐丄俋侽亱偲偄偭偨搙悢朄乮俇侽暘朄乯偑堦
斒揑偱偁偭偨丅
丂屖搙朄傪梡偄傞棟桼偼扨弮柧夣偱丄嶰妏娭悢偺旝暘愊暘偺彅岞幃傪娙扨柧椖壔偡傞偨
傔偱偁傞丅傕偪傠傫丄旝暘愊暘傪傗傞埲忋丄妏搙偼幚悢偲偄偆惂栺傕娷傑傟傞丅
丂巹偑崅峑惗偺崰丄屖搙朄偼丄崅峑侾擭偺乽悢妛 I 乿偱妛傫偩妎偊偑偁傞丅乮偙傫側偙偲傪彂
偔偲丄擭偑偽傟偪傖偆偐側丠乯偦偺屻偺妛廗巜摫梫椞偱偼媣偟偔崅峑俀擭偱妛傫偱偄偨偑丄
捈嬤偺媽妛廗巜摫梫椞偱偼丄乽悢妛 III 乿偵捛偄傗傜傟偰偄偨丅娫堘偄偵婥偯偄偨偺偐丄怴
妛廗巜摫梫椞偱偼丄尦偺宍乽悢妛 II 乿偵暅妶偟偰偄傞丅
丂屖搙朄偼丄彫妛峑俆擭偱妛傫偩岞幃丗乽墌廃偺挿偝亖捈宎亊墌廃棪乿偵戝偄偵娭學偡傞丅
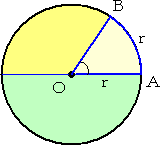 |
丂丂丂妏偺捀揰俷傪拞怱偲偡傞墌廃忋偱丄屖俙俛偺挿偝偑敿宎偺
丂丂挿偝乮 倰 乯偵摍偟偄偲偒丄拞怱妏俙俷俛傪丄侾儔僕傾儞乮倰倎倓倝倎値乯
丂丂偲偄偆丅
丂丂丂捠忢丄扨埵儔僕傾儞偼徣棯偝傟傞丅偙傟傪扨埵偲偟偰應傞偺
丂丂偑丄屖搙朄偱偁傞丅
丂丂墌廃偺挿偝 俀兾倰 亐 敿宎 倰 亖俀兾 偵傛傝丄慡墌廃偺拞怱妏偼丄
丂丂俀兾 乮儔僕傾儞乯 |
丂偟偨偑偭偰丄岞幃 丗 兾亖侾俉侽亱偑摼傜傟傞丅
偙偺偙偲偐傜丄侾儔僕傾儞偼戝懱丄俆俈搙偖傜偄偱偁傞丅乮徻偟偔偼丄俆俈亱侾俈乫係係乭丏俉侽俇丒丒丒乯
丂傑偨丄俁侽亱偼丄兾/俇丂丄俇侽亱偼丄兾/俁丂丄俋侽亱偼丄兾/俀丂側偳傕捈偪偵抦傜傟傞丅
丂偙傟傜偼寁嶼偵傛偭偰傕媮傔傜傟傞偑丄偦傟偼乽屖搙朄乿偺梸偡傞偲偙傠偱偼側偄丅
俋侽亱偵懳偡傞屖偺挿偝偑丄敿墌廃偺敿暘側偺偱丄兾/俀 偩偲偄偆姶妎傪恎偵偮偗傞傋偒偱
偁傠偆丅俇侽亱偺応崌偼丄敿墌廃偺俁暘偺侾丄俁侽亱偺応崌偼丄敿墌廃偺俇暘偺侾丄丒丒丒丅
丂屖搙朄偺掕媊偐傜丄拞怱妏偺戝偒偝偲偙傟偵懳偡傞屖偺挿偝偼斾椺偟丄
拞怱妏 兤 偵懳偡傞屖偺挿偝 俴 偼丄丂俴亖倰兤丂偱梌偊傜傟傞丅
乮偙偺傛偆側岞幃偼丄搙悢朄傪梡偄偰傕摼傜傟傞偑丄岞幃偺娙柧偝偵娭偟偰偼丄偙偪傜偵孯攝偑偁偑傞偩傠偆丅偦
丂偺堄枴偱傕屖搙朄偺桪廏惈偑暘偐傞偲巚偆丅乯
嶰妏娭悢偺摫擖
丂嶰妏斾偵偮偄偰偼丄崅峑侾擭偱妛傇乽悢妛 I 乿偱埖傢傟傞丅偦偙偱偼丄拞妛峑偱妛傫偩憡
帡斾偺墑挿偲偟偰丄庡偵恾宍偺夝愅偵梡偄傜傟傞丅娭悢揑側埖偄偼丄乽悢妛 II
乿偵偍偄偰妛
廗偡傞丅嶰妏娭悢偺僌儔僼偑儊僀儞偩偲巚偆偑丄壛朄掕棟傗扨怳摦偺崌惉偺岞幃傕娷傔偰丄
懡條側岞幃偑峖悈偺傛偆偵墴偟婑偣偰偔傞偲偄偆偺偑棪捈側姶憐偱偁傞丅
丂偍偦傜偔懡偔偺惗搆偑丄偦偺岞幃孮偺慜偵嵙愜傪枴傢偭偰偄傞偺偱偼側偄偐偲巚偆丅
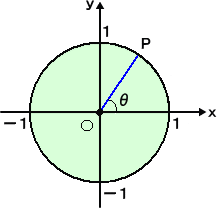 |
丂丂尨揰拞怱丄敿宎侾偺扨埵墌偵偍偄偰丄廃忋偺揰俹偲墌
丂偺拞怱俷傪寢傇摦宎俷俹偑巒慄俷倶偲嶌傞妏乮堦斒偵偼丄
丂摦宎俷俹偺昞偡妏偲偄偆丅乯偑兤偱偁傞偲偒丄揰俹偺嵗昗
丂偼丄
丂丂丂俹乮們倧倱兤丆倱倝値兤乯
丂偱梌偊傜傟傞丅
丂丂偙傟偑丄兤偵懳偡傞嶰妏娭悢 倱倝値兤丄們倧倱兤偺掕媊偱
丂偁傞丅
丂乮傕偪傠傫丄偙偺応崌偺兤偼丄屖搙朄偱梌偊傜傟傞丅乯 |
嶰妏娭悢偺嬌尷偺岞幃
丂
丂師偵丄忋婰偺岞幃傪弞娐榑朄偵側傜側偄傛偆偵拲堄偟偰徹柧偟偰傒傛偆丅
乮嶲峫丗傎偦傗傫偝傫偺俫俹乯
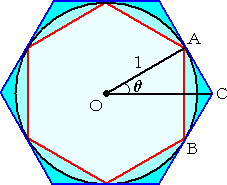 |
丂丂嵍恾偺傛偆偵丄敿宎 侾 偺墌 俷 偵惓 値 妏宍偑撪愙丒
丂奜愙偟偰偄傞丅乮嵍恾偼丄値亖俇 偺応崌乯
丂丂俙俛亖俀倱倝値兤丄俙俠亖倲倎値兤丂側偺偱丄
丂丂惓 値 妏宍偺廃偺挿偝偲丄墌廃偺挿偝偺娭學偐傜丄
丂丂俀値丒倱倝値兤亙俀値丒兤亙俀値丒倲倎値兤
丂丂偡側傢偪丄丂丂倱倝値兤亙兤亙倲倎値兤 |
乮僐儊儞僩乯丂惓 値 妏宍偺廃偺挿偝偲丄墌廃偺挿偝偺娭學偼丄捈姶揑偵柧傜偐偲偟偰傛偄傕偺偐
丂丂丂偳偆偐丄旝柇偱偡偹両嵍懁偺乽亙乿偼帺柧偲偟偰傕丄塃懁偺乽亙乿偼丄屖偑嬋偑偭偰偄傞偺
丂丂丂偱丄恀偭捈偖偵偺偽偟偰傒偰丄兤偵懳偡傞屖偺挿偝偑丄俙俠 傛傝挿偔側傜側偄偲偄偆偙偲傪
丂丂丂妋擣偟側偔偰傕偄偄偺偩傠偆偐丠丂懡暘丄嫵壢彂偱忋婰偺晄摍幃傪帵偡偲偒偵丄帇妎揑
丂丂丂偵暘偐傝傗偡偄柺愊傪梡偄傞偺偼丄弞娐榑朄偵側傞偺傪彸抦偱丄柺搢側妋擣嶌嬈傪旔
丂丂丂偗傞偨傔偲悇嶡偝傟傞丅乯
丂摉俫俹撉幰偺俫俶乽倛倧倣倎倰倕乿偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俇擭侾寧侾係擔晅偗乯
丂忋婰偺僐儊儞僩偱偄傠偄傠媈栤傪帩偨傟偰偄傞傛偆偱偡偑丄偙偺働乕僗偱偼丄嬋慄乮墌屖乯偑
扨挷偵嬋偑偭偰偄傞偺偱乮嵍塃偵僋僱僋僱嬋偑偭偰偄側偄偺偱乯丄捈姶揑偵柧傜偐偲偟偰偄偄
偺偱偼側偄偺偱偟傚偆偐丅偲偄偆偺傕丄傕偟屖偺挿偝偑AC+CB偲摍偟偄側傜偽丄屖偼AC偲CB偺
俀慄暘偵偒傟偄偵増偭偰廳側傞偼偢偱丄恾偺傛偆偵拞嬻偵傇傜壓偑偭偨傛偆側忬懺偵偼側傜
側偄偐傜偱偡丅嶰妏宍偺侾曈偑丄懠偺俀曈偺榓傛傝抁偄偺偲帡偰偄傑偡偹丅尩枾側専徹偲偼
偄偊傑偣傫偑丄捈姶揑偵偼偙傟偱廫暘捠偠傞偲巚偄傑偡丅
丂嬻廙偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俇擭侾寧侾俆擔晅偗乯
丂捈姶揑偵偼傕偪傠傫偦傟偭傐偄偱偡偑丄偦傟偑尩枾偵柧傜偐偱側偄偺偱丄乽妋擣偟側偔偰傕
偄偄偺偩傠偆偐丠乿偲媈栤傪帩偭偰偄傞傢偗偱偟傚偆丅
丂屖偺挿偝偑丄AC+CB傛傝挿偄偐傕偟傟側偄偲偄偆庡挘傪尩枾偵斲掕偡傞偺偼娙扨偱偼側偄
偼偢偱偡丅嬋慄偺挿偝偺掕媊傑偱栠傞偐偦傟偲摨摍側壗偐傪巊傢側偄偲帵偣側偄偼偢偱偡丅
乮嶨姶乯丂偦偆偡傞偲捈姶偱柧傜偐偱丄尩枾偵傕捈偪偵帵偣傞傛偆側応崌偵崱屻弌偔傢偟偨帪
丂丂偵偼丄乽捈姶揑偵柧傜偐乿偲偼尵傢偢偵扨偵乽柧傜偐乿偲尵偭偨曽偑椙偄偺偐側偲偐巚偄
丂丂傑偟偨丅
丂俧俙俬 偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俇擭侾寧侾俆擔晅偗乯
丂捈姶偑棤愗傜傟傞椺偲偟偰丄僔儏儚儖僣乮Schwarz乯偺採摂偲偄偆傕偺偑偁傝傑偡丅僒僀僩偱専
嶕偝傟偰丄恖偺捈姶偱偼墌拰偺懁柺愊偵側傞偼偢偑丄偦偆偲傕尵偄愗傟側偄偙偲偑偁傞丅乮恖
娫偺姶妎偩偗偱偼尒岆傞丄偁傞偄偼娫堘偄傪婲偙偡椺偑悢妛偺帠椺偺拞偵嶳傎偳偁傞傛偆
側婥偑偟傑偡丅偩偐傜媡偵柺敀偄丅乯
丂摉俫俹偱偼丄乽惓 値 妏宍偺廃偺挿偝偲丄墌廃偺挿偝偺娭學偼丄捈姶揑偵柧傜偐乿偱偁傞偲偄
偆棫応偱師偺寁嶼偵恑傓傕偺偲偡傞丅乮忋婰偺乽倛倧倣倎倰倕乿偝傫偵姶幱偟傑偡丅乯
丂忋婰偺 兤 偼丄侽亙兤亙兾/俀 傪枮偨偡傕偺偲偟偰傛偄丅乮値 偺抣傪廫暘戝偒偔偲傟偽傛偄丅乯
偙偺偲偒丄倱倝値兤亜侽丄們倧倱兤亜侽丂側偺偱丄丂丂們倧倱兤亙倱倝値兤/兤亙侾丂偑惉傝棫偮丅
傑偨丄亅兾/俀亙兤亙侽丂偺偲偒丄侽亙亅兤亙兾/俀丂側偺偱丄
丂們倧倱乮亅兤乯亙倱倝値乮亅兤乯/乮亅兤乯亙侾丂丂偡側傢偪丄丂丂們倧倱兤亙倱倝値兤/兤亙侾
偑惉傝棫偮丅
丂偟偨偑偭偰丄兤 仺 亄侽丂丄兤 仺 亅侽丂偺壗傟偵懳偟偰傕丄倱倝値兤/兤 仺 侾丂偲側傞丅
丂埲忋偐傜丄
丂
偺惉傝棫偮偙偲偑帵偝傟偨丅
嶰妏娭悢偺旝暘丒愊暘
丂忋婰偱帵偟偨嬌尷偺岞幃傪梡偄偰丄丂丂乮倱倝値倃乯乫亖們倧倱倃丂丂偲偄偆旝暘偺岞幃偑娙扨偵
媮傔傜傟傞丅
丂幚嵺偵丄倱倝値乮倃亄倛乯亅倱倝値倃亖俀們倧倱乮倃亄倛/2乯倱倝値(倛/2)丂側偺偱丄倛
仺 侽丂偺偲偒丄
丂乮倱倝値乮倃亄倛乯亅倱倝値倃乯/倛亖們倧倱乮倃亄倛/2乯丒(倱倝値(倛/2))/(倛/2) 仺 們倧倱倃
偐傜柧傜偐偱偁傞丅
丂旝暘偺岞幃偐傜丄師偺愊暘偺岞幃偑媮傔傜傟傞丅
丂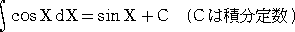 丂
丂
墌偺柺愊偺岞幃偺徹柧
 |
丂丂丂偄傛偄傛墌偺柺愊偺岞幃傪徹柧偡傞弨旛偑惍偭偨
丂丂傛偆偱偁傞丅
丂丂丂尨揰拞怱丄敿宎 倰 偺墌偺曽掱幃偼丄
丂丂丂丂倃2亄倄2亖倰2丂
丂丂丂偵傛傝梌偊傜傟傞丅偦偺巐暘墌偺柺愊傪 俽 偲偍偔偲丄
丂丂丂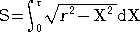 |
偟偨偑偭偰丄丂倃亖倰丒倱倝値兤丂偲偍偄偰丄抲姺愊暘偺岞幃傪梡偄傞偲丄
丂
偲側傞丅丂埲忋偐傜丄
丂敿宎 倰 偺墌偺柺愊偺岞幃偼丄丂敿宎亊敿宎亊墌廃棪乮亖兾 倰2乯
偱偁傞偙偲偑帵偝傟偨丅
乮捛婰乯丂嵟嬤丄摉俫俹傪偛棗偵側偭偨曽偐傜儊乕儖傪捀懻偟偨丅乮暯惉侾俇擭侾侽寧俉擔晅偗乯
丂偦偺曽偵傛傟偽丄乽 兤 仺丂侽丂偺偲偒丄(倱倝値兤)/兤丂仺丂侾丂乿傪丄墌偺柺愊傪梡偄偰徹柧偡
傞曽朄偑弞娐榑朄偲側傞傜偟偄偐傜暿曽朄偱嫵偊傞傋偒偩偲丄抦傝崌偄偺曽偐傜尵傢傟偰
媍榑偵側偭偨偲偺偙偲偱偁傞丅
丂忋婰偱偼丄墌偺柺愊傪媮傔傞摴嬶偲偟偰偺嶰妏娭悢偺旝暘愊暘偑丄
丂丂
傪弌敪揰偲偟偰偍傝丄偦偺徹柧偵崅峑偺嫵壢彂偱偼墌偺柺愊傪梡偄偰偄傞偲偄偆帠偐傜弞
娐榑朄偵側傞偲偄偆榑揰偱偟偨丅
丂偦偺弞娐榑朄傪夞旔偡傋偔丄忋婰偱弎傋偨傛偆偵丄乽傎偦傗傫乿偝傫偑庢傝慻傑傟偰偄傞偙
偲傪徯夘偟傑偟偨丅
丂儊乕儖傪捀懻偟偨曽偵傛傟偽丄倱倝値 兤 偺愊暘傪巊傢偢偵敿宎 倰 偺墌偺柺愊偑
兾倰2 偲尵
偆帠偼嬌尷偺奣擮傪梡偄偰丄惗搆偵愢柧偱偒傞偲偺偙偲偱偁傞丅
乮墌偺柺愊偵偮偄偰偼屆戙偐傜抦傜傟偰偍傝丄偦偺徹柧偼墌偵撪愙丒奜愙偡傞惓懡妏宍偱嬤帡偡傞偙偲偵傛傝
丂摼傜傟偰偄傞丅乮傾儖僉儊僨僗揑曽朄乯乯
丂埲壓偑丄捀偄偨徹柧偺奣棯偱偁傞丅乮堦晹廋惓偟偰宖嵹乯
乣 敿宎 倰 偺墌偺柺愊偑 兾倰2 偲側傞偙偲丂乣
乮徹柧乯丂師偺俁偮偺僗僥僢僾傪摜傫偱帵偡丅
[侾] 丂敿宎 倰 偺墌偵撪愙偡傞惓 俁亊俀n 懡妏宍偺廃偺挿偝傪 俴(値)丄奜愙偡傞惓 俁亊俀n 懡
妏宍偺廃偺挿偝傪 俴乫(値) 偲偡傞偲丄
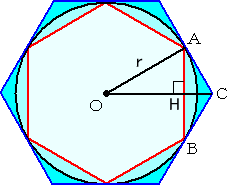 |
丂丂 俴(値) 亙 俴乮墌廃偺挿偝乯 亙 俴乫(値)
偑惉傝棫偪丄値 傪尷傝側偔戝偒偔偟偨偲偒丄
丂丂俴(値)丄俴乫(値) 偼偲傕偵 俴 偵廂懇偡傞丅
|
幚嵺偵丄乷俴(値)乸偼忋偵桳奅側扨挷憹壛楍偱丄乷俴乫(値)乸 傕壓偵桳奅側扨挷尭彮楍偱偁傞
偺偱丄偲傕偵廂懇偡傞丅偙偺偲偒丄仮俙俫俷 佷 仮俠俙俷丂偱偁傞偙偲偵拲堄偟偰丄
丂俴乫(値) 亅俴(値) 亖乮乮倰/併(倰2-l(値)2)乯亅侾乯俴(値)丂丂丂乮 偨偩偟丄l(値) 亖 俙俫丂乯
偐傜丄 値 仺 亣 偲偟偨偲偒偵丄俴乫(値) 亅俴(値) 仺 侽 偲側傞丅
偟偨偑偭偰丄乷俴(値)乸丄乷俴乫(値)乸 偲傕偵摨偠嬌尷抣傪桳偟丄嫴傒寕偪偺尨棟偵傛傝丄
丂値 仺 亣 偲偟偨偲偒丄俴(値) 仺 俴
偲側傞丅
乮曗懌乯丂忋婰偺晄摍幃丂俴(値) 亙 俴乮墌廃偺挿偝乯 亙 俴乫(値)丂偱丄俴(値) 亙 俴乮墌廃偺挿偝乯
丂偱偁傞偙偲偼丄帺柧偲偟偰傛偄偩傠偆丅
丂乮側偤側傜丄俀揰傪寢傇慄暘偺挿偝偑丄偦偺嵟抁嫍棧傪梌偊傞偐傜偱偁傞丅乯
丂偦傟偵懳偟偰丄 俴乮墌廃偺挿偝乯 亙 俴乫(値)丂傪帺柧偲偡傞偵偼彮偟掞峈偑偁傞丅
丂偙偺揰偵偮偄偰丄儊乕儖傪捀懻偟偨曽偼師偺傛偆偵愢柧偟偰偔傟偨丅
丂嬋慄偺挿偝偼丄嬋慄忋偺揰傪寢傇愜傟慄偺挿偝偺榓偺嬌尷偲偟偰梌偊傜傟傞丅
乮偦偺堄枴偱偼丄俴(値) 偑 俴 偵廂懇偡傞偺偼掕媊偦偺傕偺偱偁傞丅乯丂丂丂丂丂丂丂丂
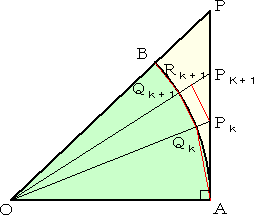 |
丂丂嵍恾偵偍偄偰丄乷俻値乸偼丄屖俙俛忋偺暘揰偱偁傞丅
丂奺暘揰偲揰俷傪寢傇捈慄偑揰俙偵偍偗傞愙慄俙俹偲
丂岎傢傞暘揰偑乷俹値乸偱偁傞丅俹倠俼倠亄侾偲俻倠俻倠亄侾
丂偼暯峴偲偡傞丅偙偺偲偒丄
丂丂俻倠俻倠亄侾亙俹倠俼倠亄侾亙俹倠俹倠亄侾
丂偑惉傝棫偮丅
丂丂偙偺晄摍幃偐傜丄屖俙俛偺挿偝 亙 慄暘俙俹偺挿偝
丂偱偁傞偙偲偑暘偐傝丄傛偭偰丄
丂丂俴乮墌廃偺挿偝乯 亙 俴乫(値)
丂偱偁傞丅 |
乮僐儊儞僩丗暘偐傝傗偡偄徹柧偱偡偹両偙傟偱丄偙傟傑偱偺儌儎儌儎偑層嶶柖徚偟偨姶偠偱偡丅乯
丂偲偙傠偱丄捈宎偲惓懡妏宍偺廃偺挿偝偼憡帡斾偺娤揰偐傜斾椺偟丄偐偮丄偙偺乵侾乶偺帠幚
偵傛傝丄師偺[俀]偑柧傜偐偲側傞丅
[俀]丂乮墌廃)乛(捈宎) 偼忢偵堦掕偱丄 乮[侾] 偺嬌尷抣乯亐俀 倰丂偑偦偺抣偱偁傝丄偙偺抣偑墌
丂丂廃棪 兾 偱偁傞丅
丂乵侾乶偲[俀]偑墌廃偐傜偺 兾 偺夝庍偲偟偰廃抦偺帠幚偲偡傟偽丄師偺[俁]偑杮幙揑側晹暘偱
偁傞丅
[俁] 丂(傾儖僉儊僨僗偺曽朄乯
丂敿宎 倰 偺墌偵撪愙偡傞惓 俁亊俀n 懡妏宍偺柺愊傪 俽(値) 偲偍偔丅
丂撪愙偡傞惓懡妏宍偼丄椬傝崌偆捀揰俀屄偲墌偺拞怱 俷 傪捀揰偲偡傞 俁亊俀n 屄偺崌摨側
擇摍曈嶰妏宍 仮(値) 偵暘妱偱偒傞丅堦偮偺嶰妏宍 仮(値) 偵偍偄偰丄師偺傛偆偵偍偔丅
丂(墌偺拞怱 俷 傪抂揰偵傕偨側偄曈偺挿偝)亖俀亊l(値)
偦偺偲偒丄惓懡妏宍偺柺愊 俽(値乯偲廃偺挿偝 俴(値) 偼偦傟偧傟師偺傛偆偵昞偝傟傞丅
丂俽(値)亖俁亊俀n亊(仮(値) 偺柺愊)亖俁亊俀n亊l(値)亊併(倰2-l(値)2)
丂俴(値)亖俁亊俀n亊(仮(値) 偺曈偱抂揰偑 俷 偱側偄侾曈偺挿偝)亖俁亊俀n亊l(値)亊俀
[侾]丄[俀] 偐傜丄敿宎 倰 偺墌偵懳偟偰丄 値 仺 亣 偲偟偨偲偒丄
丂lim 俴(値) 亖 lim { 俁亊俀n亊俀亊l(値) } 亖 兾亊俀倰
偡側傢偪丄丂丂 lim { 俁亊俀n亊l(値) } 亖 兾亊倰丂丂偲側傞丅
傑偨丄 値 仺 亣 偲偟偨偲偒丄 l(値) 仺 0 偲側傞偙偲偐傜丄偙傟傜傪梡偄偰
丂lim 俽(値)亖lim[俁亊俀n亊l(値)亊併(倰2亅l(値)2)]亖乮兾亊倰乯亊併(倰2)亖兾亊倰2
偱偁傞偙偲偑摼傜傟傞丅
摨條偵偟偰丄敿宎 倰 偺墌偵奜愙偡傞惓 俁亊俀n 懡妏宍偺柺愊傪 俽乫(値) 偲偍偔偲丄
丂俽(値乯 丗 俽乫(値) 亖 倰2亅l(値)2 丗 倰2
側偺偱丄丂俽乫(値)亖 乮倰2/乮倰2亅l(値)2乯乯俽(値乯丂偑惉傝棫偮丅
丂傛偭偰丄偙偺応崌傕丄丂丂lim 俽乫(値)亖lim 俽(値)亖兾亊倰2丂丂偱偁傞偙偲偑暘偐傞丅
偟偨偑偭偰丄丂俽(値乯 亙 俽乮墌偺柺愊乯 亙 俽乫(値)丂偵偍偄偰丄嫴傒寕偪偺尨棟偵傛傝丄
丂俽乮墌偺柺愊乯亖兾亊倰2
偑惉傝棫偪丄
丂敿宎 倰 偺墌偺柺愊偺岞幃偼丄丂敿宎亊敿宎亊墌廃棪乮亖兾 倰2乯
偱偁傞偙偲偑帵偝傟偨丅丂乮徹廔乯
丂傑偨丄忋婰偺徹柧偺拞偱丄俽(値)亖 俴(値)丒乮(侾/俀)併(倰2亅l(値)2)乯
偲偄偆娭學幃偑惉傝棫偮偙偲偵拲堄偡傞偲丄師偺俀偮偺柦戣偼摨抣側柦戣偲側傞丅
[嘥]丂乮墌廃乯乛乮捈宎乯偼忢偵堦掕偱偦偺抣傪墌廃棪 兾 偲偡傞丅
[嘦]丂 (墌偺柺愊)乛(敿宎)2 偼忢偵堦掕偱偦偺抣傪墌廃棪 兾 偲偡傞丅
仸忋偺[俁]偱帵偟偨帠暱偼[嘥] 佀 [嘦]傪帵偟偨傛偆側傕偺偱偁傞偑丄[俁] 偺
俽(値)丄 俴(値) 傪
梡偄偰丄媡偵[嘦] 佀 [嘥] 傕帵偣傞帠偼柧傜偐偱偁傠偆丅
丂傕偟偐偟偨傜墌愊岞幃偼丄偙偺傛偆偵乽墌廃棪 兾 偲偼壗偧傗丠乿偲偄偆掕媊偺巇曽偵傕婲
場偡傞帠暱側偺偱丄柺搢側愢柧晹暘傪徣偄偰岞棟偲偟偰崅峑悢妛偱偼埖偭偰偄傞偲傕峫偊
傜傟傞丅
丂埲忋偑丄偄偨偩偄偨儊乕儖偺撪梕偱偁傞丅
戝曄暘偐傝傗偡偄徹柧偱丄儊乕儖傪捀懻偟偨曽偵姶幱偟偨偄丅
丂忋婰偺徹柧[侾]偵偍偗傞晄摍幃丂 俴(値) 亙 俴乮墌廃偺挿偝乯 亙 俴乫(値)丂偼丄崅峑偺嫵壢彂
偱妛傇晄摍幃丂丂倱倝値兤亙兤亙倲倎値兤丂偦偺傕偺偱偁傞丅偙偺晄摍幃偺徹柧偵丄嫵壢彂偱偼丄
墌偺柺愊傪梡偄偰偄傞偲偄偆偙偲偱丄弞娐榑朄偵側偭偰偄傞偲偄偆榑揰偱偁偭偨丅
嫵壢彂偱偼丄偙偺晄摍幃傪嫆傝強偲偟偰丄
丂
傪徹柧偟丄嶰妏娭悢偺旝愊暘偺岞幃偐傜丄掕愊暘偺寁嶼偱丄墌偺柺愊傪媮傔偰偄傞丅
丂忋婰偺徹柧偱偼丄偦偺傛偆側曽岦傪偲傜側偄偱丄扨側傞嬌尷偺寁嶼偺斖醗偱墌偺柺愊偺
岞幃傪偲傜偊偨傕偺偱偁傞丅
丂lim { 俁亊俀n亊l(値) } 亖 兾亊倰丂偲偄偆嬌尷偺幃偵丄岻柇偵丄
丂
偲偄偆娭學偑尒偊側偄宍偱杽傔崬傑傟偰偄傞丅
丂嫵壢彂偱丄倱倝値兤亙兤亙倲倎値兤丂偺徹柧偵丄婃側偵墌偺柺愊傪梡偄傞棟桼偼丄嬌尷榑傪夞
旔偡傞偨傔偺嫵堢揑攝椂偲棟夝偡傋偒側偺偩傠偆丅
丂偨偩丄偙偺傛偆側嬌尷傪巊偭偨寁嶼偼丄崅峑悢妛偺儗儀儖傪挻偊傞傛偆側晹暘偑偁傞偟丄
傑偨丄戝懡悢偺崅峑惗偑廗傢側偄偱偁傠偆乽悢妛III乿偺榖側偺偱丄擔杮偺崅峑惗偺戝懡
悢偑墌偺柺愊偵偮偄偰丄帺屓姰寢偟側偄傑傑妛嬈傪廔椆偟偰偟傑偭偰偄傞偲偄偆尰幚偵偼
曄傢傝偑側偄丅
乮捛婰乯丂暯惉俀俀擭侾侽寧俀俀擔晅偗
丂俫俶乽埥傞闉偡偲乿偝傫偑丄乽sin兤亙兤亙tan兤偺徹柧乿偵偮偄偰丄摉俫俹偺宖帵斅乽弌夛偄
偺愹乿偵彂偒崬傑傟傑偟偨丅埲壓偼丄偦偺敳悎偱偡丅
丂忋婰偺乽sin兤亙兤亙tan兤乿偺徹柧偵偍偗傞丄兤亙tan兤偺晹暘偼擺摼偟傑偟偨丅偦偙偱丄
sin兤亙兤偺徹柧傪峫偊偰傒傑偟偨丅
乮徹柧乯丂敿宎侾偺墌丂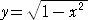 丂傪峫偊丄揰乮侽丆侾乯偐傜揰乮倎丆
丂傪峫偊丄揰乮侽丆侾乯偐傜揰乮倎丆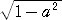 乯傑偱偺墌屖傪
乯傑偱偺墌屖傪
丂兤偲偟丄倱倝値兤亖倎丂偲偡傞丅墌屖偺挿偝偼
丂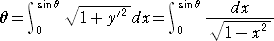
偱梌偊傜傟傞丅偙偙偱丄
丂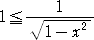
側偺偱丄
丂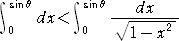
偡側傢偪丄丂sin兤亙兤丂偑惉傝棫偮丅丂乮徹廔乯
丂埲忋偺徹柧偱偼丄嶰妏娭悢偺旝暘丂(倱倝値兤)乫亖們倧倱兤偼梡偄偰偄側偄偨傔丄弞娐榑朄偺
栤戣偼偝偗傜傟偰偄傑偡丅
丂摉俫俹偺宖帵斅乽弌夛偄偺愹乿偵偍偄偰丄埥傞闉偡偲偝傫偼丄乽俀揰娫偺嵟抁嫍棧偼偦傟傪
寢傇慄暘偱偁傞乿偲偄偆柦戣偑儐乕僋儕僢僪婔壗妛偵偍偄偰岞棟側偺偐偳偆偐傪栤傢傟偰偄
傑偡丅乮暯惉俀俀擭侾侽寧侾俉擔晅偗乯
丂忋婰偱弎傋傜傟偰偄傞傛偆偵丄嬋慄偺挿偝偼丄嬋慄忋偺暘揰傪寢傇愜慄偺榓偺忋尷偲偟
偰掕媊偝傟傑偡丅傑偨丄俠1媺偺嬋慄偵偍偄偰偼丄挿偝傪掕愊暘偵偰昞偣傞偨傔丄嬋慄傗捈
慄偺挿偝偺戝彫斾妑偼掕愊暘偺抣偺斾妑偵傛傝峴偆偙偲偑偱偒傑偡丅
丂偡傞偲丄乽俀揰娫偺嵟抁嫍棧偼偦傟傪寢傇慄暘偱偁傞乿偲偼丄挿偝傪掕愊暘偱偼昞偡偙偲偑
弌棃側偄嬋慄丄椺偊偽楢懕偱偁偭偰傕旝暘弌棃側偄嬋慄摍偑偁傞偐傜偙偦岞棟偲偟偰梫惪
偝傟傞偙偲側偺偐側丠偲偄偆媈栤偱偡丅
丂嶰妏宍偺俀曈偺榓偼懠偺侾曈傛傝挿偄偲偄偆偙偲偐傜丄俀揰傪寢傇愜傟慄偺拞偱捈慄偑堦
斣抁偄偲偄偆偙偲丄傑偨丄嬋慄偺挿偝偼丄嬋慄忋偺揰傪寢傇愜傟慄偺挿偝偺榓偺嬌尷偲偟偰
梌偊傜傟傞偙偲偐傜丄乽俀揰傪寢傇嬋慄偺偆偪嵟抁嫍棧傪梌偊傞偺偼慄暘乿偲偄偆偙偲偼丄偁傞
忦審傪枮偨偡嬋慄偵娭偟偰帵偝傟傞傛偆側丏丏丏暤埻婥偱偡偐偹丠
丂埥傞闉偡偲偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俀擭侾侽寧俀俀擔晅偗乯
丂嬋慄偺挿偝偺掕媊傪庤尦偺嫵壢彂偐傜梫栺偟偰堷梡偟傑偡丅側偍丄愜慄偺挿偝偼掕媊嵪
傒偲偟傑偡丅
乲掕媊乴丂嬫夋 乵倎丆倐乶 偵偰掕媊偝傟傞嬋慄俠偵偍偄偰丄嬫夋偺暘妱
丂儮丗丂倎亖倲0亙倲1亙丒丒丒亙倲倣亖倐
偵懳墳偟偰惗偢傞俠忋偺揰 俥乮倲0乯丄俥乮倲1乯丄丒丒丒丄俥乮倲倣乯 傪弴斣偵寢傫偱惗偢傞愜慄傪丄俠
偺嬤帡愜慄偲屇傃丄偦偺挿偝
丂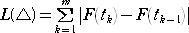
偺偁傜備傞嬫夋偺暘妱儮偺廤崌偺忋尷傪丄俠偺挿偝偲掕媊偡傞丅
丂偙偺掕媊偵偍偄偰丄嬋慄俠偼楢懕丄旝暘壜擻側偳偺惂尷偼側偔丄擟堄偱偡丅傑偨楢懕丄旝
暘壜擻偺嬋慄偵尷傝丄暯嬒抣偺掕棟傪梡偄偰嬋慄偺挿偝俴傪
丂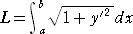
偲偄偆傛偆偵丄掕愊暘傪梡偄偰昞偣傞傛偆偱偡丅
丂掕愊暘偵偰昞偣傞嬋慄偵偍偄偰偼丄俀揰傪寢傇嵟抁嫍棧偼捈慄偱偁傞偲娙扨偵寢榑(徹
柧)偱偒傞偺偱偡偑丄偦偆偱偼側偄嬋慄偵偍偄偰傕乽捈慄=嵟抁嫍棧乿偼徹柧壜擻側偺偱偟傚
偆偐丠偙偙偑丄暘偐傜側偄偺偱偡丅
丂偨偩乽嶰妏宍偺擇曈偺榓偼巆傝偺曈傛傝戝偒偄乿偼嬋慄偺挿偝偺掕媊偲偼柍娭學偵徹柧
壜擻側偨傔丄嬋慄偺挿偝偺掕媊偵愜慄傪峫偊偰偄傞帪揰偱丄婛偵捈慄亙嬋慄傪擣傔偰偄傞
偲偄偊傞偲傕巚偊傑偡丅
丂偲側傞偲丄乽俀揰娫偺嵟抁嫍棧偼偦傟傪寢傇慄暘偱偁傞乿偲偄偆柦戣偼丄乽嶰妏宍偺擇曈偺
榓偼巆傝偺曈傛傝戝偒偄乿偵娨尦偝傟丄岞棟偲偼偄偊側偄偲偄偆偙偲偵側傞偺偱偟傚偆偐丅
丂偟偐偟丄悢妛幰偺埨攞陰巵偺挊嶌偵偰婥偵側傞婰弎偑偁傝傑偟偰丄偦偺傑傑堷梡抳偟傑偡丅
丂埨攞 陰丂挊 乽旝愊暘偺曕傫偩摴乿丂乮怷杒弌斉乯丂倫丏侾俆俀丄侾俆俁
丂曄暘朄偵偰嵟抁嫍棧傪梌偊傞嬋慄偺栤戣丗
丂俀掕揰 俹乮倶1丆倷1乯丄俻乮倶2丆倷2乯傪寢傇嬋慄 倷亖倷乮倶乯偺偆偪丄倷乮倶乯偑楢懕旝暘壜擻忦審傪枮
懌偟偰偄傞偲偄偆忦審偺傕偲偵丄嵟傕抁偄嬋慄傪媮傔傛丅
丂丂(偙偺椺戣傪夝偄偰捈慄偺曽掱幃傪摫弌偟偨屻)
丂(拲堄)丂偙偺徹柧傪尒傟偽丄乽俀揰娫偺嵟抁嫍棧偼偦傟傪寢傇慄暘偱偁傞乿偲偄偆岞棟偼徹
丂丂丂丂丂柧偝傟傞傛偆偵巚偊傞偑丄偙傟偼偳偙傑偱傕乽岞棟乿偱偁偭偰徹柧偼弌棃側偄丅忋偺応
丂丂丂丂丂崌偼丄乽俠1媺偺嬋慄懓乿偵惂尷偟偰丄偦偺夝偼慄暘偱偁傞偙偲傪徹柧偟偰偄傞偙偲偵
丂丂丂丂丂拲堄偝傟偨偄丅
丂帇揰傪曄偊偰丄乽嵟抁嫍棧=捈慄乿偑岞棟偐丄偡側傢偪徹柧壜擻偐偳偆偐傪帵偡偵偼丄俀揰傪
寢傇捈慄傛傝抁偄嬋慄偑乽懚嵼偟側偄乿偙偲傪帵偣傞偐丄偲傕偄偊傞偲巚偄傑偡丅偟偐偟丄偙傟偼
慜弎偺捠傝丄愜慄亜捈慄偺偨傔捈慄亙愜慄亙嬋慄偲側傝丄傗偼傝丄嵟抁嫍棧偼捈慄偲寢榑偱
偒偦偆側婥偑偟傑偡偑丅
丂偙偺條偵巹偺拞偱媍榑偼偐側傝嶖憥偟偰偍傝傑偡丅尩枾惈偽偐傝戝帠偵偡傞偺偼偁傑傝椙
偄偲傕巚偊側偄偺偱偡偑丄傗偼傝嵟抁嫍棧=捈慄偑岞棟偐偳偆偐婥偵側傝傑偡丅
丂摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞俫俶乽俥俶乿偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俀擭侾侽寧俀俀擔晅偗乯
丂乽俀揰傪寢傇嵟抁嫍棧偼慄暘(捈慄)乿偲偄偆偺偼丄乽俀揰傪寢傇嬋慄偺偆偪偱丄偦偺挿偝偑嵟
彫偱偁傞偺偼慄暘偱偁傞乿偲偄偆堄枴偱偡傛偹丅傑偢丄乽俀揰傪寢傇嬋慄乿偺掕媊偲乽偦偺挿偝乿
偺掕媊偑昁梫偱偡丅乽俀揰傪寢傇嬋慄乿傪峀傔偵掕媊偟偰傕丄乽偦偺挿偝乿偑懚嵼偟側偄偙偲偵
側傞偺偱傎偳傎偳側強偵側傞偱偟傚偆丅楢懕惈偖傜偄偼壖掕偡傞偺偐側丅挿偝偼埥傞闉偡偲偝
傫偑彂偐傟偰偄傞宍偱掕媊偡傞偲巚偄傑偡丅挿偝偑懚嵼偟側偄嬋慄偼偨偔偝傫偁傞偙偲偵側傝
傑偡丅偩偐傜丄忋偺柦戣偼丄
丂俀揰傪寢傇嬋慄偱偦偺挿偝偑偁傞傕偺偆偪偱偦偺挿偝偑嵟彫偱偁傞偺偼慄暘偱偁傞
偲偄偆偙偲偵側傞偲巚偄傑偡丅偙傟偼挿偝偺掕媊偐傜偡傟偽徹柧偼擄偟偔側偄偱偟傚偆丅
丂挿偝偑懚嵼偟側偄偺偼丄埥傞闉偡偲偝傫偑彂偐傟偨掕媊偱忋尷偑側偄応崌丄懄偪忋偵桳奅
偱側偄応崌偱偡偐傜丄偦偺偲偒偼挿偝傪柍尷戝偲掕媊偡傞偙偲偵偡傟偽嵟弶偺宍偱傕偄偄偐
傕偟傟傑偣傫丅偁偲偼乽俀揰傪寢傇嵟抁嫍棧偼慄暘(捈慄)乿偲偄偆偺傪傕偭偲堘偆堄枴偵夝偡傞
偙偲偑偱偒傞偐偳偆偐偱偡丅
丂埥傞闉偡偲偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俀擭侾侽寧俀俁擔晅偗乯
丂FN偝傫偺夝愢偼丄憡摉偵寛掕揑側媍榑偵巚偊傑偡丅妋偐偵乽寢傇乿傢偗偱偡偐傜丄楢懕惈
偺壖掕偼昁梫偱偡偹丅傗偼傝丄岞棟偱偼側偔丄乽掕棟乿偲偄偆偙偲偵側傝偦偆偱偡偹丅
丂偟偐偟丄FN偝傫偺巜揈傪庴偗傑偟偰丄巹帺恎丄戝愗側偙偲傪庢傝偙傏偟偰偄傞偙偲偵婥晅偒傑
偟偨丅埨攞 陰 巵偺拲堄偺撪梕偼丄乽俀揰娫偺嵟抁嫍棧偼丄偦傟傪寢傇慄暘偱偁傞乿偲偄偆柦
戣偼岞棟偱偁傞偲偄偆偙偲偱偡丅忋婰偺埨攞 陰 巵偺庡挘偺彂偒崬傒偼丄巹偺岆夝偵傛傞岆
怉偱偡丅乮掶惓嵪傒乯
乮乽俀揰傪寢傇嵟抁嫍棧偼慄暘乿偼岞棟偲偼尵偭偰偄側偐偭偨偺偱偟偨両偙傟偼丄傗偼傝掕棟偱偡偹丅乯
丂夵傔偰傑偟偰丄埨攞巵偺拲堄偵偮偄偰専摙傪偍婅偄偟偨偄偺偱偡丅傑偢丄乽俠1媺偺嬋慄懓
偵惂尷偟偰乿偲尵媦偟偰偄傞偙偲偐傜丄嵟抁嫍棧偺柦戣偼丄俠0媺偺嬋慄偲晄楢懕嬋慄傕嬋慄
偵娷傔偨忋偱丄乽嵟抁嫍棧亖慄暘乿偼岞棟偱偁傞偲偄偭偰偄傞偺偩偲夝庍偟傑偟偨丅
丂楢懕嬋慄偵偮偄偰偼丄乽嵟抁嫍棧=慄暘乿偼丄乽嶰妏宍偺擇曈偺榓偼懠偺堦曈傛傝戝偒偄乿
偐傜徹柧偱偒傞偺偩偲巚偄傑偡丅
丂偱偼丄帄傞偲偙傠晄楢懕側嬋慄偺挿偝偼偳偆側傞偺偱偟傚偆偐丅椺偊偽丄嬫娫乵倎丆倐乶偵偍偄
偰丄桳棟悢偵偰丄侾丄柍棟悢偵偰丄侽偺抣傪偲傞條側晄楢懕側嬋慄偺挿偝偼掕媊偝傟偆傞傕偺
側偺偱偟傚偆偐丅
丂挿偝偑掕媊偝傟側偄偺偱偁傟偽丄挿偝傪柍尷戝偲傕掕媊弌棃側偄嬋慄偑偁傞偙偲偵側傝丄偦
偆偄偭偨帠忣傪娷傔偰埨攞巵偼丄乽俀揰娫偺嵟抁嫍棧偼偦傟傪寢傇慄暘乿傪岞棟偲偟偰偄傞偺
偐丅傕偟偔偼丄偦偆偄偭偨嬋慄偵傕挿偝傪掕媊弌棃傞偑丄壗傜偐偺帠忣偵偰慄暘傛傝抁偄嬋慄
偑側偄偙偲傪帵偡偙偲偑弌棃側偄偨傔偵岞棟偲尵偭偰偄傞偺偐丅
丂俠1媺偺嬋慄懓偵惂尷偟側偄応崌丄乽俀揰娫偺嵟抁嫍棧偼偦傟傪寢傇慄暘偱偁傞乿偼壥偨偟
偰岞棟偲偄偊傞偺偱偟傚偆偐丅
丂俥俶偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俀擭侾侽寧俀俁擔晅偗乯
丂乽俀揰娫偺嵟抁嫍棧乿偲偄偆尵梩偵丄悢妛偺尵梩偲偟偰偼(擔忢尵岅偱偼晛捠偵巊偄傑偡乯堘
榓姶偑偁傝傑偡丅俀揰娫偺嫍棧偑堦堄揑側堄枴傪帩偮偺偱丄偦傟偵嵟抁偲偄偆廋忺岅傪偮偗
傞偺偑傛偔傢偐傝傑偣傫丅嵟抁傪庢偭偰偟傑偊偽丄乽俀揰娫偺嫍棧偼偦傟傪寢傇慄暘(偺挿偝)
偱偁傞乿偱丄偙傟偼岞棟偱偼側偔掕媊偱偡偹丅
丂傑偨丄乽桳棟悢偵偰丄侾丄柍棟悢偵偰丄侽偺抣傪偲傞條側晄楢懕側嬋慄偺挿偝乿偵偮偄偰丄
丂嬫夋 乵倎丆倐乶 偺暘妱丂儮丗丂倎亖倲0亙倲1亙丒丒丒亙倲倣亖倐丂偱丄岎屳偵桳棟悢丄柍棟悢傪庢傟偽
俴(儮)亖倣丂偱偡偐傜丄忋偵桳奅偱偼側偔挿偝偼柍尷戝偵側傝傑偡丅偁傞偄偼忋尷偼側偄偺偱
挿偝偼掕媊偱偒側偄偙偲偵側傝傑偡丅偙偙傑偱晄楢懕偵偟側偔偰傕丄偁傞揰偱塃嬌尷偐嵍嬌尷
偑懚嵼偟側偄埵偱挿偝偼柍尷戝偵側傞偲巚偄傑偡丅
丂偝傜偵丄乽俠1媺偺嬋慄懓偵惂尷偟側偄応崌丄乽俀揰娫偺嵟抁嫍棧偼偦傟傪寢傇慄暘偱偁傞乿
偼壥偨偟偰岞棟偲偄偊傞偺偱偟傚偆偐丅乿偵偮偄偰丄
丂俀揰娫偺嵟抁嫍棧傪丄俀揰傪寢傇嬋慄偺挿偝偺嵟彫抣偲峫偊丄嬋慄偺挿偝傪慄暘偺挿偝偲
嬫娫偺暘妱傪巊偭偨宍偱掕媊偡傞尷傝丄岞棟偱偼側偔掕棟偵側偭偰偟傑偆偲巚偄傑偡丅偩偐傜
偙傟偑岞棟偱偁傞偨傔偵偼彮側偔偲傕偳偪傜偐傪曄偊側偄偲偄偗側偄偙偲偵側傝傑偡丅
丂埥傞闉偡偲偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俀擭侾侽寧俀俁擔晅偗乯
丂傗偼傝丄偛巜揈捠傝丄乽俀揰娫偺嫍棧乿偵嵟抁傪偮偗傞偺偼曄偱偡偹丅挊幰偼應抧慄偺掕
媊偺偙偲傪偄偭偰偄傞偺偐丏丏丏丅
丂俠1媺偺嬋慄懓偵惂尷偲偄偆偙偲側偺偱丄帄傞偲偙傠晄楢懕側娭悢傪採埬偟偰傒偨偺偱偡偑丄
傗偼傝丄偦傟傪嬋慄偲屇傇偵偼憡摉偺堘榓姶偑偁傝丄忋弎偺堄枴偼撲偺傑傑偱偡丅尵梩偺
堄枴傪慺捈偵夝偡傟偽丄儐乕僋儕僢僪暯柺偵偍偄偰丄俠1媺偱偼側偄嬋慄偵娭偟偰偼丄慄暘傛
傝抁偄嬋慄偑懚嵼偟側偄偙偲傪懠偺岞棟偐傜偼徹柧偱偒側偄丄偲尵偭偰偄傞傛偆偵巚偊傑偡丅
壗偩偐掕媊偲岞棟傪崿摨偟偰偄傞傛偆側丏丏丏丅
丂埥傞闉偡偲偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俀擭侾俀寧俁侽擔晅偗乯
丂乽儐乕僋儕僢僪婔壗妛偵偍偄偰丄俀揰娫偺嵟抁嫍棧偼捈慄偱偁傞乿偲偄偆柦戣偼岞棟偐掕棟
偐偲偄偆偙偲傪媍榑偝偣偰偄偨偩偒傑偟偨丅
丂埨攞陰巵偺乽俀揰娫偺嵟抁嫍棧偼慄暘偲偄偆岞棟偼丄偳偙傑偱傕岞棟偱偁傝徹柧偼弌棃側
偄乿偲偄偆尵媦偑傗偼傝婥偵側偭偰偍傝傑偟偨偺偱丄偦偺屻峫偊偨偙偲傪偛徯夘偄偨偟傑偡丅
丂傑偢丄俀揰乮倶1丆倷1乯丄俻乮倶2丆倷2乯娫偺嫍棧偺掕媊偼丄
丂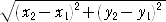
偲偟傑偡丅偙偺嫍棧傪挿偝偲偟偰傕偮偺偼捈慄偱偡丅偙偺帪揰偱(儐乕僋儕僢僪婔壗妛偺岞棟
傛傝)丄嶰妏宍偺擇曈偺榓偼懠偺堦曈傛傝戝偒偄偼乽徹柧偝傟傑偡乿丅
丂師偵丄嬋慄偺挿偝偼丄嬋慄忋偺暘揰傪寢傇愜傟慄偺榓偺忋尷偲偟偰掕媊偝傟傑偡丅
丂偙偺掕媊偲暯嬒抣偺掕棟傛傝丄嬋慄偑C侾媺偺偲偒偼丄偦偺挿偝傪掕愊暘傪梡偄偰昞偣傞
偙偲偑乽徹柧偝傟傑偡乿丅
丂偦偟偰丄偦偺嵺(C侾媺偺応崌)偼丄嬋慄偺挿偝傪掕愊暘偱昞偣傞偲偄偆掕棟偐傜丄偦偺嵟
彫抣傪梌偊傞嬋慄偼慄暘偱偁傞偙偲偑徹柧偝傟傑偡丅
丂偙偙偱拲栚偝傟傞偺偼丄嬋慄偺挿偝偼丄捈慄側偄偟愜傟慄偺挿偝傛傝傕戝偒偄偲丄掕媊偝
傟偰偄傞偙偲偱偡丅(嶰妏宍偺擇曈偺榓)亜(懠偺堦曈)偼丄掕棟偱偡偟丄嬋慄偑C侾媺偺偲偒
偵掕愊暘偱挿偝傪昞偣傞偺傕掕棟偱偡丅
丂偟偐偟丄嬋慄帺懱偺挿偝偼捈慄側偄偟愜傟慄傛傝戝偒偄(忋尷)偲掕媊偡傞偟偐埖偄傛偆偑
側偔丄偙偺偙偲偼徹柧偝傟偰偄傑偣傫丅偦傕偦傕嬋慄偺挿偝偵偮偄偰丄憖嶌揑側掕媊傪梌偊
側偔偰偼悢妛揑偵嬋慄偺挿偝傪埖偆偙偲偼偱偒傑偣傫偺偱丄摉偨傝慜偲偄偊偽摉偨傝慜偱偡
偑丏丏丏丅
丂偙偺偙偲傪丄埨攞陰巵偼丄乽俀揰娫偺嵟抁嫍棧偼偦傟傪寢傇慄暘偱偁傞偲偄偆岞棟偼丄偳
偙傑偱傕岞棟偱偁傞乿偲昞尰偟偨偺偐偲巚偆偺偱偡丅
丂嵟抁嫍棧偲偄偆昞尰偵彮偟堘榓姶偑偁傝傑偡偑丄偙傟偼偍偦傜偔俀揰偺嵟抁楢寢慄偺挿
偝偵偍偄偰嵟彫偺傕偺偼慄暘偱偁傞丄偲偄偆偙偲側偺偩傠偆偲巚偄傑偡丅
丂偦偟偰丄偦偺慄暘埲壓偺挿偝傪傕偮嬋慄傪儐乕僋儕僢僪婔壗妛偱偼掕媊弌棃側偄丄偲偄偆
條偵夝庍偟偰偍傝傑偡丅捈慄偲愜傟慄偺挿偝偱偁傟偽丄梕堈偵斾妑弌棃傑偡偟丄C侾媺偱偁
傞嬋慄摨巑偱偁傟偽丄掕愊暘傪斾妑偡傟偽挿偝偺斾妑偼壜擻偱偡丅
丂偟偐偟丄C侾媺偱偼側偄嬋慄偲捈慄偺挿偝偺斾妑偼丄偦傕偦傕嬋慄傪愜傟慄偺忋尷偲偟偰
掕媊偟偰偁傞偨傔丄偳偪傜偑挿偄偐偲偄偆斾妑偺媍榑偼柍堄枴偱偡丅偱偡偐傜丄俀揰傪寢傇
嬋慄偺挿偝偑丄俀揰娫偺慄暘偺挿偝傛傝戝偒偔側傞偙偲偼徹柧偡傋偒柦戣偱偼側偔丄梫惪偝
傟傞傋偒(掕媊偝傟傞傋偒)柦戣偩偲偄偆偙偲偐偲巚偄傑偡丅
丂忕挿偵側傝傑偡偑丄傑偲傔偱偡丅
丂乽儐乕僋儕僢僪婔壗妛偵偍偄偰丄慄暘偲愜傟慄丄偝傜偵丄C侾媺偺嬋慄偵尷傟偽丄俀揰偺嵟
抁楢寢慄偼慄暘偱偁傞偲偄偆柦戣偼徹柧偱偒傞丅偟偐偟丄堦斒偺嬋慄傪傕娷傔傞偲丄嬋慄
偺挿偝偺掕媊傪嬋慄忋偺暘揰傪寢傇愜傟慄偺榓偺忋尷偲偟偰掕媊偡傞傎偐側偄偨傔丄俀
揰傪寢傇嬋慄偑慄暘傛傝挿偄偺偼掕媊偱偁傝丄亀俀揰偺嵟抁楢寢慄偼慄暘亁偱偁傞偲偄偆
柦戣偼徹柧偺懳徾偲偼側傜側偄丅傛偭偰丄俀揰偺嵟抁楢寢慄偼慄暘偱偁傞偲偄偆柦戣偼
岞棟偱偁傞丅乿
丂埲忋偑丄偦偺屻峫偊偰傒偨偙偲偱偡丅傑偲傔偰傒偨傕偺偺丄偳偆傕帺怣偑偁傝傑偣傫丅偳
偆偟偰傕偙偺媍榑偵寛掕揑側摎偑梸偟偄偺偱丄偳偆偐奆條丄専徹傪媂偟偔偍婅偄偄偨偟傑偡丅
丂埥傞闉偡偲偝傫偐傜儊乕儖傪偄偨偩偄偨丅乮暯惉俀俁擭侾寧俋擔晅偗乯
丂忋婰偱丄嶰妏娭悢偺旝暘丂(倱倝値兤)乫亖們倧倱兤傪梡偄側偄偱丄 sin兤亝兤傪徹柧偟傑偟偨偑丄
摨條偵兤亝tan兤偺徹柧傕峴偊傑偡丅
乮徹柧乯丂尨揰拞怱偱敿宎侾偺墌 倷亖併(侾亅倶2)傪峫偊丄俀揰(侽丆侾)丄(倎丆併乮侾亅倎2乯)傪寢傇
墌屖偺挿偝傪兤偲偡傞丅 偡傞偲丄丂倲倎値兤亖倎/併乮侾亅倎2乯丂偲側傞丅
偙偙偱丄丂
丂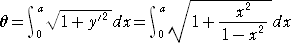
偄傑丄丂倲亖倶/併乮侾亅倶2乯丂偲偍偔偲丄丂倶亖倲/併乮侾亄倲2乯丂偱丄倓倶/倓倲亖侾/乷併乮侾亄倲2乯乸3
側偺偱丄
丂 丂丂丂乮徹廔乯
丂丂丂乮徹廔乯
乮僐儊儞僩乯
丂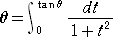
偼丄墌屖偲偄偆偙偲傪棧傟偰帺柧側幃側偺偱丄徹柧偺慜敿晹暘偼偄傜側偄傛偆側丏丏丏梊姶丅
丂偝偰丄埥傞闉偡偲偝傫偺榖偵栠傝傑偡丅
丂寢嬊偺偲偙傠丄墌偼C侾媺偺嬋慄偱偡偐傜丄掕愊暘偱挿偝傪寁應偱偒傞偨傔丄嶰妏娭悢偺
旝暘傪梡偄傛偆偑梡偄傑偄偑丄嬋慄偺挿偝偺掕媊偐傜帺偢偲丂sin兤亝兤亝tan兤丂偼摫偐
傟偰偟傑偆偲偄偆偙偲偵側傝傑偡丅
丂偦偺掕媊偲偼丄嬋慄偺挿偝傪偦偺忋偺暘揰傪寢傇愜傟慄偺榓偺忋尷偲偡傞傕偺偱偡丅
丂傑偨丄墌偺応崌丄撪愙 値 妏宍偺廃埻偼丄値 傪偄偔傜戝偒偔偲偭偰傕丄昁偢奜愙n妏宍偺廃
埻傛傝彫偝偔側傝傑偡丅
丂偙偺偙偲傛傝丄掕愊暘傪梡偄偢丄傛傝崻杮揑側丂sin兤亝兤亝tan兤偺暿徹柧傪峴偭偰傒傑
偡丅
乮徹柧乯丂0亝兤亙兾/俀丂偵偰丄丂sin兤亝tan兤丂丄丂sin兤亝兤丂偼丄嬋慄偺挿偝偺掕媊偐傜
丂帺柧(栜榑丄C侾媺偺嬋慄偱偡偐傜徹柧傪偟偨曽偑挌擩側媍榑偱偡偑)丅
傑偨丄0亙兤偺偲偒丄兤傪廫暘彫偝偔偲傟偽丄擟堄偺惓偺幚悢兠偵懳偟偰丄兤-sin兤亙兠
偲偱偒傞(嬋慄偼愜傟慄偺榓偺乽忋尷乿偱偡偐傜)丅
丂偙偙偱丄tan兤亙兤偲側傞奜愙 値 妏宍偑偁傞偲壖掕偡傞丅
丂廫暘偵 値 傪戝偒偔偲傟偽丄丂tan兤亙sin兤亙兤偲側傞 値 偑懚嵼偡傞丅
偟偐偟丄偙傟偼墌偺撪愙懡妏宍偺廃埻偑奜愙懡妏宍偺廃埻傛傝戝偒偔側傞偨傔柕弬丅
丂備偊偵丄0亙兤亙兾/俀丂偵偰丄sin兤亙兤亙tan兤偲側傝丄兤亖侽丂偺偲偒丄
丂sin兤亖兤亖tan兤偲側傞丅丂乮徹廔乯
丂偙偺懠偵暿徹柧偲偟偰丄sin兤傪廂懇偡傞柍尷媺悢偵偰掕媊偡傞傕偺偑偁傝傑偡丅慜弎偺
徹柧偱偼嶰妏娭悢偲墌屖偼婔壗妛揑側掕媊傪梌偊傜傟偰偄傑偟偨偑丄夝愅揑側掕媊傪峴
偄傑偡丅
乮徹柧乯丂sin兤亖儼乷(亅侾)n/(俀値亄侾)両乸兤2n亄1
丂cos兤=儼乷(亅侾)n/(俀値)両乸兤2n丂丂丂乮丂儼偼丄値亖侽乣亣丂乯丂偲掕媊偡傞丅
偙傟傜偺惍媺悢偼丄慡偰偺兤偵偍偄偰愨懳廂懇偡傞丅
傑偨丄偙偺掕媊偐傜丄0亝兤亝兾/俀偵偍偄偰丄丂侽亝cos兤亝侾丂偑徹柧偝傟傞丅
偦偟偰丄丂0亙sin兤偵偍偄偰丄丂sin兤/兤亙侾丂偲側傞偨傔丄丂sin兤亙兤丂偲側傞丅
偝傜偵丄
丂
偱偁傞偐傜丄擟堄偺惓偺幚悢兠偵懳偟偰丄丂兤亅sin兤亙兠側傞兤偑懚嵼偡傞丅
丂傑偨丄丂侽亙cos兤亝侾丂偵偍偄偰丄丂sin兤亝sin兤/cos兤丄
偡側傢偪丄丂sin兤亝tan兤丂(摍崋偼丄兤亖侽丂偵偰惉棫)
丂偙偙偱丄tan兤亙兤側傞兤偑懚嵼偡傞偲壖掕偡傞偲丄tan兤亙sin兤亙兤丂偲側傞偙偲偵側傝
柕弬丅備偊偵丄丂0亝兤亙兾/俀丂偵偍偄偰丄丂sin兤亝兤亝tan兤丂偑惉棫偡傞丅丂乮徹廔乯
丂屻敿偺晹暘偺媍榑偼慜弎偺媍榑偲傎傏摨偠偱偡丅婔壗妛揑側媍榑偱偼丄嬋慄傪嬋慄忋
偺暘揰傪寢傇愜傟慄偺榓偺忋尷偲偟偰媍榑偟偰偄傞偺偵懳偟偰丄夝愅揑側媍榑偱偼丄愨
懳廂懇偡傞惓媺悢傪梡偄偰sin兤傪掕媊偟偰偄傑偡丅
丂墌屖偺応崌偵尷傝丄偦偺挿偝偵偮偄偰丄婔偮偐偺徹柧傪偛徯夘抳偟傑偟偨偑丄堦斒偺嬋
慄偵偍偄偰傕丄乽俀揰偺嵟抁楢寢慄偼慄暘偱偁傞乿偲偄偆柦戣偼丄嬋慄偺挿偝傪偆傑偔掕媊
偡傞偨傔偵梫惪偝傟傞乽徹柧偺懳徾偲偼側傜側偄柦戣乿偲峫偊傜傟傑偡丅
(抐尵偟偰偍偒側偑傜丄帺怣偑側偄偺偨傔丄偛憡択偝偣偰捀偔師戞偱偡丅偙偺庡挘偺摉斲傪偛専摙捀偗
傞偲彆偐傝傑偡)
丂楌巎揑側榖偟偵側傝傑偡偑丄偙偺傛偆側嬋慄偺挿偝偺惈幙偵弶傔偰尵媦偟偨偺偼傾儖僉
儊僨僗偱偡丅栜榑丄斵偺帪戙偵偼乽挿偝乿偲偄偆帺柧側傕偺傪悢妛揑偵掕媊偡傞偲偄偆峫偊曽
偑側偄偨傔丄嬋慄偺挿偝偺戝彫娭學傪岞棟偲偟偰梫惪偟傑偟偨丅
丂朻摢偱庢傝忋偘傜傟偰偄傞媮愊朄偼丄傾儖僉儊僨僗偺弶婜偺傕偺偲峫偊傜傟傞榑暥乽墌偺
寁應乿偵偰埖傢傟偰偄傞曽朄偱偡丅偦偺榑暥偱偼丄sin兤亙兤亙tan兤(栜榑丄嶰妏娭悢偵傛傞
昞尰偱偼偁傝傑偣傫偑)偼帺柧偺偙偲偲偟偰埖傢傟偰偄傑偡偑丄偦偺屻彂偐傟偨榑暥乽媴偲墌
拰偵偮偄偰乿偵偰丄sin兤亙兤亙tan兤傪徹柧偡傞偨傔偺嬋慄偺挿偝偺惈幙傪岞棟偲偟偰徻
嵶側愢柧傪敽偄掕幃壔偟傑偡丅
丂偦偺偙偲傪摜傑偊偰丄悢妛嘨偵偍偗傞乽墌偺媮愊偺弞娐榑朄乿偵偮偄偰丄巹偺峫偊傪怽偟
忋偘傑偡丅
丂妋偐偵崅峑惗偵尩枾側徹柧傪棟夝偝偣傞昁梫偼側偄偲巚偄傑偡丅偟偐偟丄業崪側弞娐榑
朄傪巜摫偟懕偗傞偺傕摨帪偵栤戣偱偁傞偲峫偊傑偡丅栤戣偺崻尮偼丄嬋慄偺挿偝偺掕媊傪
峴偆偨傔偺摴嬶偑懙偭偰偄側偄偙偲偵偁傞偺偱偡偐傜丄傾儖僉儊僨僗偵曧偄
丂(撪愙懡妏宍偺廃埻)亙(墌廃)亙(奜愙懡妏宍偺廃埻)
傪丄偁傞掱搙偺愢柧傪敽偄岞棟揑偵擣傔偰偟傑偆偺傕椙偄偐偲巚偆偺偱偡丅
丂偦偆偡傞偲丄乽挿偝乿偲偼壗偐丄偲偄偆栤戣堄幆偑敪惗偡傞宊婡偵傕側傞偺偱偼側偄偱偟傚偆偐丅
丂摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞俫俶乽嬻廙乿偝傫偑忋婰榖戣偵偮偄偰峫嶡偝傟傑偟偨丅
乮暯惉俀係擭俋寧俋擔晅偗乯
丂墌廃偺挿偝/捈宎亖兾偲偟偨偲偒丄巹偑巚偆偵偼丄埲壓偺乮侾乯乣乮俆乯偼摨抣偩偲巚偄傑偡丅
偮傑傝偳傟偐傪帵偡偵偼偳傟偐傪慜採偲偡傞昁梫偑偁傝傑偡丅媡偵丄偳傟偐傪慜採偲擣傔傟
偽懠傪摫偔偙偲偑偱偒傑偡丅
乮侾乯丂墌偺柺愊偑兾r2偱偁傞偙偲
乮俀乯丂墌廃偺挿偝偑愜傟慄偺忋尷乮嬌尷乯偱偁傞偙偲
丂丂丂乮摿偵撪愙惓懡妏宍偺廃偺嬌尷偱偁傞偙偲乯
乮俁乯丂扨埵墌偺廃偺敿暘亖兾偑 併[1+(y乫)2] 偺[-1丆1]偱偺掕愊暘抣偱偁傞偙偲
丂丂丂乮偙偙偱丄倷=併(1-倶2)丂乯
乮係乯丂墌廃偺屖偺挿偝偑奜懁傪捠傞愜傟慄傛傝抁偄偙偲
乮俆乯丂lim倶仺0 sin(倶)/倶 亖 1 偱偁傞偙偲
丂崅峑悢妛偱偼乮侾乯傪慜採偲偟偰榖傪恑傔偰偄傞傛偆偵尒偊傑偡丅乮彫妛峑偱廗偭偨偙偲偼巊
偭偰偄偄偲偄偆棫応乯偦偆偄偆尒曽偱惍棟偝傟偰傒傞偲偡偭偒傝偡傞偺偱偼側偄偱偟傚偆偐丅
乮僐儊儞僩乯丂嬻廙偝傫丄偛巜揈偁傝偑偲偆偛偞偄傑偡丅
丂埥傞闉偡偲偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀係擭俋寧侾係擔晅偗乯
丂墌偺柺愊傪寁嶼偡傞嵺偺弞娐榑朄偵偮偄偰丄嬻廙偝傫偐傜偺偛巜揈偵偮偄偰専摙偟偰傒
傑偟偨丅嬻廙偝傫偼俆偮偺柦戣傪摨抣偲偟偰丄偳傟傪弌敪揰偲偡傞偺偐偺栤戣偱偁傞偲峫偊
傜傟偰偄傑偡丅
丂柺愊丄挿偝傪丄掕愊暘偲嬌尷偱掕媊偡傞棫応偱偡偲丄乮侾乯偼丄佺01併(1-倶2)d倶=侾/係偱偁傞
偙偲傪岞棟偲偟偰丄嶰妏娭悢偺嬌尷傗旝暘傪掕棟偲偟偰摫偔棫応偲偄偊傑偡丅
丂乮俀乯偵偮偄偰偼丄偄傢備傞乽尩枾乿偲偄傢傟傞嫵壢彂偱嵦梡偝傟偰偄傞丄嬋慄偺挿偝偺掕媊
偦偺傕偺偱偡丅
丂乮俁乯偼乮侾乯偲摨條偵丄墌廃偺挿偝偑丄佺-11 併[1+(y乫)2] =兾偱偁傞偙偲傪岞棟偲偟偰偄傑偡丅
丂乮係乯偵偮偄偰偼丄墌廃偺挿偝乮埲屻L乯偑奜愙値妏宍偺廃埻偺挿偝乮埲屻Qn乯傛傝傕抁偄偙偲
傪岞棟偲偡傟偽丄乮侾乯乣乮俁乯乮俆乯傪掕棟偲偟偰摫弌偱偒傞偲偄偆帠偩偲巚偆偺偱偡偑丄巹偼彮
偟栤戣偑偁傞偲峫偊傑偡丅
丂L亙Qn丂偲梫惪偡傞偩偗偱偼丄L偼Qn傛傝傕抁偄壗偐丄偲偟偐偟傔偝傟偰偍傜偢丄撪愙値妏宍
偺廃埻偺挿偝傪Pn偲偡傞偲丄L亙Pn亙Qn偲偄偆壜擻惈傕巆偝傟傑偡偺偱丄墌偺媮愊偵偼巊梡
弌棃傑偣傫丅偱偡偺偱丄乮係乯偼丄
丂乮係亅侾乯丂L亙Qn丂偐偮丂擟堄偺幚悢兠偵偮偄偰丄Qn亅L亙兠丂偲側傞値偑懚嵼偡傞
丂丂傑偨偼
丂乮係亅俀乯丂Pn亙L亙Qn
偺偄偢傟偐傪岞棟偲偡傋偒偲峫偊傑偡丅
丂乮俆乯偵偮偄偰偼丄嶰妏娭悢傪婔壗妛揑堄枴傪棧傟偰丄lim倶仺0 sin倶/倶亖侾丂偵偰掕媊偡傞棫
応偱偡丅偙傟偼丄偁傞堄枴丄嶰妏娭悢傪柍尷媺悢偵偰掕媊偡傞棫応偲帡偰偄傑偡丅
丂埲忋傪専摙偡傞偲丄乮俀乯埲奜偺棫応偱偼丄墌廃偺挿偝丄堦斒揑偵偼嬋慄偺挿偝偲偼壗偐丄
偲偄偆偙偲偑掕媊偝傟偰偄傑偣傫丅偨偩偟丄乮係亅侾乯乮係亅俀乯偵偮偄偰偼丄昞尰偼堎側傝傑偡偑丄
乮俀乯偲摨條偵墌廃偺挿偝傪掕媊偡傞柦戣偱偁傞偲峫偊傑偡丅
丂乮侾乯乣乮俆乯偺摨抣惈偑帵偝傟偰傕丄乮俀乯埲奜偼丄嬋慄偺挿偝偺懚嵼偑捈娤偵婎偯偄偰偄傞
偙偲傪娪傒傑偡偲丄傗偼傝丄乮俀乯偙偦偑僔儞僾儖偝偲偄偆揰偐傜媍榑偺弌敪揰偲偟偰揔愗偲峫偊
傑偡丅
丂側偍丄傾儖僉儊僨僗偑墌偺媮愊偵乮係亅俀乯傪梫惪偟偨偺偼丄斵偺帪戙丄挿偝傗柺愊偼乽柧傜
偐側懚嵼乿偱偁傞偨傔丄偦傟傜傪掕媊偡傞偲偄偆峫偊偑側偐偭偨偙偲偲丄悢妛偵偍偗傞掕媊偺
峫偊曽偑丄嬤戙埲崀偲偼堎側傞偨傔偲峫偊傜傟傑偡丅
丂嬻廙偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀係擭俋寧侾係擔晅偗乯
丂専摙捀偒偁傝偑偲偆偛偞偄傑偡丅巹偼丄乽俀揰傪寢傇嵟抁嫍棧偼慄暘乿偼慜採偲偟偰巊偭偰
傕椙偄偮傕傝偱乮係乯傪彂偄偰偄傑偟偨丅偦偆偄偆堄枴偱
丂乮係亅俁乯丂L亙Qn丂俀揰傪寢傇嵟抁嫍棧偼慄暘
傪採帵偟偰偍偒傑偡丅
丂埥傞闉偡偲偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀係擭俋寧侾俆擔晅偗乯
丂侾擭埲忋慜偺媍戣偱偡偑丄偳偆傕婥偵側偭偰偍傝傑偟偨偙偺弞娐榑朄偵傑偮傢傞媈栤傪嬻
廙偝傫偲媍榑偡傞偙偲偱嵞峫偱偒傞偙偲傪偁傝偑偨偔巚偄傑偡丅
丂乮俆乯偼丄嶰妏娭悢偺嬌尷傪婔壗妛揑捈娤傪棧傟偰掕媊偡傞棫応偱偁傝丄偙偺掕媊偵偼丄
栤戣偼側偄偲巚偄傑偡丅偨偩丄偙偺傛偆偵嶰妏娭悢傪掕媊偟偨応崌丄偙偺掕媊偐傜丄嶰妏娭
悢偺惈幙丄婔壗妛揑側掕媊偲偺堦抳側偳傪妋擣丄摫弌偡傞昁梫偑偁傞偼偢偱偡丅偄傢備傞
乽尩枾攈嫵壢彂乿偱偁傞丄悪塝岝晇挊丂乽夝愅擖栧嘥乿偱偼丄弞娐榑朄傪夞旔偡傞偨傔丄嶰
妏娭悢傪惍媺悢偵偰掕媊偟丄偦偙偐傜丄壛朄掕棟丄僆僀儔乕偺岞幃傪徹柧偟丄偦偟偰丄婔壗
妛揑掕媊偲偺堦抳傪妋擣偟偰偄傑偡丅
丂lim倶仺0 sin倶/倶亖侾丂偼嬋慄偺挿偝傪掕媊偡傟偽丄弞娐榑朄傪夞旔偟偰丄寁嶼壜擻偱偡丅偱
偡偺偱丄lim倶仺0 sin倶/倶亖侾丂傪掕媊偲偟偰埖偆応崌丄偦偙偐傜嶰妏娭悢偺惈幙傪摫弌偟側偗
傟偽側傜側偄傛偆偵巚偄傑偡丅嶰妏娭悢偼婔壗妛揑偵掕媊偟丄偦偺嬌尷偼婔壗妛揑側挿偝
偺掕媊傪旔偗偰捈愙丄侾偲掕媊偡傞偺偼傗偼傝堘榓姶偑偁傝傑偡丅
丂傑偨丄乮侾乯乣乮係乯偱偡偑丄墌偼堦斒揑側嬋慄偺側偐偺侾偮偵偡偓側偄偨傔丄堦斒揑側嬋慄
偺挿偝丄嬋慄偵埻傑傟傞柺愊傪掕媊偟偰埖偆棫応偐傜偡傞偲丄墌廃偺挿偝傗墌偺柺愊丄墌廃丄
愙慄丄撪愙慄暘偺挿偝偲偺娭學傪屄暿偵掕媊偡傞乮侾乯乣乮係乯偼彮偟夁忚偵巚偊傑偡丅
丂嬻廙偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀係擭俋寧侾俆擔晅偗乯
丂偛巜揈偁傝偑偲偆偛偞偄傑偡丅乮俆乯偼丄巹偼嶰妏娭悢傪婔壗妛揑偵掕媊偡傞棫応偺偮傕傝
偱偟偨丅偦偺堘榓姶丄尵傢傟偰傒傟偽偦偺捠傝偱偡丅婔壗妛揑偵掕媊偟偨側傜嬌尷偼傕偆
寛傑偭偰偄傞偼偢偩丄偲偄偆偙偲偱偟傚偆偐丅崻尮偵偁傞栤戣揰偼丄兾偑幚悢偲偟偰掕傔傜傟
偰偄側偄偙偲偱偼側偄偐偲巚偄傑偡丅偦偙偱丄乮俆乯偼師偺傛偆偵彂偔偲椙偐偭偨偱偟傚偆偐偲
巚偄傑偡丅
乮俆'乯丂lim倶仺0 倶sin(180亱/倶)亖兾
丂偙偺嬌尷偼丄乽扨埵墌偵撪愙偡傞惓n妏宍偺廃挿/捈宎乿偺嬌尷偱偡丅偦偆偄偆堄恾偱偟偨丅
丂側偍丄崱夞偺乮侾乯乣乮俆乯偼丄傑偁丄懡彮嫮堷側偺偼彸抦偟偰偍傝傑偡丅偨偩丄巹偑巜揈偟偨
偐偭偨偺偼丄
丒乮侾乯乣乮俆乯偺偳傟偐傪擣傔傟偽懠偑摼傜傟傞
丒乮侾乯乣乮俆乯偺偳傟偐傪擣傔側偄偲懠偼摼傜傟側偄乮弞娐榑朄偵側傞乯
偲偄偆惍棟傪偟偨偐偭偨婥帩偪偱偦偺傛偆偵彂偒弌偟偰傒偨師戞偱偡丅
丂乮侾乯乣乮俆乯偑岞棟偲偟偰懨摉偩偲偼巹傕巚傢側偄偱偡丏丏丏丅
丂埥傞闉偡偲偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀係擭俋寧侾俋擔晅偗乯
丂傕偆彮偟怺孈傝偟偰傒傑偡丅怲廳偵専摙偟偰偄傞偮傕傝偱偡偑丄媍榑偺旘桇偑偁傟偽丄嬻廙
偝傫傪偼偠傔丄偛棗偺傒側偝傑偛巜揈偔偩偝偄丅
丂(俆'乯偼乮俀乯偲傎傏摨偠撪梕偲偄偆偙偲偵側傝傑偡偑丄lim倶仺亣 倶丒sin(180搙/倶)亖兾偲偟偰墌廃
偲捈宎偲偺斾偲偄偆婔壗妛揑検偵懳偟偰丄兾偲偄偆幚悢傪懳墳偝偣偰偄傑偡丅偙偙偱
lim倶仺亣 倶丒sin(180搙/倶)偑敪嶶偣偢丄嬌尷抣傪帩偮偙偲偑婔壗妛揑偵偼乽柧傜偐乿側偺偼嬋
慄偺挿偝偺掕媊傪丄乽婛偵擣傔偰偄傞乿偐傜偩偲峫偊傜傟傑偡乮懡暘乯丅
丂婔壗妛揑捈娤傪棧傟偰丄偮傑傝幚悢榑偵偰嬌尷抣傪帩偮偙偲傪徹柧偟傛偆偲偡傟偽丄嬫娫
弅彫朄偺尨棟偵偰徹柧偡傞傛偆偵巚偄傑偡偑丄偦偺嵺丄惓尫娭悢傪媺悢揥奐偡傞昁梫偑偁
傞偼偢偱偡乮懡暘乧乯丅偟偐偟嶰妏娭悢偺媺悢揥奐偵偼丄sin兤/兤偺嬌尷傪巊偄傑偡偺偱丄
弞娐傪旔偗傞偨傔丄傗偼傝嶰妏娭悢傪惍媺悢偵偰掕媊偡傞偺偼揔愗偲偄偊傑偡丅偡傞偲丄
cos兛亖侽偲側傞幚悢偑侽亙兛亙俀偵偰懚嵼偡傞偙偲偑丄拞娫抣偺掕棟傪梡偄偰徹柧偱偒傑
偡偺偱丄偦傟傪傕偭偰丄俀兛亖兾偲幚悢兾傪掕媊偡傟偽丄lim倶仺亣 倶丒sin(180搙/倶)亖兾傕掕
棟偲側傝傑偡丅偦偟偰丄偦傟傜傪婔壗妛偵棙梡偡傞嵺丄兾偑墌廃偲捈宎偺挿偝偲偺斾偱偁傞
偲偟偰傕柕弬側偔媍榑偑峴偊傞偙偲偑妋擣偱偒傞偲偄偆偙偲偩偲巚偄傑偡丅
丂婔壗妛揑偵嶰妏娭悢偺嬌尷傪埖偆偲丄偦偙偵偼嬋慄偺挿偝偺掕媊偑慜採偝傟偰偍傝丄杮
戣偱偁傝傑偡丄墌偺媮愊偺弞娐偺椫傪抐偪愗傞偵偼丄乽嬋慄偺挿偝乿偝偊掕媊偝傟傟偽廫暘
偱偁傞偲偄偆偺偑巹偺峫偊偱偡丅
丂嬻廙偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀係擭俋寧俀侽擔晅偗乯
丂乽婔壗妛揑偵嶰妏娭悢偺嬌尷傪埖偆偲丄偦偙偵偼嬋慄偺挿偝偺掕媊偑慜採偝傟偰偍傝乿偵
偼巀惉偱偒側偄偱偡丅儔僕傾儞傪帩偪偩偡帪偵嬋慄偺挿偝偑尰傟傞偺偼妋偐偱偡偑丄搙悢
朄偱偺嶰妏娭悢偱偼嬋慄偺挿偝偼傑偭偨偔尰傟偰偄側偄偱偡丅儔僕傾儞傪帩偪偩偟偰傕丄扨
弮偵丄乽兾/倶儔僕傾儞亖180/倶搙乿偲偄偆掕媊側傜丄嬋慄偺挿偝偺掕媊傪慜採偲偟側偔偰傕丄埖
偆偙偲偑偱偒傞偲巚偄傑偡丅
丂傑偨丄乽lim倶仺亣 倶丒sin(180搙/倶)偑敪嶶偣偢丄嬌尷抣傪帩偮偙偲偑婔壗妛揑偵偼亀柧傜偐亁
側偺偼嬋慄偺挿偝偺掕媊傪丄亀婛偵擣傔偰偄傞亁偐傜偩偲峫偊傜傟傑偡乮懡暘乯乿偵傕巹偼巀
惉偱偒側偄偱偡丅偙偙偱嬋慄偺挿偝偺掕媊偑偱偟傖偽傞棟桼偼柍偄偲巚偄傑偡丅
丂椺偊偽丄崅峑偺曽朄偵側傜偭偰(墌偺柺愊偑桳尷抣S偱懚嵼偡傞偙偲傪慜採偲偟傑偡偑)
乮侾乯丂扨埵墌偱拞怱妏(360搙/倶)偺尫偑挘傞柺愊亖sin(180搙/倶)
乮俀乯丂扨埵墌偱拞怱妏(360搙/倶)偺愵宍偺柺愊亖S/倶
乮俁乯丂妏A亖(180搙/倶)丄AB=1丄B偑捈妏偺嶰妏宍偺柺愊*2亖tan(180搙/倶)
丂乮俀乯亝乮俁乯丄乮侾乯亝乮俀乯傪巊偊偽丄S丒cos(180搙/倶)亝倶丒sin(180搙/倶)亝S丂傪摼傞偺偱丄偼
偝傒偆偪偱嬌尷(亖S)偑懚嵼偡傞丄偲偡傞偺偼偳偆偱偟傚偆偐丅
丂埥傞闉偡偲偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀係擭俋寧俀侾擔晅偗乯
丂偛専摙偁傝偑偲偆偛偞偄傑偡丅偙偺栤戣傪峫偊傞偙偲偼偲偰傕桳堄媊側帪娫偱偡丅屻彮偟丄
孈傝壓偘偰傒傑偡丅
丂搙悢朄傪梡偄傟偽丄兤傪墌屖偺挿偝偲夝庍偣偢偲傕丄偮傑傝丄嬋慄偺挿偝偺掕媊側偟偱傕丄
廫暘偵婔壗妛揑偵埖偊傞偲偄偆偺偼巀惉偱偡丅扨埵墌O忋偵偰掕媊偝傟偨丄sin佢AOB偼
尫AB偺挿偝偲偟偰夝庍偱偒丄佢AOB偼墌屖偺挿偝偲偼柍娭學偵妏AOB偺乽奐偒嬶崌乿傪昞
偡検偲偟偰夝庍弌棃傑偡丅偟偐偟丄 sin兤/兤偼丄偳偆偄偭偨婔壗妛堄枴傪帩偮偺偐丅兤傪墌
屖偺挿偝偲夝庍偡傞応崌偼丄尫偲墌屖偺挿偝偺斾偲偟偰夝庍偱偒丄墌屖偲尫偼嬌尷偵岦偐
偆偲摍偟偄挿偝偵嬤偯偔偲夝庍弌棃傑偡丅偙偺応崌偼丄捈娤揑偵柧傜偐側偙偺惈幙偵丄幚偼
嬋慄偺挿偝偺掕媊偑墶偨傢偭偰偄傞偲偄偆偙偲偑慜夞偺庡挘偱偟偨丅
丂偱偼丄兤傪挿偝偱偼側偔丄妏搙偲偟偰夝庍偡傞応崌丄sin兤/兤偼偳偆偄偭偨堄枴傪帩偮偺偐丅
傕偪傠傫丄僊儕僔儍悢妛偱偼偁傝傑偣傫偺偱丄婔壗妛揑側堄枴傪梌偊偢丄幚悢偺斾偲偟偰埖
偆偺傕壜擻偱偡丅sin兤/兤傪婔壗妛揑堄枴偵夝庍偡傞応崌丄偦傟偑桳尷妋掕抣傪帩偮偙偲
偼丄嬋慄偺挿偝偺掕媊偵巟偊傜傟偰偄傑偡偺偱丄徹柧壜擻偐偮丄捈娤揑偵傕棟夝偱偒傑偡丅
偟偐偟丄幚悢sin兤/兤偑嬌尷抣傪帩偮偙偲偼丄傗偼傝徹柧偟偨偔側傞偺偱偡丅幚悢偺懚嵼徹
柧偵娭傢傞媍榑偱偡偑丄悢楍丄娭悢偺嬌尷偼揤壓傝揑偵掕傔偢丄徹柧偡傋偒偙偲偺傛偆偵
巚偊傑偡丅
丂傑偨丄扨埵墌偺柺愊S亖兾偱偡偑丄慜採偲偟偰丄墌偺柺愊偑桳尷抣S偲偟偰懚嵼偡傞偙偲傪
梫惪偟偰丄嫴傒寕偪偺尨棟偱丄嬌尷抣S偑懚嵼偡傞偲偄偆偺偼弞娐偺傛偆側乮懡暘乯丅岆夝
偱偟偨傜怽偟栿側偄偱偡丅
丂幚悢偺岞棟丄僨乕僨僉儞僩偺愗抐傗嬫娫弅彫朄偺尨棟側偳偼丄姰慡偵摨抣側撪梕偱偁
傝丄偳傟傪岞棟偲偡傞偐偼丄偁傞堄枴帺桼偱偡丅偟偐偟丄岞棟偲偟偰偺傆偝傢偟偝偼丄傛傝懡
偔偺柦戣傪掕棟偲偟偰徹柧偱偒傞偙偲偵偁傞偲巚偆偺偱偡丅
丂嬻廙偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀係擭俋寧俀俀擔晅偗乯
丂墌偺柺愊偼丄S亖佺-11 2併(1-倶2)d倶 偱丄旕愊暘娭悢偼楢懕桳奅側偺偱丄偙偺掕愊暘偼桳
尷抣偱偁傞偲偄偆偺偼嬋慄偺挿偝摍偲偼娭學側偄偺偱弞娐偟偰側偄偲巚偄傑偟偨丅
丂埥傞闉偡偲偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀係擭俋寧俀俀擔晅偗乯
丂嶰妏娭悢偺嬌尷偑桳尷妋掕抣傪帩偮偙偲偼丄墌偺柺愊偑掕愊暘偵傛傝掕媊偝傟傞偙偲偵
巟偊傜傟偰偄偰丄偦偺嬌尷抣偼乽侾乿偱偁傞偲掕媊偡傞偲偄偆偙偲偱偡偹丅偦偆偡傟偽丄弞娐榑
朄偵娮傜側偄丅懡暘丄巹偼媍榑偺榑揰傪攃埇偟偰偄側偐偭偨偺偐傕偟傟傑偣傫丅
丂柺愊偼愊暘偱掕媊偡傞偺偑晛捠偱偡丅嬋慄偺挿偝傕嬋慄忋偺暘揰傪寢傇愜傟慄偺挿偝
偺榓偺忋尷偱掕媊偡傞偺偑椙偄偱偟傚偆丅偦偙偐傜丄嶰妏娭悢偺嬌尷丄奜愙懡妏宍偺廃埻
偺挿偝偺榓偑墌廃偺挿偝傛傝傕戝偒偄偙偲丄墌廃偺挿偝偑俀兾倰偱偁傞偙偲側偳偑徹柧偱偒傞
偨傔丄岞棟傗掕媊偼傛傝懡偔偺掕棟傪廂妌偱偒傞曽偑桪傟偰偄傞偲偄偆堄枴偱丄嬋慄偺挿
偝偺掕媊偺摫擖偵偙偩傢偭偨傢偗偱偡丅偟偐偟丄乽墌偺媮愊乿偲偄偆庡戣偺側偐偺弞娐榑朄
偺椫傪抐偪愗傞偲偄偆偙偲偵娭偟偰偼丄嬻廙偝傫偺媍榑丄偦偺偲偍傝偱偁傞偲巚偄傑偡丅偁傝
偑偲偆偛偞偄傑偟偨丅傾儖僉儊僨僗偑墌偺媮愊偺偨傔偵丄嬋慄偺挿偝偺掕媊側偟偵丄嬋慄偲
慄暘偺挿偝偺斾妑偺岞棟傪採帵偟偨偺偲摨條偵丄嶰妏娭悢偺嬌尷傪岞棟偲偟偰傕丄墌偺媮
愊偲偄偆栚揑偺斖埻撪偱偼廫暘偱偁傞偲峫偊傞偵帄傝傑偟偨丅
乮捛婰乯丂暯惉俀俆擭俁寧俇擔晅偗
丂暯惉俀俆擭搙偺戝嶃戝妛棟宯丂慜婜擖帋偱丄師偺傛偆側慺杙側栤戣偑弌戣偝傟偨丅
丂嶰妏娭悢偺嬌尷偵娭偡傞岞幃
丂
傪帵偡偙偲偵傛傝丄倱倝値倶 偺摫娭悢偑們倧倱倶 偱偁傞偙偲傪徹柧偣傛丅
丂嫵壢彂偵偁傞傛偆側婎杮栤戣偩偑丄堦斣庴尡惗偑嬯庤偲偡傞栤戣偩偲巚傢傟傞丅懡暘弌
棃偼偦傟傎偳傛偔側偄偩傠偆丅
丂暥宯丂慜婜擖帋偱傕丄倶倷暯柺偵偍偄偰丄揰乮倶0丆倷0乯偲捈慄 倎倶亄倐倷亄們亖侽 偺嫍棧偺岞幃
傪徹柧偝偣傞栤戣偑弌戣偝傟偨丅嫵壢彂偵彂偐傟偰偄傞偙偲傪偟偭偐傝妛傫偱偒側偝偄偲偄偆
戝嶃戝妛偺堄巚昞帵偲巚傢傟傞丅
乮捛婰乯丂椷榓俇擭侾侽寧俋擔晅偗
丂嶰妏娭悢偺嬌尷偵娭偡傞岞幃
丂
傪梡偄傞栤戣偼丄戝妛擖帋偱傕昿弌偱偁傞丅
丂師偺搶杒戝妛丂棟宯乮侾俋俉俀乯偺栤戣傕婎杮揑偲尵偊傞偩傠偆丅
栤戣俁丂丂倠 傪惓偺掕悢偲偡傞丅嬋慄 倷亖們倧倱倠倶 偲俁捈慄
丂丂倶亖亅兤丄倶亖侽丄倶亖兤丂乮侽亙兤亙俀兾/倠乯
偲偺岎揰傪捠傞墌偺拞怱傪俹偲偡傞丅兤偑侽偵嬤偯偔偲偒丄俹偼偳偺傛偆側揰偵嬤偯偔偐丅
乮夝乯丂俹乮侽丆倲乯 偲偍偗傞丅俹偲乮侽丆侾乯偲偺嫍棧偼丄丂侾亅倲
丂俹偲乮兤丆們倧倱倠兤乯偲偺嫍棧偼丄丂併乮兤2亄乮們倧倱倠兤亅倲乯2乯
戣堄傛傝丄丂兤2亄乮們倧倱倠兤亅倲乯2亖乮侾亅倲乯2丂側偺偱丄
丂倲亖乮侾亄們倧倱倠兤亅兤2/乮侾亅們倧倱倠兤乯乯/俀
兤 仺 侽丂偺偲偒丄們倧倱倠兤 仺 侾
丂兤2/乮侾亅們倧倱倠兤乯亖乮倠兤乯2/倱倝値2倠兤丒乮侾亄們倧倱倠兤乯/倠2 仺 俀/倠2丂側偺偱丄
丂倲 仺 侾亅侾/倠2
傛偭偰丄揰乮侽丆侾亅侾/倠2乯偵嬤偯偔丅丂丂乮廔乯
乮捛婰乯丂椷榓俇擭侾俀寧係擔晅偗
丂師偺搶杒戝妛丂棟宯乮侾俋俉俈乯偺栤戣傕丄嶰妏娭悢偺嬌尷偵娭偡傞岞幃傪梡偄傞傕偺偱偁傞丅
栤戣俇丂丂侽亙倎亙兾/俀 偲偟丄俥倎乮倶乯傪師偺幃偱掕媊偡傞丅
丂丂乥倶乥亝俀倎丂偺偲偒丄丂俥倎乮倶乯亖乮俀倎亅乥倶乥乯/乮俀倎2乯
丂丂俀倎亙乥倶乥亝兾丂偺偲偒丄丂俥倎乮倶乯亖侽
偙偺偲偒丄嬌尷抣 倢倝倣倎仺0 佺-兾兾 俥倎乮倶乯乥們倧倱倎倶乥倓倶丂傪媮傔傛丅
乮夝乯丂俥倎乮倶乯偺僌儔僼偼壓恾偺捠傝丅
丂丂
丂俥倎乮倶乯丄乥們倧倱倎倶乥偼嬼娭悢側偺偱丄
丂佺-兾兾 俥倎乮倶乯乥們倧倱倎倶乥倓倶亖俀佺0兾 俥倎乮倶乯乥們倧倱倎倶乥倓倶
傑偨丄侽亝倶亝俀倎亙兾丂偡側傢偪丄侽亝倎倶亝俀倎2丂偵偍偄偰丄
丂倎 仺 侽丂偐傜丄丂俀倎2亙兾/俀丂偡側傢偪丄丂倎2亙兾/係丂偲偟偰傛偄丅
偙偺偲偒丄丂們倧倱倎倶亜侽丂側偺偱丄丂乥們倧倱倎倶乥亖們倧倱倎倶
傛偭偰丄倎 仺 侽丂偺偲偒丄
佺-兾兾 俥倎乮倶乯乥們倧倱倎倶乥倓倶亖俀佺02a 乮俀倎亅倶乯/乮俀倎2乯們倧倱倎倶倓倶
丂亖乮侾/倎2乯佺02a 乮俀倎亅倶乯們倧倱倎倶倓倶
丂亖乮侾/倎2乯乮[乮俀亅倶/倎乯倱倝値倎倶]02a亄乮侾/倎乯佺02a 倱倝値倎倶倓倶
丂亖乮侾/倎3乯佺02a 倱倝値倎倶倓倶亖乮侾/倎4乯[亅們倧倱倎倶]02a亖乮侾/倎4乯乮侾亅們倧倱俀倎2乯
丂亖俀乮倱倝値2倎2乯/倎4亖俀乷乮倱倝値倎2乯/倎2乸2 仺 俀
埲忋偐傜丄丂倢倝倣倎仺0 佺-兾兾 俥倎乮倶乯乥們倧倱倎倶乥倓倶亖俀丂偱偁傞丅丂丂乮廔乯
丂丂丂埲壓丄岺帠拞








