円板の移動 
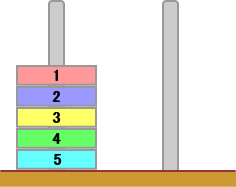 左図のように、地面に柱が2本立っていて、その
左図のように、地面に柱が2本立っていて、その
うちの左側の柱には、1から5までの番号のつけら
れた円板が、上から番号順に積まれている。
いま、1回の操作で、上から、1枚または2枚の円
板を、他の柱へ移動させる。ただし、2枚のときは、
上下の順番は、そのままとする。
何回か操作をして、右側の柱に、円板が、上から
順番に1から5まで並ぶようにしたい。
一体、何回の操作でできるであろうか?
(参考文献:ピーター・フランクル 著 中学生でも分かる 大学生にも解けない
数学問題集<2> (日本評論社))
Flash で、円板を実際に動かしてみよう。
Flash 版は、こちら HTML 版は、こちら をクリックしてください。
セキュリティ保護のため、コンピュータにアクセスできるアクティブ コンテンツが表示されないように、
Internet Explorer で制限していると、HTML版、Flash版ともに見られません。ブロックされている
コンテンツを許可してください。(すみません、自己の責任でお願いします。)
(答) 15回
(2枚ずつ2回、1枚を1回移動させて、一方の柱の円板を全て他方の柱に移す。この操作
を、1セットとする。左側の柱より始めて、5セット目で、題意を満たす。)
当HPがいつもお世話になっているHN「FN」さんが、上記の問題の一般化を考えられた。
(平成22年8月5日付け)
上記の問題で、1から5までになっているのを、n を自然数として、1から
n までとする。
n=1、2 のときは、明らかに1手でできるから、n≧3 とする。また、縦だと書きにくいので
横に書くことにする。
n=5の場合、初期状態は(12345, )、完成形は( ,12345)である。
(追記) 令和5年5月15日付け
(12345, )→(345,12)→(5,3412)→( ,53412)→(53,412)→(4153,2)→(24153, )→(153,24)
→(3,1524)→( ,31524)→(31,524)→(5231,4)→(45231, )→(231,45)→(1,2345)→(
,12345)
の15手
n=5の場合の解答は15手で長いから、n=3のときの手順を書いてみよう。
(123, )→(3,12)→( ,312)→(31,2)→(231, )→(1,23)→( ,123)
※6手が最短であることの証明はできないが、多分最短だろう。
さらに、括弧を書くのは面倒なので省略し、コンマの代わりに「0」にすると、上記の手順は
1230→3012→0312→3102→2310→1023→0123
と書ける。そこで、問題です。
(1) まず、n=4 のときの手順を考えてください。
(解) 12340→23401→40231→24031→02431→20431→43201→
32041→41320→13204→20134→12034→01234 以上 12手
(2) 次に、n=6、7、8あたりを考えてください。
(3) そして、一般の n で考えてください。
最短であることの証明は難しいので考えないことにします。n が奇数の場合は、5の場合
と同様にできそうです。偶数の場合はさてどうなるのでしょうか。
この問題に対して、HN「攻略法」さんが解法の手順を考えられた。(平成22年8月6日付け)
● n が奇数の場合・・・次のまとまった手順で、左→右と右→左に移動させる。
・12、34、45、…のように2枚ずつ移動する( (n-1)/2 回)
・残り1枚を移動する(1回)
この (n+1)/2 手を「1巡」とする操作を、n 回繰り返す。
従って、総手数は n(n+1)/2 手。
例 n=7 のとき
12345670→34567012→56703412→70563412→07563412→75063412→63750412→
41637502→24163750→16375024→37501624→50371624→05371624→53071624→
71530624→62715304→46271530→27153046→15302746→30152746→03152746→
31052746→52310746→74523106→67452310→45231067→23104567→10234567→
01234567 以上 28手
この流れは、2枚を1枚と考えると、(正順, )→ … →(逆順, )→( ,正順)として解を得てい
る。n が偶数の場合で、このような状態が存在するだろうか?
攻略法さんが、n が偶数の場合の手順を一般化された。(平成22年8月6日付け)
● n が偶数の場合・・・次のまとまった手順で、右または左に移動させる。
・1番上の1枚を移動する(1回)
・23、45、67、…のように2枚ずつ移動する。( n/2 回)
ただし、この操作の INT(n/4) 回目の後に1枚戻す。(1回)
この (n+4)/2 手を「1巡」とする操作を、n-1 回繰り返す。
従って、総手数は (n-1)(n+4)/2 手。
例 n=4 の場合 12手
0
12340
1 23401
2 40231 + 1
3 24031 ←
4 02431 1 巡
5
20431
6 43201 + 1
7 32041 ←
8 41320 2 巡
9 13204
10 20134
+ 1
11 12034 ←
12 01234 3 巡
n=6 の場合 25手
0 1234560
1
2345601
2 4560231 + 1
3 2456031 ←
4 5602431 + 2
5 0562431 1
巡
6 5062431
7 6250431 + 1
8 2506431 ←
9 6425031 + 2
10
3164250 2 巡
11 1642503
12 4250163 + 1
13 1425063 ←
14 2501463 +
2
15 0251463 3 巡
16 2051463
17 5120463 + 1
18 1205463 ←
19
5412063 + 2
20 6354120 4 巡
21 3541206
22 4120356 + 1
23 3412056
←
24 1203456 + 2
25 0123456 5 巡
n=8 の場合 42手
0 123456780
1
234567801
2 456780231 + 1
3 678045231 + 2
4 467805231 ←
5
780465231 + 3
6 078465231 1 巡
7 708465231
8 847065231 + 1
9
658470231 + 2
10 584706231 ←
11 625847031 + 3
12 316258470 2
巡
13 162584703
14 258470163 + 1
15 847025163 + 2
16 284705163
←
17 470285163 + 3
18 047285163 3 巡
19 407285163
20 724085163 +
1
21 857240163 + 2
22 572408163 ←
23 815724063 + 3
24 638157240
4 巡
25 381572406
26 157240386 + 1
27 724015386 + 2
28 172405386
←
29 240175386 + 3
30 024175386 5 巡
31 204175386
32 412075386 +
1
33 754120386 + 2
34 541207386 ←
35 735412086 + 3
36 867354120
6 巡
37 673541208
38 354120678 + 1
39 412035678 + 2
40 341205678
←
41 120345678 + 3
42 012345678 7 巡
|
|
n=10 の場合 63手
0
123456789A0
1 23456789A01
2 456789A0231 + 1
3 6789A045231 +
2
4 46789A05231 ←
5 789A0465231 + 3
6 9A078465231 + 4
7
09A78465231 1 巡
8 90A78465231
9 A7908465231 + 1
10 84A79065231 +
2
11 4A790865231 ←
12 864A7905231 + 3
13 52864A79031 + 4
14
3152864A790 2 巡
15 152864A7903
16 2864A790153 + 1
17 64A79028153 +
2
18 264A7908153 ←
19 4A790268153 + 3
20 7904A268153 + 4
21
0794A268153 3 巡
22 7094A268153
23 9470A268153 + 1
24 A2947068153 +
2
25 29470A68153 ←
26 A6294708153 + 3
27 81A62947053 + 4
28
5381A629470 4 巡
29 381A6294705
30 1A629470385 + 1
31 6294701A385 +
2
32 1629470A385 ←
33 2947016A385 + 3
34 4702916A385 + 4
35
0472916A385 5 巡
36 4072916A385
37 7240916A385 + 1
38 9172406A385 +
2
39 1724096A385 ←
40 9617240A385 + 3
41 A3961724085 + 4
42
85A39617240 6 巡
43 5A396172408
44 396172405A8 + 1
45 617240395A8 +
2
46 361724095A8 ←
47 172403695A8 + 3
48 240173695A8 + 4
49
024173695A8 7 巡
50 204173695A8
51 412073695A8 + 1
52 734120695A8 +
2
53 341207695A8 ←
54 763412095A8 + 3
55 957634120A8 + 4
56
A8957634120 8 巡
57 8957634120A
58 5763412089A + 1
59 6341205789A +
2
60 5634120789A ←
61 3412056789A + 3
62 1203456789A + 4
63
0123456789A 9 巡
|
|
n=12 の場合 88手
0 123456789ABC0
1 23456789ABC01
2
456789ABC0231 + 1
3 6789ABC045231 + 2
4 89ABC06745231 + 3
5
689ABC0745231 ←
6 9ABC068745231 + 4
7 BC09A68745231 + 5
8
0BC9A68745231 1 巡
9 B0C9A68745231
10 C9B0A68745231 + 1
11
A6C9B08745231 + 2
12 87A6C9B045231 + 3
13 7A6C9B0845231 ←
14
847A6C9B05231 + 4
15 52847A6C9B031 + 5
16 3152847A6C9B0 2 巡
17
152847A6C9B03
18 2847A6C9B0153 + 1
19 47A6C9B028153 + 2
20
A6C9B04728153 + 3
21 4A6C9B0728153 ←
22 6C9B04A728153 + 4
23
9B06C4A728153 + 5
24 09B6C4A728153 3 巡
25 90B6C4A728153
26
B690C4A728153 + 1
27 C4B690A728153 + 2
28 A7C4B69028153 + 3
29
7C4B690A28153 ←
30 A27C4B6908153 + 4
31 81A27C4B69053 + 5
32
5381A27C4B690 4 巡
33 381A27C4B6905
34 1A27C4B690385 + 1
35
27C4B6901A385 + 2
36 C4B690271A385 + 3
37 2C4B69071A385 ←
38
4B6902C71A385 + 4
39 6904B2C71A385 + 5
40 0694B2C71A385 5 巡
41
6094B2C71A385
42 9460B2C71A385 + 1
43 B29460C71A385 + 2
44
C7B294601A385 + 3
45 7B29460C1A385 ←
46 C17B29460A385 + 4
47
A3C17B2946085 + 5
48 85A3C17B29460 6 巡
49 5A3C17B294608
50
3C17B294605A8 + 1
51 17B294603C5A8 + 2
52 B29460173C5A8 + 3
53
1B2946073C5A8 ←
54 294601B73C5A8 + 4
55 460291B73C5A8 + 5
56
046291B73C5A8 7 巡
57 406291B73C5A8
58 624091B73C5A8 + 1
59
916240B73C5A8 + 2
60 B79162403C5A8 + 3
61 7916240B3C5A8 ←
62
B37916240C5A8 + 4
63 C5B37916240A8 + 5
64 A8C5B37916240 8 巡
65
8C5B37916240A
66 5B379162408CA + 1
67 379162405B8CA + 2
68
916240375B8CA + 3
69 391624075B8CA ←
70 162403975B8CA + 4
71
240163975B8CA + 5
72 024163975B8CA 9 巡
73 204163975B8CA
74
412063975B8CA + 1
75 634120975B8CA + 2
76 976341205B8CA + 3
77
763412095B8CA ←
78 957634120B8CA + 4
79 B8957634120CA + 5
80
CAB8957634120 10 巡
81 AB8957634120C
82 8957634120ABC + 1
83
5763412089ABC + 2
84 6341205789ABC + 3
85 5634120789ABC ←
86
3412056789ABC + 4
87 1203456789ABC + 5
88 0123456789ABC 11 巡 |
FNさんからこの問題についての考え方をご教示頂きました。(平成22年8月6日付け)
基本的な考え方は、次の通りです。
まず、n が奇数の場合、例えば、n=5 の場合
3手で、123450 を 053412 にします。これを、「0」を除いた部分だけ見れば、即ち、右側か
左側かは無視して、12345 がどの順に並んでいるかだけに注目すれば、12345 を
53412 に
してます。これを置換と見れば長さ5の巡回置換(15234)です。これの位数は5だから5回で
元に戻ります。そして、5回ということは右側にきてるので、3×5=15手で完成です。
次に、n が偶数の場合、例えば、n=4 の場合は同様にすると、巡回置換(1423)が得られ
るが、これの位数は4だから、4回で元に戻る。4回では左側なので駄目。そこで、1つだけ
動かないようにして、長さ3の巡回置換を作ることを考えます。
12340→23401→40231→24031→02431
これだと、3 が動いてなくて長さ3の巡回置換(124)になっています。だから、3回で元に戻
ります。3回だから右側なのでできています。
手数は、12340→・・・→024314 が4手より、 4×3=12手です。
n=6 のときの手順
1234560→3456012→5603412→3560412→6035412→0635412
これだと、4 が動いていなくて長さ5の巡回置換(16235)になっています。
手数は、1234560→・・・→0635412 が5手より、 5×5=25手です。
n=8 のときの手順
123456780→345678012→567803412→356780412
→678035412→806735412→086735412
これだと、5 が動いていなくて、長さ7の巡回置換(1826437)になっています。
手数は、123456780→・・・→0867354126 が6手より、 6×7=42手です。
n=2k のときは、k+2=(n+4)/2手で長さ n−1 の巡回置換が作れそうに思います。
だから、(n+4)(n−1)/2手で、できそうな気がします。
当HPがいつもお世話になっているHN「GAI」さんも手順を考えられた。
(平成22年8月6日付け)
n=6の場合 25手
1234560→3456012→5603412→3560412→6035412→0635412→6305412→5463012→
4630512→5146302→2514630→1463025→6301425→1630425→3016425→0316425→
3106425→6431025→4310625→6243105→5624310→2431056→3102456→2310456→
1023456→0123456
n=8の場合 42手
123456780→345678012→567803412→356780412→678035412→806735412→
086735412→860735412→738605412→386075412→753860412→417538602→241753860→
175386024→538601724→153860724→386015724→603815724→063815724→630815724→
816305724→163085724→851630724→728516304→472851630→285163047→516302847→
251630847→163025847→301625847→031625847→310625847→623105847→231065847→
652310847→846523107→784652310→465231078→523104678→452310678→231045678→
102345678→ 012345678
FNさんからのコメントです。(平成22年8月7日付け)
n=4k の場合の攻略法さんの手順が確認できました。
巡回置換 (1,4k-1,3,4k-3,・・・,2k-3,2k+3,2k-1,2k,2k+2,・・・,4,4k-2,2,4k) で、動かないのは
2k+1でした。奇数番目だけ偶数番目だけを別々に書けばそれぞれ
1,3,5,7,・・・,2k-3,2k-1,2k+2,2k+4,・・・4k-2,4k で、2k-1から2k+2だけが +3
です。
4k-1,4k-3,4k-5,・・・,2k+3,2k,2k-2,2k-4,・・・4,2 で、2k+3から2kだけが -3
です。
長さ n-1 の巡回置換だと確認されたから、(n+4)(n-1)/2手でできます。
N=4k+2も多分同様にできるのでしょう。これは省略。
次に、最短手数かどうかですが、理論的に考えるのは困難なので全数チェックに挑戦しま
した。
n=3 のときは、0123の順列は全部で24通りで、6手は最短でした。
n=4 のときは、01234の順列は全部で120通り。さすがに手計算は無理なので、ExcelVBA
でプログラムを書いて調べました。
n=4、5、6、7、8 については最短であることが確認できました。
(n=8 は2時間近くかかりました。)
以上から、らすかるさんの結果(平成22年8月8日付け)も含めて
| |
| n |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
| 最短手数 |
6 |
12 |
15 |
25 |
28 |
42 |
45 |
63 |
66 |
|
この表から、
3≦ n ≦11 において、
n が奇数のとき、 n(n+1)/2手 、 n が偶数のとき、 (n+4)(n−1)/2手
が最短手数である
ことが成り立つことになりますね。
ところで、n が偶数の場合に面白い現象がありました。n=8 の場合で書きます。
012345678 の順列は、9!=362880通りあります。この362880通りのすべての状態に到達で
きるのですが、012345678 のみ42手かかり、それ以外の362879通りは、すべて41手以下で
到達できます。n=4、n=6 でも同じことが起こっています。
n が奇数のときは、このようなことは起こっていません。例えば、n=7のとき
01234567 には、28手で到達できますが、28手以上かかる状態はたくさんあります。
65432107は32手かかります。
(コメント) FNさん、攻略法さん、らすかるさん、GAI さん、ありがとうございます。こんなにも
豊富に数学的考察が加えられることに感動しました!
攻略法さんから、状態の表現の仕方として次のような提案があった。
(平成22年8月22日付け)
| たとえば、 |
| 3 |
|
|
の場合、 ├6543─12┤ のように棒の先端部分で
連結させる。 |
| 4 |
|
|
| 5 |
|
1 |
| 6 |
|
2 |
| ┴ |
|
┴ |
|
したがって、先の表現 3456012 は、6543012
となる。
ここで、数字の移動の効果を見てみる。
2つを右へ
6543012 →
6503412 となるが、0と隣接する2つの数字に着目すれば、430 → 034
のよ
うに反転させる。
言い換えれば、「4と0を交換する」ということになる。
1つを右へ
6543012
→ 6540312 となるが、0と隣接する1つの数字に着目すれば、30 → 03
のように
反転させる。
言い換えれば、「3と0を交換する」ということになる。
2つを左へ
6543012
→ 6543210 となるが、0と隣接する2つの数字に着目すれば、012 → 210
のよう
に反転させる。
言い換えれば、「2と0を交換する」ということになる。
1つを左へ
6543012
→ 6543102 となるが、0と隣接する1つの数字に着目すれば、01 → 10
のように
反転させる。
言い換えれば、「1と0を交換する」ということになる。
また、開始の並びと終了の並びは、N=6 の場合、6543210 、0123456 となる。
以上により、これらは、「あみだくじ」(置換)で表現することができる。
| 2つを右へ |
|
1つを右へ |
|
2つを左へ |
|
1つを左へ |
6 5 4 3 0 1 2
││├─┤││
6 5 0 3 4 1 2 |
|
6 5 4 3 0 1 2
│││├┤││
6 5 4 0 3 1 2 |
|
6 5 4 3 0 1 2
││││├─┤
6 5 4 3 2 1 0 |
|
6 5 4 3 0 1 2
││││├┤│
6 5 4 3 1 0 2 |
ただ、通常と違って、
・「隣接」と「1つ飛び」のいずれかで横線を引くことになる。
・0を必ず移動させるように横線を引く。(任意の位置には引けない)
となる。
このとき、円板の移動の問題は、『横線の数を最少にするあみだくじをつくる』という問
題に置き換えられる。
N=5 の場合、15本
5 4 3 2 1 0
│││├─┤ 543012
│├─┤││ 503412
├┤││││ 053412 1巡
├─┤│││
350412
││├─┤│ 351402
││││├┤ 351420 2巡
│││├─┤ 351024
│├─┤││
301524
├┤││││ 031524 3巡
├─┤│││ 130524
││├─┤│ 132504
││││├┤
132540 4巡
│││├─┤ 132045
│├─┤││ 102345
├┤││││
012345 5巡
0 1 2 3 4 5
※各横線に対して、数字の並びを記しているが、
数字がどう移動するかは、実際のあみだくじと
同様に線を辿っていけばよい。 |
|
N=6 の場合、25本
6 5 4 3 2 1 0
│││││├┤
│││├─┤│
│││├┤││
││├─┤││
├─┤││││ 1巡
├┤│││││
│├─┤│││
││├┤│││
││├─┤││
││││├─┤ 2巡
│││││├┤
│││├─┤│
│││├┤││
││├─┤││
├─┤││││ 3巡
├┤│││││
│├─┤│││
││├┤│││
││├─┤││
││││├─┤ 4巡
│││││├┤
│││├─┤│
│││├┤││
││├─┤││
├─┤││││ 5巡
0 1 2 3 4 5 6 |
あみだくじを作成する要領で解のパターンを手作業で見つけることができる。
この攻略法さんの問題の言い換えに対して、FNさんからのコメントです。
(平成22年8月21日付け)
とてもいいアイデアという気がします。状態の表現の仕方として明らかにこの方が優れて
いますね。
N=6の場合であれば最初の形 6543210 を最終形 0123456 にする。許される操作は、
0と隣の交換または0と1つ離れた隣との交換のみ。
この「円板の移動」の問題に関連して、攻略法さんが新しい問題を作られた。
(平成22年9月2日付け)
蛙の整列1
N匹の蛙が並んでいる。逆順に並べ替える手順を示せ。
例 N=4 の場合 1234_ → 4321_
<移動条件>
・隣の葉が空いていれば、そこに移動できる。 例. 12_34 → 1_234
・他の1匹の蛙を挟んでその隣の葉が空いていれば、その1匹の蛙を飛び越えて移
動できる。
(1度に2匹以上の他の蛙を飛び越えることはできない) 例. 123_4 → 1_324
・1枚の葉には、同時に2匹以上乗れない。
(解)
| |
N=1・・・1通り
1_
→ 1_
0: 1_
(0回)
N=2・・・2通り
12_ → 21_
0: 12_ 2
1: 1_2 1
2:
_12 2
3: 21_
(3回)
N=3・・・2通り
123_ → 321_
0: 123_ 2
1:
1_32 1
2: _132 3
3: 31_2 1
4: 3_12 2
5:
321_
(5回) |
|
N=4・・・4通り
1234_ → 4321_
0: 1234_ 3
1: 12_43 1
2:
_2143 2
3: 2_143 4
4: 241_3 3
5: 2413_ 1
6: 24_31 2
7:
_4231 4
8: 4_231 3
9: 432_1 1
10:
4321_
(10回)
N=5・・・22通り
(16回)
N=6・・・4通り
(21回)
N=7・・・530通り
(31回) |
|
回数について、
Nが奇数の場合、 N(N+3)/2−4 (ただし、N≧3)
※奇数の場合の一般解は不明
Nが偶数の場合、 N(N+1)/2
蛙の整列2
N匹の蛙が並んでいる。逆順に並べ替える手順を示せ。
ただし、終了時の空き位置が先頭にくるものとする。
例 N=4 の場合 1234_ → _4321
<移動条件>
・隣の葉が空いていれば、そこに移動できる。 例. 12_34 → 1_234
・他の1匹の蛙を挟んでその隣の葉が空いていれば、その1匹の蛙を飛び越えて移
動できる。
(1度に2匹以上の他の蛙を飛び越えることはできない) 例. 123_4 → 1_324
・1枚の葉には、同時に2匹以上乗れない。
(解)
| |
N=1・・・1通り
1_
→ _1
0: 1_ 1
1: _1
(1回)
N=2・・・1通り
12_ → _21
0: 12_ 1
1: _21
(1回)
N=3・・・2通り
123_ → _321
0: 123_ 2
1: 1_32 1
2:
_132 3
3: 31_2 2
4: 312_ 1
5: 3_21 3
6: _321
(6回) |
|
N=4・・・30通り
1234_ → _4321
0: 1234_ 4
1: 123_4 2
2:
1_324 3
3: 13_24 1
4: _3124 3
5: 3_124 2
6: 321_4 1
7:
32_14 4
8: 3241_ 1
9: 324_1 2
10: 3_421 4
11: 34_21 3
12: _4321
(12回)
N=5・・・2通り
(15回)
N=6・・・854通り
(25回)
N=7・・・2通り
(28回) |
|
回数について、
Nが奇数の場合、 N(N+1)/2
Nが偶数の場合、 (N−1)(N+4)/2
攻略法さんが、蛙の整列1について、別な視点で考えられた。(平成22年9月3日付け)
平面グラフをつくって、1周する巡回路(ハミルトン閉路、ハミルトン路)を考える。
(解) 偶数の場合、N手(N/2)巡 + (N/2)手・・・・・(N+1)N/2手
| |
N=2・・・2通り
12_ → 21_
0: 12_ 1
1: _21 2
2:
2_1 1
3: 21_
0: 12_ 2
1: 1_2 1
2: _12 2
3:
21_
平面グラフ
1
/\
2──○ 巡回路 ○12 |
|
N=4・・・4通り
1234_ → 4321_
0:
1234_ 3
1: 12_43 1
2: _2143 2
3: 2_143 4
4: 241_3 3
5:
2413_ 1
6: 24_31 2
7: _4231 4
8: 4_231 3
9: 432_1 1
10:
4321_
0: 1234_ 4
1: 123_4 2
2: 1_324 1
3: _1324 3
4: 31_24 4
5: 3142_ 2
6: 314_2 1
7: 3_412 3
8: _3412 4
9: 43_12 2
10: 4321_
|
|
0: 1234_ 3
1: 12_43 4
2:
124_3 2
3: 1_423 1
4: _1423 4
5: 41_23 3
6: 4132_ 2
7:
413_2 1
8: 4_312 3
9: 43_12 2
10: 4321_
0: 1234_ 3
1: 12_43 2
2: 1_243 4
3: 142_3 3
4: 1423_ 2
5: 14_32 1
6: _4132 4
7: 4_132 3
8: 431_2 1
9: 43_12 2
10: 4321_
|
|
|
平面グラフ
1
/\
2──3
│ /
│
4──○ 巡回路 ○3124、○4213 |
|
また、終了時の空き位置を先頭にした場合(蛙の整列2)
(解) 奇数の場合、N手(N+1)/2巡・・・・・(N+1)N/2手
| |
N=1・・・1通り
1_
→ _1
0: 1_ 1
1: _1
平面グラフ
1─
○ 巡回路 ○1
N=3・・・2通り
123_ → _321
0: 123_ 3
1: 12_3 1
2: _213 2
3: 2_13 3
4: 231_ 1
5: 23_1 2
6: _321
0:
123_ 2
1: 1_32 1
2: _132 3
3: 31_2 2
4: 312_ 1
5:
3_21 3
6: _321
|
|
N=5・・・2通り
12345_ → _54321
0: 12345_ 5
1:
1234_5 3
2: 12_435 1
3: _21435 2
4: 2_1435 4
5:
241_35 5
6: 24153_ 3
7: 2415_3 1
8: 24_513 2
9:
_42513 4
10: 4_2513 5
11: 452_13 3
12: 45231_ 1
13:
4523_1 2
14: 45_321 4
15: _54321
|
|
0: 12345_ 4
1:
123_54 2
2: 1_3254 1
3: _13254 3
4: 31_254 5
5:
3152_4 4
6: 31524_ 2
7: 315_42 1
8: 3_5142 3
9:
_35142 5
10: 53_142 4
11: 5341_2 2
12: 53412_ 1
13:
534_21 3
14: 5_4321 5
15: _54321
|
平面グラフ
1
/\
2──3
\/
○ 巡回路 ○312、○213 |
|
平面グラフ
1
/\
2──3
│ / │
4──5
\/
○ 巡回路 ○53124、○42135 |
|
FNさんからのコメントです。(平成22年9月3日付け)
円板の移動と蛙の整列が実質的に同じであるというのは大変面白いです。ついでに列車
の入れ替えも実質的に同じです。
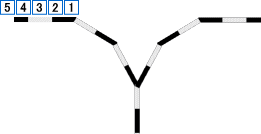
列車が1を先頭に右向きに54321と並んで
いる。これを右図のような引き込み線を利用
して右側に12345の順に並べよ。
但し、一度に動かせるのは1台か2台とする。 |
 |
54321_から1手で移れるのは、5432_1か543_12である。円板の移動を攻略法さんが
提案された記法で書けば、上から12345と並んだ状態は、54321_であり、これから1手で
移れるのは5432_1か543_12である。
円板の移動でも列車の入れ替えでも、654_123から移れるのは、
65_4123 、6_45123 、6541_23 、65421_3
のどれかである。これが蛙の整列で許される操作と同じであることは容易にわかる。
即ち、3つとも_とその隣の交換または_と1つ離れた隣との交換が許される操作である。
許される操作が同じだという意味で円板の移動と列車の入れ替えと蛙の整列は実質的に
同じ問題と言えるが、最終的に作るべき形が違えば当然別の問題になる。
「お茶の時間」の「円板の移動」は、54321_を_12345にせよであった。
「蛙の整列」では、普通は、54321_を12345_にせよである。だから当然同じ問題ではな
い。「円板の移動」で54321_を12345_にせよという問題設定はもちろん可能である。
54321_を_12345にするのを(A)型、54321_を12345_にするのを(B)型と呼ぶことに
する。5の場合で書いたが5をNにした形で考えよう。
(A)型については、次の手数でできることは確認できている。
Nが奇数のとき、N(N+1)/2手 、Nが偶数のとき、(N−1)(N+4)/2手
そして最短ではないかと予想されている。らすかるさんによれば、N≦11では正しい。
(B)型については、攻略法さんによると、
Nが偶数のとき、N(N+1)/2手 、Nが奇数のとき、N(N+3)/2−4手 (N≧3)
(ただし、Nが奇数のときは一般解は不明とのこと。)
Nが偶数のときは、比較的容易に確認できそうです。Nが奇数のときは私は全くわかりま
せん。面白いのは、(A)型ではNが奇数のときが比較的簡単でN(N+1)/2手、(B)型ではNが
偶数のときが比較的簡単でN(N+1)/2手であることです。
最短であることが証明できるとすれば一番可能性があるのは(B)型でNが偶数のときでは
ないかと思います。
続けて、FNさんからのコメントです。(平成22年9月4日付け)
上記で、「 54321_を_12345にするのを(A)型、54321_を12345_にするのを(B)型と
呼ぶことにする。」としましたが、もともとの「円板の移動」は、この形の(A)型なのでこのよう
にしましたが最初の形が逆順ぽいので攻略法さんが書かれている形のほうがいいかもしれ
ません。
12345_を_54321にするのを(A)型、12345_を54321_にするのを(B)型とする。
もちろんどちらでも同じことですが。また、説明するにはアンダーバーの方がいいと思います
が定式化できてしまえば、0でいいかなと思います。すなわち、
123450 を 054321 にするのを、(A)型
123450 を 543210 にするのを、(B)型
とする。
許される操作は、0と隣の交換、0と1つ離れた隣との交換である。
(B)型のN=6の場合の手順を書いておきます。
0:1234560
1:1234065
2:1204365
3:0214365
4:2014365
5:2410365
6:2416305
7:2416350
これで、最後が 0 になり、前の6個の文字の置換は巡回置換(124653)である。これを3回
繰り返すと即ち3乗すると(16)(25)(34)になる。以上の操作により、「123456」は「654321」に
置換され、丁度、7×3=21手でできている。
同様に、Nが偶数の場合は、N+1回で最後が 0 で、前のN文字は巡回置換にできる。
これを、N/2回繰り返すと、位数は2であるがそれだけではなく、123・・・N を逆向けN・・・321
に並べ替えるものになっている。従って、N(N+1)/2手でできる。
攻略法さんが新しい問題を考えられた。(平成22年9月6日付け)
蛙の入れ替え 2種類の蛙がM匹とN匹ずついる。(M+N+1)枚の葉の上に1匹ずつ、1つ
空けて両側に分かれて対峙している。配置を入れ替える手順を示せ。
例 M=4、N=3の場合 1111_222 → 222_1111
移動条件
・隣の葉が空いていれば、そこに移動できる。 例 11_22 → 1_122
・他の1匹の蛙を挟んでその隣の葉が空いていれば、その1匹の蛙を飛び越えて移動
できる。(1度に2匹以上の他の蛙を飛び越えることはできない) 例
112_2 → 1_212
・1枚の葉には、同時に2匹以上乗れない。
・仲間の蛙を飛び越すことはできない。 例 111_22 → 1_1122 は不可
ヒント …121212…のように交互に並ぶように移動させる。
答え
●移動回数
飛び越さないで移動させるには、M匹の蛙に対してそれぞれN+1回ずつ。
同様に、N匹の蛙ではM+1回。また、飛び越す回数はM*N回である。
したがって、M*N+M+N回(
= M*(N+1)+N*(M+1)-M*N )となる。
●蛙の種類による移動の表現
M=N=1
0: 1_2 1
1:
_12 2
2: 21_ 1
3: 2_1
M=N=2
0: 11_22 1
1: 1_122 2
2:
121_2 2
3: 1212_ 1
4: 12_21 1
5: _2121 2
6: 2_121 2
7:
221_1 1
8: 22_11 |
|
M=N=3
0: 111_222 1
1: 11_1222 2
2:
1121_22 2
3: 11212_2 1
4: 112_212 1
5: 1_21212 1
6:
_121212 2
7: 21_1212 2
8: 2121_12 2
9: 212121_ 1
10:
21212_1 1
11: 212_211 1
12: 2_21211 2
13: 22_1211 2
14:
2221_11 1
15: 222_111 |
|
M=N=4
0: 1111_2222 1
1:
111_12222 2
2: 11121_222 2
3: 111212_22 1
4: 1112_2122 1
5:
11_212122 1
6: 1_1212122 2
7: 121_12122 2
8: 12121_122 2
9:
1212121_2 2
10: 12121212_ 1
11: 121212_21 1
12: 1212_2121 1
13:
12_212121 1
14: _21212121 2
15: 2_1212121 2
16: 221_12121 2
17:
22121_121 2
18: 2212121_1 1
19: 221212_11 1
20: 2212_2111 1
21:
22_212111 2
22: 222_12111 2
23: 22221_111 1
24:
2222_1111 |
●葉の位置による移動の表現
M=N=1
123
0: 1_2 1
1: _12 3
2: 21_ 2
3: 2_1
M=N=2
12345
0: 11_22 2
1: 1_122 4
2: 121_2 5
3: 1212_ 3
4:
12_21 1
5: _2121 2
6: 2_121 4
7: 221_1 3
8:
22_11 |
|
M=N=3
1234567
0: 111_222 3
1: 11_1222 5
2:
1121_22 6
3: 11212_2 4
4: 112_212 2
5: 1_21212 1
6:
_121212 3
7: 21_1212 5
8: 2121_12 7
9: 212121_ 6
10:
21212_1 4
11: 212_211 2
12: 2_21211 3
13: 22_1211 5
14:
2221_11 4
15: 222_111 |
|
M=N=4
123456789
0: 1111_2222 4
1:
111_12222 6
2: 11121_222 7
3: 111212_22 5
4: 1112_2122 3
5:
11_212122 2
6: 1_1212122 4
7: 121_12122 6
8: 12121_122 8
9:
1212121_2 9
10: 12121212_ 7
11: 121212_21 5
12: 1212_2121 3
13:
12_212121 1
14: _21212121 2
15: 2_1212121 4
16: 221_12121 6
17:
22121_121 8
18: 2212121_1 7
19: 221212_11 5
20: 2212_2111 3
21:
22_212111 4
22: 222_12111 6
23: 22221_111 5
24:
2222_1111 |
(コメント) 単純な円板の移動の問題から始まって、こんなに豊富な応用例があることに驚
いています。
以下、工事中!

 左図のように、地面に柱が2本立っていて、その
左図のように、地面に柱が2本立っていて、その