
当HPがいつもお世話になっているHN「GAI」さんからの出題です。
(平成27年12月7日付け)
四角形ABCDがあり、AD‖BC、∠ABC=∠BDC=∠ACB/2であり、直線BDは∠ABCの2等
分線になっているという。
このとき、∠ABCは? 出そうで出にくいです。
(出典:日本数学オリンピック2000年予選問題)
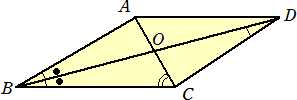
(答) 20°(問題の趣旨に合う図が少し書きにくかったです...。)
∠ACD=4θとおくと、題意より、∠ABC=∠BDC=2θ、∠ABD=∠CBD=θ
このとき、平行線ADとBCの距離をhとすると、
AD=h/tanθ−h/tan2θ=h/tan4θ+h/tan3θ
である。すなわち、 1/tanθ−1/tan2θ=1/tan4θ+1/tan3θより、
cosθ/sinθ−cos2θ/sin2θ=cos4θ/sin4θ+cos3θ/sin3θ
sin(2θ−θ)/sinθsin2θ=sin(4θ+3θ)/sin4θsin3θ
すなわち、 1/sin2θ=sin7θ/sin4θsin3θ
よって、両辺に sin4θ=2sin2θcos2θ を掛けて、 2sin3θcos2θ=sin7θ
積和の公式より、 sin5θ+sinθ=sin7θ なので、
sinθ=sin7θ−sin5θ=2cos6θsinθ
sinθ≠0 なので、 cos6θ=1/2
よって、 6θ=60°より、 θ=10°なので、 ∠ABC=2θ=20°
(コメント) 初等幾何的に求めようとしましたが、背水の陣で結局三角関数のお世話になっ
てしまいました。初等幾何的な解法は難しいのでしょうか?
当HPがいつもお世話になっているHN「DD++」さんが初等幾何的な解法に挑戦されました。
(平成27年12月11日付け)
初等幾何で頑張ってみましたが、超アクロバティック解法しかできませんでした。もっと簡単
な初等幾何的解法もありそうなものですが...。(なんでこんな解法を思いついたのか自分でも謎…)
対角線BD上に、BE=CE となる点Eをとる。辺BCと線分AEの延長の交点をFとする。辺BCに
ついて点Eと対称な点をGとする。辺ADの延長上に、AH=BH となる点Hをとる。
このとき、実は △ABG≡△ADC であり、また四角形 AHBF は菱形である。(証明は後で)

これを用いて、△AFG の内角をそれぞれ考える。
∠FAG=∠BAG-∠BAF=∠DAC-∠ABF(合同、菱形の性質)
=∠ACB-∠ABF(平行線の錯角)=2∠ABC-∠ABC=∠ABC
∠AFG=2∠AFC=2∠HBC=4∠ABC
また、∠AFC=2∠ABC、∠ACF=2∠ABC より AF=AC で、三角形の合同から AG=AC なの
で、AF=AG よって、∠AGF=∠AFG=4∠ABC
したがって、 ∠FAG+∠AFG+∠AGF=9∠ABC=π より、∠ABC=π/9
[補] △ABG≡△ADC の証明
∠CED=2∠EBC=∠ABC、∠CDE=∠ABC より、∠CED=∠CDE なので、CE=CD
また、点Eや点Gの取り方から BE=CE、BE=BG なので、結局、 BG=DC
そして、∠ABD=∠CBD=∠ADB(二等分線、平行線の錯角)より、AB=AD
さらに、∠ABG=∠ABC+∠GBC=∠ABC+∠EBC=∠CDB+∠BDA=∠ADC
したがって、二辺夾角相等なので、△ABG≡△ADC
[補] 四角形AHBFは菱形の証明
∠CED=2∠EBC=∠ABC、∠CDE=∠ABC、∠HAB=∠ABC、∠HBA=∠HAB=∠ABC より、
二角相等なので、△HAB∽△CED である。
また、∠ABD=∠CBD=∠BDA より、AB=AD である。これらを用いると、
BE:ED=CE:ED=HA:AB=HA:AD となるので、HB//AE である。
したがって、四角形AHBFは、HA//BF、HB//AF、HB=HA なので菱形である。
(コメント) DD++さんの素晴らしい証明に感動しました。ありがとうございました。