
最近、基本的な図形についての塗り分けの問題を考える機会があった。これらについて、
このページに整理しておこうと思う。
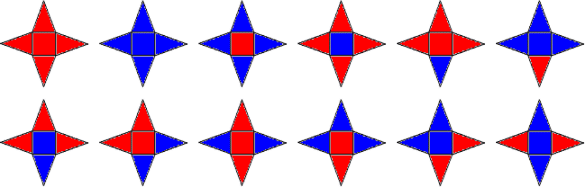
(1) 正四角錐を2色で塗り分ける方法
塗り分けの方法 
最近、基本的な図形についての塗り分けの問題を考える機会があった。これらについて、
このページに整理しておこうと思う。
(1) 正四角錐を2色で塗り分ける方法
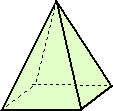 |
この場合の数は全部で、12通りある。 |
(計算による確認) 2色を、赤と青とする。
5面全部が、赤または青の場合は、それぞれ1通りずつの2通り。
4面が同色で、残り1面が他色の場合
残り1面が底面のとき、 赤または青のそれぞれ1通りずつ。
残り1面が底面でないとき、 同色が赤または青のそれぞれ1通りずつ。
よって、 この場合の数は、 4通り。
3面が赤で、残り2面が青の場合
底面が青のとき、 側面の塗り方は、1通り。
底面が赤のとき、 側面の塗り方は、2通り。
よって、 この場合の数は、 3通り。
3面が青で、残り2面が赤の場合
底面が青のとき、 側面の塗り方は、2通り。
底面が赤のとき、 側面の塗り方は、1通り。
よって、 この場合の数は、 3通り。
以上から、求める場合の数は、 2+4+3+3=12(通り)
(図示による確認) 2色を、赤と青とする。
(2) 正四面体を4色で塗り分ける方法
 |
この場合の数は全部で、2通りある。 |
(計算による確認) 底面に塗る色を一つ固定すると、側面の色の塗り方は、異なる3色の
円順列となる。
したがって、 (3−1)!=2(通り) となる。
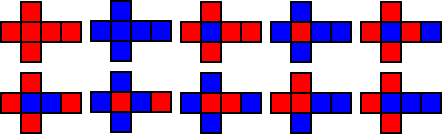
(3) 立方体を2色で塗り分ける方法
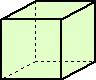 |
この場合の数は全部で、10通りある。 |
(計算による確認) 2色を、赤と青とする。
6面全部が、赤または青の場合は、それぞれ1通りずつの2通り。
5面が同色で、残り1面が他色の場合は、それぞれ1通りずつの2通り。
4面が赤で、残り2面が青の場合
上面と底面が青のとき、 側面の塗り方は、1通り。
上面と底面が赤と青のとき、 側面の塗り方は、1通り。
よって、 この場合の数は、 2通り。
4面が青で、残り2面が赤の場合
上面と底面が赤のとき、 側面の塗り方は、1通り。
上面と底面が赤と青のとき、 側面の塗り方は、1通り。
よって、 この場合の数は、 2通り。
3面が赤で、残り3面が青の場合
上面が青のとき、底面の塗り方は、赤または青の 2通り。このうちの1通りに対して、側
面の塗り方は、1通りしかない。
よって、 この場合の数は、 2×1=2(通り)。
以上から、求める場合の数は、 2+2+2+2+2=10(通り)
(図示による確認) 2色を、赤と青とする。
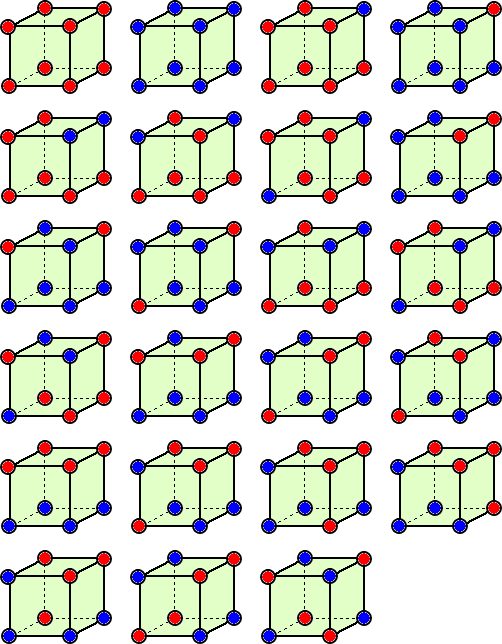
(4) 格子点を2色で塗り分ける方法
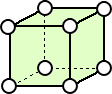 |
この場合の数は全部で、23通りある。 |
(図示による確認) 2色を、赤と青とし、使用面数で場合分けして地道に考える。
(5) 正八面体の8面の内、4面を赤、他の4面を青で塗り分ける方法
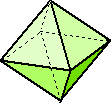 |
この場合の数は全部で、7通りある。 |
(図示による確認)
       |
当HPがいつもお世話になっているHN「FN」さんが、この話題について考察された。
(平成23年10月22日付け)
上記で、次のような問題が取り上げられている。
(1) 正四角錐を2色で塗り分ける方法 (2) 正四面体を4色で塗り分ける方法
「2色で」、「4色で」、という表現は曖昧さを含み、(1)(2)で違う意味で使われている。(1)で
は「2色以下で」の意味で、(2)では「ちょうど4色で」の意味で使われている。日常言語で、
どちらの意味で解釈される場合が多いかはどちらとも言えないが、数学では曖昧さを含ま
ない表現が望ましい。
(1A) 正四角錐をちょうどn色で塗り分ける方法の数 A(n) を求めよ。(n=1、2、3、4、5)
(2A) 正四面体をちょうどn色で塗り分ける方法の数 B(n) を求めよ。(n=1、2、3、4)
(3A) 立方体をちょうどn色で塗り分ける方法の数 C(n) を求めよ。(n=1、2、3、4、5、6)
(1B) 正四角錐をn色以下で塗り分ける方法の数 A’(n) を求めよ。(n=1、2、3、4、5)
(2B) 正四面体をn色以下で塗り分ける方法の数 B’(n) を求めよ。(n=1、2、3、4)
(3B) 立方体をn色以下で塗り分ける方法の数 C’(n) を求めよ。(n=1、2、3、4、5、6)
もちろん何れも回転によって同じになる塗り分け方は同じとみなす。
(1A)、(2A)、(3A) の方がやりやすいでしょう。その結果を使って、(1B)、(2B)、(3B) を解くこ
とになると思います。
(1A)の場合は、底面を固定すれば円順列の問題になる。ただし、同じものを含む円順列
なので、公式に入れれば終わりとはいかない。まず、同じものを含む4個のものの円順列の
個数を考えよう。
4個のうち異なるものがm個ある場合の円順列の個数を、Cir(4,m) と書く。
m=4 のときは、普通の円順列で、Cir(4,4)=3!=6
m=1 のとき、Cir(4,1)=1 は明らか。
m=2 のとき、 1122なら、1122と1212で、2通り
1222や1112のときは、1通り 従って、Cir(4,2)=4
m=3 のとき、 1123のとき、 3を固定すれば、112の順列で、3通り
1223や1233も同じだから、Cir(4,3)=3×3=9
(1A)の解について、
A(1)=1 は明らか
A(2) 底面が1のとき、側面は、(1と2)または(2だけ)で、これらの円順列となる。
底面が2のときも同じだから、 A(2)=(Cir(4,2)+Cir(4,1))×2=10
A(3)=(Cir(4,3)+Cir(4,2))×3=39
A(4)=(Cir(4,4)+Cir(4,3))×4=60
A(5)=Cir(4,4)×5=30
正しいかどうかあまり自信はありません。(1A)より、(2A)、(3A)の方が難しそうです。考えて
見てください。
FNさんからの続報です。(平成23年10月23日付け)
(2A)は難しいと思ったのですが、場合の数が非常に少ないので簡単なようです。
B(1)=1 は、明らか
B(4)=2 は、上記を参照
B(2) 2色を1と2とする。使う色は、1112、1122、1222 のどれかであるが、何れも塗り分け
方は、1通りしかないので、B(2)=3
B(3) 2色を1と2と3とする。使う色は、1123、1223、1233 のどれかであるが、何れも塗り分
け方は、1通りしかないので、B(3)=3
(1B)、(2B) は、(1A)、(2A)から出ます。(3A)は、多分本当に難しいと思いますが、実はそれ
ほどでもないのかもしれません。となると、正八面体も不可能ではないのでしょうか。
(4A) 正八面体をちょうどn色で塗り分ける方法の数D(n)を求めよ。(n=1、2、・・・、8)
これは、さすがに難しそうです。n=8とn=2ぐらいはなんとかなるでしょうか。
ぽっぽさんからのコメントです。(平成23年10月23日付け)
(4A)は、コーシー・フロベニウスの定理というので、漸化式の範囲でですが、解けそうで
す。
コーシー・フロベニウスの定理(バーンサイドの定理)
ある集合Xと、それに作用する置換群Gがあるとき、Gの部分群 g で不変であるXの
集合を、Xg とおく。ここで、軌道の個数│X/G│は、
│X/G│=(1/│G│)Σg∈G│Xg│
まず、正8面体をn色で塗り分けるということは、立方体の頂点をn色で塗り分ける方法と
場合の数は変わりません。ここである問題を考えます。
(4AS) 立方体の頂点ををn色で塗り分ける(使わない色があってもよい)方法の数
DS(n) を
求めよ。(n=1、2、・・・、8)
ここで、Xは立方体の頂点をn色で塗り分けるものの集合を、Gは立方体を回転させる回
転群とします。│G│=24 である。
実際に、 恒等置換の場合が1通り、ある面の中心と向いの面の中心を結んだ直線を軸
に90度右に回転する場合が6通り、ある面の中心と向いの面の中心を結んだ直線を軸に
180度に回転する場合が3通り、互いに向かい合う頂点を貫く軸によって、120度回転させる
場合が8通り、ある辺の中点と向かい合う辺の中点を軸として180度回転させる場合が6通
りあるので、 1+6+3+8+6=24(通り)
次に、Σg∈G│Xg│を求める。
(1) g が、恒等置換のとき、 │Xg│=n8
(2) g が、ある面の中心と向いの面の中心を結んだ直線を軸に90度右に回転するとき、6 つ
の回転群があり、Xgは、これらの2つの正方形(上面と底面)の頂点がそれぞれ全て同じ
色である集合なので、│Xg│=n2
(3) g がある面の中心と向いの面の中心を結んだ直線を軸に180度に回転するとき、3つの
回転群があり、Xgは、これらの正方形(上面と底面)の向かいの頂点が同じ色である集
合なので、│Xg│=n4
(4) 互いに向かい合う頂点を貫く軸によって120度回転させるとき、8つの回転群があり、軸
を通る頂点の色はそれぞれ自由で、軸によって対称的である3点の2組はそれぞれ全て
同じ色なので、│Xg│=n4
(5) ある辺の中点と向かい合う辺の中点を軸として180度回転させるとき、6つの回転群があ
り、軸と交わる辺の端点はそれぞれ同じ色で、他の点はそれぞれ向かい合う点と同じ色
なので、│Xg│=n4
したがって、立方体の頂点を全て使わないでいいとして、n色で塗り分ける方法の数は
DS(n)=(n8+17n4+6n2)/24
である。ここで、次のような漸化式が立つことがわかる。
Σk=1〜n nCk・D(k)=DS(n) より、 D(n)=DS(n)-Σk=1〜n-1 nCk・D(k)
ただし、D(1)=1、DS(n)=(n8+17n4+6n2)/24
これより、D(1)=1、D(2)=21、D(3)=267、…、D(8)=1680 が分かる。
FNさんからのコメントです。(平成23年10月23日付け)
もう少しゆっくりやりたかったのですが、あっさり解かれてしまったようです。(群の位数が
24であることすらすぐにはわからないので理解できてはいません)
コーシー・フロベニウスの定理(旧称バーンサイドの補題)は名前ぐらいは知っていますが
よくわかっていません。まともにやるなら、これになるのだろうとは思っていましたが、高校
数学の範囲でも、そこそこはいけるかなと考えていました。真面目に勉強して理解する努
力をしてみます。
コーシー・フロベニウスの定理を使うやり方だと、(2A)、(3A)、(4A)より、(2B)、(3B)、(4B)
の方が自然な問題ということのようです。(3A)、(3B)がまだ解かれていません。コーシー・
フロベニウスの定理を使うやり方と使わないやり方の両方での解を考えてみようと思いま
す。他の人も考えてみてください。
攻略法さんが、44通りの場合を直接に描画されました。(平成23年10月24日付け)
正四面体
使用した色数
\ 1 2 3 4 計
1色 1 - - - 1通り
2色 2 3 - - 5
3色 3 9 3 - 15
4色 4 18 12 2 36
:
n色 n nC2*3 nC3*3 nC4*2 0 …
| No. 1 ( 1 色) | No. 2 ( 2 色) | No. 3 ( 2 色) | No. 4 ( 2 色) | No. 5 ( 2 色) |
| ▲ ▲▼▲ |
▲ ▲▼▲ |
▲ ▲▼▲ |
▲ ▲▼▲ |
▲ ▲▼▲ |
| No. 6 ( 3 色) | No. 7 ( 3 色) | No. 8 ( 2 色) | No. 9 ( 3 色) | No. 10 ( 2 色) |
| ▲ ▲▼▲ |
▲ ▲▼▲ |
▲ ▲▼▲ |
▲ ▲▼▲ |
▲ ▲▼▲ |
| No. 11 ( 2 色) | No. 12 ( 3 色) | No. 13 ( 3 色) | No. 14 ( 3 色) | No. 15 ( 4 色) |
| ▲ ▲▼▲ |
▲ ▲▼▲ |
▲ ▲▼▲ |
▲ ▲▼▲ |
▲ ▲▼▲ |
| No. 16 ( 4 色) | No. 17 ( 3 色) | No. 18 ( 2 色) | No. 19 ( 3 色) | No. 20 ( 3 色) |
| ▲ ▲▼▲ |
▲ ▲▼▲ |
▲ ▲▼▲ |
▲ ▲▼▲ |
▲ ▲▼▲ |
| No. 21 ( 2 色) | No. 22 ( 1 色) | No. 23 ( 2 色) | No. 24 ( 2 色) | No. 25 ( 2 色) |
| ▲ ▲▼▲ |
▲ ▲▼▲ |
▲ ▲▼▲ |
▲ ▲▼▲ |
▲ ▲▼▲ |
| No. 26 ( 3 色) | No. 27 ( 2 色) | No. 28 ( 2 色) | No. 29 ( 3 色) | No. 30 ( 3 色) |
| ▲ ▲▼▲ |
▲ ▲▼▲ |
▲ ▲▼▲ |
▲ ▲▼▲ |
▲ ▲▼▲ |
| No. 31 ( 2 色) | No. 32 ( 1 色) | No. 33 ( 2 色) | No. 34 ( 2 色) | No. 35 ( 2 色) |
| ▲ ▲▼▲ |
▲ ▲▼▲ |
▲ ▲▼▲ |
▲ ▲▼▲ |
▲ ▲▼▲ |
| No. 36 ( 1 色) | ||||
| ▲ ▲▼▲ |
以 上 |
FNさんからのコメントです。(平成23年10月24日付け)
SB(4)=36通りをすべて実際に書くとは驚きです。それも色つきで。(2A)、(2B)も解かれてい
ます。(2A)と(2B)はどちらが自然なのでしょう。
(2B)について、コーシー・フロベニウスの定理を使って、SB(4)を計算してみます。(正四面
体の場合は使わない方が簡単ですが、正六面体(立方体)、正八面体・・・となれば、使うこと
の有利さが段々と増えていくと思います。立方体等を考える練習とすれば、コーシー・フロベ
ニウスの定理を使ってみるのも意味があるでしょう)
そのためには正四面体群についての情報が必要ですが、「私の備忘録」の「正四面体群」
にあります。そのページにあることは既知とし記号等はそのまま使います。
色は、1、2、3、4の4色とし、4つの面ABC、ACD、ADB、BCDの順に考えるものとして、それ
ぞれに、1、2、3、4を塗る塗り方を。1234のように書くことにする。
4色以下で塗る塗り方は、44=256通り。
正四面体群の位数は12で、その元は、(1)=X のタイプが、(1)〜(8)の8個で、(9)=Y のタイプ
が、(9)〜(11)の3個、(12)=I (恒等変換)が、1個 である。
I によって不変なものは、すべてだから 256通り。
X によって不変なものは、1112のタイプ 12通りと、1111のタイプ 4通りで、計16通り。
(2)〜(8)も同じだから、全部で、16×8=128通り。
Y によって不変なものは、1221のタイプ 12通りと、1111のタイプ 4通りで、計16通り。
(10)(11)も同じだから、全部で、16×3=48通り。
コーシー・フロベニウスの定理より、SB(4)=(1/12)(256+128+48)=432/12=36
SB(n)もほとんど同様にできます。SB(1)は、もちろん1だから、n≧2とする。ここで、n≦4で
ある必要はない。n≧5でも同じである。
n色以下で塗る塗り方は、n4通り。
I によって不変なものは、すべてだから、n4通り。
X によって不変なものは、1112のタイプと1111のタイプだから、n(n-1)+n=n2通り。
Y によって不変なものは、1221のタイプと1111のタイプだから、n(n-1)+n=n2通り。
従って、SB(n)=(1/12)(n4+8n2+3n2)=n2(n2+11)/12
ここで、問題「nが整数のとき、n2(n2+11)は12の倍数であることを示せ」が派生する。
ごく簡単に証明できますが...。
実際に、自然数 n に対して、 n2≡0、1 (mod 3) 、n2≡0、1 (mod 4) なので、
n2(n2+11)≡0 (mod 3) かつ n2(n2+11)≡0 (mod 4) より明らか。
攻略法さんからのコメントです。(平成23年10月24日付け)
(1A) 正四角錐をちょうどn色で塗り分ける方法の数 A(n) を求めよ。(n=1、2、3、4、5)
(1B) 正四角錐をn色以下で塗り分ける方法の数 A’(n) を求めよ。(n=1、2、3、4、5)
使用した色数
\ 1 2 3 4 5 計
1色 1 - - - - 1通り
2色 2 10 - - - 12
3色 3 30 39 - - 72
4色 4 60 156 60 - 280
5色 5 100 390 300 30 825
:
n色 n nC2*10 nC3*39 nC4*60 nC5*30 0 … 計 n2(n3+n+2)/4
(3A) 立方体をちょうどn色で塗り分ける方法の数 C(n) を求めよ。(n=1、2、3、4、5、6)
(3B) 立方体をn色以下で塗り分ける方法の数 C’(n) を求めよ。(n=1、2、3、4、5、6)
立方体(正6面体)
使用した色数
\ 1 2 3 4 5 6 計
1色 1 - - - - - 1通り
2色 2 8 - - - - 10
3色 3 24 30 - - - 57
4色 4 48 120 68 - - 240
5色 5 80 300 340 75 - 800
6色 6 120 600 1020 450 30 2226
:
n色 n nC2*8 nC3*30 nC4*68 nC5*75 nC6*30 0 … 計 n2(n4+3n2+12n+8)/24
FNさんからのコメントです。(平成23年10月25日付け)
(1A)、(1B)について、私も、n≦5について同じ結果を得ました。nについてはやってなかっ
たので、コーシー・フロベニウスでやってみました。
底面(正方形)の中心を通って、底面に垂直な直線の周りの90度の回転をgとする。群は、
g、g2、g3、g4=1(恒等変換) からなる位数4の巡回群。
1で不変なものは、塗り分け方の総数で、n5個
gで不変なものは、側面がすべて同じだから、底面、側面それぞれn通りで、n2個
g2で不変なものは、向かい合う側面が同じだから、底面、隣り合う側面がn通りで、n3個
g3は、gと同じで、n2個
従って、(1/4)(n5+n3+2n2)=n2(n3+n+2)/4
(2B)を、コーシー・フロベニウスで解くときに、「Xによって不変なものは、1112のタイプと
1111のタイプだから、n(n-1)+n=n2通り」のように書きましたが、側面3つは同じで任意、底
面も任意だから、直接、n2と書く方がいいです。n≧2とする必要もありません。
(コメント) 平成29年8月23日付け
数学セミナー(日本評論社)1994年11月号の「エレガントな解答をもとむ」に次のような
問題が出題されていました。
立方体の6面を絵の具で塗り分ける。使える色は6色までで、すべて違う色でも、2色か3
色だけを使っても、全くの自由。違う塗り方は何通りあるか。
ただし、立方体を転がしたとき、同じ塗り方になるものは1通りと数えるものとする。
この問題に対して、立方体の3組の対面に着目し上手い解釈をするとエレガントな解答が
得られるようだ。
立方体の6面は反対側に向かい合った2面を1組として、上下、前後、左右の3組あるも
のと考えられる。この3組の対面の塗り方を指定する。
対面を同色にする塗り方は、6C1=6(通り)、異なる色にする塗り方は、6C2=15(通り)
なので、合わせて、6H2=7C2=21通りある。この中から重複を許して3通り選ぶ場合の
数は、 21H3=23C3=23・22・21/6=1771(通り)
特に、3組の対面が異なる色で、どの2組の対面にも同じ2色を使わない塗り方は2通り
(鏡映で同じになるもの)あるので、15C3=15・14・13/6=455(通り)だけ加算が必要
である。よって、求める場合の数は、 1771+455=2226(通り) となる。
攻略法さんからのコメントです。(平成23年10月25日付け)
正多角錐、正多面体の塗り分けは、数学と図工の教材
・展開図を考える ・全ての塗り方で塗り分ける ・組み立てる ・同じものを見つけて分類
と考えたとき、4、5人のグループ作業では、正4面体が手頃だと思います。
視覚的に理解するには、「私の備忘録」の中の「円順列の数え上げ」があります。実際に、
81通りすべてを塗るのがポイントです(笑)
練習問題 「私の備忘録」の中の「エイト・クィーン問題」で、92個のすべての解が求まって
いる。この一覧から異なる解を求めよ。
(解) この表は、12行で構成され、行単位が同じグループになっている。回転、裏返しなど
すれば確認できる。従って、例えば、各行1列目を選んだ計12個とすればよい。(終)
攻略法さんからのコメントです。(平成23年10月25日付け)
ぽっぽさんの漸化式について、Excel ワークシートを使って、
行\列 A B C … I
1: 1 … 1=(A1^8+17*A1^4+6*A1^2)/24
2: 2 21=I2-A2 … 23=(A2^8+17*A2^4+6*A2^2)/24
3: 3 63=3C2*B2 267=I3-A3-B3 … 333=(A3^8+17*A3^4+6*A3^2)/24
などセル参照の式を使って、左上から順に埋めていきました。
ただし、nCr の計算式は、FACT(n)/(FACT(n-r)*FACT(r))
正8面体
使用した色数
\ 1 2 3 4 5 6 7 8 計
1色 1 - - - - - - - 1
2色 2 21 - - - - - - 23
3色 3 63 267 - - - - - 333
4色 4 126 1068 1718 - - - - 2916
5色 5 210 2670 8590 5250 - - - 16725
6色 6 315 5340 25770 31500 7980 - - 70911
7色 7 441 9345 60130 110250 55860 5880 - 241913
8色 8 588 14952 120260 294000 223440 47040 1680 701968
:
n色 n nC2*21 nC3*267 nC4*1718 nC5*5250 nC6*7980 nC7*5880 nC8*1680 0 …
計 n2(n6+17n2+6)/24
正m面体のm個の面をm色すべて使って塗る場合、1面が正L角形とすると、
(m-1)!/L 通り
実際に、mは、4、6、8、12、20 の5つ(→ 参考:「正多面体が5種類しかない理由」)で、
それぞれに対して、L=3、4、3、5、3
よって、 m=4 のとき、(4-1)!/3=2
m=6 のとき、(6-1)!/4=30
m=8 のとき、(8-1)!/3=1680
m=12 のとき、(12-1)!/5=7983360
m=20 のとき、(20-1)!/3=40548366802944000
FNさんからのコメントです。(平成23年10月25日付け)
(3A)、(3B)については、問題として出しましたが、ほとんど考えていませんでした。C(6)=30
だけはよくある問題なのでわかりましたが...。
攻略法さんがすべて答えを出されたので考えてみましたが、攻略法さんの答えを見て、そ
れにあわせたようなところもあります。
(3A)ができれば、即ち、上の図の対角線の 1、8、30、68、75、30 が出れば、(3B)、即ち、
最後の行はそんなに難しくない。色を、1、2、・・・、n として、C(n)を求める。
C(6):底面を固定する。上面は5通り。側面は4個の円順列。よって、C(6)=5・3!=30
C(5):112345のとき、5を底面に置く。1が上面にくれば、1234の円順列で、3!=6
2が上面にくれば、1134の円順列で、3通り。3、4のときも同じだから、計15通り。
122345等もすべて15通りだから、C(5)=15・5=75
C(2):111112のとき、1通りしかない。122222も同じ。111122のとき、22を隣合わせに置くか
向かい合わせに置くかで2通り。112222も同じ。111222のとき、1が向かい合った位置
にくるとき、1通り。こないときも、1通り。よって、C(2)=8
C(4):111234のとき、4を底面におく。1が上面なら、1123の円順列で、3通り。2が上面なら
1113の円順列で、1通り。3のときも同じで、計5通り。122234等も同じだから、このタイ
プで、4・5=20通り。112234のとき、4を底面に、1が上面なら1223の円順列で3通り。2
のときも同じ。3が上面なら、1122の円順列で2通りの計8通り。112334等も同じだから
このタイプで、8・4C2=48。 よって、C(4)=68
C(3):111123のとき、3を底面におく。2が上面にくるとき、1通り。1が上面にくるとき、1112の
円順列で、1通り。122223、123333も同じだから、2・3=6通り。111223のとき、3を底面
におく。1が上面にくるとき、1122の円順列で2通り。2が上面にくるとき、1222の円順列
で1通りの計3通り。1、2、3を交換しても同じく3通りずつで、1、2、3の交換は6通りだか
ら、このタイプ全体で、3・6=18通り。112233のとき、3が向かい合わせなら、1122の円
順列で、2通り。3が隣り合わせなら、11が向かい合うとき、1通り、22が向かい合うとき
1通り、12が向かい合うとき、多分2通り。よって、C(3)=30
1つだけという色が1つでもあれば、それを底面におけば、底面に垂直な直線の周りの回
転だけだから、円順列だけ気にすればいいので比較的楽だけど、どの色も2つ以上あると
きは考えにくいです。112233の場合は、すっきり理解できてません。
立方体の6面を2面を赤、2面を青、2面を白で塗る。回転で同じになるものは同じとみなし
て何通りの塗り方があるか。
FNさんからの続報です。(平成23年10月26日付け)
コーシー・フロベニウスの定理(旧称バーンサイドの補題:以下CF定理と略す)を使う練習
をすることが目的です。最初の練習が正多面体群であるのは妥当ではありません。まず、
巡回群あたりから始めるのが妥当です。空間における回転は難しいので、平面における回
転で考えようということです。
円順列とは、円周上に並べるが、回転によって重なるものは同一とみなすということです。
並べるものの個数がnであるとすると、2π/n の回転によって重なるものは同じとみなしま
す。これらの回転の全体は位数 n の巡回群になります。
n個のもののうちに、1個だけであるものが1つでもあれば、それを固定して考えればすぐ
にできます。もう少し一般にすれば、1がa1個、2がa2個、・・・、kがak個 (n=a1+a2+・・・+ak)
あり、これらすべてを並べる円順列を考えるとき、a1、a2、・・・、ak の最大公約数が1であ
れば、回転によって自分自身になるような並べ方はないので簡単です。CF定理で言えば、
Σのうち恒等変換以外では不動元はないということになります。同じものを含む順列の公
式をnで割るだけです。
(1) 1、1、2、2、3、3のすべてを円形に並べる並べ方は何通りあるか。ただし、回転によ
って重なるものは同じとみなす。
このような順列を、「112233の円順列」と呼ぶことにします。
もちろんCF定理を使わなくてできます。
112233の1つの順列、例えば、121323に対して、1つずつずらした
213231 、132312 、323121 、231213 、312132
は円順列としては同じである。従って、だいたい順列の総数は円順列の総数の6倍である。
ただし、順列123123の場合は、231231 、312312 が同じ円順列になる。このタイプのも
のは、円順列としては、123123 と 132132 だけである。これらの場合は、円順列1個に対
して、順列3個が対応する。これら以外は、円順列と順列の対応は、1:6である。
従って、円順列の総数を x とすれば、順列の総数は、
(x-2)・6+2・3=6x-6 これが、6!/(2!2!2!)=90 であるから、6x-6=90 より、x=16
CF定理を使った形で書けば、112233の順列は、6!/(2!*2!*2!)=90
恒等変換 e によって不変なのは、90個
60度の回転を g とすると、g、g2、g4、g5で不変なものはない。
g3(180度の回転)によって不変なのは、
123123 、231231 、312312 、132132 、321321 、213213
の6個 ゆえに、(1/6)・(90+6)=16
実質的には同じです。慣れれば、CF定理を使う方が書きやすいと思います。両方でやっ
てみて、CF定理というのは当たり前だという感覚を身に着けるのがいいのかもしれません。
下記の練習問題をやってみてください。
(2) 11223344の円順列の総数を求めよ。
(3) 111222333の円順列の総数を求めよ。
(4) 1、2、3 から重複を許して、5個取ってできる円順列の総数を求めよ。
(5) 1、2、3、4 から重複を許して、6個取ってできる円順列の総数を求めよ。
攻略法さんから解答を頂きました。(平成23年10月27日付け)
(別解) (1/R)・Σj=1〜R Ngcd(R,j) で求まる(ようだ)。
(4) 1、2、3 から重複を許して、5個取ってできる円順列の総数を求めよ。
(解) N=3、R=5 より、
σj 3gcd(5,j)
-----------------
σ1 31=3
σ2 31=3
σ3 31=3
σ4 31=3
+) σ5 35=243
------------------------
255 ÷ 5 = 51通り (終)
(5) 1、2、3、4 から重複を許して、6個取ってできる円順列の総数を求めよ。
(解) N=4、R=6 より、
σj 4gcd(6,j)
-----------------
σ1 41=4
σ2 42=16
σ3 43=64
σ4 42=16
σ5 41=4
+) σ6 46=4096
--------------------------
4200 ÷ 6 = 700通り
FNさんからのコメントです。(平成23年10月27日付け)
そのようですね。一般的な公式があるようです。本によっては、「CF定理より明らか」と書
かれてしまうかもしれないほど、CF定理に近い形ですね。でもやはり証明として書きたい気
はします。今のところうまく書けません。
一般の場合の証明をする練習という意味で、(5)を少し一般化した形でやってみます。
(5A) 異なるn個のものから重複を許して、6個とってできる円順列の総数を求めよ。
(解) 360/6=60度の回転を g とする。
g によって不変なもの 1つ隣と同じだから、xxxxxx の形で、n通り
g2 によって不変なもの 2つ隣と同じだから、xyxyxy の形で、n2通り
g3 によって不変なもの 3つ隣と同じだから、xyzxyz の形で、n3通り
g4 によって不変なもの 4つ隣と同じだから、xyxyxy の形で、n2通り
g5 によって不変なもの 5つ隣と同じだから、xxxxxx の形で、n通り
g6 =1によって不変なもの 何でもよいから、n6通り
(x、y、zは同じであってもよい)
従って、CF定理より、円順列の総数は、(1/6)(n+n2+n3+n2+n+n6)=(1/6)(n6+n3+2n2+2n)
これと一般の場合の次の公式との距離はごく短いようです。
異なるn個のものから重複を許して、r個とってできる円順列の総数は、
(1/r)Σk=1〜r ngcd(r,k) ただし、gcd(r,k)は、rとkの最大公約数
で求められる。
FNさんから解答を頂きました。(平成23年10月30日付け)
(2) 11223344の円順列の総数を求めよ。
2π/8=π/4 の回転を g とする。G={g,g2,g3,g4,g5,g6,g7,g8=1}
1で不変なものは、すべてで、8!/(2!2!2!2!)=2520(通り)
g4で不変なものは、12341234等、1234の順列の繰り返しで、4!=24(通り)
g,g2,g3,g5,g6,g7 で不変なものはない。
従って、(1/8)(2520+24)=318(通り)
(3) 111222333の円順列の総数を求めよ。
2π/9の回転を g とする。
1で不変なものは、9!/(3!3!3!)=1680(通り)
g3,g6 で不変なものは、3!=6(通り)で、それ以外で不変なものはない。
従って、(1/9)(1680+6+6)=188(通り)
このタイプの問題についても一般的な公式があるようです。でも、(1)(2)(3)から一般の式を
類推するのは無理でしょう。少なくとも個数の最大公約数が素数でなくて、最大公約数で割
ったとき、商がすべて同じではだめで、できれば3種類ぐらいはあった方がいいので、次の
問題ぐらいにしたほうがいいようです。
(6) 1が18個、2が12個、3が6個、全部で36個ある。これらすべてを並べてできる円順列の
総数を求めよ。
これだと、1つの数になるので計算しなければならないと感じるかもしれないから、式で終
わっていいように、次の形にしてみました。どちらでもいいからやってみてください。もちろん
(6)の場合でも式で終わっていいです。
(6A) 1が18個、2が12個、3、4、・・・、n がいずれも6個ずつ、全部で 6(n+3)個ある。これら
すべてを並べてできる円順列の総数を求めよ。(n≧3) N=n+3とおいて、Nの式で表せ。
FNさんから、(6A)の解答を頂きました。(平成23年11月2日付け)
N=n+3 とおく。6N個を円形に並べることになる。2π/6N の回転を g とする。
自然数 k (1≦k≦6N)に対して、gk により不変な順列 a(1)、a(2)、・・・、a(6N) があるとする。
a(t)=a(t+k) は当然成り立つが、もう少し強く次が成り立つ。
k と 6N の最大公約数を K とするとき、a(t)=a(t+K)。これは、kp+6Nq=K をみたす整数
p、q
が存在することから、gkp=gK-6Nq=gK が成り立ち、gk で不変なものは、gkp
従って、gK で不変であることからわかる。
a(t)=a(t+K) を満たすから、a(1)、a(2)、・・・、a(6N) は、a(1)、a(2)、・・・、a(K)
を繰り返すことに
なる。K は、6N の約数であるから、m=6N/K とおく。すなわち、6N=mK
a(1)、a(2)、・・・、a(6N) は、a(1)、a(2)、・・・、a(K) を m 回繰り返すことになる。
a(1)、a(2)、・・・、a(K) は、1、2、・・・、n のすべてを少なくとも1つ含む。
a(1)、a(2)、・・・、a(K) のうちの n の個数を t とする。このとき、mt=6。
従って、m、t は、6の約数で、1、2、3、6 のどれかである。だから、(m,t,K)
は、
(m,t,K)=(1,6,6N)、(2,3,3N)、(3,2,2N)、(6,1,N)
のどれかである。このうち前の2つは、(m,t,k) も同じである。後の2つについては、(m,t,k)
はそれぞれ2つずつあり、 (m,t,k)=(3,2,2N)、(3,2,4N)、(6,1,N)、(6,1,5N)
(m,t,k) のとき、a(1)、a(2)、・・・、a(K) の中に、3、・・・、n はそれぞれ
t 個ずつあり、1 は、
3t 個、2 は、2t 個ある。K=t(n+3)=tN。
a(1)、a(2)、・・・、a(6N) の個数を求めるのだが、それは、a(1)、a(2)、・・・、a(K)
の個数である。
同じものを含む順列の公式により、(tN)!/{(3t)!(2t)!(t!)N-5}
(m,t,K,k)=(1,6,6N,6N) のとき、(6N)!/{18!12!(6!)N-5}
(m,t,K,k)=(2,3,3N,3N) のとき、(3N)!/{9!6!(3!)N-5}
(m,t,K,k)=(3,2,2N,2N) のとき、(2N)!/{6!4!(2!)N-5}
(m,t,K,k)=(3,2,2N,4N) のとき、(2N)!/{6!4!(2!)N-5}
(m,t,K,k)=(6,1,N,N) のとき、N!/(3!2!)
(m,t,K,k)=(6,1,N,5N)のとき、N!/(3!2!)
これらの和を、6N で割ったものが求めるものである。一般の場合の公式は次の形である。
n(1)個が同じもの、n(2)個が別の同じもの、・・・・、n(r)個がまた別の同じものである
とき、これらすべてを並べてできる円順列の総数は、
N=n(1)+n(2)+・・・+n(r) とし、n(1)、n(2)、・・・、n(r)の最大公約数を d とするとき、
次式で与えられる。
(1/N)Σ[(N/k)!/{(n(1)/k)!(n(2)/k)!・・・(n(r)/k)!}]φ(k)
ただし、Σは、d の約数 k すべてにわたり、φ(k)はオイラーのφ関数である。
これのCF定理を使わない証明は下記のページ等にある。(平成23年11月3日付け)
「木村の数学小ネタ」 「同じものを含む円順列の個数について」
この証明も面白そうだが、数ページは必要なようだ。CF定理を使えば、前の(6A)の解答と
ほぼ同じで、具体的に k=N、2N、・・・、6N のケースを書いてる部分が不要になるから、やや
短かくなるかもしれない。実際に証明を書いたわけではないので、意外な困難があるかもし
れないが...。
同じものを含む円順列は、「同じものを含む円順列の公式」と「重複円順列の公式」で、一
応かたがついたとみなしてもいいかと思います。もちろん、どちらも特殊な状況における公式
で、例えば、次のような問題でも相当に面倒です。
(7) 1、2、2、3、3、3、4、4、4、4 のうちの 6 個を使ってできる円順列の総数を求めよ。
円順列が済めば、次は、じゅず順列です。回転の他に裏返し(鏡映)で同じになるものを同
じとみなすので、CF定理における群は、正2面体群という非可換群になります。非可換群の
中では最も簡単かもしれませんが、可換群のなかで最も簡単な巡回群と比べれば、相当難
しいと思います。このことから具体的な問題がどの程度難しくなるかがわかるわけではあり
ませんが...。
(8) 1、1、2、2、3 をすべて使ってできるじゅず順列の総数を求めよ。
(9) 1、1、2、2、3、3 をすべて使ってできるじゅず順列の総数を求めよ。
(10) 1、2、3 から重複を許して、5個とってできるじゅず順列の総数を求めよ。
(11) 1、2、3、4 から重複を許して、6個とってできるじゅず順列の総数を求めよ。
できれば、CF定理を使うやり方と使わないやり方の両方の解が欲しいところです。
攻略法さんが、(7)の解答を与えられました。(平成23年11月5日付け)
(解) 4を、0個使った場合、 1、2、2、3、3、3 の6個なので、公式より、
(1/6)・6!/(1!2!3!)=10(通り)
4を、1個使った場合、 1、2、2、3、3、3、4 の7個なので、1、2、3 の組合せは、
1、2、2、3、3、4 の6個のとき、30通り
1、2、3、3、3、4 の6個のとき、20通り
2、2、3、3、3、4 の6個のとき、10通り
4を、2個使った場合、 1、2、2、3、3、3、4、4 の8個なので、
1、2、2、3、4、4 の6個のとき、30通り
1、2、3、3、4、4 の6個のとき、30通り
1、3、3、3、4、4 の6個のとき、10通り
2、2、3、3、4、4 の6個のとき、16通り ※
(3/6)回転して不変なもの 234┃234で、2、3、4 の並べ方から、3!=6通り
2、3、3、3、4、4 の6個のとき、10通り
4を、3個使った場合、 1、2、2、3、3、3、4、4、4 の9個なので、
1、2、2、4、4、4 の6個のとき、10通り
1、2、3、4、4、4 の6個のとき、20通り
1、3、3、4、4、4 の6個のとき、10通り
2、2、3、4、4、4 の6個のとき、10通り
2、3、3、4、4、4 の6個のとき、10通り
3、3、3、4、4、4 の6個のとき、4通り ※
(2/6)、(4/6)回転して不変なもの 34┃34┃34で、3、4 の並べ方から、2!=2通りずつ
4を、4個使った場合、 1、2、2、3、3、3、4、4、4、4 の10個なので、
1、2、4、4、4、4 の6個のとき、5通り
1、3、4、4、4、4 の6個のとき、5通り
2、2、4、4、4、4 の6個のとき、3通り ※
(3/6)回転して不変なもの 244┃244で、2、4、4 の並べ方から、3!/(1!2!)=3通り
2、3、4、4、4、4 の6個のとき、5通り
3、3、4、4、4、4 の6個のとき、3通り ※
(3/6)回転して不変なもの 344┃344で、3、4、4 の並べ方から、3!/(1!2!)=3通り
以上、計251通り (終)
CF定理では、 (1490+0+2+12+2+0)/6=251通り
(検算) すべての解の個数は、「私の備忘録」の「母関数」より、
指数型母関数
(1+x)(1+x+x2/2!)(1+x+x2/2!+x3/3!)(1+x+x2/2!+x3/3!+x4/4!)・6!
= … + 1490x6 + …
上記※印より、k=1、2、3、4、5 で、(k/6)回転で不変なものは、 0、2、6+3+3=12、2、0
FNさんからのコメントです。(平成23年11月5日付け)
(7)は、問題として書いたのですが、とても面倒でやる気はしないなと思っていました。実際
にやれば、面倒なのは確かですが、できないこともないのですね。
「CF定理では、(1490+0+2+12+2+0)/6=251通り」とありますが、この「1490」を普通に求めて
みました。即ち、(7)の円順列を順列にした場合です。
(7A) 1、2、2、3、3、3、4、4、4、4 のうちの 6 個を使ってできる順列の総数を求めよ。
(解) AAAABC の型の場合 6!/4!=30(通り)
このうちの1通りに対して、Aの選び方は、1通りで、B、Cの選び方は、3通りなので、
30×3=90(通り)
AAAABBの型の場合 6!/(4!2!)=15(通り)
このうちの1通りに対して、Aの選び方は、1通りで、Bの選び方は、2通りなので、
15×2=30(通り)
AAABCDの型の場合 6!/3!=120(通り)
このうちの1通りに対して、Aの選び方は、2通りで、B、C、Dの選び方は、1通りなので、
120×2=240(通り)
AAABBCの型の場合 6!/(3!2!)=60(通り)
このうちの1通りに対して、Aの選び方は、2通りで、BもCも2通りなので、
60×2×2×2=480(通り)
AAABBBの型の場合 6!/(3!3!)=20(通り)
このうちの1通りに対して、A、Bの選び方は、1通りなので、 20×1=20(通り)
AABBCDの型の場合 6!/(2!2!)=180(通り)
このうちの1通りに対して、A、Bの選び方は、3通りで、C、Dは1通りなので、
180×3=540(通り)
AABBCCの型の場合 6!/(2!2!2!)=90(通り)
このうちの1通りに対して、A、B、Cの選び方は、1通りなので、 90×1=90(通り)
以上から、 90+30+240+480+20+540+90=1490(通り)
(※なかなか1490になりませんでした。何回も間違えました。)
また、同じものを含む順列(すべてを使うわけではないとき)の公式が母関数の形で与えら
れることも知りませんでした。Maximaに入れれば、1490は出ました。手計算で展開する気に
はなりませんでした。
(追記) 平成27年3月17日付け
立方体の各面に数字の1〜6を用いて互いに異なる数字を書き込む方法の数は、よく知ら
れているように、 5×(4−1)!=30(通り) である。
それでは、立方体の各面に、数字の1、2、2、3、3、3を書き込む方法の数は、何通りあ
るだろうか?ちょっと気になったので計算してみた。
(解) 上面に数字の「1」を固定するとき、底面の数字は、「2」または「3」の2通り。
底面の数字が「2」のとき、側面は、2、3、3、3の円順列で、その場合の数は、1通り
底面の数字が「3」のとき、側面は、2、2、3、3の円順列で、その場合の数は、2通り
以上から、求める場合の数は、 1+2=3(通り)
(コメント) もっと多いと思ったら意外に少ないですね!
(追記) 当HPがいつもお世話になっているHN「GAI」さんが正多面体の色分け方法を考察
された。(平成27年5月27日付け)
上記では、正n多面体(n=4,6,8,12,20)をr色(1≦r≦n)を使って色を塗り分ける方法が研究
されており、その結果、正n面体を異なるr色で塗り分けたとき、何通りが可能かのIROn(r)の
表は、下記のフロベニウスの定理から手に入るk色から何色かを使って塗り分ける構成式
f4 (k)=k2(k2+11)/12
f6 (k)=k2(k+1)(k3-k2+4k+8)/24
f8 (k)=k2(k6+17k2+6)/24
f12 (k)=k4(k8+15k2+44)/60
f20(k)=k4(k16+15k6+20k4+24)/60
を利用して、ちょうどr色で塗り分けられる方法が、
IRO4(r)=sum(i=0,r,(-1)^(r-i)*binomial(r,i)*f4(i)))
IRO6(r)=sum(i=0,r,(-1)^(r-i)*binomial(r,i)*f6(i)))
IRO8(r)=sum(i=0,r,(-1)^(r-i)*binomial(r,i)*f8(i)))
IRO12(r)=sum(i=0,r,(-1)^(r-i)*binomial(r,i)*f12(i)))
IRO20(r)=sum(i=0,r,(-1)^(r-i)*binomial(r,i)*f20(i)))
で各数字を算出してみると(右は辺で隣り合う面は異なる色になっている条件を付加した場合の数字か?)
正4面体
IRO4(1)=1-------------*
IRO4(2)=3-------------*
IRO4(3)=3-------------*
IRO4(4)=2-------------2
正6面体
IRO6(1)=1-------------*
IRO6(2)=8-------------*
IRO6(3)=30------------1
IRO6(4)=68------------6
IRO6(5)=75------------15
IRO6(6)=30------------30
正8面体
IRO8(1)=1-------------*
IRO8(2)=21------------1
IRO8(3)=267-----------?
IRO8(4)=1718----------?
IRO8(5)=5250----------?
IRO8(6)=7980----------?
IRO8(7)=5880----------?
IRO8(8)=1680----------1680
正12面体
IRO12(1)=1------------*
IRO12(2)=94-----------*
IRO12(3)=8814---------*
IRO12(4)=245008-------4
IRO12(5)=2759250------?
IRO12(6)=15884004-----?
IRO12(7)=52701264-----?
IRO12(8)=106866144----?
IRO12(9)=134719200----?
IRO12(10)=103118400---?
IRO12(11)=43908480----?
IRO12(12)=7983360-----7983360
正20面体
IRO20(1)=1----------------------*
IRO20(2)=17822------------------*
IRO20(3)=58076586---------------2
IRO20(4)=18093064608------------?
IRO20(5)=1498413498750----------?
IRO20(6)=51672950917308---------?
IRO20(7)=936058547290608--------?
IRO20(8)=10194866756893728------?
IRO20(9)=72644237439379200------?
IRO20(10)=357895538663241600----?
IRO20(11)=1264592451488446080---?
IRO20(12)=3281293750348373760---?
IRO20(13)=6337930306906598400---?
IRO20(14)=9157388718839961600---?
IRO20(15)=9858321678965760000---?
IRO20(16)=7794071905639219200---?
IRO20(17)=4394429252269056000---?
IRO20(18)=1672620130621440000---?
IRO20(19)=385209484627968000----?
IRO20(20)=40548366802944000-----40548366802944000
ただし、この数字は隣接する面は同じ色になっているものが含まれているので、各辺で隣
り合う面が異なった色に塗られていたら何通りになるかが知りたくなった。
そこで、勝手に右にその数を入れ込んだのであるが、不明な部分が数多く残った。ここま
での部分で間違いの部分があれば、知らせてほしい。また、未定の部分の数が分かれば教
えてほしい。
らすかるさんからのコメントです。(平成27年5月27日付け)
「*」はどういう意味かと思ったら、「0」の意味だったのですね。(0と書けば良いように思いました。)
全通り探索で調べたところ、
正四面体の 0,0,0,2 、正六面体の 0,0,1,6,15,30
はその通りで、
正八面体は、 0,1,12,103,730,2400,3360,1680
正十二面体は、 0,0,0,4,1320,58896,840672,5308800,16934400,28425600,23950080,7983360
となりました。正二十面体は、5色までは 0,0,144,2808880,1862688076 でしたが、その先は単
純全通り探索で求めるのは不可能ですね。
# r=n-1の場合の値は計算で出せますね。隣接する2面が同じ色になるパターンを全体の
パターンから引くのが簡単そうです。
r=n-1で隣接する2面が同じ色になるパターンは、(n-1)!/2通りですから
n=4 のとき、 3-(4-1)!/2=0通り
n=6 のとき、 75-(6-1)!/2=15通り
n=8 のとき、 5880-(8-1)!/2=3360通り
n=12 のとき、 43908480-(12-1)!/2=23950080通り
n=20 のとき、 385209484627968000-(20-1)!/2=324386934423552000通り
よって、n=20、r=19 の隣接同色禁止パターン数は、 324386934423552000 となりますね。
# n=20以外はプログラムで調べた値と一致しています。n=20のときの値は、地道に場合分け
して計算する方法でも同じ値になりましたので、間違いないと思います。
まだn=20の6≦r≦18の値がわかっていませんが、どうしたものでしょうか。
以下、工事中