
正4面体というと、非常に均整のとれた美しい立体という印象がある。単位球面に内接す
る正4面体は無数にあるが、そのうち、下図のように配置したものが標準的だろう。
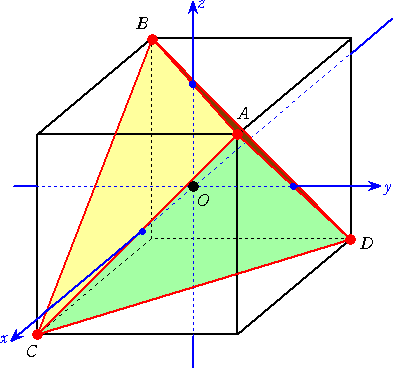
正4面体A-BCDの4頂
点の座標は、
と規則的だ。
この正4面体を回転させてピッタリ自分自身と重なるような操作は12通りある。
(1) 直線OAを回転軸として、120°回転
(2) 直線OAを回転軸として、240°回転
(3) 直線OBを回転軸として、120°回転
(4) 直線OBを回転軸として、240°回転
(5) 直線OCを回転軸として、120°回転
(6) 直線OCを回転軸として、240°回転
(7) 直線ODを回転軸として、120°回転
(8) 直線ODを回転軸として、240°回転
(9) 辺ADと辺BCの中点を結ぶ直線を回転軸として、180°回転
(10) 辺ACと辺BDの中点を結ぶ直線を回転軸として、180°回転
(11) 辺ABと辺CDの中点を結ぶ直線を回転軸として、180°回転
(12) 回転も何もしない(恒等変換)
これら12個の操作は、4つの操作の合成で表される。
X : 直線OAを回転軸として、120°回転 ・・・ (1)
この変換では、 A → A 、B → C 、C → D 、D → B と移動する。
これは、巡回置換 ( B C D ) を意味する。
Y : 辺ADと辺BCの中点を結ぶ直線を回転軸として、180°回転 ・・・ (9)
この変換では、 A → D 、B → C 、C → B 、D → A と移動する。
これは、互換の積 ( A D )( B C ) を意味する。
Z : 辺ACと辺BDの中点を結ぶ直線を回転軸として、180°回転 ・・・ (10)
この変換では、 A → C 、B → D 、C → A 、D → B と移動する。
これは、巡回置換 ( A C )( B D ) を意味する。
I : 恒等変換 ・・・ (12)
これは、恒等置換(単位置換) e を意味する。
とする。(以下では、変換 X のあと変換 Y を施すことを、YX と表記する)
いくつか変換の合成を計算してみよう。
X2 ・・・ ( B C D )( B C D )=( B D C ) なので、
この変換で、 A → A 、B → D 、C → B 、D → C と移動する。
すなわち、操作の(2)を意味する。
XY ・・・ ( B C D )( A D )( B C )=( A B D ) なので、
この変換で、 A → B 、B → D 、C → C 、D → A と移動する。
すなわち、操作の(5)を意味する。
XZ ・・・ ( B C D )( A C )( B D )=( A D C ) なので、
この変換で、 A → D 、B → B 、C → A 、D → C と移動する。
すなわち、操作の(4)を意味する。
YZ ・・・ ( A D )( B C )( A C )( B D )=( A B )( C D ) なので、
この変換で、 A → B 、B → A 、C → D 、D → C と移動する。
すなわち、操作の(11)を意味する。
XYZ ・・・ ( B C D )( A D )( B C )( A C )( B D )=( A C B ) なので、
この変換で、 A → C 、B → A 、C → B 、D → D と移動する。
すなわち、操作の(8)を意味する。
X2Y ・・・ ( B D C )( A D )( B C )=( A C D ) なので、
この変換で、 A → C 、B → B 、C → D 、D → A と移動する。
すなわち、操作の(3)を意味する。
X2Z ・・・ ( B D C )( A C )( B D )=( A B C ) なので、
この変換で、 A → B 、B → C 、C → A 、D → D と移動する。
すなわち、操作の(7)を意味する。
X2YZ ・・・ ( B D C )( A D )( B C )( A C )( B D )=( A D B ) なので、
この変換で、 A → D 、B → A 、C → C 、D → B と移動する。
すなわち、操作の(6)を意味する。
以上から、
正4面体を回転させてピッタリ自分自身と重なるような操作(1)〜(12)は順番に、
X 、X2 、X2Y 、XZ 、XY 、X2YZ 、X2Z 、XYZ 、Y 、Z 、YZ 、I
と表される。
X3 = I なので、12通りの操作は、基本的に、3種類の操作 X、Y、Z の組合せで得ら
れることになる。
このことについて、実は、2種類の操作の組合せでも表されることが知られている。
次の2つの変換を考える。
A : 直線OAを回転軸として、120°回転
この変換では、 A → A 、B → C 、C → D 、D → B と移動する。
これは、巡回置換 ( B C D ) を意味する。
D : 直線ODを回転軸として、120°回転
この変換では、 A → B 、B → C 、C → A 、D → D と移動する。
これは、巡回置換 ( A B C ) を意味する。
この2つの変換 A 、D で、12通りの変換
X 、X2 、X2Y 、XZ 、XY 、X2YZ 、X2Z 、XYZ 、Y 、Z 、YZ 、I
が表されることを以下に示す。
まず、 X=A 、 X2=A2 、 X2Z=D 、 XYZ=D2 、 I=A3 は明らか。
次に、直線OBを回転軸として、120°回転させる場合、変換 D-1 を施し、直線OAが
回転軸の場合に変換して、120°回転させ、その後で、変換 D を施せばよい。
よって、 X2Y=DAD-1 、 XZ=DA2D-1 と表される。
同様にして、 XY=D-1AD 、 X2YZ=D-1A2D と表される。
これより、 Y=A-1D-1AD と表される。
ここで、 AD=( B C D )( A B C )=( A C )( B D ) なので、この操作は、
辺ACと辺BDの中点を結ぶ直線を回転軸として、180°回転させる場合に相当する。
よって、 Z=AD と表される。
ここで、 DA=( A B C )( B C D )=( A B )( C D ) なので、この操作は、
辺ABと辺CDの中点を結ぶ直線を回転軸として、180°回転させる場合に相当する。
よって、 YZ=DA と表される。
以上から、12通りの変換は、2つの変換 A 、D により、
A、A2、DAD-1、DA2D-1、D-1AD、D-1A2D、D、D2、A-1D-1AD、AD、DA、A3
と表されることが示された。
以下、工事中