
当HPがいつもお世話になっているHN「らすかる」さんからの出題です。
(平成27年3月23日付け)
思い付いただけで自分では解いていません。
すべての辺が自然数で面積も自然数である最小の台形の面積はいくらか。
ただし、二組の辺が平行である図形は含まない。
(答え) GAI さんが考察されました。(平成27年3月24日付け)
下図の台形の面積は9で、最小値か?
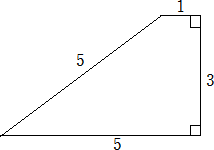
らすかるさんからのコメントです。(平成27年3月24日付け)
私もそれが最小ではないかと思っているのですが、それが最小であることが証明できてい
ません。
DD++さんが、面積の最小性を示されました。(平成27年3月25日付け)
(上底+下底)×高さ÷2が整数になるので、高さは有理数です。よって、台形を平行四辺形
と三角形に分割すると、それぞれ辺は全て整数で面積は有理数になります。
三角形側の面積が有理数ということは、ヘロンの公式より、周長が偶数なら、それは整数、
周長が奇数なら、「奇数/4」のはずですが、後者がありえないことは簡単に示せます。
(4S)2=(a2+b2+c2)2-2(a4+b4+c4) において、a、b、c のうち1つまたは3つが奇数だと、4で割っ
た時の余りが左辺は1で右辺は3になるため。
つまり、三角形側は面積が整数、つまり、これはヘロン三角形で、この時点で、面積が9以
下のものは、(3,4,5) のものしかありません。
これに、面積が整数の平行四辺形をくっつけます。5を底辺に用いると高さが12/5なせい
で、幅5、面積12の平行四辺形をくっつけるはめになります。
ということで、次点の4を底辺に用いて、幅1、面積3の平行四辺形をくっつけた面積9のもの
が最小です。
らすかるさんからのコメントです。
なるほど、台形を平行四辺形と三角形に分ければ良かったのですね。気付きませんでした。
ありがとうございます。
りらひいさんからのコメントです。
なるほど、周長が奇数で面積が奇数/4の三角形が存在しないことは簡単に示せるのです
ね。それがわからずに昨日今日と悶々としていた人がここに・・・(私です)。
分割の方は早々にわかっていてもそれだけでは解決にならないので・・・。
さくっと示してくださるDD++さん、さすがです。
(追記) よおすけさんから問題をいただきました。(令和元年7月21日付け)
GAIさんの示された下図の台形を、面積が等しい3つの図形に分割してください。
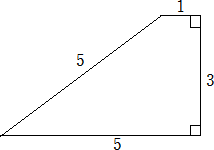
よおすけさんからのコメントです。(令和元年7月22日付け)
解はいくつかあるが、その一例を略解で示す。
GAIさんの示した台形を、3×1の長方形と、垂辺3・底辺4・斜辺5の直角三角形に分ける。
更に、垂辺3・底辺4・斜辺5の直角三角形で、垂辺と底辺に挟まれた角から斜辺へ垂線を
引く。元の台形の面積は9なので、これで面積3の三つの図形へ分割となる。
(コメント) 別解はいろいろありますね...。
以下、工事中!