曈偲妏偺旤偟偄娭學嘦丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂偙偺儁乕僕偼丄慜嶌乽曈偲妏偺旤偟偄娭學乿傪偝傜偵奼廩偝偣偨傕偺偱偁傞丅
壓恾偺撌巐妏宍乮曈俉偲曈俆亄俁偺側偡妏偼丄侾俉侽亱傛傝庒姳彫偝偄両丒丒丒係亱偔傜偄乯偺拞
偵丄偙傫側旤偟偄曈偲妏偺娭學偑偁傞偲偼丄嬃偒偱偡丅
丂丂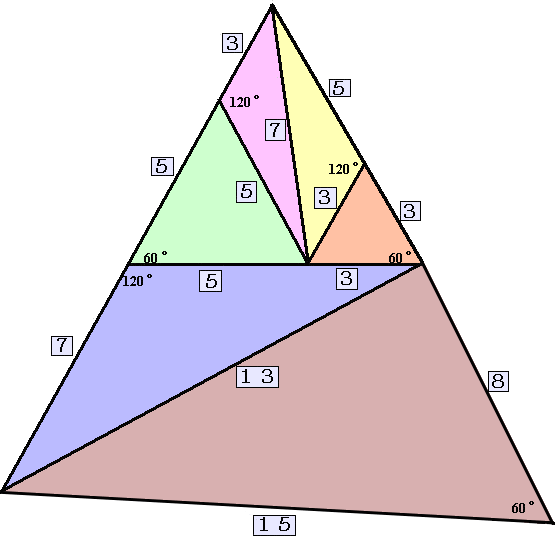
丂丂丂儚乕僾儘僜僼僩偺嶌恾婡擻傪巊梡偟偰偄傞偨傔丄懡彮丄恾宍偼僨僼僅儖儊偝傟偰偄傑偡丅
乮 暯惉侾俉擭俋寧俀係擔側傒偆偝偓條偐傜丄恾偺岆傝偺偛巜揈傪偄偨偩偒傑偟偨丅傜偡偐傞條偵偛専徹偄偨偩偒丄
丂妋偐偵恾偺岆傝偑妋擣偝傟傑偟偨丅恾偼婛偵廋惓嵪傒両偱偡丅彫偝偄嶰妏宍傪僽儘僢僋偺傛偆偵愊傒廳偹偰
丂擇摍曈嶰妏宍傜偟偒傕偺傪嶌偭偨偺偱偡偑丄廫暘側妋擣傪偟側偄傑傑丄偦偺傑傑偵偟偰偄傑偟偨丅捈慄偩傠偆
丂偲巚偭偰偄偨偲偙傠偑幚偼乽偔偺帤乿偵嬋偑偭偰偄偨偲偼丏丏丏丅偪傚偭偲丄偆偭偐傝偟傑偟偨両
丂丂恾偺岆傝傪偛巜揈偄偨偩偄偨乽側傒偆偝偓乿條丄偛専徹偄偨偩偄偨乽傜偡偐傞乿條偵姶幱偄偨偟傑偡丅乯
乮捛婰乯丂妏偑俇侽搙傑偨偼侾俀侽搙偵側傞傛偆側曈偺慻傒崌傢偣偼丄忋婰埲奜偵傕丄傕偪傠傫
丂丂丂丂丂偨偔偝傫懚嵼偡傞丅
丂丂偙偺偙偲偵偮偄偰丄撊栘導偺孨搰丂娹愭惗偑徻偟偔挷傋傜傟偰偄傞丅
丂俇侽搙偺妏偺応崌
丂俇侽搙偺懳曈偺挿偝傪 倸 偲偟丄巆傝偺擇曈偺挿偝傪 倶 丄倷 偲偡傞偲丄梋尫掕棟偐傜丄
丂丂丂丂丂丂倸2亖倶2亄倷2亅倶倷
偑惉傝棫偮丅強梫偺寢壥傪摼傞偨傔偵偼丄偙偺曽掱幃偺帺慠悢夝傪媮傔傟偽傛偄丅
丂偦偺偨傔偵丄丂倶亖倸亅兛丂丄倷亖倸亅兝丂偲偍偔丅
丂丂丂丂丂丂乮孨搰愭惗傕巜揈偝傟偰偄傞偑丄忋婰偺曽掱幃傪夝偔偨傔偵偼丄偙偺傛偆側抲偒曽偑桳岠傜偟偄丅乯
傛偭偰丄
丂丂丂丂丂丂倸2亖乮倸亅兛乯2亄乮倸亅兝乯2亅乮倸亅兛)(倸亅兝乯
傛傝丄
丂丂丂丂丂丂乮兛亄兝乯倸亖兛2亄兝2亅兛兝亖乮兛亄兝乯2亅俁兛兝
偲側傞丅
丂屻偼丄惍悢 兛丄兝傪丄倸 偑帺慠悢乮傕偪傠傫丄倶丄倷 傕帺慠悢乯偵側傞傛偆揔媂慖傫偱偁偘傟偽
傛偄丅
丂兛亄兝亖侾丂偺偲偒丄兛亖倠丂乮丂倠 偼惍悢 乯偲偍偔偲丄兝亖侾亅倠丂偱丄
丂丂丂丂倸亖侾亅俁倠乮侾亅倠乯亖俁倠2亅俁倠亄侾丂丄倶亖俁倠2亅係倠亄侾丂丄倷亖俁倠2亅俀倠
丂丂偙偺応崌丄偨偲偊偽丄乮 倶 丆 倷 丆 倸 乯亖乮 俆 丆 俉 丆 俈 乯丄乮
侾俇 丆 俀侾 丆 侾俋 乯丄丒丒丒
丂兛亄兝亖亅侾丂偺偲偒偼丄帺慠悢夝偼懚嵼偟側偄丅
丂兛亄兝亖俀丂偺偲偒丄兛亖倠丂乮丂倠 偼惍悢 乯偲偍偔偲丄兝亖俀亅倠丂偱丄
丂丂丂丂倸亖乮係亅俁倠乮俀亅倠乯乯/俀亖乮俁倠2亅俇倠亄係乯/俀丂丄
丂丂丂丂倶亖乮俁倠2亅俉倠亄係乯/俀丂丄倷亖乮俁倠2亅係倠乯/俀
丂丂偙偺応崌丄偨偲偊偽丄乮 倶 丆 倷 丆 倸 乯亖乮 侾侽 丆 侾俇 丆 侾係 乯丄丒丒丒
丂兛亄兝亖亅俀丂偺偲偒偼丄帺慠悢夝偼懚嵼偟側偄丅
丂兛亄兝亖俁丂偺偲偒丄兛亖倠丂乮丂倠 偼惍悢 乯偲偍偔偲丄兝亖俁亅倠丂偱丄
丂丂丂丂倸亖俁亅倠乮俁亅倠乯亖倠2亅俁倠亄俁丂丄倶亖倠2亅係倠亄俁丂丄倷亖倠2亅俀倠
丂丂偙偺応崌丄偨偲偊偽丄乮 倶 丆 倷 丆 倸 乯亖乮 俁 丆 俉 丆 俈 乯丄乮
俉 丆 侾俆 丆 侾俁 乯丄丒丒丒
乮 偙偺寢壥偐傜丄朻摢偺恾偺岆傝偑敪尒偝傟偨丅恾偼婛偵廋惓嵪傒両偙偺儁乕僕偑弶傔偰傾僢僾儘乕僪偝傟偨
丂偺偼丄暯惉侾俁擭侾侽寧俀俋擔側偺偱丄娵乆俁擭娫岆偭偨傑傑偱偁偭偨丅惤偵怽偟栿側偄偱偡丏丏丏m(_ _)m丂乯
丂兛亄兝亖亅俁丂偺偲偒偼丄帺慠悢夝偼懚嵼偟側偄丅
埲壓摨條偵偟偰丄兛亄兝 偑惍悢偺応崌傪峫偊傟偽丄柍悢偵夝傪摼傞偙偲偑弌棃傞丅
丂侾俀侽搙偺妏偺応崌丂丒丒丒丂俇侽搙偺応崌偲摨條偵偟偰媮傔傜傟傞丅
丂侾俀侽搙偺懳曈偺挿偝傪 倸 偲偟丄巆傝偺擇曈偺挿偝傪 倶 丄倷 偲偡傞偲丄梋尫掕棟偐傜丄
丂丂丂丂丂丂倸2亖倶2亄倷2亄倶倷
偑惉傝棫偮丅強梫偺寢壥傪摼傞偨傔偵偼丄偙偺曽掱幃偺帺慠悢夝傪媮傔傟偽傛偄丅
丂偦偺偨傔偵丄丂倶亖倸亅兛丂丄倷亖兝亅倸丂偲偍偔丅
丂丂丂丂丂丂乮屻偱丄倸2 偺崁傪徚嫀偡傞偨傔偵丄倷亖倸亅兝 偱偼側偔丄倷亖兝亅倸 偲抲偄偰偄傞偙偲偵拲堄両乯
傛偭偰丄
丂丂丂丂丂丂倸2亖乮倸亅兛乯2亄乮兝亅倸乯2亄乮倸亅兛)(兝亅倸乯
傛傝丄
丂丂丂丂丂丂乮兛亄兝乯倸亖兛2亄兝2亅兛兝亖乮兛亄兝乯2亅俁兛兝
偲側傞丅
丂屻偼丄惍悢 兛丄兝傪丄倸 偑帺慠悢乮傕偪傠傫丄倶丄倷 傕帺慠悢乯偵側傞傛偆揔媂慖傫偱偁偘傟偽
傛偄丅
丂兛亄兝亖侾丂偺偲偒丄兛亖倠丂乮丂倠 偼惍悢 乯偲偍偔偲丄兝亖侾亅倠丂偱丄
丂丂丂丂倸亖侾亅俁倠乮侾亅倠乯亖俁倠2亅俁倠亄侾丂丄倶亖俁倠2亅係倠亄侾丂丄倷亖亅俁倠2亄俀倠
丂丂偙偺応崌丄帺慠悢夝偼懚嵼偟側偄丅
丂埲壓摨條偵偟偰丄
丂丂丂兛亄兝亖亅侾丄亇俀丄亇俁丄亇係丄亇俆丄亇俇丄亇俈丄亇俉丄亇俋丄亇侾侽丄亇侾侾丂偺偲偒偼丄
丂丂帺慠悢夝偼懚嵼偟側偄丅乮 仼 偙偙偺妋擣嶌嬈偼彮偟恏偐偭偨偱偡両乯
丂兛亄兝亖侾俀丂偺偲偒丄兛亖倠丂乮丂倠 偼惍悢 乯偲偍偔偲丄兝亖侾俀亅倠丂偱丄
丂丂丂丂倸亖乮侾係係亅俁倠乮侾俀亅倠乯乯/侾俀亖乮倠2亅侾俀倠亄係俉乯/係丂丄
丂丂丂丂倶亖乮倠2亅侾俇倠亄係俉乯/係丂丄倷亖乮亅倠2亄俉倠乯/係
丂丂丂偙偙偱丄 倷 亜侽丂傛傝丄 倠亖侾丄俀丄俁丄係丄俆丄俇丄俈丂偱偁傞偑丄
倶 丄 倷 丄倸 偑偲傕偵帺慠
丂丂悢偲側傞偺偼丄倠亖俀丂偺応崌偺傒偱丄偙偺偲偒丄乮 倶 丆 倷 丆 倸 乯亖乮
俆 丆 俁 丆 俈 乯
埲壓摨條偵偟偰丄兛亄兝 偑惍悢偺応崌傪峫偊傞偙偲偵傛傝夝傪摼傞偙偲偑弌棃傞丅
乮僐儊儞僩乯丂忋恾偐傜傕暘偐傞傛偆偵丄乮 倶 丆 倷 丆 倸 乯亖乮 俉 丆 俈
丆 侾俁 乯傕夝偵側傞偑丄偙傟
丂丂丂丂丂丂偼丄兛亄兝亖俀俆丂偺応崌偵憡摉偡傞丅俇侽搙偺応崌偵斾傋偰丄侾俀侽搙偺応崌偼丄
丂丂丂丂丂丂夝偺専弌偺擻棪偑旕忢偵埆偄丅傕偭偲暿側庤棫偰偼側偄傕偺偩傠偆偐丠
乮嶲峫暥專丗丂孨搰丂娹丂挊丂丂倸2亖倶2亄倷2亇倶倷丂偺帺慠悢夝丂乮悢尋捠怣乮悢尋弌斉乯乯乯
乮捛婰乯丂暯惉侾俉擭俋寧俀俆擔晅偗
丂摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞傜偡偐傞偝傫偐傜丄
丂丂侾俀侽搙偺応崌偼丄俇侽搙偺応崌偐傜摼傜傟傞両
偲偺偛巜揈傪偄偨偩偒傑偟偨丅
丂乽夝偺専弌偺擻棪偑旕忢偵埆偄乿偲偄偆偺偼丄乽曽掱幃傪夝偄偰傕丄揔偡傞夝偑側偐側偐
尒偮偐傜側偄乿偲偄偆堄枴偱偡偑丄恾偱峫偊偨曽偑丄偙偺応崌偼傛偄傛偆偱偡丅
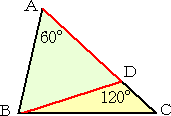 |
丂丂丂仮俙俛俠偱丄俙亖俇侽亱丄俙俛亙俙俠丂偺偲偒丄曈俙俠忋偵
丂丂俙俛亖俙俢偲側傞傛偆偵揰俢傪偲傞偲丄
丂丂丂丂丂丂佢俛俢俠亖侾俀侽亱
丂丂偲側傞丅 |
丂偙偺偙偲偐傜丄俇侽搙偺応崌偵摼傜傟偨寢壥傪梡偄傞偲丄侾俀侽搙偺応崌傕摨帪偵摼傜傟傞
偙偲偑暘偐傞丅媡偵丄侾俀侽搙偺嶰妏宍偵惓嶰妏宍傪偔偭偮偗傟偽乮椺偊偽丄忋恾偺仮俛俢俠
偵懳偟偰仮俙俛俢傪捛壛乯丄俇侽搙偺嶰妏宍偑摼傜傟傞丅偙偙偱丄曈偺挿偝傪帺慠悢偲尷掕偡
傟偽丄侾俀侽搙偺嶰妏宍偼擇摍曈嶰妏宍偵偼側傜側偄偺偱丄侾俀侽搙偺嶰妏宍偐傜俇侽搙偺
嶰妏宍偼俀屄嶌傜傟傞丅乮俛俢偱偔偭偮偔応崌偲俠俢偱偔偭偮偔応崌偺俀捠傝両乯
丂傜偡偐傞偝傫偑嶌傜傟偨昞傪庒姳曗懌偟偰丄壓昞傪摼傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮偨偩偟丄 倶 亙 倷丂偱丄俇侽亱偵懳偡傞曈偑丂倸丂偲偡傞丅乯
|
俇侽亱 |
仺 |
侾俀侽亱 |
仺 |
俇侽亱 |
|
乮 倶 丆 倷 丆 倸 乯 |
|
乮 倶 丆 倷亅倶 丆 倸 乯 |
|
乮 倶 丆 倷 丆 倸 乯 |
丂 |
乮 倷 丆 倷亅倶 丆 倸 乯 |
| 乮侾乯 |
乮丂5 丆 8 丆丂7 乯 |
|
乮丂5 丆 3 丆丂7 乯 |
|
乮丂5 丆 8 丆丂7 乯 |
|
乮丂8 丆 3 丆丂7 乯 |
| 乮俀乯 |
乮丂8 丆15 丆13 乯 |
|
乮丂8 丆 7 丆13 乯 |
|
乮丂8 丆15 丆13 乯 |
|
乮 15 丆 7 丆13 乯 |
| 乮俁乯 |
乮 10 丆16 丆14 乯 |
|
乮 10 丆 6 丆14 乯 |
|
乮 10 丆16 丆14 乯 |
|
乮 16 丆 6 丆14 乯 |
|
丂丂丂偙偺嶰妏宍偼丄乮侾乯偺嶰妏宍偲憡帡両 |
| 乮係乯 |
乮 16 丆21 丆19 乯 |
|
乮 16 丆 5 丆19 乯 |
|
乮 16 丆21 丆19 乯 |
|
乮 21 丆 5 丆19 乯 |
乮僐儊儞僩乯丂侾俀侽搙偺応崌偼帺摦揑偵俇侽搙偺応崌偐傜惗惉偝傟傞偲抦偭偰埨怱偟傑偟偨丅
丂丂丂丂丂丂傜偡偐傞偝傫偵姶幱偄偨偟傑偡丅
乮捛婰乯丂暯惉俀俀擭侾侽寧俀俇擔晅偗
丂侾俀侽搙偺懳曈偺挿偝傪 倸 偲偟丄巆傝偺擇曈偺挿偝傪 倶 丄倷 偲偡傞偲丄梋尫掕棟偐傜丄
丂丂丂丂丂丂倸2亖倶2亄倷2亄倶倷
偑惉傝棫偮丅偙偺惍悢夝偑丄屳偄偵慺側帺慠悢 倣丄値 傪梡偄偰
丂丂丂丂丂倶亖倣2亅値2丂丄丂倷亖俀倣値亄値2丂丄丂倸亖倣2亄倣値亄値2
偲彂偗傞偲偄偆偙偲傪嵟嬤抦傞偙偲偑偱偒偨丅擔杮戝妛暥棟妛晹悢妛壢偺搉曈宧堦愭惗偵
姶幱偟傑偡丅
丂傾僾儘乕僠偺曽朄偼丄乽僺僞僑儔僗悢偺敪尒乿偲摨條偱偁傞丅
乮徹柧乯丂忦審傪枮偨偡俁偮偺悢傪媮傔傞偙偲偼丄懭墌 倎2亄倐2亄倎倐亖侾 忋偺桳棟揰傪媮傔傞
丂丂丂丂偙偲偵摍偟偄丅揰乮亅侾丆侽乯傪捠傞孹偒 倠 偺捈慄偺曽掱幃偼丄倐亖倠(倎亄侾)
偲彂偗傞丅
丂丂丂丂丂偙偺捈慄偲懭墌偲偺岎揰傪媮傔傞偲丄
丂丂丂丂丂丂丂丂倎亖乮侾亅倠2乯/乮侾亄倠亄倠2乯丂丄丂倐亖乮俀倠亄倠2乯/乮侾亄倠亄倠2乯
丂丂丂丂偱偁傞丅偙偺偲偒丄倠亖値/倣丂乮 倣丄値 偼屳偄偵慺側帺慠悢乯傪戙擖偟偰丄
丂丂丂丂丂丂丂丂倶亖倣2亅値2丂丄丂倷亖俀倣値亄値2丂丄丂倸亖倣2亄倣値亄値2
丂丂丂丂偲彂偗傞偙偲偑暘偐傞丅丂乮徹廔乯
丂偙偺岞幃傪梡偄傞偲丄捀妏偺侾偮偑侾俀侽搙偱偁傞嶰妏宍偑検嶻偱偒傞丅
| 倣 |
値 |
倶 |
倷 |
倸 |
丂 |
| 俀 |
侾 |
俁 |
俆 |
俈 |
丂 |
| 俁 |
侾 |
俉 |
俈 |
侾俁 |
丂 |
| 俁 |
俀 |
俆 |
侾俇 |
侾俋 |
丂 |
| 係 |
侾 |
侾俆 |
俋 |
俀侾 |
仼丂倣亖俀丄値亖侾丂偺応崌偵憡帡丂 |
| 係 |
俁 |
俈 |
俁俁 |
俁俈 |
丂 |
| 丂丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒 |
乮捛婰乯丂暯惉俀俉擭俆寧侾俈擔晅偗
丂俇侽亱傗侾俀侽亱傪偼偝傓嶰妏宍偺俁曈偺斾偺妎偊曽傪嵟嬤抦傞偙偲偑偱偒偨丅
乮俇侽亱傪偼偝傓嶰妏宍乯丂俈丗俆丗俉丂柤屆壆丂丄俈丗俉丗俁丂擸傒
丂丂丂丂丂丂丂丂丒丒丒壗傟傕丄挿偝乽俈乿偺懳妏偺戝偒偝偑俇侽亱偲側傞丅
乮侾俀侽亱傪偼偝傓嶰妏宍乯丂俈丗俆丗俁丂幍屲嶰
丂丂丂丂丂丂丂丂丒丒丒挿偝乽俈乿偺懳妏偺戝偒偝偑侾俀侽亱偲側傞丅
丂僇儖僺僗偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俀擭侾侾寧俀俇擔晅偗乯
丂嶰妏宍偵偍偄偰丄幍屲嶰
丂丂俈俆俁亄侽侽俆亖俈俆俉乮柤屆壆乯
丂丂俈俆俁亄侽俁侽亖俈俉俁乮擸傒乯
丂弶傔偰抦偭偨丅
丂倣倧倧値倢倝倗倛倲偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俀擭侾侾寧俀俉擔晅偗乯
丂悘暘愄偵昤偄偨傕偺傪偳偆偧丅偲偼偄偊丄偙偺愭偑偆傑偔懕偒傑偣傫丅(5,16,19)側偳偑忋庤
偵擖傟偽椙偄偺偩偗偳...丅
丂丂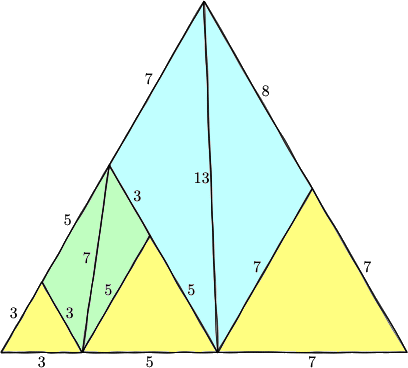
丂傝傜傂偄偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俀擭侾侾寧俁侽擔晅偗乯
丂(5,16,19)側偳偼擖傝傑偣傫偑丄摿掕偺宯楍傪懕偗傞偩偗側傜偽丄嵍壓偐傜塃曽岦偵3,5,7偲
偄偆暲傃偲丄嵍壓偐傜塃忋60亱曽岦偵3,5,7偲偄偆暲傃偺愭偵丄婏悢傪懕偗偰偄偗偽偄偄偩偗
偱偼側偄偱偟傚偆偐丠
丂堦曈3偺惓嶰妏宍傪戞0抜丄
丂堦曈5偺惓嶰妏宍偲挿偝5,3偺暯峴巐曈宍傪戞1抜丄
丂堦曈7偺惓嶰妏宍偲挿偝7,8偺暯峴巐曈宍傪戞2抜丄
丂丂乧
偲偡傞丅
丂戞k抜偺惓嶰妏宍偺堦曈偺挿偝偼 2k+3 丅
丂戞k抜偺暯峴巐曈宍偺堦偮偺曈偺挿偝偼 2k+3 丄傕偆堦偮偺曈偺挿偝偼 k(k+2) 丅
丂戞k抜偺暯峴巐曈宍偺挿偄傎偆偺懳妏慄偺挿偝偼 k^2+3k+3 丅
丂偦偆偄偆堄枴偱偼側偐偭偨偺側傜偡傒傑偣傫丅
丂偲偙傠偱丄乽曈偲妏偺旤偟偄娭學嘦乿偵娭偟偰師偺傛偆側偙偲傪巚偄傑偟偨丅
丂z^2=x^2+y^2+xy丂偺帺慠悢夝傪媮傔傞偲偒偵丄z=x+y-t丂偲偍偗偽丄(x-2t)(y-2t)=3t^2丂偲側
傞偺偱丄3t^2傪擇偮偺帺慠悢偺愊偱昞偡曽朄偺偦傟偧傟偵懳偟偰丄懳墳偡傞x,y,z偺慻偑媮
傑傞丅
丂傜偡偐傞偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俀擭侾侾寧俁侽擔晅偗乯
丂(5,16,19)丄(7,33,37)丄(9,56,61)丄(11,85,91)側偳偼丄偦傟帺懱偼擖傝傑偣傫偑丄
丂戞6抜偑(5,16,19)偺3攞
丂戞9抜偑(7,33,37)偺3攞
丂戞12抜偑(9,56,61)偺3攞
丂戞15抜偑(11,85,91)偺3攞
偺傛偆偵側偭偰丄憡帡宍偼偐側傝僇僶乕偝傟偰偄傑偡偹丅
乮偦傟偱傕(16,39,49)傗(24,95,109)側偳偼僇僶乕偝傟傑偣傫偑乯
丂屳偄偵慺偐偦偺3攞偺偳偪傜偐側偺偱丄
丂戞1抜偼丄(5ft,3ft,7ft)
丂戞2抜偼丄(7ft,8ft,13ft)
丂戞3抜偼丄(3yd,5yd,7yd)
丂戞4抜偼丄(11ft,24ft,31ft)
丂戞5抜偼丄(13ft,35ft,43ft)
丂戞6抜偼丄(5yd,16yd,19yd)
丂戞7抜偼丄(17ft,63ft,73ft)
丂丂丒丒丒
偺傛偆偵丄ft(僼傿乕僩)偲yd(儎乕僪)偺扨埵傪晅偗傟偽寢峔鉟楉側恾偑嶌傟傞偲巚偄傑偡丅
丂倣倧倧値倢倝倗倛倲偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俀擭侾侾寧俁侽擔晅偗乯
丂朸強偱榖戣偵側偭偰傞偺偱丄傕偆彮偟丅彮偟僀儗僊儏儔乕偵尒偊傞慄傪昤偒崬傓偲丄傎傏栐
梾偝傟偰偄傞傛偆偱偡丅偁偲丄傾僀僛儞僔儏僞僀儞偲偄偆柤慜偑弌偰偒傑偟偨丅傾僀僛儞僔儏僞
僀儞惍悢偲偐偺恖側偺偐娭學偁傞偺偐...丅
丂丂丂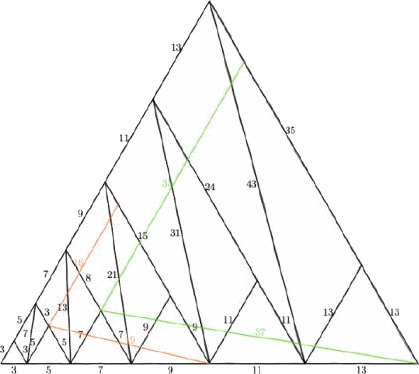
乮捛壛乯丂俫俶乽堦撉幰乿偝傫偐傜忣曬傪偄偨偩偒傑偟偨丅乮椷榓俁擭侾寧侾擔晅偗乯
丂忋婰偺榖戣偵娭楢偡傞婰帠傪尒偮偗傑偟偨丅
丂丂栘懞壝岹丂挊丂乽昞寁嶼僜僼僩偱梀傇乿乮悢尋捠怣97崋 2020擭5寧乯
乮捛婰乯丂椷榓係擭俀寧侾侾擔晅偗
丂倣倧倧値倢倝倗倛倲偝傫偐傜偄偨偩偄偨嶰妏宍傪嵞搙娙棯壔偟偰昤偄偰傒傑偟偨丅
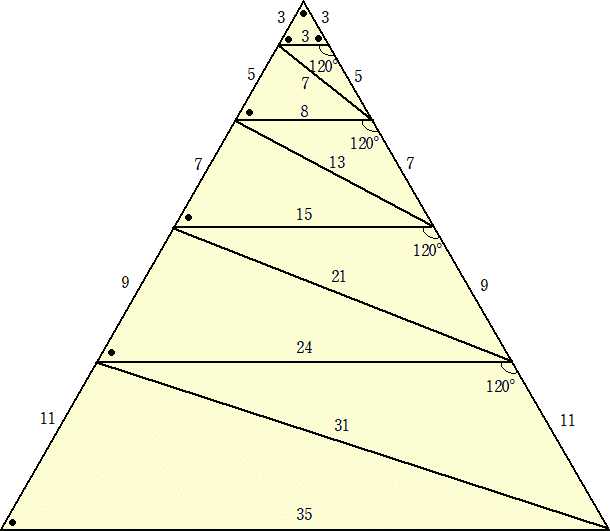
丂栤戣嶌惉偵壗偐偲巊偊偦偆側丏丏丏梊姶丅
乮捛婰乯丂椷榓係擭俋寧俀俉擔晅偗
丂柤屆壆乮俈丗俆丗俉乯丄擸傒乮俈丗俉丗俁乯丄幍屲嶰乮俈丗俆丗俁乯偺嶰妏宍傪慻傒崌傢偣傞偲丄師偺傛
偆側嶰妏宍傪峔惉偡傞偙偲偑偱偒傞丅栤戣嶌惉偵妶梡偱偒傞偐側丠
丂丂丂丂丂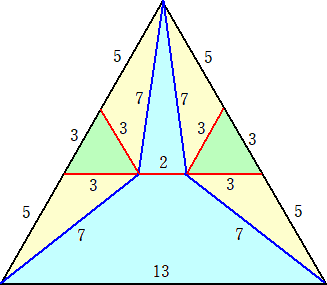
丂丂埲壓丄岺帠拞両






