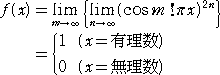僈僂僗偺婰崋丂丂丂丂丂 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 丂
丂
丂巹偑崅峑惗偺崰丄怴慛偵姶偠偨娭悢偑偁傞丅偦傟傑偱娭悢偲偄偊偽丄偡傋偰楢懕娭悢偱
偁偭偨丅懡暘丄晄楢懕側娭悢偲偺嵟弶偺弌夛偄偩偭偨偲巚偆丅
丂偨偟偐丄偦傟偼悢妛嘨乮尰峴偺悢妛嘨偲偼斾傋傕偺偵側傜側偄埵丄枺椡揑側榖戣偑朙晉
偱偁偭偨両乯 偺庼嬈偺偲偒偱偁偭偨丅愭惗偑丄崟斅偵師偺傛偆側栤戣傪弌偝傟偨丅
栤戣丂丂娭悢丂倄亖乵倃乶丂偺僌儔僼傪昤偗丅扐偟丄乵倃乶丂偼丄倃 傪墇偊側偄嵟戝偺惍悢傪昞偡丅
丂乵倃乶丂偼丄僈僂僗偺婰崋偲偄傢傟傞丅嵟弶偺崰丄亀 倃 傪墇偊側偄嵟戝偺惍悢亁 偲偄偆暥尵
偑傛偔棟夝偱偒側偐偭偨丅偟偐偟丄
丂丂乵倃乶亖値丂佁丂値亝倃亙値亄侾
偲偄偆晄摍幃偱丄椆夝偱偒偨丅偙偺晄摍幃偵傛傟偽丄乵俁丏侾係乶亖俁丄乵侽乶亖侽丄乵亅兾乶亖亅係
偼丄柧傜偐偱偁傞丅摢偺拞偵丄師偺傛偆側悢捈慄傪憐婲偟偰傕傛偄丅
丂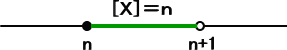
丂晄摍幃傪棙梡偟偰丄娭悢丂倄亖乵倃乶丂偺僌儔僼偼梕堈偵昤偔偙偲偑偱偒傞丅
 丂
丂
丂掕媊堟傪桳尷偺斖埻偵尷掕偡傟偽丄偙偺娭悢偼丄奒抜娭悢乮傑偨偼扨弮娭悢乯偺侾偮偺
椺傪梌偊偰偄傞丅乮堦斒偵丄扨弮娭悢偲偼丄抣堟偑桳尷廤崌偺傕偺傪偄偆丅乯擟堄偺娭悢偼丄
扨弮娭悢偱嬤帡偱偒傞偲偄偆掕棟側偳傕偁傝丄扨弮娭悢偼丄俴倕倐倕倱倗倳倕愊暘榑偵偍偄偰丄
婎杮揑側栶妱傪壥偨偟偰偄傞丅乮崅峑偱妛傇愊暘偼丄俼倝倕倣倎値値愊暘榑偺偛偔堦晹偱丄偙傟
傪怴偟偄帇揰偱峔惉偟捈偟偨傕偺偑丄俴倕倐倕倱倗倳倕愊暘榑偱偁傞丅乯
丂娭悢丂倄亖乵倃乶丂偼丄柍尷屄偺揰乮倃亖惍悢偺偲偒乯偱丄晄楢懕偱偁傞丅
偲偙傠偑丄悽偺拞偵偼丄傕偭偲偡偛偄娭悢偑偁傞丅
丂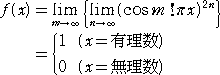
丂偙偺娭悢偼丄儚僀僄儖僔儏僩儔僗乮倂倕倝倕倰倱倲倰倎倱倱乯偺娭悢偲偄傢傟丄摓傞偲偙傠晄楢懕
偱偁傞丅亀摓傞偲偙傠晄楢懕亁偲偄傢傟偰傕丄偦偺僌儔僼偼憐憸偡傜偱偒側偄丅
丂僈僂僗偺婰崋 乵倃乶丂偵偼丄丂乵倃乶亖値丂佁丂値亝倃亙値亄侾丂偲偄偆惈幙埲奜偵丄師
偺傛偆側惈幙偑偁傞丅
乮侾乯丂擟堄偺幚悢 倃丄倄 偵懳偟偰丄丂乵倃乶亄乵倄乶亝乵倃亄倄乶
乮俀乯丂擟堄偺幚悢 倃 偲惍悢 俶 偵懳偟偰丄丂乵倃亄俶乶亖乵倃乶亄俶
乮俁乯丂桳棟悢丂俛/俙丂乮俙丄俛偼屳偄偵慺側帺慠悢乯偱丄
丂俛亖俙丒倯亄俼丂乮倯 丄俼偼侽埲忋偺帺慠悢偱丄侽亝俼亙俙乯
偺偲偒丄丂乵俛/俙乶亖倯丂丄丂乵俛/俙2乶亖乵乵俛/俙乶/俙乶
乮徹柧乯乮侾乯丂乵倃乶亖倣丂丄乵倄乶亖値丂偲偍偔偲丄丂倣亝倃亙倣亄侾丂丄値亝倄亙値亄侾
丂偙偺偲偒丄丂倣亄値亝倃亄倄亙倣亄値亄俀丂傛傝丄丂乵倃亄倄乶亖倣亄値丂傑偨偼丄倣亄値亄侾
丂傛偭偰丄丂乵倃乶亄乵倄乶亝乵倃亄倄乶丂偑惉傝棫偮丅
乮俀乯丂乵倃乶亖倣丂偲偍偔偲丄丂倣亝倃亙倣亄侾丂側偺偱丄丂倣亄俶亝倃亄俶亙倣亄俶亄侾
丂傛偭偰丄丂乵倃亄俶乶亖倣亄俶亖乵倃乶亄俶丂偑惉傝棫偮丅
乮俁乯丂俛亖俙丒倯亄俼丂乮侽亝俼亙俙乯丂傛傝丄丂俛/俙亖倯亄俼/俙丂偱丄丂侽亝俼/俙亙侾
丂傛偭偰丄丂倯亝倯亄俼/俙亙倯亄侾丂傛傝丄丂乵俛/俙乶亖倯丂偑惉傝棫偮丅
丂傑偨丄丂俛/俙亖倯亄俼/俙丂傛傝丄丂俛/俙2亖倯/俙亄俼/俙2
丂偙偙偱丄侽埲忋偺帺慠悢丂倯乫偲 俼乫傪梡偄偰丄丂倯亖俙倯乫亄俼乫丂乮侽亝俼乫亙俙乯偲彂偔偲偒丄
丂俛/俙2亖倯/俙亄俼/俙2亖倯乫亄俼乫/俙亄俼/俙2亖乵乵俛/俙乶/俙乶亄俼乫/俙亄俼/俙2
丂偙偺偲偒丄丂侽亝俼乫/俙亄俼/俙2亙乮俙亅侾乯/俙亄俙/俙2亖侾丂乮仼丂忋庤偄両乯側偺偱丄
丂乵俛/俙2乶亖乵乵俛/俙乶/俙乶
偑惉傝棫偮丅丂乮徹廔乯
丂僈僂僗偺婰崋偼丄偲偭偮偒偵偔偄斀柺丄偦偺墳梡偼丄偲偰傕枺椡揑偱偁傞丅
傂偲偮偺墳梡椺傪偁偘傛偆丅
椺丂帺慠悢 俶 偺奒忔乮 俶両乯偺拞偵丄慺悢 俹 偼壗屄娷傑傟偰偄傞偐丠
丂崱偺悽偺拞偱偼丄寁嶼偲偄偊偽揹戩偲憡応偑寛傑偭偰偄傞偑丄偙偺傛偆側栤戣偵懳偟偰丄
揹戩偼丄旕忢偵柍椡偱偁傞丅侾侽寘偺揹戩偩偲丄侾係両亖俇丆俀俀俈丆侽俀侽丆俉侽侽丂偑惛堦攖
偱偁傞丅巗斕偝傟偰偄傞娭悢揹戩偱偼丄俇俋両傑偱偼寁嶼偱偒傞偑丄巜悢昞帵側偺偱丄偙偺
栤戣偵偼巊偊側偄丅
丂偙偺栤戣偼丄僈僂僗偺婰崋傪梡偄傞偲丄娙扨偵夝寛偝傟傞丅
丂椺偊偽丄侾侽両亖侾侽丒俋丒俉丒俈丒俇丒俆丒係丒俁丒俀丒侾亖俁丆俇俀俉丆俉侽侽丂偺拞偵丄慺悢
俀 偑壗屄
娷傑傟偰偄傞偐尒偰傒傛偆丅
丂俀 傪娷傓場悢偼丄俀 偺攞悢偱偁傞 俀丆係丆俇丆俉丆侾侽 偺俆屄偁傞丅
丂丂俀亖俀丒侾丂偱丄侾屄 俀 偑娷傑傟偰偄傞丅
丂丂係亖俀丒俀丂偱丄俀屄 俀 偑娷傑傟偰偄傞丅
丂丂俇亖俀丒俁丂偱丄侾屄 俀 偑娷傑傟偰偄傞丅
丂丂俉亖俀丒俀丒俀丂偱丄俁屄 俀 偑娷傑傟偰偄傞丅
丂侾侽亖俀丒俆丂偱丄侾屄 俀 偑娷傑傟偰偄傞丅
丂埲忋偺寁嶼偐傜丄侾侽両偵偼丄慺悢 俀 偑 俉 屄娷傑傟偰偄傞偙偲偑暘偐傞丅
偙偺傛偆側寁嶼傪堦斒壔偡傞偨傔偵丄師偺傛偆側昞傪嶌偭偰傒傛偆丅
| 俀 |
係 |
俇 |
俉 |
侾侽 |
寁 |
丂 |
堄枴 |
| 仠 |
仠 |
仠 |
仠 |
仠 |
俆 |
丒丒丒丒丒 |
侾侽埲壓偺 俀 偺攞悢偺屄悢 |
| 丂 |
仠 |
丂 |
仠 |
丂 |
俀 |
丒丒丒丒丒 |
侾侽埲壓偺 係 偺攞悢偺屄悢 |
| 丂 |
丂 |
丂 |
仠 |
丂 |
侾 |
丒丒丒丒丒 |
侾侽埲壓偺 俉 偺攞悢偺屄悢 |
| 侾 |
俀 |
侾 |
俁 |
侾 |
俉 |
丂 |
丂 |
丂帺慠悢 俶 傪丄俹 偱妱偭偨彜傪丄倣丄梋傝傪丄値 偲偡傞偲丄
丂俶 埲壓偺 俹 偺攞悢偼丄倣 屄
偁傞丅偲偙傠偱丄妱傝嶼偺摍幃偐傜丄
丂俶亖俹丒倣亄値丂丂乮 侽亝 値 亙俹 乯
偟偨偑偭偰丄
丂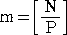
偑惉傝棫偮丅
丂偙偺婰朄傪梡偄傟偽丄忋婰偺栤戣偼丄師偺傛偆偵寁嶼偟偰傕傛偄偙偲偵側傞丅
丂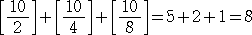
丂埲忋傪堦斒壔偟偰丄師偺岞幃傪摼傞丅
丂帺慠悢 俶 偺奒忔乮 俶両乯偺拞偵丄慺悢 俹 偼師偺屄悢娷傑傟傞丅
丂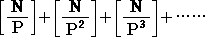
丂傑偨丄偙偺抣偼師偺傛偆偵昡壙偝傟傞丅
丂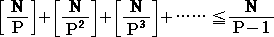
丂徹柧偼丄堈偟偄丅
乮徹柧乯丂[俶/俹]亝俶/俹丂丄[俶/俹2]亝俶/俹2丂丄[俶/俹3]亝俶/俹3丂丄丒丒丒丂傛傝丄
丂丂丂嵍曈亝俶/俹亄俶/俹2亄俶/俹3亄丒丒丒亖俶/俹乷侾/乮侾亅侾/俹乯乸亖俶/乮俹亅侾乯丂丂乮徹廔乯
丂尩枾偵偼丄
丂帺慠悢 俶 偺奒忔乮 俶両乯偺拞偵丄慺悢 俹 偼師偺屄悢娷傑傟傞丅
丂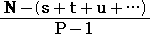
乮偨偩偟丄俶 偺 俹 恑朄揥奐傪丄倱倲倳丒丒丒 偲偡傞丅乯
偱偁傞丅偙偺偙偲傪師偵峫偊傛偆丅
丂屄悢傪媮傔傞忋婰偺岞幃偼丄師偺傛偆偵曄宍偝傟偰梡偄傜傟傞丅
丂丂 |
丂偲偍偔偲偒丄媮傔傞屄悢偼丄 |
丂 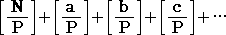
偙偺婰朄偱丄嵞搙栤戣偺摎偊傪寁嶼偟偰傒傞偲丄
丂 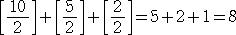
偲側傞丅
丂偲偙傠偱丄侾侽 仺 俆 仺 俀丂偲偄偆寁嶼傪尒偰偄傞偲丄侾侽 傪 俀恑悢偵揮姺偡傞寁嶼偲偺椶
帡惈偵婥偑偮偔丅偡側傢偪丄
丂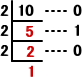
丂偟偨偑偭偰丄侾侽両偺拞偵丄慺悢 俀 偑壗屄娷傑傟偰偄傞偐傪寁嶼偡傞応崌丄侾侽
傪 俀恑悢
偵揮姺偡傞寁嶼傪偟偰丄偦偺拞偺愒帤偺晹暘偺榓傪媮傔偰傕傛偄丅
丂偝傜偵丄忋婰偺寁嶼偐傜丄侾侽 偺 俀恑朄揥奐偼丄侾侽侾侽丂側偺偱丄
丂侾侽亖侾丒俀3亄侽丒俀2亄侾丒俀亄侽丒侾
椉曈傪 俀 偱妱偭偰丄偦偺彜傪 倎 偲偡傞偲丄丂倎亖侾丒俀2亄侽丒俀亄侾
偝傜偵丄椉曈傪 俀 偱妱偭偰丄偦偺彜傪 倐 偲偡傞偲丄丂倐亖侾丒俀亄侽
偝傜偵丄椉曈傪 俀 偱妱偭偰丄偦偺彜傪 們 偲偡傞偲丄丂們亖侾
| 丂偟偨偑偭偰丄 |
|
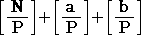 |
亖倎亄倐亄們亖侾丒乮俀2亄俀亄侾乯亄侽丒乮俀亄侾乯亄侾丒侾 |
丂丂丂丂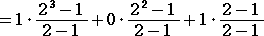 |
丂丂丂丂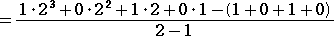 |
丂丂丂丂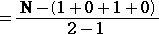 |
忋婰偺寁嶼偲摨條偵偟偰丄師偺岞幃偑摼傜傟傞偙偲偑暘偐傞丅
丂帺慠悢 俶 偺奒忔乮 俶両乯偺拞偵丄慺悢 俹 偼師偺屄悢娷傑傟傞丅
丂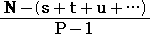
乮偨偩偟丄俶 偺 俹 恑朄揥奐傪丄倱倲倳丒丒丒 偲偡傞丅乯
(椺乯丂侾侽侽両偼丄枛旜偵 侽 偑壗屄懕偔偐丠
丂侾侽侽 偺俀恑朄揥奐偼丄侾侾侽侽侾侽侽丂側偺偱丄侾侽侽両偺拞偵慺悢 俀
偼丄侾侽侽亅俁亖俋俈 屄
娷傑傟傞丅
丂侾侽侽 偺俆恑朄揥奐偼丄係侽侽丂側偺偱丄侾侽侽両偺拞偵慺悢 俆 偼丄乮侾侽侽亅係乯/係亖俀係
屄
娷傑傟傞丅
丂偟偨偑偭偰丄侾侽侽両偺拞偵丄侾侽 偼丄俀係 屄娷傑傟傞偺偱丄侾侽侽両偼丄枛旜偵
侽 偑俀係 屄
懕偔丅
幚嵺偵丄昞寁嶼僜僼僩 俤倶們倕倢丂偺彆偗傪庁傝偰丄侾侽侽両傪寁嶼偡傟偽丄師偺傛偆側抣偲側傞丅
93326 21544 39441 52681 69923 88562 66700 49071 59682 64381 62146 85929
63895 21759 99932 29915 60894 14639 76156 51828 62536 97920 82722 37582
51185 21091 68640 00000 00000 00000 00000 000
丂妋偐偵丄侽 偑俀係屄暲傫偱偄傞偙偲偑暘偐傞丅
偙偺傛偆側戝曄側寁嶼傪偟側偔偰傕丄僈僂僗偺婰崋傪梡偄傞偲丄娙扨側巐懃寁嶼偱摨偠傕偺偑
媮傔傜傟傞偲偄偆偙偲偵姶摦傪妎偊傞丅僈僂僗偺執戝偝偑丄傂偟傂偟偲姶偠傜傟傞丅
乮拲乯丂奺帺慠悢俶偵懳偟偰丄偦偺奒忔 俶両傪曉偡娭悢 俥 偍傛傃娭楢偡傞娭悢偼丄倁俛俙傪
梡偄偰師偺傛偆偵婰弎偝傟傞丅
Function s1(a As String, b As String, c As Single) As String
丂If a = "" Then
丂丂If c = 0 Then s1 = "" Else s1 = c
丂Else
丂t = Val(Right(a, 1)) + Val(Right(b, 1)) + c
丂s1 = s1(Left(a, Len(a) - 1), Left(b, Len(b) - 1), Int(t / 10)) &
(t Mod 10)
丂End If
End Function
Function s(a As String, b As String)
丂Dim aa As String
丂Dim bb As String
丂aa = a
丂bb = b
丂If Len(aa) > Len(bb) Then bb = String(Len(aa) - Len(bb), "0") & bb
丂If Len(aa) < Len(bb) Then aa = String(Len(bb) - Len(aa), "0")
& aa
丂s = s1(aa, bb, 0)
End Function
Function d(a As String) As String
丂While Left(a, 1) = "0"
丂a = Right(a, Len(a) - 1)
丂Wend
丂If a = "" Then d = "0" Else d = a
End Function
Function m(a As String, b As String) As String
丂If b = "" Then m = "": Exit Function
丂For i = 1 To Val(Right(b, 1))
丂丂m = s(m, a)
丂Next i
丂m = d(s(m(a, Left(b, Len(b) - 1)) & "0", m))
End Function
Function 俥(n)
丂If n = 0 Then 俥 = 1 Else 俥 = m(Str(n), 俥(n - 1))
End Function
乮忋婰偺倁俛俙偵偮偄偰偼丄媑壀復晇偝傫傛傝丄偛嫵帵偄偨偩偄偨傕偺偱丄崅惛搙偺墘嶼寢
壥傪抦傝偨偄応崌偵桳岠偱偁傞丅巹偺婱廳側曮暔偱偁傞丅乯
丂丂 丂俤倶們倕倢丂傪婲摦偟丄[僣乕儖]亅[儅僋儘]亅[倁倝倱倳倎倢丂俛倎倱倝們丂俤倓倝倲倧倰]丂偲僋儕僢僋偟偰
丂丂丂俤倓倝倲倧倰 傪婲摦偟丄[憓擖]亅[昗弨儌僕儏乕儖]丂傪慖戰偟偰丄忋婰傪婰弎偡傟偽傛偄丅
丂丂丂屻偼丄俤倶們倕倢偺擟堄偺僙儖偵丄椺偊偽丄丂亖俥乮俆乯丂偲懪偪崬傓偲丄弖帪偵丄侾俀侽
偲
丂丂丂偄偆抣偑曉偝傟傞丅場傒偵丄俥乮俆乯亖俆丒係丒俁丒俀丒侾亖侾俀侽 偱偁傞丅
乮嶲峫暥專丗揷搰堦榊丂挊丂惍悢丂乮嫟棫弌斉乯乯
丂俶両偺拞偵慺悢 俹 偑婔偮娷傑傟傞偐偼丄戝妛擖帋栤戣偱傕嶶尒偝傟傞丅
憗堫揷戝妛丂嫵堢妛晹乮俀侽侽俉擭乯
丂値 傪帺慠悢偲偡傞丅俀侾俋両偼俀値偱妱傝愗傟傞偑丄俀値+1偱偼妱傝愗傟側偄偲偡傞偲丄
値亖乮丂丂乯偱偁傞丅
乮夝乯丂俀侾俋亐俀亖侾侽俋丒丒丒侾丂丄侾侽俋亐俀亖俆係丒丒丒侾丂丄俆係亐俀亖俀俈丒丒丒侽
丂俀俈亐俀亖侾俁丒丒丒侾丂丄侾俁亐俀亖俇丒丒丒侾丂丄俇亐俀亖俁丒丒丒侽丂丄俁亐俀亖侾丒丒丒侾
傛偭偰丄丂侾侽俋亄俆係亄俀俈亄侾俁亄俇亄俁亄侾亖俀侾俁丂傛傝丄
丂俀侾俋両偺拞偵慺悢俀偼丄俀侾俁屄娷傑傟偰偄傞偙偲偑暘偐傞丅
偟偨偑偭偰丄媮傔傞 値 偺抣偼丄丂俀侾俁丂偱偁傞丅丂丂乮廔乯
乮僐儊儞僩乯丂偙偺栤戣偼丄戞侾栤偺乮侾乯偺栤戣偱偁傞偑丄忋婰偺岞幃傪抦傜側偄偲夝偗側偄偺
丂丂丂丂偱偼側偄偐偲巚偆丅庴尡僥僋僯僢僋偲偟偰丄昁偢儅僗僞乕偡傋偒峫偊曽側偺偩傠偆丅
乮捛婰乯丂僈僂僗偺婰崋傪梡偄偰丄 偺柍棟悢惈偑帵偝傟傞偙偲傪丄嵟嬤丄峀搰岺嬈戝妛
偺柍棟悢惈偑帵偝傟傞偙偲傪丄嵟嬤丄峀搰岺嬈戝妛
丂丂丂丂偺戝愳尋媶幒偺儂乕儉儁乕僕偱妛傫偩丅捠忢偼丄婛栺暘悢偱昞偟偰丄柕弬傪摫偔曽
丂丂丂丂朄偑堦斒揑偩偑丄僈僂僗偺婰崋傪梡偄偨僄儗僈儞僩側夝朄偵丄偲偰傕旤偟偝傪姶偠偨丅
丂崱丄 偑桳棟悢偱偁傞偲偡傞丅柧傜偐偵丄
偑桳棟悢偱偁傞偲偡傞丅柧傜偐偵丄 偼惍悢偱偼側偄丅偙偺偲偒丄
偼惍悢偱偼側偄丅偙偺偲偒丄 丒値 偑惍悢
丒値 偑惍悢
偲側傞傛偆側丄嵟彫偺帺慠悢 値 偑懚嵼偡傞丅
丂偙偙偱丄乮 亅乵
亅乵 ]乯丒値 亖倣 偲偍偔偲丄倣 偼惍悢偱丄侽亙
]乯丒値 亖倣 偲偍偔偲丄倣 偼惍悢偱丄侽亙 亅乵
亅乵 ]亙侾 偐傜丄
]亙侾 偐傜丄
丂侽 亙 倣 亙 値
偑惉傝棫偮丅偙偺偲偒丄 丒倣亖俀丒値亅乵
丒倣亖俀丒値亅乵 ]丒乮
]丒乮 丒値乯 偼惍悢偲側傞丅
丒値乯 偼惍悢偲側傞丅
丂偙傟偼丄値 偑丄 丒値 偑惍悢偲側傞傛偆側嵟彫偺帺慠悢偱偁傞偙偲偵柕弬偡傞丅
丒値 偑惍悢偲側傞傛偆側嵟彫偺帺慠悢偱偁傞偙偲偵柕弬偡傞丅
丂傛偭偰丄 偼丄柍棟悢偱偁傞丅丂乮徻偟偔偼丄偙偪傜傪嶲徠乯
偼丄柍棟悢偱偁傞丅丂乮徻偟偔偼丄偙偪傜傪嶲徠乯
乮捛婰乯丂僈僂僗偺婰崋 乵倃乶 偼丄悢妛偺悽奅偱偼廳曮偡傞婰崋偱偁傞偑丄偙偺屇傃柤偼擔杮
丂丂屌桳偺傕偺傜偟偄丅
丂嵟嬤偱偼丄彫悢揰埲壓愗傝幪偰偼丄婰崋 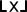 丂偱昞偟丄乽倃偺倖倢倧倧倰乮彴乯乿偲屇傇偙偲偑懡偄
丂偱昞偟丄乽倃偺倖倢倧倧倰乮彴乯乿偲屇傇偙偲偑懡偄
偦偆偩丅
丂偪側傒偵丄彫悢揰埲壓愗傝忋偘偼丄婰崋 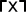 偱昞偝傟丄乽倃偺們倕倝倢倝値倗乮揤堜乯乿偲屇傇傜偟偄丅
偱昞偝傟丄乽倃偺們倕倝倢倝値倗乮揤堜乯乿偲屇傇傜偟偄丅
乮嶲峫暥專丗崻忋惗栫丄拞杮撝峗丂挊丂婎慴悢妛椡僩儗乕僯儞僌丂乮擔杮昡榑幮乯乯
丂墷暷偺悢妛嫵壢彂偱偼丄僈僂僗偺婰崋偼婛偵攑傟偰偄偰丄戙傢傝偵乽彴乿娭悢偲偐乽揤堜乿
娭悢偑巊傢傟偰偄傞傜偟偄丅
椺丂僈僂僗偺婰崋傪梡偄偰丄
丂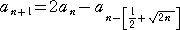
偲昞偝傟傞悢幃偼丄丂倎値+1亖俀倎値亅倎値-floor(1/2+併乮2値乯)丂偲傕昞偝傟傞丅丂乮仺丂嶲峫椺乯
丂僈僂僗偺婰崋偵娭偡傞戝妛擖帋栤戣傕悢懡偄丅
撧椙彈巕戝妛丂棟妛晹丒惗妶娐嫬妛晹乮侾俋俋俉擭乯
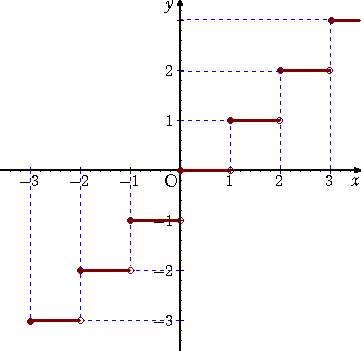
丂幚悢 倶 偵懳偟偰丄偦偺惍悢晹暘傪 [ 倶 ] 偱昞偡丅偡側傢偪丄[ 倶 ] 偼晄摍幃
丂[ 倶 ] 亝 倶 亙[ 倶 ] 亄侾
傪枮偨偡惍悢偱偁傞丅
乮侾乯丂幚悢 倶 偵懳偟偰丄摍幃丂[ 倶 ] 亄[ 倶亄侾/俁 ] 亄[ 倶亄俀/俁 ] 亖[ 俁倶 ] 丂傪帵偣丅
乮俀乯丂惓偺惍悢 値 丄幚悢 倶 偵懳偟偰丄
丂摍幃丂[ 倶 ] 亄[ 倶亄侾/値 ] 亄[ 倶亄俀/値 ] 亄丒丒丒亄[ 倶亄乮値亅侾乯/値 ] 亖[ 値倶 ] 丂傪帵偣丅
乮夝乯乮侾乯丂[ 俁倶 ]亖倣丂偲偍偔偲丄丂倣亝俁倶亙倣亄侾丂偱偁傞丅
丂倣亖俁倠丂偺偲偒丄丂倠亝倶亙倠亄侾/俁丂側偺偱丄
丂丂[ 倶 ] 亄[ 倶亄侾/俁 ] 亄[ 倶亄俀/俁 ] 亖倠亄倠亄倠亖俁倠亖倣亖[ 俁倶 ]
丂倣亖俁倠亄侾丂偺偲偒丄丂倠亄侾/俁亝倶亙倠亄俀/俁丂側偺偱丄
丂丂[ 倶 ] 亄[ 倶亄侾/俁 ] 亄[ 倶亄俀/俁 ] 亖倠亄倠亄倠亄侾亖俁倠亄侾亖倣亖[ 俁倶 ]
丂倣亖俁倠亄俀丂偺偲偒丄丂倠亄俀/俁亝倶亙倠亄侾丂側偺偱丄
丂丂[ 倶 ] 亄[ 倶亄侾/俁 ] 亄[ 倶亄俀/俁 ] 亖倠亄倠亄侾亄倠亄侾亖俁倠亄俀亖倣亖[ 俁倶 ]
丂埲忋偐傜丄壗傟偵偟偰傕丄[ 倶 ] 亄[ 倶亄侾/俁 ] 亄[ 倶亄俀/俁 ] 亖[ 俁倶 ] 丂偑惉傝棫偮丅
乮俀乯丂[ 値倶 ]亖倣丂偲偍偔偲丄丂倣亝値倶亙倣亄侾丂偱偁傞丅
丂倣亖値倠亄倛丂乮倛亖侽丄侾丄俀丄丒丒丒丄値亅侾乯丂偺偲偒丄倠亄倛/値亝倶亙倠亄乮倛亄侾乯/値丂側偺偱丄
丂倠亄乮倛亄倲乯/値亝倶亄倲/値亙倠亄乮倛亄倲亄侾乯/値
傛偭偰丄丂倛亄倲亄侾亝値丂偡側傢偪丄丂侽亝 倲 亝値亅倛亅侾丂偺偲偒丄
丂倠亝倶亄倲/値亙倠亄侾丂側偺偱丄丂[ 倶亄倲 ] 亖倠
丂倛亄倲亞値丂偡側傢偪丄丂値亅倛亝倲亝値亅侾丂偺偲偒丄
丂倠亄侾亝倶亄倲/値亙倠亄俀丂側偺偱丄丂[ 倶亄倲 ] 亖倠亄侾
偟偨偑偭偰丄丂値亅侾亅乮値亅倛乯亄侾亖倛丂側偺偱丄
丂[ 倶 ] 亄[ 倶亄侾/値 ] 亄[ 倶亄俀/値 ] 亄丒丒丒亄[ 倶亄乮値亅侾乯/値 ]
亖乮値亅倛乯倠亄倛乮倠亄侾乯亖値倠亄倛亖倣亖[ 値倶 ]
偑惉傝棫偮丅丂丂乮廔乯
丂忋婰偺栤戣偺弌揟偼丄偍偦傜偔憡摉愄偺柤屆壆巗棫戝妛偺師偺栤戣偩傠偆丅
丂擟堄偺幚悢 倶 偵懳偟偰丄晄摍幃丂倎亝倶亙倎亄侾丂傪枮偨偡惍悢 倎 傪婰崋 [ 倶 ] 偱昞偡丅幚
悢 倶 偍傛傃惓偺惍悢 値 偑梌偊傜傟偨偲偒丄
乮侾乯丂晄摍幃丂[ 倶 ] 亄倠/値亝 倶 亙[ 倶 ] 亄乮倠亄侾乯/値丂傪枮偨偡惍悢 倠 偑懚嵼偡傞偙偲傪帵偣丅
乮俀乯丂摍幃丂[ 倶 ] 亄[ 倶亄侾/値 ] 亄[ 倶亄俀/値 ] 亄丒丒丒亄[ 倶亄乮値亅侾乯/値 ] 亖[ 値倶 ] 丂偑惉棫偡
丂丂傞偙偲傪徹柧偣傛丅
乮夝乯乮侾乯丂嬫娫丂[ 倶 ] 亝 倶 亙[ 倶 ] 亄侾丂傪 値 摍暘偡傞丅
丂[ 倶 ] 亝 倶 亙[ 倶 ] 亄侾/値丄[ 倶 ] 亄侾/値亝 倶 亙[ 倶 ] 亄俀/値丄丒丒丒丄
[ 倶 ] 亄乮値亅侾乯/値亝 倶 亙[ 倶 ] 亄侾
倶 偼偙偺偳傟偐偺嬫娫偵娷傑傟傞偐傜丄偁傞惍悢 倠 乮侽亝倠亝値亅侾乯偑懚嵼偟偰丄
丂[ 倶 ] 亄倠/値亝 倶 亙[ 倶 ] 亄乮倠亄侾乯/値
乮俀乯丂乮撧椙彈巕戝妛偺乮俀乯偲摨條乯丂丂乮廔乯
丂憗堫揷戝妛丂棟岺妛晹乮俀侽侽俋擭乯偱弌戣偝傟偰偄傞栤戣傕柺敀偦偆偩丅
丂幚悢 倶 偵懳偟偰丄倶 埲壓偺嵟戝偺惍悢傪丂[ 倶 ] 偱昞偡丅埲壓偺栤偄偵摎偊傛丅
乮侾乯丂侾係/俁亙倶亙俆丂偺偲偒丄[ 俁倶/俈 ]亅 [ 俁[ 倶 ]/俈 ] 傪媮傔傛丅
乮俀乯丂偡傋偰偺幚悢 倶 偵偮偄偰丄[ 倶/俀 ]亅 [ [ 倶 ]/俀 ]亖侽丂傪帵偣丅
乮俁乯丂値 傪惓偺惍悢偲偡傞丅幚悢 倶 偵偮偄偰丄[ 倶/値 ]亅 [ [ 倶 ]/値
] 傪媮傔傛丅
乮夝乯乮侾乯丂侾係/俁亙倶亙俆丂傛傝丄丂俀亙俁倶/俈亙侾俆/俈亙俁丂側偺偱丄丂[
俁倶/俈 ]亖俀
丂傑偨丄丂係亙侾係/俁亙倶亙俆丂傛傝丄丂[ 倶 ]亖係丂側偺偱丄丂[ 俁[ 倶 ]/俈 ]亖[ 侾俀/俈 ]亖侾
丂傛偭偰丄丂[ 俁倶/俈 ]亅 [ 俁[ 倶 ]/俈 ]亖俀亅 侾亖侾
乮俀乯丂[ 倶 ] 亖俀倣丂乮倣偼惍悢乯丂偺偲偒丄俀倣亝倶亙俀倣亄侾丂側偺偱丄丂倣亝倶/俀亙倣亄侾/俀
偙偺偲偒丄丂[ 倶/俀 ]亅 [ [ 倶 ]/俀 ]亖倣亅[ 倣 ]亖倣亅倣亖侽
[ 倶 ] 亖俀倣亄侾丂乮倣偼惍悢乯丂偺偲偒丄俀倣亄侾亝倶亙俀倣亄俀丂側偺偱丄倣亄侾/俀亝倶/俀亙倣亄侾
偙偺偲偒丄丂[ 倶/俀 ]亅 [ [ 倶 ]/俀 ]亖倣亅[ 倣亄侾/俀 ]亖倣亅乮倣亄[ 侾/俀 ]乯亖倣亅倣亖侽
埲忋偐傜丄壗傟偵偟偰傕丄丂[ 倶/俀 ]亅 [ [ 倶 ]/俀 ]亖侽丂偑惉傝棫偮丅
乮俁乯丂[ 倶 ] 亖値倠亄倰丂乮倠丄倰 偼惍悢偱丄侽亝倰亙値乯丂偺偲偒丄値倠亄倰亝倶亙値倠亄倰亄侾丂側偺偱丄
丂倠亝倠亄倰/値亝倶/値亙倠亄乮倰亄侾乯/値亝倠亄侾
偙偺偲偒丄丂[ 倶/値 ]亅 [ [ 倶 ]/値 ]亖倠亅[ 倠亄倰/値 ]亖倠亅倠亖侽丂丂乮廔乯
丂忋婰偺乮夝乯偱偼丄[ 倶 ] 偺忚梋偱暘椶偟偰夝傪摫偄偨偑丄師偺傛偆側暿夝傕峫偊傜傟傞丅
乮暿夝乯乮侾乯偼忋婰偲摨偠丅
乮俀乯丂[ [ 倶 ]/俀 ]亖[ 倶 ]/俀丂傑偨偼丂乮[ 倶 ]亅侾乯/俀丂側偺偱丄
丂乮[ 倶 ]亅侾乯/俀亝[ [ 倶 ]/俀 ]亝[ 倶 ]/俀
偡側傢偪丄丂[ 倶 ]亝倶亙[ 倶 ]亄侾丂傛傝丄丂倶亅侾亙[ 倶 ]丂丄丂[ 倶 ]亝倶丂傪梡偄偰
丂倶/俀亅侾亙乮[ 倶 ]亅侾乯/俀亝[ [ 倶 ]/俀 ]亝[ 倶 ]/俀亝倶/俀
傛偭偰丄丂倶/俀亅侾亙[ [ 倶 ]/俀 ]亝倶/俀丂丒丒丒(*)
傑偨丄丂倶亅侾亙[ 倶 ]亝倶丂傛傝丄丂倶/俀亅侾亙倶/俀亅侾/俀亙[ 倶 ]/俀亝倶/俀丂側偺偱丄
丂亅倶/俀亝亅[ 倶 ]/俀亙亅倶/俀亄侾丂丒丒丒(**)
(*)偲(**)傪曈乆壛偊偰丄丂亅侾亙[ [ 倶 ]/俀 ]亅[ 倶 ]/俀亙侾
[ [ 倶 ]/俀 ]亅[ 倶 ]/俀丂偼惍悢偱偁傞偺偱丄丂[ [ 倶 ]/俀 ]亅[ 倶 ]/俀亖侽
乮俁乯丂乮俀乯偲摨條偵峫偊偰丄[ [ 倶 ]/値 ]亖[ 倶 ]/値丂丄乮[ 倶 ]亅侾乯/値丂丄丒丒丒丄乮[ 倶 ]亅値亄侾乯/値
側偺偱丄丂乮[ 倶 ]亅値亄侾乯/値亝[ [ 倶 ]/値 ]亝[ 倶 ]/値
偡側傢偪丄丂[ 倶 ]亝倶亙[ 倶 ]亄侾丂傛傝丄丂倶亅侾亙[ 倶 ]丂丄丂[ 倶 ]亝倶丂傪梡偄偰
丂倶/値亅侾亙乮[ 倶 ]亅値亄侾乯/値亝[ [ 倶 ]/値 ]亝[ 倶 ]/値亝倶/値
丂傛偭偰丄丂倶/値亅侾亙[ [ 倶 ]/値 ]亝倶/値丂丒丒丒(*)
丂傑偨丄丂倶亅侾亙[ 倶 ]亝倶丂傛傝丄丂倶/値亅侾亙倶/値亅侾/値亙[ 倶 ]/値亝倶/値丂側偺偱丄
丂亅倶/値亝亅[ 倶 ]/値亙亅倶/値亄侾丂丒丒丒(**)
(*)偲(**)傪曈乆壛偊偰丄丂亅侾亙[ [ 倶 ]/値 ]亅[ 倶 ]/値亙侾
丂[ [ 倶 ]/値 ]亅[ 倶 ]/値丂偼惍悢偱偁傞偺偱丄丂[ [ 倶 ]/値 ]亅[ 倶 ]/値亖侽丂丂乮廔乯
丂僈僂僗偺婰崋偺堄枴偑暘偐偭偰偟傑偊偽壗偱傕側偄偑丄姷傟偰偄側偄恖偵偲偭偰偼偲偰偮
傕側偔擄偟偔姶偠傞傜偟偄丅摨偠栤戣偱傕丄僈僂僗偺婰崋傪梡偄偨偩偗偱擄搙偼忋偑傞丅懡暘
擖帋栤戣偱僈僂僗偺婰崋偑巊傢傟傞偺偼弌戣幰懁偺榑棟偩傠偆丅庴尡惗傪乽傃傃傜偣傞乿
偨傔偵丏丏丏丅
丂偨偩師偺栤戣偼丄偦傫側晽忣傪姶偠偝偣側偄埵偵丄傛偔峫偊傜傟偨椙栤偩偲巚偆丅
丂搶嫗戝妛慜婜丂棟宯乮侾俋俋俉擭乯
丂幚悢 倎 偵懳偟偰丄倠亝倎亙倠亄侾 傪枮偨偡惍悢 倠 傪 [ 倎 ] 偱昞偡丅値
傪惓偺惍悢偲偟偰丄
丂
偲偍偔丅俁俇値亄侾屄偺惍悢
丂[ 俥乮侽乯 ] 丄[ 俥乮侾乯 ] 丄[ 俥乮俀乯 ] 丄丒丒丒丄[ 俥乮俁俇値乯 ]
偺偆偪憡堎側傞傕偺偺屄悢傪 値 傪梡偄偰昞偣丅
丂値亖侾 偲偟偰丄幚嵺偵 俁俈屄偺抣傪媮傔偰傒偨丅
乮庴尡応偱丄栙乆偲幚峴偡傞曽偑傕偟偐偟偨傜丏丏丏偄傞偐傕丠婔偽偔偐偺晹暘揰偼傕傜偊傞
丂偐傕偟傟側偄丅乯
丂俥乮倶乯亖倶2乮俆係亅倶乯/俉俇係丂偵偮偄偰丄
| 値 |
俥乮値乯 |
[ 俥乮値乯] |
屄悢 |
| 0 |
0.00 |
0 |
1 |
| 1 |
0.06 |
0 |
| 2 |
0.24 |
0 |
| 3 |
0.53 |
0 |
| 4 |
0.93 |
0 |
| 5 |
1.42 |
1 |
2 |
| 6 |
2.00 |
2 |
3 |
| 7 |
2.67 |
2 |
| 8 |
3.41 |
3 |
4 |
| 9 |
4.22 |
4 |
5 |
| 10 |
5.09 |
5 |
6 |
| 11 |
6.02 |
6 |
7 |
| 12 |
7.00 |
7 |
8 |
| 13 |
8.02 |
8 |
9 |
| 14 |
9.07 |
9 |
10 |
| 15 |
10.16 |
10 |
11 |
| 16 |
11.26 |
11 |
12 |
| 17 |
12.38 |
12 |
13 |
| 18 |
13.50 |
13 |
14 |
| 19 |
14.62 |
14 |
15 |
| 20 |
15.74 |
15 |
16 |
| 21 |
16.84 |
16 |
17 |
| 22 |
17.93 |
17 |
18 |
| 23 |
18.98 |
18 |
19 |
| 24 |
20.00 |
20 |
20 |
| 25 |
20.98 |
20 |
| 26 |
21.91 |
21 |
21 |
| 27 |
22.78 |
22 |
22 |
| 28 |
23.59 |
23 |
23 |
| 29 |
24.33 |
24 |
24 |
| 30 |
25.00 |
25 |
25 |
| 31 |
25.58 |
25 |
| 32 |
26.07 |
26 |
26 |
| 33 |
26.47 |
26 |
| 34 |
26.76 |
26 |
| 35 |
26.94 |
26 |
| 36 |
27.00 |
27 |
27 |
|
 |
丂埲忋偐傜丄値亖侾偺偲偒丄媮傔傞屄悢偼丄俀俈屄偱偁傞偙偲偑暘偐傞丅
丂摨條偵丄値亖俀 偺偲偒傕媮傔偰傒傛偆丅
丂俥乮倶乯亖倶2乮侾侽俉亅倶乯/俁係俆俇丂偵偮偄偰丄
| 値 |
俥乮値乯 |
[ 俥乮値乯] |
屄悢 |
| 0 |
0.00 |
0 |
1 |
| 1 |
0.03 |
0 |
| 2 |
0.12 |
0 |
| 3 |
0.27 |
0 |
| 4 |
0.48 |
0 |
| 5 |
0.75 |
0 |
| 6 |
1.06 |
1 |
2 |
| 7 |
1.43 |
1 |
| 8 |
1.85 |
1 |
| 9 |
2.32 |
2 |
3 |
| 10 |
2.84 |
2 |
| 11 |
3.40 |
3 |
4 |
| 12 |
4.00 |
4 |
5 |
| 13 |
4.65 |
4 |
| 14 |
5.33 |
5 |
6 |
| 15 |
6.05 |
6 |
7 |
| 16 |
6.81 |
6 |
| 17 |
7.61 |
7 |
8 |
| 18 |
8.44 |
8 |
9 |
| 19 |
9.30 |
9 |
10 |
| 20 |
10.19 |
10 |
11 |
| 21 |
11.10 |
11 |
12 |
| 22 |
12.04 |
12 |
13 |
| 23 |
13.01 |
13 |
14 |
| 24 |
14.00 |
14 |
15 |
| 25 |
15.01 |
15 |
16 |
| 26 |
16.04 |
16 |
17 |
| 27 |
17.09 |
17 |
18 |
| 28 |
18.15 |
18 |
19 |
| 29 |
19.22 |
19 |
20 |
| 30 |
20.31 |
20 |
21 |
| 31 |
21.41 |
21 |
22 |
| 32 |
22.52 |
22 |
23 |
| 33 |
23.63 |
23 |
24 |
| 34 |
24.75 |
24 |
25 |
| 35 |
25.88 |
25 |
26 |
| 36 |
27.00 |
27 |
27 |
| 37 |
28.12 |
28 |
28 |
| 38 |
29.25 |
29 |
29 |
| 39 |
30.37 |
30 |
30 |
| 40 |
31.48 |
31 |
31 |
| 41 |
32.59 |
32 |
32 |
| 42 |
33.69 |
33 |
33 |
| 43 |
34.78 |
34 |
34 |
| 44 |
35.85 |
35 |
35 |
| 45 |
36.91 |
36 |
36 |
| 46 |
37.96 |
37 |
37 |
| 47 |
38.99 |
38 |
38 |
| 48 |
40.00 |
40 |
39 |
| 49 |
40.99 |
40 |
| 50 |
41.96 |
41 |
40 |
| 51 |
42.90 |
42 |
41 |
| 52 |
43.81 |
43 |
42 |
| 53 |
44.70 |
44 |
43 |
| 54 |
45.56 |
45 |
44 |
| 55 |
46.39 |
46 |
45 |
| 56 |
47.19 |
47 |
46 |
| 57 |
47.95 |
47 |
| 58 |
48.67 |
48 |
47 |
| 59 |
49.35 |
49 |
48 |
| 60 |
50.00 |
50 |
49 |
| 61 |
50.60 |
50 |
| 62 |
51.16 |
51 |
50 |
| 63 |
51.68 |
51 |
| 64 |
52.15 |
52 |
51 |
| 65 |
52.57 |
52 |
| 66 |
52.94 |
52 |
| 67 |
53.25 |
53 |
52 |
| 68 |
53.52 |
53 |
| 69 |
53.73 |
53 |
| 70 |
53.88 |
53 |
| 71 |
53.97 |
53 |
| 72 |
54.00 |
54 |
53 |
|
 |
丂埲忋偐傜丄値亖俀偺偲偒丄媮傔傞屄悢偼丄俆俁屄偱偁傞偙偲偑暘偐傞丅
丂忋婰偺幚尡偐傜丄丂俀俈丆俆俁丆丒丒丒丂偲偄偆悢楍偑摼傜傟丄堦斒偺帺慠悢
値 偵偮偄偰丄媮傔
傞屄悢偼丄
丂俀俇値亄侾乮屄乯
偱偁傞偙偲偑悇嶡偝傟傞丅
丂嬶懱揑側 値 偵偮偄偰丄揹戩偑偁傟偽梕堈偵屄悢偑媮傔傜傟傞偑丄揹戩側偟偱屄悢傪媮傔
傞偲偄偆搶嫗戝妛偺栤戣偵丄暯惉俀係擭搙偐傜幚巤偺怴妛廗巜摫梫椞偱婜懸偝傟傞乽壽戣妛
廗乿偺曅椮傪尒傞傛偆側巚偄偱偁傞丅
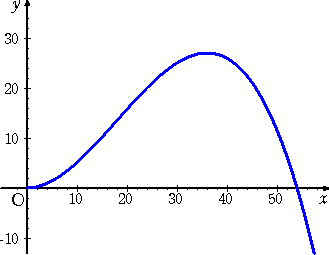
丂値亖侾偺偲偒偲 値亖俀偺偲偒偺僌儔僼傪昤偄偰傒偰嬃偄偨偙偲偑偁傞丅弅広偼丄値亖侾偺偲偒傪
侾偲偡傞偲丄値亖俀偺偲偒偼俀偵偟偨偺偩偑丄俀偮偺僌儔僼傪摨偠弅広偵偟偰廳偹偰傒傞偲僺僢僞儕
廳側偭偰尒偊傞偺偩両偙傟偭偰丏丏丏嬼慠丠
丂偒偭偲娭悢偺偙偺鉟楉側惈幙偑栤戣夝朄偵惗偐偝傟傞偺偩傠偆丅
丂嬻廙偝傫偐傜忋婰栤戣偺夝摎傪捀偒傑偟偨丅乮暯惉俀係擭侾寧俀俀擔晅偗乯
丂搶嫗戝妛慜婜丂棟宯乮侾俋俋俉擭乯
丂幚悢 倎 偵懳偟偰丄倠亝倎亙倠亄侾 傪枮偨偡惍悢 倠 傪 [ 倎 ] 偱昞偡丅値
傪惓偺惍悢偲偟偰丄
丂
偲偍偔丅俁俇値亄侾屄偺惍悢
丂[ 俥乮侽乯 ] 丄[ 俥乮侾乯 ] 丄[ 俥乮俀乯 ] 丄丒丒丒丄[ 俥乮俁俇値乯 ]
偺偆偪憡堎側傞傕偺偺屄悢傪 値 傪梡偄偰昞偣丅
乮夝乯丂倶/俁俇値亖倷丂偲偍偔偲丄幃偑懡彮尒傗偡偔側傝傑偡丅
丂俧乮倷乯亖俀俈倷2乮俁亅俀倷乯値
丂偙偺偲偒丄[ 俧乮侽乯 ] 丄[ 俧乮侾/俁俇値乯 ] 丄[ 俧乮俀/俁俇値乯 ] 丄丒丒丒丄[ 俧乮侾乯 ] 丂傪挷傋傞偙偲偵側
傝傑偡丅
丂旝暘偟偰丄丂俧乫乮倷乯亖侾俇俀倷乮侾亅倷乯値
丂嬫娫 [侽丆侾] 偱丄丂俧乫(倷)亞0 傛傝丄俧乮倷乯偼扨挷偵憹壛偟丄偝傜偵丄俧乫(倷) 偼丄倷亖侾/俀丂偺
帪嵟戝偱偁傞丅
丂俧乫(侾/俀)亖俉侾値/俀亜俁俇値丂偲偄偆偙偲偼丄倷亖侾/俀丂晅嬤偱偼丄倷
偑丄侾/俁俇値 摦偄偨偲偒丄
俧乮倷乯偼侾埲忋摦偔偙偲偑暘偐傝傑偡丅
丂偪傚偆偳丄俧乫乮倷乯亖俁俇値丂偲側傞 倷 傪媮傔偨偔側傝傑偡偹丅媮傔偰傒傞偲丄倷亖侾/俁丄俀/俁丂偲
側傝傑偡丅偦偺帪偺俧乮倷乯偺抣偼丄俈値丄俀侽値丂偲側傝傑偡丅傑偨丄俧乮侽乯亖侽丄俧乮侾乯亖俀俈値
丂偙偺傛偆側峫嶡偐傜丄
(a)丂侽亝倷亝侾/俁丂偱偼丄倷 偑丄侾/俁俇値摦偄偨帪丄俧乮倷乯偺曄壔偼侾埲壓偱偁傞偐傜丄
丂[俧乮倷乯] 偼丄侽偐傜俈値傑偱偺惍悢傪栐梾偡傞丅
(b)丂侾/俁亝倷亝俀/俁丂偱偼丄倷 偑丄侾/俁俇値摦偄偨帪丄俧乮倷乯偺曄壔偼侾埲忋偱偁傞偐傜丄
丂[俧乮倷乯] 偼丄偡傋偰堎側傞惍悢偲側傞丅
(c)丂俀/俁亝倷亝侾丂偱偼丄(a)偲摨條偵丄俀侽値偐傜俀俈値傑偱偺惍悢傪栐梾偡傞丅
丂傛偭偰丄丂(a)偺斖埻偱丄俈値亅侽亄侾亖俈値亄侾屄偺惍悢
(b)偺斖埻偱丄俀係値亅侾俀値亄侾亖侾俀値亄侾屄偺惍悢
丂乮拲堄丗侾/俁亖侾俀値/俁俇値丄俀/俁亖俀係値/俁俇値乯
(c)偺斖埻偱丄俀俈値亅俀侽値亄侾亖俈値亄侾屄偺惍悢
丂俀売強偺嫬奅偱廳暋偟偰悢偊偰偄傑偡偺偱丄崌寁偼丄俀俇値亄侾屄丂偲側傞丅
乮僐儊儞僩乯丂暘偐傝傗偡偄寁嶼偱偡偹両嬻廙偝傫偵姶幱偟傑偡丅
丂俥俶偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀係擭侾寧俀俁擔晅偗乯
丂搶戝偺栤戣偼偛偮偛偮偟偨姶偠偱偄偐偵傕擄偟偦偆偵尒偊傑偡丅峫偊傛偆偲巚偆婥椡傪堔偊
偝偣傞岠壥偼偁傝偦偆偱偡丅偙傫側偵暋嶨側幃偱弌戣偟側偗傟偽側傜側偄偺偱偟傚偆偐丅2師
娭悢偱弌偟偰傕偄偄偺偱偼側偄偐偲巚偆偺偱偡偑丄偦傟偱偼娙扨偡偓傞偲偄偆偙偲偱偟傚偆偐丅
偦傟偲傕2師娭悢側傜婛偵弌戣偝傟偨偙偲偑偁傞偲偄偆偙偲側偺偱偟傚偆偐丅
丂師偺掱搙偺栤戣偱傕偄偄偺偱偼側偄偐偲巚偄傑偡丅
(1)丂幚悢 倎 偵懳偟偰丄倠亝倎亙倠+1 傪枮偨偡惍悢 倠 傪丄[倎] 偱昞偡丅値
傪惓偺惍悢偲偟丄
丂丂F(倶)亖倶(倶+俁値)/(俋値)丂偲偍偔丅俇値+侾屄偺惍悢 [F(0)]丄[F(1)]丄[F(2)]丄ゥA[F(俇値)]
偺偆偪
丂憡堎側傞傕偺偺屄悢傪 値 傪梡偄偰昞偣丅
丂栤戣偲偟偰偼偐側傝扨弮偵側偭偰偄傑偡偑丄栤戣偲偟偰偺峔憿偵偼戝偒側堘偄偼偁傝傑偣
傫丅尒偨姶偠偑偪傚偭偲寉偄偺偱丄庤傪晅偗傗偡偄偺偱偼側偄偱偟傚偆偐丅偙偺掱搙偺栤戣
偐傜傗偭偰傒傞偺偑偄偄偲巚偄傑偡丅
丂栤戣傪嶌傞曽偐傜尵偆偲丄2師娭悢偺応崌偼偐側傝偄偄壛尭偵嶌偭偰傕栤戣偲偟偰惉棫偟
傑偡丅3師娭悢偱嶌傠偆偲偡傞偲丄偐側傝柺搢側傛偆偱偡丅3師娭悢偱丄偙偺宍偺栤戣偑偱偒
傞偨傔偺忦審傪挷傋偰傒傞偺傕柺敀偦偆偱偡丅
丂(1)傪堦斒壔偟偰師偺宍偵偟偰傒傑偡丅
(2)丂幚悢 倎 偵懳偟偰丄倠亝倎亙倠+1 傪枮偨偡惍悢 倠 傪丄[倎] 偱昞偡丅値丄倎丄倐
傪惓偺惍悢偲偟丄
丂丂F(倶)亖倶(倶+倎)/倐丂偲偍偔丅値+侾屄偺惍悢 [F(0)]丄[F(1)]丄[F(2)]丄ゥA[F(値)]
偺偆偪憡堎側傞
丂傕偺偺屄悢傪 値 傪梡偄偰昞偣丅
丂棟孅偼摨偠偱偡偑丄堦斒壔偟偨暘柺搢偵側傝傑偡丅値丄倎丄倐 偵偮偄偰偺斚囹側応崌暘偗偑
昁梫偵側傞傛偆偱偡丅巹傕夝偗偰傞傢偗偱偼偁傝傑偣傫丅倎丄倐 偺嬼婏偑摨偠偱偁傞応崌偼偱
偒偦偆側婥偑偟傑偡丅
丂嬻廙偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀係擭侾寧俀係擔晅偗乯
亀(2)丂幚悢 倎 偵懳偟偰丄倠亝倎亙倠+1 傪枮偨偡惍悢 倠 傪丄[倎] 偱昞偡丅値丄倎丄倐傪惓偺惍悢偲
丂丂偟丄F(倶)亖倶(倶+倎)/倐丂偲偍偔丅値+侾屄偺惍悢 [F(0)]丄[F(1)]丄[F(2)]丄ゥA[F(値)]
偺偆偪憡堎
丂側傞傕偺偺屄悢傪 値 傪梡偄偰昞偣丅亁偵偮偄偰丄
丂惓偺惍悢偲偟偨応崌偼丄埲壓偺(倎)(倐)(們1)(們2)偺応崌暘偗偲側傝傑偟偨丅
丂F乫(倶)=(2倶+倎)/倐丂丄F乫(倶)=侾丂傪壓偐傜捠夁偡傞揰偼丄丂倶=(倐-倎)/2
丂尒傗偡偔偡傞偨傔丄倶=A 傑偱栐梾丄埲崀偽傜偽傜偺帪偺屄悢丗 [F(A)]+1+(n-A)
傪 G(A) 偲
彂偔偙偲偵偟傑偡丅
(倎)丂倐-倎亝0 側傜 n+1屄偺抣偑慡晹偽傜偽傜偱丄n+1屄
(倐)丂倐-倎亞2値 側傜 0 偐傜 [F(値)] 傪栐梾偡傞僞僀僾偱丄G(0)屄
(們)丂0亙倐-倎亙2値 偺応崌偼丄
(們1)丂倐-倎 偑嬼悢偺帪丄倶=(倐-倎)/2 傑偱偼栐梾丄埲崀偽傜偽傜側偺偱丄G((倐-倎)/2)屄
(c2)丂倐-倎 偑婏悢偺帪丄丂F((倐-倎+1)/2)-F((倐-倎-1)/2)=(倐-倎+倎)/倐=1丂側偺偱丄
丂丂倶=(倐-倎-1)/2 傑偱偼栐梾丄埲崀偽傜偽傜偲峫偊偰丄丂G((倐-倎-1)/2)屄
偲側傝傑偡偹丅F乫(倶)偺偐傢傝偵丄傛傝捈愙 F(倶)-F(倶-1)傪挷傋傞庤傕偁傝傑偟偨丅
丂俥俶偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀係擭侾寧俀係擔晅偗乯
丂倐-倎偑婏悢偺偲偒偼丄寁嶼傕偟側偄偱丄柺搢偐側偲巚偭偨偺偱偡偑丄幚嵺偵寁嶼偟偨傜丄偦
傟傎偳偱傕側偄偺偱偡偹丅旝暘偱側偔嵎暘(奒嵎)偱傕偄偄偺偐両嵎暘偱傗偭偰偄傟偽丄
丂丂F((倐-倎+1)/2)-F((倐-倎-1)/2) = (倐-倎+倎)/b = 1
偼丄偁傜偨傔偰寁嶼偡傞傑偱傕側偔丄丂F(倶)-F(倶-1)=1丂傪枮偨偡抣偲偟偰媮傔偰偄偨敜偩偐傜
嵎暘偺傎偆偑妝側偺偐傕偟傟傑偣傫丅
丂俁師娭悢偺応崌偼嵎暘偱偼柍棟側傛偆偱偡丅偲偄偆偙偲偼丄俀師偲俁師偱杮幙揑側堘偄偑偁
傞偲偄偆偙偲偵側傝傑偡丅傗偼傝丄俁師娭悢偱弌戣偡傞昁慠惈偑偁傞偲偄偆偙偲偐傕偟傟傑偣傫丅
丂偁偲偼丄俁師娭悢偱弌戣偡傞偲偒丄搶戝偺幃掱搙偺幃偟偐側偄偺偐丄傑偨丄婥偑岦偄偨傜挷
傋偰傒傑偟傚偆丅(倐)偺G(0)屄偼丄G(値)=[F(値)]+1屄偱偡偹丅
乮捛婰乯丂暯惉俀俉擭俉寧俈擔晅偗
丂忋婰偱師偺栤戣傪峫偊偨丅庴尡悢妛偺桳柤栤戣偱傕偁傞丅
(椺乯丂侾侽侽両偼丄枛旜偵 侽 偑壗屄懕偔偐丠
丂偦偙偱偼丄岞幃 丗
丂帺慠悢 俶 偺奒忔乮 俶両乯偺拞偵丄慺悢 俹 偼師偺屄悢娷傑傟傞丅
丂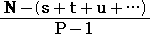
乮偨偩偟丄俶 偺 俹 恑朄揥奐傪丄倱倲倳丒丒丒 偲偡傞丅乯
傪梡偄偰丄侾侽侽 偺俆恑朄揥奐 係侽侽 傛傝丄侾侽侽両偺拞偵 俆 偼丄乮侾侽侽亅係乯/係亖俀係 乮屄乯娷
傑傟傞偙偲偐傜丄侾侽侽両偺枛旜偵 侽 偑俀係 屄懕偔偙偲傪尒偨丅
丂傕偪傠傫丄偙偺寁嶼偼丄僈僂僗偺婰崋傪梡偄偰傕弌棃傞丅
丂乵侾侽侽/俆乶亄乵侾侽侽/俆2乶亖俀侽亄係亖俀係乮屄乯
丂嵟嬤丄斞崅丂栁丂挊丂乽悢妛偺尋媶傪偼偠傔傛偆乮嘥乯乿乮尰戙悢妛幮乯丂傪撉傫偱偄偨傜丄
偙偺寁嶼傪師偺傛偆偵偟偰偄傞偙偲偑拲栚偝傟偨丅
丂値両偵娷傑傟傞俆偺屄悢傪俥乮値乯偲偍偔丅偙偙偱丄侾偐傜値傑偱偺悢偺偆偪丄俆偺攞悢偺屄悢傪
倣偲偡傞偲丄師偺摍幃偑惉傝棫偮丅
丂俥乮値乯亖倣亄俥乮倣乯
偟偨偑偭偰丄丂俥乮侾侽侽乯亖俀侽亄俥乮俀侽乯亖俀侽亄係亄俥乮係乯亖俀侽亄係亄侽亖俀係
乮僐儊儞僩乯丂嵞婣揑側摍幃偺棙梡偱姶摦偟傑偟偨丅堄枴偼僈僂僗偺婰崋偲摨條側偺偩偑丄彮
丂丂丂丂丂丂偟栚怴偟偄姶偠偑偡傞丅
乮捛婰乯丂椷榓俇擭侾侾寧侾侽擔晅偗
丂師偺搶杒戝妛丂棟宯乮侾俋俉俆乯偺栤戣偼丄僈僂僗偺婰崋偲愨懳抣偑弌偰偔傞栤戣偱偁傞丅
栤戣俁丂丂[倶]偵傛偭偰幚悢 倶 傪偙偊側偄嵟戝偺惍悢傪昞偟丄俥乮倶乯亖乥倶亅俀[乮倶亄侾乯/俀]乥偲
丂丂偍偔丅
乮侾乯丂倷亖俥乮倶乯偺僌儔僼傪昤偗丅
乮俀乯丂倢倝倣値仺亣 佺02n 倕-2x俥乮倶乯倓倶丂偺抣傪媮傔傛丅
乮夝乯乮侾乯丂[乮倶亄侾乯/俀]亖倠丂偲偍偔偲丄丂倠亝乮倶亄侾乯/俀亙倠亄侾丂偡側傢偪丄
丂俀倠亅侾亝倶亙俀倠亄侾丂偺偲偒丄丂[乮倶亄侾乯/俀]亖倠丂偱丄丂俥乮倶乯亖乥倶亅俀倠乥丂偲側傞丅
俀倠亅侾亝倶亙俀倠丂偺偲偒丄丂俥乮倶乯亖亅倶亄俀倠
俀倠亝倶亙俀倠亄侾丂偺偲偒丄丂俥乮倶乯亖倶亅俀倠
傛偭偰丄倷亖俥乮倶乯偺僌儔僼偼丄壓恾偺傛偆偵側傞丅
丂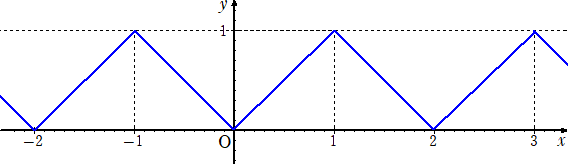
乮俀乯丂倠亖侾丄俀丄丒丒丒丄値丂偵偮偄偰丄
佺2k-22k-1 倕-2x乮倶亅俀倠亄俀乯倓倶亄佺2k-12k 倕-2x乮亅倶亄俀倠乯倓倶
亖[乮亅侾/俀乯倕-2x乮倶亅俀倠亄俀乯]2k-22k-1亄乮侾/俀乯佺2k-22k-1 倕-2x倓倶
丂亄[乮亅侾/俀乯倕-2x乮亅倶亄俀倠乯]2k-12k亅乮侾/俀乯佺2k-12k 倕-2x倓倶
亖乮亅侾/俀乯倕-4k+2亄乮侾/俀乯[乮亅侾/俀乯倕-2x]2k-22k-1亄乮侾/俀乯倕-4k+2亅乮侾/俀乯[乮亅侾/俀乯倕-2x]2k-12k
亖亅乮侾/係乯乮倕-4k+2亅倕-4k+4乯亄乮侾/係乯乮倕-4k亅倕-4k+2乯
亖乮侾/係乯倕-4k亅乮侾/俀乯倕-4k+2亄乮侾/係乯倕-4k+4
亖乮侾/係乯倕-4k乮侾亅俀倕2亄倕4)
亖乮侾亅倕2乯2/係丒倕-4k
傛偭偰丄
佺02n 倕-2x俥乮倶乯倓倶亖儼k=1n 乮侾亅倕2乯2/係丒倕-4k
亖乮侾亅倕2乯2/係丒乮侾亅倕-4n乯/乮倕4亅侾乯丂偐傜丄
丂倢倝倣値仺亣 佺02n 倕-2x俥乮倶乯倓倶亖乮倕2亅侾乯/係乮倕2亄侾乯丂丂乮廔乯
乮僐儊儞僩乯丂側偐側偐寁嶼偑僴乕僪偱偟偨偹両
丂丂丂丂丂埲壓岺帠拞
 丂
丂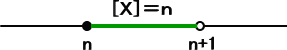
 丂
丂