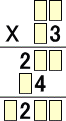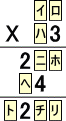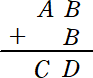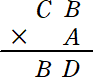・虫食い算の攻略法 Ｓ．Ｈ 氏
「虫食い算」という名称は、計算式（主に筆算形式）が虫に食われたように穴が空いている
ことに由来する。１９４６年に出版された、佐野昌一氏（別名 海野十三氏、推理作家やＳＦ
作家で、日本SFの始祖の一人と呼ばれる）の著書「虫食い算大会」で「虫食い算」という言葉
が初めて使われたようだ。日本は、虫食い算で世界最高のレベルと言われる。
虫食い算の一種で「覆面算」と言われる問題がある。意味のある文や単語から作られる。
覆面算では、同じ文字には同じ数字が対応し、しかも、復元される計算式は唯一つに定ま
る。
例えば、あさしお＋おしだす＝あまのやま に対して、２つの解が存在するので、これは覆
面算とは言えない。
（１） １６７８＋８７５２＝１０４３０ （２） １５７８＋８７６２＝１０３４０
覆面算ではいくつか有名な問題が知られている。
もっとも古いものでは、作者不明の ＳＥＮＤ＋ＭＯＲＥ＝ＭＯＮＥＹ (答え⇒覆面算）や、
つゆは＋しとしと＝あめがふる （答えは、こちら）
などがある。
まず、虫食い算を体験してみよう。虫食い算の問題は巷間に溢れているが、解答のみの
場合多く、その考え方、解き方を詳しく説明しているものは少ない。次の虫食い算を例に、
その攻略法を考えてみよう。
例 次の虫食い算を解け。
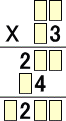
（解） 説明しやすいように、空所に次のように名前を付ける。
 |
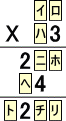３を掛けて３桁になるので、（イ）＝６〜９
このとき、必然的に、（ハ）＝１なので、（ロ）＝４、（ホ）＝２
繰り上がりを考えて、（ヘ）＝（イ）＝９しかなく、（ニ）＝８
よって、（リ）＝２、（チ）＝２、（ト）＝１ |
読者のために練習問題を残しておこう。
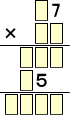
（解）
 |
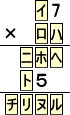まず、虫食い算の攻略法は、与えられた式から情報を取得して、分かると
ころから地道に埋めていく。これに尽きる。
その際に注意することは、数の偶奇や数の桁数に着目すると解決の糸口
が見えてくる場合が多い。 |
上記の場合だと、（イ）７×（ロ）＝（ト）５ に注目して、７に（ロ）を掛けて下１桁が５なので、
（ロ）＝５と確定する。また、（ロ）＝５を（イ）７に掛けて２桁なので、（イ）＝１、（ト）＝８と確定
する。
すると、１７に（ハ）を掛けて３桁の数（ニ）（ホ）（ヘ）になるには、（ハ）の可能性は、６、７、
８、９の何れかであるが、
１７×６＝１０２、１７×７＝１１９、１７×８＝１３６、１７×９＝１５３
より、（ト）５＝８５ と計算して繰り上がるのは、１７×９＝１５３ しかない。
よって、（ハ）＝９と確定する。
以上から、 １７×５９を計算すると、１００３となり、すべての虫食い箇所が確定する。
虫食い算の問題が次のページで取り上げられている。是非挑戦してみてください。
・虫食い算 ・完全覆面算 ・小町覆面算 ・虫食い算２ ・虫食い算３ ・虫食い算４
・虫食い算５ ・虫食い算６ ・虫食い算７ ・虫食い算８（覆面算） ・虫食い算９
・虫食い算１０ ・虫食い算１１ ・虫食い算１２ ・パズル２０１６(6) ・２０１３年頭パズル
虫食い算と同様に覆面算もお楽しみください。
・覆面算 ・覆面算２ ・クリスマス覆面算 ・行儀よい覆面算 ・覆面算２０２０
・覆面算
虫食い算の問題をいろいろと収集してみた。
問題 ０から９までの数字を一度ずつ使って足し算の式を作る。空所を補充せよ。
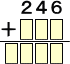
（解） 普通の計算以外に、使える数字にも制限があるので、解きやすいとは思うが、それ
ほど易しくもない虫食い算でしょう。
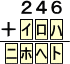
まず、すぐ気が付くのは、（ニ）＝１。ということは、（イ）の可能性は、７、８、９の何れかで
ある。
ところが、１と２がすでに使われているので、（イ）＝９の可能性はない。
ここで、（イ）＝８とすると、（ホ）＝０が確定し、残りの使える数字は、３、５、７、９
十の位での繰り上がりがないので、（ロ）＝３または５
（ロ）＝３のとき、一の位の繰り上がりがないという条件で、（へ）＝７だが、それは不可能。
（ロ）＝５のとき、一の位の繰り上がりがないという条件で、（へ）＝９だが、それは不可能。
以上から、（イ）＝７、（ホ）＝０と確定する。
このとき、残りの使える数字は、３、５、８、９
十の位での繰り上がりがあるので、（ロ）＝８または９
（ロ）＝９とすると、（ヘ）＝３だが、それは不可能。
（ロ）＝８とすると、（ヘ）＝３なので、残りの使える数字は、５、９を考えると、
（ハ）＝９、（ト）＝５と確定する。
以上から、 ２４６＋７８９＝１０３５ となる。 （終）
ＧＡＩ さんからのコメントです。（令和２年２月２０日付け）
ネットで見た虫食い算ですが、中学１年生の創作だそうです。
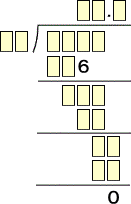
（コメント） 中学１年生創作という言葉に惹かれて考えてみました。
まず、（ソ）＝（ネ）＝０は確定で、（ヲ）＝１しか入らない。第３行が３桁で一の位が６、第７
行が２桁で一の位が０であることから、（イ）＝９、（ハ）＝５と確定し、（ニ）＝１、（ホ）＝４とな
るので、（ヌ）１、（ル）＝２、（レ）＝（ツ）＝７が確定する。
（ロ）の可能性は、１〜７があるが、３桁から２桁を引いて１桁になることから、（ロ）＝７しか
ありえず、（ヨ）＝９、（タ）＝８が確定する。
よって、（ワ）＝０、（カ）＝５で、（ヘ）＝１、（ト）＝３、（チ）＝６、（リ）＝５が確定する。
＃この虫食い算を創作されたのが中学１年生だと聞いて驚きです。出来上がったものを解
くのは根気が要りますが、そのうち解決します。それに対して解がユニークに決まる虫食
い算を作るのは解く以上に難しいことです。中学１年生の構想力に感服です。
らすかるさんからのコメントです。（令和２年２月２０日付け）
整数の方が説明しやすいので、被除数の10倍をa(5桁で一の位は0)、除数をb(2桁)、商の
10倍をc(3桁で一の位は0以外)とすると、bc=aです。
bにcを掛けると一の位が0となり、bを何倍かすると一の位が6になることから、bは偶数で、
cの一の位は5です。
一番下の部分からbを5倍しても2桁のままですから、bの十の位は1と決まります。十の位
が1である偶数を1桁倍して3桁になるのは、
12×9=108 、14×8=112 、14×9=126 、16×7=112 、16×8=128
16×9=144 、18×6=108 、18×7=126 、18×8=144 、18×9=162
で、すべてですが、このうち一の位が6になるものは、14×9=126 と 18×7=126 の二つし
かありません。
aから12600を引いた結果が1000以上ですから、aは13600以上です。
もし、b=14 とすると、 13600÷14≒971.4 なので、cは、975 か 985 か 995 となりま
すが、cの十の位を14倍して2桁ですから、975しかあり得ません。
14×975=13650 であり、1365÷14 を筆算で行うと条件を満たします。
もし、b=18 とすると、13600÷18≒755.6 なので、cは、765 か 775 か 785 か 795
となりますが、cの十の位を18倍すると、いずれも3桁になり条件を満たしません。
従って、答えは、 1365÷14=97.5 です。
（追記） 令和２年３月７日付け
虫食い算は、算数の発想を鍛えるのに最適ですね。算数の発想にこそ様々な科学の思
考法の原点のようなものが根付いているように感じます。
問題 次の空所を補充せよ。
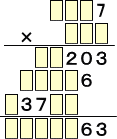
（解）
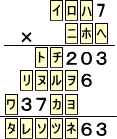
まず、７と掛けて一の位が３になることから、 （へ）＝９ と確定。□□７×９を計算して下
３桁が２０３から、（ハ）＝６、（ロ）＝４と確定。同様に、７と掛けて一の位が６になることから、
（ホ）＝８ と確定。このとき、（ヲ）＝３、（ル）＝７と確定。
このとき、上から第４行と第５行の関係から、（ニ）＝８と類推され、（カ）＝３、（ヨ）＝６で、
（ヌ）＝３ということから、（イ）＝５と確定し、（リ）＝４、（ワ）＝４である。また、（ト）＝４、
（チ）＝９である。よって、（ネ）＝１、（ツ）＝０、（ソ）＝６、（レ）＝８、（タ）＝４となる。
（追記） 令和２年３月１６日付け
問題 次の空所を補充せよ。
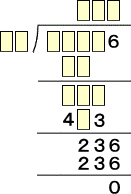
（解）
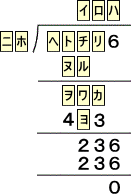
明らかに、（カ）＝６で、（リ）＝６である。また、２３６＝５９×４なので、（ニ）＝５、（ホ）＝９、
（ハ）＝４が分かる。よって、（ロ）＝７で、（ヨ）＝１が確定。
このとき、 （ヲ）＝４、（ワ）＝３で、（イ）＝１から、（ヌ）＝５、（ル）＝９から、
（ヘ）＝１、（ト）＝０、（チ）＝２が確定する。
（追記） 令和２年６月１３日付け
虫食い算と覆面算の混合問題もある。
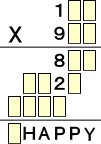
（解）
 |
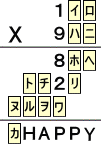まず、１**×９で４桁なので、（ヌ）＝１は確定。また、１**×（ハ）も４桁
なので、（ト）＝１も確定。このとき、（ハ）＝６、７、８、９
（ハ）＝６のとき、１**×６の十の位が２なので、１**＝１７０、１７１
１**＝１７０のとき、（ヘ）＝Ｙ＝０で、（リ）＝（ワ）＝Ｐ＝０
Ｙ＝Ｐ となり、覆面算のルールから不適。 |
１**＝１７１のとき、（ニ）＝５で、１７１×９６５＝１６５０１５ となり、覆面
算のルールから不適。
（ハ）＝７のとき、１**×７の十の位が２なので、１**＝１４６、１４７、１６０、１６１、１７５
１**＝１４６のとき、（ニ）＝６で、１４６×９７６＝１４２４９６ となり、覆面算のルールから不適。
１**＝１４７のとき、（ニ）＝６で、１４７×９７６＝１４３４７２ となり、覆面算のルールから不適。
１**＝１６０のとき、（ニ）＝５で、１６０×９７５＝１５６０００ となり、覆面算のルールから不適。
１**＝１６１のとき、（ニ）＝５で、１６１×９７５＝１５６９７５ となり、覆面算のルールから不適。
１**＝１７５のとき、（ニ）＝５で、１７５×９７５＝１７０６２５ となり、覆面算のルールから不適。
（ハ）＝８のとき、１**×８の十の位が２なので、１**＝１４１、１５３、１６５、１６６、１７８
１**＝１４１のとき、（ニ）＝６で、１４１×９８６＝１３９０２６ となり、覆面算のルールから不適。
１**＝１５３のとき、（ニ）の値が存在しないので不適。
１**＝１６５のとき、（ニ）＝５で、１６５×９８５＝１６２５２５ となり、覆面算のルールから不適。
１**＝１６６のとき、（ニ）＝５で、１６６×９８５＝１６３５１０ となり、覆面算のルールから不適。
１**＝１７８のとき、（ニ）＝５で、１７８×９８５＝１７５３３０ となり、条件に適する。
（ハ）＝９のとき、１**×９の十の位が２なので、１**＝１１４、１２５、１３６、１４７、１５８、１６９
１**＝１１４のとき、（ニ）の値が存在しないので不適。
１**＝１２５のとき、（ニ）＝７で、１２５×９９７＝１２４６２５ となり、覆面算のルールから不適。
１**＝１３６のとき、（ニ）＝６で、１３６×９９６＝１３５４５６ となり、覆面算のルールから不適。
１**＝１４７のとき、（ニ）＝６で、１４７×９９６＝１４６４１２ となり、覆面算のルールから不適。
１**＝１５８のとき、（ニ）の値が存在しないので不適。
１**＝１６９のとき、（ニ）＝５で、１６９×９９５＝１６８１５５ となり、覆面算のルールから不適。
以上から、求める覆面算は、１７８×９８５＝１７５３３０ である。
（コメント） 与えられた条件から可能な場合を列挙して検証していくという、かなりしんどい計
算でした。
（追記） 令和２年６月２４日付け
当ＨＰがいつもお世話になっているＨＮ「ｋｓ」さんから虫食い算の問題をいただきました。
問題 次の虫食い算で、被除数の各位の数の和を求めよ。
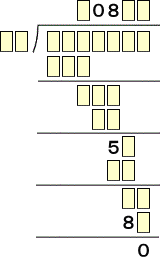
らすかるさんからのコメントです。（令和２年６月２５日付け）
除数×８が２桁で、除数×□が３桁なので、除数は、１２に決まる。
すると、下から2行目と3行目は84、4行目は48、5行目は56、6行目は96、7行目は101、8行
目は108と決まり、1090164÷12=90847 とわかる。
よって、被除数の各位の数の和は、２１
（なぜ被除数の桁の和を求める必要があるのかわかりませんが．．．。）
ｋｓさんからのコメントです。（令和２年６月２５日付け）
らすかるさん、ありがとうございます。２桁の数で、８を掛けると２桁で、９を掛けると３桁に
なるところが面白いと思いました。被除数を答えるかわりに、和は試験的 です。
（追記） 令和２年６月３０日付け
問題 次の空所を補充せよ。
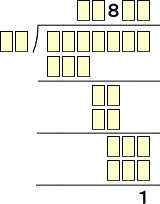
（解）
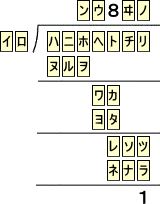
まず、（ウ）＝（ヰ）＝０ である。また、８を掛けて２桁なので、（イ）＝１である。
このとき、（ン）＝９で、９を掛けて３桁になることから、（ロ）＝２が確定する。このとき、
（ヨ）＝９、（タ）＝６、（ワ）＝９、（ヘ）＝９、（ハ）＝（ヌ）＝１、（ニ）＝（ル）＝０、（ホ）＝（ヲ）＝８
が定まる。さらに、（ノ）＝９で、（ネ）＝１、（ナ）＝０、（ラ）＝８が定まり、その結果として、
（レ）＝１、（チ）＝（ソ）＝０、（リ）＝（ツ）＝９が定まり、（カ）＝７から、（ト）＝７となる。 （終）
（追記） 令和２年６月１４日付け
次に、覆面算の攻略法を考えてみよう。
つゆは＋しとしと＝あめがふる
を例に解き方を見てみよう。
 |
左図において、Ｃ1、Ｃ2、Ｃ3、Ｃ4 は、繰り上がりの数を表す。
また、例えば、７＋６＝１３ などは、７＋６≡３ と書くことにする。 |
このとき、上式は、
は＋と≡る ・・・ （１）
Ｃ1＋ゆ＋し≡ふ ・・・ （２）
Ｃ2＋つ＋と≡が ・・・ （３）
Ｃ3＋し≡め ・・・ （４）
Ｃ4≡あ ・・・ （５）
２つの一桁の数を加えたとき、繰り上がりは高々１であるので、Ｃ1、Ｃ2、Ｃ3、Ｃ4 の値は、
０または１である。ただし、あは０ではないので、 Ｃ4＝あ＝１ と確定。
また、あ＝１であることから、 Ｃ3＝１、し＝９ も確定、め＝０ である。
さらに、Ｃ2＋つ＋と＝１０＋が≧１２ において、 １＋８＋と≧１２ から、 と≧３
ここで、と＝３のとき、 Ｃ2＝１、つ＝８ となり、が＝２ となる。
このとき、８ゆは＋９３９３＝１０２ふる において、はに４、５、６、７を順次代入すると、
は＝４ 、る＝７ 、Ｃ1＝０ 、ゆ＝６ 、ふ＝５
が条件に適する。
したがって、答えは、８６４＋９３９３＝１０２５７ となる。
読者のために、練習問題を残しておこう。
練習問題 せつめいと＋かいせつ＋と＝よくよんでよ
（解）
上記同様、明らかに、Ｃ5＝よ＝１ と確定し、Ｃ4＝１、せ＝９、く＝０ である。
このとき、 と＋つ＋と≡１ で、Ｃ1＝０、１、２ の可能性がある。
Ｃ1＝０ のとき、 と＋つ＋と＝１ を満たす数はない。
Ｃ1＝１ のとき、 せ＝９ より、 い＝で となり、不適。
よって、 Ｃ1＝２ で、 と＋つ＋と＝２１ を満たすものは、 と＝８、つ＝５
このとき、 ２＋い＋９≡で より、 １＋い＝で になる。
Ｃ2＝１ で、 １＋め＋い≡ん
また、Ｃ4＝１ なので、 Ｃ3＋５＋か＝１１ すなわち、 Ｃ3＋か＝６
か≠５ なので、 Ｃ3＝０ 、か＝６ と確定。
このとき、 １＋め＋い＝ん で、 １＋い＝で より、 め＋で＝ん
残っている数 ２、３、４、７ で、上式を満たすのは、 い＝２ 、で＝３ 、め＝４ 、ん＝７
以上から、答えは、９５４２８＋６２９５＋８＝１０１７３１ となる。 （終）
類題で、もう１問、練習問題を残しておこう。
練習問題 かいせつと＋せつめい＋と＝よくよんでよ
（解）
前問と同様にして、Ｃ5＝よ＝１ と確定し、Ｃ4＝１、か＝９、く＝０ である。
このとき、 と＋い＋と≡１ で、Ｃ1＝０、１、２ の可能性がある。
Ｃ1＝０ のとき、 と＋い＋と＝１ を満たす数はない。
Ｃ1＝１ のとき、 と＋い＋と＝１１ で、と に入る数の可能性は、 ２、３、４ の何れか。
と＝２ のとき、 い＝７
Ｃ4＝１ なので、 Ｃ3＋７＋せ＝１１ すなわち、 Ｃ3＋せ＝４
ここで、 Ｃ3＝０ ならば、せ＝４ で、 Ｃ2＋4＋つ＝ん
このとき、 Ｃ2＝０ は起こりえず、 Ｃ2＝１ 、つ＝３ 、ん＝８
しかるに、条件を満たす め は存在しない。
よって、 Ｃ3＝１ ならば、せ＝３ となるが、 Ｃ2＋３＋つ≧１４ 即ち、 Ｃ2＋つ≧１１
において、条件を満たす つ は存在しない。
と＝３ のとき、 い＝５
Ｃ4＝１ なので、 Ｃ3＋５＋せ＝１１ すなわち、 Ｃ3＋せ＝６
ここで、Ｃ3＝０ または １ であるが、
Ｃ3＝０ ならば、せ＝６ で、Ｃ2＋６＋つ＝ん
このとき、 Ｃ2＝０ で、 つ＝２ 、ん＝８ で条件を満たすためには、
め＝４ 、で＝７
Ｃ3＝１ は起こりえない。
と＝４ のとき、 い＝３
Ｃ4＝１ なので、 Ｃ3＋３＋せ＝１１ すなわち、 Ｃ3＋せ＝８
ここで、Ｃ3＝０ または １ であるが、
Ｃ3＝０ ならば、せ＝８ で、Ｃ2＋８＋つ＝ん を満たす数は存在しない。
Ｃ3＝１ ならば、せ＝７ で、Ｃ2＋７＋つ≧１２ すなわち、 Ｃ2＋つ≧５
このとき、 つ＝５ 、６ 、８
つ＝５ のとき、Ｃ2＝０ で、ん＝２ となるが、 １＋５＋め＝で を満たす め と で
は存在しない。
つ＝６ のとき、条件を満たすんは存在しない。
つ＝８ のとき、め＝６ 、で＝５ 、Ｃ2＝１ で、ん＝７ となり不適。
Ｃ1＝２ のとき、 と＋い＋と＝２１ より、 と＝８ 、い＝５
Ｃ4＝１ なので、 Ｃ3＋５＋せ＝１１ すなわち、 Ｃ3＋せ＝６
せ≠５ なので、 Ｃ3＝０ 、せ＝６
このとき、 Ｃ2＋６＋つ＝ん を満たす数は存在しない。
以上から、答えは、９５６２３＋６２４５＋３＝１０１８７１ となる。 （終）
（コメント） 覆面算には、虫食い算にはないシンドさがありますね！
覆面算に病みつきになったので、もう１題。
練習問題 かいたい＋うりもの＝うりたいね
（解）
まず、すぐ分かるのは、 Ｃ4＝う＝１
このとき、 Ｃ3＝１ 、か＝８ 、り＝０ または、Ｃ3＝１ 、か＝９ 、り＝１
または、 Ｃ3＝０ 、か＝９ 、り＝０
Ｃ3＝１ 、か＝８ 、り＝０ のとき、 い＝９ 、Ｃ2＝１ で、結果として、た＝０
これは、覆面算のルールに反する。
また、 Ｃ3＝１ 、か＝９ 、り＝１ は、覆面算のルールに反するので不適。
以上から、 Ｃ3＝０ 、か＝９ 、り＝０ と確定。
このとき、覆面算のルールから、 Ｃ2＝１ でなければならない。
い＋１＝た 、Ｃ1＋た＋も＝１０＋い 、い＋の≡ね なので、 Ｃ1＋も＝９
（い，た）＝（２，３）、（３，４）、（４，５）、（５，６）、（６，７）、（７，８）
ここで、 Ｃ1＝０ なら、 も＝９ となり、覆面算のルールに反するので不適。
Ｃ1＝１ なら、 も＝８ で、（い，た）＝（２，３）、（３，４）、（４，５）、（５，６）
この中で、 い＋の＝１０＋ね を満たすのは、 い＝５ 、の＝７ しかない。
このとき、 ね＝２ で、 た＝６ と確定するので、
９５６５＋１０８７＝１０６５２ （終）
（追記） 令和３年８月１８日付け
虫食い算の問題を更に収集してみよう。
問題 次の虫食い算を解け。
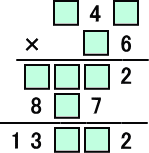
（解） 説明しやすいように、空所に次のように名前を付ける。
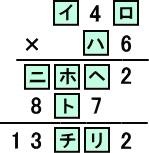
（ロ）の可能性は、２、７の２通りあるが、（ハ）×（ロ）が奇数であることから、（ロ）＝７ と
確定する。このとき、（ハ）＝１、（ト）＝４、（イ）＝８で、（ニ）＝５、（ホ）＝０、（ヘ）＝８となる。
よって、（チ）＝５、（リ）＝５ である。
（コメント） 数の性質を駆使して、一つの突破口が開かれると、一気に全てが氷解するとい
う虫食い算の醍醐味が味わえる問題である。
（追記） 令和４年６月９日付け
最近、連立型の覆面算に触れる機会があった。
次の計算式において、Ａ、Ｂ、Ｃ、Ｄ には、０〜９ の何れかが入る。ただし、同じ文字には
同じ数字が入り、違う文字には違う数字が入るものとする。数の先頭には、０は入らないも
のとする。
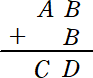
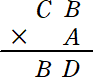
上の計算式が同時に成り立つとき、Ａ、Ｂ、Ｃ、Ｄ の値をそれぞれ求めよ。
（解） 第一の計算式から、下一桁のＢの値は、５、６、７、８、９ の何れかで、
それぞれに対して、Ｄの値は、０、２、４、６、８ の何れかである。
計算の結果、１繰り上がるので、 Ｃ＝Ａ＋１
Ｃ≦９ から、Ａの値は、１、２、３、４、５、６、７、８ の何れか。
ここで、Ａ＝１とすると、Ｂ＝Ｄ となり、条件に反する。
Ａ≧３のとき、Ｃ≧４なので、１０Ｃ×Ａは、１００以上となる。
ところが、計算結果は２桁なので、 Ａの値は、２ と確定する。
このとき、Ｃ＝３ である。Ｂ＝５、６、７、８、９ に注意して、
ＣＢ×Ａ＝３５×２、３６×２、３７×２、３８×２、３９×２
＝７０、７２、７４、７６、７８
よって、 Ａ＝２、Ｂ＝７、Ｃ＝３、Ｄ＝４ と確定する。
ＡＢ＋Ｂ＝２７＋７＝３４ より、 Ｄ＝４ となるので、適する。 （終）
以下、工事中！
