
次の覆面算で、□には 1 〜 9 の数字が各々1回入ります。

この3桁どうしの足し算はなにか探せますか?
(答)
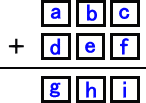
として、Excel さんにお手伝い頂いて次の結果を得た。 336通りある。
abc と def が逆な場合も含めているので、実質は、168通りの解がある。
(当HPがいつもお世話になっているHN「らすかる」さんにご検証いただきました!)
小町覆面算 
次の覆面算で、□には 1 〜 9 の数字が各々1回入ります。

この3桁どうしの足し算はなにか探せますか?
(答)

として、Excel さんにお手伝い頂いて次の結果を得た。 336通りある。
abc と def が逆な場合も含めているので、実質は、168通りの解がある。
(当HPがいつもお世話になっているHN「らすかる」さんにご検証いただきました!)
|
|
|
解があまりに多すぎるので、パズルにならないかも知れないが、ここで特筆すべきことは、
2つの3桁の整数の和の各位の数の和が18になっている
点である。これは、とても面白い結果である。
この事実を、らすかるさんが証明されました。(平成22年11月14日付け)
(証明) a+b+c=p 、d+e+f=q 、g+h+i=r とすると、
a×102+b×10+c≡a+b+c=p (mod 9)
d×102+e×10+f≡d+e+f=q (mod 9)
g×102+h×10+i≡g+h+i=r (mod 9)
p+q+r=45≡0 (mod 9) かつ p+q≡r (mod 9) から、 r≡0 (mod 9)
ここで、 6≦r≦24 なので、 r=9 または 18
r=9 のとき、
{ g , h , i }={ 1 , 2 , 6 }、{ 1 , 3 , 5 }、{
2 , 3 , 4 } のみ
(順列の総数は、 3!×3=18(通り))
このとき、
{ g , h , i }={ 1 , 2 , 6 } のとき、2数の和は700以上なので、解なし
{ g , h , i }={ 1 , 3 , 5 } のとき、2数の和は600以上なので、解なし
{ g , h , i }={ 2 , 3 , 4 } のとき、2数の和は600以上なので、解なし
なので、r=9 の場合は起こり得ない。
従って、 r=18 (証終)
(コメント) なるほど、a+b+c=p 、・・・ という見方をすればよかったんですね!
c+f=・・・・ と考えていて、青木ヶ原の樹海を彷徨っている感じでした。
スッキリしました。らすかるさんに感謝します。
FNさんが、紙と鉛筆で考えられたとのことである。(平成22年11月15日付け)
abc
+def
−−−
ghi
まず、繰り上がりがないと仮定する。
偶数+偶数=偶数 、 偶数+奇数=奇数 、 奇数+奇数=偶数
なので、縦の3つ(a、d、g等)のうち、奇数は0個または2個である。即ち偶数個ある。
このとき、全体で奇数は偶数個となるが、奇数は、1、3、5、7、9の5個なので不適。
よって、必ず繰り上がりはあることになる。
ここで、繰り上がりが1つあれば、偶奇が1つ逆になり、奇数が奇数個になり、適する。
繰り上がりが2つあれば、もう1つ偶奇が逆になり、奇数が偶数個で、不適。
従って、繰り上がりは、1つだけあることになる。
一般性を失うことなく、一の位で繰り上がりがあるとしてよい。
十の位で繰り上がりがあるときは、一の位を百の位にもっていき、百、十の位を十、一の
位とすればよい。
また、a<d、b<e、c<f としてよい。
以上の仮定のもとで出したものから、a、d
の交換、b、e
の交換、c、fの交換、繰り上がり
位置を十の位にする、の操作で別の解が得られるから、解の個数は16倍になる。
らすかるさんの出された結果からするとこの条件のもとで、336÷16=21(通り)の解が
得られるはずである。
以上の仮定を式に書くと次のようになる。
a<d<g=a+d 、b<e<h=b+e+1 、 i<c<f 、 c+f=10+i
g+h+i=18 であること
g+h+i=a+d+b+e+1+c+f−10 において、a+b+c+d+e+f+g+h+i=45
なので、 g+h+i=45−(g+h+i)−9=36−(g+h+i)
よって、 g+h+i=18
(コメント) 「足した結果の各位の数の和が18」の別証明をいただき、FNさんに感謝します。
FNさんのやられた方法を参考にして、21(通り)の解を実際に求めてみよう。
b=1 のとき
e=2 ならば、 h=4 で、 g+i=14 から、
( g , i )=(5 , 9 )、( 6 , 8 )、( 8 , 6 )、(
9 , 5 )
( g , i )=( 5 , 9
) のとき、 a+d=5 、 c+f=19 (不適)
( g , i )=( 6 , 8
) のとき、 a+d=6 、 c+f=18 (不適)
( g , i )=( 8 , 6
) のとき、 a+d=8 、 c+f=16
このとき、 a=3 、d=5 で、 c=7 、f=9 より、 317+529=846
(
g , i )=( 9 , 5
) のとき、 a+d=9 、 c+f=15
このとき、 a=3 、d=6 で、 c=7 、f=8 より、 317+628=945
e=3 ならば、 h=5 で、 g+i=13 から、
( g , i )=(4 , 9 )、( 6 , 7 )、( 7 , 6 )、(
9 , 4 )
( g , i )=( 4 , 9
) のとき、 a+d=4 、 c+f=19 (不適)
( g , i )=( 6 , 7
) のとき、 a+d=6 、 c+f=17
このとき、 a=2 、d=4 で、 c=8 、f=9 より、 218+439=657
(
g , i )=( 7 , 6 ) のとき、 a+d=7 、 c+f=16 (不適)
( g , i )=( 9 , 4
) のとき、 a+d=9 、 c+f=14
このとき、 a=2 、d=7 で、 c=6 、f=8 より、 216+738=954
e=4 ならば、 h=6 で、 g+i=12 から、
( g , i )=(3 , 9 )、( 5 , 7 )、( 7 , 5 )、(
9 , 3 )
( g , i )=( 3 , 9
) のとき、 a+d=3 、 c+f=19 (不適)
( g , i )=( 5 , 7
) のとき、 a+d=5 、 c+f=17
このとき、 a=2 、d=3 で、 c=8 、f=9 より、 218+349=567
(
g , i )=( 7 , 5 ) のとき、 a+d=7 、 c+f=15 (不適)
( g , i )=( 9 , 3
) のとき、 a+d=9 、 c+f=13
このとき、 a=2 、d=7 で、 c=5 、f=8 より、 215+748=963
e=5 ならば、 h=7 で、 g+i=11 から、
( g , i )=(2 , 9 )、( 3 , 8 )、( 8 , 3 )、(
9 , 2 )
( g , i )=( 2 , 9
) のとき、 a+d=2 、 c+f=19 (不適)
( g , i )=( 3 , 8
) のとき、 a+d=3 、 c+f=18 (不適)
( g , i )=( 8 , 3
) のとき、 a+d=8 、 c+f=13
このとき、 a=2 、d=6 で、 c=4 、f=9 より、 214+659=873
(
g , i )=( 9 , 2
) のとき、 a+d=9 、 c+f=12
このとき、 a=3 、d=6 で、 c=4 、f=8 より、 314+658=972
e=6 ならば、 h=8 で、 g+i=10 から、(
g , i )=(3 , 7 )、( 7 , 3 )
( g , i )=( 3 , 7
) のとき、 a+d=3 、 c+f=17 (不適)
( g , i )=( 7 , 3
) のとき、 a+d=7 、 c+f=13
このとき、 a=2 、d=5 で、 c=4 、f=9 より、 214+569=783
e=7 ならば、 h=9 で、 g+i=9 から、
( g , i )=(3 , 6 )、( 4 , 5 )、( 5 , 4 )、(
6 , 3 )
( g , i )=( 3 , 6
) のとき、 a+d=3 、 c+f=16 (不適)
( g , i )=( 4 , 5
) のとき、 a+d=4 、 c+f=15 (不適)
( g , i )=( 5 , 4
) のとき、 a+d=5 、 c+f=14
このとき、 a=2 、d=3 で、 c=6 、f=8 より、 216+378=594
(
g , i )=( 6 , 3
) のとき、 a+d=6 、 c+f=13
このとき、 a=2 、d=4 で、 c=5 、f=8 より、 215+478=693
b=2 のとき
e=3 ならば、 h=6 で、 g+i=12 から、
( g , i )=(4 , 8 )、( 5 , 7 )、( 7 , 5 )、(
8 , 4 )
( g , i )=( 4 , 8
) のとき、 a+d=4 、 c+f=18 (不適)
( g , i )=( 5 , 7
) のとき、 a+d=5 、 c+f=17
このとき、 a=1 、d=4 で、 c=8 、f=9 より、 128+439=567
(
g , i )=( 7 , 5 ) のとき、 a+d=7 、 c+f=15 (不適)
( g , i )=( 8 , 4
) のとき、 a+d=8 、 c+f=14
このとき、 a=1 、d=7 で、 c=5 、f=9 より、 125+739=864
e=4 ならば、 h=7 で、 g+i=11 から、(
g , i )=(5 , 6 )、( 6 , 5 )
( g , i )=( 5 , 6
) のとき、 a+d=5 、 c+f=16 (不適)
( g , i )=( 6 , 5
) のとき、 a+d=6 、 c+f=15 (不適)
e=5 ならば、 h=8 で、 g+i=10 から、
( g , i )=(1 , 9 )、( 3 , 7 )、( 4 , 6 )、(
6 , 4 )、( 7 , 3)、( 9 , 1 )
( g , i )=( 1 , 9
) のとき、 a+d=1 、 c+f=19 (不適)
( g , i )=( 3 , 7
) のとき、 a+d=3 、 c+f=17 (不適)
( g , i )=( 4 , 6
) のとき、 a+d=4 、 c+f=16
このとき、 a=1 、d=3 で、 c=7 、f=9 より、 127+359=486
(
g , i )=( 6 , 4 ) のとき、 a+d=6 、 c+f=14 (不適)
( g , i )=( 7 , 3
) のとき、 a+d=7 、 c+f=13
このとき、 a=1 、d=6 で、 c=4 、f=9 より、 124+659=783
(
g , i )=( 9 , 1
) のとき、 a+d=9 、 c+f=11
このとき、 a=3 、d=6 で、 c=4 、f=7 より、 324+657=981
e=6 ならば、 h=9 で、 g+i=9 から、
( g , i )=(1 , 8 )、( 4 , 5 )、( 5 , 4 )、(
8 , 1 )
( g , i )=( 1 , 8
) のとき、 a+d=1 、 c+f=18 (不適)
( g , i )=( 4 , 5
) のとき、 a+d=4 、 c+f=15
このとき、 a=1 、d=3 で、 c=7 、f=8 より、 127+368=495
(
g , i )=( 5 , 4 ) のとき、 a+d=5 、 c+f=14 (不適)
( g , i )=( 8 , 1
) のとき、 a+d=8 、 c+f=11
このとき、 a=3 、d=5 で、 c=4 、f=7 より、 324+567=891
b=3 のとき
e=4 ならば、 h=8 で、 g+i=10 から、(
g , i )=(1 , 9 )、( 9 , 1 )
( g , i )=( 1 , 9
) のとき、 a+d=1 、 c+f=19 (不適)
( g , i )=( 9 , 1
) のとき、 a+d=9 、 c+f=11
このとき、 a=2 、d=7 で、 c=5 、f=6 より、 235+746=981
e=5 ならば、 h=9 で、 g+i=9 から、
( g , i )=(1 , 8 )、( 2 , 7 )、( 7 , 2 )、(
8 , 1 )
( g , i )=( 1 , 8
) のとき、 a+d=1 、 c+f=18 (不適)
( g , i )=( 2 , 7
) のとき、 a+d=2 、 c+f=17 (不適)
( g , i )=( 7 , 2
) のとき、 a+d=7 、 c+f=12
このとき、 a=1 、d=6 で、 c=4 、f=8 より、 134+658=792
(
g , i )=( 8 , 1
) のとき、 a+d=8 、 c+f=11
このとき、 a=2 、d=6 で、 c=4 、f=7 より、 234+657=891
b≧4 とすると、e≧5 で、h≧10 となり、これは起こりえない。
以上から、求める場合は、
317+529=846 、 317+628=945 、 218+439=657 、
216+738=954 、 218+349=567 、 215+748=963 、
214+659=873 、 314+658=972 、 214+569=783 、
216+378=594 、 215+478=693 、 128+439=567 、
125+739=864 、 127+359=486 、 124+659=783 、
324+657=981 、 127+368=495 、 324+567=891 、
235+746=981 、 134+658=792 、 234+657=891
の21通りである。
FNさんからの問題「和を4桁にして、0から9を入れるとしたときの解を求めよ。」を攻略法
さんが求められた。(平成22年11月16日付け)
A+Bで、A<B とする。また、和の千の位は、「1」と確定する。
検索結果は下表の通りである。
| 1: 342+756=1098 2: 352+746=1098 3: 432+657=1089 4: 452+637=1089 5: 423+675=1098 6: 473+625=1098 7: 743+859=1602 8: 753+849=1602 9: 473+589=1062 10: 483+579=1062 11: 324+765=1089 12: 364+725=1089 13: 624+879=1503 14: 264+789=1053 15: 674+829=1503 16: 284+769=1053 |
17: 425+673=1098 18: 475+623=1098 19: 325+764=1089 20: 365+724=1089 21: 346+752=1098 22: 356+742=1098 23: 426+879=1305 24: 246+789=1035 25: 476+829=1305 26: 286+749=1035 27: 437+652=1089 28: 457+632=1089 29: 437+589=1026 30: 347+859=1206 31: 357+849=1206 32: 487+539=1026 |
33: 749+853=1602 34: 759+843=1602 35: 479+583=1062 36: 489+573=1062 37: 629+874=1503 38: 269+784=1053 39: 679+824=1503 40: 289+764=1053 41: 429+876=1305 42: 249+786=1035 43: 479+826=1305 44: 289+746=1035 45: 439+587=1026 46: 349+857=1206 47: 359+847=1206 48: 489+537=1026 |
上表において、1089、1035、1026 の3種類が、16通りずつで、計 48通りある。
FNさんからのコメントです。(平成22年11月16日付け)
ちょっと調べていたら、もとの問題と変わらない程度にたくさんありそうに思えて「和を4桁
にして0から9を入れるとしてもかなり解がありそうです。」と書いたのですが、もう少し調べ
るとそれほど多くなさそうに思えてきていました。きちんと調べていただいて有難うございま
す。
すべてを数えても、96通りですから、元の問題の336通りに比べて、かなり少ないですね。
一、十、百の各位について、1行目と2行目の大小を決めておいたならば、96÷8=12通り
ですから、コンピュータを使わなくてもできそうです。
□□□ +□□□ −−−−− □□□□ |
左の□に、0から9までの整数を、1つずつ入れて計算が成り立つようにし てください。すべての位で、1行目が2行目より小さいという条件のもとですべ て求めてください。 |
これなら紙と鉛筆で解ける問題と言えそうです。
FNさんが「これなら紙と鉛筆で解ける問題と言えそうです。」ということなので、実際に計算
してみた。
abc+def=1ghi において、g、h、i の何れかが0で、他は2以上9以下の自然数
繰り上がりが1回のみのとき
g<a<d 、 a+d=g+10 、b<e<h=b+e 、 c<f<i=c+f と仮定する。
g=0 のとき、 a+d=10 で、( a , d )=( 2 , 8 )、(
3 , 7 )、( 4 , 6 )
( a , d )=(2 , 8 )とする。
b=3 のとき、 ( e , h )=( 4 , 7 )、( 6 , 9 ) 何れも解なし
b=4 のとき、 ( e , h )=( 5 , 9 ) 解なし
( a , d )=(3 , 7 )とする。
b=2 のとき、 ( e , h )=( 4 , 6 )、( 6 , 8 )
( e , h )=( 4 , 6 )のとき、 解なし
( e , h )=( 6 , 8 )のとき、 ( c , f , i )=(4
, 5 ,9 )
このとき、 324+765=1089
b=4 のとき、 ( e ,
h )=( 5 , 9 )
( e , h )=( 5 , 9 )のとき、 ( c , f , i )=(2
, 6 ,8 )
このとき、 342+756=1098
( a , d )=(4 , 6 )とする。
b=2 のとき、 ( e , h )=( 3 , 5 )、( 5 , 7 )、(7 , 9 )
( e , h )=( 3 , 5 )、( 5 , 7 )のとき、 解なし
( e , h )=( 7 , 9 )のとき、 ( c , f , i )=(3
, 5 ,8 )
このとき、 423+675=1098
b=3 のとき、 ( e , h )=( 5 , 8 ) で、( c , f ,
i )=(2 , 7 ,9 )
このとき、 432+657=1089
繰り上がりが2回(百の位と十の位)のみのとき
g<a<d 、a+d=g+9 、h<b<e 、b+e=h+10 、c<f<i=c+f と仮定する。
g=0 のとき、 a+d=9 で、( a , d )=( 2 , 7 )、( 3
, 6 )、( 4 , 5 )
( a , d )=(2 , 7 )とする。
b=4 のとき、 ( e , h )=( 9 , 3 ) 解なし
b=5 のとき、 ( e , h )=( 8 , 3 )、( 9 , 4 ) 何れも解なし
b=6 のとき、 ( e , h )=( 8 , 4 )、( 9 , 5 ) 何れも解なし
( a , d )=(3 , 6 )とする。
b=4 のとき、 ( e , h )=( 8 , 2 ) 解なし
b=5 のとき、 ( e , h )=( 7 , 2 )、( 9 , 4 ) 何れも解なし
b=7 のとき、 ( e , h )=( 8 , 5 ) 解なし
( a , d )=(4 , 5 )とする。
b=3 のとき、 ( e , h )=( 9 , 2 ) 解なし
b=6 のとき、 ( e , h )=( 7 , 3 ) 解なし
b=7 のとき、 ( e , h )=( 9 , 6 ) 解なし
h=0 のとき、 b+e=10 で、( b , e )=( 2 , 8 )、(
3 , 7 )、( 4 , 6 )
( b , e )=(2 , 8 )とする。
g=3 とするとき、 ( a , d )=( 5 , 7 ) 解なし
g=4 とするとき、 ( a , d )=( 6 , 7 ) 解なし
( b , e )=(3 , 7 )とする。
g=2 とするとき、 ( a , d )=( 5 , 6 ) 解なし
g=4 とするとき、 ( a , d )=( 5 , 8 ) 解なし
g=5 とするとき、 ( a , d )=( 6 , 8 ) 解なし
( b , e )=(4 , 6 )とする。
g=2 とするとき、 ( a , d )=( 3 , 8 ) 解なし
g=3 とするとき、 ( a , d )=( 5 , 7 ) 解なし
繰り上がりが2回(百の位と一の位)のみのとき
g<a<d 、a+d=g+10 、b<e<h 、b+e−1=h 、i<c<f 、c+f=i+10 と仮
定する。
g=0 のとき、 a+d=10 で、( a , d )=( 2 , 8 )、(
3 , 7 )、( 4 , 6 )
( a , d )=(2 , 8 )とする。
b=3 のとき、 ( e , h )=( 4 , 6 )、( 5 , 7 )、(
7 , 9 ) 何れも解なし
b=4 のとき、 ( e , h )=( 6 , 9 ) 解なし
( a , d )=(3 , 7 )とする。
b=2 のとき、 ( e , h )=( 4 , 5 )、( 5 , 6 )、(
8 , 9 ) 何れも解なし
b=4 のとき、 ( e , h )=( 5 , 8 )、( 6 , 9 ) 何れも解なし
( a , d )=(4 , 6 )とする。
b=2 のとき、 ( e , h )=( 7 , 8 )、( 8 , 9 ) 何れも解なし
b=3 のとき、 ( e , h )=( 5 , 7 )、( 7 , 9 ) 何れも解なし
i=0 のとき、 c+f=10 で、( c , f )=( 2 , 8 )、(
3 , 7 )、( 4 , 6 )
( c , f )=(2 , 8 )とする。
g=3 とするとき、 ( a , d )=( 4 , 9 ) 解なし
g=4 とするとき、 ( a , d )=( 5 , 9 ) 解なし
g=5 とするとき、 ( a , d )=( 6 , 9 ) 解なし
g=6 とするとき、 ( a , d )=( 7 , 9 ) 解なし
( c , f )=(3 , 7 )とする。
g=2 とするとき、 ( a , d )=( 4 , 8 ) 解なし
g=4 とするとき、 ( a , d )=( 5 , 9 )、( 6 , 8 ) 何れも解なし
g=5 とするとき、 ( a , d )=( 6 , 9 ) 解なし
( c , f )=(4 , 6 )とする。
g=2 とするとき、 ( a , d )=( 5 , 7 ) 解なし
g=3 とするとき、 ( a , d )=( 4 , 9 )、( 5 , 8 ) 何れも解なし
g=5 とするとき、 ( a , d )=( 7 , 8 ) 解なし
g=7 とするとき、 ( a , d )=( 8 , 9 ) 解なし
次に、繰り上がりが3回のときを考える。
g<a<d 、a+d=g+9 、h<b<e 、b+e=h+9 、i<c<f 、c+f=i+10 と仮
定する。
g=0 のとき、 a+d=9 で、( a , d )=( 2 , 7 )、( 3
, 6 )、( 4 , 5 )
( a , d )=(2 , 7 )とする。
i=3 のとき、 ( c , f )=( 4 , 9 )、( 5 , 8 )
( c , f )=( 4 , 9 )のとき、 ( b , e , h )=(6
, 8 ,5 )
このとき、 264+789=1053
( c , f )=( 5 , 8 )のとき、 解なし
i=4 のとき、 ( c , f )=( 5 , 9 )、( 6 , 8 ) 何れも解なし
i=5 のとき、 ( c , f )=( 6 , 9 ) で、 ( b , e ,
h )=(4 , 8 ,3 )
このとき、 246+789=1035
( a , d )=(3 , 6 )とする。
i=2 のとき、 ( c , f )=( 4 , 8 )、( 5 , 7 ) 何れも解なし
i=4 のとき、 ( c , f )=( 5 , 9 ) 解なし
i=5 のとき、 ( c , f )=( 7 , 8 ) 解なし
i=7 のとき、 ( c , f )=( 8 , 9 ) 解なし
( a , d )=(4 , 5 )とする。
i=2 のとき、 ( c , f )=( 3 , 9 ) で、 ( b , e ,
h )=(7 , 8 ,6 )
このとき、 473+589=1062
i=3 のとき、 ( c , f )=( 6 , 7 ) 解なし
i=6 のとき、 ( c , f )=( 7 , 9 ) で、 ( b , e ,
h )=(3 , 8 ,2 )
このとき、 437+589=1026
i=7 のとき、 ( c , f )=( 8 , 9 ) 解なし
h=0 のとき、 b+e=9 で、( b , e )=( 2 , 7 )、( 3
, 6 )、( 4 , 5 )
( b , e )=(2 , 7 )とする。
g=3 のとき、 ( a , d )=( 4 , 8 ) で、 ( c , f ,
i )=(6 , 9 ,5 )
このとき、 426+879=1305
g=4 のとき、 ( a , d )=( 5 , 8 ) 解なし
g=5 のとき、 ( a , d )=( 6 , 8 ) で、 ( c , f ,
i )=(4 , 9 ,3 )
このとき、 624+879=1503
( b , e )=(3 , 6 )とする。
g=2 のとき、 ( a , d )=( 4 , 7 ) 解なし
g=4 のとき、 ( a , d )=( 5 , 8 ) 解なし
( b , e )=(4 , 5 )とする。
g=2 のとき、 ( a , d )=( 3 , 8 ) で、 ( c , f ,
i )=(7 , 9 ,6 )
このとき、 347+859=1206
g=6 のとき、 ( a , d )=( 7 , 8 ) で、 ( c , f ,
i )=(3 , 9 ,2 )
このとき、 743+859=1602
i=0 のとき、 ( c , f )=( 2 , 8 )、( 3 , 7 )、( 4
, 6 )
( c , f )=(2 , 8 )とする。
g=3 のとき、 ( a , d )=( 5 , 7 ) 解なし
g=4 のとき、 ( a , d )=( 6 , 7 ) 解なし
( c , f )=(3 , 7 )とする。
g=2 のとき、 ( a , d )=( 5 , 6 ) 解なし
g=4 のとき、 ( a , d )=( 5 , 8 ) 解なし
g=5 のとき、 ( a , d )=( 6 , 8 ) 解なし
( c , f )=(4 , 6 )とする。
g=2 のとき、 ( a , d )=( 3 , 8 ) 解なし
g=3 のとき、 ( a , d )=( 5 , 7 ) 解なし
(コメント) 数え漏れがあったので訂正しました...f(^_^;)。
上記で探索した解をベースにして、攻略法さんの解を分類してみた。
| 324+765=1089 11: 324+765=1089 12: 364+725=1089 19: 325+764=1089 20: 365+724=1089 342+756=1098 1: 342+756=1098 2: 352+746=1098 21: 346+752=1098 22: 356+742=1098 423+675=1098 5: 423+675=1098 6: 473+625=1098 17: 425+673=1098 18: 475+623=1098 432+657=1089 3: 432+657=1089 4: 452+637=1089 27: 437+652=1089 28: 457+632=1089 |
264+789=1053 14: 264+789=1053 16: 284+769=1053 38: 269+784=1053 40: 289+764=1053 246+789=1035 24: 246+789=1035 26: 286+749=1035 42: 249+786=1035 44: 289+746=1035 473+589=1062 9: 473+589=1062 10: 483+579=1062 35: 479+583=1062 36: 489+573=1062 437+589=1026 29: 437+589=1026 32: 487+539=1026 45: 439+587=1026 48: 489+537=1026 |
426+879=1305 23: 426+879=1305 25: 476+829=1305 41: 429+876=1305 43: 479+826=1305 624+879=1503 13: 624+879=1503 15: 674+829=1503 37: 629+874=1503 39: 679+824=1503 347+859=1206 30: 347+859=1206 31: 357+849=1206 46: 349+857=1206 47: 359+847=1206 743+859=1602 7: 743+859=1602 8: 753+849=1602 33: 749+853=1602 34: 759+843=1602 |
以下工事中