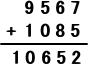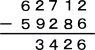覆面算　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　何とはなしに、ＮＴＶ系で新しく始まったＴＶドラマ「リモート」を見ていたら、思わず画面に
引き込まれてしまった。堂本光一演ずる氷室光三郎警視が地下室に居ながらにして、深
田恭子演ずる彩木くるみ（一応交通課所属の警察官）に携帯電話を通して指示を出し、
難事件を解決していくというストーリーである。携帯電話の度重なる使用と奇抜な場面設
定に驚いたが、今風な感じがして今後の展開が楽しみである。もちろん、深田恭子のコミ
カルで愛敬いっぱいの演技も楽しみの一つである。

　実は、私が思わず画面に引き込まれたのは、次のような覆面算が登場したからである。

　　　　　　　　　　　　　　

　この覆面算は、覆面算の世界では最も有名な問題であり、また最も古い問題でもある。
作者は不明でイギリスの Ｈ．Ｅ．Ｄｕｄｅｎｅｙ （デュードニー　1857〜1930）が紹介したとさ
れている。ドラマの中では、ＭＯディスクを読み込むためのパスワードを解く鍵として氷室
警視が、鮮やかに解いていた。しかし、見ている側は、彩木くるみ同様その解法について
いけなかった．．．(・・?)

　このページでは、上の覆面算を解いてみようと思う。生憎、ビデオに撮っていなかったの
で、下の計算はもしかしたら、氷室警視の論理と若干異なるかもしれない。（あしからず！）

左図において、Ｄ＋Ｅ＝Ｙ　または　１０＋Ｙ　であるが、これを、 　　　　　　　　　　　　Ｄ＋Ｅ≡Ｙ 　と書くことにする。他も同様。 　　また、Ｃｉ で繰り上がった数を表すものとする。 　　　　Ｃｉ ＝０　または　１　である。（ただし、ｉ ＝１，２，３，４）

　このとき、次のような連立方程式が得られる。

　　　　　　　　 Ｄ＋Ｅ≡Ｙ
　　　　　Ｃ_１＋Ｎ＋Ｒ≡Ｅ
　　　　　Ｃ_２＋Ｅ＋Ｏ≡Ｎ
　　　　　Ｃ_３＋Ｓ＋Ｍ≡Ｏ
　　　　　Ｃ_４　　　　　 ≡Ｍ

　Ｍは１桁の数であり、０と異なる数であるから、Ｍ＝Ｃ_４＝１ となる。このとき、Ｏ が２以

上とすると、Ｃ_３＋Ｓ＋１≧１２ すなわち、Ｃ_３＋Ｓ≧１１ となり、この式を満たす Ｃ_３，Ｓ は

存在しないので、矛盾。従って、Ｏ＝０ である。 Ｏ＝０ より、Ｃ_２＋Ｅ＋Ｏ　の計算から １

繰り上がることはないので、 Ｃ_３ ＝０ 。このとき、Ｓ＝９ となる。

　さらに、Ｃ_２＋Ｅ＝Ｎ を第２式に代入して、Ｃ_１＋Ｃ_２＋Ｅ＋Ｒ≡Ｅ　即ち Ｃ_１＋Ｃ_２＋Ｒ≡０

だから、８以下の数Ｒでこの式を満たすのは、Ｃ_１＝Ｃ_２＝１ で、Ｒ＝８ のみである。

よって、１＋Ｎ＋８≡Ｅ において、Ｎ≧２ だから、１＋Ｎ＋８＝１０＋Ｅ　即ち　Ｎ＝１＋Ｅ

となる。

　また、Ｄ＋Ｅ＝１０＋Ｙ において、Ｄ、Ｅ、Ｙ は異なる数で、２ ≦ Ｄ， Ｅ， Ｙ ≦ ７　より、

１２≦Ｄ＋Ｅ≦１３ となり、　Ｄ＋Ｅ＝１２，１３　である。

　このとき、　Ｎ＝１＋Ｅ　なので、Ｄ＝７，Ｅ＝５ の場合しか、この式を満たす数はない。

よって、Ｎ＝６ ，Ｙ＝２　となる。

　以上から、求める計算式は、次のようになる。

　　　　　　　　　　　
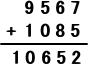
（別解）

左の計算で、　Ｍ＝１　しかありえない。 　　したがって、Ｓ＋Ｍ　の計算で、１ 繰り上がるためには、 　　　　Ｓ＝８　または　Ｓ＝９

　そこで、　Ｓ＝９　とすると、　Ｏ＝０　となる。さらに、Ｅ≠Ｎ　なので、　Ｎ＝Ｅ＋１

このとき、　Ｎ＋Ｒ＋（０または１）＝１０＋Ｅ　において、　Ｒ＋（０または１）＝９

ここで、　Ｓ＝９　としているので、　Ｒ＝８　となり、　Ｄ＋Ｅ＝１０＋Ｙ　である。

　また、　Ｄ、Ｅ、Ｙ は異なる数で、２ ≦ Ｄ， Ｅ， Ｙ ≦ ７　より、　１２≦Ｄ＋Ｅ≦１３ となり、

Ｄ＋Ｅ＝１２，１３　であるが、　Ｎ＝１＋Ｅ　なので、Ｄ＝７，Ｅ＝５ の場合しかない。

　このとき、　Ｎ＝６ ，Ｙ＝２　となる。　（終）


（参考文献　　ジョーゼフ・デグレージア　著　　金沢　養　訳
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　数のパズルはおもしろい　（白揚社））

（コメント）　別解の方がスッキリしていますね！もしかして、これが、氷室警視の解答だった
　　　　　　かも．．．？

　上記の別解では、Ｓ＝８ の場合が調べられていない。解が１つでも見つかればいいや〜
というのが、どうも上記参考文献のコンセプトらしい。

　そこで、Ｓ＝８　の場合が起こらないことを確認してみた。

　Ｓ＝８　とすると、　Ｏ＝０　で、　Ｅ＝１０＋Ｎ　、　Ｅ＝９　より、　Ｎ＝０　（矛盾）


　覆面算は、繰り上がりの処理がポイントである。練習のために、１つ課題を出しておこう。

問題　次の覆面算を解け。
　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（答）
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
（参考文献：みやたよしゆき　著　数学パズル（啓学出版））

（追記）　平成１９年２月１９日付け

　もうクリスマスの時期をとうに過ぎてしまったが、クリスマス関連の覆面算の問題を一つ追
加しておく。

　下記の計算で同じ文字には同じ数字が入る。使える数字は、０〜９までの１０個である。

どのように数字を埋めればいいだろうか？

　　　　　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（答）　例えば、

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

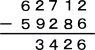
　当ＨＰがいつもお世話になっている、らすかるさんにご検証していただいたところ、解は全
部で２６通りあるとのことである。（平成１９年２月１９日付け）

　以下が、その全解。

２４０３４−１６４９２＝７５４２　　２４０３４−１７４９２＝６５４２　　２４０７４−１５４３２＝８６４２
２４０７４−１８４３２＝５６４２　　２４５３４−１６４９２＝８０４２　　２４５３４−１８４９２＝６０４２
２４７９４−１６４５２＝８３４２　　２４７９４−１８４５２＝６３４２　　２４８０４−１５４６２＝９３４２
２４８０４−１９４６２＝５３４２　　２４９７４−１６４３２＝８５４２　　２４９７４−１８４３２＝６５４２
３６１５６−２７６９３＝８４６３　　３６１５６−２８６９３＝７４６３　　３６８０６−２７６４３＝９１６３
３６８０６−２９６４３＝７１６３　　６２１３２−５４２０６＝７９２６　　６２１３２−５７２０６＝４９２６
６２１７２−５３２４６＝８９２６　　６２１７２−５８２４６＝３９２６　　６２４０２−５３２７６＝９１２６
６２４０２−５９２７６＝３１２６　　６２７１２−５３２８６＝９４２６　　６２７１２−５９２８６＝３４２６
６２９３２−５４２０６＝８７２６　　６２９３２−５８２０６＝４７２６

（コメント）　こんなに解があっては覆面算になりませんね！単なる計算問題でした．．．。


　当ＨＰがいつもお世話になっているＨＮ「ＦＮ」さんからの出題です。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２３年７月１５日付け）

　次の覆面算を解いてください。

　１９７６年３月発行の中公新書「数理パズル」に載っている問題です。その本によると、英
語の数詞を使った覆面算で文字の上でも計算が正しくて、覆面算として一意的な解を持つ
のは、著者の知る限り、この２つしかないとのことです。ただし、３５年ほど前の話なので、こ
れら以外がみつかっている可能性は高いかと思います。

　ちなみに、１９７６年というのは、日本における最初のある程度売れたマイコン TK-80 が
発売された年だそうです。私は、TK-80は知りません。多くの人が知っている事実上の初代
マイコンPC-8001、MZ-80C が発売されたのは、１９７９年です。その３年前ですから、ほと
んどの人はコンピュータに接する機会はなかったころです。

　TK-80のメインメモリは最大1KByteのようです。今は2Gはあるから6桁以上違います。速
度も同様かそれ以上に差があると思います。著者たちはコンピュータが使える環境にあった
ようですが、３５年前の大型コンピュータは現在のパソコンよりかなり劣るでしょう。


　ＧＡＩ さんが上記問題の解を求められました。（平成２３年７月１５日付け）

　ＦＮさんからのコメントです。（平成２３年７月１５日付け）

正解です。出題しながら自分では解いてなかったので、一意的であることを確認する意味も
込めて、(1)だけ解いてみました。

　(1)は、0から9までのすべての数字が出るという意味で、より完全な問題ですね。

（解）　Y+2N≡Y　(mod 10)　より、2N≡0　(mod 10)　なので、N＝0、5　　　

　 N＝0　だから、　E＝5　となる。繰り上がりは最大２だから、FOに、1か2を足して、SIにな

ることから、Oは、8か9　である。I は、0か1　だが、0はないから、I は、1 となる。

　だから、Oは、9 しかなく、100の位で、2繰りあがることになる。

　残っているのは、2、3、4、6、7、8　で、F+1＝S　より、

　　　(F，S)＝(2，3)、(3，4)、(6，7)、(7，8)

また、Xは、2以上だから、2T+R+1≧22 でなければならない。

　これを満たすT、Rは、

　　　(T，R)＝(7，8)、(8，6)、(8，7)

しかない。

　(T，R)＝(7，8)　とすると、　(F，S)＝(2，3)　または　(3，4)

　　(F，S)＝(2，3)　のとき、残っているのは、4、6　で、

　　　　　　2987Y+750+750＝31X7Y

　　　を満たすXは、3なので、不適。

　　(F，S)＝(3，4)　のとき、残っているのは、2、6　で、

　　　　　　3987Y+750+750＝41X7Y

　　　を満たすXは、3なので、不適。

　(T，R)＝(8，6)　とすると、　(F，S)＝(2，3)　または　(3，4)

　　(F，S)＝(2，3)　のとき、残っているのは、4、7　で、

　　　　　　2968Y+850+850＝31X8Y

　　　を満たすXは、3なので、不適。

　　(F，S)＝(3，4)　のとき、残っているのは、2、7　で、

　　　　　　3968Y+850+850＝41X8Y

　　　を満たすXは、3なので、不適。

　したがって、　(T，R)＝(8，7)　で、　F978Y+850+850＝S1X8Y　を満たすXは、4 となり、

　(F，S)＝(2，3)　である。このとき、Y＝6　となる。　　（終）


　らすかるさんが、この話題について調べられました。（平成２３年７月１５日付け）

　同じ数詞が複数回出現しないパターンで、解が一意的になるものは、以下の５通りありま
した。

　（１）　FIVE＋SEVEN＋ELEVEN＋TWELVE＋FIFTEEN＋TWENTY＝SEVENTY

　（２）　SIX＋SEVEN＋NINE＋TWELVE＋SIXTEEN＋TWENTY＝SEVENTY

　（３）　THREE＋SEVEN＋TEN＋TWENTY＋THIRTY＝SEVENTY

　（４）　ONE＋NINE＋TWENTY＋FIFTY＝EIGHTY

　（５）　ONE＋TWO＋FIVE＋NINE＋ELEVEN＋TWELVE＋FIFTY＝NINETY

　同じ数詞が複数回出現するパターンは、組合せが多くて調べるのは大変そうです。

　TK-80のマイナーチェンジ版であるTK-80Eを持っていました。TK-80のRAMは標準装備
で512バイトでしたので、現在の標準を２GBとすると４００万倍違いますね。

　クロックは2.048MHzでしたので、単純にクロックだけで比較すると１５００倍程度ですが、
1クロックあたりの計算量がまるで違いますので処理能力的にも１００万倍は違うと思いま
す。


　ＦＮさんからのコメントです。（平成２３年７月１５日付け）

　同じ数詞が複数回出現しないという条件でこんなにもあるのですか。しかも、ほんの短時
間で確認できてしまうとはとてもびっくりします。確かに同じ数詞が複数回出現しないほうが
問題としてはいいですね。「数理パズル」の２題はどちらもそうではなかったのでやや不満
足です。

　同じ数詞が複数回出現するパターンは、かなり膨大な数になるのでしょうね。同じ数詞が
複数回出現しないのが５個もあれば、こちらのタイプはあまり興味が持てないような気がし
ます。

　TK-80のマイナーチェンジ版を持っておられましたか。マイコンというのが世の中に出始め
たころからのユーザーですね。私はPC-8001やMZ-80Cが出たころからです。５年で１０倍ぐ
らいの感じで進歩してるようですね。


（コメント）　私のパソコンとの初めての出会いは、ＳＨＡＲＰの「ＭＺ−８０Ｂ」。カセットテープ
　　　　　　にプログラムやデータを保存するタイプで、５００人程度のデータを処理するのに
　　　　　　一晩かかった懐かしい記憶が蘇ります。夕方プログラムを実行して、翌朝その結
　　　　　　果を見るという今では考えられないことですね！


　ＧＡＩ さんが、らすかるさんの問題（１）〜（５）の解を見出されました。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２３年７月１６日付け）

（コメント）　ＧＡＩ さん、解答をお寄せいただいてありがとうございます。今日１日手計算で
　　　　　　（１）を考えていて、「おや、解なしかな？」と思っていたところです。らすかるさん、
　　　　　　ごめんなさい。ＧＡＩ さんの解答を見て、手計算に穴があったことに気づかされま
　　　　　　した。

　手計算で、（１）の解を探索してみました。

　　　　　　　　　　　　　　　　　　　この式を満たすVは存在しない。

　(E，N)＝(3，8)　のとき、　2E+3N＝30

　　このとき、　2V+9+3≡0　(mod 10)　より、　2V≡8　(mod 10)　なので、V＝4、9

　　　V＝4　のとき、　2V+9+3＝20

　　　　このとき、　Ｉ+2V+L+E+2＝Ｉ+8+L+3+2＝I+L+13≡0　(mod 10)　より、

　　　　I+L≡7　(mod 10)　なので、(I，L)＝(0，7)、(1，6)、(2，5)、(5，2)、(6，1)、(7，0)

　　　　　(I，L)＝(0，7)　のとき、　Ｉ+2V+L+E+2＝8+7+3+2＝20

　　　　　　このとき、　F+T+9+2≡0　(mod 10)　より、　F+T≡9　(mod 10)

　　　　　　　この式を満たすF、Tは存在しない。

　　　　(I，L)＝(1，6)　のとき、　Ｉ+2V+L+E+2＝1+8+6+3+2＝20

　　　　　　　このとき、　F+T+9+2≡0　(mod 10)　より、　F+T≡9　(mod 10)

　　　　　よって、　(F，T)＝(2，7)、(7，2)

　　　　　　(F，T)＝(2，7)　のとき、残りの数字は、　0、5、9　で、F+T+9+2＝2+7+9+2＝20

　　　　　　　このとき、　S+2W+6+2+2≡4　(mod 10)　より、S+2W≡4　(mod 10)

　　　　　　　0、5、9　で、この式を満たすものはない。

　　　　　(F，T)＝(7，2)　のとき、残りの数字は、　0、5、9　で、F+T+9+2＝7+2+9+2＝20

　　　　　　このとき、　S+2W+6+7+2≡4　(mod 10)　より、

　　　　　　　S+2W≡9　(mod 10)　なので、　S＝9、W＝0

　　　　　　　　よって、　S+2W+6+7+2＝24

　　　　　　　　このとき、E+2T+I+2＝3+4+1+2＝10　となり、E＝3　に矛盾。

　　　(I，L)＝(2，5)　のとき、　Ｉ+2V+L+E+2＝2+8+5+3+2＝20

　　　　このとき、　F+T+9+2≡0　(mod 10)　より、　F+T≡9　(mod 10)

　　　　　この式を満たすF、Tは存在しない。

　　(I，L)＝(5，2)　のとき、　Ｉ+2V+L+E+2＝5+8+2+3+2＝20

　　　このとき、　F+T+9+2≡0　(mod 10)　より、　F+T≡9　(mod 10)

　　　　この式を満たすF、Tは存在しない。

　　(I，L)＝(6，1)　のとき、　Ｉ+2V+L+E+2＝6+8+1+3+2＝20

　　　このとき、　F+T+9+2≡0　(mod 10)　より、　F+T≡9　(mod 10)

　　　　よって、　(F，T)＝(2，7)、(7，2)

　　　　(F，T)＝(2，7)　のとき、残りの数字は、　0、5、9　で、F+T+9+2＝2+7+9+2＝20

　　　　　このとき、　S+2W+1+2+2≡4　(mod 10)　より、

　　　　　　S+2W≡9　(mod 10)　なので、　S＝9、W＝0

　　　　　　よって、　S+2W+1+2+2＝23

　　　　　　このとき、E+2T+I+2＝3+14+6+2＝25　となり、E＝3に矛盾。

　　　　(F，T)＝(7，2)　のとき、残りの数字は、　0、5、9　で、F+T+9+2＝7+2+9+2＝20

　　　　　このとき、　S+2W+1+7+2≡4　(mod 10)　より、S+2W≡4　(mod 10)

　　　　　　0、5、9　で、この式を満たすものはない。

　　(I，L)＝(7，0)　のとき、　Ｉ+2V+L+E+2＝7+8+3+2＝20

　　　このとき、　F+T+9+2≡0　(mod 10)　より、　F+T≡9　(mod 10)

　　　　この式を満たすF、Tは存在しない。

　　　　V＝9　のとき、　2V+9+3＝30

　　　このとき、　Ｉ+2V+L+E+3＝Ｉ+18+L+3+3＝I+L+24≡0　(mod 10)　より、

　　　　I+L≡6　(mod 10)　なので、(I，L)＝(0，6)、(1，5)、(2，4)、(4，2)、(5，1)、(6，0)

　　　　(I，L)＝(0，6)　のとき、　Ｉ+2V+L+E+3＝18+6+3+3＝30

　　　　　このとき、　F+T+9+3≡0　(mod 10)　より、　F+T≡8　(mod 10)

　　　　　　この式を満たすF、Tは存在しない。

　　　(I，L)＝(1，5)　のとき、　Ｉ+2V+L+E+3＝1+18+5+3+3＝30

　　　　このとき、　F+T+9+3≡0　(mod 10)　より、　F+T≡8　(mod 10)

　　　　　よって、　(F，T)＝(2，6)、(6，2)

　　　　　(F，T)＝(2，6)　のとき、残りの数字は、　0、4、7　で、F+T+9+3＝2+6+9+3＝20

　　　　　　このとき、　S+2W+5+2+2≡4　(mod 10)　より、S+2W≡5　(mod 10)

　　　　　　　0、4、7　で、この式を満たすものはない。

　　　　(F，T)＝(6，2)　のとき、残りの数字は、　0、4、7　で、F+T+9+3＝6+2+9+3＝20

　　　　　このとき、　S+2W+5+6+2≡4　(mod 10)　より、S+2W≡1　(mod 10)

　　　　　　0、4、7　で、この式を満たすものはない。

　　　(I，L)＝(2，4)　のとき、　Ｉ+2V+L+E+3＝2+18+4+3+3＝30

　　　　このとき、　F+T+9+3≡0　(mod 10)　より、　F+T≡8　(mod 10)

　　　　　よって、　(F，T)＝(1，7)、(7，1)

　　　　　(F，T)＝(1，7)　のとき、残りの数字は、　0、5、6　で、F+T+9+3＝1+7+9+3＝20

　　　　　　このとき、　S+2W+4+1+2≡4　(mod 10)　より、S+2W≡7　(mod 10)

　　　　　　　0、5、6　で、この式を満たすものはない。

　　　　(F，T)＝(7，1)　のとき、残りの数字は、　0、5、6　で、F+T+9+3＝7+1+9+3＝20

　　　　　　このとき、　S+2W+4+7+2≡4　(mod 10)　より、S+2W≡1　(mod 10)

　　　　　　　0、5、6　で、この式を満たすものはない。

　　(I，L)＝(4，2)　のとき、　Ｉ+2V+L+E+3＝4+18+2+3+3＝30

　　　このとき、　F+T+9+3≡0　(mod 10)　より、　F+T≡8　(mod 10)

　　　　よって、　(F，T)＝(1，7)、(7，1)

　　　　　(F，T)＝(1，7)　のとき、残りの数字は、　0、5、8　で、F+T+9+3＝1+7+9+3＝20

　　　　　　このとき、　S+2W+2+1+2≡4　(mod 10)　より、S+2W≡9　(mod 10)

　　　　　　　0、5、8　で、この式を満たすものはない。

　　　　(F，T)＝(7，1)　のとき、残りの数字は、　0、5、8　で、F+T+9+3＝7+1+9+3＝20

　　　　　このとき、　S+2W+2+7+2≡4　(mod 10)　より、S+2W≡3　(mod 10)

　　　　　　0、5、8　で、この式を満たすものはない。

　　(I，L)＝(5，1)　のとき、　Ｉ+2V+L+E+3＝5+18+1+3+3＝30

　　　このとき、　F+T+9+3≡0　(mod 10)　より、　F+T≡8　(mod 10)

　　　　よって、　(F，T)＝(2，6)、(6，2)

　　　　　(F，T)＝(2，6)　のとき、残りの数字は、　0、4、7　で、F+T+9+3＝2+6+9+3＝20

　　　　　　このとき、　S+2W+1+2+2≡4　(mod 10)　より、S+2W≡9　(mod 10)

　　　　　　　0、4、7　で、この式を満たすものはない。

　　　　(F，T)＝(6，2)　のとき、残りの数字は、　0、4、7　で、F+T+9+3＝6+2+9+3＝20

　　　　　このとき、　S+2W+1+6+2≡4　(mod 10)　より、S+2W≡5　(mod 10)

　　　　　　0、4、7　で、この式を満たすものはない。

　　(I，L)＝(6，0)　のとき、　Ｉ+2V+L+E+3＝6+18+3+3＝30

　　　このとき、　F+T+9+3≡0　(mod 10)　より、　F+T≡8　(mod 10)

　　　　この式を満たすF、Tは存在しない。

　(E，N)＝(5，0)　のとき、　2E+3N＝10

　　このとき、　2V+15+1≡0　(mod 10)　より、　2V≡4　(mod 10)　なので、V＝2、7

　　　V＝2　のとき、　2V+15+1＝20

　　　　このとき、　Ｉ+2V+L+E+2＝Ｉ+4+L+5+2＝I+L+11≡0　(mod 10)　より、

　　　　I+L≡9　(mod 10)　なので、　(I，L)＝(1，8)、(3，6)、(6，3)、(8，1)

　　　　(I，L)＝(1，8)　のとき、　Ｉ+2V+L+E+2＝1+4+8+5+2＝20

　　　　　このとき、　F+T+15+2≡0　(mod 10)　より、　F+T≡3　(mod 10)

　　　　　よって、　(F，T)＝(4，9)、(6，7)、(7，6)、(9，4)

　　　　　　(F，T)＝(4，9)　のとき、残りの数字は、　3、6、7　で、F+T+15+2＝4+9+15+2＝30

　　　　　　　このとき、　S+2W+8+4+3≡2　(mod 10)　より、

　　　　　　　　S+2W≡7　(mod 10)　なので、　S＝3、W＝7

　　　　　　　　F＝4　より不適。

　　　　　(F，T)＝(6，7)　のとき、残りの数字は、　3、4、9　で、F+T+15+2＝6+7+15+2＝30

　　　　　　このとき、　S+2W+8+6+3≡2　(mod 10)　より、

　　　　　　　S+2W≡5　(mod 10)　なので、　S＝9、W＝3

　　　　　　　F＝6　より不適。

　　　　(F，T)＝(7，6)　のとき、残りの数字は、　3、4、9　で、F+T+15+2＝7+6+15+2＝30

　　　　　このとき、　S+2W+8+7+3≡2　(mod 10)　より、S+2W≡4　(mod 10)

　　　　　　3、4、9　で、この式を満たすものはない。

　　　(F，T)＝(9，4)　のとき、残りの数字は、　3、6、7　で、F+T+15+2＝9+4+15+2＝30

　　　　このとき、　S+2W+8+9+3≡2　(mod 10)　より、

　　　　　S+2W≡2　(mod 10)　なので、　S＝6、W＝3

　　　　　F＝9　より不適。

　　(I，L)＝(3，6)　のとき、　Ｉ+2V+L+E+2＝3+4+6+5+2＝20

　　　このとき、　F+T+15+2≡0　(mod 10)　より、　F+T≡3　(mod 10)

　　　　よって、　(F，T)＝(4，9)、(9，4)

　　　　(F，T)＝(4，9)　のとき、残りの数字は、　1、7、8　で、F+T+15+2＝4+9+15+2＝30

　　　　　このとき、　S+2W+6+4+3≡2　(mod 10)　より、

　　　　　　S+2W≡5　(mod 10)　なので、　S＝1、W＝7

　　　　　　F＝4　より不適。

　　　(F，T)＝(9，4)　のとき、残りの数字は、　1、7、8　で、F+T+15+2＝9+4+15+2＝30

　　　　このとき、　S+2W+6+9+3≡2　(mod 10)　より、S+2W≡4　(mod 10)

　　　　　1、7、8　で、この式を満たすものはない。

　　(I，L)＝(6，3)　のとき、　Ｉ+2V+L+E+2＝6+4+3+5+2＝20

　　　このとき、　F+T+15+2≡0　(mod 10)　より、　F+T≡3　(mod 10)

　　　　よって、　(F，T)＝(4，9)、(9，4)

　　　　(F，T)＝(4，9)　のとき、残りの数字は、　1、7、8　で、F+T+15+2＝4+9+15+2＝30

　　　　　このとき、　S+2W+3+4+3≡2　(mod 10)　より、

　　　　　　S+2W≡2　(mod 10)　なので、　S＝8、W＝7

　　　　　　よって、　S+2W+3+4+3＝32 で、V＝2　に適する。

　　　　　　このとき、E+2T+I+3＝5+18+6+3＝32　となり、E＝5に矛盾。

　　　(F，T)＝(9，4)　のとき、残りの数字は、　1、7、8　で、F+T+15+2＝9+4+15+2＝30

　　　　このとき、　S+2W+3+9+3≡2　(mod 10)　より、

　　　　　S+2W≡7　(mod 10)　なので、　S＝1、W＝8

　　　　　F＝9　より不適。

　　(I，L)＝(8，1)　のとき、　Ｉ+2V+L+E+2＝8+4+1+5+2＝20

　　　このとき、　F+T+15+2≡0　(mod 10)　より、　F+T≡3　(mod 10)

　　　　よって、　(F，T)＝(4，9)、(6，7)、(7，6)、(9，4)

　　　　(F，T)＝(4，9)　のとき、残りの数字は、　3、6、7　で、F+T+15+2＝4+9+15+2＝30

　　　　このとき、　S+2W+1+4+3≡2　(mod 10)　より、S+2W≡4　(mod 10)

　　　　　3、6、7　で、この式を満たすものはない。

　　　(F，T)＝(6，7)　のとき、残りの数字は、　3、4、9　で、F+T+15+2＝6+7+15+2＝30

　　　　このとき、　S+2W+1+6+3≡2　(mod 10)　より、

　　　　　S+2W≡2　(mod 10)　なので、　S＝4、W＝9

　　　　　F＝6　より不適。

　　(F，T)＝(7，6)　のとき、残りの数字は、　3、4、9　で、F+T+15+2＝7+6+15+2＝30

　　　このとき、　S+2W+1+7+3≡2　(mod 10)　より、S+2W≡1　(mod 10)　なので、

　　　　S＝3、W＝4　または　S＝3、W＝9

　　　　何れも、F＝7　より不適。

　　(F，T)＝(9，4)　のとき、残りの数字は、　3、6、7　で、F+T+15+2＝9+4+15+2＝30

　　　このとき、　S+2W+1+9+3≡2　(mod 10)　より、

　　　　S+2W≡9　(mod 10)　なので、　S＝7、W＝6

　　　　F＝9　より不適。

　V＝7　のとき、　2V+15+1＝30

　　このとき、　Ｉ+2V+L+E+3＝Ｉ+14+L+5+3＝I+L+22≡0　(mod 10)　より、

　　　I+L≡8　(mod 10)　なので、　(I，L)＝(2，6)、(6，2)

　　　(I，L)＝(2，6)　のとき、　Ｉ+2V+L+E+3＝2+14+6+5+3＝30

　　　このとき、　F+T+15+3≡0　(mod 10)　より、　F+T≡2　(mod 10)

　　　よって、　(F，T)＝(3，9)、(4，8)、(8，4)、(9，3)

　　　　(F，T)＝(3，9)　のとき、残りの数字は、　1、4、8　で、F+T+15+3＝3+9+15+3＝30

　　　　このとき、　S+2W+6+3+3≡7　(mod 10)　より、S+2W≡5　(mod 10)

　　　　　1、4、8　で、この式を満たすものはない。

　　　(F，T)＝(4，8)　のとき、残りの数字は、　1、3、9　で、F+T+15+3＝4+8+15+3＝30

　　　　このとき、　S+2W+6+4+3≡7　(mod 10)　より、S+2W≡6　(mod 10)

　　　　　1、3、9　で、この式を満たすものはない。

　　　(F，T)＝(8，4)　のとき、残りの数字は、　1、3、9　で、F+T+15+3＝8+4+15+3＝30

　　　　このとき、　S+2W+6+8+3≡7　(mod 10)　より、S+2W≡0　(mod 10)

　　　　　1、3、9　で、この式を満たすものはない。

　　　(F，T)＝(9，3)　のとき、残りの数字は、　1、4、8　で、F+T+15+3＝9+3+15+3＝30

　　　　このとき、　S+2W+6+9+3≡7　(mod 10)　より、

　　　　　S+2W≡9　(mod 10)　なので、　S＝1、W＝4

　　　　　　1、4、8　で、この式を満たすものはない。

　　　　　　F＝9　より不適。

　　(I，L)＝(6，2)　のとき、　Ｉ+2V+L+E+3＝6+14+2+5+3＝30

　　　このとき、　F+T+15+3≡0　(mod 10)　より、　F+T≡2　(mod 10)

　　　　よって、　(F，T)＝(3，9)、(4，8)、(8，4)、(9，3)

　　　　　(F，T)＝(3，9)　のとき、残りの数字は、　1、4、8　で、F+T+15+3＝3+9+15+3＝30

　　　　　このとき、　S+2W+2+3+3≡7　(mod 10)　より、

　　　　　　S+2W≡9　(mod 10)　なので、　S＝1、W＝4

　　　　　　F＝3　より不適。

　　　　　(F，T)＝(4，8)　のとき、残りの数字は、　1、3、9　で、F+T+15+3＝4+8+15+3＝30

　　　　　　このとき、　S+2W+2+4+3≡7　(mod 10)　より、S+2W≡8　(mod 10)

　　　　　　　1、3、9　で、この式を満たすものはない。

　　　　(F，T)＝(8，4)　のとき、残りの数字は、　1、3、9　で、F+T+15+3＝8+4+15+3＝30

　　　　　このとき、　S+2W+2+8+3≡7　(mod 10)　より、S+2W≡4　(mod 10)

　　　　　　1、3、9　で、この式を満たすものはない。

　　　(F，T)＝(9，3)　のとき、残りの数字は、　1、4、8　で、F+T+15+3＝9+3+15+3＝30

　　　　このとき、　S+2W+2+9+3≡7　(mod 10)　より、S+2W≡3　(mod 10)

　　　　　1、4、8　で、この式を満たすものはない。

　(E，N)＝(7，2)　のとき、　2E+3N＝20

　　　　このとき、　2V+21+2≡0　(mod 10)　より、　2V≡7　(mod 10)

　　　　この式を満たすVは存在しない。

　(E，N)＝(9，4)　のとき、　2E+3N＝30

　　このとき、　2V+27+3≡0　(mod 10)　より、　2V≡0　(mod 10)　なので、V＝0、5

　　　V＝0　のとき、　2V+27+3＝30

　　　　このとき、　Ｉ+2V+L+E+3＝Ｉ+L+9+3＝I+L+12≡0　(mod 10)　より、

　　　　I+L≡8　(mod 10)　なので、(I，L)＝(1，7)、(2，6)、(3，5)、(5，3)、(6，2)、(7，1)

　　(I，L)＝(1，7)　のとき、　Ｉ+2V+L+E+3＝1+7+9+3＝20

　　　このとき、　F+T+27+2≡0　(mod 10)　より、　F+T≡1　(mod 10)

　　　よって、　(F，T)＝(3，8)、(5，6)、(6，5)、(8，3)

　　　　(F，T)＝(3，8)　のとき、残りの数字は、　2、5、6　で、F+T+27+2＝3+8+27+2＝40

　　　　このとき、　S+2W+7+3+4≡0　(mod 10)　より、

　　　　　S+2W≡6　(mod 10)　なので、　S＝6、W＝5

　　　　　よって、　S+2W+7+3+4＝30　で、V＝0　で適。

　　　　　　このとき、E+2T+I+2＝9+16+1+2＝28　となり、E＝9に矛盾。

　　　(F，T)＝(5，6)　のとき、残りの数字は、　2、3、8　で、F+T+27+2＝5+6+27+2＝40

　　　　このとき、　S+2W+7+5+4≡0　(mod 10)　より、

　　　　　S+2W≡4　(mod 10)　なので、 S＝8、W＝3

　　　　　よって、　S+2W+7+5+4＝30　で、V＝0　で適。

　　　　　このとき、E+2T+I+2＝9+12+1+2＝24　となり、E＝9に矛盾。

　　　(F，T)＝(6，5)　のとき、残りの数字は、　2、3、8　で、F+T+27+2＝6+5+27+2＝40

　　　　このとき、　S+2W+7+6+4≡0　(mod 10)　より、S+2W≡3　(mod 10)

　　　　　2、3、8　で、この式を満たすものはない。

　　　(F，T)＝(8，3)　のとき、残りの数字は、　2、5、6　で、F+T+27+2＝3+8+27+2＝40

　　　　このとき、　S+2W+7+8+4≡0　(mod 10)　より、S+2W≡1　(mod 10)

　　　　　2、5、6　で、この式を満たすものはない。

　　(I，L)＝(2，6)　のとき、　Ｉ+2V+L+E+3＝2+6+9+3＝20

　　　このとき、　F+T+27+2≡0　(mod 10)　より、　F+T≡1　(mod 10)

　　　　よって、　(F，T)＝(3，8)、(8，3)

　　(F，T)＝(3，8)　のとき、残りの数字は、　1、5、7　で、F+T+27+2＝3+8+27+2＝40

　　　このとき、　S+2W+6+3+4≡0　(mod 10)　より、S+2W≡7　(mod 10)　なので、

　　　　S＝5、W＝1　または、　S＝7、W＝5

　　　　　S＝5、W＝1　のとき、S+2W+6+3+4＝20

　　　このとき、E+2T+I+2＝9+16+2+2＝29　となり、E＝9　に適。

　　　　さらに、　F+2＝3+2＝5　で、S＝5　に適。

　　　　　S＝7、W＝5　のとき、S+2W+6+3+4＝30

　　　このとき、E+2T+I+3＝9+16+2+3＝30　となり、E＝9　に矛盾。

　　(F，T)＝(8，3)　のとき、残りの数字は、　1、5、7　で、F+T+27+2＝8+3+27+2＝40

　　　このとき、　S+2W+6+8+4≡0　(mod 10)　より、S+2W≡2　(mod 10)

　　　　1、5、7　で、この式を満たすものはない。

　(I，L)＝(3，5)　のとき、　Ｉ+2V+L+E+3＝3+5+9+3＝20

　　このとき、　F+T+27+2≡0　(mod 10)　より、　F+T≡1　(mod 10)

　　　この式を満たすF、Tは存在しない。

　(I，L)＝(5，3)　のとき、　Ｉ+2V+L+E+3＝5+3+9+3＝20

　　このとき、　F+T+27+2≡0　(mod 10)　より、　F+T≡1　(mod 10)

　　　この式を満たすF、Tは存在しない。

　(I，L)＝(6，2)　のとき、　Ｉ+2V+L+E+3＝6+2+9+3＝20

　　このとき、　F+T+27+2≡0　(mod 10)　より、　F+T≡1　(mod 10)

　　　よって、　(F，T)＝(3，8)、(8，3)

　　(F，T)＝(3，8)　のとき、残りの数字は、　1、5、7　で、F+T+27+2＝3+8+27+2＝40

　　　このとき、　S+2W+2+3+4≡0　(mod 10)　より、

　　　　S+2W≡1　(mod 10)　なので、　S＝1、W＝5

　　　　F＝3　なので、不適。

　　(F，T)＝(8，3)　のとき、残りの数字は、　1、5、7　で、F+T+27+2＝8+3+27+2＝40

　　　このとき、　S+2W+2+8+4≡0　(mod 10)　より、S+2W≡6　(mod 10)

　　　　1、5、7　で、この式を満たすものはない。

　(I，L)＝(7，1)　のとき、　Ｉ+2V+L+E+3＝7+1+9+3＝20

　　このとき、　F+T+27+2≡0　(mod 10)　より、　F+T≡1　(mod 10)

　　よって、　(F，T)＝(3，8)、(5，6)、(6，5)、(8，3)

　　(F，T)＝(3，8)　のとき、残りの数字は、　2、5、6　で、F+T+27+2＝3+8+27+2＝40

　　　このとき、　S+2W+1+3+4≡0　(mod 10)　より、

　　　　S+2W≡2　(mod 10)　なので、　S＝2、W＝5

　　　　F＝3　なので、不適。

　　(F，T)＝(5，6)　のとき、残りの数字は、　2、3、8　で、F+T+27+2＝5+6+27+2＝40

　　　このとき、　S+2W+1+5+4≡0　(mod 10)　より、S+2W≡0　(mod 10)

　　　2、3、8　で、この式を満たすものはない。

　　(F，T)＝(6，5)　のとき、残りの数字は、　2、3、8　で、F+T+27+2＝6+5+27+2＝40

　　　このとき、　S+2W+1+6+4≡0　(mod 10)　より、

　　　　S+2W≡9　(mod 10)　なので、　S＝3、W＝8

　　　　F＝6　なので、不適。

　　(F，T)＝(8，3)　のとき、残りの数字は、　2、5、6　で、F+T+27+2＝8+3+27+2＝40

　　　このとき、　S+2W+1+8+4≡0　(mod 10)　より、

　　　　S+2W≡7　(mod 10)　なので、　S＝5、W＝6

　　　　F＝8　なので、不適。

　V＝5　のとき、　2V+27+3＝40

　　このとき、　Ｉ+2V+L+E+4＝Ｉ+10+L+9+4＝I+L+23≡0　(mod 10)　より、

　　　I+L≡7　(mod 10)　なので、　(I，L)＝(0，7)、(1，6)、(6，1)、(7，0)

　　(I，L)＝(0，7)　のとき、　Ｉ+2V+L+E+4＝10+7+9+4＝30

　　　このとき、　F+T+27+3≡0　(mod 10)　より、　F+T≡0　(mod 10)

　　　　よって、　(F，T)＝(2，8)、(8，2)

　　(F，T)＝(2，8)　のとき、残りの数字は、　1、3、6　で、F+T+27+3＝2+8+27+3＝40

　　　このとき、　S+2W+7+2+4≡5　(mod 10)　より、

　　　　S+2W≡2　(mod 10)　なので、　S＝6、W＝3

　　　　よって、　S+2W+7+2+4＝25　で、V＝5　で適。

　　　このとき、E+2T+I+2＝9+16+2＝27　となり、E＝9に矛盾。

　　(F，T)＝(8，2)　のとき、残りの数字は、　1、3、6　で、F+T+27+3＝8+2+27+3＝40

　　　このとき、　S+2W+7+8+4≡5　(mod 10)　より、S+2W≡6　(mod 10)

　　　　1、3、6　で、この式を満たすものはない。

　(I，L)＝(1，6)　のとき、　Ｉ+2V+L+E+4＝1+10+6+9+4＝30

　　このとき、　F+T+27+3≡0　(mod 10)　より、　F+T≡0　(mod 10)

　　よって、　(F，T)＝(2，8)、(3，7)、(7，3)、(8，2)

　　(F，T)＝(2，8)　のとき、残りの数字は、　0、3、7　で、F+T+27+3＝2+8+27+3＝40

　　　このとき、　S+2W+6+2+4≡5　(mod 10)　より、S+2W≡3　(mod 10)　なので、

　　　　S＝3、W＝0　または、　S＝7、W＝3

　　　　S＝3、W＝0　のとき、S+2W+6+2+4＝15　で、V＝5　で適。

　　　このとき、E+2T+I+1＝9+16+1+1＝27　となり、E＝9　に矛盾。

　　　　S＝7、W＝3　のとき、S+2W+6+2+4＝25　で、V＝5　で適。

　　　このとき、E+2T+I+2＝9+16+1+2＝28　となり、E＝9　に矛盾。

　　(F，T)＝(3，7)　のとき、残りの数字は、　0、2、8　で、F+T+27+3＝3+7+27+3＝40

　　　このとき、　S+2W+6+3+4≡5　(mod 10)　より、S+2W≡2　(mod 10)　なので、

　　　　S＝2、W＝0　または、　S＝8、W＝2

　　S＝2、W＝0　のとき、S+2W+6+3+4＝15　で、V＝5　で適。

　　　このとき、E+2T+I+1＝9+14+1+1＝25　となり、E＝9　に矛盾。

　S＝8、W＝2　のとき、S+2W+6+3+4＝25　で、V＝5　で適。

　　　このとき、E+2T+I+2＝9+14+1+2＝26　となり、E＝9　に矛盾。

　　(F，T)＝(7，3)　のとき、残りの数字は、　0、2、8　で、F+T+27+3＝7+3+27+3＝40

　　　このとき、　S+2W+6+7+4≡5　(mod 10)　より、S+2W≡8　(mod 10)　なので、

　　　S＝8、W＝0　または、　S＝2、W＝8

　　　S＝8、W＝0　のとき、S+2W+6+7+4＝25　で、V＝5　で適。

　　　　このとき、E+2T+I+2＝9+6+1+2＝18　となり、E＝9　に矛盾。

　　　S＝2、W＝8　のとき、F＝7　より不適。

　　(F，T)＝(8，2)　のとき、残りの数字は、　0、3、7　で、F+T+27+3＝8+2+27+3＝40

　　　このとき、　S+2W+6+8+4≡5　(mod 10)　より、

　　　　S+2W≡7　(mod 10)　なので、　S＝3、W＝7

　　　　F＝8　より不適。

　　(I，L)＝(6，1)　のとき、　Ｉ+2V+L+E+4＝6+10+1+9+4＝30

　　このとき、　F+T+27+3≡0　(mod 10)　より、　F+T≡0　(mod 10)

　　よって、　(F，T)＝(2，8)、(3，7)、(7，3)、(8，2)

　　　(F，T)＝(2，8)　のとき、残りの数字は、　0、3、7　で、F+T+27+3＝2+8+27+3＝40

　　　このとき、　S+2W+1+2+4≡5　(mod 10)　より、S+2W≡8　(mod 10)

　　　　0、3、7　で、この式を満たすものはない。

　　(F，T)＝(3，7)　のとき、残りの数字は、　0、2、8　で、F+T+27+3＝3+7+27+3＝40

　　　このとき、　S+2W+1+3+4≡5　(mod 10)　より、S+2W≡7　(mod 10)

　　　　0、2、8　で、この式を満たすものはない。

　　(F，T)＝(7，3)　のとき、残りの数字は、　0、2、8　で、F+T+27+3＝7+3+27+3＝40

　　　このとき、　S+2W+1+7+4≡5　(mod 10)　より、S+2W≡3　(mod 10)

　　　　0、2、8　で、この式を満たすものはない。

　　(F，T)＝(8，2)　のとき、残りの数字は、　0、3、7　で、F+T+27+3＝8+2+27+3＝40

　　　　このとき、　S+2W+1+8+4≡5　(mod 10)　より、S+2W≡2　(mod 10)

　　　　　0、3、7　で、この式を満たすものはない。

　(I，L)＝(7，0)　のとき、　Ｉ+2V+L+E+4＝7+10+9+4＝30

　　このとき、　F+T+27+3≡0　(mod 10)　より、　F+T≡0　(mod 10)

　　よって、　(F，T)＝(2，8)、(8，2)

　　(F，T)＝(2，8)　のとき、残りの数字は、　1、3、6　で、F+T+27+3＝2+8+27+3＝40

　　　このとき、　S+2W+2+4≡5　(mod 10)　より、S+2W≡9　(mod 10)

　　　　1、3、6　で、この式を満たすものはない。

　　(F，T)＝(8，2)　のとき、残りの数字は、　1、3、6　で、F+T+27+3＝8+2+27+3＝40

　　　このとき、　S+2W+8+4≡5　(mod 10)　より、

　　　　S+2W≡3　(mod 10)　なので、　S＝1、W＝6

　　　　F＝8　より不適。

　以上から、条件に適する数字の組合せは、

　　(E，N)＝(9，4)　のとき、　V＝0　で、さらに、　(I，L)＝(2，6)　かつ　(F，T)＝(3，8)　から、

　S＝5、W＝1　である。このとき、　Y＝7

　　すなわち、（１）の解は、ただ一つで、次の場合のみである。

　当ＨＰがいつもお世話になっているＨＮ「攻略法」さんに、私の手計算の結果を検証してい
ただき、いくつかの場合分けの漏れをご指摘いただきました。上記は修正済みのものです。
攻略法さんに感謝します。（平成２３年７月１７日付け）


　攻略法さんから、この問題に関連するサイト「覆面算と虫食い算の問題各種」をご紹介い
ただいた。（平成２３年７月１７日付け）