
次の虫食い算は、当HPがいつもお世話になっているHN「FN」さんからの出題です。
実は過剰条件で、割る数の1の位の7はなくても解は一意的です。それでは難しすぎそう
なのと、7を7個にしたかったので下記にしました。 なんらかの工夫で試行錯誤の回数を減
らせないでしょうか。
いくらかの試行錯誤が必要です。時間のある方は、挑戦してみては?
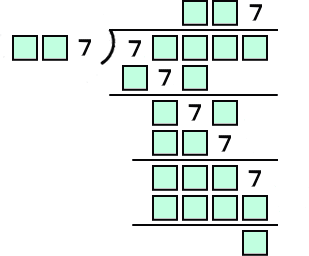
(答) 73137÷337 を計算している。
FNさんからのコメントです。(平成23年6月23日付け)
正解です。私も一応自分で解いてみて解答は得ました。しかし、これ以外にないというの
は面倒くさくなってやめました。そこそこの手順でこれ以外にないことは示せるでしょうか。
FNさんの心配を取り払うべく考察してみた。

上記の計算で、 A=B=1 と仮定すると、 117×D=G7H を満たすDは存在しない。
よって、A≧2 または B≧2 である。
このとき、G=6 または 7 で、AB7×D=G7Hとなるパターンは、
257×3 、337×2 、387×2
の3通りしかない。
(1) 257×3=771 の場合、Eが最大で9が入ってもIは2以下で、Jは0以下となり不適
(2) 387×2=774 の場合、Eが最大で9が入ってもIは2以下で、Jは0未満となり不適
(3) 337×2=674 の場合、 MNP=235 より、 JKL=236 、F=1 と確定する。
このとき、 C=3 で、さらに、I=5 なので、 E=3 となる。
以上から、解は一意的に定まる。