虫食い算６　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　次の虫食い算は、当ＨＰがいつもお世話になっているＨＮ「ＧＡＩ」さんからの出題です。

（初級）　□に１〜９を一つずつ入れよ。

１．　□＋□＝□　、□＋□＝□　、□×□＝□

２．　□＋□＝□　、□＋□＝□　、□÷□＝□

３．　□＋□＝□　、□−□＝□　、□×□＝□

４．　□＋□＝□　、□−□＝□　、□÷□＝□

（中級）

５．

６．

（上級）　７．



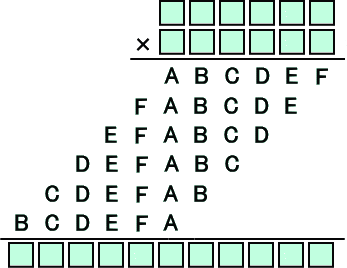
（その他）　A〜Iに１〜９の数字を一つずつ入れよ。

８．　A＋B＝B＋C＋D＝D＋E＋F＝F＋G＋H＝H＋I＝１１

９．　A＋B＝B＋C＋D＝D＋E＋F＝F＋G＋H＝H＋I＝１３

１０．　A＋B＝B＋C＋D＝D＋E＋F＝F＋G＋H＝H＋I＝１４

１１．　　出来たかな？

１２． 　　　　　　　　　 　　　　　　　　　(ヒント）ぎりぎりです。

（答）　（初級）について、ＦＮさんによる解です。（平成２３年６月２３日付け）

　　１．の解は、　１＋７＝８　、４＋５＝９　、２×３＝６

　あとは掛け算を割り算にかえたり足し算を引き算にかえたりすればよい。すなわち、
　２×３＝６　を　６÷２＝３　にかえたり、１＋７＝８　を　８−１＝７　にかえたり．．．。

　（中級）について、ＦＮさんからのコメントです。（平成２３年６月２３日付け）

　　５．は、ＷとＵが交換可能だから、解は一意的ではないですね。
　３５０＋６７３＋９３８２＝１０４０５とか。解は他にもありそうです。

　　６．は、Ｎ、Ｗ、Ｖが交換可能だから、１つ解があれば６個できます。
　６２１＋８４６＋９０７１＝１０５３８とか。解は一意的であって欲しいと思います。


　（上級）について、ＦＮさんによる解です。（平成２３年６月２３日付け）

　　多分、ABCDEF＝142857　しかないでしょう。証明も可能そうです。


　ＦＮさんの解について、らすかるさんからのコメントです。（平成２３年６月２４日付け）

　　ABCDEF＝285714 とか ABCDEF＝428571 などの可能性もあるのでは？


　ＦＮさんからのコメントです。（平成２３年６月２４日付け）

　　その通りです。それら以外にはないと思います。証明はそんなに簡単ではないかもしれ
　ません。１行目の数が999と99の倍数であることは言えそうです。あとは13の倍数である
　ことが言えれば、142857=999*11*13なので終了だと思います。

　　13の倍数も同じでできそうです。999の倍数がやや不完全なのできちんとやってみます。


　らすかるさんが上記の事実を証明されました。（平成２３年６月２４日付け）

（証明）　ABCDEF、BCDEFA、・・・、FABCDE はすべて被乗数の倍数だから

　　　　ABCDEF0−BCDEFA＝A000000−A＝（1000000−１）Ａ＝999999A

　　　　BCDEFA0−CDEFAB＝999999B

　　　　　　・・・・・・・・・・・・・・・・・・・・

　　　　FABCDE0−ABCDEF＝999999F

も被乗数の倍数である。A〜Fの最大公約数は1だから、被乗数は999999の約数。

　999999＝３³・７・１１・１３・３７ で 102345≦被乗数≦165432 なので、被乗数は、１１、１３、

３７の倍数、つまり、5291の倍数。

　19＜102345/5291＜165432/5291＜32 だから、被乗数÷5291は、21か27となり

　　5291×21=111111　、5291×27=142857

から、被乗数は142857以外にあり得ない。　　（証終）


　ＦＮさんからのコメントです。（平成２３年６月２４日付け）

　なるほど。ABCDEF0-BCDEFAを作ればいいのですね。この方が簡単そうです。私は999
の倍数を証明するのにこだわってしまいました。333の倍数までなら比較的簡単なので、こ
れと99、13の倍数であることを使って47619の倍数であるとするべきでした。

　らすかるさんからのコメントです。（平成２３年６月２４日付け）

　証明がもう少し簡単になりました。

（証明）　ABCDEF、BCDEFA、・・・、FABCDE はすべて被乗数の倍数だから

　　　　ABCDEF0−BCDEFA＝A000000−A＝（1000000−１）Ａ＝999999A

　　　　BCDEFA0−CDEFAB＝999999B

　　　　　　・・・・・・・・・・・・・・・・・・・・

　　　　FABCDE0−ABCDEF＝999999F

も被乗数の倍数である。A〜Fの最大公約数は1だから、被乗数は999999の約数。

　999999＝３³・７・１１・１３・３７ で 102345≦被乗数≦165432 なので、

　 6＜999999/165432＜999999/102345＜10 から、999999/7 または 999999/9 となるが、

後者は不適なので、被乗数は、999999/7＝142857以外にあり得ない。　　（証終）


　ＦＮさんからのコメントです。（平成２３年６月２４日付け）

　999999の約数で6桁であるのは、111111、333333、999999を除けば、142857しかないとい
うことですね。表記についてですがABCDEF0-BCDEFA=999999*A等と書く方がいいですね。


　７．について、次のページ「循環小数の不思議」が参考になると思います。


　（その他）について、ＦＮさんによる解です。（平成２３年６月２４日付け）

８．　B＋D＋F＋H＝10　で、B、Hは１になれないので、場合の数はあまり多くない。だから
　手作業でできました。左右対称を除いて一意的でした。

９．１０．は手作業でやる気がおきなかったので、コンピュータを使いました。

　A＋B＝B＋C＋D＝D＋E＋F＝F＋G＋H＝H＋I＝Ｘ　とする。

　B＋D＋F＋H＝Ｙ　とおくと、　５・Ｘ＝４５＋Ｙ　で、　10≦Y≦30　だから、11≦X≦15

　　X＝11、12、13、14、15　について、Excel VBAで調べてみたら、次のようになりました。

　ただし、1つの解に対して、AとI、BとH、CとG、DとFを交換しても解です。このようなのは左
右対称なものとして同一視することにします。

　　X=11　 (A,B,C,D,E,F,G,H,I)＝(9,2,5,4,6,1,7,3,8)

　　X=12　 解なし

　　X=13　 (A,B,C,D,E,F,G,H,I)＝(9,4,1,8,3,2,5,6,7)、(7,6,5,2,8,3,1,9,4)

　　X=14　 (A,B,C,D,E,F,G,H,I)＝(8,6,1,7,4,3,2,9,5)

　　X=15　 解なし

　コンピュータでやったあとで、もう一度手作業で考えてみました。X＝15のとき解なしは簡
単にでます。X＝14のとき上記の解しかないことも比較的容易です。X＝12とX＝13だけが
手作業でできてません。

１１．の答えは、　１９４６５０

１２．の答えは、　Ａ＝４、Ｂ＝３、Ｃ＝８、Ｄ＝９