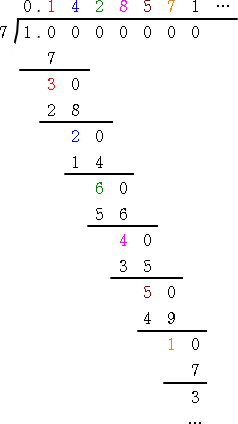分数を小数に直す場合、有限小数か循環小数の何れかになる。有限小数も、最後に 0
が循環すると考えれば、循環小数とみなせる。また、逆に、有限小数、循環小数は、必ず
分数に直すことができる。
(例) 0.6666666・・・・・・・ を、分数に直してみよう。
X=0.6666666・・・・・・・ とおくと、 10X=6.6666666・・・・・・・・ である。
これらを辺々引いて、 9X=6 となり、 X=2/3 という分数になる。
上記解答以外に、無限等比級数の公式を使った解法もあるが、上記解答に比べて相当
見劣りがする。
0.6666666・・・・・・・
=0.6+0.06+0.006+・・・・・・・=0.6/(1−0.1)=0.6/0.9=2/3
1 という数を、素数で割った場合、その余りは必ず素数より小さいので、必ず何れは循
環する。問題は、何桁目で循環するのかということである。
有限小数は、0が循環していると考えればよいが、この場合除外する。
いくつか実験してみよう。
1/3=0.33333・・・・
1/7=0.142857142857・・・・
1/11=0.0909・・・・
1/13=0.076923076923・・・・
1/17=0.05882352941176470588235294117647・・・・
1/19=0.052631578947368421052631578947368421・・・・
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
上記の実験で、ある法則を発見することができる。
(合同の記号≡については、こちらを参照)
1/3 は、1桁目で循環している。実は、101≡1 (mod 3)
1/7 は、6桁目で循環している。実は、106≡1 (mod 7)
実際に、101≡3 (mod 7) より、103≡27≡−1 (mod 7) から明らか。
1/11 は、2桁目で循環している。実は、102≡1 (mod 11)
実際に、101≡−1 (mod 11) より明らか。
1/13 は、6桁目で循環している。実は、106≡1 (mod 13)
実際に、101≡−3 (mod 13) より、103≡−27≡−1 (mod 13) から明らか。
1/17 は、16桁目で循環している。実は、1016≡1 (mod 17)
実際に、102≡−2 (mod 17) より、104≡4 (mod 17)
よって、 108≡16≡−1 (mod 17) から明らか。
1/19 は、18桁目で循環している。実は、1018≡1 (mod 19)
実際に、103≡−7 (mod 19) より、109≡−343≡−1 (mod 19) から明らか。
以下同様である。
このように、循環する小数 1/p (pは素数)が何桁目で循環するかをみるには、合同式
10n≡1 (mod p)
を満たす n の値を求めればよい。これは、とても面白い性質だと思う。
フェルマーの定理によれば、
Xp-1≡1 (mod p) (ただし、X は、p で割り切れない)
が成り立つので、そのような n は必ず存在する(即ち、必ずどこかで循環する)。
上記循環小数の計算では、Excel のマクロを活用して求めたが、筆算で計算する場合、
計算ミスも起こりやすい。循環する桁数が前もって分かっていれば、検算に活用できると思
う。
幼少の頃、天才数学者のガウスは、循環する小数 1/p をある程度暗記していたと聞く。
そういったもろもろの積み重ねが、法則の発見につながったのだろう。上記の実験で、その
雰囲気が伝われば幸いである。
(参考文献:遠山 啓 著 数学入門(下) (岩波新書))
(追記) 参考までに使用したExcel のマクロを書いておこう。
Function Q(a,b,n)
If n=0 Then
Q=””
Else
Q=Int(10*a/b) & Q(10*a Mod b,b,n−1)
End If
End Function
Excel を起動し、[ツール]−[マクロ]−[Visual Basic Editor] とクリックして Editor
を起動し、[挿入]−[標準モジュール] を選択して、上記を記述すればよい。後は、Excelの
任意のセルに、例えば、 =Q(1,7,30) と打ち込むと、瞬時に、1÷7 の小数点以下
30桁までの数列を得ることができる。
Excel のセルに普通に「=1/7」と打ち込むと、「0.142857143」と小数点以下9桁ま
でしか得ることができない。上記マクロを用いると、より詳しい小数展開が得られて重宝で
ある。
(追記) 上記では、10n≡1 (mod p)を利用して、循環小数が何桁目で循環するの
を見たが、次の性質に着目して求めることもできる。
0.66・・・ を、分数に直す際、 X=0.66・・・ とおいて、 10X=6.66・・・ から、
9X=6 を解いて、 X=2/3 を求めた。
この場合に着目するところは、 X=6/9 という形である。9=101−1 で、その逆数は、
1/9=1/(10−1)
=(1/10)・1/(1−(1/10))
=(1/10)・(1+(1/10)+(1/10)2+(1/10)3+・・・)
=1/10+1/102+1/103+・・・
と書ける。 したがって、 循環小数 1/9 は、1桁目で循環し、その循環節は「1」である。
同様に、 99=102−1 なので、その逆数は、
1/99=1/102+1/104+1/106+・・・
となり、 循環小数 1/99 は、2桁目で循環し、その循環節は「01」である。
例 分数 2/3 は、6/9 と書けるので、1桁目で循環し、その循環節は「6」である。
例 分数 5/11 は、45/99 と書けるので、2桁目で循環し、その循環節は「45」である。
もっとも、 7×(142857)=999999 となる数 142857 を発見して、分数 1/7 は、
142857/999999 と書けるので、6桁目で循環し、その循環節は「142857」であると
する方は、「多分いない!」と思う。
(追記) 平成18年5月31日付け
今頃の高校1年生は、実数という話の中で循環小数のことを学ぶ。(進学校といわれるとこ
ろでは既に終わっているかもしれないが...)
その計算の際、上記のようなことを知っていれば、自分が計算ミスをしているのかしていな
いのかの判定ができる。ただ、それは高校1年生にとっては難しすぎる判定法である。
最近、もっと簡便な判定法があることを知った。それは、
7以上の素数 p に対して、その逆数 1/p の循環節は必ず 9 の倍数になる
ということである。
たとえば、 1/7=0.142857142857・・・・ から、1/7 の循環節は、142857 で、
各位の数の和 1+4+2+8+5+7=27 が9の倍数であることから、142857 は9の
倍数となる。
1/7 程度だったら計算ミスのしようがないかもしれないが、一応簡便な検算が瞬時にで
きる。
1/17 などは、循環することが分かってはいても、
1/17=0.05882352941176470588235294117647・・・・
のような計算が続くと辟易してしまう。これも循環節 0588235294117647 について、
0+5+8+8+2+3+5+2+9+4+1+1+7+6+4+7=72
から、9の倍数となることが確かめられ、ほぼ計算は合っているものと推察される。
このような事実は次のようにして示される。
たとえば、 x=0.142857142857・・・・ とおくと、
1000000x=142857.142857142857・・・・
小数点以下が同じ数字の並びなので、辺々引いて、
999999x=142857
左辺は9の倍数なので、右辺の142857も9の倍数となる。
(参考文献:玉木英彦 著 小学生にピタゴラス (みすず書房))
(追記) 平成18年7月17日付け
上記において、循環する小数 1/p (pは素数)が何桁目で循環するかは、
10n≡1 (mod p)
を利用すればよいことが分かった。
すなわち、循環節の長さが n であるとき、10n を p で割った余りは、1 となる。
このことに関連して、次の事実も知られているようだ。
既約分数 b/a において、a は、2 および 5 を素因数に持たないものとする。
このとき、
既約分数 b/a の循環節の長さが n であるとき、10n を a で割った余りは、
b の値に無関係で、いつも 1 である。
(証明) r = b/a ( a と b は互いに素)とおくと、条件より、ある自然数 m に対して、
10m+n・r − 10m・r =s ( s は自然数)
と書ける。 すなわち、 (10n − 1)10m・b = s・a ( s は自然数)
条件より、右辺は a で割り切れ、10m・b と a は互いに素なので、10n − 1 が a で割
り切れる。したがって、10n を a で割った余りは、b によらず、いつも 1 である。(終)
例 10 を 3 で割った余りは、1 なので、既約分数 1/3 や 2/3 の循環節の長さは、1
例 1000000 を 13 で割った余りは、1 なので、既約分数 1/13 、2/13、・・・ の循環
節の長さは、6
(追記) 平成21年4月10日付け
上記において、1/7 の循環節は、「142857」であることを知ったが、この数は、さらに
次のような面白い現象を引き起こすことを最近知った。
142857×326=46571382
と、電卓を使って計算結果を求めては、その面白さはうかがい知れない。
筆算で求めると、
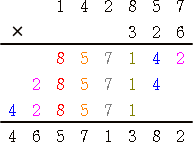
となり、同じ数字が縦に並ぶ様は、美しい!
実は、このような現象が起きるカラクリは、乗数の「326」にある。この数は、ある特殊な
計算で求められる。