丂擔忢惗妶偱壗婥側偔巊偭偰偄傞悢丄椺偊偽丄俀係俇 側偳偼丄偁傞栺懇偺傕偲偵婰弎偝傟偰偄
傞丅丂俀係俇 偼丄乽偵乕傛傫傠偔乿偲偼屇偽偢丄惓偟偔偼丄乽偵傂傖偔傛傫偠傘偆傠偔乿偱偁傞丅傕偭偲
傕丄崙摴俀係俇崋慄偼丄捠徧乽偵乕傛傫傠偔乿偲屇偽傟傞偑丄偙傟偼偁偔傑偱傕捠徧偱偁傞丅
丂偟偨偑偭偰丄摨偠悢帤偱傕丄彂偐傟偰偁傞弴斣偵傛偭偰堎側偭偨堄枴崌偄傪傕偮丅
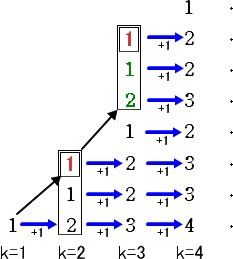
丂惍悢偱丄堦斣塃懁偺悢偼丄堦偺埵丄偦偺嵍偼丄廫偺埵丄傑偨偦偺嵍偼丄昐偺埵丄丒丒丒丂偲
尵傢傟傞丅偙偺偙偲傪柧椖偵昞偡偵偼丄師偺傛偆偵彂偗偽傛偄丅
丂丂俀係俇(10)亖俀丒侾侽2亄係丒侾侽亄俇
丂偙偺偲偒丄乽俀係俇乿偺傛偆側婰悢朄傪丄埵庢傝婰悢朄丄偦偟偰丄偦偺悢傪丄塃曈偺傛偆偵婰
偡曽朄傪 廫恑朄揥奐 偲偄偆傛偆偩丅
乮乽偠偭偟傫傎偆偰傫偐偄乿偲撉傓両抪偢偐偟側偑傜崱傑偱乽偠傘偭偟傫傎偆偰傫偐偄乿偲偢偭偲撉傫偱傑偟
丂偨 丏丏丏 倖(^^;) 乯
丂偙偺埵庢傝婰悢朄偼丄僀儞僪偱偺乽楇乮侽乯偺敪尒乿偑側偐偭偨傜丄側偐偭偨婰悢朄偩偲巚偆丅
傕偟偐偟偨傜丄崱偱傕丄嘥丄倁丄倃丄俴丄俠丄俢丄俵 偲偄偭偨儘乕儅悢帤傪巊偭偰偄偨偐傕偟傟
側偄丅乮偙傟偼丄旕忢偵恏偄婰悢朄偱偁傞丅徻偟偔偼丄偙偪傜傪嶲徠乯
丂廫恑朄偺埵庢傝婰悢朄偱偼丄侾侽偵側傞偲埵偑侾偮孞傝忋偑傞偲偄偆惈幙傪傕偮丅偙傟偑丄
埵偑堎側傞偛偲偵堘偆婰崋傪梡偄偨儘乕儅悢帤偲偺寛掕揑側堘偄偱偁傞丅
丂廫恑朄揥奐偺峫偊偼丄倫恑朄揥奐偵堦斒壔偝傟傞丅扐偟丄倫 偼丄俀埲忋偺惍悢偲偡傞丅
丂倎0倫n亄倎1倫n-1亄倎2倫n-2亄丒丒丒亄倎n-1倫亄倎n丂丂乮奺倎倠偼丄侽亝倎倠亙倫 側傞惍悢乯
偱昞偝傟偨悢傪丄倫恑朄揥奐偝傟偨悢偲偄偄丄奺埵偺悢傪暲傋偰丄倫恑朄偺埵庢傝婰悢朄
偑摼傜傟傞丅
丂倎0倎1倎2丒丒丒倎n-1倎n(p)丂
椺丂係恑朄偱丄侾俀俁 偼丄廫恑朄偱偼偄偔偮偐丠
丂侾俀俁(4)亖侾丒係2亄俀丒係亄俁亖侾俇亄俉亄俁亖俀俈
椺丂廫恑朄偱丄侾俀俁 偼丄俆恑朄偱偄偔偮偐丠
丂侾俀俁(10)亖俆丒俀係亄俁亖俆丒乮俆丒係亄係乯亄俁亖係丒俆2亄係丒俆亄俁丂傛傝丄侾俀俁 傪丄俆恑朄偱昞
偡偲丄丂係係俁(5)丂偲側傞丅
丂廫恑朄偱昞偝傟偨悢傪丄倫恑朄偵曄姺偡傞応崌丄忋婰偺傛偆偵寁嶼偡傞偙偲偼傑偢側偄丅
捠忢師偺傛偆側昅嶼偱媮傔傜傟傞丅
丂丂
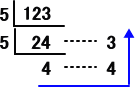
丂忋婰偱偼丄惍悢偺 倫 恑朄揥奐傪寁嶼偟偨偑丄傕偪傠傫丄彫悢偺 倫 恑朄揥奐傕偁傝偆傞丅
丂倎1倫-1亄倎2倫-2亄丒丒丒亄倎n倫-n亄丒丒丒丂丂乮奺倎倠偼丄侽亝倎倠亙倫 側傞惍悢乯
椺丂係恑朄偱丄侽丏侾俀俀 偼丄廫恑朄偱偼偄偔偮偐丠
丂侽丏侾俀俀(4)亖侾丒係-1亄俀丒係-2亄俀丒係-3亖侾俁/俁俀
椺丂廫恑朄偱丄侽丏侾俀俀 偼丄俆恑朄偱偄偔偮偐丠
丂侽丏侾俀俀亖倎1俆-1亄倎2俆-2亄倎3俆-3亄倎4俆-4亄倎5俆-5亄丒丒丒丂丂偵偍偄偰丄
丂侽丏侾俀俀亊俆亖侽丏俇侾亖倎1亄倎2俆-1亄倎3俆-2亄倎4俆-3亄倎5俆-4亄丒丒丒丂 傛傝丄倎1亖侽
丂侽丏俇侾亊俆亖俁丏侽俆亖倎2亄倎3俆-1亄倎4俆-2亄倎5俆-3亄丒丒丒丂丂傛傝丄倎2亖俁
偙偺偲偒丄侽丏侽俆亖倎3俆-1亄倎4俆-2亄倎5俆-3亄丒丒丒丂偲側傝丄
丂侽丏侽俆亊俆亖侽丏俀俆亖倎3亄倎4俆-1亄倎5俆-2亄丒丒丒丂丂傛傝丄倎3亖侽
丂侽丏俀俆亊俆亖侾丏俀俆亖倎4亄倎5俆-1亄丒丒丒丂丂傛傝丄倎4亖侾
丂侽丏俀俆亊俆亖侾丏俀俆丂乮偙傟偼忋婰抣偲摨偠偱忋偺寁嶼偑埲壓孞傝曉偝傟傞丅乯
丂丂丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒
偟偨偑偭偰丄丂侽丏侾俀俀 傪丄俆恑朄偱昞偡偲丄侽丏侽俁侽侾侾侾丒丒丒丂偡側傢偪
丂丂
偲側傞丅
丂偙偺椺偐傜傕暘偐傞傛偆偵丄廫恑朄偺悽奅偱桳尷彫悢偱偁偭偰傕丄倫恑悢偺悽奅偱偼丄弞
娐彫悢偲側傞応崌偑偁傞丅
丂惍悢偺応崌偲摨條偵偟偰丄彫悢偺応崌偼丄師偺傛偆側昅嶼偱媮傔傞偺偑晛捠偱偁傞丅
丂丂
乮捛婰乯丂暯惉俀俆擭俋寧俀侾擔晅偗
丂曻憲戝妛暥嫗峑幧偱丄乽戙悢嬋慄偲婔壗妛乿偲戣偟偰丄斞崅愭惗偺儗僋僠儍乕偑偁傞偲偄偆
偙偲偱嶲壛偟偰偒偨丅斞崅愭惗偲偼俁侽擭傎偳慜丄愬戜偺搶杒戝妛偱峴傢傟偨戙悢婔壗妛僔
儞億僕僂儉偱偍尒偐偗偟偰埲棃偱偁偭偨偑丄婥偝偔側偍恖暱偼憡曄傢傜偢偱妝偟偄帪娫傪嫟
桳偡傞偙偲偑弌棃偨丅島媊偺崌娫崌娫偺僄僺僜乕僪偑偲偰傕柺敀偐偭偨丅
丂椺偊偽丄Wikipedia偱偼丄Shafarevich偑彫暯師尦傪柤晅偗偨偙偲偵側偭偰偄傞偑丄偦傟偼岆
傝偱丄杮摉偼丄彫暯愭惗偐傜桿傢傟偰擖偭偨媔拑揦偱斞崅愭惗偑彫暯師尦偲柦柤偟偨偄偲
怽偟弌偰丄俇侽侽墌偺働乕僉僙僢僩偱椆夝偟偰傕傜偭偨偲偐丏丏丏丅斞崅愭惗偺偍榖傪巉偭偰偄傞
偲丄戙悢婔壗妛偺戝屼強偱偁傞丄彫暯朚旻丄Shafarevich丄Hartshorne丄丒丒丒偺彂愋偐傜庴偗
傞報徾偲偼傑偨堘偭偰丄偲偰傕恖娫枴偁傆傟傞恖暱偑偆偐偑偄抦傟偨丅
丂偦偺拞偱丄嶨択偱偼偁偭偨偑丄乽侾/俆偺俈恑朄揥奐偼擛壗丠乿偲偄偆偙偲偑榖戣偵側偭偨丅
巹偼丄摢偺拞偱丄忋婰偺傛偆偵丄侾/俆亖侽丏俀傪弴師俈攞偟偰惍悢晹暘傪偮側偘偰丄
丂侽丏侾俀俆係侾俀俆係丒丒丒丒
傪摼偨偑丄斞崅愭惗偼師偺傛偆側暿夝傪徯夘偝傟偨丅
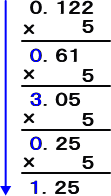
侾偼俆偱妱傟側偄偐傜侽偑偨偪丄侽傪曗偭偰侾侽乮俈恑悢乯偲偡傞丅偙傟偼廫恑朄偱俈偱丄俆偱妱傞
偲侾偑偨偪俀梋傞丅
俀侽乮廫恑朄偱侾係乯偲偟偰俆偱妱傞偲俀偑偨偪係梋傞丅
係侽乮廫恑朄偱俀俉乯偲偟偰俆偱妱傞偲俆偑偨偪俁梋傞丅
俁侽乮廫恑朄偱俀侾乯偲偟偰俆偱妱傞偲係偑偨偪侾梋傞丅埲壓丄孞傝曉偟偲側傞丅
丂廬偭偰丄侾/俆偺俈恑朄揥奐偼丄丂侽丏侾俀俆係侾俀俆係丒丒丒丒
丂偝傜偵丄斞崅愭惗偼丄師偺傛偆側惈幙傕柺敀偄偲徯夘偝傟偨丅
丂侾/俆偺俈恑朄揥奐偺弞娐愡丂侾俀俆係丂傪俀偲俆偺娫偱俀偮偺悢侾俀偲俆係偵暘偗懌偟偰傒傞偲丄
丂丂侾俀亄俆係亖俇俇
偲側傞丅偙偙偱丄俇偼丄俇亖俈亅侾偐傜偔傞丅廫恑朄揥奐偱丄侾/俈偺弞娐愡偼丄侾係俀俉俆俈丂偱偁
傞偑丄偙傟傕丄丂侾係俀亄俉俆俈亖俋俋俋丂乮俋亖侾侽亅侾乯丂偲側傝丄摨偠尰徾偱偁傞丅
乮仺丂嶲峫丗乽弞娐彫悢偺晄巚媍乿乯
乮僐儊儞僩乯丂寁嶼偺娙柧偝偐傜尵偆偲丄俈傪妡偗偨曽偑暘偐傝傗偡偄偲巚偆偑丄斞崅愭惗偺曽
丂丂丂丂丂丂朄傕桳傝偐側偲巚偆丅
丂倫恑朄揥奐偼丄惍悢偵懳偟偰丄偦偺奺埵偺悢偼堦堄偵掕傑傞偑丄彫悢偺応崌偼丄俀捠傝偵
昞偝傟傞応崌偑偁傞丅
丂偨偲偊偽丄廫恑朄揥奐偱丄桳尷彫悢偺 侽丏俆 偲偄偆悢偼丄
丂丂侽丏俆侽侽侽侽侽侽侽侽丒丒丒丒丒丒丂丂傑偨偼丂丂侽丏係俋俋俋俋俋俋俋丒丒丒丒丒丒
偲俀捠傝偵昞偝傟傞丅偟偐偟丄偦偺抣偼丄偲傕偵摍偟偄丅
椺丂崱丄偁傞惍悢偺俁恑朄揥奐偑俀捠傝偵昞偣偨傕偺偲偡傞丅偡側傢偪丄
丂倎丒俁2亄倐丒俁亄們 亖 倓丒俁2亄倕丒俁亄倖丂乮扐偟丄倎丄倐丄們丄倓丄倕丄倖 偼侽丆侾丆俀 偺壗傟偐偺悢乯
丂偙偺偲偒丄們亅倖 亖俋乮倓亅倎乯亄俁乮倕亅倐乯丂傛傝丄丂們亅倖 偼俁偺攞悢偱偁傞偑丄
丂亅俀亙們亅倖 亙俀丂側偺偱丄們亅倖 亖侽丂偲側傞丅丂傛偭偰丄們亖倖
丂摨條偵偟偰丄倐亅倕 亖俁乮倓亅倎乯丂傛傝丄倐亖倕丂偡側傢偪丄倓亖倎丂偲側傞丅
丂埲忋偲摨條偵偟偰丄惍悢偺倫恑朄揥奐偺曽朄偼丄堦堄揑偱偁傞偙偲偑暘偐傞丅
丂傑偨丄倫恑朄偺埵庢傝婰悢朄偵偍偄偰丄嵟彫偺 値 寘偺悢偼丄侾侽侽丒丒丒侽(p)亖倫値-1
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂0 偑 値-1 屄
丂丂丂丂 倫恑朄偺埵庢傝婰悢朄偵偍偄偰丄嵟戝偺 値 寘偺悢偼丄qqq丒丒丒q(p)亖倫値亅侾
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂q=p-1 偑 値 屄
丂偟偨偑偭偰丄倫恑朄偺埵庢傝婰悢朄偵偍偄偰丄値 寘偺悢偼丄
丂丂倫値-1乮倫亅侾乯 屄
偁傞丅乮偨偩偟丄侽 偼丄偙偺応崌偺寁嶼偐傜偼彍奜偝傟偰偄傞丅乯
乮嶲峫暥專丗媨尨丂斏丂挊丂丂惍悢丂丂乮壢妛怴嫽幮儌僲僌儔僼乯乯
乮捛婰乯丂暯惉俀侽擭俋寧俈擔晅偗
丂俀恑朄偱昞偝傟偨惍悢傪彫偝偄弴偵暲傋丄
丂侾丂丄侾侽丂丄侾侾丂丄侾侽侽丂丄侾侽侾丂丄丒丒丒丒丒丒
偲偟偨偲偒丄弶傔偺曽偐傜悢偊偰侾俇斣栚偺悢偼壗偐偲栤傢傟傟偽丄
丂丂
偐傜丄捈偪偵丄丂侾侽侽侽侽丂偱偁傞偙偲偑暘偐傞丅懄偪丄扨偵丄乽侾俇乿偲偄偆廫恑朄偺惍悢傪
俀恑朄偺惍悢偵捈偣偽傛偄丅
丂偲偙傠偑丄栤戣偺弌偟曽傪曄偊傞偲丄夆慠擄偟偔姶偠傜傟傞丅
丂侽丂丄侾丂丄俀丂偺俁屄偺悢帤偺傒傪偄偔偮偐巊偭偰墶偵暲傋惍悢傪嶌傞丅偨偩偟丄愭摢偐
傜暲傇乽侽乿偼柍帇偟偰峫偊傞傕偺偲偡傞丅
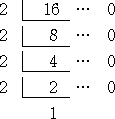
丂偙偺偲偒丄丂侾丄俀丄丒丒丒丒丂偲暲傫偱偄傞悢楍偱丄悢帤偺乽侾乿偑巊傢傟偰偄傞偲偒偼丄偦偺
惍悢偼旘偽偟偰悢偊傞傕偺偲偡傞丅嵟弶偐傜悢偊偰侾俇斣栚偺惍悢偼壗偩傠偆偐丠
丂偙傟偼丄侽 偲 俀 偺傒傪巊偭偰弌棃傞惍悢傪彫偝偄弴偵暲傋偰丄
丂俀丂丄俀侽丂丄俀俀丂丄俀侽侽丂丄俀侽俀丂丄俀俀侽丂丄俀俀俀丂丄丂丒丒丒丒丒
偲偟偨偲偒丄嵟弶偐傜悢偊偰侾俇斣栚偺惍悢傪栤偆栤戣偱偁傞丅
丂忋婰偺悢楍偼丄侽 偲 侾 偺傒傪巊偭偰弌棃傞俀恑朄偺惍悢楍
丂侾丂丄侾侽丂丄侾侾丂丄侾侽侽丂丄侾侽侾丂丄侾侾侽丂丄侾侾侾丂丄丂丒丒丒丒丒
偵懳墳偟丄廫恑朄偵捈偣偽丄
丂侾丂丄俀丂丄俁丂丄係丂丄俆丂丄俇丂丄俈丂丄丂丒丒丒丒丒
偲偄偆偙偲偱偁傞丅
丂侾俇 傪俀恑朄偵捈偣偽丄丂侾侽侽侽侽丂偱偁傞偺偱丄媮傔傞惍悢偼丄丂俀侽侽侽侽丂偲側傞丅
丂嵟嬤丄偙傫側榖戣偑丄暯惉俀侽擭俉寧俀係擔丄乽擬寣両暯惉嫵堢妛堾乿乮僼僕僥儗價宯乯偱庢
傝忋偘傜傟偨丅
丂侾丄俀丄丒丒丒丒丂偲暲傫偱偄傞悢楍偱丄悢帤偺乽係乿丄乽俋乿偑巊傢傟偰偄傞偲偒偼丄
偦偺惍悢偼旘偽偟偰悢偊傞傕偺偲偡傞丅
丂嵟弶偐傜悢偊偰係侽侽斣栚偺惍悢偼壗偩傠偆偐丠
丂偙偺栤戣傪峫偊傞偨傔偵丄壓昞偺傛偆側廫恑朄偺悢帤偲俉恑朄偺悢帤偺懳墳傪峫偊傞丅