
問達に邂逅しました。(平成23年11月10日付け)
無論、題意は誰にも容易に把握出来、接線を求めて、高校生のように解決可能ですが、我
々は、接超平面(線)Tと云えば、点∈P2(K)*で、以降、双対多様体を考えずにはいられない
体質になっている。(一例)
問達の限りなく易しい2次曲線C1、C2 について視ると、全てが氷解すべく努めました。そこ
までやるかと呆れ顔も浮かびますが、顔色を伺いつつそこまでやりました。
(数秒間、参考図を凝視願います)
C1、C2 の双対多様体 C1*、C2* を求め、その交点 p* を求め、有理写像Φj: Cj--->Cj*
の p=Φj(p*) なる p を求め、全てが氷解する図達を描きました。間違いが無いか確認をお
願い致します。(双対曲線を求める際、双方とも2次なので、飯高先生の手法が使えます。)
英文の a 以降も、双対多様体を求める発想で、全てが氷解する図付きの解説を為して
損は在りません。是非具現を。
次は所蔵しておりませんが、上の a、b、.... の手頃な実例になるでありましょう。
「計算数学」「Computer Mathematics」「コンピュータグラフィックス特論Ⅱ (大学院講義)」
その他
問達の a 以降 b.... も双対多様体を求める発想で、全てが氷解する図付きの解説を本
当に為して損は在りません。 是非具現を。ご感想を記載願います。
3次以上でも、参考図の2次の如く。
「共通理解 共通認識」について
共通接線(接超平面)問題に対峙する際、我々は接超平面(線)Tと云えば、点∈P2(K)*な
る共通認識を醸成中です。以降、双対多様体を考えずにはいられない体質になっている。
(→ 一例)
デカルトの正葉線(folium of Descartes)なる代数曲線C1:K[X,Y]/(X3-3XY+Y3)と他の代
数曲線C2の組み合わせで共通接線(接超平面)問題に対峙したい。(→ 例)
太赤線C1と細赤線C2には共通接線(接超平面)が存在するのは「火を見るよりも明らか」
ですが、
(1) それぞれの双対曲線 Cj* を求め、(C2はn=2次曲線なので飯高先生の発想で願います)
(2) C1*∩C2* を求めることを為して、
(3) 共通接線(接超平面)を求めて下さい。
資料の(b)を双対曲線 C1*を求めたので、C1*の方から解決して遊んで下さい。
大阪府立四條畷高等学校の先生が公開されておられる「2つの円の共通接線」に漂着致
しました(別解達も丁寧に述べておられます。2円を2楕円にかえた時、破綻する発想等コメ
ントが欲しいところです)
これを、C1*∩C2* を求める発想でどうぞ。
(射影幾何の講義を受講されて、もうご卒業のみなさん向けの愉しい発想例でもあります)
(1) n=2次曲線C1、C2 の双対曲線を求めると、
C1*:x2 + y2 - 1 = 0(不変) 、C2*: 12x2 + 8x - 4y2 + 1 = 0(円に非ず!)
となることを、飯高先生の発想に倣い、(先ず、射影曲線化し)必ず導出して下さい。
(2) 交点を求めると、
{-3/4 ,-(√7)/4} 、 {-3/4 , (√7)/4} 、{1/4, -(√15)/4} 、{1/4, (√15)/4}
これを、 Ax+By+1=0 の(A,B)に代入し、4本の接線を瞬時に得る。
(3) このC1*∩C2*を求める発想が初体験の方が高校数学指導者に存在するでしょう。なら
ば、興味津々で「dual variety」に深入りなさり、感激を生徒に熱く語られ、その熱さに感
化し、生徒が數學研究者を目指すに違いない。
高校生向けの次の問いを大學生と共に考察したい。
(1) C1:13x2 - 14yx + 5y2 - 16=0 、C2:13x2 - 14yx + 64x + 5y2 - 64y + 192=0
の主軸問題を解き、二曲線を図示せよ。
(2) 両曲線に接する直線達を求めよ。
なる問いの(2)を、大學生が瞬時に、次のように解いた。
二曲線 5x2 + 14yx + 13y2 - 1 = 0 、4x2 - 40yx - 8x - 92y2 - 24y - 1 =0
の交点を求め、Ax+By+1=0 の (A,B) に代入すれよい。
例えば、 1/16・(-2 + 3(√15))x + 1/16・(2 - (√15))y + 1=0 が、その答えの一つ。
お願いの重要な質問:大學生が二曲線の背景を隠匿し書き下しているが、その大學生の
二曲線の導出過程を省かず記して下さい。その際、資料1、資料2は絶対に見ないで、上
の質問の解答をお願い致します。
他の両曲線に接する直線達を求め、C1、C2 と大學生が云う二曲線と共に全てを図示願
います。
大學生に、どうやって其の二曲線の交点を求めるのかをたずねたら、次のイデアルは等
しいので、易しいI2 のZERO点を求めればよいと即答した。
I1=<5x2 + 14yx + 13y2 - 1 , 4x2 - 40yx - 8x - 92y2 - 24y - 1>
I2=<-(256y2 - 64y - 11)・(256y2 + 192y + 29) , -8192y3 - 2816y2 + 1064y - 168x + 251>
お願いの更に重要な質問:またしても『瓢箪から駒』の如く大學生は、 I1=I2 と云う。
I2の導出過程を省かず記し、I1=I2 も証明願います。
大學生はどの質問にも瞬時に応え去りゆくので、追いかけて問うた。何を専攻したら、そ
のような明解極まる発想達が得られるのですか?大學生は____専攻と答え____教授に師事
すればよいと端的に答え去ってしまった。
大阪府立四條畷高等学校の先生が公開されておられる「2つの円の共通接線」に漂着
致しました(別解達も丁寧に述べておられます)と申しました。
(平成23年11月11日付け)
更に、「分母の有理化」の(2)を路上で出会った大學生に教えを乞うたところ何と瞬時に、
分母のQ上の最小多項式を求めると、
f[x]=x8 - 64x6 - 96x5 + 808x4 + 1152x3 - 2304x2 - 1152x + 144 で
Q[x]/f[x]・Q[x]
|
Q
を考慮し、有理化は、 (1/144)・(-x7 + 64x5 + 96x4 - 808x3 -1152x2 + 2304x + 1152)
に問題の分母を代入すれば、答えを得る。
(1/6)・(6 - 6(√2) + 5(√3) + 3(√5) - 2(√6) - 3(√10) + 2(√15) - (√30)
近頃の大學生は凄いと思わず漏らし、最小多項式は、どうやって求めるのですか?と尋
ねたら、多様な発想で叶うが、Sylvester matrixが強力な助っ人なので、是非頑張ってと立
ち去るので、追いかけて問うた。何を専攻したら、そのような明解極まる発想達が得られる
のですか?
大學生は、體育系のタイ____論専攻と答え、____教授に師事すればよいと端的に答え去っ
てしまった。
更に、追いかけて、続きの問題はなく、これ(分母の有理化をしたらこれで終わり)で、終
結なのですか?と問うたら、「東京大学前期文系(1990)」の模倣をするから、解いてご覧
とさりげなく教唆し立ち去る。
上の f[x]=x8 - 64x6 - 96x5 + 808x4 + 1152x3 - 2304x2 - 1152x + 144 を例にして、
f[x]=0 の解を α とすると、他の解達は全て7次以下の α の多項式で表現されるのは自
明だが、具現してご覧と呟いて立ち去った。
どうしても具現したく頑張って得たことを吐露します。α以外の解達が體育系ではなさそう
な大學生の云う通り、
{ -α7/364-47α6/8736+283α5/1456+2371α4/4368-236α3/91-1961α2/312+2871α/364+2577/364,
-17α7/17472+α6/1092+499α5/8736+125α4/4368-2465α3/4368+16α2/39+953α/728-1641/364,
-5α7/1344-α6/224 +169α5/672+4α4/7-1061α3/336-47α2/8+459α/56+18/7,
-α7/17472+9α6/1456-67α5/8736-515α4/1456-145α3/4368+209α2/52+495α/728-1863/364,
α7/1092+23α6/4368-283α5/4368-835α4/2184+145α3/273+563α2/156+135α/364-111/182,
7α7/2496-α6/1248-233α5/1248-59α4/312+1639α3/624+707α2/312-995α/104-51/26,
11α7/2912-5α6/2912-355α5/1456-317α4/1456+2323α3/728+193α2/104-3595α/364 +927/364}
となりました。改めて、近頃の大學生は凄いと驚嘆せずにはいられませんでした。
お願いの重要な質問:大學生に示唆されて唸りながら、「東京大学前期文系(1990)」の
(2)を凝視しながら、私が導出した多項式を
σ1[α]= -α7/364-47α6/8736+283α5/1456+2371α4/4368-236α3/91-1961α2/312+2871α/364+2577/364,
等とするとき、九九の表:σi・σjを完成し、ガロア群を明記願います。
世界の高校数学指導者が分母の有理化を滔々と語る姿が目に浮かびますが、何やら変
でない方向に彷徨しそうです。大學生はどの質問にも瞬時に応え去りゆくので、更に追いか
けて問うた。何を専攻したら、そのような明解極まる発想達が得られるのですか?
大學生は____専攻と答え、(有理化すれば終わりでは毛頭なく)梅村 浩多元数理科学専攻
教授に師事すればよいと端的に答え去ってしまった。
上の1箇所の空欄を埋めて子細を記して下さい。
共通接線(接超平面)問題に対峙する際、我々は接超平面(線)Tと云えば、点∈P2(K)*な
る共通認識を醸成中です。以降、双対多様体を考えずにはいられない体質になっている。
(→ 一例)
代数曲線 C1:K[X,Y]/<13X2 - 7YX + 37Y2 - 25>、
代数曲線 C2:K[X,Y]/< -18X2 - 48YX - 20X - 32Y2 + 15Y + 25>
の共通接線(接超平面)問題に、双対多様体を求め、対峙したい。
(0) C1とC2 の主軸問題を きちんと解き、共通接線(接超平面)が存在するとフリーハンド
で図示して下さい。
例えば、-18X2 - 48YX - 20X - 32Y2 + 15Y + 25=0 の正体は「Wolfram|Alpha」にお願い
し叶うが、次の共通接線を求める発想はエレガントでしょうか?
(1) それぞれの双対曲線 Cj* を求め(その名称を云い)、
(C1、C2共、n=2次曲線なので飯高先生の発想で願います)
(2) C1*∩C2* を求めることを為して、
(3) 共通接線 Tpj(Cj)(接超平面)を求めて、 C1、C2、C1*、C2*、Tpj(Cj)を同一 R2に全て図
示願います。(無論、C1*、C2*の主軸問題を きちんと解き)
(4) 双対化したとき、曲線の名称は変るケースがありますが、次数は今回は不変なのは自
明です。何故、自明か解説願います。
高校生も、ちょっと分母の有理化を黒板で指導されたなら、誰でも、例えば、
先生「1/(41/3+21/3-1)のときは、どうするのですか?」と質問が可能ですが...。
(平成23年度11月12日付け)
先生を困らせまいと配慮しているのか、入試にでないので封印せよとか怒られることを想
定し、要領よく大人の態度を身につけ、だまっている かでしょう。
分母の有理化に郷愁を覚える方が世界に存在するようです。
その方々なら、質問者に怒声を浴びせることなく、例えば、
1/( 21/2 + 31/3 + 51/5 )
の分母の有理化を問うたら、真摯に取り組まれるにちがいない。
上の路上で出会った大學生に教えを乞うたところ、何と瞬時に、「分母のQ上の最小多項
式(当然 2*3*5=___次)を求める」とに倣い、真に求めて終わりとせず、且つ、「東京大学前期
文系(1990)」のような問を自ら作成し(入試作成者のように背景を隠匿せず)、ガロア群を
定めるにちがいない。
以上の具現をお願い致します(共軛概念が絡みます。為した後、無駄であったなら子細を
記載願います)。
中高生や指導者や世界の郷愁諸氏とともに、この分母の有理化なる知悉の概念が、「ガ
ロア理論」の入門のチャンスとなりえることは、指導者が隠匿すべきではないと考えますが
如何?(有理化絡みの定理は、このpdf の何ページに在りますか?)
「1/( (√2)+31/3+51/5) の分母の有理化をせよ。」なる問を路上で出会った大學生に教え
を乞うたところ、何と瞬時に、「分母のQ上の最小多項式(当然 2*3*5=___次)m(x)を求める」
とに倣い、真に求め、これから、すぱっと分母の有理化を為し終わりとせず云々(再掲です)。
(平成23年11月13日付け)
問題を觀て、中学生とその指導者、高校生とその指導者、大學生とその指導教授、 .....
(ジェネレーション・ギャップ(世代間断絶) generation gap) が皆無のあの有理化の問題)が
素朴過ぎて理解完了し、もう郷愁を覚えるのみのExample 達の背後に在る一理論を紫枠
に凝縮しました。紫枠の真意が捉えられないなら、捉えられるまで凝視願います。
あの體育系でなさそうな大學生が洩らした、体論に必ず、いの一番に証明されている定理
を、例えば、「可換体論」の 41p。K[α]=K(α) と明記されていても、あまりの短文故、見逃し
て体論ご卒業の方が存在しそうです。今回は、最小多項式 m(x) なる片割れが主役です。
分母の有理化 (分子 25は、解決後付与しているので無視し)分母の 3-21/3 について、あ
の体論の最初に在る定理を、実例がなくても自分で実例込みで考察し、老若男女が知悉の
有理化を瞬時に為した大學生に倣い、
(1) 3-21/3 の最小多項式m(x)を多様な発想で求め、
(2) 求めた m(x) を用いて分母の有理化を為し、それで終わりとせず、模倣が叶わぬことを、
求めたm(x)の判別式を求め、Q上ではT大の模倣は破綻するが、Qの或る2次の拡大体 k
とすれば、求めた m(x)の解をαとすれば、他の解∈k[α] とk係数のαの3-1次の多項式
と具現されることは自明でも、必ず具現し、ガロア群の構造を群表を作成し記述願います。
英文の分母 (1) 3-21/3 を觀た刹那、言語圏を問わず、ああ云えばこう云うとだれでも容
易に設問できるでしょう。
(有理化で終わりではなく、T大の如き、考察も為すべきでありますが..)
1/(3-21/4) の有理化を願います。
1/(3-21/5) の有理化を願います。
1/(3-21/6) の有理化を願います。
1/(3-21/117) の有理化を(指導者様にも必ず具現)願います。
.
.
1/(3-21/2011) の有理化を願います。(無論、各分母のQ上の共軛達が絡みます)
黄色の模範解答を視ると、共軛絡みが強調された有理化です。飯高先生は「共軛」につい
て吐露されたことがあります。Is this confusing? とある、資料の9pを御覧いただき、お考え願
います。
そこの a+b・21/3+c・22/3 について、1/(a+b・21/3+c・22/3) で、a=7、b=5、c=3 として、だれ
でも経験済みの有理化を多様な発想で為して、体論を具体例を通して学ぶ契機にしたい。
発想イ:英文の高校で指導されたような方法で...。
発想ロ:体論を履修し以前に例示してくれた発想で...。
先ず、7+5・21/3 +3・22/3 の最小多項式 f[x] を求め、此処から手間をかける価値がある
ので、次の51p以降の諸定義、諸命題を讀み、
資料、「Euclidean algorithm」、「Greatest common divisor of two polynomials」
に倣い、今回は、x(を選んだ理由は_____)と最小多項式 f[x] について、一歩一歩手続きを
踏襲し、不定方程式 x・X+f[x]・Y=1の多項式解(X,Y)∈K[x]2 を求めて、
1/(7+5・21/3 +3・22/3)
の分母の有理化をして下さい。
分母の有理化で終わりとせず、模倣が叶わぬことを、求めた f[x] の判別式を求め、Q上
では、T大の模倣は破綻するが、Qの或る2次の拡大体 k とすれば、求めた f[x] の解を α
とすれば、他の解∈k[α] と k 係数のαの3-1次の多項式と具現されることは自明でも、必
ず具現し、ガロア群の構造を群表を作成し記述願います。
分母の有理化をすいすい為し、進学志望も叶って郷愁を覚えてはいるが、その後の人生
で、そもそも分母の有理化とは...と懐疑精神を発露することもなく、其れを契機に學べるガ
ロア理論を学ぶチャンスを逸してしまった方が世界に数多存在しそう..。中、高の有理化を
指導される方にも、そういう諸氏が数多存在しそう.......。
郷愁を覚える問3の分母の有理化の草色囲みの模範解答は、教育的配慮のなせる技で
すか?郷愁を覚える問4のガロア群の考察のHint:Consider α2-1 の模範解答は、教育的
配慮のなせる技ですか?どちらも導出過程こそ重要なのに、我々に答えを明記し解けと.....。
問4の Hint をなくせば、問いかけは初心者向けのよい問でしょう。答えが明記してあるの
で、為すべきことがなく寂しいので、例えば、資料の n=3次方程式について、問4の如き問
達を創り、特に、Hint のようなαの多項式を導出過程を隠匿せず記すことは、体論を学習
する學生にも適した問いかけだと思います。是非、具現して下さい。
n=3次方程式ではつまらないと云われる方々も存在するでしょう。ならば、n=3+1次の(7p
の21th March 1797 of C.F. Gauss’diary の4次の)f(X)=X4+52X3-26X2-12X+1 について、
問4の如き問達を創り、特に Hint のようなαの3次以下の多項式∈Q[α] を導出過程を隠
匿せず記すことは、体論を指導される教授にも、(無論、學生にも、高校教師にも)適した問
いかけだと思います。必ず具現して下さい。
問 3 についても、-1-21/3-41/3 の最小多項式 f(x) を求める発想で、1/(-1-21/3-41/3)
の分母の有理化をきちんと為し、このf(x)=0 について、問4の Hint のようなαの2次以下の
多項式多項式∈(今度はQ[α]でなく改めるべき体k を明記し、k[α])を求め、ガロア群の乗
積表を作成願います。
上の全てをきちんと為した後、郷愁を覚える問4のガロア群の考察のHint: Consider α2-1
の模範解答は教育的配慮のなせる技ですか?について、再考されたお考えを是非記載願い
ます。
英文の問達 3、4 を視て、模倣したくなりました。(平成23年11月14日付け)
α=5 - 1/22/3 - 1/21/3 - (√3) +I・(-(√3)/22/3+(√3)/21/3) とする。
(1) 1/α の懐かしい分母の有理化を多様な発想で行って下さい。
私が為すと分母は 5764∈Q になりました。その顛末をAとするとき、緑囲みの如く α・A=1
となることを確認願います。(ならなければ、なるまで)
(2) α=5 - 1/22/3 - 1/21/3 - (√3) +I・(-(√3)/22/3+(√3)/21/3) の最小多項式を f[x] とす
る。f[x]を多様な発想で求めて下さい。英文問4を模倣したく、Qにαを添加した体Q(α)も
考察したいが....。
Hint の模倣;σ[α]=-2α5/15+47α4/15 - 80α3/3 +1534α2/15 - 527α/3+1742/15 も
(3) f[x]=0 の解であることを多様な発想で示して下さい。(英文は導出過程を隠匿)
(4) f[x]=0 の全ての解を明記願います(無論、6個存在します)。
(5) σ[α]、σ[σ[α]] を求め、σk[α] (k=1、2、......)としても、英文の問 4の如く解達をわた
り尽くさぬ事態が生じることを確認して下さい。
(6) ガロア群が巡回群 Z/3Z なる、英文とは異なる事態に遭遇した.......(初体験ですか?)。さ
て、あなたならどうなさいますか?再度、資料の4 の Hint を凝視し........、
(3次方程式の解達を二つも明記しておいて、あとひとつは?なんて、いくら何でも愚弄して
いる問ではありませんか?)
f(x)=(x-α)(x-(α2-2))(x-(______))
資料に酷似の同じ低次の3次のとき、f(x)=(x-α)(x-(_______))(x-(______)) はなさいましたか?
同じ低次の3次のときのT大なら、f(x)=(x-α)(x-(_______))(x-(______)) はなさいましたか?
我々が、(2)以降問題にしているのは、あと 6-2 は?で、
f(x)=(x-α)(x-(5 - 1/22/3 - 1/21/3 - (√3) +I・(-(√3)/22/3+(√3)/21/3)))・
(x-(______))(x-(______))(x-(______))(x-(______))
は如何です。matrix equation For example 8行8列・・・こんなのを觀た刹那、例えば、
1/(1+(√2)+31/3+51/4+71/5)
の分母の有理化もそうなさるの?是非、具現願います。
体論を履修された、路上で出会った大學生に教えを乞うたところ、何と瞬時に、「分母のQ
上の最小多項式 m(x)(当然_____次)を求めると 叶う」に倣うて下さい。
資料で、まだ終わりではなく、これから本腰を入れ、関連質問
Q[X]/(m[X]・Q[X])
|
|
.
.
|
Q
も数多在るのですが、創作され解決なさって下さい。
先ず、多様な発想で途中経過を明記され、有理化を、1/(1+(√2)+31/3+51/4+71/5)=_______
(3の草色囲みのような天才の模範解答でない解答を願います)
どの発想が一番お気に入りですか?
(私は、紫囲みのK[X]/<m[X]>同型K(α)=K[α] がかなりお気に入りです)。
同値関係 剰余類環
演算が「剰余類に対する演算」としてきちんと定義されていることは、結果(和や積)として
求まる剰余類が代表元の取り方に依らないこと(these definitions are well-defined)、
「Quotient ring」は代数系を學ぶ誰もが洗礼を受ける。
その一例で、有理化を商環を構築後に述べるよい云い方に遭遇しました。商環の洗礼を
受ける高校生向けに表現します。
x3=2 を解きなさい。 x1=_____、x2=____、x3=_______
1/(x1+3)、1/(x2+3)、1/(x3+3) を、4で求めた代表=________を用いて、一気呵成に分母の有
理化をして、高校で指導された手法のExample を、1/(21/3+3) にかえて真似を!)と比較し、
体論を學ぶと有理化が透明になった感想を記しなさい。
1/(x12+x1+1)、1/(x22+x2+1)、1/(x32+x3+1) を、4の下=赤線で求めた代表=__________を用い
て、一気呵成に分母の有理化をして、高校で指導された手法と比較し、体論を學ぶと有理
化が透明になった感想を記しなさい。
もう一問、愉しんで下さい。
x4=7 を 解きなさい。 x1=_____、x2=____、x3=_______、x4=_______
1/(x12+x1+2011)、1/(x22+x2+2011)、1/(x32+x3+2011)、1/(x42+x4+2011) を、4の下=赤線を
模倣し、(x2+x+2011)∈Q[x]/(x4-7) 代表=____________を用いて、一気呵成に分母の有理化をし
て、高校で指導された手法と比較し、体論を學ぶと有理化が透明になった感想を記しなさい。
有理化を商環を構築後に述べるよい云い方に遭遇しました。(平成23年11月15日付け)
商環の洗礼を受ける高校生向けに表現します。
x3=2 を解きなさい。 x1=_____、x2=____、x3=_______.
1/(x1+3)、1/(x2+3)、1/(x3+3) を 4で求めた代表=________を用いて一気呵成に分母の有理化
を(再掲)直後に、商環等の概念習得させるのが何と無理と....を想起しました...あゝ....。
大阪府立四條畷高等学校の先生が公開されておられる「数と式 問 題」
積の組み合わせの工夫の因数分解 有名な対称式・交代式の因数分解
分母の有理化 付録(an-bn の公式)
の(1)の分母の有理化を模範解答(別解?)とは異なる発想で(商環を全面に出した発想で解
きたい。
(√2)+(√3)+(√5) の最小多項式 f[x] を多様な発想で求め、商環の洗礼を受ける高校生
向けに表現します。
f[x]=0 を解きなさい。 x1=_____、x2=____、x3=_______、......、x8=_________.
1/x1、1/x2、1/x3、.....、1/x8 を、4 の下=赤線を模倣し、x∈Q[x]/(f[x]) 代表=_______を自ら
求め、其れを用いて一気呵成に分母の有理化を。問題の 4 や東大(背景を隠匿)の模倣を
致します。(東大の出題教授よりは、背景を明記します。)
f[x]=0 の解をαとするとき、他の解は、資料を真似て有理式表現の方でなく、7次以下の多
項式表現を試みた。(疲労困憊しました)一部掲載します。
-α、 59α/6 - 95α3/18+97α5/144 -5α7/28
8つのうち、3つも提示しました。間違いがないことを証明して、残りの5つを是非求めてくだ
さい。
8次方程式 f[x]=0 のガロア群を決定して下さい。(有理化など誰でも知悉の概念からガロ
ア群へ)
今まで、日々多くの問題を提示してまいりましたが、新たな問題を真剣に提示します。
上で貴方が決定した8次方程式 f[x]=0 のガロア群は可解群であることを証明して下さい。
(8次方程式 f[x]=0 が可解であったから自明なんて云わないで!)
有理化の有理化なる所以を述べよ、と云いましたが、明らか過ぎて不要です。可解群の可
解群なる所以を述べよ、は全然明らかでないので是非願います。)
可解群の可解群なる所以を述べた學生諸氏、更に、f[x]=0 の解をαとするとき、他の解
は資料を真似て有理式表現の方でなく7次以下の多項式表現を試みた。一部掲載します。
-α 、59α/6 - 95α3/18+97α5/144 -5α7/28 、・・・
間違いがないことを証明してください。残りを是非求めてください。8次方程式 f[x]=0 のガロ
ア群を決定して下さい。即座に為さずにはいられない筈で具現の証を残される(無論群表も)。
上智大学の有理化せよなる問いかけ自体が既視感が在り過ぎ解く意義すら消失でしょう。
しかし、問いかけ方が重要だと思いませんか?(この中では、7が一番優れている設問)
英文の2問の商環(実は体) Q[x]/<f[x]> での設問なら、為す意義が明確で誰でも學びた
くなる筈。
草色囲みも a、b、c、d∈Q は明記し、左辺を一瞥すれば、Qに堕ちることを説明させ、計
算などさせない方が学べる。計算した學生は、「これって覚えなければ」と、そうする輩も輩
出しそう...。
(右辺のみを与え、Q上既約であることを証明させ、Q(
すのもよい)
(1) 此処の全ての問を、英文の赤囲み、紫囲みの視座で解いて下さい。(と高校生や体論を
學習しはじめた人たちに勧められると、有理化せよではフンであった態度が豹変し、対峙
の様変わりが好ましいでしょう)
(2) 以前からの資料達は中学、高校、数学教員の(自主)研修用の資料としても英文の赤囲
み、紫囲みの視座で、Q[x]/<f[x]> を考察してるんだと意義が見いだせ、問いかけ方も教
材研究のひとつとして取り組み甲斐があるでしょう。
問題の Symplify の 1/(1+41/3) については、
(3) 分母の最小多項式 f[x]を求めて下さい。無論低次です。具体的に、f[x]=0 の解を明記し
て、 1+41/3、________、_________。次を考察願います。
(4) α が f[x]=0 の解なら、もうひとつの解は、
σ[α]=1-1/(2・22/3)-I・
と 、k[α] (Q[x]では不可で、k=Q(____))の元として表されることを(導出して欲しいが...)確
認願います。
(5) 最後のもう一つは、σ[σ[α]]と予想されるでしょうが、確かめてT大との相違点を論じ
てください。
資料の真意をご理解いただけるまで、本当に n 回ご覧願います。
(平成23年11月16日付け)
Find 等お願いしている問題が少数あります。特に、商環絡みの問題に対峙され、真摯に
解答をお願いします。Abel の苦闘のおかげで、中高生及び指導者が、Abel 忖度可能なこ
とも在る...........。
問題について考える。(平成23年11月17日付け)
p(x)=2x2 + 21/5x + 21/5
p(x)=0 を「Wolfram|Alpha」に挿入しても、完璧に___∈Q[x]のZERO点とは答えてくれないで
しょうから、自分で多様な発想で、____∈Q[x]を導出して下さい。
(導出するまで下の問を視ないで下さい)
上の青囲みのような問に遭遇し、解いた経験がありますか?「ガロア理論」のどの定理の
具体例として考察すべき問題ですか?
模倣した問は、1/(1 + 21/5 +
設問を試みる中で産声をあげた問です。
p(x)=2x2 + 21/5x + 21/5
から得られた基礎体Q係数の方程式を、f[x]=0 とすると、(解く前の予想の次数ですが無論、
5*2=__次です)
α=1 + 21/5 +
の分母の有理化を為して下さい。
昔、指導された方法での有理化も試み、比較して遊んで下さい。
β=1 - 1/(2・24/5) +
も f[x]=0 の解であることを確かめ、1/βの分母の有理化も為して下さい。
以上で、f[x]=0 の解を2つ明記した。他の解(10-2個)を全て求め、Gauss平面上に綺麗
にZERO点が分布している様子を図示願います。
青囲みのような問を創るほど易しいことはありません。(解くのは、やり甲斐があります)
「代数的数」、「Algebraic number」等から、無限に作問叶うので、幾つか作問し、解いてと
お世話になっている諸師に逆質問して、人それぞれに発想が異なることを學んで下さい。
此処に、f[x]=x4 - 4x3 - 6x2 + 4x + 1 の円函数解が在る、と明記されていますが、それに
とらわれず資料の4の如く、Gal(Q[x]/(x4 - 4x3 - 6x2 + 4x + 1)Q[x],Q) を 求 め た い。
私が試みると、 -α3/2 + 3α2/2 + 9α/2 + 3/2 と なった。
自らガロア群の生成元を導出して下さい。(導出過程をも隠匿せず明記願います)私が導
出したのが誤りであれば、修正願います。その際、円函数絡みの導出法に倣うべきではな
いかも......。T大に倣うべきか模索を ......
(私が試みると、について:
f[-α3/2 + 3α2/2 + 9α/2 +3/2] の因数分解ほど易しいものはないので試みて。
1/16・(α4-4α3-6α2+4α+1)(α8-8α7-8α6+128α5+126α4-632α3-1400α2-1024α-239)
となったので、私が導出したガロア群の生成元はぜったい間違いがありません)
今の時代ですから、世界のガロア群探究者が皆此処を視ているので、ミスで済ませたくな
いので、念には念を入れております。恥ずかしいので、「求めたガロア群が可解群であること
を証明せよ」は封印します。
p(x)=2x2 + 21/5x + 21/5
p(x)=0 を「Wolfram|Alpha」に挿入しても、完璧に___∈Q[x]のZERO点とは答えてくれないで
しょうから、自分で多様な発想で、____∈Q[x]を導出して下さい。(導出するまで下の問を視
ないで下さい)上の青囲みのような問に遭遇し、解いた経験がありますか?と訊ね放浪した
ところ、共軛概念を用いた事例に邂逅しました。(平成23年11月18日付け)
この4つの式∈Q(
明を要求した方がよい)御丁寧な発想に倣い、上の青囲みや草色囲みを解くことを試みて
下さい。
此の種の問を、元のg[x]∈Q(α1,α2,.....,αm)[x] から係数を基礎体Qに落とし f(x)∈Q[x]
を得るので、「落とす問題」と命名したくなりました。「落とす問題」は誰でも軽く創作出来ます。
(恐らく人生で創作する問題の内、もっとも容易な創作問題でしょう) 10問試しに創作を!
一例: 49・71/3x7 + 36x6 + 5・52/3x5 + 4・22/3x4 + 3x3 + 22/3x2 + x + 19
解くのは、共軛絡みは理解していても煩雑すぎて容易ではない......。(試しに創作した問を
恩師に捧げて、本気で解いてくれるまで側を離れぬこと!)
上の諸問題、青色囲み、草色囲みや上記事例や創作された10問も統一的なもっとスカッ
とした発想で是非解いて下さい。「ガロア理論」の 88p Q2に類比の問題があり、次数6とあ
りますが、次数5じゃダメなんですかと云いたくなりませんか?
大阪教育大 問6.5を、先ず、指示通りに解いて下さい。(平成23年11月19日付け)
(3)(4)の指示に背き、次の発想でガロア群を考察願います。
α=
他の解が、 αの3次以下の多項式∈Q[α]で一意的に表現可能ことは自明でしょうが、多
様な発想で具現して下さい。
σ1[α]=α、σ2[α]=______、σ3[α]=______、σ4[α]=______
乗積 σj・σk 表を作成し、ガロア群を詳しく考察願います。無論、σjn(n=1、2、3、4)等も
本当に求め、このガロア群 {σj| j∈{1、2、3、4}}の考察と問6.5の指示の置換表現と何れが
お気に入りですか?
分母の有理化に郷愁(ノスタルジア)を覚え 為さずにはいられない方へ
1/(5/8 + α + α2 + α3 ) の分母の有理化を多様な発想で具現して下さい。
α=
Q(
f(x)が、α=
虚部に分け、イデアル I1=<x4 - 6y2x2 + 2x2 + y4 - 2y2 + 25,4yx3 - 4y3x + 4yx>の共通
実ZERO点を求めればよいことを確かめ、生成元を取り替え、
I2=<y(y2 - 3)(y2 + 2)(y4 - 2y2 + 25),-xy(y2 - 3)(y2 + 2),
y(5y6 - 14y4 + 133y2 -154x2 - 100),
15y8 - 42y6 + 322y4 - 146y2 - 77x4 - 154x2 - 1925>
の共通実ZERO点を求めればよいことを 証明 し、実際解いて下さい。
共通実ZERO点は全て、x2+y2=r2 上に在る。それを視て、一つをαとして、他をαの3次
以下の多項式∈Q[α]で表わせますか?
Example の25を無視した 1/(3-21/3) の分母の有理化を(5)での言い回しで行います。
(平成23年11月22日付け)
Q[3-21/3]は体なので、1/(3-21/3)∈Q[3-21/3]は自明。よって、1/(3-21/3)がα=(3-21/3)
の多項式で表されるのは自明だと悉皆の人が云う。
自明なら具現をお願いします、と云われても、為さぬ方が存在するかも....。それではいけ
ないので、或る発想で具現すると、α2/25 - 9α/25 + 27/25 となった。
その後、α=(3-21/3)を代入し計算すると、(9 + 3・21/3 + 22/3)/25 で答えと一致した。
この(5)のF[a] が体なので、1/a∈F[a]を具現可能で、赤と草色のアンダーラインは、実に
明解。(有理化について、此れ程有限次代数拡大体の文脈のなかで指導された経験が御
座いますか?)
【お願い:今後、分母の有理化を指導される方々も、aを添加した体F(a)=F[a]なる文脈を前
面に押し出して、1/aをaの多項式で具現を必ず為し、有理化のご指導願います】
(と、お願いしても、従来の指導法を止められない方が存在しそうで.....あゝ)
2問:赤のアンダーラインを必ず具現することにより、分母の有理化を為してください。更に、
次の数問についても、赤のアンダーラインを必ず具現することにより、分母の有理化を 為
してください。
その赤のアンダーラインの導出過程を隠匿せず、為した証を願います。
「Galois Group of Order 8」は真に傾聴に値するでしょう。
(K/Qが、2*2*2=8次拡大体では物足りないと感じ、すぐ次数をあげて、ガロア群を考察願い
ます )
Q((√2),(√3),(√5),(√7),(√11),(√13),(√17),(√19),(√23),(√29),(√31),
(√37),(√41),(√43),(√47),(√53),(√59),(√61),(√67),(√71),(√73),
(√79),(√83),(√89),(√97),(√101))
のガロア群も念頭におきつつ、知悉の次の分母の有理化をお願いします。
1/{2011+(√2)+(√3)+(√5)+(√7)+(√11)+(√13)+(√17)+(√19)+(√23)+(√29)+(√31)+
(√37)+(√41)+(√43)+(√47)+(√53)+(√59)+(√61)+(√67)+(√71)+(√73)+(√79)+
(√83)+(√89)+(√97)+(√101)}
赤のアンダーラインを必ず具現することにより、分母の有理化を為してください。
(5) を、a=(√2)+(√3)+(√5)+(√6)+(√10)+(√15)+(√30)、1/a の場合に具現したい。
(平成23年11月23日付け)
1/((√2)+(√3)+(√5)+(√6)+(√10)+(√15)+(√30))
=(a7 - 284a5 - 2416a4 - 4882a3 + 5152a2 + 8436a - 3632)/71
となることを多様な発想で証明願います。
大阪府立四條畷高等学校の先生が公開されておられる「分母の有理化」にも倣い、上の
事実を確認願います。上では、Q[(√2)+(√3)+(√5)+(√6)+(√10)+(√15)+(√30)]が実は体
なる事実しか用いていないが、「Galois Group of Order 8」は拡大体Q[(√2),(√3),(√5)]/Q
を詳しく考察していて、「可換体論」の74pの問題の詳しい解答を与えています。
Q[(√2),(√3),(√5)]=Q((√2)+(√3)+(√5))は想定外ではないでしょう。事実なら証明して
下さい。
上の問題を考察する際、 f[x]=x8 - 40x6 + 352x4 - 960x2 + 576 が必要となる筈です。
東大の模倣をしたい。
n=3<8次方程式 f[x]=0 の解をαとするとき、他の解がαの7次以下の多項式で一意的に
表現可能は想定外ではないでしょう。
例えば、σ1[α]=α、σ2[α]=-α、σ3[α]=-5α7/288+97α5/144-95α3/18+59α/6
となるでしょう。あと8-3個のσj[α] を求めて群表σj・σi を作成し、「Galois Group of Order 8」
の Find Aut[Q[(√2),(√3),(√5)]/Q] の説明と比較検討を願います。
「ガロア理論」の29p 近傍の理論とも照合しつつ、共軛に郷愁を覚える方数多在り。
f[x]=0 のひとつの解は、α=(√2)+(√3)+(√5) です。したがって、当然Q上共軛な元、例え
ば、β=(√2)-(√3)+(√5) も解です。βをαの7次以下の多項式で表現可能は自明で済ま
せず具現して下さい。他のQ上共軛な元達を全て求めて下さい。
各共軛元 xj について、その逆元が xj の多項式で表されることは自明と片付けず具現願
います。ガロア理論で 「必須」な 『変わらざるもの』概念が目につきます。
参考資料を視つつ、赤囲みをじっと見る。(平成23年11月24日付け)
「Polynomials 著者: Victor V. Prasolov」のabelian equationsをじっと見る。
「日々のつれづれ」・・・ある任意次数の方程式の根は、すべての根がそれらのうちのひとつ
を用いて有理的に表示されるという様式で相互に結ばれているとしよ
う。
じっと見たことを具現したい。
(1) 最初の体 Q(√(2+
「X^4-4*X^2+2」を「Wolfram|Alpha」に挿入し、体がQの正規拡大体を知る。他の解を、
√(2+
√(2+√(2+
Gal[Q[X]/<f[X]>/Q] を考察したい。
f[x]=0 の解をαとし、東大の模倣をし(と云いながら、本当のところは逆に東大(入試問題作成教授氏)
が模倣したことを疑う人は世の中に存在しない)
(1) 他の解達は、
{α,-α, 3α-α3,α3-3α,-α5+5α3-5α,α5-5α3+5α,-α7+7α5-14α3+7α,α7-7α5+14α3-7α}
で尽くされることを導出してください。上から順に、σj[α]と定義するとき、
(2) 全てのσj[σk[α]]について乗積表を完成して下さい。そして、再三再四凝視し感じる
ことを述べて下さい。
念のため、√(2+√(2+
ながら、Q上の√(2+√(2+
各σj について、σjn[α]=αなる最小のnを求めて下さい。
(3) Q[X]/<f[X]>
|
|
Q
の中間体達を 求めて下さい。
「Polynomials 著者: Victor V. Prasolov」は、所蔵しておらず、覗き見のみですが、非常に
気になります!具現例達が欲しい。
次の α について、最小多項式を求め、Q(α)で因数分解願います。Exercise1を試みて
下さい。(平成23年11月25日付け)
(1) α=√(2 +
(4) α=√(17 + √17) (5) α=√(2011 + √2011)
熊本大学「数学演習I」の1の(2)に遭遇した。(平成23年11月28日付け)
(3x2 + 4yx + 8zx + 5y2 - 2yz - 1=0 の主軸問題を解き、その代数曲面Sも描けが良いか
も。更に、その双対曲面 S* も求め、主軸問題を解き、S* を描けなら更に良問かも...。
大學生で、双対曲面 S* 初体験で深みに嵌る方続出かも...)
解答の「f[x]=0、D[f[x],x]=0 が共通解を持たぬ」について、他の発想達で論じて下さい。
この f[x]=x3 - 8x2 - 6x + 99 に ついて、参考資料の4の如き考察を お願い致します。
但し、修正箇所在り。Gal(K,k) k=Q(√D) (b) のHint consider ________を願います。
Hint: (164(√2981)α2 - 469(√2981)α - 8943α - 2904√2981 + 隠匿の項)/17886
(一部隠匿しました) Exercise 19.6 をも気にし、具現しながら...。
紫、草色枠の問題は多様な発想で解けるが、(平成23年11月29日付け)
(0) 黒色枠の最小多項式を求める問題を先ず解いて下さい。(4行4列となり)
「Cayley-Hamilton theorem」を使うでしょう。「Minimalpolynom」にも其の発想が在ります。
その最小多項式を求める発想で、
(1) 紫枠の b=a3 - a2 + a + 1 のQ上の最小多項式f(x)を求め、b-1を求めて下さい。
(共軛に郷愁を覚える方数多在り)
b のQ上の共軛元を求めることは、易しい(f[x]=0 を解けばよい)ので求め、分母・分子に
共軛元達を掛けるいつもの発想で再び、b-1 を求めて下さい。
その最小多項式を求める発想で、
(2) 草色枠の b=a3 -1 のQ上の最小多項式f(x)を求め、b-1 を求めて下さい。
(共軛に郷愁を覚える方数多在り)
b のQ上の共軛元を求めることは、易しい(f[x]=0 を解けばよい)ので求め、分母・分子に
共軛元達を掛けるいつもの発想で再び、b-1 を求めて下さい。
紫枠や草色枠は、分母の有理化なので、高校で指導された手法で、1/b の分母の有理
化を試みて下さい。
高校で指導されておられる方曰く、タイプ1・タイプ2で、あとはパズルのようなものと(→「分
母の有理化」)高校で指導されておられる方のご意見です。
(5)を多様な発想(体論を体験し)で解き、パズルでは断じてないことを体験し、体を揺すっ
て解く喜びを体で表現して下さい。
論理学的には、複数解が矛盾してしまう「ジレンマ」、論理的に解けそうでいて不思議と解
答が見つからない「パラドックス」に対して、唯一解が出せるものを「パズル」と定義すること
ができる。しかし一般的にパズルといえば、娯楽として提供される問題や謎全般を指すこと
が多い。学問的な命題に対して娯楽の要素が強いものがパズル、または知識に頼るものが
クイズで思考で解くものがパズル、など多くの意見がある(ちなみに20世紀前半には、クロス
ワードパズルの様にクイズとパズルの中間と思われる問題を「クイズル (Quizzle)」という造語
で呼んだこともある)。
「Minimalpolynom」に、「Endomorphismus」を用いて最小多項式を求める発想が在ります。
(平成23年11月29日付け)
その最小多項式を求める 発想で、黄色枠を我々は解いた。
(0) 先ず、紫枠と8を上の「Endomorphismus」を用いて最小多項式を求める発想で解いて下
さい。
(1) ▼高校生は、2つの囲みを解いた経験から紫枠を視た刹那、その3次方程式が東大と
全く同じなので、f[x]=0 の3つの解の多項式表現を、
σ1[α]=α、σ2[α]=-α2 +隠匿1・α+隠匿2、σ3[α]=σ2[σ2[α]]
を求め、(2ヶ所隠匿しました) (1+t+t2)/4 のtにσj[α]を代入し、其れを解とする 3次方程
式をつくり、α3-3α2+1=0 を用いて、x3 - 9x2/4 + 9x/8 + 隠匿 = 0 を得る筈。具現して
下さい。
(2) 紫枠を視た大學生は終結式を用いる発想で瞬時に、x3 - 9x2/4 + 9x/8 + 隠匿 = 0 を
得る筈。具現して下さい。
この大學生の発想を視た高校生は、はやく大人になりたいと切望するに違いない。
(3) もっと大人の、例えば、高校生の指導者や大學院生の指導者は更に大學生を超えた
多様な発想達で紫枠の最小多項式を求めるでしょう。必ず具現をお願い致します。
宮西先生は、終結式について、(増田佳代・宮西正宜 両先生が)丁寧な解説をされてお
られます。(増田佳代 関西学院大学理工学部数理科学科教授)
問;8 についても、(1)(2)の発想達で解決願います。(→ 参考:「判別式と終結式」)
問;紫枠と8 の判別式達を求め、ガロア群達の相違点を論じて下さい。
「判別式と終結式」に幾つか代数曲線 Cj が例示されている。各曲線 Cjについて、その双
対曲線 Cj* を求め、図示願います。
上の双対曲線 Cj* を求める問題が、(巧く誘導され)出題される予感在り....。
【体論のいの一番 4.5 Satz 】から、一歩も出ない所を彷徨っているダメな私。で、自己嫌
悪に陥いっているのですが...。(平成23年11月30日付け)
「4.5 Satzを視た刹那、どいつもこいつもかっこつけやがって定理」と命名せずにはいられ
ない私。(はやる気持ちを抑えて・・・ね、と云われても)
青枠の問題は黄色枠が、「4.5 Satzを視た刹那、どいつもこいつもかっこつけやがって定
理」から、問38 1/(1 - 21/3 + (21/3)2)∈Q(21/3)=Q[21/3] で表示可能なのは自明。で、そ
れなら未定係数法で、 1/(1 - 21/3 + (21/3)2)= c0 + c1・21/3 + c2・(21/3)2 で世界一簡単
な連立一次方程式を解けば、解決し、話は終わり、と指導されるのは嫌な私ですので、代
わりに連立一次方程式を明記し、c0 + c1・21/3 + c2・(21/3)2 を定めて下さい。
未定係数法が嫌な私が、それなら他の如何なる発想達で、青枠達の問達を未定係数法
以外の発想達で解いてと願うのは想定の範囲内でしょう。青枠達の問達を多様な発想で必
ず解いて下さい。
「4.5 Satzを視た刹那、どいつもこいつもかっこつけやがって定理」の証明を中・高校生に
も心底わかるように為し、黄色枠=東大や青枠∈英語圏 が証明済の「4.5 Satzを視た刹那、
どいつもこいつもかっこつけやがって定理」から自明でも自明と片付けず、具現願います。
黄色枠=東大や青枠∈英語圏 に酷似の問(係数を色々かえ)達を100問創作し、近傍の
大人(例:指導者)に東大の如く他の解の具体的な表示を自明でも具現し、ガロア群がZ/3Z
を具現してと願うて下さい。
(其の大人は真に大人の態度を示し、√[判別式]∈Q を確かめつつ、東大の如く他の解の
具体的な表示を必ず具現なさるで ありましょう)
英語圏で遭遇した青囲みの低次n=3の事例に、彷徨うて独逸語圏での同じ事例に遭遇し
た。(平成23年12月1日付け)
英語圏と同じく独逸も肝心の導出法に触れないで、α2-2 も解と説く。
(特に、独逸語圏のは易し過ぎる実數解の個数にあれほど費やし、「も解」の導出法には皆
目触れず)
(2) ガロア群を観察すれば、X3-3X+1 の解の公式がつくれないことはないことが証明でき
る。
定理 n=>5 でないならば、解を根号m√と加減乗除によって、係数 a0、 a1、・・・、an で表
示することはできないことはない。
とびっきり易しい事例を梅村 浩 (多元数理科学専攻)教授が提示され曰く。
f(x)=x3+6x2-8=0 のガロア群とは、その3つの解 x1=-5.76...、x2=-1.31...、x3=-1.06...(誤植在
り)のある性質を保った入れ換えとのことである。
私も不本意ですが、独逸語&英語圏(肝心の導出法に触れず全面的に隠匿)に倣い
σ[α]= -α2/2 +隠匿1α+隠匿2∈Q[α]
も解(と不本意ですが二箇所だけ隠匿し)。2ヶ所の隠匿を定め、
x3+6x2-8=(x-α)(x-σ[α])(x-σ[σ[α]])
を証明して下さい。(高校生向けの問です)
Artin & 独逸語&英語圏&日本語圏の教授諸氏(無論飯高先生も)様への真摯な質問:
肝心の導出法に触れないで、σ[α] も解と説くのは、Gaussに倣うての隠匿なのでしょう
か?(教育的配慮の為せるワザ?)
X4+52X3-26X2-12X+1=0 の解を α とするとき、他の解を σ[α]∈Q[α]で表現可能なの
は(一つは私が為し明記しました)自明でしょうが、導出過程を隠匿なさらず明記され、必ず
具現願います。
(具現していただけると世界の高校生や大學生も欣喜雀躍します)
(そして、ガロア理論の真髄に触れる努力を <落ちこぼれた學生も死ぬまで>為すでしょう)
質問に対する回答に絡む具体例が以下のメインです。(平成23年12月1日付け)
(飯高先生から助言をいただきましたが、殆ど到る所不透明で悩み続けております。飯高先
生のタイプミス->負正則数など直ぐ修正叶い、不正則数 (irregularity) 揚げ足なんてとりま
せん)
独逸のtの消去をたどって下さい。そして、得た 4x2 - 4yx - 15x + y2 + 7y + 13=0 のみを
視て(出だしの (x,y)∈Q(t)2は視ないで!)、問を創り、t∈Q(x,y) を自ら求めて下さい。
<問19-3のような t = (1-x)/y∈Q(x,y) は誰でも経験済故求める>
飯高先生出題の赤線の双対曲線は、上の独逸と同種の放物線=青線となることを示し、青
線のパラメタ-表示を導出過程も明記し求めて下さい。 x=_____∈Q[t] ,y=____∈Q[t]
宮西先生は、終結式について、(増田佳代・宮西正宜 両先生が)丁寧な解説(共著)をさ
れておられます。(増田佳代 関西学院大学理工学部数理科学科教授)
「判別式と終結式」の16p 以降に、終結式を用いての t---->(x,y)∈K(t)2 に於ける t の
消去法が明記されています。
上で導出された x=_____∈Q[t] ,y=____∈Q[t] から t を消去したい。
(イ) 独逸の t の消去に倣って、t を消去願います。
(ロ) 終結式を用いて、t を消去願います。
(ハ) 他の発想で、t を消去願います。
私は、x=μ[t]∈Q(t) , y=ξ[t]∈Q(t) から t を消去するよりも逆に、有理曲線であること
が知られた曲線の具現化の方に関心が在ります。
「判別式と終結式」の(増田佳代・宮西正宜 両先生が)丁寧な解説(共著) の例 2.10 の
終結式を用いて、t を消去した顛末の例
C: x3 - yx2 - yx - 3x + y2 + 2y + 2=0 のみを視て、有理曲線であることを再現したい。
t= -(-x2 - x + y + 2)/y∈Q(x,y) として、Cが有理曲線化叶うことを、問19.3 に倣い見つ
けました。(無論、別の t=___でもよく多義性があります)
実際 t= -(-x2 - x + y + 2)/y∈Q(x,y) としたら、 x=(t2 + 1)/t、 y=(t3 + 1)/t2 が得られ
ることを確認願います。多義性が在るので、上とは異なる t=_____∈Q(x,y)を見出して下さい。
C の双対曲線 C* を私が求めたら、
4x4 + 4yx3 + 27y2x2 - 18yx2 - x2 + 54y3x -18y2x + 27y4+ 隠匿・y =0
となった。(一部隠匿しましたので、多様な発想で導出なさって下さい)
Cが有理曲線なので、双対曲線 C* が有理曲線 なのは自明ですが、
4x4 + 4yx3 + 27y2x2 - 18yx2 - x2 + 54y3x -18y2x + 27y4+ 隠匿・y =0
のみを視て、有理曲線であることを是非具現願います。
私が、或る発想で具現すると、
x=-((t(t3 - 隠匿))/(2t3 - 3t2 - 1)) 、y= -((t2 - t4)/(2t3 - 3t2 - 1))
(一部 隠匿しましたので 多様な発想で 導出 なさって下さい)
無論、私が有理曲線化した上が嘘ではいけないので、或る発想で t を消去し、元の
4x4 + 4yx3 + 27y2x2 - 18yx2 - x2 + 54y3x -18y2x + 27y4+ 隠匿・y =0
になることを確認しております。
上は、下(以前に言及)と関係した話題ですが、(増田佳代・宮西正宜 両先生が)丁寧な
解説をされている終結式を讀まれ、再考願います。
(0) Cox の英文の紫枠の模倣である黄色枠のh[x,y] を求めて下さい。得たh[x,y]は、x に
ついて何次ですか。h[x,y]は、y について何次ですか。続いて、以下如何なる自分自身に
問うべき問題達が想定されますか?想定の範囲内の問達を記述願います。
「志村五郎 著 数学をいかに使うか」
超越拡大体 3.12 Lurothの定理 <----- の具体例達が欲しいです。
参考資料に漂着し、學ぶ契機をいただき讀んでおります。(平成23年12月3日付け)
10頁の 2X2 + Y2 - 5Z2=0 のパラメタ-表示にミスが在れば修正願います。ミスがないか
否か、パラメタ-表示から終結式を 用いる発想で、元の(射影)曲線が得られるか確認願い
ます。(→参考:「判別式と終結式」)
2X2 + Y2 - 5Z2=0 の双対曲線を多様な発想で求め、双対曲線上の有理点の存在、非存
在を論じて下さい。
2X2 + Y2 - 5Z2=0 の双対曲線は、低次のn=2次ですから、「発想1」・「発想2」なる発想も
具現しがいが在る筈です。是非具現し、双対曲線上の有理点の存在、非存在を論じて下さ
い。
「集合の相等」であるが、下の Q(
(平成23年12月4日付け)
Q(
逆の Q(
(1) 緑枠と紫枠の何れがお気に入り でしょうか?
(2) この一番上の √7∈ Q(√7+√5+√3) を紫枠方式で証明願います。
√5∈ Q(√7+√5+√3) を紫枠方式で試みました。
√5=18731(√7+√5+√3)/3776 - 8485(√7+√5+√3)3)/3776
+ 841(√7+√5+√3)5)/3776 - 15(√7+√5+√3)7)/3776∈Q(√7+√5+√3)
上は、「ガロア理論」のprimitive element theorem, 28pの具体例ですが、
(3) 具体例で具現して欲しい.....と願わずにはいられないですか?.
(スイスイと何時でもこんな証明を容易になさるのでしょうか?)
Theorem 14.4. (The primitive element theorem)
Every separable finite extension F/K is simple(こんなシンプルな定理も 稀有)
(4) 直ぐ証明願います。
「Theoreme de l'element primitif」 Un exemple explicite も紫枠方式です。
(en fait, la methode proposee en note aboutit a 云々にも留意。)
(5) 創造性を育むには如何に學べばよいのでしょうか?「ガロア理論」の定理達の証明を
辿り、事例で具現程度では創造性は産まれないことは嫌というほど分かります。
「Cubic function」に、
Viete's trigonometric expression of the roots in the three-real-roots case lends itself to
a geometric interpretation in terms of a circle. (図解在り)
英語圏、独逸語圏以外で大學生に如何に講義を? と彷徨い遭遇しました。
「Tschirnhaus transformation」により、東大の「x3+3x2-1=0」は、英文の「x3-3x2+1=0」にな
るので本質的に異なる問ではないが、双方の解を黒囲みの解の公式で求め、一度は考察
したい。
公式の暗記に強い受験生は、条件付きの3次方程式の解の円函数表示に当て嵌め、英
文の「x3-3x2+1=0」の解は、________、________、________。
解をぐっと睨んで、α、α2 - 2、__________(∈Q[α]の2次以下の表示)
東大の「x3+3x2-1=0」は、上で解けた解を変換し、_________、________、_________。
解をぐっと睨んで、α、__________、__________∈Q[α]の2次以下の表示)として合格したに違い
ない。上の受験生に倣い、空欄を埋めてと高校生にお願いして下さい。
解の円函数表示による表示より、下を好む方が存在する筈。その所以は?
英文の「x3-3x2+1=0」の解の表示:
{ e-2πi/9 + e2πi/9,e-8πi/9 + e8πi/9,e-4πi/9 + e4πi/9}
東大の「x3+3x2-1=0」の解の表示:
{-1 + e-2πi/9 + e2πi/9, -1 + e-8πi/9 + e8πi/9, -1 + e-4πi/9 + e4πi/9}
この表示により、正確な解の位置が定まるので、具現して下さいと高校生にお願いして下
さい。
吉田輝義氏の「ガロア理論」のどの部分が創造性に満ちたものでしょうか?
(平成23年12月5日付け)
その primitive element theorem は、
(3) 具体例で具現して欲しい.....と願わずにはいられないですか?
(スイスイと何時でもこんな証明を容易になさるのでしょうか?)
Theorem 14.4. (The primitive element theorem)
Every separable finite extension F/K is simple(こんなシンプルな定理も稀有)
(4) 直ぐ証明願います。
(以上 再掲)
資料1、資料2に構成的な証明が在り、且つ、欲しい事例が在りました。
Q(21/3,ζ)=Q(21/3+ζ)
21/3を wa=21/3+ζのQ係数の多項式で表現(21/3=_________∈Q[wa])し、ζを wa=21/3+ζ
のQ係数の多項式で表現(ζ=_______∈Q[wa])することにより、自明でない方の包含関係
Q(21/3,ζ)⊂Q(21/3+ζ)
を証明願います。
私が為すと、ζ=(-2・wa7 + 隠匿・wa4 + 36・wa)/27 (一部隠匿) となりました。
上は紫枠論法です。
wa=21/3+ζの最小多項式 f[x] を多様な発想で求め、他の解をαの 3-1次以下の多項
式σj[α]∈Q[α](英文の x3-3x+1=0 のは一つ与えられているので、
α、α2 - 2、__________(∈Q[α]の2次以下の表示)
あと一つは多様な発想で求められてしまう...。「表わせ」なる東京大學等に倣い、
αがf[x]=0の解なら 6-1次以下の多項式σj[α]∈Q[α]も解を総計6個必ず求めて下さい。
σ1[α]=α
σ2[α]= (4*α^5)/9 + (2*α^4)/3 + (4*α^3)/3 - (4*α^2)/3 + α + 3
σ3[α]=
・・・・
σ6[α]=
(ひとつ私が求めて明記しましたが、σ2k[α] (k=1、2、3、...)としても、{σj| j=1、・・・、6}を尽
くさぬでしょう)
「EinfAuhrung in die Algebra MusterlAosungen Blatt 12」の46に倣い、
Q((1 + I)/
であることを示して下さい。(平成23年12月6日付け)
発想をかえて、Q((1 + I)/
紫枠論法で証明願います。
即ち、 (1 + I)/
(1 + I)/
し、2^(1/4) =______∈Q[wa]
他の解を、αの 3-1次以下の多項式σj[α]∈Q[α]で表わせる東京大學等に倣い、
(英文のx3-3x+1=0 のは、一つ与えられているので、α、α2 - 2、______(∈Q[α]の2次以下
の表示) あと一つは多様な発想で求められてしまう.....)
wa=(1 + I)/
なら 8-1次以下の多項式σj[α]∈Q[α]も解を総計8個必ず求めて下さい。
σ1[α]=α
σ2[α]=-37/14 - 9α/14 + 34α2/21 + 19α3/7 - 65α4/42 + 11α5/42 - 8α6/21 + 4α7/21
(真に、f[σ2[α]]=0 か確認願います)
σ3[α]=
・・・・・・・・
σ8[α]=
(ひとつ私が求めて明記しましたが、σ2k[α] (k=1、2、3、・・・)としても、{σj| j∈{1、・・・、8}}
を尽くさぬでしょう)
Q[X]/f[X]*Q[X]
|
Q の中間體を全て求めて下さい。
「共軛」に絡む問題です。出題ミスであることを証明願います。
再掲でありますが、この近傍の諸問題を視て解いて提示下さい。
(平成23年12月7日付け)
領域:0≦s≦1、0≦t≦1 は、任意の四角形 A(0,0)、B(a,b)、C(c,d)、D(e,f)に変換
れる。
<与えられた四角形は、凸四角形であるものとする。点Aが原点にくるように平行移動し>
(1) 非線型写像 F によって、正方形が四角形に、(あの青線の円Cjが赤線の代数曲線に)
写される様子を為さずにはいられなかったので為しました。是非、味読、視讀願います。
(2) 更に、楕円 E: 100x2 - 100x + 400y2 - 400y + 109=0 の像 F(E) の代数曲線を導出過
程を明記し求めて下さい。
私が為すと、90000x4 - 630000x3 + 240000yx2 + 3846925x2
+ 1447500yx - 8861550x + 722500y2 - 3154100y + 5883929=0
となりました。(過ちが在れば即座に改めます。)
(3) F(E) の双対曲線 F(E)* を是非求めて下さい。
受講者がもう少し高次 2<n の代数曲線の双対曲線をもと、卒業後も取り組んでいる問題
です。
双対曲線の定義については、京都大学や(京都大学)に推奨されている氏は、例えば、
「対数的極小モデル理論の最近の発展について」等、公にしておられる。
(4) 解読された箇所を敷衍願います。
第0部 デカルトから現代の代数幾何学まで
第1部 代数曲線の幾何学(高次曲線論
アフィン代数曲線
射影代数曲線(に、飯高先生の手計算時代の数例の具現達が在ります)
微分型式の理論
曲線の種数とワイエルシュトラス因子
第2部 曲線と曲面の幾何学(複素多様体としての代数曲線
代数曲面
代数多様体のモジュラスの理論
モジュラス多様体のコンパクト化と代数多様体の退化
代数曲線の合同ゼータ関数)
第3部 体験的=代数幾何学論
第4部 増補(3次元代数多様体の双有理幾何学
数理物理学と代数幾何学
数学Cのニューフェース (<---此処は視たことがないのですが、想定は可能です。)
『代数曲線・代数曲面入門』安藤哲也(著)にも在るようです。定義と(C*)*=C を自明でも証
明せよ。(以外、いっさい触れず無念....)
事例も添え、代数曲面の双対曲面達をも著書に付け加え、誤植を皆無にされれば、購入
&読者の厚い層が世界に在る筈。
「Gを群とし、HをGの部分群、KをHの部分群とすると、KはまたGの部分群でもあることを
示せ」に遭遇しました。(検索して、感想を記載願います)
他の代数的構造で、例えば、正規拡大体ついて、上と類比な命題は真でしょうか?真なら
証明し、偽なら反例達を明記願います。
主に、体論絡み、代数曲線・曲面絡みの問題提起は、大學生や高等學校の指導者にと
ってヤル気の出る素材にはなり得る でしょう。(平成23年12月9日付け)
是非解いて、とお願いしているので、考え中の方が数多存在の筈。私の日々の問題提起
を視て、解いて損であったと罵声を 浴びたこともないので、暫くすれば解答を寄せられる筈
で、期待しております。高等學校の指導者にも解きがいの在る問題となるよう心がけており
ます。
大學生の指導者も此処をみておられますが、こたえると沽券にかかわるなんてお考えでは
なく、そんなことに悩んでいるの かぁと憐憫の情を示され、無論、瞬時に解かれ、解答者が
現れるのを愉しみにまっておられ、解答達の公表を敢えて差し控えておられるのでしょう。
屈折した表現を致しましたが、大學教授諸氏に問い合わせて、メールで丁寧な解答やpdf
添付つきの示唆を頂いたことも数例(1、2、・・・これは、高等學校の指導者が真摯に対峙し、
高校生にヤル気を、元気を与える良問だと為されておられる筈の代数幾何入門の入門の問
です)在ります。
私の日々の自問非自答の問題提起をEPUB保存し、電子書籍化し、更に、印刷し、店頭に
並べれば、小中高大院と世代を問わず購入し、日々ヤル気が継続し、数學を研究する道に
進まれるかも...。
非線形写像 F(X,Y)∈C(X,Y)2 の正体を明記し、赤裸々に晒しました。
(平成23年12月10日付け)
Jacobian determinant(Jacobian)を求め、青線の同心円が赤線に写されることを多様な
発想で証明願います。
発想(1) 無論、先ず、F の逆写像(が存在すること証明し)を求め、F-1(u,v)=__________.
発想(2)
発想(3)
・・・・・・
赤線の直線 L も円と見做すのが普通です。図を視て、F-1(L)を求めて下さい。
単位円上を (x,y) が一定の速さで動くとき、F(x,y) の速度vector、加速度vector をも求
め観察されたことを記載願います。
青線の円族をさらに増やし、Cr:x2+y2=r2 の像F(Cr)を求め図示願います。
{3,4,......,2011,2012,...}∋r--->Cr------>F(Cr)
上の非線型写像は研究し尽くされていますが、一般論への補助手段としても永遠に不滅
です。
F は等角写像であることは明らかでも具体的に交点の在る代数曲線f1[x,y]=0、f2[x,y]=0
を定め、その為す角をきちんと求め、像達も求め、その為す角が不変であることを示して下
さい。
ついでに、双対曲線f1*[x,y]=0、f2*[x,y]=0 も是非求め、同様な不変性を示して下さい。
提示したF に酷似の問題(高校生向けと云えなくもない)を創り、上の如き考察を願います。
上の非線型写像 F は研究し尽くされていますが、変換はそうでもないかも...。
このF は全然等角写像ではないことを証明して下さい。
非線型写像Fを考察したい。(平成23年12月11日付け)
Cr:x2+y2=r2 について、下の各青線=Cr とその像赤線=F(Cr)は図示しました。
(1) F(C1/2) の像を求めて下さい。(連動して動く様も説明願います)
(2) F(C1) の像を求めて下さい。(連動して動く様も説明願います)
(3) F(C3/2) の像を求めて下さい。(連動して動く様も説明願います)
(4) F(C2) の像を求めて下さい。
(5) F(D) の面積 A(F(D))を求め、A(F(D))/A(D)も求めて下さい。
(6) r→∞のとき、F(Cr)はどうなりますか?
此処までは、高校生も為す事柄と云えなくもない。以下は、そうでもなく、大學生や院生も
學生でない大人も食指が動かないなんてありえない問群です。
(無論、飯高先生の講義履修済の諸氏にも)
出所が明確な非線型写像Fについて、上の(1)から(5) までの考察を是非願います。
(上とは異なる想定の範囲外のことが生じましたか?)
そして、各F(Cr)の双対曲線を是非求め、特異点の考察をも是非願います。要求されなくて
も、非線型写像Fの第一次近似写像 は如何? と、「Jacobi-Matrix」を求めて考察される
筈です。(無論、Falte=襞も求め)
(重要な注記) 非線形写像の「Jacobi-Matrix」は、例えば、「松島与三 著 多様体入門」の
最後に近い261pに在ります。等角写像であることは明らかです。
C: -256y5 + 128x2y3 - 144xy2 - 16x4y + 27y + 4x3 = 0 の双対曲線C*を求めて下さい。
C* には二重接線が存在します。それを多様な発想で求めて下さい。(→発想例)
R2で考察したことと、複素数も許容し C2 で考察したこととの対比願います。私が後者を
考察したら、( i ,-2i )、( -i ,2i ) が接点となりました。
( x , y )=t・( i ,-2i )+(1-t)・( -i ,2i ) から t を消去すれば、二重接線の一つが得られます。
「連立方程式の回避」の高校生が求める4次函数のグラフG(f)に於ける二重接線には、双
対曲線G(f)* の通常二重点(特異点)が対応していますが、C*の二重接線には、(C*)* = C の
如何なる点が対応しますか?
そもそも (C*)* = C には特異点が存在しないことを確認して下さい。
C: -256y5 + 128x2y3 - 144xy2 - 16x4y + 27y + 4x3 = 0 を「Wolfram|Alpha」に挿入して視
ても然りです。
上の相違点は想定の範囲内でしたか?
さて、此処から非線型写像の探訪ですが、
(イ) Fで、上の C: -256y5 + 128x2y3 - 144xy2 - 16x4y + 27y + 4x3 = 0 と C* と二重接
線を写したF(C)、F( C*)、F(二重接線)を多様な発想で求めて、図示をも願います。
二重接線----->F(二重接線)は円円対応でしたか?
C* と二重接線の接する接点を求め、F(C*) とF(二重接線)の接する接点を求めて下さい。
さらに、今度は、参考図の F で、
(ロ) 上の C: -256y5 + 128x2y3 - 144xy2 - 16x4y + 27y + 4x3 = 0 と C* と二重接線を
写したF(C)、F( C*)、F(二重接線)を多様な発想で求めて、図示をも願います。
C* と二重接線の接する接点を求め、F(C*) とF(二重接線)の接する接点を求めて下さい。
(イ) (ロ)の様々な相違点を述べて下さい。
高校生の指導者が教え過ぎて(指導法如何?ガロア拡大に絡まるHilbert 90をもか?)高
校生すら「知りすぎたのね」と云われそうな命題達;19-3、6-15を熟視され(ご覧いただき)
味読されて忌憚のないご意見をお聞かせいただければ幸甚です。
(平成23年12月12日付け)
6-15 の行間を讀ませる証明でなく丁寧な証明を是非お願い致します。命題達;紫枠=19-3、
6-15 は高校生が知悉の事柄を難解な用語を散りばめ述べたのでしょうか?
これは飯高先生が絶賛されておられる津山高専の2年生2人の研究発表(参考)にも関係
が在ります。
再度、お願い致します。6-15 の行間を讀ませる証明でなく丁寧な証明を是非お願い致しま
す。命題達;紫枠=19-3、6-15 は高校生が知悉の事柄を難解な用語を散りばめ述べたので
しょうか?草色枠を知りたく在れば、先ず、なんとしてもイデアルI のZERO点を知らねば話に
ならず。視てしまったので、二重接線の存在は線が引ける幼児にも叶うが、知らぬ存ぜぬフ
リをして、その双対曲線を必ず求め、その特異点から二重接線を求め愉しんで下さい。
無論、「二重接線」なる発想からも二重接線を具現願います。その際、多様な発想で叶うで
しょうが、必ず判別式を(何度か)用い具現願います。横道に逸れましたので、再三願います。
紫枠= 6-15 の行間を讀ませる証明でなく丁寧な証明を是非お願い致します。命題達;19-3、
6-15 は高校生が知悉の事柄を難解な用語を散りばめ述べたのでしょうか?
高校生の指導者が教え過ぎて(指導法如何?ガロア拡大に絡まるHilbert 90をもか?)に目
を奪われて果てし無き=死ぬまで、探究中でありましょうが、(ガロア拡大に絡まるHilbert 90
に逢えてよかったか、是非正直に告白願います)(→参考例)
再四願います。紫枠= 6-15 の行間を讀ませる証明でなく丁寧な証明を是非お願い致します。
命題達;19-3、6-15 は高校生が知悉の事柄を難解な用語を散りばめ述べたのでしょうか?
高校生すら「知りすぎたのね」と云われそうな命題達;19-3、6-15を熟視され(ご覧いただき)
味読されて忌憚のないご意見をお聞かせいただければ 幸甚です。
果てしなき(お願い)続き:草色枠の如き問題達を未来永劫創作し、解説をお願い致します。
再五願います。
紫枠= 6-15 の 行間を讀ませる証明でなく丁寧な証明を是非お願い致します。
命題達;19-3、 6-15 は高校生が知悉の事柄を難解な用語を散りばめ述べたのでしょうか?
飯高先生が絶賛されておられることはインパクトが強すぎて、私の質問は取るに足らない
と無視されることは百も承知の上で、再六願います。
紫枠= 6-15 の行間を讀ませる証明でなく丁寧な証明を是非お願い致します。命題達;19-3,
6-15 は高校生が知悉の事柄を難解な用語を散りばめ述べたのでしょうか?
無論、「二重接線」なる発想からも二重接線を具現願います。その際、多様な発想で叶うで
しょうが、必ず判別式を(何度か)用い具現願います。
この件は霞んでしまったでしょうが、双対曲線絡みと把握し、飯高先生の講義の受講者に
なりすまし、明解な解答を必ず願います。(飯高先生は、この代数曲線なら初体験なので、
即座に具現せずにはいられないでしょう)世界の皆んなでお願いしましょう。
「多様な発想で導出された其の双対を導出法達をも赤裸々に隠匿せず記載して!」
以下で双対曲線を幾つか求めます。双対曲線に初めて「デカルトの精神と代数幾何」で
邂逅し、例示されておられる19p から學び、代数曲線に遭遇したら必ず双対曲線を求め學
んでまいりました。(平成23年12月13日付け)
そこでは、最初からK[X,Y]/<f[X,Y]>、K[X,Y,Z]/<f[X,Y,Z]>
を考えることが重要と「可換環論」(所持しておりませんが)の松村英之氏が書評を書いて
おられます。
(一時期の京大は、永田、広中、小田忠雄、宮西雅宜、松村英之、中野茂男を擁していた)
書評を 讀みたいでしょう。『数学にかけし若き命』のこと(飯高茂 46)も在り。
陰陽表示の曲線の交点に遭遇しました。
パラメタ-表示の後半の曲線は、次のC2なる代数曲線であることを確認して下さい。
C1: x2 + 2x + y + 1 = 0(とする。高1で履修)、C2: -2x2 + 2yx + 2x - y2 - y = 0
後半の交点を示す t の(近似)値に、ミスが在ることを示して下さい。未来 t=1 に通過せず、
過去に通過しています。後半の交点を双方共パラメタ-表示で求めて遊んで下さい。後半の
交点を双方共陰的表示で求めて遊んで下さい。陰的表示した曲線の主軸問題を解いて、以
下を考察願います。
もう嬉々として飯高先生の講義履修生が解くn=2次曲線C1、C2 の双対曲線を必ず求め、
交点C1*∩C2*も求めて下さい。交点C1∩C2={P1,P2} を求めて下さい。
草色枠の非線型写像Fについて、代数曲線F(C1)、F(C2)を求めて下さい。
交点 F(C1)∩F(C2) を求めて下さい。代数曲線F(C1)の双対曲線F(C1)*を求めて、特異点も
求めて図示して下さい。代数曲線F(C2)の双対曲線F(C2)*を求めて、特異点も求めて図示し
て下さい。交点 F(C1)*∩F(C2)* を求めて下さい。
C1: x2 + 2x + y + 1 = 0、C2: -2x2 + 2yx + 2x - y2 - y = 0 とする。(→参考図)
交点C1∩C2={P1,P2} に於ける接線 T1、T2 を求めて為す角を求めて下さい(高校で履修)。
求めた接線 T1、T2 の紫色枠の非線型写像Fによる像F(T1)、F(T2) を求め、円円対応であ
る事の定理が具体例で心底理解できたと、函数論履修者に云わしめて下さい。
紫色枠の非線型写像Fについて(函数論で一番易しいと履修)、F(C1)を求めて下さい。
F(C1)を含む最小の代数曲線を求めて下さい。代数曲線F(C2)を求めて下さい。
赤い太線には特異点(3,0)が在る。(3,0)∈F(C1) ではないことを示し、このような現象が
生じる理由を述べて下さい。F(C2)にはこのような現象が生じない理由を述べて下さい。交
点F(T1)∩F(T2)を求めて下さい。接線T3、T4 を求めて、為す角を求めて下さい。等角写像
でしたか?(函数論で一番易しいと履修)
C1とC2で囲まれる部分の面積を求めて下さい。F(C1)とF(C2) で囲まれる部分の面積を求
めて下さい。F(C1)を含む最小の代数曲線の双対曲線 f1*(x,y)=0 を求めて、特異点も求
めて図示して下さい。代数曲線F(C2)の双対曲線 F(C2)* を求めて、特異点も求めて図示し
て下さい。交点{(x,y)|f1*(x,y)=0}∩F(C2)* を求めて下さい。
上で双対曲線を幾つか求めたでしょうが、多様な発想で再び求めて下さい。
真摯な問:双対曲線、双対曲面、_______、________、......、______、....... に具体的に触れている飯
高先生の著書以外の書籍が在れば御教示願います。もし稀有なら、その理由を御教示願
います。双対曲面を具現されておられるなら提示願います。(導出法は、隠匿されても不満
は云いません。導出の努力を致します)
今回は高校生にも射影曲線履修者にも性格の良い正則函数の函数論履修者にも性格
の悪い非線型写像探訪者にも具体例を通じて理解の一助となるべく努めました。
此れで小中高生が世代間のギャップをものともせず、ドンドン上の世代を困らす質問を投
げかけることが可能になれば、上の世代も安閑としていられなく、研究意欲を失うことはなく
なるでありましょう。.
(1) 代数曲線 C: (-1 + x2 + y2)3 -x2y3=0 の特異点を求めて下さい。(→参考図)
(2) 二つの特異点は自明ですが、他の出現する特異点に疑問点が生じる筈です。如何に
疑問点を解消なさいますか?
(3) 非線型写像F:R2-->R2 を F[x,y]=[x+y,y2] によるCの像F(C)は参考図となりますか?
(4) また、F(F(C))も求め、F(C)、F(F(C))の特異点を求めて下さい。
(5) C、F(C)、F(F(C)の双対曲線達を求めてください。
(6) 各双対曲線に如何なる特異点が出現しましたか?
孤立特異点を有する代数曲線の量産を為します。
2x4 + 16yx3 + 26x3 + 48y2x2 + 12yx2 - 151x2 + 64y3x - 264y2x - 1702yx
- 1560x + 32y4 - 368y3 + 1250y2 + 4386y + 6723 = 0
2x4 + 16yx3 + 26x3 + 48y2x2 + 12yx2 - 327x2/2 + 64y3x - 264y2x - 1752yx
- 1720x + 32y4 - 368y3 + 1200y2 + 4516y + 6608 = 0
2x4 + 16yx3 + 26x3 + 48y2x2 + 12yx2 - 181x2 + 64y3x - 264y2x - 1822yx
- 1944x + 32y4 - 368y3 + 1130y2 + 4698y + 6489 = 0
2x4 + 16yx3 + 26x3 + 48y2x2 + 12yx2 - 407x2/2 + 64y3x - 264y2x - 1912yx
- 2232x + 32y4 - 368y3 + 1040y2 + 4932y + 6408 = 0
2x4 + 16yx3 + 26x3 + 48y2x2 + 12yx2 - 231x2 + 64y3x - 264y2x - 2022yx
- 2584x + 32y4 - 368y3 + 930y2 + 5218y + 6419 = 0
2x4 + 16yx3 + 26x3 + 48y2x2 + 12yx2 - 527x2/2 + 64y3x - 264y2x - 2152yx
- 3000x + 32y4 - 368y3 + 800y2 + 5556y + 6588 = 0
2x4 + 16yx3 + 26x3 + 48y2x2 + 12yx2 - 301x2 + 64y3x - 264y2x - 2302yx
- 3480x + 32y4 - 368y3 + 650y2 + 5946y + 6993 = 0
2x4 + 16yx3 + 26x3 + 48y2x2 + 12yx2 - 687x2/2 + 64y3x - 264y2x - 2472yx
- 4024x + 32y4 - 368y3 + 480y2 + 6388y + 7724 = 0
2x4 + 16yx3 + 26x3 + 48y2x2 + 12yx2 - 391x2 + 64y3x - 264y2x - 2662yx
- 4632x + 32y4 - 368y3 + 290y2 + 6882y + 8883 = 0
2x4 + 16yx3 + 26x3 + 48y2x2 + 12yx2 - 887x2/2 + 64y3x - 264y2x - 2872yx
- 5304x + 32y4 - 368y3 + 80y2 + 7428y + 10584 = 0
2x4 + 16yx3 + 26x3 + 48y2x2 + 12yx2 - 501x2 + 64y3x - 264y2x - 3102yx
- 6040x + 32y4 - 368y3 - 150y2 + 8026y + 12953 = 0
各曲線Cj の双対曲線Cj*を求め、双方の特異点を求めて図示も願います。如何にして量産
したかを暴いて下さい。そして、逆に、そのような量産された曲線達を提示願います。
孤立特異点を有する代数曲線(=高橋和巳型代数曲線と命名)の量産を為します。
(平成23年12月14日付け)
草色枠
-2x4 - 16yx3 + 142x3 - 48y2x2 + 834yx2 - 3936x2 - 64y3x + 1632y2x - 13215yx
- 33733x - 32y4 + 1064y3 - 12711y2 + 65153y - 121838 = 0
-32x4 - 256yx3 + 2272x3 - 768y2x2 + 13344yx2 - 62814x2 - 1024y3x + 26112y2x
- 210792yx - 537568x - 512y4 + 17024y3 - 202728y2 + 1034888y - 1926539 = 0
-8x4 - 64yx3 + 568x3 - 192y2x2 + 3336yx2 - 15663x2 - 256y3x + 6528y2x - 52536yx
+ 133852x - 128y4 + 4256y3 - 50520y2 + 256832y - 475958 = 0
-32x4 - 256yx3 + 2272x3 - 768y2x2 + 13344yx2 - 62490x2 - 1024y3x + 26112y2x
- 209496yx - 533248x - 512y4 + 17024y3 - 201432y2 + 1019768y - 1881287 = 0
-4x4 - 32yx3 + 284x3 - 96y2x2 + 1668yx2 - 7791x2 - 128y3x + 3264y2x - 26106yx
+ 66386x - 64y4 + 2128y3 - 25098y2 + 126526y - 232363 = 0
上の各曲線Cj の特異点を求め、孤立特異点であることを示して下さい。更に、双対曲線
Cj*を求め、特異点も調べて下さい。
紫線型
通常二重点なる特異点を有する代数曲線(=捻り曲線と命名)の量産を為します。
2x4 + 16yx3 - 142x3 + 48y2x2 - 834yx2 - 81
- 324
+ 11091y2 + 3780
4x4 + 32yx3 - 284x3 + 96y2x2 - 1668yx2 - 162
- 3264y2x - 648
- 648
2x4 + 16yx3 - 142x3 + 48y2x2 - 834yx2 - 81
- 324
+ 10767y2 + 3780
上の各曲線Cj の特異点を求め、孤立特異点ではなく図のような点であることを示して下さ
い。更に、双対曲線Cj*を求め、特異点も調べて下さい。
例示した紫線には線が引ける幼児すら二重接線の存在を認め具現してしまう。
各曲線Cj の二重接線を、この解答達に倣わず、双対曲線絡みと把握し、飯高先生の講義
の受講者になりすまし、明解な解答を必ず願います。(飯高先生は、この代数曲線なら初体
験なので、即座に具現せずにはいられないでしょう)世界の皆んなでお願いしましょう。
「多様な発想で導出された其の双対を導出法達をも赤裸々に隠匿せず記載して!」と叫び
つつ読者各位も求めた双対曲線Cj*から二重接線の方程式を提示してください。
また、各曲線Cj の二重接線のみでなく変曲点に於ける接線等をも一気呵成に求める発想
をも開発し具現して下さい。
手始めに、「二重接線」からどうぞ。(私が具現したら、この場合 0.00000000000001 秒で
した)激白します。「判別式と終結式」(増田佳代 関西学院大学理工学部数理科学科教授)
から學んだ手法を使いました。増田佳代・宮西正宜 両先生(丁寧な解説)(共著)に感謝致
します。
最初からK[X,Y]/<f[X,Y]>、K[X,Y,Z]/<f[X,Y,Z]>を考えることが重要と「可換環論」の
松村英之氏が書評を書いておられます。
(一時期の京大は、永田、広中、小田忠雄、宮西雅宜、松村英之、中野茂男を擁していた。)
「デカルトの精神と代数幾何」 飯高茂、上野健爾、浪川幸彦著
第0部 デカルトから現代の代数幾何学まで
松村英之氏 曰く;
第1部 代数曲線の幾何学(高次曲線論)は良くも悪くも型破りで、いわば八方破れで飯高
氏が喋りまくっている。最初の10頁ぐらいは高校生でも読めるように書かれているが、その
辺から先は______________________.
最後に、「ともあれ毒にも薬にもならぬ課外書物(加害書物)が多い中にあって、本書は強
烈なものをたっぷり含んでいる本である」と松村英之氏(名古屋大學)
容易ですが、数行に亘る丁寧な解説付きの[問題]に遭遇しました。
以下、「鶏を割くに焉いずくんぞ牛刀を用いんや」と揶揄されても為す価値が存在します。
これはまさに「双対曲線の出番」の 問なので、是非紫枠のC* を求め、その特異点を求め
る方法で解いて下さい。そのC* の導出は多様な発想でお願いします。
(無論、有理写像:C---Φ--->C* も明記願います)
但し、今回は(可約な -x4 + 4x3 - 4x2 - 4yx + y2 + 4y=0)4次曲線なので、飯高先生の発
想は通じません。(履修者は今回の4次曲線の「双対曲線も」求めずにはいられないでしょう)
双対曲線の定義は明確です。
黄色枠の易しい問題を御覧ください。(選択肢から選ばないで!)この黄色枠の易しい問題
について、長い解説が在ります。ちらっと視て、聴いて、行く末は想定の範囲内でしょう。紫
枠の双対曲線を先ず求め、その特異点を求める発想で答えに着地下さい。
Cを、x4/9 - 8x3/9 - 5y2x2/36 - x2 + 2y2x + 8x - y2 - y4/4 = 0 (と、2<n 次曲線とQ上
可約な代数曲線であることを 伏せ)、そのn=2 の倍の次数の4次の曲線 C の双対曲線C*
を求めて、と設問する方がやり甲斐が在りますので、是非多様な発想で4次曲線 C の双対
曲線 C*を求めて下さい。(無論、有理写像C---Φ--->C* も明記願います)
上は、n=2次に取り組み、より高次なものも具現したい、なる強い欲求を満たす問題です。
倍の4次曲線 C の双対曲線 C* の具現ですから。
(云うまでも在りませんが、飯高先生の3次の行列の逆行列の発想は無効です)
飯高先生が、年度変り後、m度射影幾何學と代数曲線、曲面、.....の講義をされ、講義の
理解度を試される際は、行列問題に必ずしも帰着しない、より高次なn=5、6、....、2011、....
な代数曲線、曲面、....の双対を求めなさい、と出題されるにちがいない。
(授業料を支払うのは困難ですが、受講したいです!)
双対曲線 C* の特異点を求め、ハイ終わり(QED)も礼を失するので、最後まで聴いてあ
げて下さい(私もそうするつもりです)。そして、縷縷英語で解説された発想と私がお願いし
た発想の何れが将来使えそうかをも論じて下さい。
以上 「鶏を割くに焉いずくんぞ牛刀を用いんや」と揶揄されても為す価値が存在すると考
えに考えてお願いを致しました。
私は「鶏を割くに牛刀を用いるのが大好き」です。その所以は、今回の例で云えば、超容
易な何れにも接すると云う問題から 代数曲線の双対曲線がタダで學べてしまうのですか
ら!まさに、「ザ チャンス」です。逸してはもったいない。
鶏を割くに、牛刀を用いた経験の問題達を提示願います。
「数学をいかに使うか」の事例達に不可解なことがありすぎますが、双対を如何に使って
遊ぶかなら、今回の体験・具現で有効であったことが身に沁みてわかった筈です。
次のような易しい問題を、書籍「デカルトの精神と代数幾何」を購入し、この視座から解い
て視るとこうなると、多様な発想による解説付きの本を上梓されれば、読者層が小中高生、
数学教師を目指す数学科学生、現場の小中高(大院)の数学教師(教授)全てで、「どうも
売れそうにもない」は解消されます。(平成23年12月15日付け)
次のような易しい問題とは、参考資料に酷似ですが、お茶の水女子大学:
2曲線 y=x2+1、y=-2x2-1 の共通接線を求め、接点も求めよ。
なる超易な問を、講義の履修者になりすまし、
各 n=2 次の代数曲線 C1:xn-y+1=0 、 C2: -2xn-y-1=0 の双対曲線を先ず射影化し、行
列の逆行列を求める発想に倣い、お茶の水女子大学の問をといて下さい。
C1*:________________________、C2*:___________________________
n=2 に固執しては損なので、敢えて、(xn-y+1)(-2xn-y-1) を展開し、4次の代数曲線
C:-2x4 + yx2 - 3x2 + y2 - 1=0
の双対曲線 C* を多様な発想で求め、その特異点を求め、再び、お茶の水女子大学の問
をといて下さい。(無論、有理写像C---Φ--->C* も明記願います)
私が或る発想で具現すると、 C*: x4-12y2x2+4yx2+32y4-32y2=0 と今回は想定通りの次
数不変の4次の代数曲線になったので、間違いはない筈です。
これを、 「Wolfram|Alpha」に挿入すれば、可約曲線だと視えるし、実際、左辺を高校生に
倣い、Q上で因数分解すれば、上の飯高先生の云われる発想で為したC1*、C2* に一致し、
ますます想定通りで愉しい。
有理写像C---Φ--->C* も私が具現したところ、
Φ(x,y)=((2x(2x2 + y + 1) - 4x(-x2 + y - 1))/(-8x4 + 3yx2 - 6x2 + 2y2),
(-x2 - 2y)/(-8x4 + 3yx2 - 6x2 + 2y2))
となりました。(ミスが在れば修正願います)
以上、「鶏を割くに焉いずくんぞ牛刀を用いんや」と揶揄されても、為す価値が存在するこ
とを合点していただけましたでしょうか?
「どうも売れそうにもない」は解消されます、に戻り、書籍の副題は「入試問題を牛刀を用
いて解き、代数幾何學入門」となされば、購読者層が小中高生、数学教師を目指す数学科
学生、現場の小中高(大院)の数学教師(教授)、更に、院生指導者も講義の際、易しすぎ
る事例として(その書籍を見せつつ、購入を勧め)俎上に載せられ、院生も心底理解し、挫
折しつつ、次の難題達に立ち向かう姿勢を示すに違いない。
例えば、「Die 28 Doppeltangenten」も多様な発想で双対曲線を求めずにはいられないと
即座に具現し、解決されるでしょう。
今まで多様な発想で双対曲線、双対曲面を求めてまいりましたが、「Duale Kurven」の発
想は初めてです。(平成23年12月16日付け)
さっそく この通りの終結式を用いる発想で、双対曲線を求めずにはいられないのですが、
人の愉しみを奪うのもいけないことなので、もっと容易な「二重接線」をともと食指が動き始
めたのですが、やはりいけないことなので、易し過ぎる問題を、双対曲線を独逸語でなされ
た懇切丁寧な終結式を用いる発想で、私が具現した事実を晒します。
記号も独逸に合わせて、終結式の全てを隠さず提示する努力は致しましたが、今回のは
行列のサイズの関係で収まりきれませんでした。
(が、綺麗に行儀よく要素が並んでいるので、補うのは容易です。)
その行列式は、紫枠=因数分解 をも為し、全て晒しました。
此れより、赤線: ((-2 + y0)2 + y1)(-y02 + y1) = 0 の双対曲線は、
( y02 - 4y1)( y02 + 4y1 + 8y0y1) = 0 (想定通り、可約曲線=青線です)
(x、y と云う記号にかえたいのですが、独逸にあわせて為される方に利するべくその儘にしておきます)
青線の特異点を求め、それから赤線の共通接線が求められることを確認願います。
如何でしたでしょうか?終結式をもっと愛す為に私が禁欲した上の問題達を必ず解いて
愉しんで下さい。今回の発想で、有理写像C---Φ--->C* が得られますか?
例の問題をも今回の独逸の終結式の発想で必ず求めて下さい。飯高先生も即座にそう為
され、次回の講義の際こんな発想も 在ると黒板に記されるでしょう。すると、世界にその発
想が拡散し、誰でも必ずその発想でも為すことでしょう。その発想を、「終結式でどいつも法」
と命名します。(品のない命名には理由が在るので許して下さい。)
飯高先生の発想は、n=2だから「偶々行列で出来る法」と命名します。
教えた通りの発想でないと「0点だぞ!」なるお硬い指導者が存在するようです。私は、あ
あ云えば(指導されれば)こう云う、更にこうも云う発想を求め続けて彷徨うております。
問題については、4次ですが可約なので、n=2だから、「偶々行列で出来る法」でも為して下
さい。
この発想をタダで世界につかってねと公表されておられる方は、Ruth Kellerhals教授です。
飯高先生と學会で数度逢われておられそうな予感在り。
上記の終結式を用いる発想で、問題の双対曲線を求めずにはいられないのですが、人の
愉しみを奪うのもいけないことなので、同程度に容易な
C: 27x4 + 482yx3 + 2187y2x2 + 438yx2 + 4374y2x - 192yx + 2187y2 - 256y = 0
の双対曲線 C* を、終結式を用いる発想で是非求めて下さい。(平成23年12月17日付け)
為さずにはいられないので、私が為すと、高校生が描ける
-x4 + x3 + (隠匿)x2 - 5x + y + 2 = 0 (x--->y=_____ は複接線をもつ4次函数)
実は、「志学 数学」(参考:書評)の125p 推敲;ミスプリ訂正だけでも一回では無理で、云
々に関わることですが、「デカルトの精神と代数幾何」第1章 高次曲線論 のなんと最初の
ページに誰でもグラフから気付くミスがあります。(其れを素材にしたので隠匿した部分は直
ぐバレてしまいます)
y=_____ の右辺を因数分解すれば、誤字:五次 (x+2)2(x-1)3ではなく4次 (x+2)(x-1)3 です。
(此処で飯高先生が高校時代の立ち読みを回顧され熱く語られておられる事柄は何度讀ん
でも感動的ですので、未だ未購入の世界の方々は是非購入し味読なさって下さい)
おすすめしたい確認法は、自ら求めたC*の双対曲線(C*)*を求めて、
27x4 + 482yx3 + 2187y2x2 + 438yx2 + 4374y2x - 192yx + 2187y2 - 256y = 0
になれば誰にも頼ることなく自己解決しますので、是非今回は終結式を用いる発想でどうぞ!
4次 y=(x+2)(x-1)3 の複接線を双対曲線を求めて、その特異点をもとめて、瞬時に求め
ることを飯高先生は為されておられないので為して下さい。
また、発想は、第1章 高次曲線論 のなんと最初のページ+1 と同じですが、
(x+2)(x-1)3 - (ax + b)=(x - p)2(x - q)2 から係数を比較して云々ではなく、
(x+2)(x-1)3 - (ax + b) の判別式を多様な発想で求め、代数曲線 判別式=0 の特異点を
求める発想で求めてください。
(この発想での複接線を求めるのが初めてであれば感動するでしょう)
代数曲線 判別式=0 の特異点は一つだけとは限らないでしょう、複接線を求める為に用
いた特異点以外の特異点は何を表していますか?(→ 参考:「判別式と終結式」)
複接線を求める為に「16-12次方程式」の判別式を用い、上で感動されたでしょう。
16+α次方程式の判別式計算を愉しんで為し、応用例も示して下さい。
上記の箇所の一部のみ具現します。(平成23年12月18日付け)
代数曲線 判別式=0 は、
-27a4 + 6412a3 - 8760ba2 - 380880a2 - 2688b2a
+ 1924272ba - 256b3 + 300816b2 - 105122880b=0
となりました。
(この代数曲線やその双対曲線を多様な発想で本当に求め、図示することは要求されなくて
も為さずにはいられないでしょう。是非、具現を!)
この特異点達は、
(a,b)=(140,-100)、(140 + 3
(140 - 3
で、最初の(a,b)=(140,-100)を用いて、非日本語圏の提示された解と異なる道から同じ
地点(David said... The answer is y = 140x - 100.)に着地しました。言葉が通じないにも関
わらず数式で意思の疎通が叶ってしまい感激です。
以下、幾度か双対曲線を求めますが、その際は、「Duale Kurven」なる発想で是非お願い
致します。(Doppeltangenteの図も在ります)
唐突ですが、代数曲線 C: 4a3 - 72a2 - 108ba + 324a - 27b2 + 108b=0 の特異点を求
めて下さい。その双対曲線 C* と C* の特異点を求め、双方を観察された感想を記してくだ
さい。即ち、Cの特異点の名称をのべ、C* の何を反映しているか?C* の特異点の名称を
のべ、Cの何を反映しているか?を観察された感想を記してください。
実は、上の発端は、判別式を考察する際、生じた問題です。
例えば、易しい曲線: y=x3 - 6x2 + 9x と y=ax+b から、(x3 - 6x2 + 9x) - (ax+b) の判別
式(導出する際、多様な発想が望ましいが)を、3次の場合の公式にあてはめて、D[a,b]を
求めることは頻繁に行うでしょう。
ここで止めず、もう一押しして、代数曲線D[a,b]=0 (これを判別曲線 DC と命名)の特異
点を求めて、その双対曲線 DC* と DC* の特異点を求め、互いに他を観察してください。
即ち、DCの特異点の名称をのべ、DC*の何を反映しているか?DC*の特異点の名称をの
べ、DC の何を反映しているか?を考察し、この場合は高校生が知悉の事柄に他ならない
ことを確認願います。
今後は、恒に、曲線に遭遇したら直ぐ上の如き考察をなさって下さい。代数多様体の特異
点は、その多様体の何かの特徴を強烈に反映させる筈故。
こんどは、第1章 高次曲線論の最初のページの例で、(x+2)(x-1)3 -(ax+b)=0 の判別式
を求め、D[a,b]=____________________
ここで止めず、もう一押しして、代数曲線D[a,b]=0 (これを判別曲線 DC と命名)の特異
点(今回は複数在るので、正しくは特異点達に留意され)を求めて、その双対曲線 DC* と
DC* の特異点を求め、互いに他を観察してください。即ち、DCの特異点の名称をのべ、DC*
の何を反映しているか?DC*の特異点の名称をのべ、DC の何を反映しているか?を考察
し、この場合は高校生が知悉の事柄に他ならないことを確認願います。
もとの曲線 y=(x+2)(x-1)3 と上で考察された事実から、3本の接超平面T1,T2,T3を C と
共に図示願います。一つは複接線で、他の二つはなんと命名されますか?
飯高先生は、双対曲線を求め、もとの高次曲線の複接線、変曲点の有無を探る等論じて
おられます。
上は、判別代数曲線D[a,b]=0 (DC)の特異点達を求め、もとの曲線の複接線、変曲点の
有無を探れることの例証です。(→参考)
C: x4 + yx3 - 10x3 + 10y2x2/9 - 10yx2 + 23x2 + y3x/9
- 10y2x + 24yx + 10x + y4/9 + 215y2/9 - 24 = 0
の双対曲線C* を、「Duale Kurven」なる発想で是非求めて下さい。
(Doppeltangenteの図も在ります)
C* はQ上可約な代数曲線K1∪K2 であることを示し、交点K1∩K2 を求め、それから生じ
るCに於ける接超平面が4つ Tj 在ることを示し、CとTj を図示して下さい。
同じ結論:CとTj の図示を今度は双対なる手法を用いず、判別式を用いて是非導出願い
ます。(→「判別式と終結式」)
以上を解かれたなら、次の発想も為さずにはいられない筈です。
CはQ上可約な代数曲線C1∪C2 で、双方ともn=2次である(高校生が為します)ので、講義
の発想で、双対曲線達C1*、C2* を是非求めて下さい。そして、交点C1*∩C2*を求め、それ
から生じるC1∪C2に於ける接超平面が4つ Tj 在ることを示し、CとTj を図示して下さい。
以上、同じ問題を3通りの発想で解いた筈です。此等の発想達で、このような問を誰か解
いたことがあるでしょうか?世界初かも知れません...。
「早稲田大学 理工学部(2007)」の「共通接線を求めよ。」なる問は誰にも経験が在るで
しょう。これも上の3通りの発想で求めて遊んで下さい。(→ 参考:「共通接線」)
参考図を視て、すべてを合点いただけましたでしょう、が説明等を加えます。
(平成23年12月19日付け)
5次の可約代数曲線C:
yx4 + y2x3 + 2yx3 + x3/2 + y3x2 - 2y2x2 - 15yx2/2
+ 5x2/2 - 3y3x - 3y2x/2 - 25yx/2 + 3x + y3 + y2 + 6y = 0
の双対曲線C* を多様な発想で求めて欲しいのですが、「Duale Kurven」なる発想で是非求
めて下さい。(Doppeltangenteの図も在ります)
そして、双対曲線C* の特異点達を求め、そのうちの2つを使い、Cの複接線を求めて下
さい。まだ未使用の特異点は、Cの如何なる特徴を反映しているか推察願います。
以上からも飯高先生の感動を追体験できたでありましょう。
Cの複接線だけが知りたいのであれば、「二重接線」の発想や曲線Cと y=ax+b から(y、x
を消去し) 判別曲線D[a,b]=0 の特異点を求める方法も是非!
(これなら複接線以外の情報もゲット叶いますので)
参考図を隠匿することなく提示したように、Cは赤線=円錐曲線∪3次曲線です。
円錐曲線 C1 : x2 + yx + 5x + y2 + y + 6=0 (は主軸問題も解き)の双対曲線C1* は、講
義の発想で求めて下さい。
3次曲線 C2 の双対曲線 C2* は講義の発想では不可なので、例えば、「Duale Kurven」
なる発想で是非求めて下さい。
上の2つのC1*、C2* の左辺の積=0 で、参考図もゲットされたことを確認願います。
3次曲線 C2 の双対曲線 C2* の特異点を求め、C2には変曲点が在ることが判明した筈
です。その特異点を求め、C2 の変曲点に於ける接超平面を求め図示も願います。
無論、3次曲線 C2 の変曲点に於ける接超平面は、高校生も双対曲線C2*を求めず、二
回微分し求めるので、どうぞ!また、判別式を使う手も高校生が為すので コレも どうぞ!
(→ 参考:「円錐曲線」)
n=2 次でない代数曲線(非円錐曲線)C:
-x5 - yx4 - 3x4 - y2x3 - 3x3 + y2x2 - yx2 - 3x2 + y3x + 2y2x - 2x + y4 + 2y2=0
の双対曲線C*を多様な発想で求めて欲しいのですが、「Duale Kurven」なる発想で是非求め
て下さい。(Doppeltangenteの図も在ります)(平成23年12月20日付け)
上を完了されるまで絶対下を視ないで下さい。
双対曲線C*をゲットされたのですね!有難う御座います。
図のようになり、特異点達も求め、飯高先生の感動を追体験なさいましたね。
(微分幾何學絡みの曲線を今回草色で明示しました。草色の曲線の方程式を是非求めて愉
しんで下さい)
草色の曲線の方程式、双対曲線C*の方程式を隠匿せず必ず明記下さい。特異点達をも
明記下さい。その名称をも付記願います。複接線を明記下さい。変曲点に於ける接線を明
記下さい。
赤線から瞬時にバレタでしょうが、この曲線は、Q上可約で、一つは知悉の円錐曲線の楕
円です。もうひとつは、飯高先生が変曲点を求めることはかなり大変である(図6)と11行解
説されておられる楕円曲線です。各々の双対曲線を求めることは(行列を為して叶うのも)易
しいので具現し、その左辺の積の展開をどうぞ!
数学のかんどころ シリーズ 7番目+n 番目として、参考図等を含んだ書籍が店頭に並
べば、初体験の事柄が書いてあり、立ち読みではもったいないと購買層は廣く、世界の人々
が行列を為して購入し、読破し、感激するでしょう。
「デカルトの精神と代数幾何」のはじめの章に書かれてあったことを、今回のように易しい
事例で具現すれば、こんなことになるのかぁ---と相乗効果で「デカルトの精神と代数幾何
飯高茂、上野健爾、浪川幸彦著」は売れに売れ増版される。
既版の数学のかんどころ(数学のかんどころ 飯高 茂,中村 滋,岡部恒治,桑田孝泰
編)シリーズに追加されたコレは既版のを凌駕してるかも...(そうありたく、日々厚かましく投
稿しております。)
<中村 滋,岡部恒治,桑田孝泰先生も此処を視て視ぬフリは為さらないで下さい>
ぜひ、数学のかんどころシリーズに追加願います。一番売れます。
(追伸) 赤点に於ける接線の方程式の具現は容易で高校生も為す。草色の曲線の導出過
程を隠匿せず、世界のだれにも分かるよう、勘所をも明記し、必ず導出願います。
飯高先生は知悉だが具現となると數分を要し想定通りの次数の代数曲線Q[X,Y]/<f[X,Y]>
が眼前にと安堵されるに違いない。(そして、次回の数名の受講生に出題されるに違いない。)
九州大學の問題を改竄した緑枠の問題を
(1) 双対曲線 C* を先ず求め、
(2) C* の特異点達 pj を求め、
(3) 2+2=4 次曲線Cの共通接超平面 Tpj(C)を(3)を用いて求め、
(4) 得たものを全て同一R2 に図示し、鑑賞し、感想を記して下さい。
(5) 近傍の諸氏へもこの発想で、九州大の問で必ず解いて!とお願いして下さい。
志村五郎&岩堀長慶&佐武一郎&山崎圭次郎&___&___共著で、2円について、
internal common tanjent,external common tanjent
なる用語が定義されているのを視ました。(→ 参考)
(6) 2+2=4 次曲線C=可約=C1∪C2=楕円∪放物線の
internal common tanjent,external common tanjent は全て在りますか?
(九州大の赤の4次曲線に共通接線達を有限本ひくことは、幼い無垢な子供が為すことが叶
うことです。)
(1)--(4) を 手計算で具現したものと_____の助けを借りて具現したものとで要した時間を教
えて下さい。
________の助けの例: 「PARI/GP」 (常用されておられますか?)
視れば必ず心底分かり、飯高先生の感動を追体験すべく努めました。図をじっと視て、す
べてを合点いただけましたでしょう。より易しい問達です。
C: x4 + yx3 - 10x3 + 10y2x2/9 - 10yx2 + 23x2 + y3x/9
- 10y2x + 24yx + 10x + y4/9 + 215y2/9 - 24 = 0
の双対曲線C*を、「Duale Kurven」なる発想で是非求めて下さい。
(Doppeltangenteの図も在ります)
C* はQ上可約な代数曲線K1∪K2 であることを示し、交点K1∩K2を求め、それから生じる
Cに於ける接超平面が4つ Tj 在ることを示し、CとTj を図示して下さい。
同じ結論:CとTj の図示を、今度は双対なる手法を用いず、判別式を用いて是非導出願い
ます。
やり取りを改竄して、『楕円E1と楕円E2で双対E1*、E2* を求めて解決も亦悦しからずや』
(平成23年12月21日付け)
易し過ぎる、例えば、線をひける幼児でも為す問も改竄したり、次元を上げに あげても通
用する「鶏を割くにいずくんぞ牛刀を用いんと揶揄されても牛刀が欲しい」ので為しました。
(初等的解法は、成年後は訳ありてやだと断じて為さぬ気構えは失いたくない難題だが...)
問題、即ち、易し過ぎる問題をも、飯高先生の講義で學んだ「牛刀=双対多様体」を用い解
決し、次元をあげた問題群にも近未来挑む企てを自らに課し.......、参考の如く共通接線達の
問題を解く(解いてしまいましたが行間を必ず埋めて下さい)
視れば分かるのに説明を加えたのが逆効果で何を云いたいのか曖昧だと云われそうで、
(→参考)図を視れば分かるので再々視願います。(解いてしまいましたが行間を必ず埋め
て下さい)
(初等的解法は、成年後は訳ありてやだと断じて為さぬ気構えは失いたくない.....難題だが...)
(→ 参考文献)
「Ellipse and Line」の最後の例に、易しい 4x2 + 9y2 = 36、x2 + y2 = 5 の共通接線の解説
が在ります。(平成23年12月22日付け)
参考図に明記したように、初等的な問題を牛刀をもって鶏を割くことが先の學習に繋がる
ので、今回も (x2 + y2 - 5)(4x2 + 9y2 - 36)=0 を敢えて可約か不透明にし、4次の代数曲
線 C: 4x4 + 13y2x2 - 56x2 + 9y4 - 81y2 + 180 = 0 について
(1) 双対曲線C* を求め、
(2) C* の特異点を求め、
(3) 如何なる名称の特異点か、知らぬ存ぜぬフリをして調査し、
(4) _____なる名称の特異点だから、それならもとのCの共通接線は、参考図の最後に示さ
れた通りだ、と牛刀=双対曲線C* を求めて解決したい。
C: 4x4 + 13y2x2 - 56x2 + 9y4 - 81y2 + 180 = 0 の双対曲線C* を私が「Duale Kurven」
なる発想で求めると、 45x4 + 65y2x2 - 14x2 + 20y4 - 9y2 + 1 = 0 となりました。
確認する術は幾つも在りますが、特に易しいのは、Cは易しい可約曲線:
C1: x2 + y2 - 5 = 0 、C2: 4x2 + 9y2 - 36 = 0
なる双方とも、n=2 次曲線なのですから、行列を用いて、それぞれの双対曲線が得られます。
C1*: f1*(x,y)=0 、C2*: f2*(x,y)=0 を講義の手法で必ず求め、積 f1*(x,y)・f2*(x,y)
を展開し、私が得た上の左辺になるか、確認願います。
(2) C* の特異点を求め、
(3) 如何なる名称の特異点か、知らぬ存ぜぬフリをして調査し、
(4) _____なる名称の特異点だから、それならもとのCの共通接線は4本存在する。
志村五郎・岩堀長慶・佐武一郎・山崎圭次郎・( )・( )共著で、2円について、
internal common tanjent,external common tanjent なる用語が定義されているのを視ました。
と以前申しましたが、今回の易しい楕円と楕円は容易に解けてしまう例でしたが、この用語が
使いたくなるような位置関係に在る問を自ら創作し、牛刀=双対曲線C* を求めて解決して提
示下さい。
一番上に酷似ですが、主軸問題をも考察し、次問を
(イ) 英文に倣う発想 と (ロ) 牛刀=双対曲線C* を用いる発想
で、次問を解いて下さい。
n=2次曲線 -72x2 + 60yx - 73y2 + 4356=0 と -13x2 + 20yx - 17y2 + 605=0 の共通接
線を求めて下さい。(せめて両曲線の正体を主軸問題を解いて、把握して、丁寧に図示し)
4次曲線 936x4 - 2220yx3 + 3373y2x2 - 100188x2 - 2480y3x
+ 123420yx + 1241y4 - 118217y2 + 2635380 = 0
の双対曲線C*を求める発想をも(以下、真摯な願いです)
(イ) は、高校生が解いて損はない問題ですので、近傍の高校生へ
(ロ) は、射影幾何學と n=二次 曲線の講義がなされている大學の受講生が、解いて損は
ない問題ですので、近傍の大學生へ
射影幾何學と n∈{3,4,・・・} 曲線、曲面、・・・の講義が為されている大學をご存知なら教
示願います。そして、双対曲線、双対曲面、双対曲__、・・・の講義が為されている大學をご存
知なら教示願います。
射影幾何學とn=二次曲線の講義がなされている受講生諸氏(解いていないにも関わらず
卒業認定されてしまった頃の)あんなに少人数で、至れり尽くせりの大學が在るであろうか。
卒業認定されてしまった受講生諸氏は、いくら何でも今回の
45x4 + 65y2x2 - 14x2 + 20y4 - 9y2 + 1 = 0
の双対曲線は求めずにはいられないと仕事の合間に具現なさって、あの当時為せばよかっ
たと振り返ってもしょうがないと思いつつ、しまったなぁ-と...飯高先生が再考査(追試験)をな
されば、その後の人生もかわったかもと...。
「一を聞いて十を知る」だそうですが、私は、一を聞いて(例えば1次元代数多様体)二を知
る(例えば2次元代数多様体)、二を聞いて三を知る(例えば3次元代数多様体) なんてすらあ
りえません。(平成23年12月23日付け)
しかし、直前達の可約因子2つの代数曲線Cの双対曲線C* を求めて、もとのCに関わる
問題を幾つも解決したので、可約因子3つの代数曲線C、問題がない筈がないと検索する
と、やはり在り解決しました。
問題自体は、3つの適当に配置された円の internal common tanjent,external common tanjent
(志村五郎&岩堀長慶&佐武一郎&山崎圭次郎&___&___共著で 2円について
internal common tanjent,external common tanjent なる 用語が定義されているのを視ました。)
を幼児でも叶うので、真似て引きまくると、図が得られました。
(さいた さいた チューリップのはなが ならんだ ならんだ あか P1 しろ P2 きいろ P3
3点が collinear (ならんだ ならんだ) を双対から解決。
視れば瞬時に何を為すべきかは分かるようにしましたが、手順を書きます。
先ず、(1) n=2 でない6次代数曲線C:
((x + 2)2 + (y - 9)2 - 4)((x - 7)2 + (y - 7)2 - 9)((x - 1)2 + (y - 1)2 - 1)=0
即ち、 x6 - 12x5 + 3y2x4 - 34yx4 + 135x4 - 24y2x3 + 280yx3 - 1016x3
+ 3y4x2 - 68y3x2 + 622y2x2 - 3388yx2 + 8879x2 - 12y4x
+ 280y3x - 2024y2x + 7224yx - 15196x + y6 - 34y5
+ 487y4 - 3612y3 + 13103y2 - 17154y + 7209 = 0
の双対曲線C*を求めてください。(添付の青になる筈です。曲線も描きましたが錯綜しています)
(2) 得た双対曲線C*の特異点を全て求めてください。
(3) 得た特異点達から、もとの曲線Cの接線の方程式を全て此処に記し、
(4) CとC*と接線達を全て同一 R2 に描くと私が為した図のようになることを確認し、
(5) 接線達の全ての交点達を計算で求め、適当な3点を選んで結ぶと、幼児が歌う通り、な
らんだ ならんだ あか P1 しろ P2 きいろ P3となることを計算もし確認願います。
(いっぱい一列に並んでいるので色分けし線で結んでください)
私は、n=2 でないこの6次代数曲線Cの双対曲線C*は、「Duale Kurven」なる発想で求めま
したので、そうなさって下さい。可約なので、飯高先生の講義の手法でも偶々叶うので具現し
て下さい。今回もまた牛刀をもって鶏を割きましたが愉しくありませんか?
(さらなる切れ味抜群の牛刀が在れば、使いながら解説願います)
幼児でも為す黒線達=代数曲線の接超平面達を描くことは、次の手順で可能です。
先ず、(1) 2次でない6次の可約曲線 C の双対曲線C*を「Duale Kurven」なる発想で必ず
求めてください。(可約で各因数が2次故、容易に叶うので、其れからも必ず)
(2) 得た双対曲線C*の特異点を全て求めてください。
(3) 得た特異点達から、もとの曲線Cの接線の方程式を全て此処に記し、
(4) CとC*と接線達を全て同一 R2 に描くと私が為した図のようになることを確認し、
(5) 接線達の全ての交点達を計算で求めて下さい。
こんどは、参考図とは異なり、幼児が歌う通りとはならない。
共線ではありませんが、楕円にしたら、どの程度共線具合が逸脱したか、幾つかの楕円
の3組を自ら設定し、各組毎に逸脱度を調査願います。
共線という数學的概念は、過去も現代も未来も未来永劫重要と素敵な丁寧な解説が存在
しました。西山先生は双対曲線の視座から未だ考察されておられないので、此処を訪問願
いたいです。
「 同一直線上」で検索すると、「シムソンの定理」に漂着しました。もう遅いので明日以降味
読させていただく所存です。
解説をお読み下さい。(平成23年12月23日付け)
この事実は、古来著名で何にも新たな発見でもなく取り上げるまでもないと一蹴されそう
ですが、故きを温ねて新しきを知るなんて為せる問題です。手順を記します。
(1) 先ず、赤の楕円 C: f(X,Y)=0 の双対曲線C*を求めて下さい。n=2次曲線なので、飯高
先生の講義の手法でも偶々叶うし、私が記した発想でも叶うので具現して下さい。
x2+yx+y2-4/3=0 の正体は想定通りの挿入、顛末です。
(2) 2点C∋(xj,yj)に於ける接超平面を考えると、
x1x + y1y + 1=0、 x2x + y2y + 1=0、 f*(x1,y1)=0、f*(x2,y2)=0、x1x2 + y1y2=0
から、 {x1, y1}、 {x2, y2} を消去するだけでよい。(下のシルベスター行列式でどうぞ!)
消去と云えば、常套手段;シルベスター行列式
(3) 消去して、(2)で得た結論 x2+y2=___ が正しいかの確認法は数多在り。
首を傾けて、絵のようになっていれば、ほぼ間違いない。高校生の練習とおもって、C上の
具体的な点を定め、その点に於ける接線Tを求め、接線Tと x2+y2=___ の交点を通るTと垂
直な直線LがCの接線になっていれば文句なし。(2)がメインです。
灘高校の問題で、常套手段:シルベスター行列式を用いて、a を消去すれば楕円が得られ
るでしょう。この楕円について、上の(1)(2)を為して下さい。
無論、n=2次曲線だから、双対曲線C* は講義の手法でも偶々叶うので即座に行列を使い
どうぞ!
此処に出現する4つの二次曲線(飯高先生出題の y=x/(x+5)、その双対曲線、赤線、青線)
のそれぞれについて双対曲線を用いて、P (X,Y) からひいた2本の接線が90度となるような
点 P の軌跡を求めて下さい。
双対曲線を用いて、1+1+4問も解いた感想を記して下さい。恐らく世界初でしょう。もし、先
達がみあたりましたら、ご教示下さい。近傍の方々に、この種の問を双対曲線をもちいて解
いて!とお願いして下さい。
条件を緩和して、束縛条件として、2接線の為す角が48度のときの軌跡をも多様な発想で
求めて下さい。(π/3でもいいです)
(外部の点 P (X,Y) からひいた2本の接線が48度となるような点 P の軌跡を求めて下さい)
備考;「 P (X,Y) からひいた2本の接線が90度となるような点 P の軌跡を求めて下さい。」
なる各問題に存在すれば、とか留意点を付記する必要がありますか?
f(x,y)=2x2-5yx+2y2+2x+ 2y とする。代数曲線C: f(x,y)=0 (双曲線であることを確認し)
の、P(X,Y) から C へひいた2本の接線が90度となるような点 P の軌跡を求めよ、と云うよ
くある問題に、次の発想で取り組んで下さい。
(1) 先ず、C: f(x,y)=0 の双対曲線C* を求めて下さい。n=2次曲線なので、飯高先生の講
義の手法でも偶々叶うし、私が記した発想でも叶うので具現して下さい。
f*(x,y)=____________________________________.(曲線の名称は______)
(2) 2点 C∋(xj,yj)に於ける接超平面を考えると、
x1x + y1y + 1=0、 x2x + y2y + 1=0、 f*(x1,y1)=0、f*(x2,y2)=0、x1x2 + y1y2=0
から、 {x1, y1}、 {x2, y2} を消去するだけでよい。(下のシルベスター行列式でどうぞ!)
消去と云えば、常套手段;シルベスター行列式
減点パパがいると警戒し、(2)よりP の軌跡を求めて下さい。
f(x,y)=4x2 - 8yx + 36x + 4y2 + 36y + 9 とする。代数曲線C: f(x,y)=0 (名称は_____)の
P(X,Y) から C へひいた2本の接線が90度となるような点 P の軌跡を求めよ、と云うよくあ
る問題に、次の発想で取り組んで下さい。
(1) 先ず、C: f(x,y)=0 のP(X,Y) から C へひいた2本の接線が90度となるような点 P の
軌跡を求めよ、と云うよくある問題を求めて下さい。n=2次曲線なので、飯高先生の講義
の手法でも偶々叶うし、私が記した発想でも叶うので具現して下さい。
f*(x,y)=____________________________________.(曲線の名称は______)
(2) 2点 C∋(xj,yj)に於ける接超平面を考えると、
x1x + y1y + 1=0、 x2x + y2y + 1=0、 f*(x1,y1)=0、f*(x2,y2)=0、x1x2 + y1y2=0
から、 {x1, y1}、 {x2, y2} を消去するだけでよい。(下のシルベスター行列式でどうぞ!)
消去と云えば、常套手段;シルベスター行列式
(2)よりP の軌跡を求めて下さい。
P(X,Y) から C へひいた2本の接線が90度となるような点 P の軌跡を求めよ、と云う問題
は、今後も廃れることなく入試、院試等にも出題されます。
そのとき、上の如く双対曲線C* を求めて解決する発想が、よい意味で蔓延すべく教育に
携われておられる諸氏へ協力要請を致します。採点者様も此の解法を受認してくださる世
の中であって欲しい。
上では、標準型でない2次曲線を標準形にすることなく自然に結論に到達しました。
下の既に標準型のCの、そのような問題の解説達を讀み、双対曲線C*を求めて解決して
みて下さい。(愉しい筈です)
参考図をちらっと視て下さい。(こんなのが考査、入試、院試で出題されると皆んな喰らい
付く) (平成23年12月24日付け)
問題は、R2 に於ける曲線Cを定め、K=拘束された点C上の点 A、B に於ける接線TA(C)、
TB(C)の為す角に於ける拘束条件:例 AKB=84度と自由度を奪われたKの軌跡。
まず、今までの人生で遭遇した諸問題の内でもっとも容易に問題が把握できてしまう問:
易しい曲線C: y=xn (n=2) に点Kから2つの接線TA(C)、TB(C)をひき、其れ等の交角AKB
が 90度なのは知悉なので少し変え、例えば、60度であるよう拘束された点Kの軌跡を求め
て下さい。
もう一度、参考図を視れば、題意は火を見るより明らかでしょう。この題意が非常に明確
な問を、飯高先生の講義受講者になりすまし、習得した証の例として解きたい。即ち、
(1) 何よりも先ず、y=x2 の双対曲線を求めることを為して下さい。
(2) は既出の通りです。
(2)を用いて、気持よく拘束されたKの軌跡を求めて下さい。
(草色曲線の一部の上に拘束されて自由度を奪われ可哀想でしょう)
終結式により、上で容易に K の軌跡を求められたでしょうが、傾きを、m1、m2 とし、正接
の公式等を持ち出し、黒板で解説されそうな解法をも為し、双対曲線を用いる発想で解放さ
れたことを感受願います。
世界に、「双対化し、気持よく解決する発想」を廣めて下さい。此れで、全て氷解したので
はないので止めず、例えば、手計算で叶うのを選択し、AKB=2π/m (m∈{24,12,5,17,.....}
等とし、定めた各角について、(2)を(すこし改めて)用いて、気持よく拘束されたKの軌跡を求
めて下さい。
問題が未だ解けていない方や解いてそれでおしまいの方や高校生にも解いて欲しいので
易しい問を記します。
次のn=2次の代数曲線 Cj を定める主軸問題を解き、図示して下さい。
C1: 41x2 - 20yx + 20x - 16y2 - 4y + 2=0
C2: 3y2 + 4xy - 2y + 4x - 1=0
(1) 共有点 C1∩C2 が在れば求めて下さい。
(2) 双対曲線C1*、C2*を求め、図示し、C1*∩C2*が在れば求めて下さい。
(3) C1*、C2*の共通接線達を直に求めないで、(C1*)*、(C2*)*を求めて図示して下さい。
(4) C1、C2には共通接線が存在しないことを証明して下さい。
2次曲線の双対曲線は、もう行列のあの発想で解いてもう學習済で為すべきことがないと
自らに云ってらっしゃる方へ:
(41x2 - 20yx + 20x - 16y2 - 4y + 2)(3y2 + 4xy - 2y + 4x - 1)=0
が可約な代数曲線であることを、知らぬフリし、左辺を心のなかで展開し、その履修済の
n=2の倍の4次の代数曲線Cの双対曲線 C*を多様な発想で求め、正しくC*を求めたかの
確認は、(C*)* を多様な発想で求めて為して下さい。無論、C---rational map--->C* も明
記してください。
双対曲線の定義は(短文で且つ)明確。(平成23年12月25日付け)
飯高先生の射影幾何學を受講された方、したかった方の世界の方々への、こう問題を提
示されたなら誰でも瞬時に出来てしまうという緊急自信速報です。受講生に出題された単位
認定用の問題に即して云えば、高次とはとても云えないn=2次方程式
(x+5)y-x=0 (函数: x ---> y=x/(x+5))
の(疑う余地もない滑らかな曲線)の接線の方程式を中學で教わった y=mx+n とせず、
Ax+By+1=0 と超平面認識に改め、其れが (x+5)y-x=0 とただ一点のみを共有すべく所望
すれば、多様な発想で(微分學を既習の方は其れで、未習の方は終結式で、終結式が嫌い
な方は D=0で)飯高先生の方針では大変でしたと述べられておられることが必ず頗る容易
に叶います。直ぐ具現を為します。
一番低学年の手法で云うと、連立方程式 (x+5)y-x=0 と Ax+By+1=0 をさぼらず本当に
解いて、
x={-1/2 - 5A/2 - B/2 - (1/2)√((1 - 5A - B)2 + 4B])}/A
y={-1 + 5A + B + √((1 - 5A - B)2 + 4B])}/(2B)
または、
x={-1/2 - 5A/2 - B/2 + (1/2)√((1 - 5A - B)2 + 4B])}/A
y={-1 + 5A + B - √((1 - 5A - B)2 + 4B])}/(2B)
を得て、√((1 - 5A - B)2 + 4B]) の中が 0 であればよく、(1 - 5A - B)2 + 4B=0 で、高1の
學生がとけてしまった!
なんなら A を x、 B を y にして、飯高先生が__分取り組み、ゲットされた結論と当然
同じです。図示すると、もとの試験の赤線=C よりは難しい青線=C* です。
(限りなく 0 人に近い解いた受講生は、あれ?ミスはない筈なのに、自分が得たC*の主軸
問題も解かなければ単位認定されないのだろうかと忖度。
一番低学年の手法で云うと、上の如く、手計算で3分も要し、人生が短いので、もっと短時
間所望なら、知悉の判別式で、1分以内程度で叶います。射影幾何學履修の認定の証書が
付与されます。
できなくても履修認定されてしまって、自信のないことの自覚者への緊急自信速報です。
出だしに吐露したように、ふと思うことが、こんなに大切だと初めて経験し、講義も受講し
ていないのにできてしまいました。これまで、私が数多の双対曲線具現をお願いしてまいり
ましたが、今回のふとおもうからの視座で、全て具現される筈です。是非お願い致します。
(無論、飯高先生への次回以降の講義の際、指導内容に含めて下さいとお願い用でもあり
ます)
数多の双対曲線具現は、もう為し、忘却の彼方の方へ。直前のを再掲しますので、ふと
おもうの発想で瞬時に次問達を解いて下さい。
次のn=2次の代数曲線 Cj を定める主軸問題を解き、図示して下さい。
C1: 41x2 - 20yx + 20x - 16y2 - 4y + 2=0
C2: 3y2 + 4xy - 2y + 4x - 1=0
(1) 共有点 C1∩C2 が在れば求めて下さい。
(2) 双対曲線C1*、C2*を求め、図示し、C1*∩C2*が在れば求めて下さい。
(3) C1*、C2*の共通接線達を直に求めないで、(C1*)*、(C2*)*を求めて図示して下さい。
(4) C1、C2には共通接線が存在しないことを証明して下さい。
2次曲線の双対曲線は、もう行列のあの発想で解いてもう學習済で為すべきことがないと
自らに云ってらっしゃる方へ:
(41x2 - 20yx + 20x - 16y2 - 4y + 2)(3y2 + 4xy - 2y + 4x - 1)=0
が可約な代数曲線であることを、知らぬフリし、左辺を心のなかで展開し、その履修済の
n=2の倍の4次の代数曲線Cの双対曲線 C*を多様な発想で求め、正しくC*を求めたかの
確認は、(C*)* を多様な発想で求めて為して下さい。無論、C---rational map--->C* も明
記してください。
ふと思ったことを誰にも理解し具現願いたいと考えます。無論、飯高先生の行列の発想
も愛して、高次元の2次限定超曲面、双対曲面の際も倣いたいですが、確実に挫折しそう
ですが頑張ります。
(追伸) 飯高先生は、試験まえに、例えば、 (x+1)y=x の双対曲線はカクカクシカジカと数
分、行列をいじり具現し、類似のを必ず出題するから解いてくれたまえと黒板に提示
された筈.......。このリハーサル問題を、ふとおもう発想で、1分以内に解いて下さい。
無論、数多の以前のお願いのC達をもお願いします。
(コメント) (x+1)y=x と Ax+By+1=0 が接するときの A、B の関係式を求めると、
A2+2AB+B2-2A+2B+1=0 となる。
このことから、C:(x+1)y=x に対して、C*:x2+2xy+y2-2x+2y+1=0 を得る。
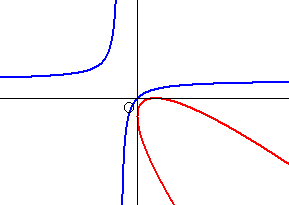
双曲線Cに対して、曲線C*は、C*を
原点の周りに45°回転させると、
y2 =
となるので、放物線である。
(コメント) 飯高先生の問題の図に似てい
てよかったです!
受講生でもないのに出来てしまいました。(平成23年12月26日付け)
今度は、終結式をm=2度用いて、
(1) 解読 されたら、それが正しいか、逆に
(2) 25X2 + 10YX - 10X + Y2 + 2Y + 1=0 の双対曲線を終結式をm=2度用いて其の行列も
明記し求め、飯高先生出題のy=x/(x+5) になる迄為して下さい。
(3) また、25X2 + 10YX - 10X + Y2 + 2Y + 1=0 の双対曲線を、前に記した、高校1年が為
す方法で求めて下さい。
双対曲線を終結式で求めるには、m=2度使用し解決した。
(4) 双対曲面を終結式で求めるには、____度使用し解決。事例で具現願います。
(5) 双対__を終結式で求めるには、____度使用し解決。事例で具現願います。
上の高校1年が双対曲線を求めたについて、紫枠で問いかけたからです。いっそのことと
紫枠を付加しました。
(6) 途方もなく容易な双対曲線の導出を、いっそのこと、ふと思う法で為して下さいと、近傍
の方にお願いして下さい。(海外に居られる非近傍の方にも)無論、終結式で2度使用す
る導出法をも。
(7) 味をしめ、もうどうにもとまらなくなる筈です。y=xn (n∈{3,4,5,...} の双対曲線の導出
を、いっそのことふと思う法で為さずにはいられないと。
終結式を好きになりましたでしょうか?他の諸問題で溺愛されておられれば、事例達を御
教示願います。
次の各代数曲線について、双対曲線を、いっそのことふと思う法 (なら高校生が為す)や
終結式をm=2度使用法等で求めてください。そして、「デカルトの精神と代数幾何 飯高茂、
上野健爾、浪川幸彦著」の自己双対曲線を讀んで下さい。
{y2 - x3 = 0,,y2 - x5 = 0, y2 - x7 = 0, y2 - x9 = 0, y2 - x11 = 0,, y2 - x13 = 0}
{y3 - x4 = 0, y3 - x5 = 0, y3 - x7 = 0, y3 - x10 = 0, y3 - x11 = 0, y3 - x13 = 0}
= {y4 - x5 = 0, y4 - x7 = 0, y4 - x9 = 0, y4 - x11 = 0, y4 - x13 = 0}
いっそのことふと思う法で、飯高先生の黒板に提示されたリハーサル問題を、高校生なら
こうして解けてしまう!と提示していただきました。緑枠のmapをも是非具現願います。
講義手順 何よりも先ず為すべき射影化に________分、行列表現に______分、逆行列を求め
るのに____分、それから双対曲線を求めるのに____分、そして、最終局面の逆射影化を為す
時間に_____分。答が不安になり多様なチェックが存在するだろうと思案に要する時間が___分。
一番手早い手段を選択し為す時間____秒。(または、(A-1)-1=A だから、(C*)*=C は自明で、
確認の必要なしと自信満々かも) 総計 手計算で_____分。
やっと、講義通り解けて、親に経済的な負担をこれ以上かけずに卒業できると安堵・・・と
思いきや、C のどの点がC* のどの点に対応していることを示せと設問にないが為すべきだ
と再考を開始:_______________。いくら教えられた手順を視ても、map が導出不可なので、やっと
自ら考え始める(履修を認められた試験後も考え続け) __分かけて、map を導出し、やれや
れやっと解けたぁ!いや、待てよ、飯高先生は、ひっかけ問題は今まで出題されなかったの
で本番で悪戯に複雑なn=2次曲線を与えて、双対曲線を求めよ、なんて為されないが、単純
な問題で、講義が理解出来ているか、いつものように出題なさるに違いない。
例えば、単純なn=2次曲面Sを与え、上の如く、双対化すると名称が変わるような問を自ら
創作し(自分に不利にならぬよう超易しいのを)行列を用いて解きなさい、と本番で為される
ことは誰にも想定の範囲内の予想問題です。
この大學生に倣い、単純なn=2次曲面Sを与え、何よりも先ず射影化し、...等の手順を
踏み、最後まで時間を測りながらやりとげて下さい。
(無論、出題される教授が解くに要すと心中で考えられる時間内で____分)
そして、この問題、曲面の問題を、いっそのことふと思う法で、高校生ならこうすると必ず
示して下さい。無論、S、S* を図示もし、map も隠匿せず明記してください。
大學生は、試験後ずっと、例えば、何で射影化しないとだめなんですかと懐疑。2<n次曲
線(曲面)の双対をなぜ出題していただけなかったのか...。試験後、為してみると、次数
は大抵高くなり、疲労困憊(行列のせいじゃない)。なぜ、わざわざ難化するの?
C、S、...、C*、S*、...の少数の黒板に為されたのを視ると、どれもC*、S*の方が難。
なぜ、わざわざ難化するの?
特に、講義のC*が放物線(parabola)(本番のも然り)なんて、何処の天体の住民なのと云
われそう。主軸問題をきちんと解いたなら、疑う余地はないのに...と、等々、卒業後も未
解決の諸問題に悶々として社会生活を送っているのです。
以上、教えられる方の目線で発すべき問題達を記してみました。此処で、「志村五郎」を想
起致しました。139p---教える身になってと。x=3 を、X・x+Y・y+1=0 と認識にも関わる記載在
り。飯高先生は、代数幾何学Ⅲ 315p では、X・x+Y・y=1 流派(何れが主流?)
( X・x+Y・y=1 で正しい答を導出したら、×印をなさる先生が存在か? )
今回のを、X・x+Y・y=1 流で高校生に勧めてください。大學生は、行列の方をも。
今回のは、CにもC*にも特異点がなく、次数も不変の2次なので寂しい、ので易しい例。
(X・x+Y・y+1=0 、X・x+Y・y=1 流、双方の流派で)
無論、C*を用いて、複接線を。(高校生なら代数幾何を學ぶ契機になる易しい問題です)
これでは未だ次数が4次と不変でわびしいと次の問題。何れも、いっそのことふと思う法で、
高校生も叶うので具現し、他の例えば終結式を使う大學生の模倣をも。無論、先ず為すべ
きは射影化ですね...。
紫枠 = 講義の通りの射影化を頑張って為し た方へのふとおもう法を視てご理解願います。
具体例に即して記載します。
先ず、何をさておいても早速にやらなけれはならないことが、と講義の通りの射影化を頑
張って為し、XY + ZY - XZ=赤文字の右上まで為し、此処まで出来て手が止まった學生が
存在(部分点:_____点)。その先の行列表現に行き詰った學生に「行列のできない相談所」
救済策を講じたい故、青色で強調した言い回しの(今回の云われた通りの射影化までし頓
挫した方へ)
射影化まで為して、頓挫者向けのふとおもう法で、答の
X2 + 2YX - 2ZX + Y2 + Z2 + 2YZ =0
に高校1年生も辿り着き、教えてもいないのに、よく出来ましたと満点+αを飯高先生が与え
られる。
行列未履修の高校1年生も辿り着くプロセスを省くことなく記述願います。
云う必要のないHint:{AX + BY + CZ = 0、XY + ZY - XZ = 0} この連立方程式を解く前に、
一文字Xを多様な発想で消去し、BY2 - AZY - BZY + CZY - CZ2=0
を得て、例えば、Y について易しい2次方程式だ!それなら_________ で
瞬時に答の X2 + 2YX - 2ZX + Y2 + Z2 + 2YZ =0 に高校1年生も辿
り着く。
(プロセスを省くことなくとお願いしましたが、殆ど到る所記してしまい
ました)
講義の、先ず射影化は、その重要性を認知したいが、その直後、行列表現し、更に、逆行
列をは、ネクタイでぎゅうぎゅう自分で自分の首を締め墓穴を掘るような気がしてなりません。
(しかも、2次限定)何とか草色枠でもっと安価にC*を得たい。
今回の射影化後、行列表現することなく瞬時に安価にC*が得られないかと、ふと思う法と
は、告白します!定義に戻れば、瞬時です。是非、このふと思う法で瞬時に飯高先生出題
問題を解いて下さい。
如何でしたか?逆行列が嫌いな方もそうでない方も「掃き出し法(sweep out method)」とか
を用いて解き、上のふと思う法と対比願います。
草色枠の下に、硲先生に言及しました。「代数幾何学」で、射影化後、行列表現され、逆
行列を求めておられます。其れを回避し、ふと思う法で瞬時とメールしたいくらいです。
ふと思う法を何度も引用し、しつこいと云われそうですが、私はそんな性格ではありません。
しつこいには理由が数多在ります。
飯高先生は出来がよくなかったと記載され、それから1ケ月後何故不出来であったか、分
析結果を公表されました。私なりに、何故不出来かを分析し、遂に、高校1年でさえ出来ちゃ
ったと言わしめるまで、問いかけを工夫致しました。
何故不出来であったかの理由は判明しているのですが、硲 文夫先生も双対曲線を求め
る際、次の手順を何故か踏まれておられるので、學生向けに主旨を述べつつ、それに従順
に従うよう設問を試みます。
二次形式と云えば、対称行列と固執し過ぎると、出来が良くないことが判明した。
各問は指示された通りにせよ。
7x2 + 5yx + 3y2 - 1=0 を先ず射影化せよ。途中経過を必ず書け。
C: 7X2 + 5YX + 3Y2 - Z2=0 となった筈。
此の左辺の二次形式(quadratic form) を、線型代数で必ず為すよう講義されたように、行
列M(q)表現せよ。(対称行列になっていなければ、誤りがあるので留意せよ)
此処で、M(q) について、
「二次形式論における最も重要な問いは、変数の斉次線型変換によって、二次形式 q が
どの程度まで簡約できるかということである。」
を線型代数で履修し、単位が認められておれば考察しなくてよい。即ち、単位が認められて
いないなら詳しく考察せよ。
次に、M(q)-1 を求めよ。
M(q) の逆行列を求める発想は線型代数で履修した筈。例えば、掃き出し法で教授された
なら、その途中経過を省くことなく記せ。解答欄に書けないなら 裏まで使え。
M(q)-1 に対応する二次形式を記せ。
以上から、射影幾何の講義で為したCの双対曲線C*が得られた。
講義で、(C*)* =C は証明したので為さないでもよい。(為してもよい)
が、上で君が得たC*から開始し、上の全ての指示した手順を忠実に実行し、(C*)* =C とな
るまで努力せよ。ならなければ、君の云う努力は認めない。
射影化の逆を為したら、f*(x,y) を線型代数で講義されたように行列表現を為し、固有値
問題を解き、f*(x,y)=0 を綺麗に図示せよ。無論、主軸も明記し図示すること。
今回の再考査用のリハーサルの上の設問で、元の曲線と f*(x,y)=0 の名称は同一であっ
たことが判明した筈。逆行列を求めるのが大変であったろう。労は労わないので、元の曲線
と f*(x,y)=0 で囲まれた部分の面積でも求めて、自分で疲れを癒せ。
本番の問題を解いた人が、CとC*の名称が変わっていたと云っていただろう。何故、名称
がコロコロ変わる、または、不変なのか、実例で100個為し、レポートとして2日後までに提出
せよ。(無論、上の行列を用いる指導した方法に限る)
(2<n次曲線の双対曲線を求める自由は保証するが、単位としては認めない)
代数曲線全体の集合⊃n=2次の代数曲線の全体の集合∋{C1,C2,......,C100}について、
Ck、Ck* 其々の定義式と名称を記せ。。
以下がメインのお願いです。(次回の射影幾何の講義用)
ふと思う法により、7x2 + 5yx + 3y2 - 1=0 の「射影化後、行列に固執しない」ことを許容さ
れるなら、瞬時に双対射影曲線が得られますので、是非具現願います。
(コメント)
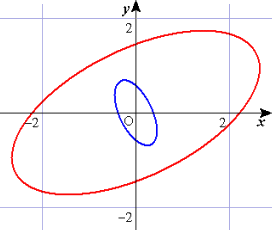 C:7x2 + 5yx + 3y2 - 1=0 を射影化して、
C:7x2 + 5yx + 3y2 - 1=0 を射影化して、7x2 + 5yx + 3y2 - z2=0
このとき、ふと思う法により、
12x2 - 20yx + 28y2 - 59z2=0
即ち、 C*:12x2 - 20yx + 28y2 - 59=0
C、C* はともに楕円である。
(← 青:C 、赤:C* )
Oに関する円、球、...の反転Fによる像は、何処にも在る問題です。
(平成23年12月28日付け)
超平面Hに関する鏡映(対称)変換:Rn---S(H)--->Rn では、其処に在るものを何でも変
換する(鏡はそうする)。反転では、何でも写してやろう精神が欠如してるなぁと思っていたら
図の如く、中学生が學ぶ y=ax2+k (m=2) の像を求めようとする気配が在る。
それなら匂わすだけに終わらず是非具現して視たい。端的に諸問題を記載していますの
で、即座に取り組んで下さい。
反転Fは、F(x,y)=(x/(x2 + y2), y/(x2 + y2)) です。先ず、F・Fを求めることにより、F-1を
求めて、易しい赤線のFによる像F(C)を必ず求めて下さい。
上では、F-1 を利用して、像F(C)を求めましたが、他の発想で、像F(C)を求めて下さい。
(この発想が、あらゆる場面で有効で諸々の問題が瞬時に解決しますので是非!)
あとは、双対曲線を幾つか求め、どの点がどの点に写されるか明記する問題達ですが、
飯高先生の講義に潜り込んで、贋學生になったつもりで、先ず、射影化し、云々の指導に
従い、各曲線の双対曲線 を 求められるものは 求め、そうでないの は諦 め て。
ふと思う法(参考1、参考2)で、行列では求められないものまで完璧に求めてください。
端的に諸問題を記載していますので、即座に取り組んで下さい。さあ、開始せずにはいら
れない、どうぞ!(写像図式を記していますが、可換図式ですか?)
求めたF(C)=青線 には、線を引ける幼児が為す複接線が在る故、もとめる前から、その
双対曲線には____なる名称の特異点が在る筈と想定し、本当に、その双対曲線を求め(黒
線で図示されている通りの)想定の範囲内の特異点が在ると座標を求め、それから、もと
の複接線を求める若い頃の飯高先生の感動を再現して、代数幾何學へ猛進して下さい。
無論、想定の範囲外の壁に直ぐぶち当たります。
私がF(C)を求める際、殆どの人が為さぬが重視している発想で頑張って為したら、中學生
が知悉の2次曲線が高次曲線: 3x4 + 6y2x2 - 4yx2 - 4x2 + 3y4 - 4y3=0 に変換されたの
で、私が為したことにミスが珍しく存在しないならば、この高次曲線は飯高先生のリハーサル
問題を遥かに凌駕している問題で、解かずに解けたなんて云っている場合じゃないことが分
かり、解かずにはいられない。
難でも、非線型写像で写像してみんとて為しました(過去形でなく始まりです)
代数曲線Cが在れば、必ず直ぐ具現したい曲線C*が在る。無論、C*の特異点達も調査開
始(ことを知らぬ儘、卒業し単位認定証もあるぞと云う人が存在するに違いない)
(ことを知らぬ儘、卒業し数學教育にたずさわっておられる人<中高大院>も存在するに違い
ない)
代数曲線全体の集合AC⊃2次の代数曲線の全体の集合∋Cj--*-->Cj*∈2次の代数曲線の全体の集合⊂AC
写像*を、この部分集合に限定すれば、即ち、高次の代数曲線を禁欲すれば、
n=2次の代数曲線の全体の集合∋Cj---*--->Cj*∈n=2次の代数曲線の全体の集合
次数は不変で、* は全単射と見做して(少し断わりを付与し)構わない。ただし、C*の名は
不変とは限らない。その例を快く為していただきました。
Cの双対曲線C*をCの影=C*と命名する。これで、もう恒に付随していて、今後の人生で
片方のみ考えて理解終了なんてなくなる。各Ckの影Ck* を慕いて→参考図
問題 この楕円族の双対曲線族を、今の時点で双対曲線化最速の手法で直ぐ為し、影
Ck* を慕いて、影Ck* が改名されて 楕円にならないkを求め、更に、双曲線、放物線にな
るものに分類して下さい。kを動かし、如何なるkで名が激変するか探究願います。
どうにも止まらなくなり、楕円曲面族 Sk の影 Sk* を慕いて、同様な愉しみを奪うことは控
えますので、ご自分でどうぞ!
Table[-1 + 7(-k + x)2 + 5(-k + x)(-k2 + y) + 3(-k2 + y)2 = 0, {k, -3, 3, 1/4}]
を「Wolfram|Alpha」に挿入しても、 かもめ(楕円族)を描いてくれないのかぁ...。私が描く
と、有心n=2次曲線が放物線上に綺麗に並び、飛んでる姿が眼前に。
次数は不変で、* は全単射と見做して(少し断わりを付与し)構わない。ただ、C*の名は不
変とは限らない。その例を、快く為していただきました、と上で謝辞を述べましたが、引用図
は射影化後のではなく、射影化しない儘の、ふと思う法でご協力いただいたようです。
射影化後のふと思う法で瞬時に双対曲線化を具現願います。射影双対曲線のところまで
で構いません。
代数曲面 Sk の影 Sk* を慕いて、具体例の参考図(資料:Geometric Inversion)を視た刹
那、一つ次元を上げ、球面反転なる非線型写像を考察しないではいられないでしょう。
易しい二次曲線 C のかわりに易しい二次曲面Sからスタートし、各問題を必ず解いて下さ
い。
この写像図式のF(S)は、もはや、二次曲面ではなく、おそらく、邂逅初夜の特異点の在る
高次曲面でありましょう。更に、F(S)* は次数も激変し、特異点の在る高次曲面でありましょ
う。具現すれば、世界初でしょう。創作された問題で、ふと思う法が使える2次曲面が現れた
ときは射影化し、行列表現を為す等やり遂げて下さい。また、行列表現をすることなく、ふと
おもう法で瞬時に双対射影曲面をも求めて対比願います。
どうにも止まらなくなり、代数曲面 Sk--F--> F(Sk) の影 F(Sk)* を慕いて。
(→話題3へ続く)