高校数学から大学数学へ進化していく過程で、「Ｗｅｌｌ Ｄｅｆｉｎｅｄ」ということが、否応にも
意識され始める。私自身最初のころは、その本質を理解しないまま、見よう見まねでなんと
なく使っていた覚えがある。
「ある概念の定義をする場合、そう決めることによって、何も矛盾なく上手くいく」ということ
が確認されているということを「Ｗｅｌｌ Ｄｅｆｉｎｅｄ」という。今回、次の書籍：
土基善文 著 ＸのＸ乗のはなし （日本評論社）
を読んでいたら、「Ｗｅｌｌ Ｄｅｆｉｎｅｄ」の話があって、改めてその奥の深さを認識させられた。
「Ｗｅｌｌ Ｄｅｆｉｎｅｄ」という言葉に初めて接するのは、おそらく「位相空間論」の講義におい
てだろう。または、「群論」の講義かもしれない。
例 集合 Ｓ 上の同値関係を、Ｒ とする。
直積集合 Ｓ×Ｓ の部分集合 Ｒ を関係といい、（ｘ ，ｙ）∈ Ｒ のとき、ｘＲｙ と表す。
関係 Ｒ が、次の３つの条件を満たすとき、同値関係という。
（１） ｘＲｘ （反射律）
（２） ｘＲｙ ならば ｙＲｘ （対称律）
（３） ｘＲｙ 、ｙＲｚ ならば ｘＲｚ （推移律）
今、ｘ の剰余類を Ｃｘ ＝｛ ｙ∈Ｓ｜ｘＲｙ ｝ とし、商集合 Ｓ/Ｒ＝｛Ｃｘ｜ｘ∈Ｓ ｝ が定ま
る。 ２つの集合 Ｓ、Ｔ に対して、写像 f ：Ｓ → Ｔ を考える。
ｘ ，ｙ∈Ｓ に対して、ｘＲｙ のとき、ｆ（ｘ）＝ｆ（ｙ）
が成り立つとき、 ｆ は、同値関係 Ｒ に関して、Ｗｅｌｌ Ｄｅｆｉｎｅｄ であるという。
これは、商集合 Ｓ/Ｒ の各剰余類に対して、その代表元の選び方に関係なく、ｆ（ｘ） の値
が一定であることを意味する。
このとき、写像 ｇ ： Ｓ/Ｒ → Ｔ が、 ｇ(Ｃｘ)＝ｆ（ｘ） により、自然に定義される。
すなわち、「Ｗｅｌｌ Ｄｅｆｉｎｅｄ」とは、この対応が確かに写像といえることが確認されている
ということである。
この写像 ｇ のことを、ｆ より誘導された写像または自然な射影という。
例 ２つの集合 Ｘ、Ｙ と、その上の同値関係をそれぞれ Ｒ、Ｓ とおく。
いま、写像 ｆ ：Ｘ → Ｙ について、
ｘＲｙ ならば、 ｆ（ｘ）Ｓｆ（ｙ）
が成り立つとする。
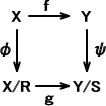
このとき、ある写像 ｇ ： Ｘ/Ｒ → Ｙ/Ｓ で、ｇ・φ＝ψ・ｆ となるものが、ただ一つ存在する。
ただし、φ ： Ｘ → Ｘ/Ｒ φ（ｘ）＝Ｃｘ 、ψ ： Ｙ→ Ｙ/Ｓ ψ（ｙ）＝Ｃｙ とする。
実際に、Ｃｘ∈Ｘ/Ｒ に対して、φ（ｘ）＝Ｃｘ となる ｘ ∈Ｘ をとり、ｇ（Ｃｘ）＝ψ（ｆ（ｘ））
と定めればよい。この写像 ｇ が求めるものである。
まず、写像 ｇ は、Ｗｅｌｌ Ｄｅｆｉｎｅｄ である。即ち、ｇ（Ｃｘ） の値は、代表元 ｘ の選び方に
関係なく一意に定まる。
なぜならば、φ（ｘ1）＝Ｃｘ 、φ（ｘ2）＝Ｃｘ のとき、 ｘ1Ｒｘ2 なので、ｆ（ｘ1）Ｓｆ（ｘ2）である。
よって、ψ（ｆ（ｘ1））＝ψ（ｆ（ｘ2））が成り立つので、
Ｃｘ＝Ｃｘ1＝Ｃｘ2 のとき、 ｇ（Ｃｘ1）＝ｇ（Ｃｘ2）
であることがいえる。ゆえに、写像 ｇ は、Ｗｅｌｌ Ｄｅｆｉｎｅｄ である。
また、上記の性質を持つ写像が、２つ（ｇ1、ｇ2）あったとする。
任意の Ｃｘ に対して、φ（ｘ）＝Ｃｘ となる ｘ ∈Ｘ をとるとき、
ｇ1（Ｃｘ）＝ｇ1（φ（ｘ））＝ｇ1・φ（ｘ）＝ψ・ｆ （ｘ）
ｇ2（Ｃｘ）＝ｇ2（φ（ｘ））＝ｇ2・φ（ｘ）＝ψ・ｆ （ｘ）
よって、 ｇ1（Ｃｘ）＝ｇ2（Ｃｘ） より、 ｇ1 ＝ ｇ2
したがって、条件を満たす写像は存在して、しかもただ一つに定まる。
、 
