長方形変換　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　戻る

　「重積分の計算」で見たように、適切な座標変換を行うことにより、いろいろな領域が長方
形に変換された。

例１　円板 ： ｘ2＋ｙ2≦ａ2 上の点（ ｘ ，ｙ ）は、変数変換　ｘ＝ｒ・ｃｏｓθ、ｙ＝ｒ・ｓｉｎθ　（ｒ≧０）

　　により、長方形の周および内部 ：　０≦ｒ≦ａ　、０≦θ≦２π の点（ ｒ ，θ ）に移される。

　　　 　　　

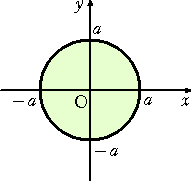例２　楕円板 ： ｘ2/ａ2＋ｙ2/ｂ2≦１ 上の点（ ｘ ，ｙ ）は、変数変換　ｘ＝ａ・ｕ、ｙ＝ｂ・ｖ　により、

　　円板 ： ｕ2＋ｖ2≦１ 上の点（ ｕ ，ｖ ）　に移される。さらに、例１の変換を施せば、長方形

　　に変換される。

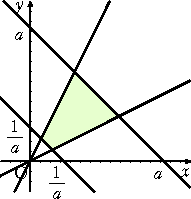
例３　台形の内部及び周　１/ａ≦ｘ＋ｙ≦ａ 、ｘ/ａ≦ｙ≦ａｘ　（ａ＞０） 上の点（ ｘ ，ｙ ）は、変数

　　変換　ｘ＋ｙ＝ｕ、ｘ＝ｕ・ｖ　（ｕ＞０、ｖ＞０）　により、長方形の内部及び周

　　　　　１/ａ≦ｕ≦ａ 、１/（ａ＋１）≦ｖ≦ａ/（ａ＋１）

　　上の点（ ｕ ，ｖ ）　に移される。

　　　 　　　

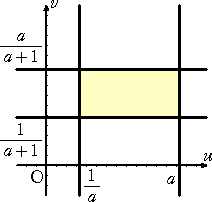例４　４つの放物線　ｙ＝２ｘ2　、ｙ＝３ｘ2　、ｙ2＝２ｘ　、ｙ2＝３ｘ　で囲まれた領域

　　　　　　　　　　

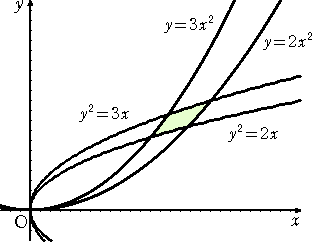
　　は、変数変換 により、長方形の内部及び周

　　　　　　　１/３≦ｕ≦１/２　、２≦ｖ≦３

　　という領域に移される。


　平成２３年１１月２６日付けで、当ＨＰ読者のＫ．Ｎ．さんより、メールを頂いた。

　様々な図形について、面積や面積モーメントなどを計算する必要があり、高校で習った数
ＩＩＩの積分を思い出しながら、計算しておりました。重積分をする必要が出てきたときに、やり
方がさっぱり思い出せず往生してしまいましたが、「重積分の計算」を参考にやり方を思い
出し、なんとか解を求めることができました。

　具体的には、半径１の四分円内について、∬ｘｙdｘdｙ を計算したかったのです。

　次の段階として、一般的な問題として、４つの直線で囲まれた区域について、面積や面積
モーメントなどを計算したいと思い、適切に変数を置換すると、長方形の面積に変換して計
算できるということが見えてきました。

　たとえば、下図のような４直線で囲まれる図形で、６種類の重積分をしたいのです。

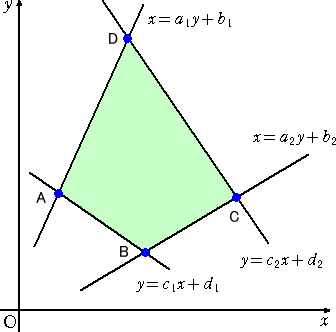　　　　Ａ＝∬dｘdｙ

　　　　Ｍｘ＝∬ｘdｘdｙ

　　　　Ｍｙ＝∬ｙdｘdｙ

　　　　Ｄｘ＝∬ｘ2dｘdｙ

　　　　Ｄｙ＝∬ｙ2dｘdｙ

　　　　Ｄｘｙ＝∬ｘｙdｘdｙ

　しかし、こういう場合、具体的にどういう置換関数を作ればいいのか、考えてみたのですが
分かりませんでした。どうやって計算したら良いのでしょうか。

　計算が1回きりなら、累次積分で済むのですが、実は、WEBプログラムを作っておりまして、
任意の四角形についての計算式ないし計算方法を得たいのです。

　任意の四角形となると、左上の点が左下の点より右に来るか左に来るかで分割が違って
くるので、長方形に変換し計算する方が良いのではと考えております。

　なお、私は、機械や鉄構物の設計をした経験を生かすべく、梁の断面性能計算プログラム
を作っています。９月末に、やっと第一段階のものが出来まして下記サイトで公開しておりま
す。（→　http://iseccalc.sakura.ne.jp）

　そこでは、I形断面しか計算しませんが、次段階として各種形状の断面の計算もできるよう
に拡張したいと思い、その準備としていろいろな図形について計算をしております。


　Ｋ．Ｎ．さんからの問いかけであるが、率直に言って「難しい！」のかな？果たして、任意の
四角形は、長方形に変換できるのだろうか？


　当ＨＰがいつもお世話になっているＨＮ「ＦＮ」さんからのコメントです。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２３年１２月５日付け）

　実用性は全く考えてません。理論的に可能かどうかだけです。変換T：(ｘ，ｙ)→(ｘ’，ｙ’)で、
ｘ’、ｙ’がｘ、ｙの1次式で書ける場合、即ち、一次変換と平行移動の合成で書ける場合、即ち
アフィン変換の場合は一般の四角形を平行四辺形に移すのは不可能です。アフィン変換は
平行四辺形を平行四辺形に移すからです。アフィン変換を2つつなぎ合わせたものなら可能
なようです。

　O(0，0)、P(1，,0)、Q(1，1)、R(0，1)とし、四角形を正方形OPQRに移す変換を考える。四角
形をABCDとする。対角線BDに関してAとCが反対側にあるとする。(凸性を仮定すれば成り
立つ。仮定しなくてもどちらかの対角線について成り立つような気がする。)

　AをOに、BをPに、DをRに移すアフィン変換はある。BDによって分けられた半平面のうち、
Aを含む側については、このアフィン変換をとる。同様に、CをQに、BをPに、DをRに移すア
フィン変換はある。Cを含む半平面については、このアフィン変換をとる。2つのアフィン変換
は直線BD上では同じである。

　射影変換だと、つなぎあわせたりしないで可能なようです。ただし、1次分数式ですから、
実用性から言えば、アフィン変換を２つ貼り付けたものの方がいいような気がします。実際
に計算に乗るかどうかはわかりません。大きな勘違いがあるかもしれません。重積分の計
算は大昔学生のころにほんの少しやっただけです。


（コメント）　ＦＮさん、お考えいただきありがとうございます。今日１日講義がなかったので、
　　　　　　紙と鉛筆で手計算に没頭していましたが、途中で挫折．．．。

　計算の方針は、次の通りです。

　与えられた四角形は、凸四角形であるものとする。上図で点Ａが原点にくるように平行移

動し、与えられた四角形の４頂点の座標を、Ａ（０，０）、Ｂ（ａ，ｂ）、Ｃ（ｃ，ｄ）、Ｄ（ｅ，ｆ）とする。

　線分ＡＢ、線分ＤＣを、ｓ ： １−ｓ の比に分ける点をそれぞれＰ、Ｑとおく。

同様に、線分ＡＤ、線分ＢＣを、ｔ ： １−ｔ の比に分ける点をそれぞれＲ、Ｓとおく。

　このとき、線分ＰＱと線分ＲＳの交点（ ｘ ，ｙ ）は、ｓ、ｔ の分数式で与えられる。

　この分数式を変換式と考えれば、上記の任意の四角形は、正方形の内部及び周を表す

領域：　０≦ｓ≦１、０≦ｔ≦１　に変換される。

　今度は、ａ、ｂ、ｃ、ｄ、ｅ、ｆ に具体的な数字を入れて計算を実行してみようと思う。

例　　下図のように、Ａ（０，０）、Ｂ（３，１）、Ｃ（１，４）、Ｄ（−１，２）とする。



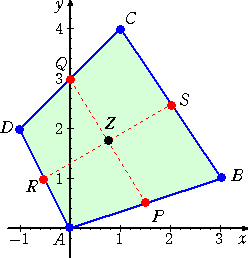　線分ＡＢ、線分ＤＣを、ｓ ： １−ｓ の比に分ける点を

　それぞれＰ、Ｑとおくと、

　　　Ｐ（３ｓ，ｓ）　、Ｑ（２ｓ−１，２ｓ＋２）

　　同様に、線分ＡＤ、線分ＢＣを、ｔ ： １−ｔ の比に分

　ける点をそれぞれＲ、Ｓとおくと、

　　　Ｒ（−ｔ，２ｔ）　、Ｓ（−２ｔ＋３，３ｔ＋１）

　　線分ＰＱと線分ＲＳの交点をＺとする。

　線分ＰＱを、ｍ ： １−ｍ の比に分ける点と線分ＲＳを、ｎ ： １−ｎ の比に分ける点が一致

することから、連立方程式：

　　（ｓ＋１）ｍ＋（−ｔ＋３）ｎ＝３ｓ＋ｔ　、（ｓ＋２）ｍ＋（−ｔ−１）ｎ＝−ｓ＋２ｔ

が得られる。これを解いて、　ｍ＝ｔ　、　ｎ＝ｓ　（←　これは当然の帰結ですね！）

　よって、交点Ｚの座標を（ ｘ ，ｙ ）とおくと、

　　ｘ＝−ｓｔ＋３ｓ−ｔ　、ｙ＝ｓｔ＋ｓ＋２ｔ

となる。この変換の様子を図示すれば下図となる。

　　　

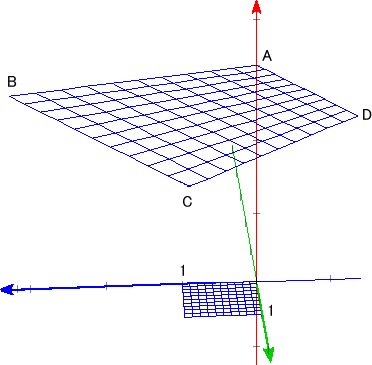
　この変換の函数行列式（Ｊａｃｏｂｉａｎ）を計算してみる。

　　　ｘｓ＝−ｔ＋３　、ｘｔ＝−ｓ−１

　　　ｙｓ＝ｔ＋１　　、ｙｔ＝ｓ＋２

なので、　４ｓ−ｔ＋７　となる。すなわち、

　　ｄｘｄｙ＝（４ｓ−ｔ＋７）ｄｓｄｔ

となる。

例　上記で与えられた四角形ＡＢＣＤにおいて、Ａ＝∬dｘdｙ　を計算せよ。

（解）
　　　　　　（終）

（コメント）　当然にして、Ａの値は四角形ＡＢＣＤの面積（１７/２）に等しい。


　当ＨＰがいつもお世話になっているＨＮ「Ｓ（Ｈ）」さんが上記話題について考察されました。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２３年１２月６日付け）

　任意の四角形は、正方形（角砂糖）の内部及び周を表す領域：　０≦ｓ≦１、０≦ｔ≦１　に
変換される（次元を上げても）を拝見し、参考資料中程の荷重平均の図（天秤棒）をご覧くだ
さい。

　W={(w1，w2，w3，w4}|w1+w2+w3+w4=1，wj≧0} の任意の点に、

    w1・A+w2・B+w3・C+w4・D　----->　w1・(0，0)+w2・(1，0)+w3・(1，1)+w4・(0，1)

（→　計算例）

　　W---->w1・A+w2・B+w3・C+w4・D　 は、Hom[R4，R2]　　（具体的に行列表現）

　　W---->w1・(0，0)+w2・(1，0)+w3・(1，1)+w4・(0，1)　　は、Hom[R4，R2]
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（具体的に行列表現）

参考：「Baryzentrische Koordinaten」、「重心座標」

　「長方形変換」に触発され、その非線型写像 F を求め具現してみました。（→参考：「写像」）

　私は、代数曲線＆双対曲線、代数曲面＆双対曲面、・・・に関心が在ります。

　非線型写像 F の具現は世界初かも．．．。(  F(C)* も無論、世界初 )


（コメント）　Ｓ（Ｈ）さん、ありがとうございます。非線形写像の具現、世界初とか．．．。感動
　　　　　　しました。

　上記の具体的な計算を一般化するのは容易だろう。

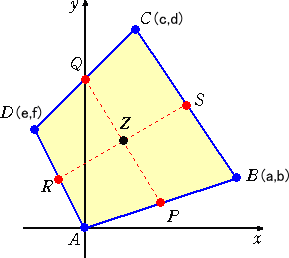　　与えられた四角形は、凸四角形であるもの
　とする。

　　点Ａが原点にくるように平行移動し、与えら
　れた四角形の４頂点の座標を、

　　　Ａ（０，０）、Ｂ（ａ，ｂ）、Ｃ（ｃ，ｄ）、Ｄ（ｅ，ｆ）

　とする。

　　線分ＡＢ、線分ＤＣを、ｓ ： １−ｓ の比に分
　ける点をそれぞれＰ、Ｑとおき、同様に、線
　分ＡＤ、線分ＢＣを、ｔ ： １−ｔ の比に分ける
　点をそれぞれＲ、Ｓとおく。

　このとき、　　　Ｐ（ｓａ，ｓｂ）　、Ｑ（（ｃ−ｅ）ｓ＋ｅ，（ｄ−ｆ）ｓ＋ｆ）

　　　　　　　　　　Ｒ（ｔｅ，ｔｆ）　、Ｓ（（ｃ−ａ）ｔ＋ａ，（ｄ−ｂ）ｔ＋ｂ）

となる。線分ＰＱと線分ＲＳの交点Ｚの座標を、（ ｘ ，ｙ ）とおくと、点Ｚは線分ＰＱを、ｔ ： １−ｔ
の比に分ける点である。よって、変換式は、

　　　ｘ＝ｔ｛（ｃ−ｅ）ｓ＋ｅ｝＋（１−ｔ）ｓａ＝（ｃ−ｅ−ａ）ｓｔ＋ａｓ＋ｅｔ

　　　ｙ＝ｔ｛（ｄ−ｆ）ｓ＋ｆ｝＋（１−ｔ）ｓｂ＝（ｄ−ｆ−ｂ）ｓｔ＋ｂｓ＋ｆｔ

により与えられる。この計算結果は、上記のＳ（Ｈ）さんのものと一致する。

　この変換式の函数行列式（Ｊａｃｏｂｉａｎ）は、

　　　ｘｓ＝（ｃ−ｅ−ａ）ｔ＋ａ　、ｘｔ＝（ｃ−ｅ−ａ）ｓ＋ｅ

　　　ｙｓ＝（ｄ−ｆ−ｂ）ｔ＋ｂ　　、ｙｔ＝（ｄ−ｆ−ｂ）ｓ＋ｆ

なので、　｛ａ（ｄ−ｆ）＋ｂ（ｅ−ｃ）｝ｓ＋｛ｆ（ｃ−ａ）＋ｅ（ｂ−ｄ）｝ｔ＋ａｆ−ｂｅ　となる。すなわち、

　　ｄｘｄｙ＝［｛ａ（ｄ−ｆ）＋ｂ（ｅ−ｃ）｝ｓ＋｛ｆ（ｃ−ａ）＋ｅ（ｂ−ｄ）｝ｔ＋ａｆ−ｂｅ］ｄｓｄｔ

　この変換式を、Ａ（０，０）、Ｂ（３，１）、Ｃ（１，４）、Ｄ（−１，２）の場合に適用すれば、

　　　ｘ＝−ｓｔ＋３ｓ−ｔ

　　　ｙ＝ｓｔ＋ｓ＋２ｔ

となり、上記例における計算結果と一致する。

　Ｋ．Ｎ．さんの問題設定では、四角形の４頂点Ａ、Ｂ、Ｃ、Ｄの座標のかわりに各辺の方程
式が与えられている訳であるが、連立１次方程式を解くことは、プログラムを書くことにより
可能だろう。そうすれば、四角形の４頂点Ａ、Ｂ、Ｃ、Ｄの座標もコンピュータ上で容易に求
められる。

　このような手順を尽くせば、Ｋ．Ｎ．さんの問題は完全解決と判断して良いと思う。

　試しに、Ａ＝∬dｘdｙ　を計算してみよう。簡単な重積分の計算から、

　　　Ａ＝｛ｄ（ａ−ｅ）＋ｃ（ｆ−ｂ）｝/２

となる。これは、公式として覚えておくと役に立つときがあるかな．．．？

　上記のように配列した方が覚え易いと思ったが、ここは素直に

　　　Ａ＝｛（ａｄ−ｂｃ）＋（ｃｆ−ｄｅ）｝/２

とした方がいいように思えてきた。（→　参考：「三角形の面積の公式」）

　他の　Ｍｘ＝∬ｘdｘdｙ、Ｍｙ＝∬ｙdｘdｙ、Ｄｘ＝∬ｘ2dｘdｙ、Ｄｙ＝∬ｙ2dｘdｙ、Ｄｘｙ＝∬ｘｙdｘdｙ
も同様に計算できる。


　攻略法さんが上記話題について考察されました。（平成２３年１２月８日付け）

　上記の例の　Ａ（０，０）、Ｂ（３，１）、Ｃ（１，４）、Ｄ（−１，２）とした場合について、種々の量
を計算してみました。

　S= 17/2　、Sｘ= 22/3　、Sｙ= 91/6　、Xg= 44/51　、Yg= 91/51　、
　Jｘ= 133/4　、Jｙ= 149/12　、Jｘｙ= 103/8

　実務レベルでは、次のように計算できるのではないでしょうか。

●多角形の断面性能

　反時計まわりに与えられた多角形の頂点が示す座標を、(Xｋ，Yｋ)　（ｋ=1、2、…、N） とす
る。また、XＮ+1＝X1　、YＮ+1＝Y1　とする。

（１）　断面積　・・・　反時計まわりを正とする符号付面積である。

　　　　　Ｓ＝∫dＳ＝(1/2)Σｋ=1〜N { Xｋ・Yｋ+1−Xｋ+1・Yｋ }

　　辺と原点からなる三角形の面積の和（２次元外積による）
（→参考：「三角形の面積の公式」　あるいは、台形の面積による場合、「多角形の面積」）

（２）　原点から ｘ 軸方向、原点から ｙ 軸方向の断面１次モーメント

　Sｘ=∫ｙdＳ=(1/6)Σｋ=1〜N { （Xｋ・Yｋ+1−Xｋ+1・Yｋ）（Xｋ＋Xｋ+1） }
　Sｙ=∫ｘdＳ=(1/6)Σｋ=1〜N { （Xｋ・Yｋ+1−Xｋ+1・Yｋ）（Yｋ＋Yｋ+1） }

（３）　図心　・・・　荷重分布が均一なら、重心となる。

　Xg=Sｘ/Ｓ
　Yg=Sｙ/Ｓ

（４）　ｘ 軸回り、ｙ 軸回り断面２次モーメント

　Jｘ=∫ｙ2dＳ=(1/24)Σｋ=1〜N { （Xｋ・Yｋ+1−Xｋ+1・Yｋ）（（Yｋ＋Yｋ+1）2＋Yｋ2＋Yｋ+12） }
　Jｙ=∫ｘ2dＳ=(1/24)Σｋ=1〜N { （Xｋ・Yｋ+1−Xｋ+1・Yｋ）（（Xｋ＋Xｋ+1）2＋Xｋ2＋Xｋ+12） }

（５）　原点回りの断面相乗モーメント

　Jｘｙ

　=∫ｘｙdＳ

　=(1/24)Σｋ=1〜N { （Xｋ・Yｋ+1−Xｋ+1・Yｋ）（（Xｋ＋Xｋ+1）（Yｋ＋Yｋ+1）＋XｋYｋ＋Xｋ+1Yｋ+1） }


　Ｓ（Ｈ）さんからの続報です。（平成２３年１２月７日付け）

　参考資料に近い「捩り写像」なる定義が欲しい。その所以は、参考図を視ていただくと理
解していただけるでしょう。

　非線型写像　R2---F--->R2　F[s，t]=(2s + t， -3ts - 2s + 4t)　について、黄色枠は既に
お願い済みですが、真ん中の写像される様子の描写を熟視願います。

X=[0，1]×[0，1]---F--->Y=F[X] が局所微分同相写像は、視て理解可能でしょう。

　参考図の草色囲みを考察したい。

　円の半径 ｒ が、或る値より小さいとき、F[Cｒ]は捩れていない！例えば、C1 とF[C1] を図示
していますが、代数曲線　F[C1] を私が求めると、

　　9ｘ4 - 36ｘ3 + 24ｙｘ2 + 55ｘ2 + 180ｘ + 25ｙ2 - 60ｙ - 464=0　(確認願います。）

　円の半径 ｒ が、或る値より大きくなると、F[Cｒ]は捩れてしまう！

　例えば、C4 とF[C4] を図示していますが、代数曲線F[C4] を求めて、図示もして、草色囲
みの図のようになることを示して下さい。

　上のように様相が異なる原因を探りたい。「Jacobi-Matrix」を参照しつつ、

　　　　　ｄFｐ： Tp(R2)------>TF(p)(R2)

を求め、Det[dFp]=0 なる点ｐ が満たす代数曲線Cを求めて下さい。

　Cと代数曲線F(C) を図示すると、草色の図になることを示してください。そして、代数曲線
F[C1]の特異点を求め、その特異点の名称を云うて下さい。

　代数曲線F[C4]の特異点を求め、その特異点の名称を云うて下さい。特異点の名称がガ
ラリと異なる境目の ｒ を求めて下さい。

　代数曲線F[C1] の双対曲線 F[C1]* を求め、図示もし、特異点を求め、その特異点の名
称を云って下さい。

　代数曲線F[C4] の双対曲線 F[C4]* を求め、図示もし、特異点を求め、その特異点の名
称を云って下さい。

　上は、「Sard’s Theorem」の事例になっていて、理解の助けとしたいのです。

　「Introduction to Differential Geometry」の17p 近傍も。
Definition 1.3.2　ｄFｐ： Tp(R2)------>TF(p)(R2)
Theorem 1.3.4　 Sard’s Theorem


　Ｓ（Ｈ）さんからの続報です。（平成２３年１２月８日付け）

　「中心 (1/2，1/2) の青線の同心円 Cｒ ： ((ｘ-1/2)2+(y-1/2)2=ｒ2 がだんだん大きくなる」に
連動し、赤線の閉曲線F(Cｒ)が変化する様子をご覧ください。

　青い同心円 Cｒ が、[0，1]×[0，1] に収まるとき、F(Cｒ)は捩れていない同心閉曲線と命名。
（赤線が囲む面積や赤線の弧長を求めたくて堪らないでしょう...。)

　[0，1]×[0，1] に収まる色々な四角形（小学生が縦×横で面積を求める）が四角形に写さ
れる（高校生が像F(四角形)の面積を求める）様子も描写。

　青い同心円 Cｒ が、[0，1]×[0，1] に収まらず、はみ出して行くと、F(Cｒ)に捩れ（特異点）
が出現。

　青い同心円 Cｒ が一線を越えると今まで(出現した特異点の名称は?)とは異なる特異点
（その名称は?)が出現！

　私が得た

54ｘ4 - 378ｘ3 + 144ｙｘ2 - 1080ｘ2 - 1539ｘ2 - 162ｙｘ
　　　　　　　　　　　+ 5616ｘ + 13038ｘ + 150ｙ2 - 1440ｙ - 4196ｙ + 5088 + 6086=0
を工夫し、「Wolfram|Alpha」に挿入して、捩れ（特異点）を感受なさって下さい。

　再び、参考図にかえり、F(C1/5)を含む最小の代数曲線 C：f[ｘ，ｙ]=0 を求め、その特異点
を求めて、C∪{特異点}=F(C1/5) となるか考察願います。

　F(C1/3)を含む最小の代数曲線 C：f[ｘ，ｙ]=0 を求め、その特異点を求めて、
C∪{特異点}=F(C1/3) となるか考察願います。

　F(C1)を含む最小の代数曲線 C：f[ｘ，ｙ]=0 を求め、その特異点を求めて、
C∪{特異点}=F(C1) となるか考察願います。

　青い同心円 Cｒ が草色の一線を越えるときの、例えば、C19 のとき、F(C19) を表す代数曲
線 C：f[ｘ，ｙ]=0 を求め、その特異点を求めて下さい。

　F(s，t)=特異点 となる C19 上の点達も求めて観察願います。

　上で得た各代数曲線の双対曲線を求めて、その特異点を求めて、もとの代数曲線の何を
反映しているか記載願います。


　Ｓ（Ｈ）さんからの続報です。（平成２３年１２月９日付け）

　「点Ａが原点にくるように平行移動し、与えられた四角形の４頂点の座標を、Ａ（０，０）、
Ｂ（ａ，ｂ）、Ｃ（ｃ，ｄ）、Ｄ（ｅ，ｆ）とする。」としても一般性を失わないは理解できますが、
Ｂ（ａ，ｂ）、Ｃ（ｃ，ｄ）、Ｄ（ｅ，ｆ）の　選び方によっては、参考図の如く、ｓｔ が片方に出現せず
「不公平感」が否めないので、F[ｓ，ｔ]の双方に非線型項が出現すべく四角形の４頂点の座
標を指定し、Ａ≠（０，０）なる問題提起を致しました。

　{{ｘ1，ｙ1}、{ｘ2，ｙ2}、{ｘ3，ｙ3}、{ｘ4，ｙ4}}={{3，1}、 {4， 3}、 {8， 7}、 {6， 2}}

　ｓｔ 項が双方に出現の非線型写像F；F[ｓ，ｔ]=(ｔｓ + ｓ + 3t + 3， 3ｔｓ + 2ｓ + ｔ + 1)　による
諸々の代数曲線Cj の像F(Cj)を求め、その特異点を求め、更に、その双対曲線F(Cj)* を
求め、その特異点を求める等、為すべきことをなさって提示下さい。



　　　以下、工事中