多角形の面積　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　面積の計算問題は、小学校から中学校、高校、大学を通じて、身近な問題と言える。そこ
には該当の学年に応じた種々の公式が介在する。

　最近、任意の多角形に対して常に成り立つ求積公式を知ることができたので紹介したい。

たとえば、皆さんは下記の図形の面積はどのようにして求めるだろうか？



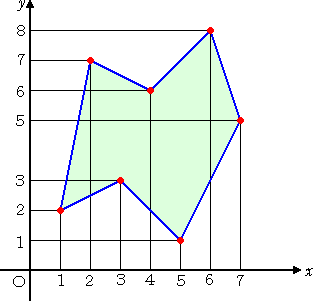
　　　多分、多くの方は左図の図形を含む
　　長方形を考えて、その面積から余計な
　　部分の面積を差し引いて、所要の面積
　　を求めることだろう。

　　　実は、一般的に次の公式により、機
　　械的な計算で面積は求められる。

　　　ｎ 個の頂点の座標を、（Ｘ_k ，Ｙ_k）とす
　　ると、面積Ｓは、

　　　

　　　　　但し、Ｘ_ｎ＋１＝Ｘ_１ ，Ｙ_ｎ＋１＝Ｙ_１　


　試しに、上記の図形の面積を求めてみよう。

　したがって、　Ｓ＝（−１０−８−１２＋１３＋２８＋２６＋９）÷２＝２３　となる。

（コメント：この公式の素晴らしい点は、図形の形状を気にせずに機械的に計算できるところ
　　　　　　だろう。）

（参考文献：　西山　豊　著　サイエンスの香り　生活の中の数理　（日本評論社））