シムソンの定理　　　　　　 　　　　　　　　　　　　　　　　　　

　新学習指導要領になって一時ある程度の幅をきかせていた平面幾何が勢いをなくしつつ
ある。平面幾何によって、数学の面白さに開眼したという方も多いと思うのだが．．．。

　私自身も、中学時代に高校入試の勉強で平面幾何を統一的に学び、平面幾何の魅力に
取りつかれた一人である。

　当ＨＰの別のページ「蝴蝶定理」で、いろいろな幾何の問題に触れる中で、大事な定理を
見逃していたことに気づかされた。

　中国では、４つの重要な定理として、次のものをあげているＨＰサイトが多い。

　　メネラウスの定理　、チェバの定理　、トレミーの定理　、シムソンの定理

　トレミーの定理を除いた他の定理は、共線・共点の定理で、作図題でも活躍することは
ご存じのことと思う。（→参考：基本の作図）

　また、共線・共点の定理は、代数学的意味を有しており、その顕著な例が、デザルグの
定理であろう。

　このページでは、共線・共点の定理について、いろいろ整理したいと思う。

　まずは、シムソンの定理から始めよう。


シムソンの定理　　（正しくは、ウォーレスの定理といわれるらしい！）

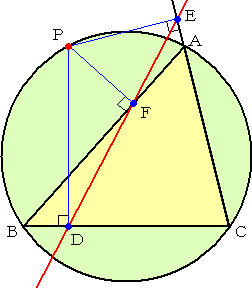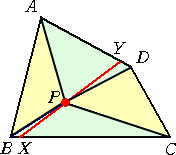
△ＡＢＣの外接円周上の点Ｐから、ＢＣ、ＣＡ、 　　ＡＢ　に下ろした垂線の足を Ｄ、Ｅ、Ｆ とする。 　　　このとき、３点 Ｄ、Ｅ、Ｆ は１直線上にある。 　　　この直線のことを、シムソン線という。 　　　「１直線上にある」ということを、如何に示すか 　　が証明のポイントだろう。

　平成２２年４月２０日付けで、ＨＮ「ｍｕｔｕｒａｊｃｐ」さんから下記の証明に対して、次のような
ご指摘を頂いた。

　「４点 Ｐ、Ｆ、Ａ、Ｅ が同一円周上にあっても、この順序に並んでいる保証はなく、
　∠ＰＦＥ＝∠ＰＡＥ であるとは言えないのではないでしょうか?」

　ご指摘はごもっともで恐縮です。ただ、△ＡＢＣが直角三角形とか鈍角三角形の場合、そ
して点Ｐの位置まで考慮するとなると証明する前に気が滅入ってしまいます。本質を見失っ
てしまいそうです。

　当ＨＰの趣旨、教育的配慮から、以下では、上図の場合に限定して証明を行っている点
を是非ご理解ください。一つの場合について証明の方法が理解されれば、他の場合につい
ても同様に示されると考えます。

　これに対して、ｍｕｔｕｒａｊｃｐ さんから、

　「図に依存する証明は好ましくないし、図の場合に限定して証明を行う場合も、一般性を
　失わない事を示す必要があると思う。」

とのご指摘を頂きました。（平成２２年４月２３日付け）

　以下は、ｍｕｔｕｒａｊｃｐ さんによる証明である。（一部文言等を修正させて頂きました。）

　（証明）　題意より、点Ｐが弧ＡＢ上にあるとしても一般性を失わない。

　このとき、四角形ＰＢＣＡ は、円に内接するので、　∠ＰＢＣ＋∠ＰＡＣ＝１８０°

　∠ＰＢＣ＝９０°のとき、Ｄ（＝Ｂ）、Ｅ（＝Ａ）、Ｆ　が１直線上にあることは明らかである。

　∠ＰＢＣ＞９０°のときは、∠ＰＡＣ（＜９０°）について論ずればよいので、∠ＰＢＣ＜９０°

　と仮定しても一般性を失わない。

　このとき、　∠ＰＡＣ＞９０°であるので、点Ｅは辺ＣＡの延長上にある。

　４点 Ｐ、Ｆ、Ａ、Ｅ は、同一円周上にあるので、　∠ＰＦＥ＝∠ＰＡＥ

　また、　∠ＰＡＥ＋∠ＰＡＣ＝１８０°なので、　∠ＰＡＥ＝∠ＰＢＣ

　∠ＰＢＣ＜９０°より、Ｄ、ＦはＰＢに対して同じ側にあり、四角形ＰＢＤＦは円に内接するの

で、　∠ＰＢＤ＋∠ＰＦＤ＝１８０°が成り立つ。

　　よって、　∠ＰＦＥ＋∠ＰＦＤ＝１８０°となり、３点 Ｄ、Ｅ、Ｆ は１直線上にある。　（証終）

（コメント）　ｍｕｔｕｒａｊｃｐ さん、証明ありがとうございます。何とか一般的な証明になりました
　　　　　　ね！FNさんも４月２３日付けで指摘されていますが、

　　　Ｐが孤ＡＢ上にあり、∠ＰＢＣ＜９０°のときを証明すれば十分

　ということがキーポイントのようです。

　以下の証明は、上記の議論を踏まえて簡略化したものである。

（証明）　４点 Ｐ、Ｆ、Ａ、Ｅ は、同一円周上にあるので、　∠ＰＦＥ＝∠ＰＡＥ

　同様に、四角形ＰＢＣＡは円に内接するので、　∠ＰＡＥ＝∠ＰＢＤ

　四角形ＰＢＤＦは円に内接するので、　∠ＰＢＤ＋∠ＰＦＤ＝１８０°

　　よって、　∠ＰＦＥ＋∠ＰＦＤ＝１８０°となり、３点 Ｄ、Ｅ、Ｆ は１直線上にある。　（証終）


　証明があまりにも鮮やかすぎて、じっくり味わう余裕がないほどである。脳裏に焼き付ける
ために下図を補充しておこう。
　　　　　　　　　　

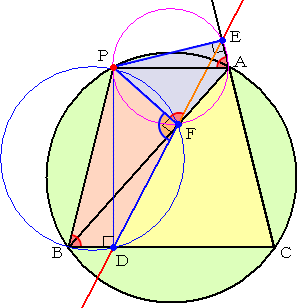
　シムソンの定理に対して、我が敬愛する安田　亨先生は、極座標を用いて代数的に証明
されている。（　→　参考）

　興味ある証明なので、少し整理しておくことにする。

　まず、次の２つの事実を活用する。

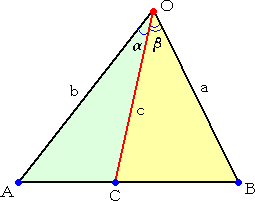線分 ＡＢ 上に点 Ｃ が存在するとき、 　　直線 ＡＢ 上にない点 Ｏ により、 　　　　　　△ＯＡＢ＝△ＯＡＣ＋△ＯＣＢ 　　すなわち、 　　　 　　が成り立つ。

逆に、線分 ＡＢ と点 Ｃ があり、直線 ＡＢ 上にない点 Ｏ について、

　　　　　　　

が成り立つとき、点 Ｃ は、線分 ＡＢ 上に存在する。

（証明）　△ＯＡＢ＝△ＯＡＣ＋△ＯＣＢ　より、

　　　　（1/2）ａｂ・ｓｉｎ（α＋β）＝（1/2）ｂｃ・ｓｉｎα＋（1/2）ｃａ・ｓｉｎβ

　が成り立つので、等式が成り立つことは明らかであろう。

　　逆に、点 Ｃ が、線分 ＡＢ 上に存在しないと、△ＯＡＢ＝△ＯＡＣ＋△ＯＣＢ　が成り立

　たないので、等式が成り立てば、必然的に、点 Ｃ は、線分 ＡＢ 上に存在する。（証終）


　また、半径 ｒ の円 Ｏ において、直径の端点 Ｐ を極座標の極、有向線分ＰＯを始線と
する。

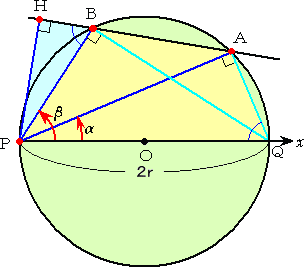このとき、円 Ｏ 上の２点Ａ、Ｂの座標は、 　　 　　Ａ（ ２ｒ・ｃｏｓα ， α ） 　　 　　Ｂ（ ２ｒ・ｃｏｓβ ， β ） 　と書ける。 　　このとき、点Ｐより直線ＡＢに下ろした 　垂線の足Ｈの座標は、 　　　Ｈ（ ２ｒ・ｃｏｓα・ｃｏｓβ ， α＋β ） 　と書ける。

（証明）　４角形 ＡＢＰＱ は、円Ｏに内接するので、　∠ＡＱＰ＝∠ＨＢＰ　が成り立つ。

　　よって、　△ＨＰＢ∽△ＡＰＱ　なので、　∠ＢＰＨ＝α　が成り立つ。

　　このことから、明らかであろう。　　（証終）


　以上により、極座標による、シムソンの定理の証明の準備ができた。

（証明）　点Ｐが△ＡＢＣの頂点のいずれかで 　　　　　あるときは定理は明らかに成り立つ 　　　　　ので、点Ｐは頂点に一致しないものと 　　　　　してよい。 　　点Ｐを極、点Ｐより円の中心Ｏを通る有向 　線分を始線とする極座標を考える。 　　円Ｏの半径を ｒ とし、３点 Ａ、Ｂ、Ｃ の座 　標をそれぞれ 　　Ａ（ ２ｒ・ｃｏｓα ， α ） 　　Ｂ（ ２ｒ・ｃｏｓβ ， β ） 　　Ｃ（ ２ｒ・ｃｏｓγ ， γ ） 　とおく。

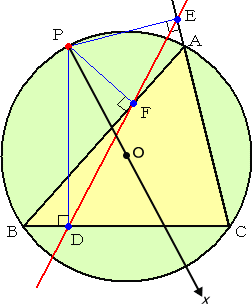　このとき、Ｅ（ ２ｒ・ｃｏｓα・ｃｏｓγ ， α＋γ ）　、Ｆ（ ２ｒ・ｃｏｓα・ｃｏｓβ ， α＋β ）

　　Ｄ（ ２ｒ・ｃｏｓβ・ｃｏｓγ ， β＋γ ）　　が成り立つ。

　よって、

　

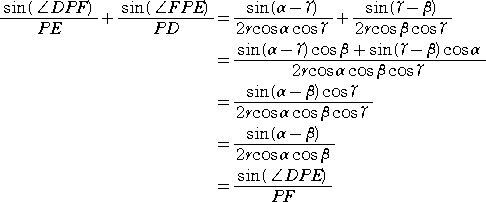
　したがって、線分ＤＥ上に点Ｆが存在し、３点 Ｄ、Ｅ、Ｆ は、同一直線上にある。　　（証終）


（コメント）　確かに代数的には示されたが、平面幾何の性質を用いた証明の美しさにはか
　　　　　　なわない。

　旧学習指導要領で何十年ぶりかで復活した複素数平面は、新学習指導要領で、あえな
く消えてしまった。複素数平面で幾何の問題を考えることは、一度体験すると、その美しさ
から病みつきになるくらいである。

　複素数を用いてシムソンの定理を証明するとどうなるか大いに興味のあるところである。

　過去の記憶を呼び戻すべく、私自身の勉強も兼ねて、証明を考えたいと思う。


　以下において、座標平面の原点を Ｏ とし、Ｏ と複素数 α で表される点を結ぶ線分を
Ｏα 、点Ａ（ｚ₁）のことを、点 ｚ₁ と表すことにする。

　まず、直線の平行と垂直の条件を確認しておこう。

　２点 α、β を通る直線を Ｌ、２点 γ、δ を通る直線を Ｍ とする。このとき、

（平行条件）

　　

（垂直条件）

　　

（証明）　平行条件は、（α−β）/（γ−δ） の偏角が ０ または π 即ち、実数から明らか。

　垂直条件は、（α−β）/（γ−δ） の偏角が ±π/２ 即ち、純虚数から明らか。　　（証終）


　ある条件の下に、いくつかの直線の方程式を求めてみよう。

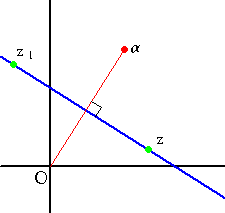（１）　点 ｚ1 を通り、Ｏα に垂直な直線の方程式は、 　　　　　　　　 　　　上式の分母を払って整理すれば、 　　　　　　　　（ｃ は実数、α≠０） 　　　これは、Ｏα に垂直な直線の一般形を表す。

（証明）　２点 ｚ 、ｚ₁ を通る直線と、２点 Ｏ、α を通る直線が垂直なので、垂直条件から明
　　　　　らか。後半も同様。　　（証終）


（２）　点 ｚ₀ を通り、直線 に平行な直線の方程式は、

　　　

（証明）　直線の方程式に、 ｚ₀ を代入して、ｃ が得られ、明らかであろう。　　（証終）


（３）　点 ｚ₀ を通り、直線 に垂直な直線の方程式は、

　　　

（証明）　２点 ｚ 、ｚ₀ を通る直線と、２点 Ｏ、α を通る直線が平行なので、平行条件から明
　　　　　らか。（証終）


（４）　２点 ｚ₀ 、ｚ₁ を通る直線の方程式は、

　　

（証明）　２点 ｚ 、ｚ₀ を通る直線と、２点 ｚ₁ 、ｚ₀ を通る直線が平行なので、平行条件から
　　　　　明らか。　　（証終）


　これまで得られた直線の方程式を見て分かるように、とても美しいとは言えない形になっ
ている。それは、一般の平面で考えているからである。このページの当面の目標は、シム
ソンの定理を証明することであったが、そこには円が関わっている。

　半径 １ の円すなわち単位円の世界で幾何の問題を考えると、上記で得られた関係式
が、とても美しい関係式に生まれ変わることを上記のＨＰで学ぶことが出来た。

　以下で、円は単位円としても一般性を失うことはない。

単位円周上の２点 ｚ₀ 、ｚ₁ を通る直線の方程式

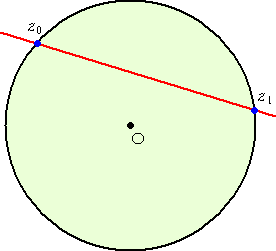	（証明）　（４）において、 　　　　　　　　 　　　　を代入して整理すると、所要の式が得 　　　　られる。（証終） 　　ここで、特に、ｚ1 → ｚ0 とすれば、 　点 ｚ0 における接線の方程式 　　　　 　が得られる。

平行条件　　４点 α 、β 、γ 、δ は単位円周上にあるものとする。

　２点 α 、β を通る直線と、２点 γ 、δ を通る直線が平行であるとき、

　　　　αβ − γδ ＝ ０

が成り立つ。

（証明）　平行条件

　　　　

において、

　　　　

を代入して整理すると、所要の式が得られる。　　（証終）


垂直条件　　４点 α 、β 、γ 、δ は単位円周上にあるものとする。

　２点 α 、β を通る直線と、２点 γ 、δ を通る直線が垂直であるとき、

　　αβ ＋ γδ ＝ ０

が成り立つ。

（証明）　垂直条件

　　

において、

　　

を代入して整理すると、所要の式が得られる。　　（証終）


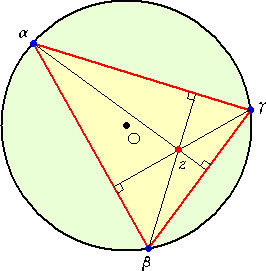
三角形の垂心

△αβγ の外接円の中心を Ｏ とし、垂心 を ｚ とすると、 　　　ｚ＝α＋β＋γ が成り立つ。 （コメント）　これは、座標幾何では決して得 　　　　　　ることのない美しさである！

（証明）　２点 α 、ｚ を通る直線および２点 γ 、ｚ 　　　　を通る直線と円 Ｏ との交点をそれぞれ 　　　　 ｘ 、 ｙ とする。 　　このとき、２点 α 、ｘ を通る直線の方程式は 　　　　　　 　　　また、２点 γ 、ｙ を通る直線の方程式は 　　　　　　 　　　である。 ここで、２点 α 、ｘ を通る直線と２点 β 、γ　を

通る直線は垂直なので、垂直条件より、　αｘ ＋ βγ ＝ ０　が成り立つ。

　同様に、２点 γ 、ｙ を通る直線と２点 α 、β を通る直線は垂直なので、垂直条件より、

　γｙ ＋ αβ ＝ ０　が成り立つ。これらを直線の方程式に代入して、

　　　　　　　、　　

　このとき、　　　、　　

なので、辺々引いて、　（α−γ）ｚ＝（α−γ）（α＋β＋γ）　より、　ｚ＝α＋β＋γ　（証終）


αより２点β、γを通る直線に下ろした垂線の足は、ｈ＝（α＋β＋γ−βγ/α）/２

（証明）　上図において、明らかに、　△γｘｈ ≡ △γｚｈ　なので、　ｈ は、２点 ｚ 、 ｈ を結ぶ

　線分の中点である。よって、中点の公式により、所要の式を得る。

　ただし、　αｘ＋βγ＝０　より、　ｘ＝−βγ/α　であることに注意する。　（証終）


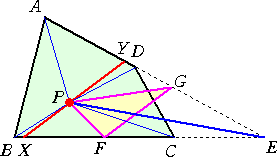
　さて、いよいよ複素数平面において、シムソンの定理を証明する準備が出来たようである。

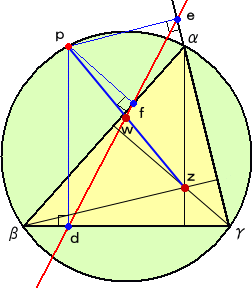（証明）　左図において、上記の公式から 　　　　ｄ ＝ （ｐ＋β＋γ−βγ/ｐ）/２ 　　　　ｅ ＝ （ｐ＋α＋γ−αγ/ｐ）/２ 　　　　ｆ ＝ （ｐ＋α＋β−αβ/ｐ）/２ 　　と書ける。　ここで、 　　垂心 ｚ ＝ α＋β＋γ で、２点 ｐ 、ｚ を結ぶ線分 　の中点 ｗ は、ｗ ＝ （ｐ＋α＋β＋γ）/２　となる。 　このとき、　２ｐｄ ＝ ｐ（ｐ＋β＋γ）−βγ 　　　　　　　　　　　＝ ｐ（２ｗ−α）−βγ

　　よって、　ｐ（ ｗ − ｄ ） ＝ （ｐα＋βγ）/２　が成り立つ。

同様に、　ｐ（ ｗ − ｅ ） ＝ （ｐβ＋αγ）/２　、ｐ（ ｗ − ｆ ） ＝ （ｐγ＋αβ）/２　が成り立つ。

　いま、　ｐ（ ｗ − ｄ ） ＝ （ｐα＋βγ）/２　と　ｐ（ ｗ − ｅ ） ＝ （ｐβ＋αγ）/２　において、

４点 ｐα 、βγ 、ｐβ 、αγ　は、単位円 Ｏ の周上の点で、平行条件

　　ｐα × βγ − ｐβ × αγ ＝ ０

が成り立ち、２点 ｐα 、βγ を結ぶ直線と２点 ｐβ 、αγ を結ぶ直線は平行となる。

　よって、その中点 （ｐα＋βγ）/２　と （ｐβ＋αγ）/２　は同一直線上にある。

同様にして、中点 （ｐβ＋αγ）/２　と （ｐγ＋αβ）/２　は同一直線上にある。

　以上から、３つの中点は同一直線上にあるので、ｐ（ ｗ−ｄ ）、ｐ（ ｗ−ｅ ）、ｐ（ ｗ−ｆ ）

すなわち、 ｗ − ｄ 、 ｗ − ｅ 、 ｗ − ｆ　も同一直線上にある。

　したがって、　４点 ｗ 、ｄ 、ｅ 、 ｆ　は、同一直線上にある。

　すなわち、　３点 ｄ 、ｅ 、 ｆ　は、１直線上にある。　（証終）


（注意）　上記において、点 ｐ と垂心 ｚ の中点 ｗ が、３点 ｄ 、ｅ 、 ｆ　と同一の直線上に
　　　　　あることも示された。このことを格好よく表現すれば、

　　線分 ｐｚ は、点 ｐ の△ＡＢＣに関するシムソン線によって２等分される

となる。　この事実は、シュタイナーの定理と言われるそうだ。

　以上において、シムソンの定理の証明を、３つの立場（平面幾何・極座標・複素数平面）
から眺めてきた。それぞれの特徴を十分に生かした証明で、とても面白い。


＃複素数によるシムソンの定理の証明を整理したものを、「複素数の底力」に掲載しました。
　ご高覧いただければ幸いです。


　さて、シムソンの定理は逆も成り立つが、このことは他のＨＰサイトではあまり触れられて
いないように思う。

シムソンの定理の逆

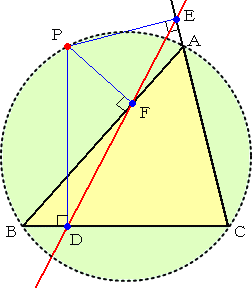△ＡＢＣの外部にある点Ｐから ＢＣ、ＣＡ、ＡＢ 　に下ろした垂線の足を Ｄ、Ｅ、Ｆ とする。 　このとき、３点 Ｄ、Ｅ、Ｆ が同一直線上にあれ 　ば、点Ｐは、△ＡＢＣの外接円の周上にある。 　　（証明） ∠ＢＤＰ＝∠ＢＦＰ＝９０°より、四角形 　　　　　　ＰＢＤＦは円に内接する四角形である。 　　　　よって、　∠ＢＰＤ＝∠ＢＦＤ

３点Ｄ、Ｅ、Ｆ が１直線上より、 　　∠ＢＦＤ＝∠ＡＦＥ 　∠ＡＥＰ＝∠ＡＦＰ＝９０°より、 　四角形ＰＢＤＦは円に内接する　 四角形である。 　よって、　∠ＡＦＥ＝∠ＡＰＥ 　ゆえに、　∠ＢＰＤ＝∠ＡＰＥ

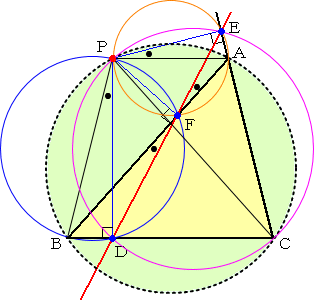　直角三角形ＰＤＣにおいて、　　∠ＰＣＤ＋∠ＣＰＤ＝９０°

　直角三角形ＰＥＣにおいて、　　∠ＰＣＥ＋∠ＣＰＥ＝９０°

　２式を辺々加えて、　∠ＡＣＢ＋∠ＣＰＤ＋∠ＣＰＥ＝１８０°

　ここで、∠ＣＰＤ＋∠ＣＰＥ＝∠ＣＰＤ＋∠ＣＰＡ＋∠ＡＰＥ
　　　　　　　　　　　　　　　　＝∠ＣＰＤ＋∠ＣＰＡ＋∠ＢＰＤ＝∠ＡＰＢ

なので、　∠ＡＣＢ＋∠ＡＰＢ＝１８０°

　したがって、点Ｐは△ＡＢＣの外接円の周上の点である。　　（証終）


　当ＨＰ読者のＨＮ「まるこ」さんから、シムソンの定理の拡張について、ご投稿いただきまし
た。（令和６年１月２３日付け）

　平面上の点 P、Q、R が同一直線上にないとき、それらを３頂点とする三角形の面積を
△PQR で表す。また、P、Q、R が同一直線上にあるときは、△PQR = 0 とする。

　A、B、C を平面上の３点とし、△ABC = 1 とする。この平面上の点 X が、△ABC の外接
円の周および内部を動く。ただし、△ABC の周上は除く。点 X から直線 BC、CA、AB にお
ろした垂線の足を L、M、N とするとき、０≦ △LMN ≦１/４ となることを示せ。また、等号が
成り立つのはどのようなときか。


　壊れた扉さんからのコメントです。（令和６年１月２３日付け）

　等号が成り立つのはどのようなときか。

　「＝０」の場合は、シムソンの定理より、点Xが円周上にある場合ですね。

「＝１/４」の場合は、中点連結定理より、点L、M、N が各辺の中点の場合ですから、点Xが
外心の場合ですね。

　０≦ △LMN ≦１/４ となることを示せ。

　その後、つい、検索してしまいました。



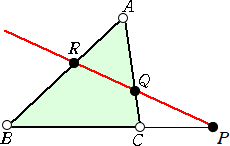
　次は、メネラウスの定理について、まとめよう。

メネラウスの定理　　（Ｍｅｎｅｌａｏｓ　西暦９８年頃？）

　　△ＡＢＣの３辺 ＢＣ、ＣＡ、ＡＢ またはその延長線上に、三角形の頂点とは異なる

３点 Ｐ、Ｑ、Ｒ がある。

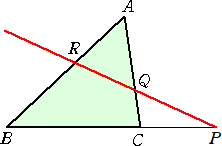このとき、３点 Ｐ、Ｑ、Ｒ が、１つの直線上に存在 するための必要十分条件は、

（証明）　まず、必要条件であることを示す。

　△ＡＢＣの３頂点 Ａ、Ｂ、Ｃ より直線上に垂線の足 Ａ’、Ｂ’、Ｃ’ を下ろす。

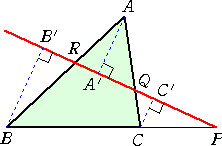このとき、　ＢＰ ： ＰＣ ＝ ＢＢ’ ： ＣＣ’ 　　　　　　　　ＣＱ ： ＱＡ ＝ ＣＣ’ ： ＡＡ’ 　　　　　　　　ＡＲ ： ＲＢ ＝ ＡＡ’ ： ＢＢ’ 　であるので、明らかに等式は成り立つ。

　次に、十分条件であることを示す。等式を満たす点Ｐが辺ＢＣの延長上にあるとしても一

般性は失われない。いま、直線ＱＲと直線ＢＣの交点を、Ｐ’とする。このとき、

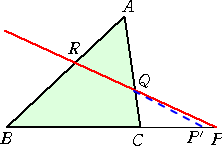よって、　ＢＰ/ＰＣ＝ＢＰ’/Ｐ’Ｃ　より、Ｐ、Ｐ’は、線 　分ＢＣを同じ比に分けるので、Ｐ＝Ｐ’　すなわち、３点 　 Ｐ、Ｑ、Ｒ は１直線上にある。　　（証終）

（追記）　令和元年１２月３日付け

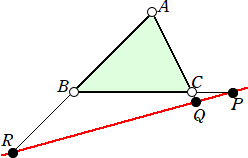
　メネラウスの定理は、三角形に直線が交わる場合が一番馴染みがあるが、直線が三角
形と交わらない場合は、私自身もそうであるが、多分読者の方もあまり馴染みがない場面
ではないだろうか。

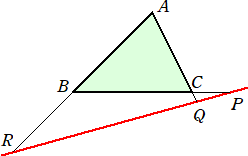３点 Ｐ、Ｑ、Ｒ が、１つの直線上に存在 　　するための必要十分条件は、

　証明は上記と同様である。


（覚え方）　今までメネラウスの定理というと、「世界一周」の合言葉で覚えてきたが、このよう
　　　　　　に三角形と交わらない直線に対しては無力である。

　この場合は、白黒白黒白黒（もちろん、黒白黒白黒白も可）の順番で線分の比を書き出し
ていくとよいようだ。

　　


メネラウスの定理の応用例１

　１辺の長さが８の正三角形ＡＢＣにおいて、辺ＢＣの延長上にＣＤ＝２となる点Ｄをとる。辺
ＡＢの中点ＭとＤを結び、辺ＡＣとの交点をＮとする。このとき、線分ＡＮの長さを求めよ。
　　　　　　　　　　　　　　　　　　　　　　　（平成２６年度神奈川県公立高校入試　数学　改題）

（解）　下図において、メネラウスの定理より、

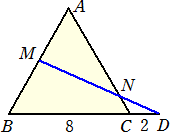（ＡＭ/ＭＢ）・（ＢＤ/ＤＣ）・（ＣＮ/ＮＡ）＝１　なので、 　　（４/４）・（１０/２）・（ＣＮ/ＮＡ）＝１　より、　ＣＮ/ＮＡ＝１/５ 　　したがって、　ＡＮ＝８×（５/６）＝２０/３　　（終）

　中学校では、メネラウスの定理は教えられていないと思うので、別解を考えてみた。

（別解）　下図のように、Ｍより辺ＢＣと平行な線を引き、辺ＡＣとの交点をＰとおく。

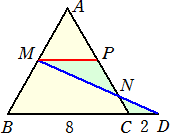中点連結定理より、　△ＮＣＤ∽△ＮＰＭ　なので、 　　ＣＮ ： ＮＰ＝ＣＤ ： ＰＭ＝２ ： ４＝１ ： ２ 　したがって、　ＡＮ＝ＡＰ＋ＰＮ＝４＋４×２/３＝２０/３　　（終）

メネラウスの定理の応用例２

　△ＡＢＣにおいて、∠Ａの外角、∠Ｂ、∠Ｃの２等分線が辺ＢＣの延長、辺ＣＡ、辺ＡＢ
と交わる点をそれぞれ Ｐ、Ｑ、Ｒ とする。

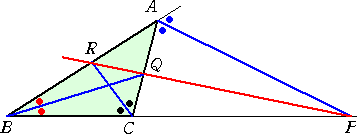このとき、 ３点 Ｐ、Ｑ、Ｒ は、１直線上にある。

（証明）　角の２等分線の性質から、　　ＢＰ ： ＰＣ ＝ ＡＢ ： ＡＣ　、ＣＱ ： ＱＡ ＝ ＢＣ ： ＡＢ

　ＡＲ ： ＲＢ ＝ ＣＡ ： ＢＣ　　であるので、明らかに等式

　　

　が成り立つ。よって、メネラウスの定理より、３点 Ｐ、Ｑ、Ｒ は、１直線上にある。　（証終）


メネラウスの定理の応用例３

　△ＡＢＣにおいて、ＡＣ＝ｎ・ＡＢ　（ｎ＞１）とする。∠Ａの２等分線Ｌが辺ＢＣと交わる
点をＤとし、ＣよりＬに下ろした垂線の足をＥとする。このとき、ＡＤ ： ＤＥ を求めよ。

　　　

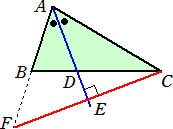
（解）　直線ＡＢとＣＥの交点をＦとおくと、△ＡＦＥ≡△ＡＣＥ　なので、

　　　ＢＦ＝ＡＦ−ＡＢ＝ＡＣ−ＡＢ＝（ｎ−１）ＡＢ

　　このとき、△ＡＦＥにおいて、メネラウスの定理より、（ＡＤ/ＤＥ）（ＥＣ/ＣＦ）（ＦＢ/ＢＡ）＝１

　が成り立つので、　（ＡＤ/ＤＥ）（１/２）（ｎ−１）＝１　より、　ＡＤ/ＤＥ＝２/（ｎ−１）

　したがって、　ＡＤ ： ＤＥ ＝ ２ ： ｎ−１ である。　　（終）


　通常幾何の証明には、ベクトル概念が有効だが、上記の証明の簡明さを考えたら、敢え
てベクトルを用いた別証をあげようという気力が湧かない。次の、チェバの定理もまた然り
である。


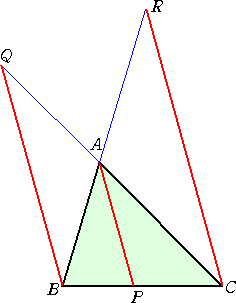
チェバの定理　　（Ｃｅｖａ　1647〜1734）

　　△ＡＢＣの３辺 ＢＣ、ＣＡ、ＡＢ またはその延長線上に、三角形の頂点とは異なる

３点 Ｐ、Ｑ、Ｒ がある。３直線 ＡＰ、ＢＱ、ＣＲ が、１点で交わるとき、

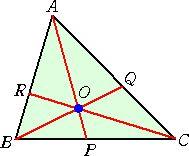が成り立つ。逆に、上記の等式が成り立てば、３直線 　　ＡＰ、ＢＱ、ＣＲ は１点で交わるか、又は、平行である。 　　　　 　　　　（ただし、３点の全てまたは１点のみが辺上にあるものとする。）

（証明）　前半は、　ＢＰ ： ＰＣ ＝ △ＯＡＢ ： △ＯＣＡ

　　ＣＱ ： ＱＡ ＝ △ＯＢＣ ： △ＯＡＢ　　　　ＡＲ ： ＲＢ ＝ △ＯＣＡ ： △ＯＢＣ

であるので、明らかに等式は成り立つ。

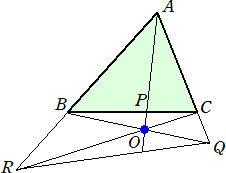
　後半は、等式を満たす点Ｐが辺ＢＣの延長上にあるとしても一般性は失われない。

　直線ＢＱと直線ＣＲが交わるとき、その交点を Ｏ 、ＯＡ と ＢＣ の交点を、Ｐ’とする。

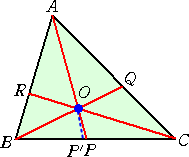このとき、 　　　　　　 　　よって、　ＢＰ/ＰＣ＝ＢＰ’/Ｐ’Ｃ　より、Ｐ、Ｐ’は、線 　分ＢＣを同じ比に分けるので、Ｐ＝Ｐ’　すなわち、３直 　 線 ＡＰ、ＢＱ、ＣＲ は１点で交わる。

　直線ＢＱと直線ＣＲが平行であるとき、その交点を Ｏ 、ＯＡ と ＢＣ の交点を、Ｐ’とする。

このとき、　△ＡＢＱ∽△ＡＲＣ　なので、 　　　　ＡＢ ： ＡＲ ＝ ＡＱ ： ＡＣ　 即ち、　ＲＢ ： ＡＲ ＝ ＣＱ ： ＡＣ　より、 　　　　　　　 となり、 　　　　　　　 　よって、ＡＰ と ＢＱ は平行となる。したがって、 　３直線 ＡＰ、ＢＱ、ＣＲ は平行である。　　（証終）

（コメント）　メネラウスの定理、チェバの定理は平面幾何ではワンセットという認識がありま
　　　　　　すが、歴史的には随分年代差があるのですね！驚きました．．．。


（追記）　令和元年１２月５日付け

　　　

　メネラウスの定理同様に、チェバの定理においても、３直線の交点Ｏが三角形の内部にな
い場合も成立する。証明は上記と同様である。

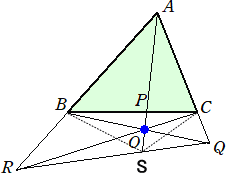（証明）　ＱＲとADの延長との交点をＳとおくと、 　　△ARQにおいて、チェバの定理より、 　　（ＡＢ/ＢＲ）（ＲＳ/ＳＱ）（ＱＣ/ＣＡ）＝１ 　　これを三角形の面積比で表すと、

　（△ＡＢＳ/△ＢＲＳ）（△ＲＳＡ/△ＳＱＡ）（△ＱＣＳ/△ＣＡＳ）＝１

すなわち、　（△ＲＳＡ/△ＢＲＳ）（△ＡＢＳ/△ＣＡＳ）（△ＱＣＳ/△ＳＱＡ）＝１

　よって、　（ＡＲ/ＲＢ）（ＢＰ/ＰＣ）（ＣＱ/ＱＡ）＝１　より、

　　（ＢＰ/ＰＣ）（ＣＱ/ＱＡ）（ＡＲ/ＲＢ）＝１　　　（証終）


チェバの定理の応用例

△ＡＢＣ の内接円が辺 ＢＣ 、ＣＡ 、ＡＢ と 　接する点をそれぞれ Ｐ 、Ｑ 、Ｒ とする。 　　このとき、３直線 ＡＰ 、ＢＱ 、ＣＲ は、１点 　で交わる。

（証明）　円外の１点から引いた接線の長さは等しいので、

　　ＢＰ＝ＲＢ　、　ＣＰ＝ＣＱ　、　ＱＡ＝ＡＲ

よって、このとき、

　

が成り立つので、チェバの定理により、３直線 ＡＰ 、ＢＱ 、ＣＲ は、１点で交わる。　　（証終）


（コメント）　三角形の内接円に、こんな性質があったとは今まで気がつきませんでした！


（追記）　令和５年６月１９日付け

　チェバの定理というと、三角形に関する定理とずっと思っていたが、実は、円に関する定理
であることを再認識させられた。

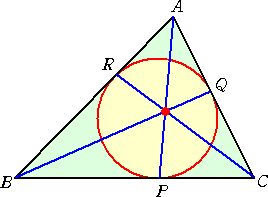
弦に対するチェバの定理

　円周上の６点Ａ、Ｂ、Ｃ、Ｄ、Ｅ、Ｆ をこの順に結ぶと、六角形ＡＢＣＤＥＦが出来る。
このとき、対角線ＡＤ、ＢＥ、ＣＦが１点で交わるための必要十分条件は、

　（ＡＢ/ＢＣ）・（ＣＤ/ＤＥ）・（ＥＦ/ＦＡ）＝１

である。
　　

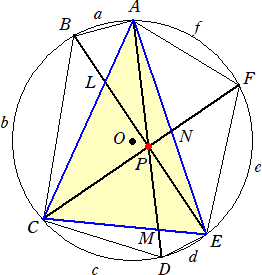
（証明）　円の直径は１としても一般性を失うことはない。このとき、弧の長さ ａ に対して、そ

の弧に対する円周角をθとすると、　ａ ： π＝２θ ： ２π　から、　θ＝ａ　である。他も同様

である。△ＡＣＥ において、３直線 ＡＭ、ＣＮ、ＥＬ が１点Ｐで交わる必要十分条件は、チェバ

の定理より、　（ＡＬ/ＬＣ）・（ＣＭ/ＭＥ）・（ＥＮ/ＮＡ）＝１　である。このとき、

　（ＡＥｓｉｎ ａ/ＣＥｓｉｎ ｂ）・（ＡＣｓｉｎ ｃ/ＡＥｓｉｎ ｄ）・（ＣＥｓｉｎ ｅ/ＡＣｓｉｎ ｆ）＝１　より、

　（ｓｉｎ ａ/ｓｉｎ ｂ）・（ｓｉｎ ｃ/ｓｉｎ ｄ）・（ｓｉｎ ｅ/ｓｉｎ ｆ）＝１

正弦定理より、　ｓｉｎ ａ ＝ＡＢ　、ｓｉｎ ｂ ＝ＢＣ　、ｓｉｎ ｃ ＝ＣＤ　、ｓｉｎ ｄ ＝ＤＥ

　ｓｉｎ ｅ ＝ＥＦ、ｓｉｎ ｆ ＝ＦＡ　なので、　（ＡＢ/ＢＣ）・（ＣＤ/ＤＥ）・（ＥＦ/ＦＡ）＝１　　（証終）


（コメント）　この定理は、覚えておくと役に立ちそう・・・。 チェバの定理と同様に、「世界一周」
　　　　　　と覚えればいいかな。


　メネラウスの定理やチェバの定理を用いると、幾何の証明が鮮やかに示されることは上記
で若干堪能したが、さらに様々な定理の証明にも有効に活用される。

　まず、ニュートン線で有名なニュートンの定理を見てみよう。この定理は、２種類ある。

ニュートン（Ｎｅｗｔｏｎ）の定理（Ａ）

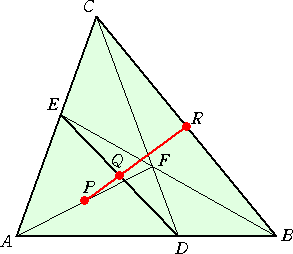△ＡＢＣ において、辺ＡＢ 、辺ＡＣ 上 　に、２点 Ｄ 、Ｅ をとる。線分ＢＥ と ＣＤ 　の交点を Ｆ とする。 　　また、線分ＡＦ 、ＤＥ 、ＢＣ の中点を 　それぞれ Ｐ 、Ｑ 、Ｒ とする。 　　このとき、３点 Ｐ 、Ｑ 、Ｒ は１直線上 　にある。

（証明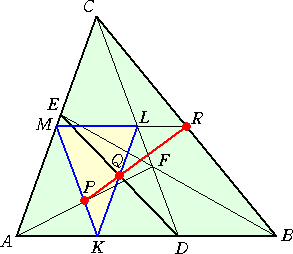）	△ＡＤＣ の３辺 ＡＤ、ＤＣ、ＣＡ の中点をそれ ぞれ Ｋ、Ｌ、Ｍ とおく。 　このとき、中点連結定理により、 　　２ＫＰ＝ＤＦ　、２ＰＭ＝ＦＣ　、２ＭＲ＝ＡＢ 　　２ＲＬ＝ＢＤ　、２ＬＱ＝ＣＥ　、２ＱＫ＝ＥＡ が成り立つ。 　ここで、△ＡＤＣ において、３点 Ｅ、Ｆ、Ｂ は １直線上にあるので、メネラウスの定理より、

　よって、上記の関係式を代入して、

　　　

が成り立つ。

　メネラウスの定理により、△ＫＬＭ において、３点 Ｐ、Ｑ、Ｒ は１直線上にある。　　（証終）


（コメント）　△ＫＬＭに気がつくことは至難の技ですね！証明のエレガントさに感動しました。


　この定理をベクトルを用いて示すことは一見難しく思える。実際に、そうなのだが、怖いも
の見たさにちょっと覗いてみよう。

（ベクトルによる証明）

左図で、　ＡＤ＝２ｂ 、ＡＥ＝２ｃ　とおくと、 　　　ＡＦ＝ｍＡＤ＋ｎＡＥ　（ｍ、ｎ は実数） とおける。明らかに、ｍ≠１、ｎ≠１　である。 　よって、　ＡＰ＝ｍｂ＋ｎｃ　、ＡＱ＝ｂ＋ｃ ところで、　ｎＡＥ＝ＡＦ−ｍＡＤ　より、 　　｛ｎ/（１−ｍ）｝ＡＥ 　　　　　　＝（ＡＦ−ｍＡＤ）/（１−ｍ）

　上式の左辺は直線ＡＥ上の点であることを表し、右辺は直線ＦＤ上の点であることを表す。

　よって、　　ＡＣ＝｛ｎ/（１−ｍ）｝ＡＥ　となる。

　同様にして、　　ＡＢ＝｛ｍ/（１−ｎ）｝ＡＤ　となる。

このとき、　ＡＲ＝（ＡＢ＋ＡＣ）/２＝｛ｍ/（１−ｎ）｝ｂ＋｛ｎ/（１−ｍ）｝ｃ　なので、

　　　ＰＲ＝ＡＲ−ＡＰ＝｛ｍ/（１−ｎ）｝ｂ＋｛ｎ/（１−ｍ）｝ｃ−（ｍｂ＋ｎｃ）

　　　　　　　　　　　　　＝｛ｍｎ/（１−ｎ）｝ｂ＋｛ｍｎ/（１−ｍ）｝ｃ

　　　ＰＱ＝ＡＱ−ＡＰ＝（ｂ＋ｃ）−（ｍｂ＋ｎｃ）＝（１−ｍ）ｂ＋（１−ｎ）ｃ

　よって、　（１−ｍ）（１−ｎ）ＰＲ＝ｍｎＰＱ　となる。

　以上から、　３点 Ｐ、Ｑ、Ｒ は１直線上にある。　（証終）

（コメント）　計算上は納得できても、メネラウスの定理の美しさには到底かないませんね！

ニュートン（Ｎｅｗｔｏｎ）の定理（Ｂ）

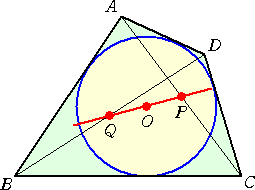円Ｏ に外接する四角形 ＡＢＣＤ において、 　対角線ＡＣ 、ＢＤ の中点をそれぞれ 　Ｐ 、Ｑ とする。 　　このとき、３点 Ｐ 、Ｑ 、Ｏ は１直線上 　にある。

　この定理を平面幾何的に証明する場合、次の補題が本質的に利用される。

補　題

辺ＡＤと辺ＢＣが平行でない四角形ＡＢＣＤ の内部の点Ｐ 　において、常に 　　　　　△ＰＡＢ＋△ＰＣＤ が一定 　であるとき、点Ｐはある線分ＸＹ上の点である。

（証明）　直線 ＢＣ と ＡＤ の交点を Ｅ とし、線分ＢＥ上に、ＢＣ＝ＦＥ となる点 Ｆ をとる。

同様に、線分ＡＥ上に、ＡＤ＝ＧＥ となる点 Ｇ をとる。このとき、△ＰＡＢ＋△ＰＣＤ が一定な ので、△ＰＢＣ＋△ＰＡＤ も一定である。即ち、 　△ＰＦＥ＋△ＰＧＥ が一定となる。△ＦＥＧは、

面積不変で △ＰＦＧ が一定より、点Ｐ は ＦＧ に平行な線分 ＸＹ 上を動く。　　（証終）


（定理の証明）　四角形ＡＢＣＤが平行四辺形であるとき、３点 Ｐ、Ｑ、Ｏ は一致するので、

命題は、明らかに成り立つ。

　そこで、四角形ＡＢＣＤは平行四辺形でないものとする。辺ＡＤと辺ＢＣが平行でないとして

も一般性を失わない。便宜上、四角形ＡＢＣＤの面積を、２Ｓ とおく。

　まず、　２△ＰＡＢ＋２△ＰＣＤ＝△ＡＢＣ＋△ＡＣＤ＝２Ｓ　より、　

　△ＰＡＢ＋△ＰＣＤ＝Ｓ（＝一定）

同様にして、　２△ＱＡＢ＋２△ＱＣＤ＝△ＡＢＣ＋△ＡＣＤ＝２Ｓ　より、

　△ＱＡＢ＋△ＱＣＤ＝Ｓ（＝一定）

また、円Ｏの半径を ｒ とすると、

　△ＯＡＢ＋△ＯＣＤ＝（ＡＢ＋ＣＤ）・ｒ　　、　△ＯＢＣ＋△ＯＤＡ＝（ＢＣ＋ＡＤ）・ｒ

で、円の接線の性質から、　ＡＢ＋ＣＤ＝ＢＣ＋ＡＤ　なので、

　△ＯＡＢ＋△ＯＣＤ＝Ｓ（＝一定）　となる。

したがって、補題により、３点 Ｐ、Ｑ、Ｏ は同一直線上にある。　　（証終）


（コメント）　最後の結論への導き方がとてもおしゃれですね！



　　　　　　　以下、工事中