蝴蝶定理　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　当ＨＰの掲示板「出会いの泉」で、ａａａ 様より紹介されたＨＰを拝見したところ、とても興
味ある幾何の定理が紹介されていた。

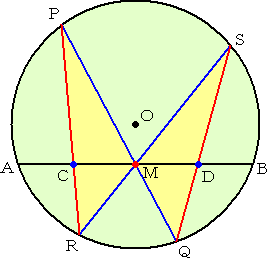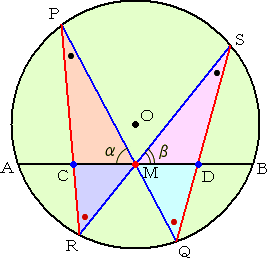
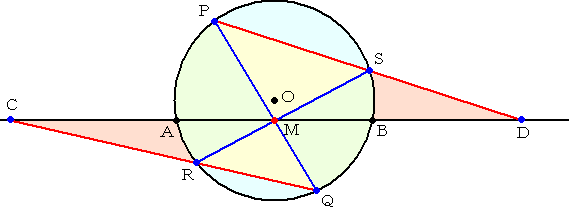
円Ｏにおいて、弦ＡＢを引き、その中点 　　をＭとする。 　　　さらに、Ｍを通る任意の２つの弦ＰＱ、 　　ＲＳを引く。 　　　これらの弦の端点ＰとＲ、ＱとＳを結び、 　　弦ＡＢとの交点をそれぞれＣ、Ｄとする。 　　　このとき、Ｍは、線分ＣＤの中点となる。

　この定理は、羽を開いた蝶を真上から描いたように見えるので、蝴蝶定理と言われる。

とても、美しい定理で、思わず感動してしまった。

　ａａａ 様より紹介されたＨＰでは、証明が書かれていないようなので、証明を知りたいと
いう衝動にかられた。

　この「蝴蝶定理」で検索すると、中国のものばかりがヒットした。（漢字ばかりに思わず閉口！）

また、「Butterfly　Theorem」として検索をかけると、案の定、英語のＨＰサイトがヒットする。
何れも、日本語のサイトはあまり（ほとんど？）登録されていないようだ。

（かなり有名な定理なようで、３０年ほど前に数学セミナーにも紹介されたそうである。（広島工業大学
大川研究室より情報提供）　したがって、日本語のサイトもあると思うのだが、現在、ａａａ 様より紹介さ
れたＨＰ以外見つけていない。）

　なお、蝴蝶定理について、１８１５年に Ｈｏｒｎｅｒ’ｓ　ｍｅｔｈｏｄ で有名な Ｗ．Ｇ．Ｈｏｒｎｅｒ が
一つの証明を与えたとのことである。

　いろいろなＨＰサイトで行われている証明を参考に、少し整理したいと思う。

（証）　与えられた図において、線分ＡＢの 　　　垂直２等分線と円との交点を、Ｅ、Ｆ 　　　とする。 　線分ＥＦに関して点Ｐと対称な点を、Ｐ’ とする。 　△ＭＰＣと△ＭＰ’Ｄについて考える。 　対称性から、ＭＰ＝ＭＰ’　・・・　（１） 　　　　∠ＰＭＣ＝∠Ｐ’ＭＤ　・・・　（２） 　円周角の定理より、 　　　　∠ＭＰＣ＝∠ＭＳＤ 　また、４点Ｐ、Ｐ’、Ｓ、Ｑが同一円周上に
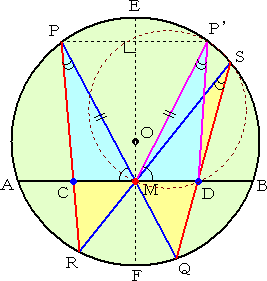あるので、 　∠Ｐ’ＰＱ＋∠ＱＳＰ’＝１８０°　が成り立つ。さらに線分ＰＰ’と線分ＡＢは平行なので、 　∠Ｐ’ＭＤ＝∠Ｐ’ＰＱ　　より、　∠Ｐ’ＭＤ＋∠ＱＳＰ’＝１８０°　すなわち、 　∠Ｐ’ＭＤ＋∠ＤＳＰ’＝１８０°　が成り立つ。 　よって、４点Ｍ、Ｄ、Ｓ、Ｐ’は同一円周上にある。 　このことから、円周角の定理により、　∠ＭＰ’Ｄ＝∠ＭＳＤ 　したがって、　∠ＭＰＣ＝∠ＭＰ’Ｄ　・・・　（３） （１）（２）（３）により、　△ＭＰＣ≡△ＭＰ’Ｄ　　であるので、　ＭＣ＝ＭＤ　となる。（証終）

　上記の証明は、初等幾何的証明であるが、三角比を用いると、次のようにも証明する
ことが出来る。

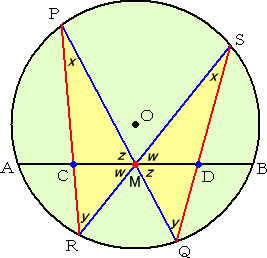	（別証）　ＡＢ＝２ｋ　、ＭＣ＝ｍ、ＭＤ＝ｎ　と 　　　　　　おく。 　　　△ＭＰＣにおいて、正弦定理により、 　　　　　　 　　　△ＭＲＣにおいて、正弦定理により、
方べきの定理より、　ＡＣ×ＢＣ＝ＰＣ×ＲＣ　なので、上式を代入して、 　　　　　　　　　　　　　 　　　が成り立つ。同様にして、 　　　　　　　　　　　　　 　　　これより、　（ｋ2−ｍ2）/ｍ2＝（ｋ2−ｎ2）/ｎ2　なので、　ｋ2ｍ2＝ｋ2ｎ2　から 　　　　ｍ ＝ ｎ　が成り立ち、　ＭＣ＝ＭＤ　となる。（証終）

　当初、冒頭の証明が最も初等的で分かりやすいと思ったが、その後の調査で、もっと簡
明な初等幾何的証明があるようだ。

（Ｓｈｋｌｙａｒｓｋｙ による証明）

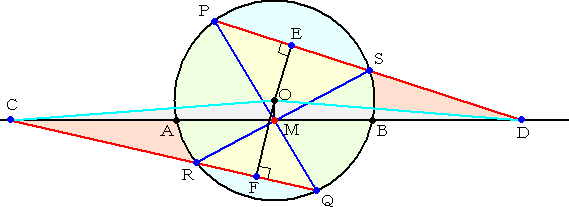
（証）　円の中心Ｏと点Ｍを結び、さらに、 　　　点Ｏより弦ＰＲ、ＳＱにそれぞれ垂 　　　線の足Ｅ、Ｆを下ろす。Ｅ、Ｆはそれ 　　　ぞれの弦の中点である。 　　　△ＭＲＰ∽△ＭＱＳ　なので、 　　　　　　ＲＰ：ＲＭ＝ＱＳ：ＱＭ 　　　すなわち、 　　　　　　ＲＥ：ＲＭ＝ＱＦ：ＱＭ 　　　が成り立つ。 　　また、∠ＭＲＰ＝∠ＭＱＳ　なので、 　△ＭＲＥ∽△ＭＱＦ　となる。 　　　よって、　∠ＭＥＲ＝∠ＭＦＱ
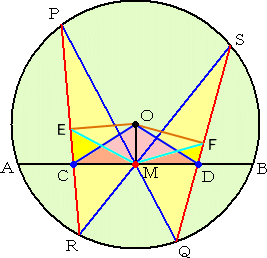ところで、∠ＯＥＣ＋ＯＭＣ＝１８０°なので、４点Ｏ，Ｅ，Ｃ，Ｍは同一円周上にある。 よって、　∠ＭＥＲ＝∠ＭＯＣ　で、また、同様にして、　∠ＭＦＱ＝∠ＭＯＤ　である。 　このとき、　∠ＭＥＲ＝∠ＭＦＱ　なので、　∠ＭＯＣ＝∠ＭＯＤ　となる。 また、ＯＭは共通なので、２つの直角三角形ＯＭＣとＯＭＤにおいて、 　　　△ＯＭＣ≡△ＯＭＤ　　となり、したがって、　ＭＣ＝ＭＤ　が成り立つ。（証終）

　また、Ｃｏｘｅｔｅｒ　ａｎｄ　Ｇｒｅｉｔｚｅｒｌ によれば、次のような証明も考えられる。

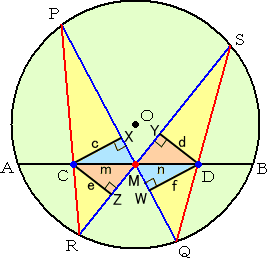	（証）　ＡＢ＝２ａ　、ＭＣ＝ｍ　、ＭＤ＝ｎ　とし、 　　　２点Ｃ、Ｄより弦ＰＱ、ＲＳに垂線を下ろし、 　　　その長さをそれぞれ　ｃ、ｄ、ｅ、ｆ　とする。 　　　△ＭＣＸ∽△ＭＤＷ　より、　ｍ/ｎ＝ｃ/ｆ 　　　△ＭＣＺ∽△ＭＤＹ　より、　ｍ/ｎ＝ｅ/ｄ 　　　△ＰＣＸ∽△ＳＤＹ　より、　ｃ/ｄ＝ＰＣ/ＳＤ 　　　△ＲＣＺ∽△ＱＤＷ　より、　ｅ/ｆ＝ＲＣ/ＱＤ 　　このとき、　（ｍ/ｎ）2＝(ｃ/ｄ)(ｅ/ｆ) 　　　　　　　　　　　　　＝（ＰＣ・ＲＣ）/（ＳＤ・ＤＱ） 　　また、方べきの定理より、 　　　ＰＣ・ＲＣ＝ＡＣ・ＢＣ＝(ａ−ｍ)(ａ＋ｍ) 　　　ＳＤ・ＤＱ＝ＡＤ・ＢＤ＝(ａ＋ｎ)(ａ−ｎ) 　　が成り立つ。
よって、　　ｍ2(ａ＋ｎ)(ａ−ｎ)＝ｎ2(ａ−ｍ)(ａ＋ｍ)　より、　ｍ＝ｎ　が成り立つ。（証終）

　さらに、メネラウスの定理を用いて証明する方法もある。あまりに技巧的なところに思わ
ず唸ってしまう。

（証）　円Ｏにおいて、弦ＡＢを引き、その 　　　中点をＭとする。 　また円外の１点Ｘより２つの割線ＸＰＲ、 ＸＳＱを引き弦ＡＢとの交点をそれぞれＣ、 Ｄとする。 　さらに、２点ＰとＱ、２点ＲとＳを結び、弦 ＡＢとの交点をそれぞれＥ、Ｆとする。 　△ＸＣＤにおいて、メネラウスの定理よ り、次の２つの等式が成り立つ。 　　(ＣＰ/ＰＸ)・(ＸＱ/ＱＤ)・(ＤＦ/ＦＣ)＝１ 　　(ＣＲ/ＲＸ)・(ＸＳ/ＳＤ)・(ＤＥ/ＥＣ)＝１ 　２つの式を辺々かけて、
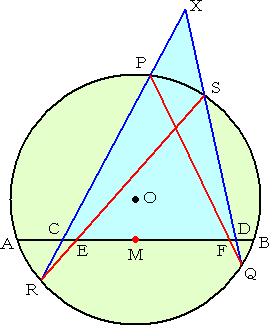(ＣＰ・ＣＲ/ＰＸ・ＲＸ)・(ＸＱ・ＸＳ/ＱＤ・ＳＤ)・(ＤＥ・ＤＦ/ＥＣ・ＦＣ)＝１ ここで、方べきの定理より、 　　　　ＣＰ・ＣＲ＝ＣＡ・ＣＢ　、　ＰＸ・ＲＸ＝ＸＱ・ＸＳ　、　ＱＤ・ＳＤ＝ＤＡ・ＤＢ なので、　　(ＣＡ・ＣＢ/ＤＡ・ＤＢ)・(ＤＥ・ＤＦ/ＥＣ・ＦＣ)＝１　が成り立つ。 　いま、ここで、Ｅ＝Ｆ＝Ｍ　とすると、上式から、 　　　　　　　(ＣＡ・ＣＢ/ＤＡ・ＤＢ)・(ＭＤ/ＭＣ)2＝１ が成り立つ。　ＡＢ＝２ａ　、ＭＣ＝ｘ　、ＭＤ＝ｙ　とおくと、上式は、 　　　　　(ａ−ｘ)(ａ＋ｘ)ｙ2＝(ａ＋ｙ)(ａ−ｙ)ｘ2 となり、明らかに、　ｘ＝ｙ　が成り立つ。　したがって、　ＭＣ＝ＭＤ　が成り立つ。（証終）

（コメント）　この証明の面白いところは、上記証明中には明記していないが、ＥとＦが限り
　　　　　　なくＭに近づくという極限の状態で証明しているところだろう。従って、ＰＲとＱＳ
　　　　　　が平行になる場合の疑問にも耐えうるものと考える。

　　上記の証明で、「ここで、Ｅ＝Ｆ＝Ｍ　とすると、」としたが、ＭＥ＝ＭＦ＝ｂ　であるよう
　にはじめから設定しておくと、面白いことに、ＭＣ＝ＭＤ　が示される。（ｂ＝０　の場合が、
　蝴蝶定理である。）

　　このことを示唆した人は、Ｍ．Ｋｌａｍｋｉｎ（１９６５）で、蝴蝶定理の一般化を与えている
　といえる。

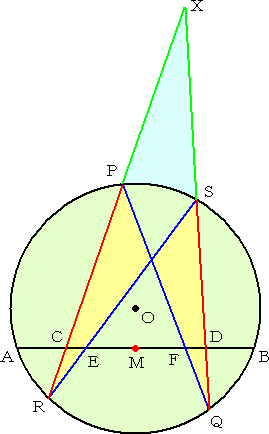円Ｏにおいて、弦ＡＢを引き、その中点 　　をＭとする。 　　　さらに、弦ＡＢ上に、ＭＥ＝ＭＦとなる２ 　　点Ｅ、Ｆをとる。 　　　Ｅ、Ｆを通る任意の２つの弦ＰＱ、ＲＳを 　　引く。ただし、これらの弦は円内で交わる 　　ものとする。 　　　これらの弦の端点ＰとＲ、ＱとＳを結び、 　　弦ＡＢとの交点をそれぞれＣ、Ｄとする。 　　　２つの弦ＰＲとＱＳの延長は、円外の１ 　　点Ｘで交わるものとする。 　　　このとき、Ｍは、線分ＣＤの中点となる。

（証）　△ＸＣＤにおいて、メネラウスの定理より、次の２つの等式が成り立つ。

　　　　(ＣＰ/ＰＸ)・(ＸＱ/ＱＤ)・(ＤＦ/ＦＣ)＝１　、　(ＣＲ/ＲＸ)・(ＸＳ/ＳＤ)・(ＤＥ/ＥＣ)＝１

　　　２つの式を辺々かけて、

　　　　(ＣＰ・ＣＲ/ＰＸ・ＲＸ)・(ＸＱ・ＸＳ/ＱＤ・ＳＤ)・(ＤＥ・ＤＦ/ＥＣ・ＦＣ)＝１

　　　ここで、方べきの定理より、

　　　　　　ＣＰ・ＣＲ＝ＣＡ・ＣＢ　、　ＰＸ・ＲＸ＝ＸＱ・ＸＳ　、　ＱＤ・ＳＤ＝ＤＡ・ＤＢ

　　　なので、　　(ＣＡ・ＣＢ/ＤＡ・ＤＢ)・(ＤＥ・ＤＦ/ＥＣ・ＦＣ)＝１　が成り立つ。

　いま、　ＡＢ＝２ａ　、ＭＣ＝ｘ　、ＭＤ＝ｙ　、ＭＥ＝ＭＦ＝Ｂ　とおくと、上式は、

　　　　　(ａ−ｘ)(ａ＋ｘ)/｛(ａ＋ｙ)(ａ−ｙ)｝・(ｙ＋ｂ)(ｙ−ｂ)/｛(ｘ−ｂ)(ｘ＋ｂ)｝＝１

　よって、　（ａ²−ｘ²）（ｙ²−ｂ²）＝（ａ²−ｙ²）（ｘ²−ｂ²）　より、　（ａ²−ｂ²）（ｘ²−ｙ²）＝０

　となり、明らかに、　ｘ＝ｙ　が成り立つ。　したがって、　ＭＣ＝ＭＤ　が成り立つ。（証終）


　また、面積計算から示す方法も面白いと思う。

（証）　左図において、 　　　△ＭＰＣ/△ＭＱＤ＝ＭＰ・ＭＣ/ＭＱ・ＭＤ 　　　△ＭＱＤ/△ＭＲＣ＝ＭＱ・ＤＱ/ＭＲ・ＣＲ 　　　△ＭＲＣ/△ＭＳＤ＝ＭＲ・ＭＣ/ＭＳ・ＭＤ 　　　△ＭＳＤ/△ＭＰＣ＝ＭＳ・ＤＳ/ＭＰ・ＣＰ 　　が成り立つ。 　　これらを辺々かけて、 　　　ＭＣ2・ＤＱ・ＤＳ/ＭＤ2・ＣＲ・ＣＰ＝１ 　　ここで、方べきの定理より、 　　ＤＱ・ＤＳ＝ＤＡ・ＤＢ、ＣＲ・ＣＰ＝ＣＡ・ＣＢ 　が成り立つ。 　　これより、　ＭＣ＝ＭＤ　が成り立つことが 　分かる。（証終）

　何となくこれまで、座標幾何による証明を避けてきた。多分計算が煩雑になるだろうとい
う理由からである。

　このことについて、次のような証明が知られているようだ。

　　　　　　　　　

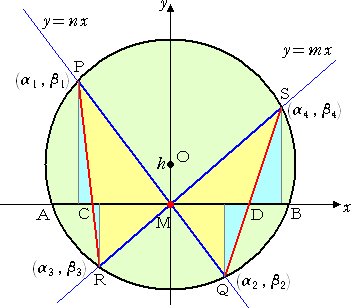
（証）　上図において、Ｍ（ ０ ， ０ ）、ＯＭ＝ｈ、半径を ｒ とすると、

　　　円Ｏの方程式は、　ｘ²＋（ｙ−ｈ）² ＝ ｒ²　となる。

　　　　いま、直線ＰＱ、ＲＳの方程式を、それぞれ　ｙ ＝ ｎｘ　、ｙ ＝ ｍｘ　とおく。

　　　この２直線と円との交点Ｐ、Ｑ、Ｒ、Ｓの座標を、それぞれ

　　　　（ α₁， β₁ ） 、（ α₂ ， β₂ ） 、（ α₃ ， β₃ ） 、（ α₄ ， β₄）

　　　とおく。　また、　Ｃ（ ｃ ， ０ ） 、Ｄ（ ｄ ， ０ ）　とおく。

　　ｘ²＋（ｙ−ｈ）² ＝ ｒ²　に、　ｙ ＝ ｎｘ　を代入して整理すると、

　　　　　（ｎ²＋１）ｘ²−２ｎｈｘ＋ｈ²−ｒ²＝０

　解と係数の関係により、　α₁＋ α₂ ＝ ２ｎｈ/（ｎ²＋１）　、α₁・α₂ ＝ （ｈ²−ｒ²）/（ｎ²＋１）

　同様にして、　　ｘ²＋（ｙ−ｈ）² ＝ ｒ²　に、　ｙ ＝ ｍｘ　を代入して整理すると、

　　　　　（ｍ²＋１）ｘ²−２ｍｈｘ＋ｈ²−ｒ²＝０

　解と係数の関係により、 α₃ ＋ α₄ ＝ ２ｍｈ/（ｍ²＋１）　、α₃・α₄ ＝ （ｈ²−ｒ²）/（ｍ²＋１）

　 以上の４式より、　ｎ・α₁・α₂/（ α₁ ＋ α₂ ） ＝ ｍ・α₃・α₄/（ α₃ ＋ α₄ ）

　すなわち、　　（ｎα₁−ｍα₃）/（ｎα₂−ｍα₄）＝−α₁α₃/α₂α₄　　が成り立つ。

　このとき、点Ｃについて、水色の三角形は相似なので、　α₃−ｃ ： ｃ−α₁ ＝ −ｍα₃ ： ｎα₁

　よって、　 ｃ ＝ （ｎ−ｍ）α₁α₃/（ｎα₁−ｍα₃）　である。

　同様にして、点Ｄについて、水色の三角形は相似なので、

　　　　　　　α₄−ｄ ： ｄ−α₂ ＝ ｍα₄ ： −ｎα₂

　よって、　 ｄ ＝ （ｎ−ｍ）α₂α₄/（ｎα₂−ｍα₄）　である。

　このとき、　ｄ/ｃ ＝ （α₂α₄/α₁α₃）（ｎα₁−ｍα₃）/（ｎα₂−ｍα₄） ＝ −１　となり、

　ｄ ＝ −ｃ　すなわち、　ＭＣ＝ＭＤ　が成り立つ。（証終）

（コメント）　単なる計算なのだが、目標に向かっての巧妙な仕掛けが散りばめられていて、
　　　　　　ワクワクしますね！


　さて、Ｍ．Ｋｌａｍｋｉｎ（１９６５）により与えられた一般の蝴蝶定理以外にも、次のような形に
一般化することもできる。

定理（Ｂｅｔｔｅｒ　Ｂｕｔｔｅｒｆｌｙ　Ｔｈｅｏｒｅｍ）

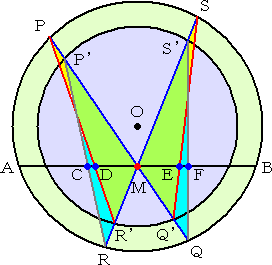　　２つの同心円Ｏにおいて、弦ＡＢを引き、
　その中点を、Ｍとする。

　　さらに、Ｍを通る任意の２つの弦ＰＰ’Ｑ’Ｑ、
　ＲＲ’Ｓ’Ｓを引く。

　　点Ｐ’とＲ、点ＰとＲ’、点ＳとＱ’、点Ｓ’とＱ
　を結び弦ＡＢとの交点をそれぞれＣ、Ｄ、Ｅ、
　Ｆとする。

　　このとき、次の等式が成り立つ。

　　　　



（注意）　２つの同心円が一つの円になるとき、２点ＣとＤ、２点ＥとＦは一致し、蝴蝶定理の
　　　　結果を得ることができる。

　この定理を証明するために、次の事実が有効に用いられる。


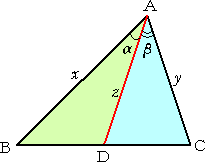
　　左図の△ＡＢＣにおいて、

　　　　

　が成り立つ。



　　　　　　この事実の証明は易しい。

　　　　　　　　　　△ＡＢＣ＝△ＡＢＤ＋△ＡＣＤ　なので、

　　　　　　　　　　(1/2)・ｘ・ｙ・ｓｉｎ (α＋β)＝(1/2)・ｘ・ｚ・ｓｉｎ α ＋ (1/2)・ｚ・ｙ・ｓｉｎ β

　　　　　　が成り立つ。この式より、所要の結果が得られる。


　この事実を用いて、いよいよ定理の証明に入ろう。

（証）　与えられた図において、Ｍ1、Ｍ2 　　　を定める。 　△ＭＰ’Ｒ において、 　　　ｓｉｎ(α＋β)/ＭＣ 　　＝ｓｉｎβ/ＭＰ’＋ｓｉｎα/ＭＲ 同様にして、 △ＭＰＲ’ において、 　　　ｓｉｎ(α＋β)/ＭＤ 　　＝ｓｉｎβ/ＭＰ＋ｓｉｎα/ＭＲ’ 　△ＭＳＱ’ において、 　　　ｓｉｎ(α＋β)/ＭＥ 　　＝ｓｉｎβ/ＭＱ’＋ｓｉｎα/ＭＳ

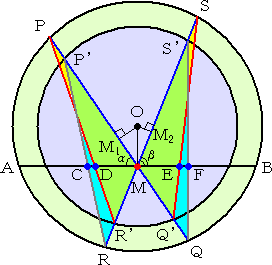△ＭＳ’Ｑ において、　　　ｓｉｎ(α＋β)/ＭＦ＝ｓｉｎβ/ＭＱ＋ｓｉｎα/ＭＳ’ が成り立つ。　したがって、 　　ｓｉｎ(α＋β)（１/ＭＣ＋１/ＭＤ−１/ＭＥ−１/ＭＦ） 　＝ｓｉｎβ/ＭＰ’＋ｓｉｎα/ＭＲ＋ｓｉｎβ/ＭＰ＋ｓｉｎα/ＭＲ’ 　　−ｓｉｎβ/ＭＱ’−ｓｉｎα/ＭＳ−ｓｉｎβ/ＭＱ−ｓｉｎα/ＭＳ’ 　＝ｓｉｎα（１/ＭＲ−１/ＭＳ）＋ｓｉｎα（１/ＭＲ’−１/ＭＳ’） 　　＋ｓｉｎβ（１/ＭＰ−１/ＭＱ）＋ｓｉｎβ（１/ＭＰ’−１/ＭＱ’） 　ここで、方べきの定理より、　ＭＰ・ＭＱ＝ＭＲ・ＭＳ 　　　　　　　　　　　　　　　　　　ＭＰ’・ＭＱ’＝ＭＲ’・ＭＳ’ が成り立ち、さらに、　ＭＰ−ＭＱ＝ＭＰ’−ＭＱ’＝２ＭＭ1＝２ＯＭｓｉｎα 　 　　　　　　　　　　　　ＭＳ−ＭＲ＝ＭＳ’−ＭＲ’＝２ＭＭ2＝２ＯＭｓｉｎβ であるので、　　ｓｉｎ(α＋β)（１/ＭＣ＋１/ＭＤ−１/ＭＥ−１/ＭＦ）＝０ となる。　よって、 　　　　　　　　　　　　 が成り立つ。（証終）

（コメント）　この証明では、三角比が用いられているが、もっと初等幾何的な証明はできな
　　　　　　いものだろうか？


　蝴蝶定理の新たな拡張として、次のような事実が成り立つことを最近知ることが出来た。

　北海道の高倉　亘　さんという方が、「初等幾何における抽象化と一般化」の中で、次の
性質について証明されている。

　円Ｏにおいて、弦ＡＢを引き、その中点をＭとする。さらに、Ｍを通る２つの弦ＰＱ、
ＲＳを引く。ただし、直線ＰＳ、直線ＱＲは、直線ＡＢと交わるものとする。

　その交点をＣ、Ｄとするとき、Ｍは、線分ＣＤの中点となる。



　証明については、少し文言等を整理して示したいと思う。

（証明）　下図のように、Ｏより、線分ＰＳ、ＱＲに垂線ＯＥ、ＯＦを下ろす。



　直角三角形ＯＭＣと直角三角形ＯＭＤにおいて、両者が合同であることを示せばよい。

　まず、∠ＯＭＣ＝∠ＯＦＣ＝９０°より、４点Ｏ、Ｍ、Ｆ、Ｃ は同一円周上にある。

よって、　∠ＭＯＣ＝∠ＭＦＱ　である。

　同様に、∠ＯＭＤ＝∠ＯＥＤ＝９０°より、４点Ｏ、Ｍ、Ｄ、Ｅ は同一円周上にある。

よって、　∠ＭＯＤ＝∠ＭＥＳ　である。

　ここで、　△ＭＰＳ∽△ＭＲＱ　なので、　△ＭＥＳ∽△ＭＦＱ　である。

よって、　∠ＭＦＱ＝∠ＭＥＳ　なので、　∠ＭＯＣ＝∠ＭＯＤ　が成り立つ。

　ＯＭは共通なので、　直角三角形ＯＭＣ≡直角三角形ＯＭＤ

したがって、　ＭＣ＝ＭＤ　となり、Ｍは線分ＣＤの中点となる。（証終）

（コメント）　蝴蝶定理の新たな進展に感動しました。高倉さんに感謝いたします。

　Ｍ．Ｋｌａｍｋｉｎ（１９６５）による拡張と、北海道の高倉さんによる拡張をまとめて、次のよう
に、蝴蝶定理の新たな拡張を発見された方がおられる。（平成１７年１２月２日付け）

　ＨＰサイト：「数学教材の部屋」に、そのことが詳しく述べられている。

　　ＣＡＢＲＩ　ＪＡＶＡ　ＡＰＰＬＥＴによる数学教材　：　「胡蝶定理とその応用」

　上記のことを、当ＨＰの統一した記号を用いると、次のようになるであろう。

　円Ｏにおいて、弦ＡＢを引き、その中点をＭとする。さらに、弦ＡＢ上に ＭＥ＝ＭＦ と
なる２点Ｅ、Ｆをとり、２点Ｅ、Ｆを通る２つの弦ＰＱ、ＲＳを引く。ただし、直線ＰＳ、ＱＲ
は、直線ＡＢと交わるものとする。その交点をＣ、Ｄとする。
　このとき、次が成り立つ。
（１）　Ｍは、線分ＣＤの中点である。　　（２）　Ｍは、線分ＸＹの中点である。



　証明は、「胡蝶定理とその応用」をご覧下さい。

（コメント）　（２）は、Ｍ．Ｋｌａｍｋｉｎ（１９６５）による拡張と同じですが、（１）は、高倉さんのも
　　　　　　のを、より一般化したもので成り立つことに感動しました！証明も、対称な点を利
　　　　　　用したもので分かりやすかったです。「数学教材の部屋」様に感謝いたします。


　　　以下、工事中