高次方程式の解の近似計算 
代数学の基本定理によれば、n次方程式は、n個の解をもつ。特に、3次方程式は、3次
関数のグラフの特徴から、3つの解のうち、少なくとも1つは実数解である。
その実数解の1つが有理数解であるとき、3次式は容易に因数分解され、2次方程式の
解の公式を用いて3次方程式の3つの解は完全に記述される。
問題は、実数解が有理数解でないときである。この場合は、方程式の解を完全に記述す
るのは困難で、近似解を求めることになる。
最近のグラフ描画ソフトを使えば、解の小数第1位ぐらいまでだったら正しく読み取ること
ができる。
このページでは、その近似解を手計算で求める方法について紹介する。
例 3次方程式 X3+2X−5=0 の実数解を求めよ。
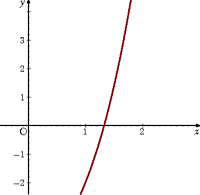 |
F(X)=X3+2X−5 とおくと、
F(X) は連続で、F(1)=−2<0、F(2)=7>0
よって、中間値の定理により、方程式 F(X)=0 は、
1 と 2 の間に実数解をもつ。
この実数解の近似値を求める方法として、古くから
次のような Newton の方法が学校教育で教えられ
ている。
|
Newton の方法
| 第2次導関数 F”(X) が F(X1) と同符号のとき、 |
 |
| は、X1 より詳しい近似値を与える。 |
この X と真の解 α との差は次のように評価される。
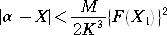
ただし、M、K は、αの近くで、
0<K≦|F’(X)| 、|F”(X)|≦M
を満たす定数である。 |
上記例において、
F”(X)=3X2+2>0 、 F(2)=7>0 なので、 X1=2 として、X を求めれば、
X=1.5 である。(この値は、2より解に近い。)
今度は、 X1=1.5 として、この計算を繰り返すと、 X≒1.3428・・・ となり、さらに真
の値に近くなる。 (1.3・・・位までは、上図のグラフからも読み取れる。)
(因みに、この方程式の実数解の正しい値(近似値)は、1.328・・・ 。)
このページのタイトルから外れるかも知れないが、方程式が多項式でない場合について
も、ここで考察しておこう。
例 方程式 ex = x2 を解け。(平成18年11月3日・HN「虫さされかゆみ・しっしんに」さんより出題)
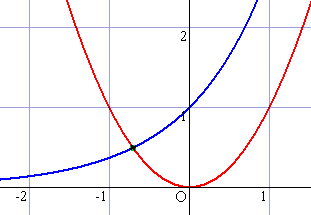 |
グラフ描画ソフトを用いて、グラフを
書かせてみた。
交点は1つで、その x 座標は、だい
たい−0.70くらいであることが読み
取れる。
このことを計算で確かめてみよう。 |
(解) F(x)=ex − x2 とおくと、 F(x) は連続で微分可能ある。
F’(x)=ex − 2x で、さらに、 F”(x)=ex − 2 、F”’(x)=ex である。
F”’(x)>0 より、 F”(x) は単調に増加し、 F”(log2)=2 − 2=0
よって、 x<log2 のとき、 F”(x)<0 より、F’(x) は単調に減少する。
x>log2 のとき、 F”(x)>0 より、F’(x) は単調に増加する。
ここで、 F’(log2)=2−2log2=2log(e/2)>0 なので、
すべての x に対して、 F’(x)>0 となり、F(x) は単調に増加する。
F(−1)=e-1 − 1<0 、F(0)=1>0 なので、中間値の定理により、
方程式 F(X)=0 は、 −1 と 0 の間にただひとつの実数解をもつ。
−1<x<0 において、 F”(x)<0 なので、Newton の方法における X1 として、
X1=−1 とおく。このとき、Newton の方法により、
X=−1−F(−1)/F’(−1)=−1+(1−e-1)/(e-1+2)=−(2+e)/(1+2e)
ここで、 ネイピアの数 e ≒ 2.7182818284 として、 X の値を求めると、
X =−0.733043605249721 となる。 また、−1≦x≦0 において、
F’(x)≧F’(0)=1 、 |F”(x)|≦|F”(−1)|=2−e-1
なので、 K=1 、 M=2−e-1 として、誤差を計算すると、次の値より小さい。
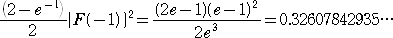
まだ、誤差が大きいので、さらなる計算が必要である。
上記と同様にして、今度は、 X1=−0.733043605249721 とする。このとき、
X=X1−F(X1)/F’(X1)=X1−(ex1 − x12)/(ex1 − 2x1)
に代入して、 X=−0.703807786328276 を得る。このときの誤差は、
上記と同様に計算して、 0.002 くらいの幅である。
このようにして得られる X は、限りなく真の解に近づくことが知られているので、真の解が、
ほぼ「 −0.70 」くらいであることは、ほぼ確実である。 (終)
(コメント) 上記の小数計算は、表計算ソフト Excel を利用した。当HPがいつもお世話に
なっている、らすかるさんは、精度1200桁の自作電卓で計算されたとのことで、
もっと詳しい値を出力された。
初期値を、−1 として、
-1
-0.7330436052454454101901278
-0.7038077863241329872803886
-0.7034674683317975063564335
-0.7034674224983924833237669
-0.7034674224983916520498186
-0.7034674224983916520498186
( e の x 乗の計算は、テイラー展開の式を使って求めたそうです。)
らすかるさんの計算結果を見ると、真の解は、
−0.7034674224983916520498186・・・
のようですね!
(追記) S(H)さんが考察されました。(平成26年11月1日付け)
(計算結果) -0.70346742249839165204981860185990213034292843103422360809328769
2219921221440677421793664607664383138547538613397017723816071706339955772
8646718168154693644676114444089404
とのことです。
このNewton の方法は、いくつか問題点がある。
問題点1. この計算を何回続ければよいのか?
問題点2. 小数を含む計算なので、電卓なしでは大変である!
理論的には優れてはいるものの、このような近似計算を電卓に頼らずに手計算で行うこ
とは、非常に厳しいものがある。
そこで、次に述べる Horner の方法が手計算の場合有効となる。
いくつか予備知識を確認しよう。
組立除法(Synthetic division)
・・・ これは、整式を1次式で割り算したときに、商と余りを簡単に求める方法である。
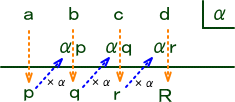
説明を簡単にするために、3次式 F(X)=aX3+bX2+cX+d の場合を考える。
F(X) を、1次式 X−α で割った商を、pX2+qX+r とし、余りを、R とする。
このとき、
F(X)=(X−α)(pX2+qX+r)+R
と書ける。この式を展開して、F(X)=pX3+(q-αp)X2+(r−αq)X−αr+R なので、もと
の式と係数比較して、
a=p、b=q-αp、c=r−αq、d=−αr+R
すなわち、
p=a、q=b+αp、r=c+αq、R=d+αr
この関係を図式化すれば次のようになる。
練習 次の割り算を計算し、商と余りを求めよ。(実際の求め方は、こちらを参照)
(1) (X3+2X−5)÷(X−1)
(2) (2X3+3X2+4)÷(2X−1)
(答) (1)商は、X2+X+3、余りは、−2 (2)商は、X2+2X+1、余りは、5
方程式の変換・・・ これは、所要の条件を満たすように方程式を書き換える方法である。
定理(解より一定数を減ずる)
F(X)=0 の解を、α、β、γ とする。このとき、
α−p、β−p、γ−p を解とする方程式は、F(X+p)=0
(証) Y=F(X) のグラフを、X軸方向に、−p だけ平行移動すればよい。
3次式 F(X)=aX3+bX2+cX+d に対して、F(X+p)=sX3+tX2+uX+v は次のようにし
て求められる。
F(X+p) の X に X−p を代入して、F(X)=s(X−p)3+t(X−p)2+u(X−p)+v となる。
この式により、s、t、u、v は、次のように定められる。
v ・・・ F(X) を X−p で割った余り
u ・・・ 上記の商を X−p で割った余り
t ・・・ 上記の商を X−p で割った余り
s ・・・ 上記の計算で、 X−p で割った商
例 3次方程式 X3−6X2+11X−6=0 の解から、2 を減じた解をもつ 3次方程式を作れ。
3次方程式を解けば、X=1、2、3 なので、それらから 2 を減じると、−1、0、1
となる。
よって、求める方程式は、X(X−1)(X+1)=X3−X より、X3−X=0 となる。
3つの解がわかれば、上記のように簡単に解かれる。しかし、3つの解が具体的にわから
ない場合、上記のような計算は無力となる。そこで、先の定理が日の目をみることになる。
上記の例の問題は、一般的に次のように解かれる。
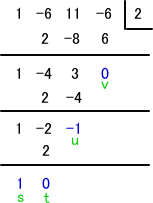 |
左図の組立除法の計算から、求める方程式は、
X3−X=0
となる。
この解法の優れている点は、計算が解に依存していない所で
ある。したがって、解が具体的にわからなくても、所要の方程式
を確実に求めることができる。 |
上記定理の応用として、次の事実はよく知られている。
3次方程式 aX3+bX2+cX+d=0 は、必ず、aX3+pX+q=0 の形に変換できる。
(証) もとの方程式の解に、b/3a を加えた解をもつ方程式を作ればよい。
 |
左図の組立除法の計算から、求める方程式は、
aX3+pX+q=0
となる。
(→ 参考:「チルンハウス変換」)
|
例 3次方程式 X3+9X2+33X+52=0 を解け。
もとの方程式の解に、b/3a=3 を加えた解をもつ方程式は、X3+6X+7=0
この式は、(X+1)(X2−X+7)=0 と因数分解されるから、直ちに解は求められる。
(参考:Cardano の解法
3次方程式 X3+3pX+q=0 において、ab=−p、a3+b3=−q を満たす a、b は、
2次方程式 X2+qX−p3=0 の解の3乗根である。
この a、b を用いて、3次方程式の解の一つ a+b が求められる。→「方程式論」を参照)
上の定理と同様にして、以下の定理が成り立つ。
定理(解に一定数を乗ずる)
F(X)=0 の解を、α、β、γ とする。このとき、
kα、kβ、kγ を解とする方程式は、F(X/k)=0
例 3次方程式 X3−6X2+11X−6=0 の解を 2倍した解をもつ方程式を作れ。
(X/2)3−6(X/2)2+11(X/2)−6=0 より、X3−12X2+44X−48=0
定理(解の逆数をとる)
F(X)=0 の解を、α、β、γ とする。このとき、
1/α、1/β、1/γ を解とする方程式は、F(1/X)=0
例 3次方程式 X3−6X2+11X−6=0 の解の逆数を解にもつ方程式を作れ。
(1/X)3−6(1/X)2+11(1/X)−6=0 より、6X3−11X2+6X−1=0
定理 実数係数の方程式において、虚数 α+βi (β≠0)が解ならば、
その共役 α−βi も解
この定理により、虚数解は必ず偶数個あり、したがって、奇数次の方程式は必ず実数解
をもつことが分かる。
定理 方程式 F(X)=0 において、
F(a)・F(b)>0 ならば、a<X<b の範囲に、偶数個(0も含む)の実数解をもつ
F(a)・F(b)<0 ならば、a<X<b の範囲に、奇数個の実数解をもつ
定理 十分大きい|X|に対して、aX3+bX2+cX+d と aX3 は同符号である。
実数解が存在する区間を定めることを、実数解を分離するという。(→参考:「解の分離」)
例 3次方程式 3X3−6X−1=0 の実数解を分離せよ。
F(X)=3X3−6X−1とおくと、F(−∞)<0、F(0)<0、F(∞)>0 だから、上記定理により、
負の解は、0 または 2個、正の解は、1 または 3個もつことが直ぐ分かる。
さらに、F(X)=3X(X2−2)−1 より、
X≦−2 のとき、F(X)<0 、 X≧2 のとき、F(X)>0
なので、−2 より小、2より大の実数解は存在しない。
また、 F(−2)<0、F(−1)>0、F(0)<0、F(1)<0、F(2)>0 なので、
したがって、3次方程式は、−2と−1の間、−1と 0 の間、1 と 2 の間に実数解をもつ。
上記例からも分かるように、解の前後で必ず符号が変化する。これについて、次に述べる
Descartes の符号法則が有名である。
例えば、5次式 X5+3X4−2X3+4X2+2X−3 の係数に着目して、
| 1 |
3 |
−2 |
4 |
2 |
−3 |
| + |
+ |
− |
+ |
+ |
− |
左の表で、符号の変化は、3箇所ある。このとき、
符号変化数は3である、という。
明らかに、係数の最初と最後の符号が
同じ場合、符号変化数は偶数 、 異符号の場合、符号変化数は奇数
である。
以下において、F(X) は、実数係数の整式とする。このとき、次の法則が成り立つ。
デカルト(Descartes)の符号法則
方程式 F(X)=0 の正の解の個数は、符号変化数より、偶数個(0も含む)少ない
(ただし、解の重複がある場合は、重複する回数で数えるものとする)
例 X3+2X+3=0 の符号変化数は、0。よって、正の解はない。
X4−3X+2=0 の符号変化数は、2。よって、正の解は2個または0個。
デカルトの符号法則を証明するために、まず次の補題を示そう。
補 題 α>0 とする。このとき、
(X−α)F(X)の符号変化数は、F(X)の符号変化数より奇数個多い
例 2次式 X2+2X−3 の符号変化数は、1 である。このとき、
(X−1)(X2+2X−3)=X3+X2−5X+3=0 の符号変化数は、2。
よって、符号変化数が、1個(奇数個)だけ多い。
(X−α)F(X)の展開式の係数の最初と最後の符号が、α>0 という条件のもとで
F(X)の展開式の係数の最初と最後の符号が同符号ならば、異符号に
F(X)の展開式の係数の最初と最後の符号が異符号ならば、同符号に
なるので、符号変化数が奇数個増えることは、ほとんど明らかだろう。
F(X)が3次式の場合について、上記補題が成り立つことを見ておこう。
(略証) F(X)=aX3+bX2+cX+d に対して、G(X)=(X−α)F(X) (α>0)を考える。
すなわち、
G(X)=(X−α)(aX3+bX2+cX+d)
=aX4+(b−aα)X3+(c−bα)X2+(d−cα)X−dα=AX4+BX3+CX2+DX+E
ここで、 A=a 、B=b−aα 、C=c−bα 、D=d−cα 、E=−dα である。
a > 0 として、 b 、 c 、 d の符号のすべての場合について調べて下表を得る。
| |
a |
b |
c |
d |
符号変化数 |
A |
B |
C |
D |
E |
符号変化数 |
| 1 |
+ |
+ |
+ |
+ |
0 |
+ |
? |
? |
? |
− |
1 または 3 |
| 2 |
+ |
+ |
+ |
− |
1 |
+ |
? |
? |
− |
+ |
2 または 4 |
| 3 |
+ |
+ |
− |
+ |
2 |
+ |
? |
− |
+ |
− |
3 |
| 4 |
+ |
+ |
− |
− |
1 |
+ |
? |
− |
? |
+ |
2 |
| 5 |
+ |
− |
+ |
+ |
2 |
+ |
− |
+ |
? |
− |
3 |
| 6 |
+ |
− |
+ |
− |
3 |
+ |
− |
+ |
− |
+ |
4 |
| 7 |
+ |
− |
− |
+ |
2 |
+ |
− |
? |
+ |
− |
3 |
| 8 |
+ |
− |
− |
− |
1 |
+ |
− |
? |
? |
+ |
2 または
4 |
上記の表の「?」部分にどんな符号が入ろうとも符号変化数は上表の通りで、何れの場
合も奇数個増えていることが分かる。 a <0 の場合も同様である。 (証終)
(デカルトの符号法則の証明)
実数係数の n 次の整式 F(X)=aXn+bXn−1+・・・+cX+d において、a>0 とし
ても一般性を失わない。
また、解 0 は符号変化数に影響を与えないので、 d≠0 としても一般性を失わない。
(イ) 方程式 F(X)=0 に正の解がない場合
d>0 なので、係数の最初と最後の符号が同符号となり、符号変化数は偶数
よって、命題は成り立つ。
(ロ) 方程式 F(X)=0 が正の解 α、β、・・・、γ を持つ場合
F(X)=(X−α)(X−β)・・・(X−γ)G(X) と因数分解できる。
このとき、方程式 G(X)=0 は正の解を持たない。
解と係数の関係から、正の解を持たない場合、符号変化数は、0
補題により、 正の解 α に対して、(X−α)G(X)の符号変化数は、G(X)より奇数個多い。
換言すれば、方程式 (X−α)G(X)=0 の正の解の個数(1個!)は、(X−α)G(X)の符
号変化数より、偶数個少ない。
同様にして、方程式 (X−α)(X−β)G(X)=0 の正の解の個数(2個!)は、
(X−α)(X−β)G(X)の符号変化数より、偶数個少ない。
・・・・・・・・・・・・・・・・・・・・・・・
よって、方程式 (X−α)(X−β)・・・(X−γ)G(X)=0 の正の解の個数は、
(X−α)(X−β)・・・(X−γ)G(X)の符号変化数より、偶数個少ない。
以上から、命題は成り立つ。 (証終)
先の例(3次方程式 3X3−6X−1=0)において、符号変化数は、1 である。
したがって、正の解をただ一つもつことが、係数だけの洞察により判断することができる。
さらに、Xに−Xを代入して、3X3−6X+1=0 この方程式の符号変化数は、2 なので、
もとの方程式の負の解は、2個または0個であることが分かる。
さて、いよいよ Horner の方法(1819年)を説明する準備ができたようだ。
例 3次方程式 X3+2X−5=0 の実数解の近似値を求めよ。
F(X)=X3+2X−5 とおく。符号変化数は 1 なので、方程式 F(X)=0 は正の解を
1個もつ。
また、F(−X)=−X3−2X−5 の符号変化数は 0 なので、もとの方程式は負の解をもたない。
(ここら辺の議論は、このページの冒頭にあるように、グラフを活用したほうが視覚的に分かるのだが、係数だけの
洞察から、これだけのことが言えることに感動を覚える。符号法則の偉大さがひしひしと伝わってくる!)
F(1)=−2<0、F(2)=7>0 なので、方程式は、1 と 2 の間にただ一つの実数解をもつ。
したがって、求める実数解は、1+α(0<α<1)の形の小数である。
方程式の解から 1 減じた解をもつ方程式は、先の定理により、
X3+3X2+5X−2=0 ・・・(*)
この方程式の解の一つが、αである。
次に、αの小数第1位を求めるために、方程式(*) の解を10倍した解をもつ方程式を作
れば、先の定理により、
X3+30X2+500X−2000=0 ・・・(**)
となる。
いま、G(X)=X3+30X2+500X−2000≒500X−2000≒0 と考えて、X≒4
そこで、G(3)=−203<0、G(4)=544>0 であることを確認して、方程式(**)
の解は、
3 と4 の間にあることが分かる。
よって、αの小数第1位は、3 であることが示された。
方程式(**) の解から 3 減じた解をもつ方程式は、先の定理により、
X3+39X2+707X−203=0 ・・・(***)
方程式(***) の解を10倍した解をもつ方程式は、
X3+390X2+70700X−203000=0 ・・・(****)
70700X−203000≒0 より、X≒3 なので、
H(X)=X3+390X2+70700X−203000
とおいて、H(2)=−60032<0、H(3)=12637>0 がすぐ分かる。
よって、方程式(****)の解は、2 と 3 の間にあることが分かる。
ゆえに、αの小数第2位は、2 であることが示された。
このような計算を続けていけば、順次小数第3位以下も求めることができる。
以上から、3次方程式 X3+2X−5=0 の実数解の近似値は、1.32・・・ である。
(注意) 上記のような計算方法が Horner の方法 といわれるものであるが、別な書籍に
よると、多項式の値の計算で、掛け算の回数を減らすような求め方(先の定理の s、t、u、
v を用いた式変形)のことも、Horner の方法 というらしい。
上記推論は、組立除法と同様に図式化される。次の練習問題を通して、その美しさを是
非、堪能して欲しいと思う。
練習問題 3次方程式 X3+2X−18=0 の実数解の近似値を小数第2位まで正しく求
めよ。
(解) H(X)=X3+2X−18 とおく。導関数 H’(X)=3X2+2>0 なので、グラフは単調
に増加する。よって、実数解はただ一つある。
さらに、H(2)=−6<0、H(3)=15>0 なので、方程式は、2 と 3
の間に解をもつ。
よって、Horner の方法により、

したがって、3次方程式 X3+2X−18=0 の実数解の近似値は、2.36・・・ (終)
読者のために、練習問題を一つ提示して、長かったこのページの筆をおくことにしよう。
(正直に告白すると、このページのアップロードまで、2週間を要した!)
練習 4の3乗根の値を、手計算で小数第2位まで正しく求めよ。
(Hint: 4の3乗根は、3次方程式 X3−4=0 の解である。) (答)1.58・・・
当HPがいつもお世話になっているHN「攻略法」さんが、上記の問題を解かれた。
(平成22年10月14日付け)
(解) H(X)=X3−4 とおく。導関数 H’(X)=3X2≧0 なので、グラフは単調に増加する。
よって、実数解はただ一つある。
さらに、H(1)=−3<0、H(2)=4>0 なので、方程式は、1 と 2
の間に解をもつ。
よって、Horner の方法により、
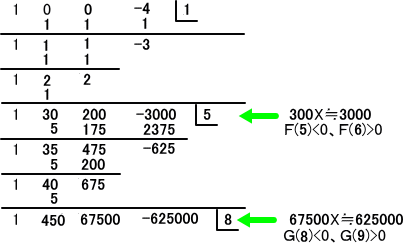
(徐々に桁数も増加して計算が難しくなっていく...(T_T)。)
したがって、4の3乗根の値を、小数第2位まで正しく求めると、1.58 である。 (終)
(コメント) 攻略法さんに感謝します。
(参考文献:福井常孝 他著 線形代数学入門(内田老鶴圃新社))







