組立除法の意外な使い道 
n 次の整式を 1次式で割り、その商と余りを求める場合、通常「組立除法」が用いられる。
例1. (X3+2X−5)÷(X−1) の商と余りを求めよ。
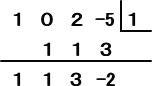 左の計算により、
左の計算により、
商は、X2+X+3、余りは、−2
例2. (2X3+3X2+4)÷(2X−1) の商と余りを求めよ。
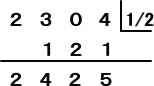
左の計算により、
商は、X2+2X+1、余りは、5
上記のような略記法で計算する場合、例1.と例2.の違いに注意を要する。
その違いは、次の等式により了解される。
例1.の場合は、 X3+2X−5 = (X−1)(X2+X+3)−2
例2.の場合は、
2X3+3X2+4 = (X−1/2)(2X2+4X+2)+5= (2X−1)(X2+2X+1)+5
基本的に、組立除法は X− α による割り算なので、aX+b による割り算に用いる場合は、
商は、a で割るという操作が一回入る。
このようなことは、F(X)÷G(X) の計算で、商を Q(X)、余りを R(X) としたとき、
F(X)=G(X)Q(X)+R(X) (R(X)=0 または degR(X)<degG(X) )
と書いて初めて理解されることである。
組立除法をこのような見方で見直すと、組立除法の意外な使い道が見えてくる。
平均変化率の計算
整式 F(X) を 1次式 X−a で割った商を S(X)、余りを T とし、商
S(X) を 1次式 X−b で
割った商を Q(X)、余りを R とする。このとき、
F(X)=(X−a)S(X)+T=(X−a)((X−b)Q(X)+R)+T
なので、F(a)=T、F(b)=(b−a)R+T が成り立つ。よって、F(b)−F(a)=(b−a)R となる。
したがって、次の公式を得る。
公式 整式 F(X) において、X の値が a から b まで変化するときの平均変化率は、
F(X) を X−a で割った商を、X−b で割った余りに等しい。
例 F(X)=2X3−3X2+X−4 において、X の値が −1 から 2 まで変化するときの平均
変化率を求めてみよう。
通常は、次のように計算される。
F(−1)=2(−1)3−3(−1)2+(−1)−4=−10、F(2)=2・23−3・22+2−4=2
よって、平均変化率は、(F(2)−F(−1))/(2−(−1))=12/3=4
上記の計算は、今の高校生にとって、とても苦手なようで、100%全員が正解になること
はない。
組立除法を用いた場合は、次のように計算される。
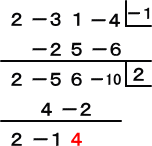
以上から、求める平均変化率は、4 である。
記数法の計算
二進法で、110101 という数は、十進法では、どのような数であろうか?
通常、このような計算は次のようになされる。
1×25+1×24+0×23+1×22+0×2+1=53
組立除法を用いた場合は、次のように計算される。
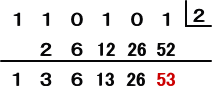
なぜ、このような計算で求められるのだろうか?
その原理は、いたって単純である。
二進法で表される数が、110101 とする。
整式 F(X)=1・X5+1・X4+0・X3+1・X2+0・X+1 に対して、
十進法で表される数は、1×25+1×24+0×23+1×22+0×2+1 すなわち F(2)
に等しい。したがって、求める数は、割り算 F(X) ÷ (X−2) の余りである。
整式の割り算
組立除法というと、整式の X− a による割り算を思い浮かべるが、実は、(X−
a)(X−b)
の割り算にも有効である。
例 (X3+2X2−3X−4)÷(X−1)(X−2) の商と余りを求めよ。
通常は、次のように計算される。(実際に、割り算を実行してもよい。)
整式 F(X) = X3+2X2−3X−4 = X(X−1)(X−2)+5X2−5X−4
= X(X−1)(X−2)+5(X−1)(X−2)+10X−14=(X−1)(X−2)(X+5)+10X−14
したがって、商は、X+5 、余りは、10X−14
組立除法を用いて計算する場合、どのような手順でやるのだろうか?
整式 F(X) を 1次式 X−a で割った商を S(X)、余りを T とし、商
S(X) を 1次式 X−b
で割った商を Q(X)、余りを R とする。このとき、
F(X)=(X−a)S(X)+T=(X−a)((X−b)Q(X)+R)+T
すなわち、F(X)=(X−a)(X−b)Q(X)+R(X−a)+T
ここで、T=F(a) 、(b−a)R=F(b)−F(a) である。
したがって、次の公式を得る。
公式 整式 F(X) を 1次式 X−a で割った商を S(X)、余りを T とし、商 S(X) を
1次式 X−b で割った商を Q(X)、余りを R とする。
今、整式 F(X) を (X−a)(X−b) で割るとき、
商は Q(X) 、余りは、 R(X−a)+F(a) で与えられる。
それでは、実際に、組立除法を適用してみよう。
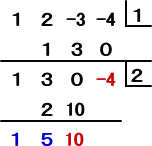 |
左の計算により、
商は、1・X+5=X+5
余りは、10(X−1)+(−4)=10X−14
となる。(これは、上の計算結果と一致する。) |
定積分の計算
定積分の計算も差の形なので、平均変化率の計算と同様にして求められる。
| 例 |
定積分 |
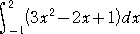 |
を求めよ。 |
通常は、
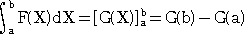
という公式から、G(X)=X3−X2+X なので、求める値は、
G(2)−G(−1)=(8−4+2)−(−1−1−1)=9
ところで、G(b)−G(a)=m(b−a) (m:平均変化率)なので、組立除法を用いた場合は、
次のように計算される。
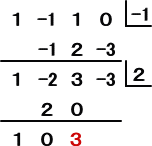 |
左の計算により、
求める値は、 3(2−(−1))=9 となる。
(これは、上の計算結果と一致する。) |
上記の計算だと組立除法を用いる有効性が視認されないが、G(X) や a、b の値に分数
が入ってくる場合は多分(?)有効だろうと思う。
その他、数列の和 Sn から一般項 an を求める公式
a1=S1 、 n≧2 のとき、 an=Sn−Sn-1
についても組立除法は使えるが、その応用は読者の練習に残しておこう。
(参考文献:熊野充博 著 組立除法の応用例 (数研通信 No.20))
(追記) 平成22年10月14日付け
当HPがいつもお世話になっているHN「攻略法」さんが、
数列の和 Sn から一般項 an を求める公式
a1=S1 、 n≧2 のとき、 an=Sn−Sn-1
について考察された。
問 題 初項から第 n 項までの和 Sn が、 Sn=n2+2n で与えられる数列の一般項
an を求めよ。
通常は、次のように解かれる。
n=1 のとき、a1=S1=3
n≧2 のとき、 an =Sn −Sn-1=(n2+2n)−{(n−1)2+2(n−1)}=2n+1
この式は、n=1 のときも成り立つ。
ゆえに、n≧1 のとき、 an =2n+1
これに対して、組立除法を用いた場合は、次のように計算される。
(解) 組立除法を使って、n2+2n を n−1 で展開する。(→ 参考:「整式の割り算」)
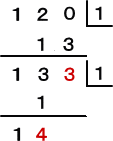 |
よって、左の計算により、
S1=3 (← n2+2n を n−1 で割った余り)
Sn=1・(n−1)2+4・(n−1)+3
また、 Sn-1=(n−1)2+2(n−1)
|
したがって、Sn−Sn-1 は、n−1 を変数とする多項式の減算だから、an= 2(n−1)+3
(普通に計算すれば、an =2n+1 であるが、一般化を意識して...)
n−1=x とおくと、n=x+1 なので、方程式 2x+3=0 の解に
1 を加えればよい。
(→ 参考:「方程式の変換」)
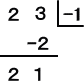 |
よって、左の計算により、求める方程式は、 2n+1=0 となり、
an=2n+1
|
(コメント) 攻略法さんに感謝します。
さらに、攻略法さんに組立除法の使用場面をまとめて頂いた。(平成22年10月16日付け)
ケース1
★整式 F(x) を x−a で割ったときの商: Q(x) 、余り: R
★整式 F(a) の値(x=a を代入する)
★記数法の計算
※ F(x)=Q(x)(x−a)+F(a) と表される。
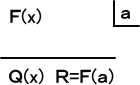
★整式 F(x) を(x−a)(x−b)で割ったときの商: Q(x) 、余り: R(X−a)+F(a)
ただし、R={F(b)−F(a)}/(b−a)
★整式 F(x) において、x の値が a から b まで変化するときの平均変化率: R
★定積分:
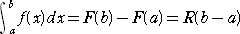
★整式 F(x) 上の2点( a ,F(a) )、( b ,F(b) ) を通る直線の方程式: y=R(x−a)+F(a)
※ F(x)=Q(x)(x−a)(x−b)+R(x−a)+F(a) と表される。
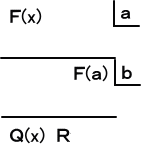 ← R:(x−a)の係数、傾き、平均変化率
← R:(x−a)の係数、傾き、平均変化率
ケース2
★整式 F(x) を x=a でテイラー展開する
★整式 F(x) を (x−a)2 で割ったの商: Q(x) 、余り: F’(a)(x−a)+F(a)
★整式 F(x) 上の点( a ,F(a) )における接線の方程式: y=F’(a)(x−a)+F(a)
★代数方程式の根をニュートン法で求める(関数値、微分係数)
※ F(x)=F(a)+F’(a)(x−a)+{F”(a)/2!}(x−a)2+・・・ と表される。
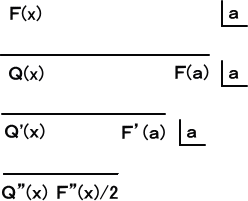
この応用として
★数列の和 Sn から一般項 an を求める公式:
a1=S1 、n≧2 のとき、 an=Sn−Sn-1
Sn を n−1 で展開すると、
S1 および Sn=C0+C1(n−1)+C2(n−1)2+C3(n−1)3+・・・
を得る。また、与式の n に n−1 を代入して、Sn-1 を得る。
よって、 an =Sn −Sn-1 は、n−1 を変数とする整式に展開される。
n−1=x とおくと、n=x+1 なので、方程式の解に 1 を加えた方程式を求めることに
より、一般項 an を得る。
★y=F(x) のグラフを、x 軸方向に a、y 軸方向に b だけ平行移動したグラフを表す式:
y=F(x−a)+b
F(x)を x+a で展開し、 y=F(x) =A+B(x+a)+C(x+a)2+D(x+a)3+・・・ を得る。
この式に、x=X−a、y=Y−b(平行移動量)を代入すると、
Y=A+b+Bx+Cx2+Dx3+・・・ を得る。
例 y=x3+2x2−3 のグラフを、x 軸方向に 2、y 軸方向に −3 だけ平行移動する場合
(解) y+3=(x−2)3+2(x−2)2−3 より、展開して整理すると、
y=x3−4x2+4x−6 (終)
この計算は、組立除法を用いると次のように計算される。
 |
左の計算により、
Y+3=X3−4X2+4X−3
なので、求める関数は、
y=x3−4x2+4x−6 |
●n次式へ拡張した組立除法は、特に、「スーパー組立除法」と言われることを、最近参加し
た数学研究会で新潟高校の先生より教わった。
整式 ax3+bx2+cx+d を x2−px−q で割った商 ax+r と余り mx+n は次のよう
にして求められる。(1次式の場合の「X−α」を意識して、2次式も「x2−px−q」の形に置く
のが自然なのだろう。)
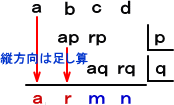
実際に、 ax3+bx2+cx+d=(x2−px−q)(ax+r)+mx+n から係数比較して、
b=−ap+r 、c=−aq−rp+m 、 d=−rq+n
より、 r=b+ap 、 m=c+rp+aq 、 n=d+rq である。
また、整式 ax4+bx3+cx2+dx+e を x2−px−q で割った商 ax2+rx+s と余り
mx+n も、
b=−ap+r 、c=−aq−rp+s 、 d=−rq−sp+m 、e=−sq+n
より、 r=b+ap 、 s=c+rp+aq 、 m=d+sp+rq 、 n=e+sq であるので、
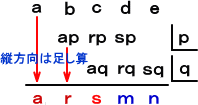
より、簡便に求められる。
除数が因数分解された場合は、ケース1に相当するが、一般の整式で与えられる場合は、
拡張された組立除法を用いて解決される。
問 題 F(x)=x3−3x2+5x−6 において、F(1+ )の値を求めよ。
)の値を求めよ。
(解) x=1+ が満たす2次方程式は、 x2−2x−2=0
が満たす2次方程式は、 x2−2x−2=0
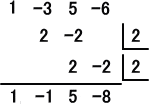 |
よって、左の計算により、
F(x)=(x2−2x−2)(x−1)+5x−8
したがって、 F(1+ )=−3+5 )=−3+5 (終) (終)
|
(コメント) 攻略法さん、分かり易く整理していただいて感謝します。
読者のために、いくつか練習問題を置いておこう。
練習問題 次の割り算の商と余りを求めよ。
(1) (2x3+4x2−3x+1)÷(x2−x−2)
(2) (3x3−5x2+2x−3)÷(x2−x−2)
(3) (2x4−3x3+x2−3x+2)÷(x2−x−2)
(4) (3x5+2x3+3x2+x+4)÷(x3−x−2)
(解)(1) 2x3+4x2−3x+1、x2−x−2 の係数を書き出す。
青丸数字は、筆算の順番を表す。
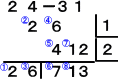
よって、(2x3+4x2−3x+1)÷(x2−x−2)の商は、2x+6 、余りは、7x+13
(2) 3x3−5x2+2x−3、x2−x−2 の係数を書き出す。

よって、(3x3−5x2+2x−3)÷(x2−x−2)の商は、3x−2 、余りは、6x−7
(3) 2x4−3x3+x2−3x+2、x2−x−2 の係数を書き出す。

よって、(2x4−3x3+x2−3x+2)÷(x2−x−2)の商は、2x2−x+4 、余りは、−x+10
(4) 3x5+2x3+3x2+x+4、x3−x−2 の係数を書き出す。

よって、(3x5+2x3+3x2+x+4)÷(x3−x−2)の商は、3x2+5 、余りは、9x2+6x+14
例 (X3+2X2−3X−4)÷(X−1)(X−2) の商と余りをスーパー組立除法により求めてみよう。
(X−1)(X−2)=X2−3X+2 なので、

したがって、商は、X+5 、余りは、10X−14
スーパー組立除法の応用例を考えてみよう。
問題 x4+ax3+bx2−x+3 を x2−x−2 で割ったときの余りが 2x+1 になるという。
このとき、定数 a、b の値を求めよ。
(解) 自明な部分は補って、スーパー組立除法により、

よって、−1−1+(ア)=2 から、 (ア)=4 よって、(イ)=2 で、(ウ)=2
a+1=2 より、 a=1 、b+2+2=−1 より、 b=−5 (終)
(コメント) x2−x−2=(x−2)(x+1) なので、剰余の定理を使った方が速いかな?
以下、工事中

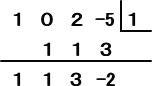 左の計算により、
左の計算により、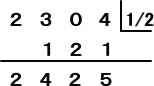
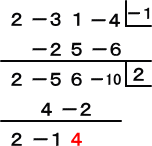


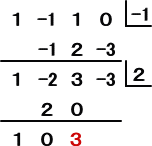

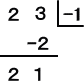
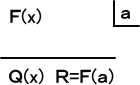
 ← R:(x−a)の係数、傾き、平均変化率
← R:(x−a)の係数、傾き、平均変化率









