解の分離 
「解の分離」と聞いて、「あ〜、あれか!」と思われた方は、相当年配の方だろう。最近の
用語では、「解の配置」とか「解の符号」などと言われている。
(因みに、私は、「2根の配置」で学んだ世代です!)
2次方程式の解は、解の公式を用いれば完璧に求められる。次の話題は、その解が数
直線上でどのような位置にあるかを問うものだろう。これが、「解の配置」と言われる所以
だ。
例えば、「正の解と負の解を持つ」と言えば、「解の符号」問題だが、2つの解の間に「0」
が分け入って、2つの解を分離していると考えれば、「解の分離」問題になる。
次の問題は、「解の分離」という言葉を理解するには打って付けだろう。
定数 a>0 とする。2次方程式 x2+ax−1=0 の2つの実数解のうち、ちょうど
1つの解だけが、2次方程式 x2−x−a=0 の2つの実数解の間にあることを示せ。
(→証明はこちら)
このページでは、「解の分離」について世に知られている所を、まとめてみようと思う。
代表的例題
2次方程式 x2−2mx+m+2=0 が次のような解を持つように定数 m の値の範
囲を求めよ。
(1) 2つの解がともに正
(2) 異符号の解を持つ
解法は、いくつか考えられるが、代表的なものをあげておこう。
(解と係数の関係を利用する解)
(1) 題意を満たすためには判別式を D とすると、 D≧0 で、かつ、2つの解 α 、 β に
ついて、 α+β>0 、 αβ>0 であることが必要十分である。
よって、 D/4=m2−m−2=(m−2)(m+1)≧0 より、 m≦−1 、m≧2
解と係数の関係より、 α+β=2m>0 より、 m>0
αβ=m+2>0 より、 m>−2
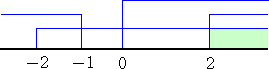
よって、求めるmの値の範囲は、 m≧2
(2) 題意を満たすためには、 αβ<0 であることが必要十分である。
よって、 m+2<0 より、 m<−2 (終)
(コメント) 私が解の分離問題を初めて学んだのは、高校1年の時。なかなか使いこなせ
なかった思い出がある。しかし、受験勉強で鍛えられたせいか、今は苦にならな
い。むしろ「解の分離」という言葉の響きを楽しめる境地になった。
解の分離問題は、関数のグラフを用いる解法が最も考えやすく分かり易いだろう。
(関数のグラフを利用する解)
(1) 2次関数 F(x)=x2−2mx+m+2=(x−m)2−m2+m+2 のグラフの軸の式は、
x=m である。題意を満たすためには、
軸 x=m>0 (あるいは、頂点の x 座標 m>0 )
頂点の y 座標 −m2+m+2≦0 (あるいは、判別式 D≧0 )
境界点での符号 F(0)=m+2>0
であることが必要十分である。
よって、 m>0
−m2+m+2≦0 より (m−2)(m+1)≧0 から、 m≦−1 、m≧2
m+2>0 より、 m>−2

よって、求めるmの値の範囲は、 m>2
(2) F(0)=m+2<0 であることが必要十分である。
よって、 m<−2 (終)
上記の代表的例題の解法を公式化すれば、下記のようになるだろう。
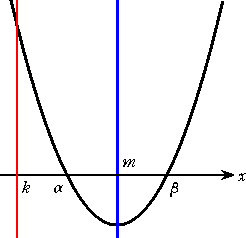
2次方程式
x2+ax+b=0 の2つの解がともに k より大きくなるための必要十分
条件は、
判別式 D≧0 、 (α−k)+(β−k)>0 、 (α−k)(β−k)>0
2次関数
F(x)=x2+ax+b のグラフを活用すれば、
軸の式 x=m>k 、 頂点の y 座標≦0 、 F(k)>0
である。
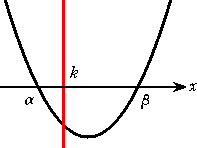
2次方程式 x2+ax+b=0
の2つの解の間に k があるための必要十分条件は、
(α−k)(β−k)<0
2次関数
F(x)=x2+ax+b のグラフを活用すれば、
F(k)<0
である。
このような考え方を会得すれば、様々な問題に対処できるようになる。
解の分離問題は受験数学のいろいろなところで登場するが、次の問題がその代表だろう。
問 題 m>0 のとき、直線 y=2mx+m2 が通過する範囲を求めよ。
直線の方程式 y=2mx+m2 を、m に関する2次方程式 m2+2mx−y=0 と考え
るところがポイントである。そして、
定数 m0>0 が定まる
↓
等式 m02+2m0x−y=0 を満たす点( x , y )が存在する
↓
実数 x 、 y に対して、2次方程式 m2+2mx−y=0 は、正の解 m0 を持つ
と考えられることから、下記のような解答を得ることが出来る。
(解) m に関する2次方程式 m2+2mx−y=0 が少なくとも一つ正の解を持つ条件を
求めればよい。
(イ) 2つとも正の解のとき、
F(m)=m2+2mx−y=(m+x)2−x2−y とおくと、求める条件は、
−x2−y≦0 、 −x>0 、 −y>0
すなわち、 y≧−x2 、 x<0 、 y<0
(ロ) 1つが正で、他の解が0のとき、
F(m)=m2+2mx−y において、 F(0)=0 より、 y=0
このとき、 m2+2mx=m(m+2x)=0 より、 m=−2x>0
よって、求める条件は、 x<0 、 y=0
(ハ) 異符号の解を持つとき、
F(m)=m2+2mx−y において、 F(0)<0 より、 −y<0
よって、求める条件は、 y>0
以上から、求める直線の通過範囲は、
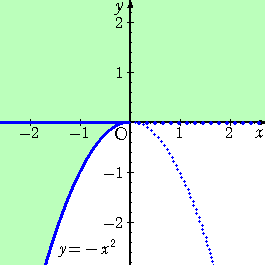
となる。ただし、境界線のうち放物線 y=−x2 (x<0)は含み、直線y=0 (x≧0)は含
まない。 (終)
上記では解の符号に注意して場合分けをしたが煩雑になるという弱点がある。軸の位置
によって場合分けする方が実戦的かもしれない。
実数 x 、 y に対して、2次方程式 m2+2mx−y=0 が正の解 m0 を持つため
の条件を求め、この条件を満たす点 ( x 、 y ) の存在範囲を図示せよ。
(別解) F(m)= m2+2mx−y = (m+x)2−x2−y とおくと、軸の式は、 m=−x
(1) −x >0 すなわち、 x <0 のとき、題意を満たすためには、判別式を D として、
D/4=x2+y≧0 すなわち、 y≧−x2 であればよい。
(2) −x≦0 すなわち、 x ≧0 のとき、題意を満たすためには、 F(0)=−y<0
すなわち、 y>0 であればよい。
以上から、求める領域は、

となる。ただし、境界線のうち放物線 y=−x2 (x<0)は含み、直線y=0 (x≧0)は含
まない。 (終)
(コメント) 解法が随分スッキリしましたね!予備校などでは、この別解の方で教えられてい
るようである。このタイプの例題はこちらを参照(→大学入試問題探訪 「013」)
冒頭で保留していた問題を証明しておこう。
問 題 定数 a>0 とする。2次方程式 x2+ax−1=0 の2つの実数解のうち、
ちょうど1つの解だけが、2次方程式 x2−x−a=0 の2つの実数解の間
にあることを示せ。
(証明) F(x)=x2−x−a とおく。x2+ax−1=0 の2つの実数解を α、β(α<β)とし、
2次方程式 x2−x−a=0 の2つの実数解を γ、δ(γ<δ)とする。
このとき、題意を満たすためには、 F(α)F(β)<0 であることを示せばよい。
F(α)F(β)
=(α2−α−a)(β2−β−a)
=(αβ)2−αβ(α+β)+αβ+a(α+β)−a(α+β)2+2aαβ+a2
=(−1)2−(−1)(−a)+(−1)+a(−a)−a(−a)2+2a(−1)+a2
=1−a−1−a2−a3−2a+a2
=−3a−a3<0 (証終)
正の解を何個持つかはいろいろな場面で問われる基本問題である。方程式の係数から、
その傾向を伺う方法として、デカルト(Descartes)の符号法則が有名である。
(→ 参考:「高次方程式の解の近似計算」)
例えば、2次方程式 X2+2X−3=0 の左辺の係数だけを左から順に書き並べると、
下表のようになる。
|
|
左の表で、符号の変化は、( + → − )の1箇所ある。
このとき、符号変化数は1である、という。 |
係数の符号の変化数に着目して、次の公式が知られている。
デカルト(Descartes)の符号法則
方程式 F(X)=0 の正の解の個数は、符号変化数より、偶数個(0も含む)少ない
上の例であげた2次方程式 X2+2X−3=0 の符号変化数は、1 なので、デカルトの
符号法則によれば、正の解を必ず1個持つことが分かる。当然残りの解は負の解である。
このデカルトの符号法則は、2次方程式に適用するには大袈裟すぎるが、3次以上の方
程式に対しては、簡便に正の解の個数を判断する方法として有効だろう。
例 3次方程式 X3+2X−3=0 の符号変化数は、1。 よって、正の解は1個。
実際に、 X3+2X−3=(X−1)(X2+X+3) から明らかだろう。
(注意) この例からも分かるように、係数が 0 の項(つまり、その項がない!)は、それを
飛ばして符号の変化数を数える。
解の分離問題をひねったものとして、次の例題も重要だろう。
例 題 実数係数の2次方程式 F(x)=x2+ax+b=0 が 0<x<1 を満たす
解を少なくとも1つもつための条件を求め、この条件を満たす点(
a , b )の
存在範囲を図示せよ。
(解) 2次方程式の2つの解を α 、 β (ただし、 0<α<1)とおく。
また、 F(x)=x2+ax+b=(x+a/2)2+b−a2/4 より、軸の式は、x=−a/2
(1) β<0 のとき、題意を満たすためには、 F(0)<0 、F(1)>0
すなわち、 b<0 、 1+a+b>0
(2) β=0 のとき、 b=0 で、このとき、 α=−a
題意を満たすためには、 0<−a<1 すなわち、 −1<a<0
(3) 0<β<1 のとき、2つの解がともに 0 と 1 の間なので、
頂点の y 座標=b−a2/4≦0 、 軸 0<−a/2<1 、
F(0)>0 、 F(1)>0
すなわち、 b≦a2/4 、−2<a<0 、 b>0 、 1+a+b>0
(4) β=1 のとき、 1+a+b=0 で、このとき、α=−a−1
題意を満たすためには、 0<−a−1<1 すなわち、 −2<a<−1
(5) β>1 のとき、題意を満たすためには、 F(0)>0 、F(1)<0
すなわち、 b>0 、 1+a+b<0
以上から、求める領域は、
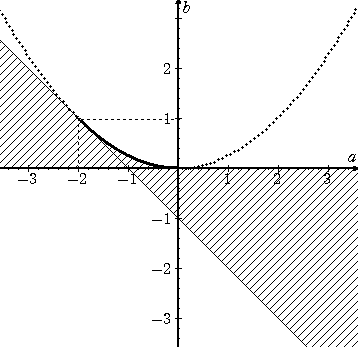
境界線は、放物線 b=a2/4 (−2<a<0)の部分のみ含み、他は含まない。 (終)
この例題の応用として、次の問題があげられる。
問 題 直線 y=x と y=−x の上にそれぞれ点A( a , a )、B( b ,
−b )を、
OA+0B= であるようにとる。この条件を満たしながら、2点 A、B がそ
であるようにとる。この条件を満たしながら、2点 A、B がそ
れぞれの直線上を動くとき、線分ABが通過する領域を図示せよ。
この問題のいやらしいところは、直線 AB ではなくて、線分 AB であるという点である。
(何となく、面倒っち〜ような...予感)
(解) 条件から、  |a|+
|a|+ |b|=
|b|= より、 |a|+|b|=1 である。
より、 |a|+|b|=1 である。
この図形はひし形で上下左右対称なので、一般性を失うことなく、 a≧0 、 b≦0 の
場合を調べれば十分である。
このとき、 a−b=1 より、 b=a−1≦0 で、 0 ≦ a ≦ 1 である。
線分 AB の方程式は、(a+b)(x−a)−(a−b)(y−a)=0 ただし、 b ≦ x ≦ a
a−b=1 なので、 (2a−1)(x−a)−(y−a)=0 すなわち、
F(a)=2a2−2(x+1)a+x+y=0 軸の式は、 a=(x+1)/2
この2次方程式の解で、「 0 ≦ a ≦ 1 、 a−1 ≦ x ≦ a 」という条件を満たすもの
が存在するように、点( x , y )が満たすべき条件を定めればよい。
ここで、 a−1 ≦ x ≦ a より、 x ≦ a ≦ x+1 、 0 ≦ a ≦ 1 なので、
(1) −1 ≦ x < 0 のとき、 0 ≦ a ≦ x+1 で、軸はこの区間の中点である。
よって、題意を満たすためには、判別式を D として、
D/4=(x+1)2−2(x+y)=x2+1−2y ≧ 0 、 F(0) = x+y ≧ 0 であればよい。
すなわち、 y ≦ (1/2)(x2+1) 、 y ≧ −x 、 −1 ≦ x < 0
(2) 0 ≦ x ≦ 1 のとき、 x ≦ a ≦ 1 で、軸はこの区間の中点である。
よって、題意を満たすためには、判別式を D として、
D/4=(x+1)2−2(x+y)=x2+1−2y ≧ 0 、F(1) = −x+y ≧ 0 であればよい。
すなわち、 y ≦ (1/2)(x2+1) 、 y ≧ x 、 0 ≦ x ≦ 1
以上から、a≧0 、 b≦0 とした場合の領域は、
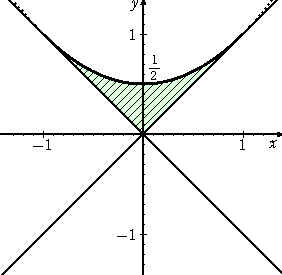
ただし、境界線も含む。
よって、求める領域は、
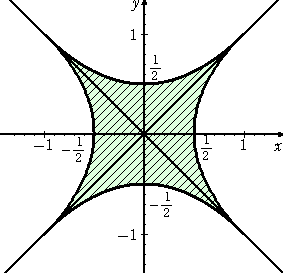
となる。
当HPがいつもお世話になっているHN「Seiichi Manyama」さんからのコメントです。
(平成28年10月5日付け)
2次方程式の実数解の存在について、素晴らしい解答がついたツイートがあったので、紹
介しておきます。
3(a - 1)x2 + 6x - a - 2 = 0 は、0 と 1 の間に少なくとも一つ解をもつことを示せ。
(証明) a = 1 のとき、x = 1/2 で、0 と 1 の間に解をもつ
a ≠ 1 のとき、2次関数 f(x) = 3(a - 1)x2 + 6x - a - 2 について、
∫01f(x) dx = a - 1 + 3 - a - 2 = 0
よって、この場合も、0 と 1 の間に少なくとも一つ解をもつ。 (証終)
厳密に示したければ、中間値の定理を持ち出してくればよい。
(コメント) なるほど!積分を用いた証明は初見です。Seiichi Manyamaさんに感謝します。
積分を用いないと大変な計算になりますね!
Seiichi Manyamaさんからのコメントです。(平成28年10月5日付け)
今更ですが、次の方が問題としてすっきりしている気がする。
3ax2 + 6x - a - 3 = 0 は、0 と 1 の間に少なくとも一つ解をもつことを示せ。
DD++さんからのコメントです。(平成28年10月6日付け)
じゃあ私は微分も積分も使わずに……。
左辺を f(x) と置くと、
f(1/6)f(3/4) = (-(11/12)a-2)((11/16)a+(3/2)) = -(1/192)(11a+24)2 ≦ 0
なので、1/6≦x≦3/4 に f(x)=0 の解が存在する。この範囲は、 0<x<1 に含まれているの
で、題意は示された。
0≦x≦2/3 や 1/3≦x≦1 だと計算は楽ですが、0<x<1 には微妙に入りきってないので
使えない……。
らすかるさんからのコメントです。(平成28年10月6日付け)
では私も別解を。
f(x)=3ax2+6x-a-3 とおくと、 f(1/ )=2
)=2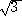 -3>0
-3>0
a≧-2のとき、f(0)=-a-3<0 なので、0<x<1/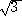 の範囲に解が存在し、
の範囲に解が存在し、
a<-2のとき、f(1)=2a+3<0 なので、1/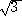 <x<1の範囲に解が存在する。
<x<1の範囲に解が存在する。
Seiichi Manyamaさんからのコメントです。(平成28年10月6日付け)
らすかるさん、私も最初不動点を利用したこの解を考えていました。
DD++さん、これはこれで素晴らしい。試行錯誤でこの範囲を見つけられたのでしょうか?
DD++さんからのコメントです。(平成28年10月7日付け)
左辺をaについて整理すると、(3x2-1)a+(6x-3) なので、
(3x2-1)/(6x-3) = (3y2-1)/(6y-3) 、x≠y
として、整理すると、 (2x-1)(2y-1)=-1/3
これがaについて綺麗に2乗にまとまる必要十分条件です。
そこから、 1×(-1/3) と思えば、x=1、y=1/3(おしい)
(-1)×(1/3) と思えば、x=0、y=2/3 (おしい)
(1/2)×(-2/3) と思えば、x=3/4、y=1/6 (OK)
(-1/2)×(2/3) と思えば、x=1/4、y=5/6 (これもOK)
と見つけました。別の方法として、片方の解を決め打ちする方法もあります。
x=1/2 が解となるとき、a=0 で、二次方程式ではなくなる(論外)
x=1/3 が解となるとき、a=-3/2 で、もう1つの解は x=1(おしい)
x=2/3 が解となるとき、a=-3 で、もう1つの解は x=0(おしい)
x=1/4 が解となるとき、a=-24/13 で、もう1つの解は x=5/6(OK)
x=3/4 が解となるとき、a=-24/11 で、もう1つの解は x=1/6(OK)
あるいは、さらに別の方法として、判別式 D/4=3a2+9a+9 が有理数の平方になると考えて、
双曲線の媒介変数表示 a=(6t+9)/(t2-3) のtに適当な有理数を放り込めばよい。
x=0 が解となるとき、a=-3 つまり、t=0、-2
x=1 が解となるとき、a=-3/2 つまり、t=-1、-3
というのを参考に、t=-1/2 を放り込むと、a=-24/11 で、このとき方程式の解は、x=1/6、3/4
Seiichi Manyamaさんからのコメントです。(平成28年10月7日付け)
DD++さん、ありがとうございます。
(追記) 「解の符号」と題して、当HPがいつもお世話になっているHN「よおすけ」さんからご
投稿いただきました。(令和2年12月13日付け)
2次方程式 x2+ax+a+12=0 は異なる2つの実数解をもつものとする。
(1) 少なくとも1つの解の整数部分は4にならないことを証明せよ。
(2) aが整数であって、1つの解の整数部分が4のとき、aの値を求めよ。
(出典:1976年 金沢大学)
スモークマンさんが考察されました。(令和2年12月14日付け)
考えてみました...
(1) 2つの実数解をα、βとすると、解と係数の関係から、 α+β=-a 、αβ=a+12
よって、aを消去して、 αβ+α+β=12 すなわち、 (α+1)(β+1)=13
いま、αの整数部分が4とすると、 4≦α<5
このとき、 13/6<β+1≦13/5 すなわち、 7/6<β≦8/5 となるので、
βの整数部分は、1 で、つまり、同時に整数部分が4にはなり得ない。
よって、少なくとも1つの解の整数部分は4にならない。
(2) αの整数部分が4とすると、βの整数部分は、1 なので、
α=4+s (0≦s<1) 、β=1+t (0≦t<1)
このとき、 -a=α+β=4+s+1+t=5+s+t から、 a=-5、-6
a=-5 のとき、 x^2-5x+7=(x-5/2)^2+7-25/4>0 で実数解が存在しない。
a=-6 のとき、 x^2-6x+6=0 から、x=3± で、3+
で、3+ の整数部分は、4
の整数部分は、4
以上から、 a=-6 である。
(コメント) (1)は、背理法による解法もあります。
2つの解がともに整数部分が4と仮定すると、
判別式 D=a2−4a−48≧0 より、 a≦2−2√13 、2+2√13≦a ・・・(イ)
軸 x=−a/2 について、4≦−a/2<5 より、 −10<a≦−8 ・・・(ロ)
F(x)=x2+ax+a+12 について、 F(4)=5a+28≧0 かつ F(5)=6a+37>0
すなわち、 a≧−28/5 かつ a>−37/6 より、 a≧−28/5 ・・・(ハ)
(イ)(ロ)(ハ)をともに満たすaは存在しないので、矛盾。
よって、少なくとも1つの解の整数部分は4にならない。
(2)について、1つの解の整数部分が4なので、 F(4)F(5)=(5a+28)(6a+37)≦0
このとき、 −37/6≦a≦−28/5 で、aは整数より、 a=−6
ここで、 −6<2−2√13<−4 なので、a=−6は、(イ)を満たす。
このとき、 x2−6x+6=0 から、x=3± で、3+
で、3+ の整数部分は、4
の整数部分は、4
以上から、 a=−6 が求めるものである。
(追記) 令和6年6月22日付け
冒頭で、次の問題を考えた。
2次方程式 x2−2mx+m+2=0 が次のような解を持つように定数 m の値の範
囲を求めよ。
(1) 2つの解がともに正
(2) 異符号の解を持つ
解法は種々考えられるが、微分法を使ってもよいのであれば、(1)(2)は統一的に次の
ように解かれる。
(解) x2−2mx+m+2=0 から、 m(2x−1)=x2+2
ここで、x=1/2 とすると、 左辺=0 、右辺=9/4 で、左辺≠右辺 から、 x≠1/2
よって、 m=(x2+2)/(2x−1) と書ける。
y=(x2+2)/(2x−1) とおくと、 y’=2(x+1)(x−2)/(2x−1)2
y’=0 を解くと、 x=−1、2 なので、次の増減表を得る。
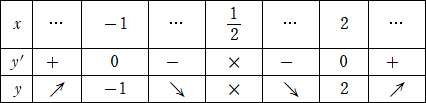
よって、グラフの概形は下図となる。
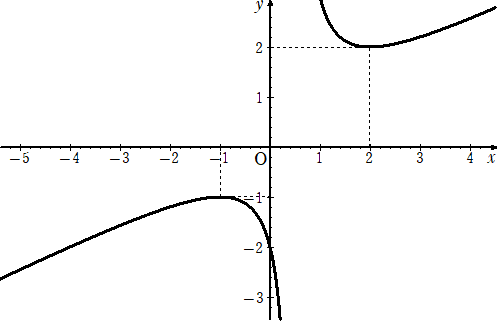
グラフから、求めるmの値の範囲は、
(1) 2つの解がともに正であるためには、x>0 の部分で、y=m が2点で交わればよい
ので、 m≧2 である。
(2) 異符号の解を持つためには、x<0 の部分とx>0 の部分のそれぞれで、y=m が
交わればよいので、 m<−2 である。 (終)
同様にして、次の問題を解いてみよう。
問題 2次方程式 x2−2mx+3m−2=0 が 0 と 2 の間に2つの解を持つように定数
mの値の範囲を定めよ。
(解) m(2x−3)=x2−2 において、x≠3/2 なので、 m=(x2−2)/(2x−3) と書ける。
y=(x2−2)/(2x−3) とおくと、 y’=2(x−1)(x−2)/(2x−3)2
y’=0 を解くと、 x=1、2 なので、次の増減表を得る。
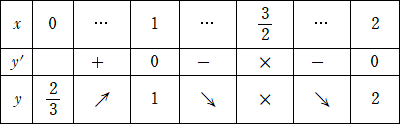
よって、グラフの概形は下図となる。
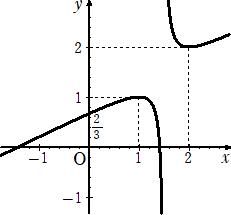
グラフから、求めるmの値の範囲は、 2/3<m≦1 である。 (終)
(コメント) 高校生の時あれほど苦労した解の分離問題が、微分法の力で鮮やかに解か
れるとは、感動しますね!
(追記) 令和6年10月19日付け
次の東北大学 文理共通(1983)の問題も、解の符号を問うている。
問題 nを3以上の整数とする。関数 F(x)=2xn+1−4xn+3 について、次の問に答えよ。
(1) F(3/2) の符号を調べよ。
(2) 方程式 F(x)=0 の正の解、負の解の個数を求めよ。
(解)(1) F(3/2)=2(3/2)n+1−4(3/2)n+3=3−(3/2)n≦3−27/8=−3/8<0
(2) F’(x)=2(n+1)xn−4nxn-1=2(n+1)xn-1(x−2n/(n+1))=0 とおくと、
x=0 、2n/(n+1)
nが偶数のとき、n−1は奇数で、 x=0 で極大で、極大値 3、
x=2n/(n+1) で極小で、極小値 F(2n/(n+1))
(1)より、F(2n/(n+1))≦F(3/2)<0
x → −∞ のとき、 F(x) → −∞
x → ∞ のとき、 F(x) → ∞
よって、正の解の個数は、2で、負の解の個数は、1個
nが奇数のとき、n−1は偶数で、x=2n/(n+1) で極小で、極小値 F(2n/(n+1))
(1)より、F(2n/(n+1))≦F(3/2)<0
x → ±∞ のとき、 F(x) → ∞
よって、正の解の個数は、2で、負の解の個数は、0個 (終)
(追記) 令和7年4月23日付け
次の東北大学 前期理系(1992)の問題は、3次方程式が実数解を3個持つ条件を問う
ている。
問題 x についての3次方程式 2x3−3(a+b)x2+6abx−2a2b=0 が3つの相異なる
実数解をもつとする。このとき、点(a,b)の存在する範囲を求め、それを図示せよ。
(解) F(x)=2x3−3(a+b)x2+6abx−2a2b とおく。
F’(x)=6x2−6(a+b)x+6ab=6(x−a)(x−b)=0 より、x=a 、b
F(x)=0 が3つの相異なる実数解をもつためには、x=a 、b で極値をとり、
(極大値)×(極小値)<0 であればよい。
よって、 F(a)F(b)=a2(a−b)2b(2a−b)<0 より、
a≠0 、a≠b 、b(2a−b)<0
よって、求める点(a,b)の存在する範囲は下図。
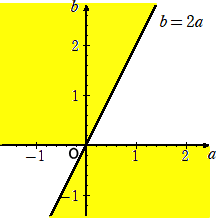
ただし、境界線および b 軸は含まない。 (終)
(コメント) 後で気がついたのですが、この問題は既に「実数解の個数」で取り上げられてい
ました!
(追記) 令和7年5月25日付け
次の東北大学 前期理系(1994)の問題は、3次方程式が負の解を持たない条件を問う
ている。
問題 x に関する3次方程式 (x+a)3−3x−a2=0 が負の解をもたないように実数 a の
範囲を定めよ。
(解) (x+a)3−3x=a2 において、F(x)=(x+a)3−3x とおく。
F’(x)=3(x+a)2−3=3(x+a+1)(x+a−1)=0 とおくと、 x=−a−1 、−a+1
F(x)は、x=−a−1 で極大で、極大値 3(a+1)−1=3a+2
−a−1≧0 すなわち、a≦−1 のとき、F(0)=a3<0 なので、y=a2>0 が x<0 に
おいて、y=F(x)と交わることはない。
よって、a>−1 で考えればよい。題意を満たすためには、
a2>3a+2 かつ F(0)=a3<a2 であればよい。
よって、 a<(3−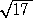 )/2 、(3+
)/2 、(3+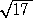 )/2<a かつ a<1 より、
)/2<a かつ a<1 より、
−1<a<(3−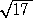 )/2
)/2
a≦−1 と合わせて求める a の値の範囲は、 a<(3−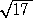 )/2 (終)
)/2 (終)
(追記) 令和7年6月9日付け
次の東北大学 後期文系(1994)の問題は、解の分離の定番だろう。
問題 実数 t に対して、xy平面上の直線Ltを次のように定義する。
Lt:y=(4tx+t2−1)/(t2+1)
(1) t が実数全体を動くとき、Ltの通りうる範囲を図示せよ。
(2) t が t≧0 のすべてを動くとき、Ltの通りうる範囲を図示せよ。
(解)(1) y=(4tx+t2−1)/(t2+1) を書き直して、 (y−1)t2−4tx+y+1=0
y=1 のとき、 2tx=1 から、実数解 t が存在するためには、 x≠0 であればよい。
y≠1 のとき、2次方程式 (y−1)t2−4tx+y+1=0 が実数解を持つためには、判別式
をDとおくと、 D/4=4x2−(y−1)(y+1)=4x2−y2+1≧0 から、 4x2−y2≧−1
以上から、Ltの通りうる範囲は、下図である。ただし、点(0,1)は除く。
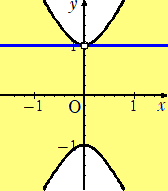
(2) (y−1)t2−4tx+y+1=0 において、
y=1 のとき、 2tx=1 が t≧0 の実数解 t が存在するためには、x>0 であればよい。
y≠1 のとき、2次方程式 (y−1)t2−4tx+y+1=0 すなわち、
(y−1)(t−2x/(y−1))2+y+1−4x2/(y−1)=0 が t≧0 の実数解 t を持つために
2x/(y−1)≦0 すなわち、 2x(y−1)≦0 のとき、t=0 において、
(y−1)(y+1)≦0 より、 −1≦y<1 であればよい。
2x/(y−1)≧0 すなわち、 2x(y−1)≧0 のとき、判別式をDとおくと、
D/4=4x2−y2+1≧0 から、 4x2−y2≧−1
以上から、Ltの通りうる範囲は、下図である。ただし、y=1(x≦0)の部分は除く。
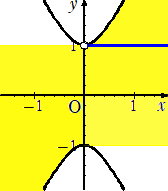
(追記) 令和7年7月6日付け
次の東北大学 前期文系(1996)の問題は、解の分離の定番だろう。
問題 直線 y=ax+b は楕円 4x2+y2=4 と相異なる2点で交わり、これらの交点の y
座標はともに正であるという。このような(a,b)の範囲をab平面上に図示せよ。
(解) a=0 のとき、題意を満たすためには、 0<b<2 であればよい。
a≠0 のとき、 x=(y−b)/a を代入して、 4(y−b)2/a2+y2=4
すなわち、 (a2+4)y2−8by+4b2−4a2=0
判別式をDとすると、相異なる2点で交わることから、
D/4=16b2−4(a2+4)(b2−a2)=−4a2b2+4a4+16a2>0
a≠0 なので、 −b2+a2+4>0 すなわち、 a2−b2>−4
軸の式 x=4b/(a2+4)>0 から、 b>0
y切片>0 から、 b2−a2>0 すなわち、 (b+a)(b−a)>0
以上から、求める(a,b)の範囲は、下図。ただし、境界線は含まない。
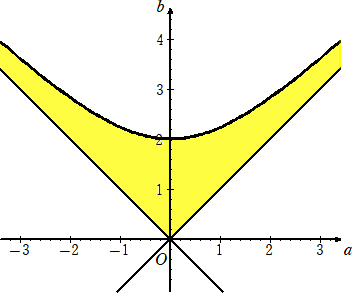 (終)
(終)
(追記) 令和7年9月24日付け
次の東北大学 後期文系(1999)の問題は、解の分離問題だろう。
問題 xy平面において、不等式 y≦x3−3p2(x−2)−q で定まる領域をD、不等式
1≦x≦2、y≦0 で定まる領域をEとする。EがDに含まれるための p、q についての条
件を求めよ。また、この条件をみたす(p,q)の領域をpq平面に図示せよ。
(解) F(x)=x3−3p2(x−2)−q とおくと、 F’(x)=3x2−3p2x=0 とおくと、x=±p
−1≦p≦1 のとき、題意を満たすためには、 F(1)=1+3p2−q≧0
−2≦p≦−1 のとき、 F(−p)=−p3+3p2(p+2)−q=2p3+6p2−q≧0
1≦p≦2 のとき、 F(p)=p3−3p2(p−2)−q=−2p3+6p2−q≧0
p≧2 のとき、 F(2)=8−q≧0
p≦−2 のとき、 F(2)=8−q≧0
以上から求める領域は、
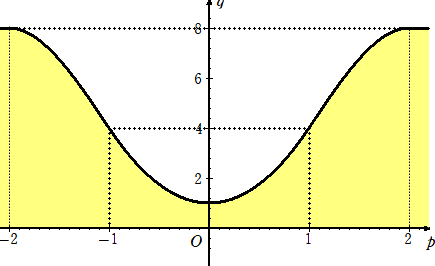 (終)
(終)
以下、工事中










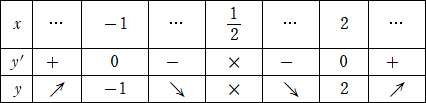
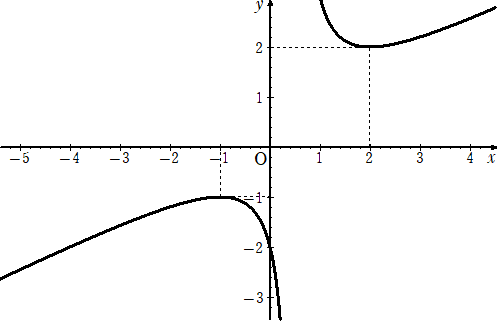
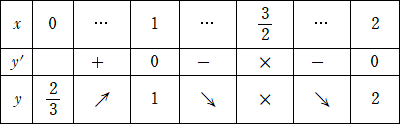




 (終)
(終) (終)
(終)