| 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 |
||||||
| 侽侾俁 | 暯惉俀侽擭搙慜婜 | 拀攇戝妛 | 慡妛 | 丒丒丒 | 懳悢娭悢乮悢妛嘦乯 | 丂昗弨 |
丂栤戣偺婰弎偼懳悢娭悢偩偑丄幚幙偼丄俀師曽掱幃偺夝偺暘棧栤戣偱掕宆揑側栤戣偲尵
偊傞丅
丂夝偺暘棧栤戣偑嬯庤側恖偵偲偭偰偼擄栤偲塮傞偩傠偆偑丄夝朄偼掕傑偭偰偄傞偺偱丄昁偢
墴偝偊偰偍偐側偗傟偽側傜側偄斖醗偺栤戣偩傠偆丅乮仺丂嶲峫丗乽夝偺暘棧乿乯
拀攇戝妛丂慡妛乮俀侽侽俉乯
丂倫丄倯 傪惓偺幚悢偲偡傞丅倶 偺曽掱幃丂倢倧倗10乮倫倶乯倢倧倗10乮倯倶乯亄侾亖侽丂偑 侾 傛傝戝偒偄夝
傪帩偮偲偒丄揰乮 倢倧倗10 倫丆倢倧倗10 倯 乯偺懚嵼偡傞斖埻傪嵗昗暯柺忋偵恾帵偣傛丅
乮夝乯丂乮倢倧倗10 倶亄倢倧倗10 倫乯乮倢倧倗10 倶亄倢倧倗10 倯乯亄侾亖侽丂傛傝丄
丂丂丂丂丂乮倢倧倗10 倶乯2亄乮倢倧倗10 倫亄倢倧倗10 倯乯倢倧倗10 倶亄乮倢倧倗10 倫乯乮倢倧倗10 倯乯亄侾亖侽
丂丂丂丂偙偙偱丄丂倢倧倗10 倶亖倃丂丄丂倢倧倗10 倫亖倎丂丄丂倢倧倗10 倯亖倐丂偲偍偔偲丄
丂丂丂俀師曽掱幃丂倃2亄乮a亄倐乯倃亄倎倐亄侾亖侽丂偑摼傜傟傞丅
丂丂丂丂傕偲偺曽掱幃偑 侾 傛傝戝偒偄夝傪帩偮偺偱丄偙偺俀師曽掱幃偼彮側偔偲傕侾屄偺惓偺
丂丂丂夝傪帩偮偙偲偵側傞丅
丂丂丂丂丂俥乮倃乯亖倃2亄乮a亄倐乯倃亄倎倐亄侾亖乮倃亄乮a亄倐乯/俀乯2亅乮a亅倐乯2/係亄侾丂偲偍偔偲丄
丂丂丂幉偺曽掱幃偼丄丂倃亖亅乮a亄倐乯/俀丂偲側傞丅
丂丂丂丂乮侾乯丂亅乮a亄倐乯/俀亜侽丂偡側傢偪丄丂a亄倐亙侽丂偺偲偒丄戣堄傪枮偨偡偨傔偵偼丄
丂丂丂丂丂丂丂捀揰偺 倄 嵗昗亖亅乮a亅倐乯2/係亄侾亝侽丂偡側傢偪丄
丂丂丂丂丂丂丂丂丂丂丂丂丂a亅倐亝亅俀丂傑偨偼丂a亅倐亞俀
丂丂丂丂乮俀乯丂亅乮a亄倐乯/俀亝侽丂偡側傢偪丄丂a亄倐亞侽丂偺偲偒丄戣堄傪枮偨偡偨傔偵偼丄
丂丂丂丂丂丂丂俥乮侽乯亖倎倐亄侾亙侽丂偡側傢偪丄丂倎倐亙亅侾
丂丂丂埲忋偐傜媮傔傞椞堟偼丄
丂丂丂丂丂丂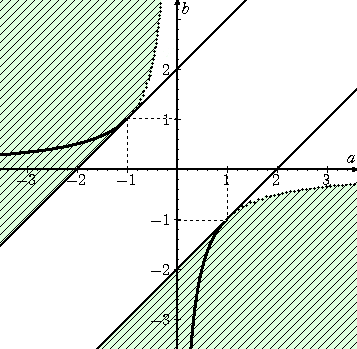
丂嫬奅慄偼丄丂倎倐亖亅侾 乮丂亅侾亝倎亙侽丂丄丂侾亝倎丂乯 偺晹暘傪彍偒娷傑傟傞丅丂乮廔乯
乮僐儊儞僩乯丂幉偺埵抲偵傛偭偰応崌暘偗偡傞偲偙傠偑億僀儞僩偱偡偹両