
高校で学ぶ数学で一番大切で感動的な出会いは、「判別式」との出会いだろう。判別式
を初めて学習するのは、2次方程式の解法においてであるが、その後、判別式は、高校数
学にとどまらず、いろいろな分野で顔を出す、言わば数学の世界の人気者である。私自身
高校で判別式を学んで以来、その華麗な技の虜になってしまった一人である。
ただ、判別式のそのような多様性、有用性に気がつく生徒は少ない。むしろ「何故こんな
所で判別式?」と疑問を持つ方が普通である。
ここでは、判別式の素性を明らかにし、その豊富な応用例をまとめていこうと思う。
判別式というと、2次方程式の判別式のことを想起する方が多いと思われるが、一般に
は、n 次(n≧2)の多項式において定義される。ただし、このページでは、n=2、3 の場合
についてのみ考えることにする。
n 次多項式 F(X)=a0Xn+a1Xn-1+・・・+an-1X+an において、方程式 F(X)=0 の根を、
α1、α2、・・・、αn とする。(→参考:根と解の違い)
このとき、異なる i 、j ( i < j )すべてについて、根の差分の平方 (αi−αj)2 の積を考え
て、
D =a02(n-1)Π(αi−αj)2
とおく。この D のことを、多項式 F(X) (または、方程式 F(X)=0 )の判別式という。
( D の定義で、差分の平方を考えるのは、D を対称式にするため、a02(n-1) を掛けるのは、
分母に a0 が残るのを避けるためである。 D の最高次の項の形が
α12(n-1)α22(n-2)・・・αn2 などから明らかだろう。)
D の定義から分かるように、
D=0 ⇔ 多項式 F(X) (または、方程式 F(X)=0 )は、重根をもつ
すなわち、判別式とは、多項式が重根を持つかどうかを判別する式である。
(高校で活躍する判別式は、解が実数かどうかを判別する方に重きが置かれるが...。)
例 2次方程式 ax2+bx+c=0 の場合、2つの解を、α、β とおくと、解と係数の関係か
ら、 α+β=-b/a 、 αβ=c/a なので、
判別式 D=a2(α−β)2=a2{(α+β)2−4αβ}=a2{b2/a2−4c/a}=b2−4ac
即ち、 2次方程式 ax2+bx+c=0 の判別式は、D=b2−4ac となる。
2次方程式の解が実数かどうかは、判別式 D が、解の公式において、根号の中味である
ことから判別できる。
また、次のようにしても、確認できるだろう。
α、β が相異なる実数 ならば、 明らかに、 D>0
α、β が等しい ならば、 明らかに、 D=0
α、β が相異なる虚数(互いに共役) ならば、 α−β は純虚数なので、 D<0
上記は全ての場合をつくしているので、転換法という証明法により、必要十分条件となる。
例 3次方程式 ax3+bx2+cx+d=0 の場合、このままで判別式を計算すると、
D=b2c2+18abcd−4ac3−4b3d−27a2d2 となり、とても長い式で覚えられない。
そこで、まず、3次方程式を変形することを考える。ax3+bx2+cx+d=0 において、
x=X−b/(3a) を代入すると、
a(X−b/(3a))3+b(X−b/(3a))2+c(X−b/(3a))+d=0
展開して、
aX3−bX2+(b2/(3a))X−b3/(27a2)+bX2−(2b2/(3a))X+b3/(9a2)
+cx−bc/(3a)+d=0
即ち、aX3+(c−b2/(3a))X−b3/(27a2)+b3/(9a2)−bc/(3a)+d=0
よって、3次方程式として、 x3+px+q=0 の場合を考えればよい。
(このような変換は、チルンハウス変換と呼ばれる。)
このとき、 3つの解を、α、β、γ とおくと、解と係数の関係から、
α+β+γ=0 、 αβ+βγ+γα=p 、 αβγ=−q
である。判別式 D=(α−β)2(α−γ)2(β−γ)2 において、
(α−β)(α−γ)=α2−(β+γ)α+βγ=α2−(−α)α+p−(αβ+γα)
=α2+α2+p−(β+γ)α=2α2+p−(−α)α=3α2+p
同様にして、(β−γ)(β−α)=3β2+p 、(γ−α)(γ−β)=3γ2+p
これら3式を辺々掛けると、
−(α−β)2(α−γ)2(β−γ)2=(3α2+p)(3β2+p)(3γ2+p)
=p3+3(α2+β2+γ2)p2+9(α2β2+β2γ2+γ2α2)p+27α2β2γ2
ここで、α2+β2+γ2=(α+β+γ)2−2(αβ+βγ+γα)=−2p
α2β2+β2γ2+γ2α2=(αβ+βγ+γα)2−2αβγ(α+β+γ)=p2
なので、−(α−β)2(α−γ)2(β−γ)2=p3−6p3+9p3+27q2=4p3+27q2
従って、3次方程式 x3+px+q=0 の判別式は、 D=−4p3−27q2
3次方程式の解については、次のように判別される。
(3次方程式は少なくとも一つ実数解をもつこと、実係数という条件で、虚数解は互いに共
役であることに注意する。)
D>0 ならば、 3つの相異なる実数解をもつ
D<0 ならば、 1つの実数解と2つの虚数解をもつ
D=0 とする。 p=q=0 ならば、 3重解(解は0のみ)をもつ
pq≠0 ならば、 3つの実数解(2重解とその他の解)をもつ
例 3次方程式 x3−3x+1=0 は、3つの実数解を持つことを示せ。
判別式D=−4(−3)3−27・12=81>0 より、3つの相異なる実数解をもつ。
(コメント) 高校生向けには、グラフを用いる方が教育的だろう。y=x3−3x+1 のグラフ
は下図の通り。

グラフより、3次方程式 x3−3x+1=0 は、3つの相異なる実数解をもつことが分かる。
私が高校時代に出会った問題で、その解法の面白さに惹かれたものは次のようなもので
ある。
問題1 実数 x 、y に対して、 3x2−4xy+6y2−8x− 4y+3=0 が成り立つ。
このとき、 x 、y の取り得る値の範囲を求めよ。
(コメント) 2次方程式の理論を学んだ後の演習問題として先生から出題されたものだが、
まだ数学がよく分かっていない高校生にとっては十分すぎるくらいの難問だった
と思う。
(解) y についての2次方程式 6y2−4(x+1)y+3x2−8x+3=0 が実数解をもつので、
判別式を D とすると、D/4=4(x+1)2−18x2+48x−18=−14x2+56x−14≧0
より、 x2−4x+1≦0 よって、 2−
同様にして、x についての2次方程式 3x2−4(y+2)x+6y2−4y+3=0 が実数解
をもつので、D/4=4(y+2)2−18y2+12y−9=−14y2+28y+7≧0 より、
2y2−4y−1≦0 よって、 (2−
(コメント) 「実数 x 、y に対して、」という点を、「実数解 x 、y をもつ」と発想の転換をすると
ころが当時とても斬新に思えました。
今風にこの問題を授業等で取り上げるとしたら、パソコンを使って、
3x2−4xy+6y2−8x− 4y+3=0 のグラフを描かせて、おおよその範囲を理解させて終
わりというのが実状でしょうか?それでは、あまりに味気ないですね!

この考え方を用いた例は数多い。一つだけ例をあげておこう。
例 次の関数の値域を求めよ。
(解) 分母を払って、 yx2−2x+y−4=0
y=0 のときは、 x=−2 なので、 y=0 も値域に含まれる。
y≠0 とする。 上式を、x についての2次方程式とみて、実数解をもつので、
判別式 D/4=1−y(y−4)=−y2+4y+1≧0 より、 y2−4y−1≦0
よって、 2−
この問題も、グラフを描かせて値域を正確に求めることはできない!判別式の有用さが
身にしみて分かるところだ。

上記のようなタイプの問題は、「判別式が絡みそう...」ということが薄々分かるが、突然
に判別式が出てきて驚く問題としては次の問題が有名だろう。
問題2 点( x , y )が、円 x2+y2=1 の内部および周上を動くとき、点( x+y , xy )の
動く範囲を求めよ。(これは、随分昔の東京大学入試問題!)
(当HPがいつもお世話になっているHN「よおすけ」さんからの情報では、上記の問題は、1954年に東京
大学が出題したものとのことです。もう出題されてから60年も経つのですね!−2013.12.2追記)
(解) u=x+y 、v=xy とおくと、 x2+y2=(x+y)2−2xy=u2−2v≦1
よって、 v≧(1/2)u2−1/2 ・・・(1)
また、 実数 x 、y は、2次方程式 t2−ut+v=0 の解なので、
判別式D=u2−4v≧0 より、 v≦(1/4)u2 ・・・(2)
(1)、(2)より、求める領域は、
 (終)
(終)(コメント) 正直に告白すると、私は高校で初めてこのような問題に出会ったとき、ものの
見事に判別式をとるという発想が思い浮かばなかった。解答を見て、すごく不自
然さを感じた。今では全く違和感がないのだが...。
問題2では、解と係数の関係が根底にあったが、より一般に、領域を求める際に判別式
が関係する例としては次の問題が有名である。
問題3 放物線 y=2x2+2ax+a2 について、a がすべての実数値をとって変わるとき、
放物線が通過する領域を求めよ。
(解) a についての2次方程式 a2+2x・a+2x2−y=0 が実数解を持つので、
判別式 D/4=x2−(2x2−y)=y−x2≧0 より、求める領域は、 y≧x2 (終)
(コメント) グラフ描画ソフト「grapes」を用いて、放物線が通過する領域を描かせてみた。
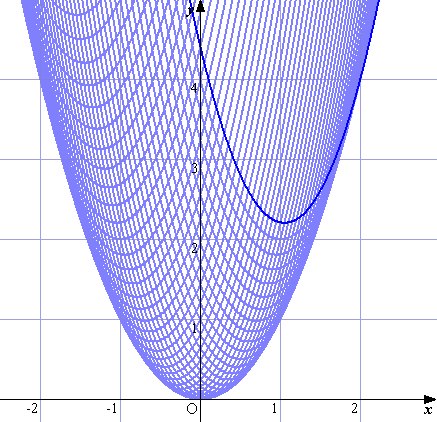
確かに、左図から求める領域が、
y≧x2
であることが分かる。
また、次の問題4と問題5も発想の豊かさ
に驚かされる。この手法は解析学の常套手
段なのだろう!
問題4 2つのベクトル a 、b に対して、内積を、a・b で表すとき、次の不等式を示せ。
|a||b|≧|a・b| (コーシー・シュワルツの不等式)
(解) 任意の実数 t に対して、|ta−b|2≧0 が成り立つので、
|a|2t2−2(a・b)t+|b|2≧0 において、
判別式D/4=(a・b)2−|a|2|b|2≦0 より、|a||b|≧|a・b| (終)
(コメント) 等号が成り立つ場合は明らかであろう。
平面上のベクトルなら強引に成分計算に持ち込んでも易しいが、一般のベクトルについて
は厳しいだろう。どこからか「任意の実数 t 」を引っ張り出してきて、
絶対不等式「 |ta−b|2≧0 」に持ち込むところが心憎い。
もっとも、この問題については、
を用いた証明の方がエレガントで、私は好きだ!
問題5 実数 x 、y に対して、x2−4x+4y2=1 のとき、x+y の最大値を求めよ。
(解) x+y = k とおく。 y=k−x を、x2−4x+4y2=1 に代入して整理すると、
2次方程式 5x2−4(2k+1)x+4k2−1=0 が実数解を持つので、
判別式 D/4=(4k+2)2−5(4k2−1)=−4k2+16k+9≧0
すなわち、 4k2−16k−9=(2k+1)(2k−9)≧0 より、−1/2 ≦ k ≦ 9/2
よって、 求める最大値は、 9/2 (終)
次の問題は、高校に入って私が受けた最初の試練である。不等号の使い回しに魅了され
た問題である。
問題6 等式 5x2−12xy+10y2−6x−4y+13=0 を満たすような実数 x 、y の値を
求めよ。
(解) x の2次方程式 5x2−2(6y+3)x+10y2−4y+13=0 が実数解を持つので、
判別式 D/4=(6y+3)2−5(10y2−4y+13)=−14(y2−4y+4)
=−14(y−2)2≧0 より、 0≦(y−2)2≦0
よって、 (y−2)2=0 となり、 y=2 で、このとき、 x=3 (終)
具体的な数を係数に持つ2次方程式には、解の公式という強力な武器があるので、解が
どのようなものであるかは直ぐ分かる。しかし、文字を係数に持つ2次方程式の場合、解が
どのような範囲にあるかを調べるときには解の公式は無力である。
次の問題は、問題1の変形バージョンである。判別式の使い方が面白い。
問題7 k が実数値をとって変わるとき、x の2次方程式 x2+(k+3)x+k2=0 の実数
解の取り得る値の範囲を求めよ。
(解) k についての2次方程式 k2+xk+x2+3x=0 が実数解をもつので、
判別式 D=x2−4x2−12x=−3x2−12x≧0 より、x2+4x≦0
よって、 −4 ≦ x ≦ 0 (終)
(コメント) 解の公式を用いて、
から、x の取り得る値の範囲を求めることは困難だろう。グラフ描画ソフトを使って、x の値
域を求めてみた。
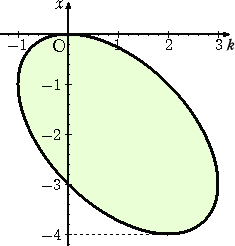
図から確かに、 −4 ≦ x ≦ 0 である。
次の問題も、問題1の変形バージョンであるが、2次方程式を作る作業が入ってくる。
問題8 実数 x 、y 、z が等式 x+y+z=3 、xy+yz+zx=−9 を満たすとき、
x の取り得る値の範囲を求めよ。(これは、随分昔の九州大学入試問題!)
(解) z=3−x−y を、 xy+yz+zx=−9 に代入して、 xy+(x+y)(3−x−y)=−9
即ち、 y2+(x−3)y+x2−3x−9=0 を、y の2次方程式とみて実数解を持つので、
判別式 D=(x−3)2−4(x2−3x−9)=−3(x+3)(x−5)≧0 より、
(x+3)(x−5)≦0 よって、−3 ≦ x ≦ 5 (終)
この問題に対して、当HPの掲示板「出会いの泉」で、U 様がラグランジュの乗数を用いた
解法があることを示唆された。(平成18年7月3日付け)
実際に、その解法をなぞってみよう。
F( x , y , z ) = x とおく。 拘束条件としては、
G( x , y , z ) = x+y+z−3=0 、 H( x , y , z ) = xy+yz+zx+9=0
このとき、ラグランジュの未定乗数法により、
Fx+λGx+μHx=0 、Fy+λGy+μHy=0 、Fz+λGz+μHz=0
よって、 1+λ+μ(y+z)=0 、λ+μ(z+x)=0 、λ+μ(x+y)=0
2式を辺々引いて、 1+μ(y−x)=0 、 μ(z−y)=0
上式から、明らかに μ≠0 で、 よって、 z−y=0 すなわち、 y=z である。
このとき、 x+2y=3 、 y2+2xy+9=0 を連立して解くと、
( x , y , z ) = ( −3 ,3 ,3 ) 、 ( 5 , −1 , −1 )
となる。この2点が、F( x , y , z ) = x の極大点、極小点の候補である。
2つの曲面:x+y+z−3=0 、 xy+yz+zx+9=0 は下図のように交わっている。
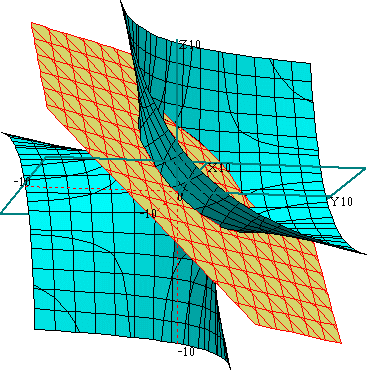
従って、幾何学的に考えて、x の取り得る値の範囲は、 −3 ≦ x ≦ 5 となる。
(コメント) ラグランジュの乗数を用いて解けるには解けるが、最後の詰めの場面で、「幾何
学的に考えて、〜」という辺りが、少し気持ち悪いような気がする。
ラグランジュ の未定乗数法は、あくまでも極値を与える候補を教えてはくれるが、それが本
当に極値を与えるかどうかについては、何ら教えてはくれない。したがって、上図のように図
形的な関係が明白な場合は有効かもしれないが、図形的に不明確な場合は、最後の結論を
記述するときに途方に暮れてしまう。この点がラグランジュ の未定乗数法の弱点なのだろう。
その点、判別式の方が明解に要求されたことに答えてくれる。
整数論で有名なディオファントス問題においても判別式は活躍する。(もっとも、この場合は
判別式の値が平方数という話になって、ちょっと意味合いが違ってくるが...。)
問題9 等式 x2−3xy+2y2+4=0 を満たすような自然数 x 、y を求めよ。
(解) x の2次方程式 x2−3xy+2y2+4=0 が、自然数解すなわち実数解を持つので、
判別式 D=9y2−4(2y2+4)=y2−16 において、x が自然数となるためには、
D=(平方数) となることが必要。そこで、y2−16=z2 (z は自然数)とおくと、
y2−z2=16から、(y+z)(y−z)=16 ( y、z は自然数 )なので、 y+z>y−z に注意
して、(y+z、y−z)=(8、2)、(4、4)より、(y、z)=(5、3)、(4、0)
(y、z)=(5、3)のとき、 x2−15x+54=0 これを解いて、 x = 6、9
(y、z)=(4、0)のとき、 x2−12x+36=0 これを解いて、 x = 6
以上から、 求める自然数の組は、 (x、y)=(6、5)、(9、5)、(6、4) (終)
上記の問題9では「自然数解→実数解」という必要条件で判別式が用いられた。ある程度
の範囲の数に絞るという意味で、このような判別式の使われ方も面白い。次は、このタイプ
の問題で、2004年度大学入試センター試験に出題されたものである。
問題10 2次関数 y=−x2+(2a−5)x−2a2+5a+3 (aは整数)のグラフが、x 軸と
異なる2点で交わるものとする。このとき、2つの交点の x 座標がともに整数となる
ように定数 a の値を定めよ。(改題)
(解) 2次方程式 −x2+(2a−5)x−2a2+5a+3=0 が、整数解すなわち実数解を持
つので、判別式 D=(2a−5)2+4(−2a2+5a+3)=−4a2+37≧0 すなわち、
a2≦37/4 である。a は整数なので、 a=0、±1、±2、±3 となる。
a=0 のとき、 2次方程式 −x2−5x+3=0 は整数解を持たない。
a=1 のとき、 2次方程式 −x2−3x+6=0 は整数解を持たない。
a=−1 のとき、 2次方程式 −x2−7x−4=0 は整数解を持たない。
a=2 のとき、 2次方程式 −x2−x+5=0 は整数解を持たない。
a=−2 のとき、 2次方程式 −x2−9x−15=0 は整数解を持たない。
a=3 のとき、 2次方程式 −x2+x=0 は整数解 0 と 1 を持つ。
a=−3 のとき、 2次方程式 −x2−11x−30=0 は整数解 −5 と −6 を持つ。
以上から、 求める a の値は、 a=±3 (終)
(追記) 平成22年9月30日付け
当HPがいつもお世話になっているHN「FN」さんから、判別式の話題を頂いた。
HPサイト「3次方程式の判別式」では、判別式を次のように定義している。
F(x)=x3+ax2+bx+c=0 に対して、F’(x)=3x2+2ax+b=0 の解を、p、q とする
とき、F(p)F(q) を、F(x)=0 の判別式という。(実際には、これの27倍をとっている...。)
確かに判別式の本来の意味は、「重解をもつかどうか」を判別するための式であるから、
判別式を名乗る資格はある。ということは、F’(α)F’(β)F’(γ)も判別式を名乗る資格を
持つ。何れも、重解をもつとき、「0」になり、そうでなければ、「0」でない。そこで、問題です。
問題 F(x)=x3+ax2+bx+c=0 の解を α、β、γ とし、F’(x)=3x2+2ax+b=0 の
解を、p、q とする。
D=(α−β)2(β−γ)2(γ−α)2 、E=F(p)F(q) 、F=F’(α)F’(β)F’(γ)
とするとき、E、F をDで表せ。
(例) 2次式 F(x)=x2+bx+c のとき、
D=b2−4c 、E=(−b2+4c)/4=−D/4 、F=−b2+4c=−D である。
(解) 解と係数の関係より、α+β+γ=−a 、αβ+βγ+γα=b 、αβγ=−c
p+q=−2a/3 、pq=b/3 が成り立つ。よって、
α+β+γ=3(p+q)/2 、 αβ+βγ+γα=3pq
このとき、(α−β)(α−γ)=α2−(β+γ)α+βγ
=α2−(3(p+q)/2−α)α+3pq−α(3(p+q)/2−α)
=3α2−3(p+q)α+3pq=3{α2−(p+q)α+pq}
=3(α−p)(α−q)=F’(α)
(ここで、 F(x)=(x−α)(x−β)(x−γ) から、
F’(x)=(x−β)(x−γ)+(x−α)(x−γ)+(x−α)(x−β)
なので、 F’(α)=(α−β)(α−γ) とした方がエレガントかもしれない。そうすると、解と係数の
関係を用いた泥臭い計算は回避される!)
同様にして、 (β−γ)(β−α)=3β2−3(p+q)β+3pq=F’(β)
(γ−α)(γ−β)=3γ2−3(p+q)γ+3pq=F’(γ)
これら3式を辺々掛けると、−(α−β)2(α−γ)2(β−γ)2
=27(α−p)(α−q)(β−p)(β−q)(γ−p)(γ−q)
=27(p−α)(p−β)(p−γ)(q−α)(q−β)(q−γ)
=27F(p)F(q)
以上から、 −D=27E なので、 E=−D/27
また、 −D=F’(α)F’(β)F’(γ)=F なので、 F=−D (終)
当HPがいつもお世話になっているHN「攻略法」さんは、2次の項がない実係数3次方程
式の場合に解かれました。(平成22年10月3日付け)
F(x)=x3+ax+b=0 とする。
●Dの算出・・・実係数3次方程式 F(x)=x3+ax+b=0 の三つの解を、α、β、γ とす
ると、解と係数の関係より、
α+β+γ=0 (ここに値打ちがある!)、αβ+βγ+γα=a
αβγ=−b (ここでは未使用! Fを求めるときに使用する)
よって、β+γ=−α より、 βγ=α2+a なので、
(α−β)(α−γ)=α2−(β+γ)α+βγ=3α2+a となる。
また、(β−γ)2=(β+γ)2−4βγ=−3α2−4a
よって、 D={(α−β)(α−γ)(β−γ)}2=(3α2+a)2(−3α2−4a)
=(9α4+6aα2+a2)(−3α2−4a)=−27α6−54aα4−27a2α2−4a3
=−27α3(α3+aα)−27aα(α3+aα)−4a3
=−27(α3+aα)(α3+aα)−4a3
=−27(−b)(−b)−4a3 ( ∵ F(α)=α3+aα+b=0 )
=−4a3−27b2
(別解) F(x)=x3+ax+b=0 の三つの解 α、β、γ について、
F(x)=(x−α)(x−β)(x−γ) より、
F’(x)=3x2+a=(x−β)(x−γ)+(x−α)(x−γ)+(x−α)(x−β) なので、
F’(α)=3α2+a 、F’(β)=3β2+a 、F’(γ)=3γ2+a の3式を辺々掛けて、
(3α2+a)(3β2+a)(3γ2+a)=−{(α−β)(α−γ)(β−γ)}2=−D
ここで、
左辺=a3+3(α2+β2+γ2)a2+9(α2β2+β2γ2+γ2α2)a+27α2β2γ2
で、また、α2+β2+γ2=(α+β+γ)2−2(αβ+βγ+γα)=−2a
α2β2+β2γ2+γ2α2=(αβ+βγ+γα)2−2αβγ(α+β+γ)=a2
α2β2γ2=b2
なので、 −D=4a3+27b2 すなわち、 D=−4a3−27b2 (終)
●FとDとの関係・・・ F(x)=x3+ax+b より、 F’(x)=3x2+a
このとき、 F’(α)=3α2+a 、F’(β)=3β2+a 、F’(γ)=3γ2+a なので、
F=F’(α)F’(β)F’(γ)=(3α2+a)(3β2+a)(3γ2+a)
=a3+3(α2+β2+γ2)a2+9(α2β2+β2γ2+γ2α2)a+27α2β2γ2
=4a3+27b2=−D
●EとDとの関係・・・F’(x)=3x2+a=0 の二つの解を、p、q とすると、
解と係数の関係より、 p+q=0 、 pq=a/3 なので、
p2+q2=(p+q)2−2pq=−2a/3 、p3+q3=(p+q)3−3pq(p+q)=0
E=F(p)F(q)=(p3+ap+b)(q3+aq+b)
=(p3q3+ap・q3+b・q3)+(ap3・q+a2pq+abq)+(bp3+abp+b2)
=(pq)3+apq(p2+q2)+b(p3+q3)+a2pq+ab(p+q)+b2
=a3/27−2a3/9+a3/3+b2=4a3/27+b2=−D/27
(コメント) 少し計算が遠回りかも...。
私と同様の感想を、FNさんも持たれたようです。(平成22年10月3日付け)
解と係数の関係でやれば、ある程度の計算がいりますが、因数分解でやれば計算はあま
りいりません。
F(x)=(x−α)(x−β)(x−γ) 、 F’(x)=3(x−p)(x−q) と書ける。
また、 F’(x)=(x−β)(x−γ)+(x−α)(x−γ)+(x−α)(x−β)
このとき、 E=F(p)F(q)=(p−α)(p−β)(p−γ)(q−α)(q−β)(q−γ)
=(α−p)(α−q)(β−p)(β−q)(γ−p)(γ−q)
=F’(α)F’(β)F’(γ)/27=F/27
F=F’(α)F’(β)F’(γ)
=(α−β)(α−γ)・(β−α)(β−γ)・(γ−α)(γ−β)
=−(α−β)2(α−γ)2(β−γ)2=−D
よって、 F=−D 、 E=F/27=−D/27
FNさんによれば、n次の場合に一般化すると、F=(−1)n(n-1)/2・D 、 F=nn・E
になるそうです。(FNさんが、多分...と仰っているので、証明はまだなのかな?)
(追記) 平成22年10月4日付け
攻略法さんが一般の3次式の判別式を計算された。
●F(x)=ax3+bx2+cx+d=0 の判別式Dの算出
定義から、 D=a4(α−β)2(β−γ)2(γ−α)2 なので、
D=a4{ (α+β+γ)2(αβ+βγ+αγ)2−4(α+β+γ)3αβγ−4(αβ+βγ+αγ)3
+18(α+β+γ)(αβ+βγ+αγ)αβγ−27(αβγ)2}
=b2c2−4b3d−4ac3+18abcd−27a2d2
となる。(この式の変形は神業だ!)
そこで、この問題の結果 E=−D/(27a2) 、F=−D/a から判別式を導いてみよう。
F(x)=ax3+bx2+cx+d とすると、F’(x)=3ax2+2bx+c となる。
F’(x)=0 の二つの解を、p、q とすると、解と係数の関係より、
p+q=−2b/(3a) 、 pq=c/(3a)
このとき、
E=F(p)F(q)=(ap3+bp2+cp+d)(aq3+bq2+cq+d)
=a2(pq)3+ab(pq)2(p+q)+ac(pq)(p2+q2)+ad(p3+q3)+b2(pq)2
+bc(pq)(p+q)+bd(p2+q2)+c2(pq)+cd(p+q)+d2
=a2(c/(3a))3+ab(c/(3a))2(−2b/(3a))+ac(c/(3a)){(−2b/(3a))2−2c/(3a)}
+ad{(−2b/(3a))3−3c/(3a)・(−2b/(3a))}+b2(c/(3a))2
+bc(c/(3a))(−2b/(3a))+bd{(−2b/(3a))2−2c/(3a)}+c2(c/(3a))
+cd(−2b/(3a))+d2
={ac3−2b2c2+4b2c2−6ac3−8b3d+18abcd+3b2c2−6b2c2+12b3d
−18abcd+9ac3−18abcd+27a2d2}/(27a2)
=(4ac3−b2c2+4b3d−18abcd+27a2d2)/(27a2)
ここで、 E=−D/(27a2) なので、D=b2c2−4b3d−4ac3+18abcd−27a2d2
(コメント) 上記の神業の計算よりも、こちらの方が計算したな〜と実感できますね!
さらに、攻略法さんは、別解を与えられた。
(別解) 終結式(シルベスター行列式)と判別式の関係:R(F,F’)=(−1)n(n-1)/2aD
より
| a b c d 0 |
| 0 a b c d |
| 3a 2b c 0 0 |=(−1){3・(3-1)/2}aD=−aD
| 0 3a 2b c 0 |
| 0 0 3a 2b c |
ここで、左辺の行列式は、1行目で展開して、
a | a b c d |-b| 0 b c d |+c| 0 a c d |-d| 0 a b d |+0
| 2b c 0 0 | | 3a c 0 0 | | 3a 2b 0 0 | | 3a 2b c 0 |
| 3a 2b c 0 | | 0 2b c 0 | | 0 3a c 0 | | 0 3a 2b 0 |
| 0 3a 2b c | | 0 3a 2b c | | 0 0 2b c | | 0 0 3a c |
それぞれを計算する。
a{a| c 0 0 |-b| 2b 0 0 |+c| 2b c 0 |-d| 2b c 0 |}
| 2b c 0 | | 3a c 0 | | 3a 2b 0 | | 3a 2b c |
| 3a 2b c | | 0 2b c | | 0 3a c | | 0 3a 2b |
=a{ac3−2b2c2+4b2c2−3ac3−8b3d+6abcd}=a(−2ac3+2b2c2−8b3d+6abcd)
-b{0-b| 3a 0 0 |+c| 3a c 0 |-d| 3a c 0 |}
| 0 c 0 | | 0 2b 0 | | 0 2b c |
| 0 2b c | | 0 3a c | | 0 3a 2b |
=−b(−3abc2 +6abc2−12ab2d+9a2cd}=a(−3b2c2+12b3d−9abcd)
c{0-a| 3a 0 0 |+c| 3a 2b 0 |-d| 3a 2b 0 |}
| 0 c 0 | | 0 3a 0 | | 0 3a c |
| 0 2b c | | 0 0 c | | 0 0 2b |
=c(−3a2c2+9a2c2−18a2bd)=a(6ac3−18abcd)
-d{0-a| 3a c 0 |+b| 3a 2b 0 |+d| 3a 2b c |}
| 0 2b 0 | | 0 3a 0 | | 0 3a 2b |
| 0 3a c | | 0 0 c | | 0 0 3a |
=−d(−6a2bc+9a2bc+27a3d}=a(3abcd+27a2d2)
したがって、
左辺=a2{(−2ac3+2b2c2−8b3d+6abcd)+(−3b2c2+12b3d−9abcd)
+(6ac3−18abcd)+(3abcd+27a2d2)}
=a2(4ac3−b2c2+4b3d−18abcd+27a2d2)=−aD
なので、 D=b2c2−4b3d−4ac3+18abcd−27a2d2 (終)
上記の計算では、「E=−D/(27a2)」であることが用いられたが、「F=−D/a」を用いても
同様に示される。
F(x)=ax3+bx2+cx+d=0 (a≠0) の三つの解を α 、β 、γ とすると、
解と係数の関係より、α+β+γ=−b/a 、αβ+βγ+γα=c/a 、αβγ=−d/a
このとき、
F=F’(α)F’(β)F’(γ)
=(3aα2+2bα+c)(3aβ2+2bβ+c)(3aγ2+2bγ+c)
=27a3(αβγ)2+6abc{(α+β)γ2+(γ+α)β2+(β+γ)α2}
+12ab2(αβγ)(α+β+γ)+9a2c(α2β2+β2γ2+γ2α2)
+18a2b(αβγ)(αβ+βγ+γα)+8b3(αβγ)+4b2c(αβ+βγ+γα)
+3ac2(α2+β2+γ2)+2bc2(α+β+γ)+c3
ここで、
(α+β)γ2+(γ+α)β2+(β+γ)α2=(α+β+γ)(αβ+βγ+γα)−3αβγ
α2β2+β2γ2+γ2α2=(αβ+βγ+γα)2−2αβγ(α+β+γ)
α2+β2+γ2=(α+β+γ)2−2(αβ+βγ+γα)
なので、解と係数の関係より、
F=(27a2d2−6b2c2+18abcd+12b3d+9ac3−18abcd−18abcd−8b3d
+4b2c2+3b2c2−6ac3−2b2c2+ac3)/a
=(−b2c2+4b3d+4ac3−18abcd+27a2d2)/a
よって、 F=−D/a より、D=b2c2−4b3d−4ac3+18abcd−27a2d2 が得られる。
FNさんからのコメントです。(平成22年10月4日付け)
上記で、「この式の変形は神業だ!」という部分で、私も、この式を計算で出そうとして、と
てもできそうになく、ネットで調べていたら、式Eの形で定義しているページを見つけ、Fと合
わせて問題として提出しました。
そして、EとFの両方を計算しました。計算量は似たようなものでした。ただし、x3 の係数は
「1」でやりました。それを使って一般の場合を出しました。
終結式というのが関係あることにも気づきました。終結式は線形代数とかの本にはよく載っ
ていますが、今まで読んだことはありません。今回はじめてきちんと読みました。
練習問題として次の問題が載ってました。
xn+ax+b の判別式を求めよ。
広島工業大学の大川研究室によれば、上記の答えは、
(−1)r・{(−1)n-1・(n−1)n-1・an+nn・bn-1} 但し、 r=n(n−1)/2
となるそうである。特に、x3+ax+b=0 について、判別式 D=−4a3−27b2 であるが、
これは、上式で、n=3 として得られるものと一致する。また、大川研究室によれば、FN さん
や攻略法さん達が議論している D 、E 、F の関係についても、E、F が D の定数倍となる
ことが分かるので、 F(x)=axn−a 或いは、 F(x)=axn−ax と置いて、「円周上の等分
点の性質」を用いて D、 E、 F を直接計算し、その定数を求めればよいとのことである。
(補足) F(x)の判別式と、F(x)、F’(x)の終結式との関係について、対称式の真実、チルン
ハウス変換、終結式の行列式表現等により出ますが、F(x)が、一般に最高次の係数
が 1 となる多項式とすると、その判別式をDとするなら、DはFの根の n(n−1) 次同
次式になり、a は、n−1 次同次式、b は、n 次同次式となるので、a、b の式で、根の
n(n−1) 次同次式となるのは、n と n−1が互いに素なる事等を用い、簡単な考察に
より、D=p・an+q・bn-1 の形になる事が分かる。
p、q を求める為に、a、b の一方が 0、もう一方が −1 の時に、「円周上の等分点
の性質」を使い、Dを定義から直接計算し、p、q が求まると云う訳です。
(厳密にはもう一寸の考察が必要ですが)
上記で、FNさんや攻略法さん等が面白い事実を活発に議論されているようですが、
それらは高次式の場合に拡張されると思う。n ≦5 の場合は、代数学講義(高木貞
治 著)に載っている。
FNさんからの出題です。(平成23年12月17日付け)
3次方程式の判別式について、高校生向きの計算練習問題です。最後まで間違えずにで
きればかなりの計算力です。
p=a+b+c 、q=ab+bc+ca 、r=abc 、A=ab2+bc2+ca2 、B=a2b+b2c+c2a
S=(a−b)(b−c)(c−a) とする。このとき、
(1) a2+b2+c2 、a2b2+b2c2+c2a2 、a3+b3+c3 、a3b3+b3c3+c3a3 、A+B
AB を、p、q、r で表せ。
(2) S=A−B であることを示し、S2 を、p、q、r で表せ。
これができると、3次方程式 x3+px2+qx+r=0 の判別式が求められたことになります。
この3次方程式の解を、a、b、c とすると、a+b+c=−p 、ab+bc+ca=q 、abc=−r
なので、上記とは、p、r の符号だけ違います。判別式は、(2)のS2 で、pを−pに、rを−rに
置き換えればいいです。結果は、(2)のS2 の式と同じです。
(解)(1) a2+b2+c2=(a+b+c)2−2(ab+bc+ca)=p2−2q
a2b2+b2c2+c2a2=(ab+bc+ca)2−2abc(a+b+c)=q2−2pr
a3+b3+c3=(a+b+c)(a2+b2+c2−ab−bc−ca)+3abc
=p(p2−3q)+3r=p3−3pq+3r
a3b3+b3c3+c3a3=(ab+bc+ca)(a2b2+b2c2+c2a2−abc(a+b+c))+3(abc)2
=q(q2−3pr)+3r2=q3−3pqr+3r2
A+B=ab2+bc2+ca2+a2b+b2c+c2a
=(ab+bc+ca)a+(ab+bc+ca)b+(ab+bc+ca)c−3abc
=(a+b+c)(ab+bc+ca)−3abc=pq−3r
AB=(ab2+bc2+ca2)(a2b+b2c+c2a)
=bca4+c3a3+a3b3+3(abc)2+abc(b3+c3)+b3c3
=abc(a3+b3+c3)+a3b3+b3c3+c3a3+3(abc)2
=r(p3−3pq+3r)+q3−3pqr+3r2+3r2=p3r−6pqr+q3+9r2
(2) A−B=ab2+bc2+ca2−a2b−b2c−c2a=(c−b)a2+(b2−c2)a+bc(c−b)
=(c−b)(a2−(b+c)a+bc)=(c−b)(a−b)(a−c)=(a−b)(b−c)(c−a)
=S
このとき、 S2=(A−B)2
=(A+B)2−4AB
=(pq−3r)2−4(p3r−6pqr+q3+9r2)
=p2q2−6pqr+9r2−4p3r+24pqr−4q3−36r2
=−4p3r+p2q2+18pqr−4q3−27r2 (終)
問題 X3−TX2+(T−3)X+1 の判別式が (T2−3T+9)2 となることを示せ。(J.P.Serre)
※ J.P.Serre:Oeuvres collected papers p.173を参照。
これを背景とした入試問題(上智大等)など、極めて色々引用されている。
X3 - TX2+(T - 3)X+1 が X の多項式として既約となる有理数 T は無限に存在する。より一
般に、二変数有理係数既約多項式 F (X,t) が与えられた時、これが X の多項式として既約
となる有理数 t は無限に存在する。(ヒルベルトの既約性定理)
(解) 公式に代入して、
D=T2(T−3)2+4T3−4(T−3)3−18T(T−3)−27
=T4−6T3+27T2−54T+81
=(T2−3T)2+18(T2−3T)+81=(T2−3T+9)2 (終)
(追記) 終結式と判別式と基本対称式と題して、当HPがいつもお世話になっているHN「GAI」
さんからご投稿いただいた。(平成27年8月24日付け)
終結式は、何か判別式と関係があったなという記憶ぐらいしかなかったので、終結式と判別
式と基本対称式の関係の変化を、改めて計算機を使って見ていたら、終結式(R)と判決式(D)
が、次数によって微妙に変化していくことに気がついた。改めて調べたら、ちゃんとn次式では、
a・D=(-1)n(n-1)/2・R(f,f’)
と書いてある。
(1) 2次関数 F2[x]=ax2+bx+c では、 Resultant[F2[x],F’2[x]]= -a・D[F2[x]]= -ab2+4a2c
基本対称式での表現 D=s12-4s2
(2) 3次関数 F3[x]= ax3 + bx2 + cx + d では、
Resultant[F3[x],F’3[x]]=-a・D[F3[x]]= -ab2c2 + 4a2c3 + 4ab3d - 18a2bcd + 27a3d2
基本対称式での表現 D=s12e22 - 4s23 - 4s13s3 + 18s1s2s3 - 27s32
(3) 4次関数 F4[x]= ax4 + bx3 + cx2 + dx + e では、
Resultant[F4[x],F’4[x]]=a・D[F4[x]]
=ab2c2d2 - 4a2c3d2 - 4ab3d3 + 18a2bcd3 - 27a3d4 - 4ab2c3e + 16a2c4e
+ 18ab3cde - 80a2bc2de - 6a2b2d2e + 144a3cd2e - 27ab4e2
+ 144a2b2ce2 - 128a3c2e2 - 192a3bde2 + 256a4e3
基本対称式での表現
D=s12s22s32 - 4s23s32 - 4s13s33 + 18s1s2s33 - 27s34 - 4s12s23s4 + 16s24s4
+ 18s13s2s3s4 - 80s1s22s3s4 - 6s12s32s4 + 144s2s32s4 - 27s14s42
+ 144s12s2s42 - 128s22s42 - 192s1s3s42 + 256s43
(4) 5次関数 F5[x]= ax5 + bx4 + cx3 + dx2 + ex + f では、
Resultant[F5[x],F’5[x]]=a・D[F5[x]]
(5) 6次関数 F6[x]= ax6 + bx5 + cx4 + dx3 + ex2 + fx + g では、
Resultant[F6[x],F’6[x]]=a・D[F6[x]]
・・・・・・・・・・・
このように関数 f が、
2、3、6、7、10、11、・・・・次関数では、 a・D=-R(f,f’)
4,5,8,9,12,13,・・・・次関数では、 a・D=+R(f,f’)
一般に、n次関数なら、 a・D=(-1)n(n-1)/2・R(f,f’) となることに初めて気がついた。
(→ 参考:「対称式の真実」)
以下、工事中