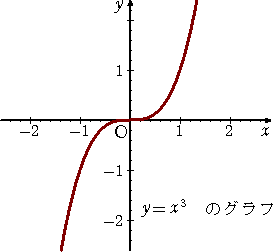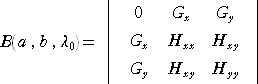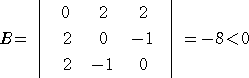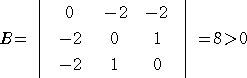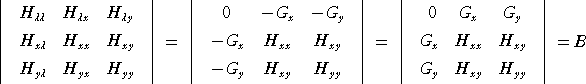儔僌儔儞僕儏偺忔悢丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 丂
丂
丂嬌戝丒嬌彫偼丄儘乕僇儖側堄枴偱偺嵟戝丒嵟彫偱偁傞丅偦偺掕媊偵偼摫娭悢偺尵梩偼梡
偄傜傟側偄丅丂俀曄悢娭悢偺応崌偵偮偄偰丄偦偺掕媊傪妋擣偟偰偍偙偆丅
丂楢懕娭悢丂倸 亖 俥乮倶 丆倷乯 偺乮倎 丆倐乯偵嬤偄揰乮倶 丆倷乯 偵偍偄偰丄忢偵
丂丂丂丂丂丂丂丂丂丂丂 俥乮倶 丆倷乯亜俥乮倎 丆倐乯
偑惉傝棫偮偲偒丄娭悢 倸亖俥乮倶 丆倷乯 偼丄乮倎 丆倐乯 偱嬌彫偲偄偄丄俥乮倎 丆倐 乯 偑嬌彫抣偱偁傞丅
摨條偵丄楢懕娭悢 倸亖俥乮倶 丆倷乯 偺 乮倎 丆倐乯 偵嬤偄揰 乮倶 丆倷乯 偵偍偄偰丄忢偵
丂丂丂丂丂丂丂丂丂丂丂 俥乮倶 丆倷乯亙俥乮倎 丆倐乯
偑惉傝棫偮偲偒丄娭悢 倸亖俥乮倶 丆倷乯 偼丄乮倎 丆倐 乯 偱嬌戝偲偄偄丄俥乮倎 丆倐 乯 偑嬌戝抣偱偁傞丅
丂嬌彫抣偲嬌戝抣傪傑偲傔偰丄嬌抣偲偄偆丅
丂侾曄悢娭悢 倷亖俥乮倶乯 偑旝暘壜擻偱偁傞偲偒丄俥乮倶乯 偑 倶亖倎 偱嬌抣傪帩偰偽丄
俥乫乮倎乯 亖 侽 偑惉傝棫偮丅丂
丂偙傟偼丄暯嬒抣偺掕棟偐傜丄娙扨偵帵偝傟傞丅
丂侾曄悢娭悢偺応崌偲摨條偵丄俀曄悢娭悢偵偮偄偰傕丄師偺帠幚偑惉傝棫偮丅
丂楢懕娭悢丂倸亖俥乮倶 丆倷乯 偑曃旝暘偱偒傞偲偒丄乮倎 丆倐乯偱嬌抣傪帩偰偽丄
丂丂丂丂丂丂丂 俥倶乮倎 丆倐乯亖侽丂丄俥倷乮倎 丆倐乯亖侽
偑惉傝棫偮丅
丂忋婰偼丄偁偔傑偱傕嬌抣傪帩偮偨傔偺昁梫忦審偱偁偭偰廫暘忦審偱偼側偄丅
椺丂丂俥乮倶乯亖倶3 偵偍偄偰丄俥乫乮倶乯亖 俁倶2 亖 侽丂傛傝丄倶 亖 侽
丂丂偟偐傞偵丄丂倶 亖 侽丂偱偼嬌抣傪帩偪摼側偄丅
丂幚嵺偵丄丂俥乭乮 倶 乯亖俇倶 側偺偱丄俥乮 倶 乯亅俥乮 侽 乯亖乮侾/俀乯俥乭乮 倛倶 乯亖俁倛倶丂乮侽亙倛亙侾乯
丂倶亖侽 偺嬤偔偱丄俥乮倶乯亅俥乮侽乯 偺晞崋偑掕傑傜側偄偺偱丄嬌抣傪帩偮偲偼尵偊側偄丅
乮暿夝丗丂俥乮 倶 乯 亖 倶3丂偺僌儔僼傪彂偗偽柧傜偐偩傠偆丅乯
丂丂丂丂丂丂丂
椺丂丂俥乮倶 丆倷乯亖倷2亅倶2 偵偍偄偰丄俥倶乮倶 丆倷 乯亖亅俀倶丂丄俥倷乮倶 丆倷 乯亖俀倷
丂丂乮侽 丆侽乯 偵偍偄偰丄俥倶乮侽 丆侽乯亖侽丂丄俥倷乮侽 丆侽乯亖侽 偱偁傞偑丄乮侽 丆侽乯偱偼嬌抣傪帩偪
丂摼側偄丅
丂丂幚嵺偵丄俥倶倶乮倶 丆倷乯亖亅俀丂丄俥倶倷乮倶 丆倷乯亖侽 丂丄俥倷倷乮倶 丆倷乯亖俀 偱丄
丂丂丂丂丂俥乮倛 丆倠乯亅 俥乮侽 丆侽乯 亖 乮1/2乯乮亅俀倛2亄俀倠2乯
丂傛偭偰丄乮侽 丆侽乯 偺嬤偔偱丄俥乮倛 丆倠乯亅 俥乮侽 丆侽乯 偺晞崋偑掕傑傜側偄偺偱丄嬌抣傪帩偮
偲偼尵偊側偄丅
丂丂乮暿夝丗丂俥乮 倶 丆 倷 乯 亖 倷2 亅 倶2丂偺僌儔僼傪彂偗偽柧傜偐偩傠偆丅乯
丂丂丂丂丂丂丂
丂偟偨偑偭偰丄曃旝暘偱偒傞揰偱偺嬌抣傪扵偡偵偼丄忋幃傪枮偨偡 乮倎 丆倐 乯 傪媮傔偰丄廫暘
惈傪妋擣偡傞昁梫偑偁傞丅
丂侾曄悢娭悢偵偍偗傞嬌戝丒嬌彫偺敾掕忦審偲偟偰丄師偺帠幚偼桳梡偱偁傞丅
丂侾曄悢娭悢 倷亖俥乮倶乯 偑旝暘壜擻丄偐偮丄倶亖倎 偱嬌抣傪傕偮偲偒丄
丂丂俥乭乮倎乯亜侽丂側傜偽丄倶亖倎丂偱嬌彫 丄俥乭乮倎乯亙侽丂側傜偽丄倶亖倎丂偱嬌戝
丂偙傟偼丄俀師偺嬤帡幃 俥乮倶乯亅俥乮倎乯 佮 乮侾/俀乯俥乭乮倎乯 傛傝丄柧傜偐偱偁傠偆丅
偙偺偙偲偐傜丄戞俀師摫娭悢偺晞崋傪寁嶼偡傞偙偲偵傛傝丄嬌戝丒嬌彫偑敾掕偱偒傞丅
丂俀曄悢娭悢偵偮偄偰傕摨條偵丄師偺岞幃偑抦傜傟偰偄傞丅
岞幃丂丂娭悢 倸亖俥乮倶 丆倷乯 偑楢懕側戞俀師曃摫娭悢傪帩偪丄
丂丂丂丂 俥倶乮倎 丆倐乯亖侽丂丄 俥倷乮倎 丆倐乯亖侽丂偲偡傞丅
丂丂傑偨丄丂俙亖 俥倶倶乮倎 丆倐乯丂丄俛亖 俥倶倷乮倎 丆倐乯丂丄俠亖 俥倷倷乮倎 丆倐乯丂偲偍偔丅
丂丂偙偺偲偒丄丂丂俙俠亅俛2亜侽丂偱丄俙亜侽丂側傜偽丄乮倎 丆倐乯 偱嬌彫
丂丂丂丂丂丂丂丂丂丂俙俠亅俛2亜侽丂偱丄俙亙侽丂側傜偽丄乮倎 丆倐乯 偱嬌戝
丂丂丂丂丂丂丂丂丂丂俙俠亅俛2亖侽丂偺偲偒偼丄偝傜偵徻偟偔惛嵏偑昁梫
丂丂丂丂丂丂丂丂丂丂俙俠亅俛2亙侽丂偺偲偒偼丄嬌抣偵偼側傜側偄
丂徹柧偼丄俿倎倷倢倧倰 偺掕棟傪梡偄偰梕堈偵帵偝傟傞丅
乮棯徹乯丂儮倸亖 俥乮倎亄倛 丆倐亄倠乯亅 俥乮倎 丆倐乯
丂丂亖乮1/2乯乮俥倶倶乮倎亄兤倛丆倐亄兤倠乯倛2亄俀俥倶倷乮倎亄兤倛丆倐亄兤倠乯倛倠亄 俥倷倷乮倎亄兤倛丆倐亄兤倠乯倠2乯
丂娭悢丂倸亖俥乮倶 丆倷乯 偑楢懕側戞俀師曃摫娭悢傪帩偮偺偱丄倛丄倠 偑廫暘彫偝偄偲偒丄
俥倶倶乮倎亄兤倛 丆倐亄兤倠乯丄俥倶倷乮倎亄兤倛 丆倐亄兤倠乯丄俥倷倷乮倎亄兤倛 丆倐亄兤倠乯 偺晞崋偼丄偦傟
偧傟 俙丄俛丄俠 偺晞崋偵摍偟偄丅偦偙偱丄倛丄倠 偑廫暘彫偝偄偲偒丄
丂丂丂儮倸丂偺晞崋偼丄乮1/2乯乮俙倛2亄俀俛倛倠亄俠倠2乯丂偺晞崋偵摍偟偄丅
丂偙偙偱丄俙倛2亄俀俛倛倠亄俠倠2亖俙乮乮倛亄乮俛/俙乯倠乯2亄乮俙俠亅俛2乯倠2/俙2乯丂傛傝丄忋婰偺
岞幃偺惉傝棫偮偙偲偑妋擣偝傟傞丅乮棯徹廔乯
丂偙偙偱丄娭悢 俥乮倶 丆倷乯 偵懳偟偰丄師偺峴楍
丂丂丂丂丂丂丂丂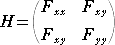
傪丄乮倎 丆倐乯 偵偍偗傞僿僢僙峴楍偲偄偆丅忋婰偺掕棟偺 俙俠亅俛2 偼丄俫偺峴楍幃偵摍偟偄丅
丂丂丂丂丂丂丂丂丂俙俠亅俛2 亖 倓倕倲 俫亖乮俫偺屌桳抣偺愊乯
丂傑偨丄 倛丄倠 偑廫暘彫偝偄偲偒丄俥乮倎亄倛 丆倐亄倠乯亅俥乮倎 丆倐乯 佮 乮侾/俀乯俫乵倶乶
丂偙偙偱丄俫乵倶乶偼丄俫傪學悢峴楍偲偡傞擇師宍幃偱丄倶 偼丄倛丄倠 傪惉暘偲偡傞楍儀僋僩儖丅
丂幚懳徧峴楍 俫 偺屌桳抣丂兩丂丄兪丂偼偡傋偰幚悢偱丄揔摉側嵗昗曄姺偵傛傝丄
丂丂丂丂丂丂丂丂丂俫乵倶乶亖兩倱2亄兪倲2
偲彂偗傞丅丂偙偙偱丄
丂偡傋偰偺 倶 乮亗侽乯 偵懳偟偰丄俫乵倶乶亜侽丂偑側傝偨偮偲偒丄丂俫 偼丄惓抣偱偁傞偲偄偆丅
丂丂乮偙偺偨傔偵偼丄俫 偺屌桳抣丂兩丂丄兪丂偼偡傋偰惓偱側偗傟偽側傜側偄丅乯
丂偡傋偰偺 倶 乮亗侽乯 偵懳偟偰丄俫乵倶乶亙侽丂偑側傝偨偮偲偒丄丂俫 偼丄晧抣偱偁傞偲偄偆丅
丂丂乮偙偺偨傔偵偼丄俫 偺屌桳抣丂兩丂丄兪丂偼偡傋偰晧偱側偗傟偽側傜側偄丅乯
傛偭偰丄嬌戝丒嬌彫偺敾掕忦審偲偟偰丄擇師宍幃偺尵梩傪梡偄傟偽丄
丂丂丂俫偑惓抣側傜偽丄嬌抣傪帩偮丂丄丂俫偑晧抣側傜偽丄埪揰偱嬌抣傪帩偨側偄
偲偄偆偙偲偵側傞丅
乮僐儊儞僩丗丂嬌抣偺廫暘惈偺妋擣偺棟榑揑攚宨偵丄擇師宍幃偺棟榑偑棈傫偱偔傞傢偗偱丄
丂丂丂丂丂丂丂壗偐柺敀偦偆丏丏丏側梊姶両丂偨偩丄峴楍偺屌桳曽掱幃傪夝偔偺偑擄偟偄偺偱丄
丂丂丂丂丂丂丂屌桳抣傪棙梡偡傞偺偼丄偁傑傝丄尰幚揑側曽朄偱偼側偄偐側丠乯
丂岞幃傪丄嬶懱揑側栤戣偵揔梡偟偰傒傛偆丅
椺丂敿媴懱丂倶2亄倷2亄倸2亖侾丂乮倸亞侽乯偵偍偄偰丄倶亄倸倸倶亖侽丄倷亄倸倸倷亖侽丂側偺偱丄
丂丂倸倶亖倸倷亖侽丂偲側傞偺偼丄乮 倶 丆 倷 乯亖乮 侽 丆 侽 乯丂偺応崌偺傒偱偁傞丅
丂丂丂偙偺偲偒丄
丂丂丂丂丂丂丂丂丂侾亄倸倶2亄倸倸倶倶亖侽丂丄丂倸倷倸倶亄倸倸倶倷亖侽丂丄丂侾亄倸倷2亄倸倸倷倷亖侽
丂丂傛傝丄丂俙亖亅侾丂丄俛亖侽丂丄俠亖亅侾丂側偺偱丄
丂丂丂丂俙俠亅俛2亖侾亜侽丂丄俙亙侽丂傛傝丄乮 侽 丆 侽 乯偱嬌戝偲側傞丅
丂丂偙傟偼丄妋偐偵敿媴懱偺恾宍揑僀儊乕僕偲堦抳偟偰偄傞丅
丂丂丂丂丂丂丂丂丂
丂撉幰偺偨傔偵丄墘廗栤戣傪偁偘偰偍偙偆丅
楙廗栤戣丂丂暯柺忋偵丄値 屄偺揰 俙1乮倎1丆倐1乯丄俙2乮倎2丆倐2乯丄丒丒丒丄俙値乮倎値丆倐値乯偑梌偊傜
丂丂丂丂丂丂丂傟偰偄傞丅偙偺偲偒丄偙傟傜偺揰偐傜偺嫍棧偺暯曽偺榓偑嬌彫乮偐偮嵟彫乯偵
丂丂丂丂丂丂丂側傞揰偺嵗昗傪媮傔傛丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮偙偺揰偼丄値 屄偺揰 俙1丄俙2丄丒丒丒丄俙値 偺廳怱偲偄傢傟傞丅乯
忦審晅嬌抣栤戣丂丂嬌戝丒嬌彫傪峫偊傞応崌丄壗傜偐偺忦審偑偮偄偰偄傞応崌偑懡偄丅
椺丂倶亄倷亄倸亖俁丂偺偲偒丄倶倷倸 偺嬌抣傪媮傔傛丅
丂乮夝乯丂俥乮倶 丆倷乯亖倶倷乮俁亅倶亅倷乯丂偲偍偔丅
丂丂丂丂俥倶乮倶 丆倷乯亖俁倷亅俀倶倷亅倷2亖倷乮俁亅俀倶亅倷乯亖侽
丂丂丂丂俥倷乮倶 丆倷乯亖俁倶亅俀倶倷亅倶2亖倶乮俁亅俀倷亅倶乯亖侽
丂
丂丂丂偙傟傪夝偔偲丄乮倶 丆倷乯亖乮 侽 丆侽 乯丄乮 侽 丆 俁 乯丄乮 俁 丆 侽 乯丄乮 侾 丆 侾 乯
丂丂傑偨丄俥倶倶乮倶 丆倷乯亖亅俀倷丂丄俥倶倷乮倶 丆倷乯亖俁亅俀倶亅俀倷丂丄俥倷倷乮倶 丆倷乯亖亅俀倶 側偺偱丄
丂乮倶 丆倷乯亖乮 侽 丆侽 乯丄乮 侽 丆 俁 乯丄乮 俁 丆 侽 乯偵懳偟偰丄
俥倶倶乮倶 丆倷乯俥倷倷乮倶 丆倷乯亅乮俥倶倷乮倶 丆倷乯乯2亖亅俋亙侽丂偱丄岞幃偵傛傝丄嬌抣傪梌偊側偄丅
丂乮倶 丆倷乯亖乮 侾 丆 侾 乯偵懳偟偰丄
俥倶倶乮侾 丆侾乯俥倷倷乮侾 丆侾乯亅乮俥倶倷乮侾 丆侾乯乯2亖乮亅俀乯乮亅俀乯亅乮亅侾乯2亖俁亜侽丂偱丄
俥倶倶乮侾 丆侾乯亖亅俀亙侽丂側偺偱丄嬌戝抣傪梌偊傞丅
乮僐儊儞僩乯丂掕宍奜梄曋暔偺嵟戝偺僒僀僘偼丄乮廲乯亄乮墶乯亄乮崅偝乯亖俋侽們倣偱偁傞丅偙偺偲
丂丂丂丂丂丂偒丄懱愊偺嵟戝偼偄偔傜偐偲偄偆栤偄偵忋婰偺栤戣偼摎偊偰偔傟傞丅摉慠丄侾曈偺
丂丂丂丂丂丂挿偝偑俁侽們倣偺偲偒丄懱愊偼嵟戝偲側傞丅
丂婔壗妛揑偵嬌抣偺懚嵼偑暘偐偭偰偄傞応崌丄師偺丂俴倎倗倰倎値倗倕 偺枹掕忔悢朄偑曋棙
偱偁傞丅
俴倎倗倰倎値倗倕 偺枹掕忔悢朄乮枹掕學悢朄乯
丂忦審丂俧乮倶 丆倷 丆倸乯亖侽丂偺偲偒丄娭悢丂俥乮倶 丆倷 丆倸乯 偺嬌抣偑偁傟偽丄偦傟偼丄師偺傛偆
偵偟偰媮傔傜傟傞丅
丂楢棫曽掱幃丂俧亖侽丂丄俥倶亄兩俧倶亖侽丂丄俥倷亄兩俧倷亖侽丂丄俥倸亄兩俧倸亖侽
傪夝偔偲丄偦偺夝 乮倎 丆倐 丆們乯偑丄嬌抣傪梌偊傞岓曗偲側傞丅
丂丂乮 拲 乯丂娭悢 俫乮 倶 丆 倷 丆 倸 丆 兩 乯亖俥亄兩俧丂偲峫偊傟偽丄忋婰偺係幃偼丄
丂丂丂丂丂俫倶亖侽丂丄俫倷亖侽丂丄俫倸亖侽丂丄俫兩亖侽丂偲偄偆偙偲偱丄忦審偺晅偐側偄晛捠偺
丂丂丂丂嬌抣偺寁嶼栤戣偵抲偒姺偊傜傟傞丅
丂偙偺偲偒偺丄兩 偺偙偲傪丄俴倎倗倰倎値倗倕 偺忔悢偲偄偆丅
丂幚嵺偵丄俧乮倶 丆倷 丆倸乯亖侽丂偺偲偒丄乮倎 丆倐 丆們乯偱丄娭悢 俥乮倶 丆倷 丆倸乯 偺嬌抣傪梌偊偰偄傞
傕偺偲偡傞丅偙偺偲偒丄俧乮倶 丆倷 丆倸乯亖侽 偐傜丄倸 偑 倶 丆 倷 偺娭悢偵側偭偰偄傞偲偡傞偲丄娭悢
俥 偼丄倶 丆倷 偺娭悢偵側傞偺偱丄乮倎 丆倐 丆們乯偵偍偄偰丄
丂丂丂丂丂丂俥倶亄俥倸丒倸倶亖侽丂丄丂俥倷亄俥倸丒倸倷亖侽
偑惉傝棫偮丅偙偙偱丄倸倶丄倸倷 偼丄師偺幃偵傛傝梌偊傜傟傞丅
丂丂丂丂丂丂俧倶亄俧倸丒倸倶亖侽丂丄丂俧倷亄俧倸丒倸倷亖侽
偦偙偱丄乮倎 丆倐 丆們乯偵偍偗傞 亅俥倸/俧倸 偺抣傪丄兩 偲偍偔偲丄俥倸亄兩俧倸亖侽丂偑惉傝棫偪丄
偝傜偵丄俥倶亄兩俧倶亖侽丂丄丂俥倷亄兩俧倷亖侽丂偑惉傝棫偮丅
丂偟偨偑偭偰丄係偮偺幃丂俧亖侽丂丄俥倶亄兩俧倶亖侽丂丄俥倷亄兩俧倷亖侽丂丄俥倸亄兩俧倸亖侽丂傪夝偔偙偲
偵傛傝丄嬌抣傪梌偊傞岓曗偺揰乮倎 丆倐 丆們乯偑媮傔傜傟傞丅
丂忋婰偺幃偼丄師偺傛偆偵峫偊偰傕摼傞偙偲偑偱偒傞丅
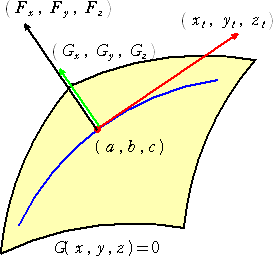 |
丂丂俧乮倶 丆倷 丆倸 乯亖侽丂偱掕傑傞嬋柺忋偵偍偄偰丄
丂丂乮倎 丆倐 丆們乯傪捠傞擟堄偺嬋慄俠傪峫偊傞丅
丂丂俠 丗丂倃亖倃乮倲乯丂丄倄亖倄乮倲乯丂丄倅亖倅乮倲乯
丂丂偙偺偲偒丄乮倎 丆倐 丆們乯偱嬌抣傪帩偮偙偲偐傜丄
丂丂俥倶倃倲亄俥y倄倲亄俥倸倅倲亖侽丂偑惉傝棫偮丅
丂丂傛偭偰丄俀偮偺儀僋僩儖丂
丂丂丂乮俥倶丆俥y丆俥倸乯丂偲丂乮倃倲丆倄倲丆倅倲乯丂
丂偼悅捈偱偁傞丅
|
丂偟偨偑偭偰丄儀僋僩儖丂乮俥倶丆俥y丆俥倸乯偼丄嬋柺偺乮倎 丆倐 丆們乯偵偍偗傞愙暯柺偺朄慄儀僋僩儖
乮俧倶丆俧y丆俧倸乯偵暯峴偱偁傞丅
丂傛偭偰丄丂乮俥倶丆俥y丆俥倸乯亄兩乮俧倶丆俧y丆俧倸乯亖侽丂偲側傞 兩 偑懚嵼偡傞丅
丂丂乮 拲 乯丂俴倎倗倰倎値倗倕 偺枹掕忔悢朄傪梡偄傞応崌丄俧乮倶 丆倷 丆倸乯亖侽 偺岡攝儀僋僩儖
丂丂丂丂丂丂丂丂丂丂丂乮 俧倶 丆 俧倷 丆 俧倸 )
丂丂丂丂丂丂偑楇儀僋僩儖偱偼側偄偲偄偆偙偲傪妋擣偡傞昁梫偑偁傞丅
丂丂丂丂椺丂乮俀曄悢娭悢偺応崌乯
丂丂丂丂丂俧乮 倶 丆 倷 乯亖倶2亅倷3亖侽丂偺偲偒偺娭悢 俥乮 倶 丆 倷 乯亖倷丂偺嬌抣傪峫偊傞丅
丂丂丂丂丂丂丂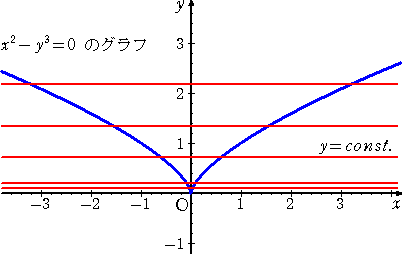
丂丂丂丂忋婰偺僌儔僼偐傜傕暘偐傞傛偆偵丄娭悢 俥乮 倶 丆 倷 乯 偼丄揰乮 侽 丆 侽 乯偱嬌彫偱偁傞丅
丂丂丂偟偐偟側偑傜丄偙偺応崌丄俴倎倗倰倎値倗倕 偺忔悢偼掕傑傜側偄丅
丂丂丂丂幚嵺偵丄揰乮侽丆侽乯偵偍偄偰丄俧倶 亖俀倶亖侽丄俧倷 亖亅俁倷2亖侽丄俥倶 亖侽丄俥倷亖侾丂側偺
丂丂丂偱丄俴倎倗倰倎値倗倕 偺忔悢偼堦堄偵掕傑傜側偄丅
丂丂丂岡攝儀僋僩儖偑楇儀僋僩儖偺偲偒偼丄俴倎倗倰倎値倗倕 偺枹掕忔悢朄偼巊偊側偄偺偱丄暿側峫
丂丂嶡偑昁梫偲側傞丅乮忋婰偺椺偵偮偄偰偼丄峀搰岺嬈戝妛偺戝愳尋媶幒傛傝偄偨偩偒傑偟偨丅乯
丂丂丂乮捛婰乯丂暯惉俀俇擭俀寧侾係擔晅偗偱丄搚昅偺巕偝傫偐傜偺僐儊儞僩偱偡丅
丂丂丂丂丂俽乮俫乯偝傫偺栤戣偵傕傛偔搊応偡傞丄儔僌儔儞僕儏偺枹掕忔悢朄偵偮偄偰偱偡丅偨偄
丂丂丂丂偰偄丄摢偐傜幃偑帵偝傟偰丄兩傪偙偆巊偊偽丄偁傞忦審幃偺壓偱丄嵟戝嵟彫栤戣偑夝
丂丂丂丂偗傞偲彂偄偰偁傞偺偱偡偑丄埲壓偺夝愢偱傛偔傢偐傝傑偟偨丅
丂丂丂丂丂曻憲戝妛島巘偺孎尨孾嶌丂挊丂乽懡曄悢偺旝暘愊暘妛乿偺戞侾俆復丄P62 偱弌夛偭偨丄
丂丂丂丂儔僌儔儞僕儏偺枹掕忔悢朄偺偙偲偑丄偄傑傂偲偮敾慠偲偟側偐偭偨偺偱偡偑丄
丂丂丂丂丂丂丂俤丏僴僀儔乕/俧丏償傽儞僫乕挊丄奍峕岾攷栿丂乽夝愅嫵掱丂壓乿
丂丂丂丂偺p丏180乣p丏183偺婰弎偱敾慠偲偟傑偟偨丅
丂丂丂g(x丆y)=0丂偲偄偆懇敍偺傕偲偱丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂娭悢f(x丆y)偺嬊強嵟戝抣乮傑偨偼嵟彫抣乯傪媮傔側偝偄丅
丂丂丂g偺儗儀儖廤崌傪丄A={(x丆y)|g(x丆y)=0}丂偲彂偗偽丄栤戣偼丄
丂丂丂丂丂(x丆y)伕A偵懳偟偰丄f(x丆y)亝f(x0丆y0)偲側傞(x0丆y0)伕A傪媮傔側偝偄丅
丂丂丂偲偄偆偙偲偵側傞丅乮拞棯乯 gradf(x0丆y0)偑儗儀儖嬋慄A偺愙儀僋僩儖(x乫(t0)丆y乫(t0))偲捈
丂丂丂岎偟偰偄傞偙偲偑暘偐傞偺偱丄嬊強揑側嬌抣偱偼丄俀偮偺儀僋僩儖
丂丂丂丂丂丂丂丂grad f(x0丆y0)丂偲丂grad g(x0丆y0)
丂丂丂偼摨偠曽岦傪帩偭偰偄傞丅偙偺偙偲偱丄昁梫忦審
丂丂丂丂丂grad f(x0丆y0)=兩丒grad g(x0丆y0)丂丒丒丒丂(*)丂丂傑偨偼丄丂g(x0丆y0)=0
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂(gradf(x0丆y0)亗0乯
丂丂丂偑摼傜傟傑偡丅偙偺僷儔儊乕僞兩傪儔僌儔儞僕儏偺忔悢偲尵偄傑偡丅
丂丂丂曽掱幃(*)偼丄俁偮偺僷儔儊乕僞 x0丆y0丆兩 偵懳偡傞俁偮偺忦審傪昞偟偰偄傑偡丅
丂丂丂俴(x丆y丆兩):=f(x丆y)-兩g(x丆y)丂傪峫偊傞偲丄grad 俴(x0丆y0丆兩)=0丂偲昞偝傟傑偡丅
丂丂丂偡側傢偪丄丂Lx(x丆y丆兩)=0丂丄L倷(x丆y丆兩)=0丂丄L兩(x丆y丆兩)=0
丂丂丂場傒偵丄乮拞棯乯偺側偐偱丄(佪f/佪x)(x0丆y0)*x乫(t0)+(佪f/佪y)(x0丆y0)*y乫(t0)=0
丂丂丂儔僌儔儞僕儏偺枹掕忔悢朄偺偙偲偑塸暥偱婰嵹偝傟偰偄傞丅
丂偄偔偮偐偺椺戣偵懳偟偰幚嵺偵丄俴倎倗倰倎値倗倕 偺枹掕忔悢朄傪揔梡偟偰傒傛偆丅
椺戣侾丂倶亄倷亖俀丂偺偲偒丄倶2亄倷2丂偺嬌抣傪媮傔傛丅
乮夝乯丂俧乮 倶 丆 倷 乯亖倶亄倷亅俀亖侽丂偺偲偒丄
丂丂丂俥乮 倶 丆 倷 乯亖倶2亄倷2丂偺嬌抣傪梌偊傞揰乮 倎 丆 倐 乯偼師偺幃傪枮偨偡丅
丂丂丂丂丂丂倶亄倷亅俀亖侽丂丄俀倶亄兩亖侽丂丄俀倷亄兩亖侽
丂丂丂傛偭偰丄丂亅兩/俀亅兩/俀亅俀亖侽丂傛傝丄兩亖亅俀
丂丂偙偺偲偒丄丂乮 倶 丆 倷 乯亖乮 侾 丆侾 乯丂偑嬌抣傪梌偊傞岓曗偱偁傞丅
丂丂丂婔壗妛揑偵峫偊偰丄乮 侾 丆侾 乯偵偍偄偰丄倶2亄倷2丂偼嬌彫偐偮嵟彫偱偁傞丅
丂丂嬌彫抣乮嵟彫抣乯偼丄俀丂偱偁傞丅
丂忋婰偺夝偲丄師偺暿夝傪惀旕斾妑偟偰傒偰壓偝偄丅俴倎倗倰倎値倗倕 偺枹掕忔悢朄偺僄儗僈儞
僩偝偑僸僔僸僔偲揱傢偭偰偔傞偙偲偱偟傚偆丅
乮暿夝乯丂倶2亄倷2亖倶2亄乮俀亅倶乯2亖俀倶2亅係倶亄係亖俀乮倶亅侾乯2亄俀丂傛傝丄倶亖倷亖侾丂偺偲偒丄
丂丂丂丂丂嬌彫偱丄嬌彫抣偼丄俀
丂俴倎倗倰倎値倗倕 偺枹掕忔悢朄偼丄曄悢偑偄偔偮偁偭偰傕丄忦審偑偄偔偮偁偭偰傕乮仼傕偪傠傫
曄悢偺屄悢傛傝偼彮側偄両乯巊偊傞偲偙傠偑慺惏傜偟偄丅
椺戣俀丂倶亄倷亄倸亖俁丂偺偲偒丄倶2亄倷2亄倸2丂偺嬌抣傪媮傔傛丅
乮夝乯丂俧乮 倶 丆 倷 丆 倸 乯亖倶亄倷亄倸亅俁亖侽丂偺偲偒丄
丂丂丂俥乮 倶 丆 倷 丆 倸 乯亖倶2亄倷2亄倸2丂偺嬌抣傪梌偊傞揰乮 倎 丆 倐 丆 們 乯偼師偺幃傪枮偨偡丅
丂丂丂丂丂丂倶亄倷亄倸亅俁亖侽丂丄俀倶亄兩亖侽丂丄俀倷亄兩亖侽丂丄俀倸亄兩亖侽
丂丂丂傛偭偰丄丂亅兩/俀亅兩/俀亅兩/俀亅俁亖侽丂傛傝丄兩亖亅俀
丂丂偙偺偲偒丄丂乮 倶 丆 倷 丆 倸 乯亖乮 侾 丆 侾 丆 侾 乯丂偑嬌抣傪梌偊傞岓曗偱偁傞丅
丂丂丂婔壗妛揑偵峫偊偰丄乮 侾 丆 侾 丆 侾 乯偵偍偄偰丄倶2亄倷2亄倸2丂偼嬌彫偐偮嵟彫偱偁傞丅
丂丂嬌彫抣乮嵟彫抣乯偼丄俁丂偱偁傞丅
乮暿夝乯丂倶2亄倷2亄倸2亖倶2亄倷2亄乮俁亅倶亅倷乯2
丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖俀倶2亄俀倶倷亄俀倷2亅俇倶亅俇倷亄俋
丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖俀乮倶亄乮倷亅俁乯/俀乯2亄乮3/2乯乮倷亅侾乯2亄俁
丂丂丂丂丂傛傝丄倶亖倷亖倸亖侾丂偺偲偒丄嬌彫偱丄嬌彫抣偼丄俁
丂栤戣偑丄係曄悢偵側傞偲丄乮暿夝乯偺傛偆側曽朄偼乽偡偛偔戝曄偵側傞側乣乿偲梊憐偝傟傞偑丄
俴倎倗倰倎値倗倕 偺枹掕忔悢朄偺曽偼丄慡偔夝摎宍幃傪曄偊傞偙偲側偔娙柧偵媮傔傜傟傞丅
丂変乆偼丄偙偺夝朄傪梌偊偰偔傟偨 俴倎倗倰倎値倗倕 偵戝偄偵姶幱偟側偗傟偽側傜側偄偱偡偹両
椺戣俁丂倶2亄倷2亄倸2亖係丂偺偲偒丄倶倷倸丂偺嬌抣傪媮傔傛丅偨偩偟丄倶 丆 倷 丆 倸 亞侽丂偲偡傞丅
丂偙偺栤戣偺婔壗妛揑堄枴偼丄乽敿宎 侾 偺媴偵撪愙偡傞捈曽懱偺懱愊偺嬌抣傪媮傔傞乿
偲偄偆偙偲偱丄柧傜偐偵嬌戝抣偺懚嵼偑偄偊傞丅偙偺偙偲傪摜傑偊偰丄俴倎倗倰倎値倗倕
偺枹掕忔
悢朄傪揔梡偡傞偺偱偁傞丅
乮傕偪傠傫丄倶2亄倷2亄倸2亖係丂傪枮偨偡揰乮 倶 丆 倷 丆 倸 乯偺廤崌偼丄俼3 偺桳奅暵廤崌偩偐
丂傜丄僐儞僷僋僩丅傛偭偰丄楢懕娭悢 倶倷倸丂偼丄嵟戝抣丒嵟彫抣傪傕偮偙偲偐傜傕嬌抣偺懚嵼
丂偼椆夝偝傟傞丅乯
丂乮夝乯丂俧乮 倶 丆 倷 丆 倸 乯亖倶2亄倷2亄倸2亅係亖侽丂偺偲偒丄
丂丂丂 俥乮 倶 丆 倷 丆 倸 乯亖倶倷倸丂偺嬌抣傪梌偊傞揰乮 倎 丆 倐 丆 們
乯偼師偺幃傪枮偨偡丅
丂丂丂丂丂倶2亄倷2亄倸2亅係亖侽丂丄倷倸亄俀兩倶亖侽丂丄倶倸亄俀兩倷亖侽丂丄倶倷亄俀兩倸亖侽
丂丂丂戞擇幃丄戞嶰幃丄戞巐幃偐傜丄丂俁倶倷倸亄俀兩乮倶2亄倷2亄倸2乯亖侽
丂丂丂丂偡側傢偪丄丂俁倶倷倸亄俉兩亖侽丂傛傝丄兩亖亅乮3/8乯倶倷倸丂偲側傞丅
丂丂丂偙偺偲偒丄
丂丂丂丂丂倷倸乮侾亅乮3/4乯倶2乯亖侽丂丄倶倸乮侾亅乮3/4乯倷2乯亖侽丂丄倶倷乮侾亅乮3/4乯倸2乯亖侽
丂丂偙傟傪夝偔偲丄
丂乮 倶 丆 倷丆 倸 乯亖乮 俀 丆侽 丆侽 乯丄乮 侽 丆俀 丆侽 乯丄乮 侽 丆侽
丆俀 乯丄乮 俀/ 丆俀/
丆俀/ 丆俀/
丆俀/ 乯
乯
婔壗妛揑偵峫偊偰丄乮 倶 丆 倷丆 倸 乯亖乮 俀/ 丆俀/
丆俀/ 丆俀/
丆俀/ 乯偱丄嬌戝偐偮嵟戝偱偁傞丅
乯偱丄嬌戝偐偮嵟戝偱偁傞丅
嬌戝抣乮嵟戝抣乯偼丄俉/乮俁 乯丂偱偁傞丅
乯丂偱偁傞丅
乮捛婰乯丂暯惉侾俇擭侾俀寧敪攧偺悢妛僙儈僫乕乮俀侽侽俆擭侾寧崋乯偵偍偄偰丄俴倎倗倰倎値倗倕
偺枹
丂丂丂丂丂掕忔悢朄偺榖戣偑庢傝忋偘傜傟偰偄傞丅
丂丂丂丂丂丂乮摉俫俹偱庢傝忋偘偨偲偒偲帪傪摨偠偔偟偰悢妛僙儈僫乕偱徯夘偝傟偨偲偄偆偙偲偱丄
丂丂丂丂丂丂丂偪傚偭偲偙偺嬼慠惈偵嬃偄偰偄傑偡丅乯
丂乮捛婰乯丂暯惉俀侽擭侾侾寧侾擔晅偗
丂丂摉俫俹偺宖帵斅乽弌夛偄偺愹乿偵俁侾擔晅偗偱俫俶乽俢丏俢丏乿偝傫偑忦審晅偒嬌抣栤戣偵偮
丂偄偰彂偒崬傑傟偨丅
丂丂俧乮 倶 丆 倷 乯亖倶2亄倷2亅侾亖侽丂偲偄偆忦審偺傕偲偱丄娭悢俥乮 倶 丆 倷 乯亖倶倷 偺嬌抣
丂傪媮傔偨偄偺偩偑丄儔僌儔儞僕儏偺忔悢朄傪梡偄丄嬌抣偺敾掕傪偡傞偲偄偆堦楢偺嶌
丂嬈偑偳偆傕忋庤偔弌棃側偄丅
丂丂忋婰偺栤戣偵丄 乽倶亞侽 丄 倷亞侽乿 偲偄偆忦審傪壛枴偡傟偽丄偙偺栤戣偼丄
丂丂丂尨揰拞怱丄敿宎侾偺墌偵撪愙偡傞挿曽宍偺柺愊偺曄壔傪栤偆
丂偙偲偵摍偟偔丄婔壗妛揑偵峫偊偰柧傜偐偵嬌抣傪帩偮偙偲偑椆夝偝傟傞丅
丂丂扨偵嬌抣傪媮傔傞偩偗偩偭偨傜丄師偺傛偆偵夝偗偽傛偄丅
丂乮夝乯丂倶2亄倷2亖侾丂傛傝丄丂倶亖們倧倱兤丄倷亖倱倝値兤丂偲偍偗傞丅偙偺偲偒丄
丂丂丂倶倷亖倱倝値兤們倧倱兤亖(侾/俀)倱倝値俀兤丂偲彂偗傞偺偱丄
丂丂丂丂丂俀兤亖俀値兾亄兾/俀丂偡側傢偪丄丂兤亖値兾亄兾/係丂偺偲偒嬌戝
丂丂丂丂丂俀兤亖乮俀値亄侾乯兾亄兾/俀丂偡側傢偪丄丂兤亖値兾亄俁兾/係丂偺偲偒嬌彫丂丂丂乮廔乯
丂丂丂丂僌儔僼偱昞偣偽壓恾偺傛偆偵側傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂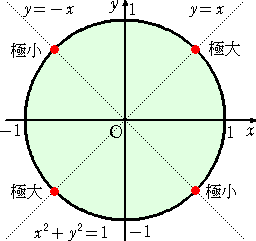
丂丂忋婰偱偼攠夘曄悢昞帵傪梡偄偰嶰妏娭悢偺僌儔僼偐傜嬌抣傪峫嶡偟偨偑丄師偺傛偆偵媮
丂傔傞曽朄偑偁傞偙偲傪俽乮俫乯條傛傝巉偭偨丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮摉俫俹偺宖帵斅乽弌夛偄偺愹乿亅暯惉俀侽擭侾侽寧俁侾擔晅偗乯
丂丂丂乮夝乯丂墌 倶2亄倷2亖侾丂偲憃嬋慄 倶倷亖倠丂偑岎傢傞偨傔偺忦審傪媮傔傟偽傛偄丅
丂丂丂丂倷亖倠/倶丂傪丄倶2亄倷2亖侾丂偵戙擖偟偰惍棟偡傞偲丄丂倶4亅倶2亄倠2亖侽丂
丂丂丂丂倶2亖倃丂偲偍偔偲丄丂倃亞侽丂偱丄俀師曽掱幃丂倃2亅倃亄倠2亖侽丂傪摼傞丅
丂丂丂丂丂墌偲憃嬋慄偑岎傢傞偨傔偵偼丄偙偺俀師曽掱幃偑彮側偔偲傕侾偮偺晧偱側偄幚悢
丂丂丂丂夝傪帩偮偙偲偑昁梫廫暘偱偁傞丅
丂丂丂丂丂俀師娭悢 倄亖倃2亅倃亄倠2丂偺幉偺曽掱幃偑丄丂倃亖侾/俀亜侽丂側偺偱丄媮傔傞忦審
丂丂丂丂偼丄敾暿幃 俢亞侽丂偵摨抣偱偁傞丅
丂丂丂丂丂傛偭偰丄丂俢亖侾亅係倠2亞侽丂偐傜丄丂亅侾/俀 亝 倠 亝 侾/俀丂偲側傞丅
丂丂丂丂丂丂丂丂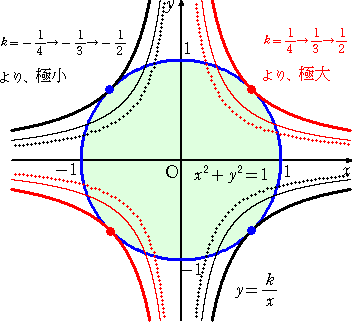
丂丂丂丂丂忋恾偐傜暘偐傞傛偆偵丄
丂丂丂丂丂丂丂倠亖侾/俀丂偺偲偒丄嬌戝偐偮嵟戝偱丄倠亖亅侾/俀丂偺偲偒丄嬌彫偐偮嵟彫偱偁傞丅
丂丂丂丂丂師偵丄嬌抣傪梌偊傞揰傪媮傔傞丅
丂丂丂丂丂丂丂倠亖亇侾/俀丂偺偲偒丄丂倃2亅倃亄侾/係亖侽丂偐傜丄丂倃亖侾/俀
丂丂丂丂丂偡側傢偪丄丂倶亖亇侾/ 丂偲側傞丅
丂偲側傞丅
丂丂丂丂傛偭偰丄丂倠亖侾/俀丂偺偲偒丄乮 倶 丆 倷 乯亖乮 侾/ 丆侾/
丆侾/ 乯丄乮 亅侾/
乯丄乮 亅侾/ 丆亅侾/
丆亅侾/ 乯
乯
丂丂丂丂傑偨丄丂倠亖亅侾/俀丂偺偲偒丄乮 倶 丆 倷 乯亖乮 侾/ 丆亅侾/
丆亅侾/ 乯丄乮 亅侾/
乯丄乮 亅侾/ 丆侾/
丆侾/ 乯
乯
丂丂丂丂丂埲忋偑媮傔傞傕偺偱偁偭偨丅丂乮廔乯
丂丂丂丂乮僐儊儞僩乯丂椉幰偺夝摎傪斾妑偡傟偽丄嶰妏娭悢傪梡偄偨曽偑偡偙傇傞娙柧偩傠偆丅
丂丂丂丂丂傑偨丄師偺傛偆側夝摎傕壜擻偱偁傞丅乮俽乮俫乯條傛傝丄偛嫵帵偄偨偩偒傑偟偨丅乯
丂丂丂丂丂丂倶2亄倷2亖侾丂傛傝丄丂 丂側偺偱丄
丂側偺偱丄 偺抣偺曄壔傪挷
偺抣偺曄壔傪挷
丂丂丂丂丂傋傟偽傛偄丅偙偺僌儔僼傪昤偔偲丄
丂丂丂丂丂丂丂丂丂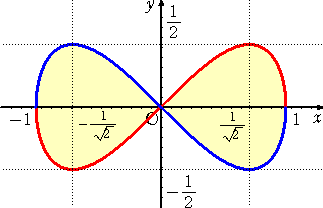
丂丂丂丂丂偙偺恾偐傜丄嬌戝揰丄嬌彫揰偑峫嶡偱偒傞丅
丂丂丂丂丂偨偩丄偙傟傜偺夝摎偱偼丄俢丏俢丏偝傫偺擸傒偵偼摎偊偰偄側偄傛偆側丏丏丏梊姶丅
丂丂丂丂儔僌儔儞僕儏偺枹掕忔悢朄傪梡偄偰忋婰偺栤戣傪夝偄偰傒傞偙偲偵偟傛偆丅
丂丂丂丂丂丂俥倶亄兩俧倶亖倷亄俀兩倶亖侽丂丄俥倷亄兩俧倷亖倶亄俀兩倷亖侽丂偐傜兩傪徚嫀偟偰丄
丂丂丂丂 倶2亅倷2亖侽丂丂乮仼丂僔儖儀僗僞乕偺徚嫀朄偵傛傞両乯丂傪摼傞丅
丂丂丂丂丂傑偨丄丂倶2亄倷2亖侾丂側偺偱丄偙傟傜傪楢棫偟偰夝偔偲丄
丂丂丂丂丂丂丂乮 倶 丆 倷 乯亖乮 侾/ 丆侾/
丆侾/ 乯丄乮 侾/
乯丄乮 侾/ 丆亅侾/
丆亅侾/ 乯丄
乯丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮 亅侾/ 丆侾/
丆侾/ 乯丄乮 亅侾/
乯丄乮 亅侾/ 丆亅侾/
丆亅侾/ 乯
乯
丂丂丂丂偲側傞丅偙偺係揰偑嬌抣傪梌偊傞岓曗偲側傞丅
丂丂丂丂丂乽倶亞侽 丄 倷亞侽乿 偲偄偆忦審偱偼丄婔壗妛揑偵峫偊偰柧傜偐偵嬌戝抣傪帩偮偺偱丄
丂丂丂丂乮 倶 丆 倷 乯亖乮 侾/ 丆侾/
丆侾/ 乯偱丄丂俥乮 倶 丆 倷
乯亖倶倷丂偼嬌戝偱偁傞丅
乯偱丄丂俥乮 倶 丆 倷
乯亖倶倷丂偼嬌戝偱偁傞丅
丂丂丂丂傑偨丄乽倶亝侽 丄 倷亝侽乿 偲偄偆忦審偼丄乽亅倶亞侽 丄亅 倷亞侽乿
偲偄偆忦審偵摨抣偱丄
丂丂丂丂丂倶倷亖(亅倶)(亅倷)丂傛傝丄乮 倶 丆 倷 乯亖乮 亅侾/ 丆亅侾/
丆亅侾/ 乯偱丄丂俥乮 倶 丆 倷 乯亖倶倷
乯偱丄丂俥乮 倶 丆 倷 乯亖倶倷
丂丂丂丂偼嬌戝偱偁傞丅
丂丂丂丂傑偨丄乽倶亞侽 丄 倷亝侽乿 偲偄偆忦審偼丄乽倶亞侽 丄亅 倷亞侽乿
偲偄偆忦審偵摨抣偱丄
丂丂丂丂倶乮亅倷乯偑嬌戝偱偁傞偲偒丄倶倷 偼嬌彫偲側傞丅
丂丂丂丂丂偟偨偑偭偰丄乮 倶 丆 倷 乯亖乮 侾/ 丆亅侾/
丆亅侾/ 乯偱丄俥乮 倶 丆 倷 乯亖倶倷丂偼嬌彫偲側傞丅
乯偱丄俥乮 倶 丆 倷 乯亖倶倷丂偼嬌彫偲側傞丅
丂丂丂丂摨條偵偟偰丄乽倶亝侽 丄 倷亞侽乿 偲偄偆忦審偼丄乽亅倶亞侽 丄 倷亞侽乿偲偄偆忦審偵摨抣偱丄
丂丂丂丂乮亅倶乯倷 偑嬌戝偱偁傞偲偒丄倶倷 偼嬌彫偲側傞丅
丂丂丂丂丂偟偨偑偭偰丄乮 倶 丆 倷 乯亖乮 亅侾/ 丆侾/
丆侾/ 乯偱丄 俥乮 倶 丆 倷 乯亖倶倷丂偼嬌彫偲側傞丅
乯偱丄 俥乮 倶 丆 倷 乯亖倶倷丂偼嬌彫偲側傞丅
丂丂丂丂乮僐儊儞僩乯丂忋婰偺寁嶼偱丄俢丏俢丏偝傫偺幙栤偺夞摎偵側偭偰偄傞偐偳偆偐丏丏丏丠
丂丂丂丂丂丂丂丂丂乮媣偟傇傝偵儔僌儔儞僕儏偺忔悢朄偺寁嶼傪偟偨偺偱尒摉堘偄偑偁傞偐傕両乯
丂丂廃偺挿偝偑 俇 偺嶰妏宍偱柺愊偑嵟戝偱偁傞傕偺傪媮傔傞偲偄偆栤戣傪峫偊傞丅
丂俴倎倗倰倎値倗倕 偺枹掕忔悢朄乮戝妛侾擭偺旝暘愊暘妛偺儗儀儖乯傪梡偄傞偲師偺傛偆偵慛傗偐
偵夝偐傟傞丅
椺戣係丂俁曈偺挿偝丂倶 丆 倷 丆 倸丂偺嶰妏宍偵偍偄偰丄丂倶 亄 倷 亄 倸 亖俇丂偺偲偒丄
丂丂丂丂俁(俁亅倶 )(俁亅倷 )(俁亅倸 )丂偑嵟戝偲側傞偺偼丄偳傫側応崌偐丠
丂仈俁(俁亅倶 )(俁亅倷 )(俁亅倸 )偺堄枴偼丄僿儘儞偺岞幃偐傜乮嶰妏宍偺柺愊乯2偱偁傞丅
乮夝乯丂俧乮 倶 丆 倷 丆 倸 乯亖倶 亄 倷 亄 倸 亅俇亖侽丂偺偲偒丄
丂丂丂 俥乮 倶 丆 倷 丆 倸 乯亖俁(俁亅倶 )(俁亅倷 )(俁亅倸 )丂偺嬌抣傪梌偊傞揰乮 倎 丆 倐 丆 們 乯偼師偺
丂丂丂幃傪枮偨偡丅
丂丂丂丂倶 亄 倷 亄 倸 亅俇亖侽丂丄亅俁(俁亅倷 )(俁亅倸 )亄兩亖侽丂丄亅俁(俁亅倶 )(俁亅倸 )亄兩亖侽
丂丂丂丂亅俁(俁亅倶 )(俁亅倷 )亄兩亖侽
丂丂丂倶 亗 俁丂丄倷 亗 俁丂丄倸 亗 俁丂偲偟偰傛偄偺偱丄忋幃偐傜丄倶 亖 倷 亖 倸 亖俀丂丄兩亖俁丂偱
丂丂丂偁傞偙偲偑梕堈偵暘偐傞丅
丂丂丂丂婔壗妛揑偵峫偊偰丄倶 亖 倷 亖 倸 亖俀丂偡側傢偪丄惓嶰妏宍偺偲偒丄柺愊偼嬌戝偐偮
丂丂丂嵟戝偲側傞丅
椺戣俆丂尨揰偐傜暯柺 倎倶亄倐倷亄們倸亄倓亖侽傑偱偺嫍棧傪媮傔傛丅
丂仈倶2亄倷2亄倸2偺嵟彫抣傪媮傔傞偙偲偵摨媊偱偁傞丅捠忢偼儀僋僩儖傪棙梡偡傞夝朄偑堦
丂丂斒揑偩傠偆丅
乮夝乯丂俧乮 倶 丆 倷 丆 倸 乯亖倎倶亄倐倷亄們倸亄倓亖侽丂偺偲偒丄
丂丂丂 俥乮 倶 丆 倷 丆 倸 乯亖倶2亄倷2亄倸2 偺嬌抣傪梌偊傞揰偼師偺幃傪枮偨偡丅
丂丂丂丂倎倶亄倐倷亄們倸亄倓亖侽丂丄俀倶亄兩倎亖侽丂丄俀倷亄兩倐亖侽丂丄俀倸亄兩們亖侽
丂丂丂偙偺偲偒丄丂俀乮倶2亄倷2亄倸2乯亄兩乮倎倶亄倐倷亄們倸乯亖侽丂偐傜丄倶2亄倷2亄倸2亖兩倓/俀
丂丂丂傑偨丄俀乮倎倶亄倐倷亄們倸乯亄兩乮倎2亄倐2亄們2乯亖侽丂傛傝丄兩亖俀倓/乮倎2亄倐2亄們2乯
丂丂丂丂婔壗妛揑偵峫偊偰丄倶2亄倷2亄倸2 偺嵟彫抣偼丄倓2/乮倎2亄倐2亄們2乯
丂丂丂傛偭偰丄媮傔傞嫍棧偼丄丂乥倓乥/併乮倎2亄倐2亄們2乯丂偱偁傞丅
乮捛乆婰乯丂俴倎倗倰倎値倗倕 偺枹掕忔悢朄偼丄偁偔傑偱傕嬌抣傪梌偊傞岓曗傪嫵偊偰偼偔傟傞偑丄
丂丂丂丂丂丂偦傟偑杮摉偵嬌抣傪梌偊傞偐偳偆偐偵偮偄偰偼丄壗傜嫵偊偰偼偔傟側偄丅
丂丂丂丂丂丂丂偟偨偑偭偰丄俴倎倗倰倎値倗倕 偺枹掕忔悢朄偼丄壗傜偐偺曽嶔偵傛傝丄嬌抣偺懚嵼偑
丂丂丂丂丂丂敾柧偟偰偄傞応崌偵桳岠偱偁傞丅
丂丂丂丂丂丂丂摉俫俹偱傕丄偦偺庯巪傪嵟戝尷桳岠棙梡偟丄乽婔壗妛揑偵峫偊偰乿偲偄偆昞尰偱丄
丂丂丂丂丂丂廫暘惈偺妋擣傪擋傢偣偰偒偨丅
丂丂丂丂丂丂丂偟偐偟丄偙偺偙偲偼丄傗偼傝丄偳偙偐偟傜婥帩偪偑埆偄丅偟偭偔傝偙側偄偺偱偁傞丅
丂丂丂丂丂丂偙偺婥暘偼丄忋婰偺尨峞傪彂偄偰偄傞偲偒偵忢偵摢偺曅嬿偵嫃嵗偭偨丅
丂丂丂丂丂丂丂偙偺審偵娭偟偰丄峀搰岺嬈戝妛偺戝愳尋媶幒傛傝傾僪僶僀僗傪捀懻偟偨丅偄偨
丂丂丂丂丂丂偩偄偨傾僪僶僀僗傪嶲峫偵偟側偑傜丄乽婔壗妛揑偵峫偊偰乿偱偼側偔丄夝愅揑側庤
丂丂丂丂丂丂朄偱丄廫暘惈偺妋擣傪峴偭偰傒偨偄丅
椺戣俇丂倶倷亖係丂偺偲偒丄俀倶亄俀倷丂偺嬌抣傪媮傔傛丅
丂乮夝乯丂俧乮 倶 丆 倷 乯亖倶倷亅係亖侽丂偺偲偒丄
丂丂丂丂丂俥乮 倶 丆 倷 乯亖 俀倶亄俀倷丂偺嬌抣傪梌偊傞揰乮 倎 丆 倐 乯偼師偺幃傪枮偨偡丅
丂丂丂丂丂丂丂丂丂丂俀亄兩倷亖侽丂丄俀亄兩倶亖侽丂丄倶倷亅係亖侽
丂丂丂丂丂丂傛偭偰丄兩2倶倷亖係丂丄倶倷亖係丂傛傝丄兩2亖侾丂偲側偭偰丄兩亖亇侾
丂丂丂丂丂偙偺偲偒丄丂乮 倎 丆 倐 乯亖乮 俀 丆 俀 乯丂丄乮 亅俀 丆 亅俀
乯
丂丂丂丂丂丂偄傑丄乮 倎 丆 倐 乯亖乮 俀 丆 俀 乯偵偮偄偰嬦枴偡傞丅
丂丂丂丂丂俧乮 俀亄倛 丆 俀亄倠 乯亖侽丂傪枮偨偡傛偆側 倛 丆 倠 傪峫偊傞偲丄
倛倠 亙 侽丂偱偁傞丅
丂丂丂丂丂側偤側傜偽丄丂倷亖係/倶丂偵偍偄偰丄倷乫亖亅係/倶2 亙侽丂傛傝丄扨挷尭彮娭悢偩偐傜
丂丂丂丂丂偱偁傞丅
丂丂丂丂丂丂偙偺偲偒丄俧乮 俀亄倛 丆俀亄倠 乯亖乮俀亄倛)( 俀亄倠乯亅係亖俀乮倛亄倠乯亄倛倠亖侽丂傛傝丄
丂丂丂丂丂俀乮倛亄倠乯亖亅倛倠丂偑惉傝棫偮丅
丂丂丂丂丂丂傛偭偰丄乮 俀 丆 俀 乯 偵嬤偄揰 乮 俀亄倛 丆 俀亄倠 乯 偵偍偄偰丄忢偵
丂丂丂丂丂丂丂丂俥乮 俀亄倛 丆 俀亄倠 乯亅俥乮 俀 丆 俀 乯亖俀乮倛亄倠乯亖亅倛倠亜侽
丂丂丂丂丂偑惉傝棫偮偺偱丄揰乮 俀 丆 俀 乯偵偍偄偰丄嬌彫偱偁傞偙偲偑暘偐傞丅
丂丂丂丂丂丂師偵丄乮 倎 丆 倐 乯亖乮 亅俀 丆 亅俀 乯偵偮偄偰嬦枴偡傞丅
丂丂丂丂丂俧乮 亅俀亄倛 丆 亅俀亄倠 乯亖侽丂傪枮偨偡傛偆側 倛 丆 倠 傪峫偊傞偲丄忋婰偲摨條偺
丂丂丂丂丂棟桼偐傜丄倛倠 亙 侽丂偱偁傞丅
丂丂丂丂丂丂偙偺偲偒丄俧乮 亅俀亄倛 丆亅俀亄倠 乯亖乮亅俀亄倛)( 亅俀亄倠乯亅係
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖亅俀乮倛亄倠乯亄倛倠
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖侽
丂丂丂丂丂傛傝丄丂俀乮倛亄倠乯 亖 倛倠丂偑惉傝棫偮丅
丂丂丂丂丂丂傛偭偰丄乮 亅俀 丆 亅俀 乯 偵嬤偄揰 乮 亅俀亄倛 丆 亅俀亄倠 乯 偵偍偄偰丄忢偵
丂丂丂丂丂丂丂丂俥乮 亅俀亄倛 丆 亅俀亄倠 乯亅俥乮 亅俀 丆 亅俀 乯亖俀乮倛亄倠乯
亖 倛倠亙侽
丂丂丂丂丂偑惉傝棫偮偺偱丄揰乮 亅俀 丆 亅俀 乯偵偍偄偰丄嬌戝偱偁傞偙偲偑暘偐傞丅
丂忋婰偺夝摎乮屻敿晹暘乯偼丄嬌抣偺掕媊偵棫偪曉偭偨徹柧偱暘偐傝傗偡偄偑丄僗儅乕僩
偝偵寚偗傞丅偟偐傕丄堿娭悢傪梲娭悢偵捈偟偰丄偦偺摫娭悢偺惈幙傪棙梡偟偰偄傞揰偑堦
斒揑偱側偄傛偆偵巚偆丅
丂嬌抣傪帩偮偨傔偺廫暘惈偺妋擣偲偟偰丄師偺帠幚偑抦傜傟偰偄傞丅丂
丂乮宑滀媊弇戝妛彜妛晹夝愅嘦乮俀侽侽俁乯偵偍偗傞楙廗栤戣偺夝摎傪嶲峫偵偝偣偰偄偨偩偒傑偟偨丅乯
丂忦審 俧乮倶 丆倷乯亖侽 偺傕偲偱丄娭悢 俥乮倶 丆倷乯 偺嬌抣偵偮偄偰峫偊傞丅
娭悢 俫乮倶 丆倷 丆兩乯亖俥亅兩俧丂偲偍偒丄丂俫倶亖侽丂丄俫倷亖侽丂丄俫兩亖侽丂傪枮偨偡揰傪
乮倎 丆倐 丆兩0乯 偲偍偔丅
丂偙偺偲偒丄師偺峴楍幃 俛 傪丄 乮倎 丆倐 丆兩0乯偱偺 墢晅偒峴楍幃 偲偄偆丅
丂丂丂丂丂丂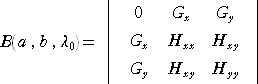
丂傕偟丄丂俛亙侽丂側傜偽丄娭悢丂俥乮倶 丆倷 乯 偼丄揰乮倎 丆倐乯偱嬌彫
丂丂丂丂丂俛亜侽丂側傜偽丄娭悢丂俥乮倶 丆倷乯 偼丄揰乮倎 丆倐乯偱嬌戝
丂忋婰偺椺戣俇偵憗懍揔梡偟偰傒傛偆丅
丂俧乮倶 丆倷乯亖倶倷亅係亖侽丂丄俥乮倶 丆倷乯亖 俀倶亄俀倷丂傛傝丄
丂丂丂俫乮倶 丆倷 丆兩乯亖俥乮倶 丆倷乯亅兩俧乮倶 丆倷乯亖 俀倶亄俀倷亅兩乮倶倷亅係乯
俴倎倗倰倎値倗倕 偺枹掕忔悢朄偵傛傝丄
丂丂丂丂丂丂丂丂丂丂俀亅兩倷亖侽丂丄俀亅兩倶亖侽丂丄倶倷亅係亖侽
丂丂丂丂丂丂傛偭偰丄兩2倶倷亖係丂丄倶倷亖係丂傛傝丄兩2亖侾丂偲側偭偰丄兩亖亇侾
丂丂丂丂丂偙偺偲偒丄丂乮倎 丆倐 丆兩乯亖乮俀 丆俀 丆侾乯丂丄乮亅俀 丆亅俀 丆亅侾乯
偙偙偱丄
丂丂丂丂丂丂俧倶亖倷丂丄俧倷亖倶丂丄俫倶亖俀亅兩倷丂丄俫倷亖俀亅兩倶
丂丂丂丂丂丂丂丂丂俫倶倶 亖 侽丂丄俫倶倷 亖 亅兩丂丄俫倷倷 亖 侽
偱偁傞偙偲偵拲堄偟偰丄揰乮俀 丆俀 丆侾乯偱偺墢晅偒峴楍幃 俛 偺抣偼丄
丂丂丂丂丂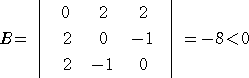
傛偭偰丄丂娭悢 俥乮倶 丆倷乯丂偼丄揰乮俀 丆俀乯偱嬌彫偲側傞丅乮愭偺寢壥偲堦抳両乯
摨條偵偟偰丄揰乮亅俀 丆亅俀 丆亅侾乯偱偺墢晅偒峴楍幃 俛 偺抣偼丄
丂丂丂丂丂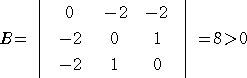
傛偭偰丄丂娭悢 俥乮倶 丆倷乯丂偼丄揰乮亅俀 丆亅俀乯偱嬌戝偲側傞丅乮愭偺寢壥偲堦抳両乯
丂傑偨丄師偺傛偆側帠幚傕抦傜傟偰偄傞傜偟偄丅
丂乮峀搰岺嬈戝妛丂戝愳尋媶幒傛傝偄偨偩偒傑偟偨丅偁傝偑偲偆偛偞偄傑偡丅乯
丂忦審 俧乮倶 丆倷乯亖侽丂偺偲偒丄揰乮倎 丆倐乯偼丄娭悢 俥乮倶 丆倷乯 偺嬌抣傪梌偊傞岓曗偲偡
傞丅丂偨偩偟丄乮俧倶 丆俧倷乯亗乮侽 丆侽乯 偲偡傞丅
丂偝傜偵丄娭悢 俫乮倶 丆倷 丆兩乯亖俥亅兩俧丂偲偍偒丄侾奒曃旝暘嶌梡慺 俢 傪丄
丂丂丂丂丂丂
偵傛傝掕傔傞丅偙偺偲偒丄揰乮倎 丆倐乯偵偍偄偰丄
丂丂丂丂丂丂俢2俥亜侽丂偺偲偒丄娭悢丂俥乮倶 丆倷乯 偼丄揰乮倎 丆倐乯偱嬌彫
丂丂丂丂丂丂俢2俥亙侽丂偺偲偒丄娭悢丂俥乮倶 丆倷乯 偼丄揰乮倎 丆倐乯偱嬌戝
乮拲堄乯丂俧乮 倶 丆 倷 乯丂偑堦斒偺擇師幃偺応崌丄婔壗妛揑偵敾掕偡傞偙偲偑擄偟偄応崌偑
丂丂丂丂丂偁傞偑丄乮 俧倶 丆 俧倷 乯 亗 乮 侽 丆 侽 乯偲偄偆忦審偝偊僋儕傾偡傟偽丄昁偢丄偙偺岞幃
丂丂丂丂丂偱丄嬌抣傪傕偮偐偳偆偐偼敾掕偱偒傞偲偺偙偲偱偁傞丅
丂丂丂丂丂丂偨偩偟丄俥乮 倶 丆 倷 乯亖俥乮 倎 丆 倐 乯 偲 俧乮 倶 丆 倷
乯亖侽 偑崅師偺愙怗傪偟偰偄傞応
丂丂丂丂丂崌乮 椺偊偽丄俧乮 倶 丆 倷 乯 亖 侽 偑丄摍崅慄 俥乮 倶 丆 倷 乯 亖 俥乮 倎 丆 倐 乯偺嬋棪墌 乯
丂丂丂丂丂偼丄偝傜偵丄俢3俥丄俢4俥丂偺寁嶼偑昁梫偵側傞偦偆偩丅
丂忋婰偺椺戣俇偵憗懍揔梡偟偰傒傛偆丅
丂俧乮 倶 丆 倷 乯亖倶倷亅係亖侽丂丄俥乮 倶 丆 倷 乯亖 俀倶亄俀倷丂傛傝丄
丂丂丂俫乮 倶 丆 倷 丆兩 乯亖俥乮 倶 丆 倷 乯亅兩俧乮 倶 丆 倷 乯亖 俀倶亄俀倷亅兩乮倶倷亅係乯
俴倎倗倰倎値倗倕 偺枹掕忔悢朄偵傛傝丄
丂丂丂丂丂丂丂丂丂丂俀亅兩倷亖侽丂丄俀亅兩倶亖侽丂丄倶倷亅係亖侽
丂丂丂丂丂丂傛偭偰丄兩2倶倷亖係丂丄倶倷亖係丂傛傝丄兩2亖侾丂偲側偭偰丄兩亖亇侾
丂丂丂丂丂偙偺偲偒丄丂乮 倎 丆 倐 丆兩 乯亖乮 俀 丆 俀 丆 侾 乯丂丄乮 亅俀
丆 亅俀 丆 亅侾 乯
偙偙偱丄
丂丂丂丂丂丂俧倶亖倷丂丄俧倷亖倶丂丄俥倶亖俀丂丄俥倷亖俀
偙偺偲偒丄丂俢俥亖俧倷俥倶亅俧倶俥倷亖俀倶亅俀倷丂側偺偱丄
丂丂丂丂丂丂丂俢2俥亖俢乮俢俥乯亖俀倶亅倷乮亅俀乯亖俀倶亄俀倷
丂丂丂丂丂丂揰乮 俀 丆 俀 乯偵偍偄偰丄俢2俥亖俉亜侽丂偲側傞偺偱丄嬌彫偱偁傞丅
丂丂丂丂丂丂揰乮 亅俀 丆 亅俀 乯偵偍偄偰丄俢2俥亖亅俉亙侽丂偲側傞偺偱丄嬌戝偱偁傞丅
乮僐儊儞僩丗寁嶼検偑偙偪傜偺曽偑彮側偔偰丄偄偄偱偡偹両乯
丂偲偙傠偱丄忋婰偱偁偘偨俀偮偺岞幃偼丄堦尒偟偰柍娭學偦偆偵尒偊傞偑丄幚偼椉幰偼枾愙
偵娭學偟偰偄傞偙偲偑師偺寁嶼偐傜暘偐傞丅
丂幚嵺偵丄峴楍幃偺惈幙偐傜丄
俛亖亅俧倶乮俧倶俫倷倷亅俧倷俫倶倷乯亄俧倷乮俧倶俫倶倷亅俧倷俫倶倶乯
丂亖亅俧倶乮俧倶乮俥倷倷亅兩俧倷倷乯亅俧倷乮俥倶倷亅兩俧倶倷乯乯亄俧倷乮俧倶乮俥倶倷亅兩俧倶倷乯亅俧倷乮俥倶倶亅兩俧倶倶乯乯
丂亖亅俧倶2俥倷倷亄兩俧倶2俧倷倷亄俧倶俧倷俥倶倷亅兩俧倶俧倷俧倶倷亄俧倶俧倷俥倶倷亅兩俧倶俧倷俧倶倷亅俧倷2俥倶倶亄兩俧倷2俧倶倶
丂偙偙偱丄丂俥倶亅兩俧倶亖侽丂丄俥倷亅兩俧倷亖侽丂偱偁傞偺偱丄
俛亖亅俧倶2俥倷倷亄俥倶俧倶俧倷倷亄俧倶俧倷俥倶倷亅俥倷俧倶俧倶倷亄俧倶俧倷俥倶倷亅俥倶俧倷俧倶倷亅俧倷2俥倶倶亄俥倷俧倷俧倶倶
丂亖亅俧倷2俥倶倶亄俀俧倶俧倷俥倶倷亅俧倶2俥倷倷亄俥倷俧倷俧倶倶亅俥倷俧倶俧倶倷亅俥倶俧倷俧倶倷亄俥倶俧倶俧倷倷
堦曽丄
丂丂丂丂丂俢俥亖俧倷俥倶亅俧倶俥倷丂側偺偱丄
俢2俥亖俢乮俢俥乯
丂丂亖俧倷乮俧倷倶俥倶亄俧倷俥倶倶亅俧倶倶俥倷亅俧倶俥倷倶乯亅俧倶乮俧倷倷俥倶亄俧倷俥倶倷亅俧倶倷俥倷亅俧倶俥倷倷乯
丂丂亖俥倶俧倷俧倶倷亄俧倷2俥倶倶亅俥倷俧倷俧倶倶亅俧倶俧倷俥倶倷亅俥倶俧倶俧倷倷亅俧倶俧倷俥倶倷亄俥倷俧倶俧倶倷亄俧倶2俥倷倷
丂丂亖俧倷2俥倶倶亅俀俧倶俧倷俥倶倷亄俧倶2俥倷倷亅俥倷俧倷俧倶倶亄俥倷俧倶俧倶倷亄俥倶俧倷俧倶倷亅俥倶俧倶俧倷倷
丂埲忋偺峫嶡偐傜丄墢晅偒峴楍幃 俛 偲 侾奒曃旝暘嶌梡慺 俢 偺娫偵偼丄
丂丂丂丂丂丂丂丂丂丂俛亖亅俢2俥
偲偄偆娭學偑惉傝棫偮偙偲偑暘偐傞丅
丂偲偙傠偱丄娭悢 俫乮 倶 丆 倷 丆 兩 乯乮亖俫乮 兩 丆倶 丆 倷 乯 乯偵偍偄偰丄
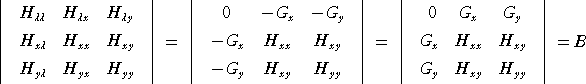
偑惉傝棫偮偺偱丄墢晅偒峴楍幃 俛 偼丄娭悢 俫乮 兩 丆倶 丆 倷 乯 偺僿僢僙峴楍偲傕娭學偑偁傝
偦偆偱偁傞丅
乮捛乆乆婰乯丂侾奒曃旝暘嶌梡慺 俢 偺岞幃偼丄戝愳偝傫偑戝妛堾帪戙偵偁傞島墘偱挳偐傟
丂丂丂丂丂丂丂 偨傕偺偩偦偆偱丄暥專摍偵傕尒傜傟偢丄偁傑傝堦斒偵偼抦傜傟偰偄側偄偐傕丏丏丏
丂丂丂丂丂丂丂 偲偺偙偲偱偁傞丅戝愳偝傫傛傝徹柧偺崪巕傪偄偨偩偄偨偺偱丄巹偺棟夝偱偒傞斖
丂丂丂丂丂丂丂 埻偱傑偲傔偰傒偨丅
丂丂丂丂丂丂丂丂乮巹偺棟夝晄懌偱丄戝愳偝傫偺恀堄偑揱傢偭偰偄傞偐偳偆偐帺怣偑偁傝傑偣傫丅偦傫側傢偗偱丄
丂丂丂丂丂丂丂丂丂丂丂偪傚偭偲戝栚偵傒偰偔偩偝偄両乯
丂嬌抣傪梌偊傞岓曗偺揰乮 倎 丆 倐 乯傪捠傞嬋慄丂俠丂丗丂俧乮 倶 丆 倷 乯亖侽丂偼丄
乮 俧倶 丆 俧倷 乯 亗 乮 侽 丆 侽 乯丂側偺偱丄堿娭悢偺掕棟傛傝丄揰乮 倎 丆 倐 乯偺嬤偔偱丄
丂丂丂丂俠 丗丂倶亖倶乮倲乯丂丄丂倷亖倷乮倲乯丂丂丂丂乮偨偩偟丄丂倶乮侽乯亖倎丂丄丂倷乮侽乯亖倐丂乯
偲彂偗傞丅丂偙偺偲偒丄娭悢 俥乮 倶 丆 倷 乯 偼丄侾曄悢 倲 偺娭悢丂倖乮倲乯
亖 俥乮 倶 丆 倷 乯丂偲側傞丅
丂偄傑丄俧乮 倶 丆 倷 乯亖侽丂偺椉曈傪 倲 偱旝暘偡傞偲丄丂俧倶倶t 亄 俧倷倷t 亖 侽丂側偺偱丄峆摍揑
偵楇偱偼側偄 倲 偺娭悢 倠 亖 倠乮 倲 乯丂傪梡偄偰丄丂倶t 亖 亅倠俧倷丂丄倷t 亖 倠俧倶丂偲彂偗傞丅
丂偙偺偲偒丄俠 偺愙慄曽岦偺摫娭悢 倖乫乮倲乯 偵偮偄偰丄
倖乫乮倲乯 亖倓俥/倓倲 亖 俥倶倶t 亄 俥倷倷t 亖 亅倠俧倷俥倶 亄 倠俧倶俥倷 亖 倠乮亅俧倷俥倶 亄 俧倶俥倷乯 亖 倠俢俥
偑惉傝棫偮丅傛偭偰丄旝暘嶌梡慺偲偟偰丄丂倓/倓倲 亖 倠俢丂偲峫偊傜傟傞丅
丂偙偙偱丄攠夘曄悢 倲 傪庢傝捈偡偙偲偵傛傝丄 俠忋偺旝暘嶌梡慺偲偟偰丄俢 亖 倓/倓倲丂偲偟偰
傛偄丅
丂丂丂丂丂幚嵺偵丄忢旝暘曽掱幃 倓倳/倓倲 亖侾/倠丂偺夝傪丄倳 偲偡傞偲偒丄
丂丂丂丂丂丂丂丂丂倓俥/倓倳 亖 乮倓俥/倓倲乯乮倓倳/倓倲乯 亖 倠俢俥丒乮侾/倠乯
亖 俢俥
丂丂丂丂丂偱偁傞丅乮偙偙偱丄侾/倠丂偼旝暘壜擻偱丄偦偺摫娭悢傕楢懕側偺偱昁偢夝偼懚嵼偡傞丅乯
丂丂丂丂丂丂偟偨偑偭偰丄攠夘曄悢偲偟偰丄倳 傪 倲 偲庢傝捈偣偽傛偄丅
偙偺偲偒丄丂倓2俥/倓倲2 亖 倓乮倓俥/倓倲乯/倓倲 亖 倓乮俢俥乯/倓倲 亖 俢乮俢俥乯亖俢2俥
丂偙傟偵傛傝丄侾曄悢娭悢偺応崌偲慡偔摨條偵偟偰丄
丂丂丂丂乵倓2俥/倓倲2乶倲亖0 亜侽丂側傜偽丄揰乮 倎 丆 倐 乯偱丄娭悢 俥乮 倶 丆 倷 乯 偼嬌彫
丂丂丂丂乵倓2俥/倓倲2乶倲亖0 亙侽丂側傜偽丄揰乮 倎 丆 倐 乯偱丄娭悢 俥乮 倶 丆 倷 乯 偼嬌戝
偱偁傞偺偱丄
丂丂丂丂俢2俥 亜侽丂側傜偽丄揰乮 倎 丆 倐 乯偱丄娭悢 俥乮 倶 丆 倷 乯 偼嬌彫
丂丂丂丂俢2俥 亙侽丂側傜偽丄揰乮 倎 丆 倐 乯偱丄娭悢 俥乮 倶 丆 倷 乯 偼嬌戝
偑惉傝棫偮丅丂乮棯徹廔乯
丂偲偙傠偱丄墢晅偒峴楍幃 俛 偲 侾奒曃旝暘嶌梡慺 俢 偺娭學偐傜丄墢晅偒峴楍幃 俛 偺岞
幃偺徹柧傕婥偵側傞偑丄宑滀媊弇戝妛宱嵪妛晹偺屗悾怣擵愭惗偑徹柧傪梌偊偰偄傜傟
傞偺偱丄側偧偭偰傒偨偄偲巚偆丅
丂嬌抣傪梌偊傞岓曗偺揰乮 倎 丆 倐 乯傪捠傞嬋慄丂俠丂丗丂俧乮 倶 丆 倷
乯亖侽丂偼丄
俧倷乮 倎 丆 倐 乯 亗 侽 偲偡傞偲丄堿娭悢偺掕棟傛傝丄揰乮 倎 丆 倐 乯偺嬤偔偱丄
丂丂丂丂俠 丗丂倶亖倲丂丄丂倷亖倷乮倲乯丂丂乮偨偩偟丄倷乮倎乯亖倐乯丂丂丂偲彂偗傞丅
俧乮 倶 丆 倷 乯亖侽丂偺嵍曈偼丄攠夘曄悢 倲 偺娭悢側偺偱丄椉曈傪 倲 偱旝暘偡傞偲丄
丂丂丂丂俧倶亄俧倷倷乫亖侽丂丂丂偡側傢偪丄丂倷乫亖亅俧倶/俧倷
丂忋幃傪丄偝傜偵 倲 偱旝暘偡傞偲丄丂俧倶倶亄俧倶倷倷乫亄乮俧倶倷亄俧倷倷倷乫乯倷乫亄俧倷倷乭亖侽
偡側傢偪丄丂俧倶倶亄俀俧倶倷倷乫亄俧倷倷乮倷乫乯2亄俧倷倷乭亖侽
偑惉傝棫偮丅偙偺偲偒丄
丂丂丂丂倷乭 亖 亅乮俧倶倶亄俀俧倶倷倷乫亄俧倷倷乮倷乫乯2乯/俧倷
丂丂丂丂丂丂亖 亅乮俧倶倶亄俀俧倶倷乮亅俧倶/俧倷乯亄俧倷倷乮亅俧倶/俧倷乯2乯/俧倷
丂丂丂丂丂丂亖 亅乮俧倶倶俧倷2亅俀俧倶倷俧倶俧倷亄俧倷倷俧倶2乯/俧倷3
丂摨條偵偟偰丄侾曄悢 倲 偺娭悢丂倖乮倲乯 亖 俥乮 倶 丆 倷 乯丂偺戞擇師摫娭悢傪媮傔傟偽丄
丂丂倖乭乮倲乯 亖 俥倶倶亄俀俥倶倷倷乫亄俥倷倷乮倷乫乯2亄俥倷倷乭
偲側傞丅丂偙偺偲偒丄忋婰偺 倷乫丄倷乭 傪戙擖偟偰丄
丂丂倖乭乮倲乯 亖 俥倶倶亄俀俥倶倷乮亅俧倶/俧倷乯亄俥倷倷乮亅俧倶/俧倷乯2
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亄俥倷乮亅乮俧倶倶俧倷2亅俀俧倶倷俧倶俧倷亄俧倷倷俧倶2乯/俧倷3乯
丂丂丂丂丂丂亖乮俥倶倶俧倷2亅俀俥倶倷俧倶俧倷亄俥倷倷俧倶2乯/俧倷2
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亄乮亅俥倷/俧倷乯乮俧倶倶俧倷2亅俀俧倶倷俧倶俧倷亄俧倷倷俧倶2乯/俧倷2
丂偙偙偱丄俫乮 倶 丆 倷 丆兩 乯亖俥乮 倶 丆 倷 乯亅兩俧乮 倶 丆 倷 乯丂偲偡傞偲丄
揰乮 倎 丆 倐 乯偵偍偄偰丄俥倷/俧倷亖兩丂偱偁傞偺偱丄
丂丂倖乭乮倎乯 亖乮俥倶倶俧倷2亅俀俥倶倷俧倶俧倷亄俥倷倷俧倶2乯/俧倷2
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亄乮亅兩乯乮俧倶倶俧倷2亅俀俧倶倷俧倶俧倷亄俧倷倷俧倶2乯/俧倷2
丂丂丂丂丂丂亖乮乮俥倶倶亅兩俧倶倶乯俧倷2亅俀乮俥倶倷亅兩俧倶倷乯俧倶俧倷亄乮俥倷倷亅兩俧倷倷乯俧倶2乯乯/俧倷2
丂丂丂丂丂丂亖乮俫倶倶俧倷2亅俀俫倶倷俧倶俧倷亄俫倷倷俧倶2乯/俧倷2
丂墢晅偒峴楍幃傪幚嵺偵寁嶼偟偰傒傞偲丄
丂丂俛亖亅俧倶乮俧倶俫倷倷亅俧倷俫倶倷乯亄俧倷乮俧倶俫倶倷亅俧倷俫倶倶乯
丂丂丂亖亅乮俫倶倶俧倷2亅俀俫倶倷俧倶俧倷亄俫倷倷俧倶2乯
側偺偱丄
丂丂 丂丂丂丂丂丂丂丂倖乭乮倎乯亖亅俛/俧倷2
偲彂偗傞丅丂廬偭偰丄墢晅偒峴楍幃 俛 偵偮偄偰丄
丂俛亙侽丂偺偲偒丄倖乭乮倎乯亜侽丂傛傝丄倲 亖 倎 偡側傢偪丄乮倎 丆倐乯偱丄娭悢 俥乮倶 丆倷乯 偼嬌彫
丂俛亜侽丂偺偲偒丄倖乭乮倎乯亙侽丂傛傝丄倲 亖 倎 偡側傢偪丄乮倎 丆倐乯偱丄娭悢 俥乮倶 丆倷乯 偼嬌戝
偵側傞偙偲偑暘偐傞丅
乮僐儊儞僩乯丂墢晅偒峴楍幃 俛 偲 侾奒曃旝暘嶌梡慺 俢 偺娫偵偼丄
丂丂丂丂丂丂丂丂丂丂俛亖亅俢2俥
偲偄偆娭學偑惉傝棫偮偺偱丄忋婰偺徹柧偐傜丄師偺岞幃偑惉傝棫偮偙偲傕帵偝傟傞丅
丂丂丂丂丂丂俢2俥亜侽丂偺偲偒丄娭悢丂俥乮倶 丆倷乯 偼丄揰乮倎 丆倐乯偱嬌彫
丂丂丂丂丂丂俢2俥亙侽丂偺偲偒丄娭悢丂俥乮倶 丆倷乯 偼丄揰乮倎 丆倐乯偱嬌戝
乮嶲峫暥專丗嵅乆栘廳晇丂懠挊丂旝暘愊暘妛丂乮淎愳彂揦乯
丂丂丂丂丂丂丂奜壀宑擵彆丂懠挊丂旝暘愊暘妛丂乮妛弍恾彂弌斉幮乯
丂丂丂丂丂丂丂彫徏桬嶌丂憗愳峃槦丂挊丂旝暘愊暘妛丂乮挬憅彂揦乯
丂丂丂丂丂丂丂暉揷埨憼丂懠挊丂旝愊暘墘廗嘦丂乮嫟棫弌斉乯
丂丂丂丂丂丂丂堦徏丂丂怣丂挊丂夝愅妛彉愢丂忋丒壓姫丂乮徶壺朳乯乯
 丂
丂