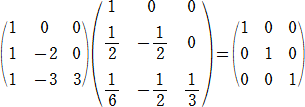�Ώ̎��̐^���@ �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�������Z�ɓ��w���čŏ��ɐ�������̂́A�u�Ώ̎��v�������B�Ώ̎����ւ����
�́A���w�T�́u���ƌv�Z�v�̓V���R�Ƃ�����ۂ������B���̓�ւ�ʂ蔲�����҂݂̂ɁA��
�̌�̐��w�����錠�����ۏ����Ƃ������Ɋ�����ꂽ�B
�@�Ώ̎��Ƃ́A�@���{�� �A���� �A ��2�{��2 �A��3���{����3 �A�E�E�E�@�Ȃǂ̂悤�ɁA�� �� �� ���������Ă�
�������ɂȂ���̂������B
�@���ۂɁA�Ⴆ�A�@��3���{����3�@�ŁA�� �� �� ����������ƁA�@��3���{����3�@�ł��邪�A����́A��
�̎��@��3���{����3�@�ɓ������B�@����āA�@��3���{����3�@�͑Ώ̎��ł���B
�@�Ώ̎��̂����A ���{�� �A�����@���A���ɁA��{�Ώ̎��Ƃ����B
�@��ʓI�ɂ́A�������@�o�i��1�C��2�C�E�E�E�C��n�j�@�ɑ��āA�C�ӂ� �� �����̒u�� �� �ɑ��āA
�@�@�@�@�@�@�@�@�o�i����(1)�C����(2)�C�E�E�E�C����(n)�j���o�i��1�C��2�C�E�E�E�C��n�j
�����藧�Ƃ��A�������@�o�i��1�C��2�C�E�E�E�C��n�j�@���Ώ̎��ł���Ƃ����B
�@�܂��A��{�Ώ̎��́A�@��1 �A��2 �A �E�E�E �A�����@�ŕ\�����B
�@�@��1����1�{��2�{�E�E�E�{��n�@�@�i�@���@��1�C��2�C�E�E�E�C��n�@�̑S�Ă̘a�j
�@�@��2����1��2�{��1��3�{�E�E�E�{��n-1��n�@�@�i�@���@��1�C��2�C�E�E�E�C��n�@�̑��قȂ�Q���̐ς̘a�j
�@�@�@ �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E
�@�@��������1��2�E�E�E��n�@�@�i�@���@��1�C��2�C�E�E�E�C��n�@�̑S�Ă̐ρj
�@�Ώ̎��ɂ����ẮA���̒藝����{�I�ł���A�d�v�ł���B
��@���@�@�Ώ̎��́A��{�Ώ̎��̑������Ƃ��ĕ\���A���̕\�����͈�ӓI�ł���B
�@���̒藝���ӎ��������̖��́A�Ώ̎��̖��ł͑�\�I�Ȃ��̂ƌ����邾�낤�B
��@���@�@���{�����P �A�������P�@�̂Ƃ��A ��2�{��2 �A��3�{��3 �A��4�{��4 �A��5�{��5 �̒l�����߂�B
�i���j�@��2�{��2���i���{���j2�|�Q�������P�|�Q���|�P
�@��3�{��3���i���{���j3�|�R�����i���{���j���P�|�R���|�Q
�@��4�{��4���i��2�{��2�j2�|�Q��2��2���P�|�Q���|�P
�@��5�{��5���i��2�{��2�j�i��3�{��3�j�|��2��2�i���{���j���Q�|�P���P�@�@�i�I�j
�i�NjL�j�@�ߘa�Q�N�T���Q�T���t��
�@�ǎ҂̂��߂ɁA�����Ώ̎�����{�Ώ̎��ŕ\�������c���Ă������B
���K���
�@���{���{�������A�����{�����{���������A�����������@�Ƃ����B�������A���A���A���̑������ŕ\���B
�i�P�j�@��2�{��2�{��2
�i�Q�j�@��3�{��3�{��3
�i�R�j�@��4�{��4�{��4
�i���j�i�P�j�@��2�{��2�{��2���i���{���{���j2�|�Q�i�����{�����{�����j����2�|�Q��
�i�Q�j�@��3�{��3�{��3
�@�@���i���{���{���j�i��2�{��2�{��2�|�i�����{�����{�����j�j�{�R�����������i��2�|�R���j�{�R������3�|�R�����{�R��
�i�R�j�@��4�{��4�{��4
�@�@���i��2�{��2�{��2�j2�|�Q�i��2��2�{��2��2�{��2��2�j
�@�@���i��2�{��2�{��2�j2�|�Q�i�i�����{�����{�����j2�|�Q�������i���{���{���j�j
�@�@���i��2�|�Q���j2�|�Q�i��2�|�Q�����j����4�|�S��2���{�S�����{�Q��2�@�@�i�I�j
�i�NjL�j�@�����P�X�N�U���Q�S���t��
�@��L�ł́A���ꂼ������߂邽�߂̎��ό`�ɉ����Čv�Z���������A����ɑ��ē���I��
���ό`�����邱�Ƃ��ŋߒm�邱�Ƃ��o�����B
�@�s���������{�����@�Ƃ����ƁA���炩�ɁA
�@�@�s���{1���s1�E�s���|�����E�s���|1
�����藧�B
�@���̎��ό`��p����A�@�B�I�Ȍv�Z�ŏ������߂���B���̓s�x�A���ό`���l����
���Ƃ���������ăX�b�L�������C���ɂȂ�܂��l�B
��2�{��2���s2���s1�s1�|�����s0���i���{���j�i���{���j�|�����i��0�{��0�j���P�E�P�|�P�E�Q���|�P
��3�{��3���s3���s1�s2�|�����s1���i���{���j�i��2�{��2�j�|�����i���{���j���P�E�i�|�P�j�|�P�E�P���|�Q
��4�{��4���s4���s1�s3�|�����s2���i���{���j�i��3�{��3�j�|�����i��2�{��2)���P�E�i�|�Q�j�|�P�E�i�|�P�j���|�P
��5�{��5���s5���s1�s4�|�����s3���i���{���j�i��4�{��4�j�|�����i��3�{��3)���P�E�i�|�P�j�|�P�E�i�|�Q�j���P
�i�Q�l�����F�������P�@���@���s�̋��ȏ��ɑ��ĎQ�l���E���W���ŕ�[���Ă���������
�@�e�i�����ʐM�@�m���D�T�W�j�i�����o�Łj�j
�@��L�̉��Ŏ��̂悤�ɍl����l�����邾�낤�B
�@�@���{�����P �A�������P�@���A�@�� �� �� �́A�Q���������@��2�|���{�P���O�@�̉��ł���B
�@����āA�@��3�{�P���i���{�P�j�i��2�|���{�P�j���O�@���A�@��3���|�P�@�ł���B
�@���̂Ƃ��A�@��3���|�P�@�A��3���|�P�@����A�@���炩�ɁA�@��3�{��3���|�Q
�@�܂��A�@��4�{��4���|�i���{���j���|�P�@�A��5�{��5���|�i��2�{��2�j���P
�i�NjL�j�@�����Q�P�N�V���W���t��
�@��L�̉��Ŏ��̂悤�ɍl����l�����邾�낤�B
�@���{�����P �A�������P�@���A�@�� �� �� �́A�Q���������@��2�|���{�P���O�@�̉��ł���B
�@�����ŁA�@�s���������{�����@�Ƃ����ƁA�@��2�����|�P�@����A�@����+2������+1�|���� �ł���̂ŁA
�@�s��+2���s��+1�|�s���@�i�����O�A�P�A�Q�A�E�E�E�j
�����藧�B����āA
�@�s0����0�{��0���Q�@�A�@�s1�����{�����P�@�A�@�s2���s1�|�s0���|�P
�@�s3���s2�|�s1���|�Q�@�A�@�s4���s3�|�s2���|�P�@�A�@�s5���s4�|�s3���P
�i�R�����g�j�@���̉�@�̕����A�u�@�s���{1���s1�E�s���|�����E�s���|1�@�v�Ƃ������ɐl�H�I�ȑQ��
�@�@�@�@�@�@���������R�ł����ˁI�����A�Ώ̎��Ƃ������Ƃ�S���ӎ����Ă��Ȃ���@�Ȃ̂ŁA
�@�@�@�@�@�@���̃y�[�W�̓��e�ɑ����������ǂ����D�D�D�����s���B
�@���̑Q������p����ƁA�utetsuya�v���A�����Q�P�N�V���X���t���œ��g�o�̌f���u�o��
���̐�v�ɏ������܂ꂽ���
���@��2�{���|�P���O�@�̂Q�� ���A�� �ɑ��A�����{�����@�����ׂĂ̎��R�� �� �Ő����l�ƂȂ�
�@�@���Ƃ������B
���@�����{�����@�́A���{���@�Ɓ@�����@�̑������ŕ\����邱�Ƃ𐔊w�I�A�[�@�Ŏ����B
�@���e�Ղɉ�����邱�Ƃ��낤�B
�@���ۂɁA�O���́A�@�s���������{�����@�ɂ����āA�@�s1�����{�����|�P�@�Ő���
�@�܂��A�������|�P�@���A�@�s2����2�{��2���i���{���j2�|�Q�������R�@�Ő���
�@�@�����ŁA�@��2���|���{�P�@����A�@����+2���|����+1�{���� �ł���̂ŁA
�@�Q�����@�s��+2���|�s��+1�{�s���@�i�����P�A�Q�A�E�E�E�j�@�����藧�B
�@�@���������āA�C�ӂ� �� �i�����P�j�ɑ��āA�s�� �A�s��+1�@�������Ɖ��肷��ƁA�s��+2 �������B
�@����āA�S�Ă̎��R�� �� �ɑ��āA�@�s���������{�����@�͐����ƂȂ�B
�@�܂��A�㔼�����l�Ɏ������B
�@�s���������{�����@�ɂ����āA�@�s1�����{���@���A���{�� �A���� �̑������ŕ\�����B
�܂��A�@�s2����2�{��2���i���{���j2�|�Q�����@���A���{�� �A���� �̑������ŕ\�����B
�@���̂Ƃ��A�@�Q�������s12�|�s2�@�Ȃ̂ŁA�� �� �� �́A�Q��������
�@�@��2�|�s1�E���{�i�s12�|�s2�j/�Q���O
�̉��ł���B����āA���̑Q���������藧�B
�@�s��+2���s1�E�s��+1�|�s���E�i�s12�|�s2�j/�Q�@�i�����P�A�Q�A�E�E�E�j
�@���������āA�C�ӂ� �� �i�����P�j�ɑ��āA�s�� �A�s��+1�@���A���{�� �A���� �̑������ŕ\������
���肷��ƁA�s��+2�@���@���{�� �A���� �̑������ŕ\�����B
�@����āA�S�Ă̎��R�� �� �ɑ��āA�@�s���������{�����@�́A���{�� �A���� �̑������ŕ\�����B
�@���l�̎�|�ŁA���g�o�����������b�ɂȂ��Ă���r�i�g�j���A���̂悤�Ȗ����N��
�����B�i�����Q�P�N�W���V���t���j
���@���{�P/�� �������Ȃ�A�����{�P/���� �������ł��邱�Ƃ������B
���@���{�P/�� �������Ȃ�A�����{�P/���� �������ł��邱�Ƃ������B
�@���ۂɁA�O���́A�@�s���������{�P/�����@�ɂ����āA�@�s1�����{�P/���@�͐���
�܂��A�@�s2����2�{�P/��2���i���{�P/���j2�|�Q�@�Ő����ƂȂ�B
�@���̂Ƃ��A���A�P/�� �́A�Q���������@��2�|�s1�E���{�P���O�@�̉��ł���B
����āA�Q�����@�s��+2���s1�E�s��+1�|�s���@�i�����P�A�Q�A�E�E�E�j�@�����藧�B
�@���������āA�C�ӂ� �� �i�����P�j�ɑ��āA�s�� �A�s��+1�@�������Ɖ��肷��ƁA�s��+2 �������B
�@����āA�S�Ă̎��R�� �� �ɑ��āA�@�s���������{�P/�����@�͐����ƂȂ�B
�@�܂��A�㔼�����l�Ɏ������B
�@�s���������{�P/�����@�ɂ����āA�@�s1�����{�P/���@�͋����ŁA
�@�s2����2�{�P/��2���i���{�P/���j2�|�Q�@�������ƂȂ�B
�@���̂Ƃ��A���A�P/�� �́A�Q���������@��2�|�s1�E���{�P���O�@�̉��ł���B
����āA�Q�����@�s��+2���s1�E�s��+1�|�s���@�i�����P�A�Q�A�E�E�E�j�@�����藧�B
�@���������āA�C�ӂ� �� �i�����P�j�ɑ��āA�s�� �A�s��+1�@���A�����Ɖ��肷��ƁA�s��+2 �������B
�@����āA�S�Ă̎��R�� �� �ɑ��āA�@�s���������{�P/�����@�͋����ƂȂ�B
�@�܂��A��L�̂悤�ȉ�@��p����ƁA
�@�@���{���{�����R�@�A�@��2�{��2�{��2���T�@�A�@��3�{��3�{��3���V�@�̂Ƃ��A
�@��4�{��4�{��4�@�A�@��5�{��5�{��5�@�̒l�����߂�B
�ȂǂƂ��������������낤�I
�@���ۂɁA�����{�����{�������o�i���{���{���j2�|�i ��2�{��2�{��2�j�p���i�X�|�T�j/�Q���Q
�@���������o�i��3�{��3�{��3�j�|�i���{���{���j�i��2�{��2�{��2�|�����|�����|�����j�p/�R
�@�@�@���o�V�|�R�E�i�T�|�Q�j�p/�R���|�Q/�R
����A �� �A�� �A���@�́A�R���������@��3�|�R��2�{�Q���{�Q/�R���O�@�̉��ƂȂ�B
�@�����ŁA�@�s���������{�����{�����@�Ƃ����ƁA�Q����
�@�s��+3���R�s��+2�|�Q�s��+1�|�i2/3�j�s���@�i�����O�A�P�A�Q�A�E�E�E�j
�����藧�B���̂Ƃ��A
�@�s0����0�{��0�{��0���R�@�A�@�s1�����{���{�����R�@�A�@�s2����2�{��2�{��2���T
�@�s3���R�s2�|�Q�s1�|�i2/3�j�s0���P�T�|�U�|�Q���V
�@�s4���R�s3�|�Q�s2�|�i2/3�j�s1���Q�P�|�P�O�|�Q���X
�@�s5���R�s4�|�Q�s3�|�i2/3�j�s2���Q�V�|�P�S�|�P�O/�R���Q�X/�R
�i�R�����g�j�@���̉�@����A�d�������� ����ɂ��肢����A�@�����{�����{�����@�̒l�����߂�̂�
�@�@�@�@�@�@���R���݁D�D�D�Ǝv������A���g�o�����������b�ɂȂ��Ă���r�i�g�j����̂��w�E
�@�@�@�@�@�@�ɂ���悤�ɁA�����ł��Ȃ��悤�ł��ˁI�Q/�R �Ƃ�������������������̂��ȁH
�@�@�@�@�@�@�i���Q�l�F�u�W�������v�j
�@���̖��̉�@�����������悤�ɁA���ʂ��悭���v�Z������\�͂��݂�Ƃ��A���낢��
�Ȓm����������ł���f�n������ȂǁA���̎�̖��́A�������҂ɂƂ��Ă̓h��
���̕p�o����Ƃ����Ă��ߌ��ł͂Ȃ����낤�B
�@���̂悤�Ȗ�肪�A���Z�������I���āu�z�b�I�v�Ƃ��Ă��鍂�Z�P�N�̂T�����~�肩�����
��������A�����Ƃ��Ă���g�ɂƂ��ẮA�ƂĂ��h�������������B�������A����Ӗ��ł́A��
�ꂪ���Z���w���ƁA���w���w�Ƃ̌��ʂ��ʂ����ɂ͏\�������鎎���ł��������B
�@���g�o�̌f���u�o��̐�v�Łu���ׁv�����̏��Ђ��Љ�ꂽ�B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����P�X�N�P���P�P���t���j
�@�@���@���v�@���@�@�u�㐔�w�v ���Ǝ��̌���I���_�@�i�X�k�o�Łj
�@�������̖{�����ݍw�����邱�Ƃ͊��킸���L����}���ٓ��ʼn{�����邵���Ȃ��B�{�ɂ́A
�@�@����������Z�̒B�l���l�����Z������ł��Ȃ��悤�ɁA���G�ȑΏ̎��̌v�Z��
�@�ÎZ�ōs�����Ƃ��ł���悤�ɂȂ�ł��낤�B
�Ƃ���A����������������̂�����B�Ώ̎��̌v�Z�ɂ́A�u�����O�}�`�v�Ƃ������̂�
�L���炵���A���ɋ������킭���e���B��V�͂̑Ώ̎��܂ł́A���َq���ق���Ȃ���A
��C�ɓǂݐi�ނ��Ƃ��ł����B
�@���̃y�[�W�ł́A��L�̖{��ǂ݂��Ȃ��Ȃ��玄�̕����Ă�A���Z����ɐ������
�Ώ̎��ɂ��āA���̐^���̎p�͂ǂ��ł��邩�A�Ώ̎��̗L��l���܂Ƃ߂Ă݂����Ǝv���B
���̋@���^���Ă����������g�m�u���ׁv����Ɋ��ӂ������B
�@��L�̖��ɂ��āA���Z�������ɉ���Ώ�L�̒ʂ�ł��邪�A���̂悤�ȉ�
���蓾��B
��@���@�@���{�����P �A�������P�@�̂Ƃ��A ��2�{��2 �A��3�{��3 �A��4�{��4 �A��5�{��5 �̒l�����߂�B
�i���j�@��1�����{���@�A��2����2�{��2�@�A��3����3�{��3�@�A��4����4�{��4�@�A��5����5�{��5�@�Ƃ����B
�@���̂Ƃ��A�@�o�i���j���i���|���j�i���|���j����2�|�i���{���j���{��������2�|���{�P�@�Ƃ����ƁA
�@�o�f�i���j/�o�i���j���P/�i���|���j�{�P/�i���|���j
�@�����ŁA
�@�P/�i���|���j���i�P/���j�i�P�{�i��/���j�{�i��/���j2�{�i��/���j3�{�i��/���j4�{�i��/���j5�{�i��/���j6�{�E�E�E�j
�@�P/�i���|���j���i�P/���j�i�P�{�i��/���j�{�i��/���j2�{�i��/���j3�{�i��/���j4�{�i��/���j5�{�i��/���j6�{�E�E�E�j
�Ȃ̂ŁA�o�f�i���j/�o�i���j���Q/���{��1/��2�{��2/��3�{��3/��4�{��4/��5�{��5/��6�{�E�E�E
����āA�o�f�i���j���o�i���j�i�Q/���{��1/��2�{��2/��3�{��3/��4�{��4/��5�{��5/��6�{�E�E�E�j�@���A
�@�Q���|�P
���i��2�|���{�P�j�i�Q/���{��1/��2�{��2/��3�{��3/��4�{��4/��5�{��5/��6�{�E�E�E�j
���Q���{��1�{��2/���{��3/��2�{��4/��3�{��5/��4�{�E�E�E
�@�|�Q�|��1/���|��2/��2�|��3/��3�|��4/��4�|��5/��5�{�E�E�E
�@�{�Q/���{��1/��2�{��2/��3�{��3/��4�{��4/��5�{��5/��6�{�E�E�E
���Q���{�i��1�|�Q�j�{�i��2�|��1�{�Q�j/���{�i��3�|��2�{��1�j/��2
�@�@�{�i��4�|��3�{��2�j/��3�{�i��5�|��4�{��3�j/��4�{�E�E�E
�@���ӂ̌W�����r���āA
��1�|�Q���|�P
��2�|��1�{�Q���O
��3�|��2�{��1���O
��4�|��3�{��2���O
��5�|��4�{��3���O
�@�E�E�E�E�E�E�E�E�E
�@�������A�@��1���P�@�A��2���|�P�@�A��3���|�Q�@�A��4���|�P�@�A��5���P�@�@�i�I�j
�i�R�����g�j�@����Ӑ}���Ȃ�����A���̂悤�ȉ�������͂܂����Ȃ��ł��傤�l�H
�@�Ώ̎��ŁA�@���������E�E�E�����@�i���������E�E�E�������O�j�@�̌`�̒P�������܂ނ��̂��A�L����
�@�@�i�����E�E�E���j
�ƕ\���B
�i�⑫�j�@�u���������E�E�E�����@�i���������E�E�E�������O�j�̌`�̒P�������܂ށv�Ƃ́A
�@�@���������E�E�E�������O�̏����������A���A�E�E�E�A���͌Œ肳��A���A���A�E�E�E�A���͂��ׂĂ�
�@���������
�Ƃ����Ӗ��ł��B
��@���{���@�́A�i�P�O�j�@ �A�����@�́A�i�P�P�j�@ �A ��2�{��2�@�́A�i�Q�O�j�@ �A��3���{����3�@�́A�i�R�P�j
�@�i�P�P�j�Ȃǂ́A�i�P2�j�Ƃ��\�����B
�@�i�P�O�j�́A�i�P�j�A�i�Q�O�j�́A�i�Q�j�@�ƒʏ�\����A�u�O�v�͏Ȃ��Ă��悢�B
�@���̋L�����g���ƁA�� �̕����@��1�C��2�C�E�E�E�C��n�@�̊�{�Ώ̎��́A
�@�@�i�P�j�@�A�i�P2�j�@�A�i�P3�j�@�A�E�E�E�A�i�P���j
�ƊȒP�ɕ\�����B
�@���āA�@�i�����E�E�E���j�@�ɂ����āA�@���{���{�E�E�E�{�������@�ł���Ƃ��A�@�i�����E�E�E���j�@�́A���R��
�� �̔��ȑg�ݕ����̕��@�������Ă���B
��@���R�� �S �̔��ȑg�ݕ����̕��@��S�ė��Ă݂悤�B
�@�@�S���R�{�P���Q�{�Q���Q�{�P�{�P���P�{�P�{�P�{�P
�@���R�� �S ���A�����S�ƍl����A��L�̕������͎��̂悤�Ȑ}�ɑ�������B
�u�b�v�������Ƃ��āA
�@�@�@�@�@�@�@ �S�@���@�@��������
�@�@�@�@�@�R�{�P�@���@�@�������b��
�@�@�@�@�@�Q�{�Q�@���@�@�����b����
�@ �@�Q�{�P�{�P�@���@�@�����b���b��
�P�{�P�{�P�{�P�@���@�@���b���b���b��
�@�����O�}�`�Ƃ́A���̂悤�Ȑ}�𐳕��`��p���ďc�����ԂȂ����ׂē�����}���̂���
�ł���B
�@���������āA��L�̎��R�� �S �̔��ȑg�ݕ����̕��@�������O�}�`��p����Ɖ��}
�̂悤�ɕ\�����B
| �i�S�j |
�i�R�P�j |
�i�Q�Q�j |
�i�Q�P�P�j |
�i�P�P�P�P�j |
 |
 |
 |
 |
 |
�@�����ŁA�ʔ�������������B��L�̃����O�}�`�̐����`�̃}�X�ڂɁA�P�A�Q�A�R�A�S�@�Ɛ���
���������ނ��Ƃ��l����B�������A������E�ցA�ォ�牺��������������悤�ɏ�������
���̂Ƃ���B
�@���̂Ƃ��A�@�i�S�j�̃^�C�v�̏������ݕ��@�́A�P�ʂ�
�@�@�@�@�@�@�@�@�i�R�P�j�̃^�C�v�̏������ݕ��@�́A�R�ʂ�
�@�@�@�@�@�@�@�@�i�Q�Q�j�̃^�C�v�̏������ݕ��@�́A�Q�ʂ�
�@�@�@�@�@�@�@�@�i�Q�P�P�j�̃^�C�v�̏������ݕ��@�́A�R�ʂ�
�@�@�@�@�@�@�@�@�i�P�P�P�P�j�̃^�C�v�̏������ݕ��@�́A�P�ʂ�
�Ȃ̂ŁA�@�P2�{�R2�{�Q2�{�R2�{�P2���P�{�X�{�S�{�X�{�P���Q�S�@�ƂȂ�A�@�Q�S���S�I�@�Ƃ���
���Ƃ���A�@�P2�{�R2�{�Q2�{�R2�{�P2���S�I�@�����藧�B�i�@���@����́A�X�S�C�I�j
�@���āA�Ώ̎��@��3���{����3�@�́A
�@��3���{����3�������i��2�{��2�j�������i�i���{���j2�|�Q�����j�������i���{���j2�|�Q�i�����j2
�Ƃ������ό`����A��{�Ώ̎��@��1�����{���@�A��2�������@��p���āA
�@��3���{����3����12��2�|�Q��22
�ƕ\�����B���̂悤�ɁA�Ώ̎�����{�Ώ̎��̑������ŕ\�����@�������O�}�`�Ƃǂ̂�
���Ȋ֘A������̂������ɍl�������B
�@�Q�ϐ��̏ꍇ�̊�{�Ώ̎��̃����O�}�`�́A
| �i�P�j |
�i�P2�j |
 |
 |
�@�����ɁA�����̊�{�Ώ̎����m���|���Ă݂悤�B
�@�@�@�@�i�P2�j�~�i�P�j�������~�i���{���j����2���{����2���i�Q�P�j
���̃����O�}�`�́A
�@
�ŁA����́A�i�P2�j�̐}�`�̉E��Ɂi�P�j�̐}�`��\�荇�킹�����̂ɓ������B
�@�i�P�j�~�i�P2�j���i���{���j�~��������2���{����2���i�Q�P�j
�Ȃ̂ŁA���������O�}�`�ƂȂ�͂��ł��邪�A����́A�i�P�j�̐}�`�̉E����i�P2�j�̐}�`��
�������`�ɕ�������A�X���C�h���Ă�����̂ƍl������B
�@�Q�ϐ����Ƃ��܂�ڍׂȋ����������Ă��Ȃ��̂ŁA���x�͂R�ϐ��̏ꍇ���l���邱�Ƃɂ�
�悤�B
��{�Ώ̎��̃����O�}�`�́A
�@�����ɁA�����̊�{�Ώ̎����m���|���Ă݂悤�B
�@�i�P2�j�~�i�P�j
���i�����{�����{�����j�~�i���{���{���j
����2���{����2�{�������{�������{��2���{����2�{����2�{�������{��2��
����2���{����2�{��2���{����2�{����2�{��2���{�R������
���i�Q�P�j�{�R�~�i�P3�j
���̃����O�}�`�́A
�@�@ |
�{�R�~ |
 |
�@���̌v�Z���ʂ́A�ǂ̂悤�ɗ�����������̂��낤���H
�@�i�P2�j�̐}�`�̉E��Ɂi�P�j�̐}�`��\�荇�킹�����̂ƁA�i�P2�j�̐}�`�̉��Ɂi�P�j�̐}�`
��\�荇�킹�����̂Ɨ�������̂��Ó��ȂƂ��낾�낤�B
�@���́A���̌W���ł���B���́A
�@�\�荇�킹�鐳���`�� �� �ŁA���̌��ʂł��铯�����̐}�`���c�����ɐ����`
�� ������Ȃ�Ƃ��A���̌W���́A���b�� �ł���
���Ƃ��m���Ă���B
�@�����ɁA��L�̃����O�}�`�̑�P���̌W���́A�@1�b1���P�@�ł���B�i���@�����Ă���I�j
��Q���̌W���́A�@3�b1���R�@�ł���B�i���@�����Ă���I�j
�@��������ƁA�@�i�P�j�~�i�P2�j�@�̃����O�}�`����L�Ɠ����ɂȂ�͂��ŁA���̂悤�ɗ�������
�̂��Ó��ȂƂ��낾�낤�B
�@�i�P�j�̐}�`�̉E����i�P2�j�̐}�`���������`�ɕ�������A�X���C�h�������̂ƁA�i�P�j�̐}�`
�̉��Ɂi�P2�j�̐}�`��\�荇�킹�����̂��l���A���̌W���́A�O�҂́A1�b1�~1�b1���P�@�ŁA
��҂́A3�b2���R�@�ł���B
�@���̂悤�ɍl����ƁA
�@�i�P2�j�~�i�P�j
���i�����{�����{�����j�~�i���{���{���j
����2���{����2�{�������{�������{��2���{����2�{����2�{�������{��2��
����2���{����2�{��2���{����2�{����2�{��2���{�R������
���i�Q�P�j�{�R�~�i�P3�j
�̂悤�ȔώG�����Ȍv�Z�����Ȃ��Ă��A��C�ɁA�@�i�P2�j�~�i�P�j���i�Q�P�j�{�R�~�i�P3�j�@�Ə�����
���ł���B
�@���̂��Ƃ����L�ŏ������`�̏W�܂�������O�}�`�ƌĂ��A�i�P2�j�A�i�P�j�A�i�Q�P�j�A�E�E�E
�Ȃǂ������O�}�`�ƌĂ�ł����������B
�@�Ƃ���ŁA�@�i�P2�j�~�i�P�j���i�Q�P�j�{�R�~�i�P3�j�@�̂悤�ȏ������ɂ͗��_������B����́A��
���̐��ɂ��Ȃ����Ƃ��B������A�����O�}�`�łP�x�����i�I�j�v�Z���Ă����A��́A����
���ʂ�p���ĕϐ��������낤�Ƃ��v�Z�������I����Ă���Ƃ������ƂȂ̂��B�������i�Q�P�j
���̈Ӗ��͕ϐ��̌��ɂ���ĕς���Ă���̂����D�D�D�B
�@�ϐ����Q�̂Ƃ�
�i�P3�j���O�@�ƍl����A�i�P2�j�~�i�P�j���i�Q�P�j�@�Ƃ������ɂ����_�������B
�@�ǎ҂̂��߂ɁA���K����������Ă������B
��@���@�@���̃����O�}�`�̐ρ@�i�R�Q�P2�j�~�i�P2�j�@���v�Z����B
�i���j�@�v�Z����ƁA
�@�i�S�R�P�P�j�A�i�S�Q2�P�j�A�i�S�Q�P3�j�A�i�R2�Q�P�j�A�i�R2�P3�j�A�i�R�Q3�j�A�i�R�Q2�P2�j�A�i�R�Q�P4�j�@�̊e��
�ɕ��������B���̂Ƃ��A
�@�i�S�R�P�P�j�̌W���́A�@1�b1�~1�b1���P
�@�i�S�Q2�P�j�̌W���́A�@1�b1�~2�b1���Q
�@�i�S�Q�P3�j�̌W���́A�@1�b1�~3�b1���R
�@�i�R2�Q�P�j�̌W���́A�@2�b1�~1�b1���Q
�@�i�R2�P3�j�̌W���́A�@2�b1�~3�b1���U
�@�i�R�Q3�j�̌W���́A�@3�b2���R
�@�i�R�Q2�P2�j�̌W���́A�@2�b1�~2�b1���S
�@�i�R�Q�P4�j�̌W���́A�@4�b2���U
�ł���̂ŁA
�@�i�R�Q�P2�j�~�i�P2�j
���i�S�R�P�P�j�{�Q�i�S�Q2�P�j�{�R�i�S�Q�P3�j�{�Q�i�R2�Q�P�j�{�U�i�R2�P3�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�{�R�i�R�Q3�j�{�S�i�R�Q2�P2�j�{�U�i�R�Q�P4�j�@�@�i�I�j
�@�v�Z�ɂ�����ƈꖕ�̕s�����o����̂ŁA�S�̕ϐ��̏ꍇ�ɂ��Ď��ۂɊm�F���Ă�
�悤�B
�i��3��2�����{��3��2�����{��3��2�����{��3��2�����{��3��2�����{��3��2�����{��3��2����
�@�@�{��3��2�����{��3��2�����{��3��2�����{��3��2�����{��3��2�����j�i�����{�����{�����{�����{�����{�����j
��
�i��4��3�����{��4��2��2���{��4��2��2���{��4��3�����{��4��2����2�{��4��2��2��
�@�@�@�@�{��3��3��2���{��3��3����2�{��3��2��2��2�{��3��3��2���{��3��3��2���{��3��2��2��2�j
�@�{
�i��4��2��2���{��4��3�����{��4��2����2�{��3��3��2���{��3��3����2�{��3��2��2��2
�@�@�@�@�{��4��3�����{��4��2����2�{��4��2��2���{��3��3����2�{��3��2��2��2�{��3��3��2���j
�@�{
�i��4��2����2�{��4��2����2�{��4��3�����{��3��3����2�{��3��2��2��2�{��3��3��2��
�@�@�@�@�{��3��3����2�{��3��2��2��2�{��3��3��2���{��4��3�����{��4��2��2���{��4��2��2���j
�@�{
�i��3��3��2���{��3��3��2���{��3��2��2��2�{��4��2��2���{��4��3�����{��4��2����2
�@�@�@�@�{��4��2��2���{��4��3�����{��4��2����2�{��3��2��2��2�{��3��3����2�{��3��3����2�j
�@�{
�i��3��3����2�{��3��2��2��2�{��3��3��2���{��4��2����2�{��4��2��2���{��4��3����
�@�@�@�@�{��3��2��2��2�{��3��3��2���{��3��3����2�{��4��2��2���{��4��3�����{��4��2����2�j
�@�{
�i��3��2��2��2�{��3��3����2�{��3��3����2�{��3��2��2��2�{��3��3��2���{��3��3����2
�@�@�@�@�{��4��2����2�{��4��2��2���{��4��3�����{��4��2����2�{��4��2����2�{��4��3�����j
��
�i��4��3�����{��4��3�����{��4��3�����{��4��3�����{��4��3�����{��4��3�����{��4��3����
�@�@�@�@�{��4��3�����{��4��3�����{��4��3�����{��4��3�����{��4��3�����j
�@�{�i
��4��2��2���{��4��2��2���{��4��2����2�{��4��2��2���{��4��2��2���{��4��2����2
�@�@�@�@�{��4��2����2�{��4��2��2���{��4��2��2���{��4��2��2���{��4��2����2�{��4��2����2
�@�@�@�@�@�{��4��2��2���{��4��2����2�{��4��2��2���{��4��2����2�{�{��4��2����2�{��4��2��2��
�@�@�@�@�@�@�{��4��2��2���{��4��2����2�{��4��2����2�{��4��2��2���{��4��2����2�{��4��2����2�j
�@�{�i��3��3��2���{��3��3����2�{��3��3��2���{��3��3��2���{��3��3����2�{��3��3��2��
�@�@�@�@�{��3��3����2�{��3��3����2�{��3��3��2���{��3��3��2���{��3��3����2�{��3��3����2
�@�@�@�@�@�{��3��3����2�{��3��3��2���{��3��3��2���{��3��3��2���{��3��3����2�{��3��3��2��
�@�@�@�@�@�@�@�{��3��3��2���{��3��3����2�{��3��3����2�{��3��3����2�{��3��3��2���{��3��3����2�j
�@�{�i��3��2��2��2�{��3��2��2��2�{��3��2��2��2�{��3��2��2��2�{��3��2��2��2�{��3��2��2��2
�@�@�@�@�{��3��2��2��2�{��3��2��2��2�{��3��2��2��2�{��3��2��2��2��3��2��2��2�{��3��2��2��2�j
��
�i��4��3�����{��4��3�����{��4��3�����{��4��3�����{��4��3�����{��4��3�����{��4��3����
�@�@�@�@�{��4��3�����{��4��3�����{��4��3�����{��4��3�����{��4��3�����j
�@�{�Q�i
��4��2��2���{��4��2��2���{��4��2��2���{��4��2��2���{��4��2��2���{��4��2��2��
�@�@�@�@�{��4��2��2���{��4��2��2���{��4��2��2���{��4��2��2���{��4��2��2���{��4��2��2���j
�@�{�Q�i��3��3��2���{��3��3��2���{��3��3��2���{��3��3��2���{��3��3��2���{��3��3��2��
�@�@�@�@�{��3��3��2���{��3��3��2���{��3��3��2���{��3��3��2���{��3��3��2���{��3��3��2���j
�@�{�R�i��3��2��2��2�{��3��2��2��2�{��3��2��2��2�{��3��2��2��2�j
�@��L�̌v�Z����A�@�i�R�Q�P2�j�~�i�P2�j���i�S�R�P�P�j�{�Q�i�S�Q2�P�j�{�Q�i�R2�Q�P�j�{�R�i�R�Q3�j
�����藧���Ă���B��L�̌v�Z�́A�S�ϐ��̏ꍇ�Ȃ̂ŁA���R
�@�i�S�Q�P3�j���O�@�A�i�R2�P3�j���O�@�A�i�R�Q2�P2�j���O�@�A�i�R�Q�P4�j���O
�ł���B���̂��Ƃ��l������A
�@�i�R�Q�P2�j�~�i�P2�j
���i�S�R�P�P�j�{�Q�i�S�Q2�P�j�{�R�i�S�Q�P3�j�{�Q�i�R2�Q�P�j�{�U�i�R2�P3�j�{�R�i�R�Q3�j�{�S�i�R�Q2�P2�j
�@�{�U�i�R�Q�P4�j
�����藧���Ă�����̂ƍl���Ă������낤�B
�i�R�����g�j�@�S�ϐ��̌v�Z�͑�ςł����I��v�Z�Ȃ��̂ŁD�D�D(T-T)�@�B�ł��A���̌o����
�@�@�@�@�@�@�Ȃ��ƁA�����O�}�`�ɂ��Ώ̎��̌v�Z�̑f���炵���������ł��Ȃ��ł���l�I
�@���āA�Ώ̎��@�o�i��1�C��2�C�E�E�E�C��n�j�@���A�������̃����O�}�`�i�����E�E�E���j�̑������Ƃ���
�\�����Ƃ������Ƃ͒����I�ɖ��炩�Ƃ��Ă������낤�B
�@������A�`���ɏq�ׂ��d�v�藝�@�F
�@�@�Ώ̎��́A��{�Ώ̎��̑������Ƃ��ĕ\���A���̕\�����͈�ӓI�ł���B
��[������ɂ́A�����O�}�`����{�Ώ̎��̑������ŕ\����邱�Ƃ�������悢�B
�@���Ƃ��A�R�ϐ��̑Ώ̎��@��3�{��3�{��3�@����{�Ώ̎��ŕ\���͍̂��Z���̕W���I�Ȗ�
�肾�낤�B
�@��3�{��3�{��3
���i���{���{���j�i��2�{��2�{��2�|�����|�����|�����j�{�R������
���i���{���{���j�i�i���{���{���j2�|�R�i�����{�����{�����j�j�{�R������
����1�i��12�|�R��2�j�{�R��3
����13�|�R��1��2�{�R��3
�@��L�������O�}�`��p������\���A�i�R�j���i�P�j�~�i�P�j�~�i�P�j�|�R�i�P�j�~�i�P2�j�{�R�i�P3�j
�ƂȂ�B�@����́A�ǂ̂悤�ɉ��߂�������̂��낤���H
�@�i�R�j�̃����O�}�`�́A�@ �@�@�ł��邪�A������@
�@�@�ł��邪�A������@ �@�Ɓ@
�@�Ɓ@ �@�ɕ������āA����
�@�ɕ������āA����
�ς��l���Ă݂�B
�@��L�̌v�Z�̑�P���ɁA�����O�}�`�@ �@�@���\��Ă���_���̗v�ł���B
�@�@���\��Ă���_���̗v�ł���B
�@���l�ɂ��āA��L�ɕ\��Ă��郄���O�}�`�@ �@���A�@
�@���A�@ �@�Ɓ@
�@�Ɓ@ �@�ɕ������āA����
�@�ɕ������āA����
| �ς��l���Ă݂�ƁA |
�@�@�@�@�@�@�@�@�@�@�@ |
�~ |
 |
�� |
 |
�{�Q |
 |
| �ł��邵�A�����O�}�` |
�@ |
�@���A |
 |
�@�� |
�@ |
�@�ɕ������āA���̐ς��l���Ă݂�ƁA |
�ƂȂ�B�@��L�̌v�Z����A�@�i�Q�j�~�i�P�j���i�R�j�{�i�Q�P�j�@���A�@�i�R�j���i�Q�j�~�i�P�j�|�i�Q�P�j
�@�����ŁA�i�P�j�~�i�P�j���i�Q�j�{�Q�i�P2�j�@���A�@�i�Q�j���i�P�j�~�i�P�j�|�Q�i�P2�j
�@�i�P2�j�~�i�P�j���i�Q�P�j�{�R�i�P3�j�@���A�@�i�Q�P�j���i�P2�j�~�i�P�j�|�R�i�P3�j
�Ȃ̂ŁA
�@�i�R�j���i�i�P�j�~�i�P�j�|�Q�i�P2�j�j�~�i�P�j�|�i�i�P2�j�~�i�P�j�|�R�i�P3�j�j
�@�@�@���i�P�j�~�i�P�j�~�i�P�j�|�Q�i�P2�j�~�i�P�j�|�i�P2�j�~�i�P�j�{�R�i�P3�j
�@�@�@���i�P�j�~�i�P�j�~�i�P�j�|�R�i�P�j�~�i�P2�j�{�R�i�P3�j
�����藧�B
�@���̂悤�ɁA�����O�}�`���c�����ɕ������A���̐ς��l���邱�Ƃɂ���āA����ƃ���
�O�}�`�̕������������邱�Ƃ��ł���B�܂�́A�����P�̃����O�}�`�i��{�Ώ̎��I�j�ŕ\
����Ƃ������Ƃł���B���̂��Ƃ���A�Ώ̎�����{�Ώ̎��̑������ŕ\�����Ƃ�������
�C�𖡂키���Ƃ��o�����悤�Ɏv���B
�@�ǎ҂̂��߂ɁA���K����������Ă������B
��@���@�@�����O�}�`�@�i�S�j�@���A��{�Ώ̎���\�������O�}�`�̑������ŕ\���B
�i���j�@�i�R�j�~�i�P�j���i�S�j�{�i�R�P�j�@���A�@�i�S�j���i�R�j�~�i�P�j�|�i�R�P�j
�@�i�R�j���i�P�j�~�i�P�j�~�i�P�j�|�R�i�P�j�~�i�P2�j�{�R�i�P3�j�@�Ȃ̂ŁA
�@�i�R�j�~�i�P�j���i�P�j�~�i�P�j�~�i�P�j�~�i�P�j�|�R�i�P�j�~�i�P�j�~�i�P2�j�{�R�i�P3�j�~�i�P�j
�܂��A
�@�i�Q�P�j�~�i�P�j���i�R�P�j�{�Q�i�Q2�j�{�Q�i�Q�P2�j�@���A�i�R�P�j���i�Q�P�j�~�i�P�j�|�Q�i�Q2�j�|�Q�i�Q�P2�j
�ł���B�@�����ŁA�@�i�Q�P�j���i�P2�j�~�i�P�j�|�R�i�P3�j�@���A
�@�i�Q�P�j�~�i�P�j���i�P2�j�~�i�P�j�~�i�P�j�|�R�i�P3�j�~�i�P�j
�܂��A�i�P2�j�~�i�P2�j���i�Q2�j�{�Q�i�Q�P�P�j�{�U�i�P4�j�@���A
�@�i�Q2�j���i�P2�j�~�i�P2�j�|�Q�i�Q�P�P�j�|�U�i�P4�j
�����ŁA�@�i�P3�j�~�i�P�j���i�Q�P�P�j�{�S�i�P4�j�@���A�i�Q�P�P�j���i�P3�j�~�i�P�j�|�S�i�P4�j�@�Ȃ̂ŁA
�@�i�Q2�j���i�P2�j�~�i�P2�j�|�Q�i�i�P3�j�~�i�P�j�|�S�i�P4�j�j�|�U�i�P4�j
���i�P2�j�~�i�P2�j�|�Q�i�P3�j�~�i�P�j�{�Q�i�P4�j
�@�܂��A�@�@�i�P3�j�~�i�P�j���i�Q�P2�j�{�S�i�P4�j�@���A�@�i�Q�P2�j���i�P3�j�~�i�P�j�|�S�i�P4�j
����āA
�@�i�R�P�j
���i�P2�j�~�i�P�j�~�i�P�j�|�R�i�P3�j�~�i�P�j
�@�@�@�|�Q�i�i�P2�j�~�i�P2�j�|�Q�i�P3�j�~�i�P�j�{�Q�i�P4�j�j�|�Q�i�i�P3�j�~�i�P�j�|�S�i�P4�j�j
���i�P2�j�~�i�P�j�~�i�P�j�|�R�i�P3�j�~�i�P�j
�@�@�@�|�Q�i�P2�j�~�i�P2�j�{�S�i�P3�j�~�i�P�j�|�S�i�P4�j�|�Q�i�P3�j�~�i�P�j�{�W�i�P4�j
���i�P2�j�~�i�P�j�~�i�P�j�|�i�P3�j�~�i�P�j�|�Q�i�P2�j�~�i�P2�j�{�S�i�P4�j
�ȏォ��A
�i�S�j���i�P�j�~�i�P�j�~�i�P�j�~�i�P�j�|�R�i�P�j�~�i�P�j�~�i�P2�j�{�R�i�P3�j�~�i�P�j
�@�@�@�@�@�|�i�i�P2�j�~�i�P�j�~�i�P�j�|�i�P3�j�~�i�P�j�|�Q�i�P2�j�~�i�P2�j�{�S�i�P4�j�j
�@���i�P�j�~�i�P�j�~�i�P�j�~�i�P�j�|�R�i�P�j�~�i�P�j�~�i�P2�j�{�R�i�P3�j�~�i�P�j
�@�@�@�@�@�|�i�P2�j�~�i�P�j�~�i�P�j�{�i�P3�j�~�i�P�j�{�Q�i�P2�j�~�i�P2�j�|�S�i�P4�j
���i�P�j�~�i�P�j�~�i�P�j�~�i�P�j�|�S�i�P�j�~�i�P�j�~�i�P2�j�{�S�i�P3�j�~�i�P�j�{�Q�i�P2�j�~�i�P2�j�|�S�i�P4�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�I�j
�@���̌v�Z�����M���Ȃ��̂ŁA�Q�ϐ��̏ꍇ�ɂ��Ċm�F���Ă݂悤�B
�@�i�S�j����4�{��4�@�ł��邪�A
�@��4�{��4���i��2�{��2�j2�|�Q��2��2�@�ŁA�@��2�{��2���i���{���j2�|�Q�������i�P�j�~�i�P�j�|�Q�i�P2�j
�Ȃ̂ŁA
�@�i�S�j���i�i�P�j�~�i�P�j�|�Q�i�P2�j�j2�|�Q�i�P2�j�~�i�P2�j
�@�@�@���i�P�j�~�i�P�j�~�i�P�j�~�i�P�j�|�S�i�P�j�~�i�P�j�~�i�P2�j�{�S�i�P2�j�~�i�P2�j�|�Q�i�P2�j�~�i�P2�j
�@�@�@���i�P�j�~�i�P�j�~�i�P�j�~�i�P�j�|�S�i�P�j�~�i�P�j�~�i�P2�j�{�Q�i�P2�j�~�i�P2�j
�@�Q�ϐ��Ȃ̂ŁA�@�i�P3�j���O�@�A�@�i�P4�j���O�@�Ƃ��Ă悢�̂ŁA�㎮�́A�Q�ϐ��̏ꍇ�ɐ���
�����Ƃ������Ă���B
�i�R�����g�j�@��L�̔ώG�ȑΏ̎��̌v�Z�����Ē����C�Â��悤�ɁA�����g�܂��A
�@�@����������Z�̒B�l���l�����Z������ł��Ȃ��悤�ɁA���G�ȑΏ̎��̌v�Z��
�@�ÎZ�ōs�����Ƃ��ł���悤�ɂȂ�ł��낤�B
�Ƃ������n�ɂ͎����Ă��Ȃ��B��̂��ɂȂ�����A���̂悤�ȋ��n�ɂȂ��̂��낤���H
�@���w�U�ő��������̔����E�ϕ����w�ԂƁA���w�̖���@�ɖ𗧂��낢��Ȍ���
����ɂ��邱�Ƃ��o����B����́A���������q���B���M������Q�[���œG��|���ĐV����
�������ɂ��A����̃L�����N�^�[�̃p���[���A�b�v����̂Ɏ��Ă���B
�@���Z����ɁA�����ł������@�̌��p�����������̂́A���̌����ł���B
�@�������@�e�i���j���O�@���d�� ��
�������߂̕K�v�\�������́A
�@�@�@�@�e�i���j���e�f�i���j���O�@�@�@�@�i�������A�@�e�i���j
�͑������j
�@���̎����́A������ �ɂ����� �e�i���j
�̂s�����������W�J���疾�炩���낤�B
�@���Z�������ɂ́A���̂悤�ɐ�������Ɨ������Ă��炦��Ǝv���B
�i�ؖ��j�@�@�e�i���j���A���|��
�Ŋ������]��́A��]�̒藝�ɂ��A�@�e�i���j�@�ł���B
�@����āA�@���� �p�i���j �Ƃ��āA�@����Z�̍P�������A�@�e�i���j���i���|���j�p�i���j�{�e�i���j
�@����ɁA�@�p�i���j���A���|�� �Ŋ���������
�q�i���j�A�]����@���@�Ƃ����ƁA
�@�@�@�@�@�@�p�i���j���i���|���j�q�i���j�{��
�@����āA�@�e�i���j���i���|���j�i�i���|���j�q�i���j�{���j�{�e�i���j���i���|���j2�q�i���j�{���i���|���j�{�e�i���j
�@�@���ӂ�������āA�@�e�f�i���j���Q�i���|���j�q�i���j�{�i���|���j2�q�f�i���j�{��
�@���������āA�@�e�f�i���j�����@�ƂȂ�A�@�e�i���j���i���|���j2�q�i���j�{�e�f�i���j�i���|���j�{�e�i���j
�@�@���̂��Ƃ���A�@�������@�e�i���j���O�@���d��
��
�����ĂA�@�e�i���j�@�́A�i���|���j2�@�Ŋ���
�@���̂ŁA���̗]��@�e�f�i���j�i���|���j�{�e�i���j���O�@����A�@�e�i���j���e�f�i���j���O
�@�@�t�ɁA�@�e�i���j���e�f�i���j���O�@�Ƃ���ƁA�@�e�i���j���i���|���j2�q�i���j�@�ƂȂ�A
�@�e�i���j�@�́A�i���|���j2�@�Ŋ����A�������@�e�i���j���O�@�͏d��
�� �����B�@�i�؏I�j
�@�@�����ŁA�@�e�i���j���e�f�i���j���O�@�Ƃ������Ƃ́A�Q�̕������@�e�i���j���O�@�A�@�e�f�i���j���O
�@�����ʉ�
��
�����Ƃ������Ƃł���B
�@���̋��ʉ��̖����A�������Z���̍��ꂵ�߂�ꂽ���̈�ł���B
�@���ʉ��̖��ɂ��ẮA�I�����Ƃ����T�O������B
�@�@��������O��ɍl����̂ŁA�ō����̌W����
�P
�Ƃ���B�@�܂��A��������ɕ����̌�
�@���𑝂₳�Ȃ����߂ɁA�R���������Ɍ��肵�čl���邱�Ƃɂ���B������������āA
�@�@�@�e�i���j���i���|���j�i���|���j�i���|���j�@�@�A�f�i���j���i���|���j�i���|���j�i���|���j
�@�Ƃ���B�@���̂Ƃ��A
�@�f�i���j�f�i���j�f�i���j���i���|���j�i���|���j�i���|���j�i���|���j�i���|���j�i���|���j�i���|���j�i���|���j�i���|���j
���l����ƁA���̍��̑S�Ẵp�^�[���������Ă���̂ŁA
�@�������@�e�i���j���O�@�A�f�i���j���O�@�����ʉ��������ƂƁ@�f�i���j�f�i���j�f�i���j���O�@�͓��l
�ł��邱�Ƃ͖��炩���낤�B
�@�f�i���j�f�i���j�f�i���j�@���@�������@�e�i���j�A�f�i���j�@���I�����Ƃ����A�ʏ�@�q�i�e�C�f�j�@�ƕ\���B
�@���Ȃ킿�A�@�@�@�q�i�e�C�f�j���f�i���j�f�i���j�f�i���j
�@�ȏ���܂Ƃ߂āA���̒藝��B
��@���@�@�������@�e�i���j���O�@�A�f�i���j���O�@�����ʉ��������߂̕K�v�\��������
�@�@�@�@�@�q�i�e�C�f�j���O�@�ł���B
�@���āA�q�i�e�C�f�j���f�i���j�f�i���j�f�i���j�̉E�ӂ͂R�ϐ�
�� �A �� �A �� �̑������ł��邪�A�����
�̏��Ԃ�C�ӂɕύX���Ă����̎��Ɠ����Ȃ̂ŁA�I���� �q�i�e�C�f�j
�͑Ώ̎��ł���B
�@�Ƃ������Ƃ́A�I�����̌v�Z�ɂ��A�����O�}�`���g����Ƃ������Ƃł���B
��@�@�e�i���j����2�{�����{�����i���|���j�i���|���j�@�A�f�i���j����2�{�����{�����i���|���j�i���|���j�@�ɑ�
�@�@���āA���̏I�����@�q�i�e�C�f�j�@���v�Z���Ă݂悤�B
�@�@�q�i�e�C�f�j���f�i���j�f�i���j���i���|���j�i���|���j�i���|���j�i���|���j
�@���ƌW���̊W���A�@���{�����|���@�A�@���������@�A�@���{�����|���@�A�@���������@�Ȃ̂ŁA
�@�q�i�e�C�f�j
���i��2�{�����{���j�i��2�{�����{���j
����2��2�{����2���{����2�{������2�{��2�����{�������{����2�{�������{��2
����2��2�{�������i���{���j�{��2�����{���i��2�{��2�j�{�����i���{���j�{��2
����2��2�{�������i���{���j�{��2�����{���i�i���{���j2�|�Q�����j�{�����i���{���j�{��2
����2�|�������{��2���{���i��2�|�Q���j�|�������{��2
������2�|�������{��2�|�������{��2���|�Q�����{��2
�@���ʂɓW�J����Ώ�L�̂悤�ł��邪�A���̓W�J�Ƀ����O�}�`���I���Ɏg����炵���B
�@�q�i�e�C�f�j �̓W�J���ŁA���A�� �Ɋւ���Ώ̎��������O�}�`�ŕ\���A
�@�q�i�e�C�f�j
����2��2�{����2���{����2�{������2�{��2�����{�������{����2�{�������{��2
����2��2�{���i��2���{����2�j�{���i��2�{��2�j�{��2�����{�����i���{���j�{��2
���i�Q2�j�{���i�Q�P�j�{���i�Q�j�{��2�i�P2�j�{�����i�P�j�{��2
�ł���B
�@���ۂ̓W�J�����烄���O�}�`�ɒ������Ƃ͈Ղ����B�ł��A�ŏ����烄���O�}�`�Ōv�Z����
�ɂ͂ǂ������炢���̂��낤���H
�@���̓W�J���ŁA ��2 �A ���� �A ��2 �A �� �A �� �A �P�@�̊e�����o��͖̂��炩���낤�B���́A
���̌W���ł���B
�@����ɂ́A�� �͉��ƌW���̊W����قȂ���̂P�����Ȃ̂ŁA�� �ɂ́A�����O�}�`�@
��Ή��Â��A�����āA��2 �ɂ́A�����O�}�`
�@�@
��Ή��Â��čl����Ƃ����炵���B
�@���l�ɁA�� �͉��ƌW���̊W����قȂ���̂Q�����Ȃ̂ŁA�� �ɂ́A�����O�}�`�@
��Ή��Â��A�����āA��2 �ɂ́A�����O�}�`
�@
��Ή��Â��邱�Ƃɂ���B
�@�e�i���j�A�f�i���j�̎����́A�Ƃ��� �Q �Ȃ̂ŁA��{�ƂȂ郄���O�}�`�́A
�@
�ł���B�e���̌W�������߂�ɂ́A���A�� �Ɋւ��郄���O�}�`����{�ƂȂ郄���O�}�`����
���������悢�B
�@��2 �̌W���́A��{�ƂȂ郄���O�}�`����
�@
�����������āA
�@
�Ȃ̂ŁA�����O�}�`�́A�i�P�P�j���i�P2�j�ł���B�i����L�̓W�J���ƈ�v�I�j
�@���� �̌W���́A��{�ƂȂ郄���O�}�`����A�@ �@�Ɓ@
�@�Ɓ@
���������������āA
�@ �@�@���@�@
�@�@���@�@ �@�@���@�@
�@�@���@�@
�Ȃ̂ŁA�����O�}�`�́A�i�P�j�ł���B�i����L�̓W�J���ƈ�v�I�j
�@��2 �̌W���́A��{�ƂȂ郄���O�}�`����
�@
�����������ĉ����c��Ȃ��̂ŌW���́A�P �ƍl����B�i����L�̓W�J���ƈ�v�I�j
�@�� �̌W���́A��{�ƂȂ郄���O�}�`����A�@ �@�����������āA
�@�����������āA
�@ �@�@���@�@
�@�@���@�@
�ƂȂ�A����́A
�@
�ƍl���A�����O�}�`�́A�i�Q�P�j�ł���B�i����L�̓W�J���ƈ�v�I�j
�@�� �̌W���́A��{�ƂȂ郄���O�}�`����A�@ �@�����������āA
�@�����������āA
�@ �@�@���@�@
�@�@���@�@
�Ȃ̂ŁA�����O�}�`�́A�i�Q�j�ł���B�i����L�̓W�J���ƈ�v�I�j
�@�P �̌W���́A��{�ƂȂ郄���O�}�`����A�������̂��Ȃ��̂ŁA
�@
�ƂȂ�A�����O�}�`�́A�i�Q�Q�j���i�Q2�j�ł���B�i����L�̓W�J���ƈ�v�I�j
�@���̂悤�ɍl����ƁA�����ɁA
�@�q�i�e�C�f�j���i�Q2�j�{���i�Q�P�j�{���i�Q�j�{��2�i�P2�j�{�����i�P�j�{��2
�ł��邱�Ƃ��������B�i���@����́A�X�S�C�I�I�ÎZ�ł��ł������D�D�D�B�j
�@��L�̓W�J���ł́A�i�Q�����j�~�i�Q�����j�Ȃ̂ŁA�����O�}�`��p���郁���b�g�͂��܂芴��
���Ȃ���������Ȃ����A�����������ɂȂ�ƁA���̌��p�����������ł��邱�Ƃ��낤�B
�@�����ɁA�i�R�����j�~�i�R�����j�̏ꍇ�ŗ��K���Ă݂悤�B
��@�@�e�i���j����3�{����2�{�����{�����i���|���j�i���|���j�i���|���j
�@�@�f�i���j����3�{����2�{�����{�����i���|���j�i���|���j�i���|���j�@�@�@�ɑ��āA
�@���̏I�����@�q�i�e�C�f�j�@�́A
�@�q�i�e�C�f�j���f�i���j�f�i���j�f�i���j
���i��3�{����2�{�����{���j�i��3�{����2�{�����{���j�i��3�{����2�{�����{���j
�@���̓W�J���ŁA
�@�P�A���A���A���A��2�A�����A�����A��2�A�����A��2�A��3�A��2���A��2���A����2�A�������A����2�A��3�A
�@��2���A����2�A��3
�̊e�����o��B�i�P�A���A���A���@�̂S�̕�������d���������ĂR���g�����́A4�g3���Q�O�ʂ��j
�@����ɂ́A�� �͉��ƌW���̊W����قȂ���̂P�����Ȃ̂ŁA�� �ɂ̓����O�}�`�i�P�j�A
��2 �ɂ̓����O�}�`�i�P2�j�A ��3 �ɂ̓����O�}�`�i�P3�j��Ή��Â���B
�@���l�ɁA�� �͉��ƌW���̊W����قȂ���̂Q�����Ȃ̂ŁA�� �ɂ́A�����O�}�`�i�Q�j�A
��2 �ɂ̓����O�}�`�i�Q2�j�A ��3 �ɂ̓����O�}�`�i�Q3�j��Ή��Â���B
�@�� �͉��ƌW���̊W����قȂ���̂R�����Ȃ̂ŁA�� �ɂ́A�����O�}�`�i�R�j�A��2 �ɂ�
�����O�}�`�i�R2�j�A ��3 �ɂ̓����O�}�`�i�R3�j��Ή��Â���B
�@�e�i���j�A�f�i���j�̎����́A�Ƃ��� �R �Ȃ̂ŁA��{�ƂȂ郄���O�}�`�́i�R3�j�A���Ȃ킿�A
�@
�ł���B�e���̌W�������߂�ɂ́A���A���A�� �Ɋւ��郄���O�}�`����{�ƂȂ郄���O�}�`
���獷�������悢�B
�P �̌W���́A��{�ƂȂ郄���O�}�`����������̂��Ȃ��̂ŁA�����O�}�`�́A�i�R3�j
�� �̌W���́A��{�ƂȂ郄���O�}�`����i�P�j�����������āA�����O�}�`�́A�i�R2�Q�j
�� �̌W���́A��{�ƂȂ郄���O�}�`����i�Q�j�����������āA�����O�}�`�́A�i�R2�P�j
�� �̌W���́A��{�ƂȂ郄���O�}�`����i�R�j�����������āA�����O�}�`�́A�i�R2�j
��2 �̌W���́A��{�ƂȂ郄���O�}�`����i�P2�j�����������āA�����O�}�`�́A�i�R�Q2�j
���� �̌W���́A��{�ƂȂ郄���O�}�`����i�P�j�A�i�Q�j���������������āA�����O�}�`�́A�i�R�Q�P�j
���� �̌W���́A��{�ƂȂ郄���O�}�`����i�P�j�A�i�R�j���������������āA�����O�}�`�́A�i�R�Q�j
��2 �̌W���́A��{�ƂȂ郄���O�}�`����i�Q2�j�����������āA�����O�}�`�́A�i�R�P2�j
���� �̌W���́A��{�ƂȂ郄���O�}�`����i�Q�j�A�i�R�j���������������āA�����O�}�`�́A�i�R�P�j
��2 �̌W���́A��{�ƂȂ郄���O�}�`����i�R2�j�����������āA�����O�}�`�́A�i�R�j
��3 �̌W���́A��{�ƂȂ郄���O�}�`����i�P3�j�����������āA�����O�}�`�́A�i�Q3�j
��2�� �̌W���́A��{�ƂȂ郄���O�}�`����i�P2�j�A�i�Q�j���������������āA�����O�}�`�́A�i�Q2�P�j
��2�� �̌W���́A��{�ƂȂ郄���O�}�`����i�P2�j�A�i�R�j���������������āA�����O�}�`�́A�i�Q2�j
����2 �̌W���́A��{�ƂȂ郄���O�}�`����i�P�j�A�i�Q2�j���������������āA�����O�}�`�́A�i�Q�P2�j
������ �̌W���́A��{�ƂȂ郄���O�}�`����i�P�j�A�i�Q�j�A�i�R�j���������������āA�����O�}�`�́A�i�Q�P�j
����2 �̌W���́A��{�ƂȂ郄���O�}�`����i�P�j�A�i�R2�j���������������āA�����O�}�`�́A�i�Q�j
��3 �̌W���́A��{�ƂȂ郄���O�}�`����i�Q3�j�����������āA�����O�}�`�́A�i�P3�j
��2�� �̌W���́A��{�ƂȂ郄���O�}�`����i�Q2�j�A�i�R�j���������������āA�����O�}�`�́A�i�P2�j
����2 �̌W���́A��{�ƂȂ郄���O�}�`����i�Q�j�A�i�R2�j���������������āA�����O�}�`�́A�i�P�j
��3 �̌W���́A��{�ƂȂ郄���O�}�`����i�R3�j�����������ĉ����c��Ȃ��̂ŌW���́A�P �ƍl����B
�ȏォ��A
�q�i�e�C�f�j
���i�R3�j�{�i�R2�Q�j���{�i�R2�P�j���{�i�R2�j���{�i�R�Q2�j��2
�@�@�{�i�R�Q�P�j�����{�i�R�Q�j�����{�i�R�P2�j��2�{�i�R�P�j�����{�i�R�j��2
�@�@�{�i�Q3�j��3�{�i�Q2�P�j��2���{�i�Q2�j��2���{�i�Q�P2�j����2�{�i�Q�P�j������
�@�@�{�i�Q�j����2�{�i�P3�j��3�{�i�P2�j��2���{�i�P�j ����2�{ ��3
�i�R�����g�j�@�ʂ����āA���̌v�Z�͐������̂��낤���H������Ǝ��M���Ȃ��I�I
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�D�D�D�P�h�A������������J�i�H�j
�@�@�@�@�@�@������ƕa�݂��ɂȂ肻���Ȍv�Z�ł��ˁD�D�D�B
�ł��A�l�I�Ȋ��z�Ȃ���A�W�J����������c�ɕ��ׂāA
�@�i��3�{����2�{�����{���j
�@�i��3�{����2�{�����{���j
�@�i��3�{����2�{�����{���j
�@�����W�J�̍��Ƃ��̌W���̌^�i�������O�}�`�j���ꏏ�Ɍv�Z�������������悤�ȋC������B
�@�I�����̌v�Z�ƌ����A�V���x�X�^�[�iSylvester�j�̍s�����L�����낤�B
��@�@�e�i���j����2�{�����{���@�A�f�i���j����2�{�����{���@�ɑ��āA���̏I�����@�q�i�e�C�f�j�@�́A
�@�@�q�i�e�C�f�j������2�|�������{��2�|�������{��2���|�Q�����{��2
�ł��������A����́A���̃V���x�X�^�[�iSylvester�j�̍s���v�Z���Ă����߂���B
�@
�@�I�������獂�Z���w�ł�����݂̔��ʎ����������B
�@�Q�����@�e�i���j����2�{�����{���@�ɑ��āA�I�����@�q�i�e�C�e�f�j���v�Z����ƁA
�@�e�i���j����2�{�����{�����i���|���j�i���|���j�@�ŁA�@�e�f�i���j���Q���{��
����āA�@�q�i�e�C�e�f�j���i�Q���{���j�i�Q���{���j���S�i�P2�j�{�Q���i�P�j�{��2
�@�i���@���������Ȃ̂Ń����O�}�`��p�����D�D�D��(�O�O;) )
�i�P�j���|���@�A�i�P2�j�����@�Ȃ̂ŁA�@�q�i�e�C�e�f�j���S���|�Q��2�{��2���S���|��2���|�i��2�|�S���j
�@�����ŁA�Q�����@�e�i���j����2�{�����{���@�̔��ʎ����A�@�c�i�e�j���|�q�i�e�C�e�f�j�@�ƒ�`����A
�@�c�i�e�j����2�|�S��
�ƂȂ�A�悭�m�������Ĉ���S�I
�@��L�ŏq�ׂ��Q�̎����@�F
�i�P�j�@�������@�e�i���j���O�@���d�� ��
�������߂̕K�v�\�������́A
�@�@�e�i���j���e�f�i���j���O�@�@�@�@�i�������A�@�e�i���j �͑������j
�i�Q�j�@�������@�e�i���j���O�@�A�f�i���j���O�@�����ʉ��������߂̕K�v�\��������
�@�@�q�i�e�C�f�j���O�@�ł���B
����A�@�Q���������@��2�{�����{�����O�@���d���������߂̕K�v�\�������́A
�@�@���ʎ��@��2�|�S�����O
�ł��邱�Ƃ��m���߂�ꂽ�B
�i�NjL�j�@�����Q�O�N�P���V���t��
�@�Ώ̎�����{�Ώ̎��ŕ\�����͎�X���邪�A���̑Ώ̎��ɂ��Ĕ��Ɏa�V�I�ȕ�
�������邱�Ƃ��ŋߒm�邱�Ƃ��o�����B
�@�@��2��2�{��2��2�{��2��2�{��2��2�{��2��2�{��2��2�@����{�Ώ̎��ŕ\���B
�@�����ŁA��{�Ώ̎��Ƃ́A
�@��1�����{���{���{��
�@��2�������{�����{�����{�����{�����{����
�@��3���������{�������{�������{������
�@��4����������
�ł��邱�Ƃ��m�F���Ă����B
�@���̕ʉ��̑f���炵���𗝉����邽�߂ɁA�������̉�@�߂Ă������B
�i���̂P�j�@�P�����̏������l���Ď��ό`�@�i���@�Q�l�F�u�O���u�i�[����v�j
��2��2�{��2��2�{��2��2�{��2��2�{��2��2�{��2��2�|��22
����2��2�{��2��2�{��2��2�{��2��2�{��2��2�{��2��2�|�i�����{�����{�����{�����{�����{�����j2
���|�Q�i��2�����{��2�����{��2�����{����2���{����2���{������2�{����2���{������2�{������2
�@�@�@�@�@�{�R���������{��2�����{����2���{������2�j
�@����āA
�@��2��2�{��2��2�{��2��2�{��2��2�{��2��2�{��2��2�|��22�{�Q��1��3���Q�����������Q��4
���������āA�@��2��2�{��2��2�{��2��2�{��2��2�{��2��2�{��2��2����22�|�Q��1��3�{�Q��4
�i�R�����g�j�@��{�Ώ̎��ŕ\���A���S���Y���ɏ]���Čv�Z���Ă݂͂����̂̔ώG�Ȍv�Z��
�@�@�@�@�@�@�S���������Ȃ��I
�i���̂Q�j�@�����O�}�`�ɂ�鎮�ό`
�@�@�Ώ̎��@��2��2�{��2��2�{��2��2�{��2��2�{��2��2�{��2��2�@�̃����O�}�`�́A�i�Q�Q�j
���Ȃ킿�A
�@
�@�ł���B���������āA���̃����O�}�`����邽�߂ɁA
�@�@ |
�@�@�� |
�@�@ |
�@�@�̐� |
�@���l����B
|
|
�@ |
�@�̌W���́A�@2�b2���P |
| �@ |
|
|
�@ �@�@ �@�@ |
�@�̌W���́A�@1�b1�~2�b1���Q |
| �@ |
|
|
�@ |
�@�̌W���́A4�b2���U�@ |
����āA�@�i�P2�j�~�i�P2�j���i�Q2�j�{�Q�i�Q�P2�j�{�U�i�P4�j�@���A
�@�@�i�Q2�j���i�P2�j�~�i�P2�j�|�Q�i�Q�P2�j�|�U�i�P4�j
�@���l�ɂ��āA
�@ |
�@�@�� |
�@�@ |
�@�@�̐� |
�@���l����B
|
|
�@ �@�@ �@�@ |
�@�̌W���́A�@1�b1���P |
| �@ |
|
|
�@ |
�@�̌W���́A4�b1���S�@ |
����āA�@�i�P3�j�~�i�P�j���i�Q�P2�j�{�S�i�P4�j�@���A�@�i�Q�P2�j���i�P3�j�~�i�P�j�|�S�i�P4�j
�@�ȏォ��A
�i�Q2�j���i�P2�j�~�i�P2�j�|�Q�o�i�P3�j�~�i�P�j�|�S�i�P4�j�p�|�U�i�P4�j
�@�@���i�P2�j�~�i�P2�j�|�Q�i�P3�j�~�i�P�j�{�Q�i�P4�j
�@���Ȃ킿�A�@��2��2�{��2��2�{��2��2�{��2��2�{��2��2�{��2��2����22�|�Q��1��3�{�Q��4
�i�R�����g�j�@�����O�}�`�͌v�Z���Ă��Ċy�����̂����A�v�Z�K����Y��₷���A���܂����
�@�@�@�@�@�@�I�ł͂Ȃ��悤�ȁD�D�D�����B������L�̌v�Z�����邽�߂ɕ��K���Ă��܂����I
�@���悢��a�V�ȕʉ����Љ�鏀�����������B�ƂĂ��A�h�z�b�N�ȉ�@�ł��邪�A������
����̂𖣗�����ł��낤�B
�i�A�h�z�b�N�i�����������j�Ƃ������t�́A�u���ɂ��̂��߂́v�Ƃ����Ӗ��B�ŋ߂�����Ƃ̃��[���̂��Ƃ�̒��ɂ���
�@�����̂ň�x�g���Ă݂��������D�D�D(^_^)v�j
�i���̂R�j�@�W����r�ɂ��v�Z
�@���̂Q�������藧���Ƃ͖��炩���낤�B
�@�i�P�{���j�i�P�{���j�i�P�{���j�i�P�{���j���P�{��1�{��2�{��3�{��4
�@�i�P�|���j�i�P�|���j�i�P�|���j�i�P����j���P�|��1�{��2�|��3�{��4
���������āA�ӁX�����āA
�@�i�P�|��2�j�i�P�|��2�j�i�P�|��2�j�i�P���2�j���i�P�{��1�{��2�{��3�{��4�j�i�P�|��1�{��2�|��3�{��4�j
���ӂ�W�J���āA�������S�ƂȂ���̂��܂Ƃ߂����̂��A
�@��2��2�{��2��2�{��2��2�{��2��2�{��2��2�{��2��2
�E�ӂ�W�J���āA�������S�ƂȂ���̂��܂Ƃ߂�ƁA
�@�P�E��4�|��1�E��3�{��2�E��2�|��3�E��1�{��4�E�P����22�|�Q��1��3�{�Q��4
����āA�@��2��2�{��2��2�{��2��2�{��2��2�{��2��2�{��2��2����22�|�Q��1��3�{�Q��4
�i�R�����g�j�@�����I������ʏ����I�ŁA���̕�����₷���ɒE�X���܂����I
�i�Q�l�����F�@���@���v�@���@�@�㐔�w�@ ���Ǝ��̌���I���_�@�@�i�X�k�o�Łj
�@�@�@�@�@�@�@�@�O�����Y�@���@���@�@�㐔�w�Ɗw�@�@�i�։ؖ[�j
�@�@�@�@�@�@�@�@�i�c��X�@���@�@���`�㐔�̊�b�@�@�i�I�ɚ������X�j
�@�@�@�@�@�@�@�@���w�Z�~�i�[�@�P�X�X�X�N�U�`�W�����@�@�i���{�]�_�Ёj�j
�i�NjL�j�@���g�o�̌f���u�o��̐�v�ɁA�����Q�T�N�S���P�V���t���łg�m�u�u�v������A��
�@�@�@�@�̎��̌v�Z���@�ɂ��Ă̏������݂��������B
�@���̃T�C�g�ɉ��L�̂悤�Ȏ��₪����A�ȉ��̂悤�ɉ��܂����B�Ώ̎��̌v�Z���ȒP
���m���ɍs�����߂̎菇��\�L���@����������Ă��������B
�i���̎���j�@���̂T���̑Ώ̎��̊W���̃G���K���g�ȏؖ��̎d��������܂���B������
�@�@�@�@�@�@�@�������B
�@(x5+y5+z5+w5+v5)
-(x4+y4+z4+w4+v4)(x+y+z+w+v)
+(x3+y3+z3+w3+v3)(xy+xz+xw+xv+yz+yw+yv+zw+zv+wv)
-(x2+y2+z2+w2+v2)(xyz+xyw+xyv+xzw+xzv+xwv+yzw+yzv+ywv+zwv)
+(x+y+z+w+v)(xyzw+xyzv+xywv+xzwv+yzwv)
-5xyzwv=0
�i���̉j�@�^���́Ax�Ay�Az�Aw�Av �̑Ώ̎��ŁA���W�J��̊e���͂��ׂĂT�����Ȃ̂�
�e���̎����� x�Ay�Az�Aw�Av �ւ̕��z�̃p�^�[���́A�������傫������
�@�@(5,0,0,0,0)�@(4,1,0,0,0)�@(3,2,0,0,0)�@(3,1,1,0,0)�@(2,2,1,0,0)�@(2,1,1,1,0)�@(1,1,1,1,1)
����āAx5�Ax4y�Ax3y2�Ax3yz�Ax2y2z�Ax2yzw�Axyzwv �̂��ꂼ��̌W�����O�ɂȂ邱�Ƃ�����
�悢�B�^����
x5�̌W�� =1-1+0+0+0+0=0�Ax4y�̌W�� =0-1+1+0+0+0=0�Ax3y2�̌W�� =0+0+0+0+0+0=0
x3yz�̌W�� =0+0+1-1+0+0=0�Ax2y2z�̌W��=0+0+0+0+0+0=0�Ax2yzw�̌W�� =0+0+0-1+1+0=0
xyzwv�̌W�� =0+0+0+0+5-5=0
�@����āA�^����0
���@�Ȃ����̎���ɂ͉��ƌW���̊W���g�����G���K���g�ȏؖ��̉�����܂����B
�@��M����̃R�����g�ł��B�i�����Q�T�N�S���P�V���t���j
�@��L�ɕ֗��ȕ\�L���Љ��Ă��܂��l�B
�@ �Ώ̎��ŁA���������E�E�E�����@�i���������E�E�E�������O�j�̌`�̒P�������܂ނ��̂��A�L����
�@�@�@�@�@�@�@�@�i�����E�E�E���j
�ƕ\���B
�@���̕\�L���g���Ɩ��̎��́A�@(5)-(1)(4)+(11)(3)-(111)(2)+(1111)(1)-(11111)�@�Ə�����
�܂��B���ꂼ��̐ς�W�J���邱�Ƃ��l����ƈȉ��̂悤�ɂȂ�܂��B
�@(11111) = (11111)�@�A(1111)(1) = (2111)+(11111)�@�A(111)(2)=(311)+(2111)�@�A
�@(11)(3)=(41)+(311)�@�A(1)(4)=(5)+(41)�@�A(5) = (5)
�@���݂ɑ������������0�ɂȂ邱�Ƃ�������܂����B
�i�R�����g�j�@�����O�}�`��������ł��ˁI
�i�NjL�j�@�����Q�T�N�W���P�O���t���ŁA�j�D�r�D������A�Ώ̎��ɂ��Ă̘b������[���Œ�
�@�@�@�@�����B�j�D�r�D����Ɋ��ӂ��܂��B
�@��{�Ώ̎�
��1����1�{��2�{�E�E�E�{��n�@�A��2����1��2�{��1��3�{�E�E�E�{��n-1��n�@�A�E�E�E�A��������1��2�E�E�E��n
�ɑ��āA�����Ώ̎�
��1����1�{��2�{�E�E�E�{��n�@�A��2����12�{��22�{�E�E�E�{��n2�@�A�E�E�E�@�A��������1n�{��2n�{�E�E�E�{��nn
���l����B���̂Ƃ��A�j���[�g���̑�����
�@�����|��1����-1�{��2����-2�|�E�E�E�{�i�|�P�j��-1����-1��1�{�i�|�P�j�����������O
�����藧�B
��@���w�ł͗L���ȍP����
�@�@��13�{��23�{�E�E�E�{��n3�|�R��1��2��3
�@���i��1�{��2�{��3�j�i��12�{��22�{�E�E�E�{��n2�|��1��2�|��2��3�|��3��1�j
����A�@��3�|�R��3����1�i��2�|��2�j�@���Ȃ킿�A�@��3�|��1��2�{��2��1�|�R��3���O�@�����藧�B
�@�j���[�g���̑��������ؖ����Ă݂悤�B�i�����Q�U�N�R���S���t���j
�i�ؖ��j�@�d�i���j���P�{��1���{��2��2�{�E�E�E�{���������@�Ƃ����ƁA�d�i���j���i�P�{��1���j�i�P�{��2���j�E�E�E�i�P�{�������j
�@���ӂ̎��R�ΐ����Ƃ��āA�@������ �d�i���j���������i�P�{��1���j�{�������i�P�{��2���j�{�E�E�E�{�������i�P�{�������j
���ӂ� �� �Ŕ������āA�@�d�f�i���j/�d�i���j����1/�i�P�{��1���j�{��2/�i�P�{��2���j�{�E�E�E�{����/�i�P�{�������j
����āA�@���i�d�f�i���j/�d�i���j�j����1��/�i�P�{��1���j�{��2��/�i�P�{��2���j�{�E�E�E�{������/�i�P�{�������j
�����ŁA�@������/�i�P�{�������j���������E����=1�`�� �i�|�P�j��-1�i�������j��-1������=1�`�� �i�|�P�j��-1�i�������j��
�Ȃ̂ŁA
���i�d�f�i���j/�d�i���j�j������=1�`�� �i�|�P�j��-1�i��1���{��2���{�E�E�E�{�������j����������=1�`�� �i�|�P�j��-1 ��������
���Ȃ킿�A�@���d�f�i���j���d�i���j�i��1���|��2��2�{�E�E�E�{�i�|�P�j��-1 ���������{�E�E�E�j�@�ɂ����āA
���ӂ� ���� �̌W�����r���āA�@���������i�|�P�j��-1 �����{��1�E�i�|�P�j��-2 ����-1�{�E�E�E�{����-1�E��1
���ӂɁA�i�|�P�j�����|���āA�@�i�|�P�j�����������|�����{��1����-1�|�E�E�E�{�i�|�P�j������-1��1
�@������A�j���[�g���̑�����
�@�����|��1����-1�{��2����-2�|�E�E�E�{�i�|�P�j��-1����-1��1�{�i�|�P�j�����������O
��B�@�@�i�؏I�j
�@�j�D�r�D����̃R�����g�ł��B�i�����Q�U�N�V���V���t���j
�@�j���[�g���̑������́A������p���Ȃ��Ă��������B
�@F(X)��(X�|��1)(X�|��2�j�E�E�E(X�|��n)�@�Ƃ����ƁA�@F(x��)���O�@(�����P�`���j
����A�W�J�������@F(X)��Xn�|S1Xn-1�{�E�E�E�{�i�|�P�j��Sn�@�Ȃ̂ŁA
F(x1) ���� F(x��) �����ׂĉ�����ƁA
�@Tn�|Tn-1S1�{�E�E�E�{�i�|�P�j���E���ESn���O
�邱�Ƃ��ł���B
�@���̂��Ƃ���A�S�Ă̑Ώ̎��͊�{�Ώ̎� ���� �ŕ\�����Ƃ��ł���̂Ƃ͋t�ɁA�����Ώ�
�� ���� �Ŋ�{�Ώ̎� ���� ��\�����Ƃ��ł���B
�@���ۂɁA�Ⴆ�A�@��1����1�@�A�@��2����12�|�Q��2�@�A�@��3����13�|�R��1��2�{�R��3�@����A
�@��1����1
�@��2����12�|�Q��2����12�|�Q��2�@����A�@��2���i1/2�j��12�|�i1/2�j��2
�@��3����13�|�R��1��2�{�R��3����13�|�R��1�o�i1/2�j��12�|�i1/2�j��2�p�{�R��3�@����A
�@��3���i1/6�j��13�|�i1/2�j��1��2�{�i1/3�j��3
�@�W���݂̂����o���čs��Ƃ��ĕ\���ƁA
�@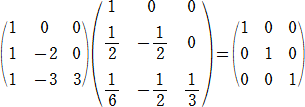
�����藧���Ă���B����ɁA
�@��4����14�|�S��12��2�{�S��1��3�|�S��4�{�Q��22
�@��5����15�|�T��13��2�{�T��12��3�|�T��1��4�{�T��5�{�T��1��22�|�T��2��3
����A
�@�@��1����1�@�A�@��2���i1/2�j�i��12�|��2�j�@�A��3���i1/3�j�i��3�|��1��2�j�{�i1/6�j�i��13�|��1��2�j
�@�@�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E
�@��L�̊�{�Ώ̎����Ώ̎���p���ĕ\����肪�A���ۂ̑�w�����ɏo�肳�ꂽ�B
���l�s����w��w���i�Q�O�P�R�j
�@���A���A�� ��萔�Ƃ��āA�`�A�a�A�b ��
�@�`�����{���{���@�A�a����2�{��2�{��2�@�A�b����3�{��3�{��3
�Ƃ����B���̂Ƃ��A������ ���`�A�a�A�b ��p���ĕ\���B
�i���j�@��3�{��3�{��3�|�R���������i���{���{���j�i��2�{��2�{��2�|�����|�����|�����j�@���A
�@�@�b�|�R���������`�i�a�|�����|�����|�����j
�@�����ŁA�@�i���{���{���j2����2�{��2�{��2�{�Q�����{�Q�����{�Q�����@���A
�@�@�`2���a�{�Q�i�����{�����{�����j
�@����āA�@�����{�����{�������i�`2�|�a�j/�Q�@�Ȃ̂ŁA�@�R���������b�|�`�i�a�|�i�`2�|�a�j/�Q�j
�@�]���āA�@���������i�`3�|�R�`�a�{�Q�b�j/�U�@�ƂȂ�B�@�@�i�I�j
�i�NjL�j�@�����Q�T�N�X���T���t���ŁA�j�D�r�D������A�����Ώ̎��ɂ��Ă̑�������[��
�@�@�@�@�Œ������B���������[���āA���̑����ǂ݉������Ƃɂ��悤�B���̂悤�ȋ@���^
�@�@�@�@���Ă����������j�D�r�D����Ɋ��ӂ��܂��B
�@�����Ώ̎�����{�Ώ̎��ŕ\�����Ƃ́A�j���[�g���̑�����
�@�����|��1����-1�{��2����-2�|�E�E�E�{�i�|�P�j��-1����-1��1�{�i�|�P�j�����������O
����A���������Ă����悢�B
��@�����|��1����-1�{��2����-2�|�E�E�E�{�i�|�P�j��-1����-1��1�{�i�|�P�j�����������O�@�ɂ��āA
�@�����Q�@�̂Ƃ��A�@��2�|��1��1�{�Q��2���O�@�ŁA�@��1����1�@�Ȃ̂ŁA�@��2����12�|�Q��2
�@�����R�@�̂Ƃ��A�@��3�|��1��2�{��2��1�|�R��3���O�@�ŁA�@��1����1�@�A��2����12�|�Q��2�@�Ȃ̂ŁA
�@�@�@��3����1��2�|��2��1�{�R��3����1�i��12�|�Q��2�j�|��1��2�{�R��3����13�|�R��1��2�{�R��3
�@�����S�@�̂Ƃ��A�@��4�|��1��3�{��2��2�|�E�E�E�{�i�|�P�j��-1����-1��1�{�i�|�P�j�����������O�@�ŁA
�@�@�@��1����1�@�A��2����12�|�Q��2�@�A��3����13�|�R��1��2�{�R��3�@�Ȃ̂ŁA
�@�@�@��4����1��3�|��2��2�{��3��1�|�S��4
�@�@�@�@����1�i��13�|�R��1��2�{�R��3�j�|��2�i��12�|�Q��2�j�{��1��3�|�S��4
�@�@�@�@����14�|�R��12��2�{�R��1��3�|��12��2�{�Q��22�{��1��3�|�S��4
�@�@�@�@����14�|�S��12��2�{�S��1��3�{�Q��22�|�S��4
�@���̌v�Z���A�����O�}�`��p���čl���Ă݂悤�B���̃y�[�W�̗��K���Ɏ��̂��̂��������B
��@���@�@�����O�}�`�@�i�S�j�@���A��{�Ώ̎���\�������O�}�`�̑������ŕ\���B
�i���j�@�i�R�j�~�i�P�j���i�S�j�{�i�R�P�j�@���A�@�i�S�j���i�R�j�~�i�P�j�|�i�R�P�j
�@�i�R�j���i�P�j�~�i�P�j�~�i�P�j�|�R�i�P�j�~�i�P2�j�{�R�i�P3�j�@�Ȃ̂ŁA
�@�i�R�j�~�i�P�j���i�P�j�~�i�P�j�~�i�P�j�~�i�P�j�|�R�i�P�j�~�i�P�j�~�i�P2�j�{�R�i�P3�j�~�i�P�j
�܂��A�i�Q�P�j�~�i�P�j���i�R�P�j�{�Q�i�Q2�j�{�Q�i�Q�P2�j�@���A�i�R�P�j���i�Q�P�j�~�i�P�j�|�Q�i�Q2�j�|�Q�i�Q�P2�j
�����ŁA�i�Q�P�j���i�P2�j�~�i�P�j�|�R�i�P3�j�@���A�i�Q�P�j�~�i�P�j���i�P2�j�~�i�P�j�~�i�P�j�|�R�i�P3�j�~�i�P�j
�܂��A�i�P2�j�~�i�P2�j���i�Q2�j�{�Q�i�Q�P�P�j�{�U�i�P4�j�@���A�i�Q2�j���i�P2�j�~�i�P2�j�|�Q�i�Q�P�P�j�|�U�i�P4�j
�����ŁA�@�i�P3�j�~�i�P�j���i�Q�P�P�j�{�S�i�P4�j�@���A�i�Q�P�P�j���i�P3�j�~�i�P�j�|�S�i�P4�j�@�Ȃ̂ŁA
�i�Q2�j���i�P2�j�~�i�P2�j�|�Q�i�i�P3�j�~�i�P�j�|�S�i�P4�j�j�|�U�i�P4�j���i�P2�j�~�i�P2�j�|�Q�i�P3�j�~�i�P�j�{�Q�i�P4�j
�܂��A�@�i�P3�j�~�i�P�j���i�Q�P2�j�{�S�i�P4�j�@���A�@�i�Q�P2�j���i�P3�j�~�i�P�j�|�S�i�P4�j
����āA
�@�i�R�P�j
���i�P2�j�~�i�P�j�~�i�P�j�|�R�i�P3�j�~�i�P�j
�@�@�|�Q�i�i�P2�j�~�i�P2�j�|�Q�i�P3�j�~�i�P�j�{�Q�i�P4�j�j�|�Q�i�i�P3�j�~�i�P�j�|�S�i�P4�j�j
���i�P2�j�~�i�P�j�~�i�P�j�|�R�i�P3�j�~�i�P�j
�@�@�|�Q�i�P2�j�~�i�P2�j�{�S�i�P3�j�~�i�P�j�|�S�i�P4�j�|�Q�i�P3�j�~�i�P�j�{�W�i�P4�j
���i�P2�j�~�i�P�j�~�i�P�j�|�i�P3�j�~�i�P�j�|�Q�i�P2�j�~�i�P2�j�{�S�i�P4�j
�ȏォ��A
�@�i�S�j
���i�P�j�~�i�P�j�~�i�P�j�~�i�P�j�|�R�i�P�j�~�i�P�j�~�i�P2�j�{�R�i�P3�j�~�i�P�j
�@�@�|�i�i�P2�j�~�i�P�j�~�i�P�j�|�i�P3�j�~�i�P�j�|�Q�i�P2�j�~�i�P2�j�{�S�i�P4�j�j
���i�P�j�~�i�P�j�~�i�P�j�~�i�P�j�|�R�i�P�j�~�i�P�j�~�i�P2�j�{�R�i�P3�j�~�i�P�j
�@�@�|�i�P2�j�~�i�P�j�~�i�P�j�{�i�P3�j�~�i�P�j�{�Q�i�P2�j�~�i�P2�j�|�S�i�P4�j
���i�P�j�~�i�P�j�~�i�P�j�~�i�P�j�|�S�i�P�j�~�i�P�j�~�i�P2�j
�@�@�{�S�i�P3�j�~�i�P�j�{�Q�i�P2�j�~�i�P2�j�|�S�i�P4�j�@�@�i�I�j
�@����āA�����ώG�����A�@��4����14�|�S��12��2�{�S��1��3�{�Q��22�|�S��4�@�����߂���B
�@�j�D�r�D����́A���̌v�Z�ɂ��āA���ځA�����̓����������߂���@���l�@���ꂽ�B
�@�����̌`���~���ɕ��ׂĈȉ��̋K���Ŕ{���̔�ŕ�����B
�@�Q���P�P�͂Q�{�A
�@�R���Q�P�͂R�{�A�Q�P���P�P�P�͂Q�{
�@�S���R�P�͂S�{�A�R�P���Q�Q�͂P�D�T�{�A�Q�Q���Q�P�P�͂Q�{
�@�T���S�P�͂T�{�A�S�P���R�Q�͂Q�{�A�R�Q���R�P�P�͂Q�{�A�R�P�P���Q�P�P�P�͂P�D�T�{
�@�U���T�P�͂U�{�A�T�P���S�Q�͂Q�D�T�{�A�S�Q���S�P�P�͂Q�{�A�S�P�P���R�R��2/3�{
��@�u�Q���P�P�͂Q�{�v�Ƃ������[���́A�����O�}�`�̌v�Z�F�@�i�P�j�~�i�P�j���i�Q�j�{�Q�i�P2�j�@����
�@�@����̂��낤���H
�@�A�[�I�ɁA�������������A�j���[�g���̑��������玟�̂悤�ɕ\����邱�Ƃ�������̂ŁA
�@�@��4��4�b0�i�S�j�|4�b1�i�R�j�{4�b2�i�Q�j�|4�b3�i�P�j
�@�@�@����14�|�S��12��2�{�U�i��22�C��1��3�j�|�S��4
�@�@�@����14�|�S��12��2�{�Q��22�{�S��1��3�|�S��4
���l�ɁA
�@�@��5��5�b0�i�T�j�|5�b1�i�S�j�{5�b2�i�R�j�|5�b3�i�Q�j�{5�b4�i�P�j
�@�@�@����15�|�T��13��2�{�P�O�i��12��3�C��1��22�j�|�P�O�i��1��4�C��2��3�j�{�T��5
�@�@�@����15�|�T��13��2�{�T��12��3�{�T��1��22�|�T��1��4�|�T��2��3�{�T��5
�@�@��6��6�b0�i�U�j�|6�b1�i�T�j�{6�b2�i�S�j�|6�b3�i�R�j�{6�b4�i�Q�j�|6�b5�i�P�j
�@�@�@����16�|�U��14��2�{�P�T�i��12��22�C��13��3�j�|�Q�O�i��23�C��12��4�C��1��2��3�j
�@�@�@�@�@�{�P�T�i��32�C��1��5�C��2��4�j�|�U��6
�@�@�@����16�|�U��14��2�{�U��13��3�{�X��12��22�|�Q��23�|�U��12��4�|�P�Q��1��2��3
�@�@�@�@�@�{�R��32�{�U��1��5�{�U��2��4�|�U��6
�@�@��7��7�b0�i�V�j�|7�b1�i�U�j�{7�b2�i�T�j�|7�b3�i�S�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�{7�b4�i�R�j�|7�b5�i�Q�j�{7�b6�i�P�j
�@�@�@����17�|�V��15��2�{�Q�P�i��14��3�C��13��22�j�|�R�T�i��13��4�C��1��23�C��12��2��3�j
�@�@�@�@�{�R�T�i��12��5�C��1��32�C��22��3�C��1��2��4�j�|�Q�P�i��1��6�C��2��5�C��3��4�j�{�V��7
�@�@�@����17�|�V��15��2�{�V��14��3�{�P�S��13��22�|�V��13��4�|�V��1��23�|�Q�P��12��2��3
�@�@�@�@�{�V��12��5�{�V��1��32�{�V��22��3�{�P�S��1��2��4�|�V��1��6�|�V��2��5�|�V��3��4�{�V��7
�@�@��8��8�b0�i�W�j�|8�b1�i�V�j�{8�b2�i�U�j�|8�b3�i�T�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�{8�b4�i�S�j�|8�b5�i�R�j�{8�b6�i�Q�j�|8�b7�i�P�j
�@�@�@����18�|�W��16��2�{�Q�W�i��15��3�C��14��22�j�|�T�U�i��14��4�C��12��23�C��13��2��3�j
�@�@�@�@�{�V�O�i��24�C��13��5�C��12��32�C��12��2��4�C��1��22��3�j
�@�@�@�@�|�T�U�i��12��6�C��22��4�C��2��32�C��1��2��5�C��1��3��4�j�{�Q�W�i��42�C��1��7�C��2��6�C��3��5�j�|�W��8
�@�@�@����18�|�W��16��2�{�W��15��3�{�Q�O��14��22�|�W��14��4�|�P�U��12��23�|�R�Q��13��2��3
�@�@�@�@�{�Q��24�{�W��13��5�{�P�Q��12��32�{�Q�S��12��2��4�{�Q�S��1��22��3�|�W��12��6�|�W��22��4
�@�@�@�@�|�W��2��32�|�P�U��1��2��5�|�P�U��1��3��4�{�S��42�{�W��1��7�{��2��6�{�W��3��5�|�W��8
�@�@��9��9�b0�i�X�j�|9�b1�i�W�j�{9�b2�i�V�j�|9�b3�i�U�j
�@�@�@�@�@�@�@�@�@�@�@�{9�b4�i�T�j�|9�b5�i�S�j�{9�b6�i�R�j�|9�b7�i�Q�j�{9�b8�i�P�j
�@�@�@����19�|�X��17��2�{�X��16��3�{�Q�V��15��22�|�X��15��4�|�S�T��14��2��3�|�R�O��13��23�{�X��1��24
�@�@�@�@�{�P�W��13��32�{�R�U��13��2��4�{�T�S��12��22��3�|�X��13��6�|�X��23��3�|�Q�V��12��2��5
�@�@�@�@�|�Q�V��12��3��4�|�Q�V��1��22��4�|�Q�V��1��2��32�{�R��33�{�X��12��7�{�X��1��42�{�X��22��5
�@�@�@�@�{�P�W��1��2��6�{�P�W��1��3��5�{�P�W��2��3��4�|�X��1��8�|�X��2��7�|�X��3��6�|�X��4��5�{�X��9
�@�K�����ɁA���܂��������ł��Ȃ����̂��ƌ��������Ƃ���A�u�����Ώ̎��̊Ȗ��ȋ��ߕ��v
�̔{�����A�����̕��ו��̏ꍇ�̐��Ɗ��S�Ɉ�v���邱�Ƃ�������ؖ����邱�Ƃ��ł���
�����B�i�����Q�T�N�X���P�T���t���j
�@�Ⴆ�A�U���̓����Ώ̎���W�J����Ƃ��A�悸�A�W���𗘗p���A
��6��6�b6�i�U���̐ς̒P�����j�|6�b5�i�T�j�{6�b4�i�S�j�|6�b3�i�R�j�{6�b2�i�Q�j�|6�b1�i�P�j
�@�@�@����16�|�U��14��2�{�P�T�i��13��3�C��12��22�j�|�Q�O�i��23�C��12��4�C��1��2��3�j
�@�@�@�@�@�{�P�T�i��32�C��1��5�C��2��4�j�|�U��6
�@���ɁA���ʂ̒���W�J����B�W�J�̎d���́A�Ⴆ�A�R�̐ς̕����ɂ��āA������
���ׂ�ꍇ�̐����v�Z����ƁA�{���䂪������܂��B
| �@ |
| ��23 |
��12��4 |
��1��2��3 |
| ��3 |
��2�� |
������ |
| �P |
�R |
�U |
|
�@��12��4 �̌W�����U�Ƃ���ƁA��23 �̌W���́A���̂P/�R�łQ�A��1��2��3 �̌W���́A���̂Q�{�łP�Q
�@�܂�A�@�Q�O�i��23�C��12��4�C��1��2��3�j���U��12��4�{�Q��23�{�P�Q��1��2��3
�@�������l�ɂ��āA
��6����16�|�U��14��2�{�U��13��3�{�X��12��22�|�Q��23�|�U��12��4�|�P�Q��1��2��3
�@�@�@�@�@�{�R��32�{�U��1��5�{�U��2��4�|�U��6
�ƓW�J�ł��܂��B
�@�Q���P�P�͂Q�{�i�P���Q�j
�@�R���Q�P�͂R�{�A�Q�P���P�P�P�͂Q�{�i�P���R���U�j
�@�S���R�P�͂S�{�A�R�P���Q�Q�͂P�D�T�{�A�Q�Q���Q�P�P�͂Q�{�i�P���S���U���P�Q�j
�@�T���S�P�͂T�{�A�S�P���R�Q�͂Q�{�A�R�Q���R�P�P�͂Q�{�A�R�P�P���Q�Q�P�͂P�D�T�{�i�P���T���P�O���Q�O���R�O�j
�@�U���T�P�͂U�{�A�T�P���S�Q�͂Q�D�T�{�A�S�Q���S�P�P�͂Q�{�A�S�P�P���R�R��2/3�{�i�P���U���P�T���R�O���Q�O�j
�@�V���U�P�͂V�{�A�U�P���T�Q�͂R�{�A�T�Q���T�P�P�͂T/�R�{�A�T�P�P���S�R�͂P�{�i�P���V���Q�P���R�T���R�T�j
�@���ʁi�@�@�j�̒��́A�����̕��ו��̏ꍇ�̐�
�@���̂悤�ɋ��߂�ƁA�����Ȗ��ɋ��߂邱�Ƃ��ł��܂��B
�@�u�s��W�J������@�v
�@
�@�Ⴆ�A�����R �̂Ƃ��A
�@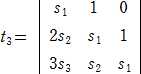
�@����āA�@��3����13�{�R��3�|��1��2�|�Q��1��2����13�|�R��1��2�{�R��3
�i�NjL�j�@�ߘa�T�N�S���Q�R���t��
�@��w�������ŁA�u���T�v���b��̖��ɑ��������̂Œ��킵�Ă݂܂����B���ƌW���̊W
�Ɋ֘A�����{�I�Ȗ��ł����B
�@���k��w�@�O�����n�i�P�X�X�X�j
�@���͂O�łȂ��萔�Ƃ��A�Q�������� ��2�|�����{�T�����O ���l����B
�i�P�j�@��2�|�����{�T�����O �̉����A�����A��5�{��5����5 ���݂����Ƃ���B���̂Ƃ��̂�
�@�@�̒l�����߂�
�i�Q�j�@��2�|�����{�T�����O �͋������������A���̂T�悪�����ł���Ƃ��A���̒l�����߂�B
�i���j�i�P�j�@���ƌW���̊W����A�@���{�������@�A�������T��
�@��5�{��5���i��2�{��2�j�i��3�{��3�j�|��2��2�i���{���j�@�Ȃ̂ŁA
�@�i��2�|�P�O���j�i��3�|�P�T��2�j�|�Q�T��3����5�@���Ȃ킿�A�@�����T
�i�Q�j�@���ʎ�����2�|�Q�O�����O�@���A�@�O�������Q�O
�@��2�������|�T���@�A��3������2�|�T���������i�����|�T���j�|�T�������i��2�|�T���j���|�T��2
�@��4���i��2�|�T���j��2�|�T��2�����i��2�|�T���j�i�����|�T���j�|�T��2�����i��3�|�P�O��2�j���|�T��3�{�Q�T��2
�@��5���i��3�|�P�O��2�j��2�|(�T��3�|�Q�T��2�j��
�@�@���i��3�|�P�O��2�j�i�����|�T���j�|(�T��3�|�Q�T��2�j������2�o�i��2�|�P�T���{�Q�T�j���|�T��2�{�T�O�p
��ӂ��A������ �� �̂T�� ��5 �������Ȃ̂ŁA�@��2�|�P�T���{�Q�T���O�@�łȂ���Ȃ�Ȃ��B
����������āA�@�����i�P�T�}�T �j/�Q
�j/�Q
����́A�O�������Q�O�@�����̂ŁA�Ƃ��ɉ��ł���B�@�@�i�I�j
�i�ʉ��j�i�P�j�@��2�������|�T���@����A�@����+2��������+1�|�T������ �ł���̂ŁA
�@�Q�����@����+2��������+1�|�T�������@�i�����P�A�Q�A�E�E�E�j�@�����藧�B
�������A�@�����������{�����@�Ƃ��� �A��1�����{�������@�A�������T���@�ł���B
�@����āA�@��2����2�{��2���i���{���j2�|�Q��������2�|�P�O��
���̂Ƃ��A�@��3������2�|�T����1����3�|�P�O��2�|�T��2����3�|�P�T��2
�@��4������3�|�T����2����4�|�P�T��3�|�T��3�{�T�O��2����4�|�Q�O��3�{�T�O��2
�@��5������4�|�T����3����5�|�Q�O��4�{�T�O��3�|�T��4�{�V�T��3����5�|�Q�T��4�{�P�Q�T��3
��ӂ��A�@��5�|�Q�T��4�{�P�Q�T��3����5�@�Ȃ̂ŁA�@�Q�T��3�i���|�T�j���O
�@�����O�@�Ȃ̂ŁA�@�����T�@�@�i�I�j
�i�R�����g�j�@���X�Ȃ���A�@��5�{��5���i��2�{��2�j�i��3�{��3�j�|��2��2�i���{���j�@�Ƃ���
�@�@�@�@�@�@���ό`�̗D�G����������ꂽ�B
�@�@�@�ȉ��A�H�����I