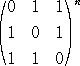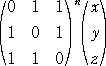S(H)����̘b��P�@�i���Q �R �S �T �U �V �W�j �@�@ �@
�@���g�o�����������b�ɂȂ��Ă���g�m�u�r�i�g�j�v����A��������̘b����Ă���B
���̃y�[�W�ł́A���������܂Ƃ߂Ă��������Ǝv���B�i�����Q�R�N�W���V���t���j
�@���̃y�[�W�̎�Șb��́A�K���A���_�ƕ������i�̂̊g��j�ɂ��Ăł���B�\���m����
���ẮA��w���ے��̑㐔�w���K�v�����D�D�D�B
�@�������@��4�{�T�Q��3�|�Q�U��2�|�P�Q���{�P���O�@�̂P�̉��� �� �Ƃ���ƁA���̉���
�@�@�|�S��/�i�P�|�āj2�@�A�i�P�|�āj/�i�P�{�R�āj�@�A�i�P�|�āj�i�P�{�R�āj/�i�|�S��2�j
�Ə�����B�����̊Ԃɂǂ̂悤�ȑΏ̐������邩�ׂ�B
�i�|�P�V�X�V�N�R���Q�P���@�K�E�X�P�X�Ƃ��̓��L���|�j
�@��L������Ɋ֘A���� �i���@�Q�l�F�g�c�P�`���́u�K���A���_�v�j
(�P)�@�ǂꂾ���V�����g��-���݂邩�T������B�i�b�x���j
(�Q) �@�Ă̂R���ȉ��̑������B��Q�ɓY�������A�L�����B��Q�ɓY�������̂͂Ȃ����H
Q[X]/�o(��4�{�T�Q��3�|�Q�U��2�|�P�Q���{�P�jQ[X]�p
��Q(�āC�|�S��/�i�P�|�āj2�C�i�P�|�āj/�i�P�{�R�āj�C�i�P�|�āj�i�P�{�R�āj/�i�|�S��2�j)
��P�@f[��]���U�S��6�|�P�P�Q��4�{�T�U��2�|�V �ɂ��āA
�@�@K��Q[��]/�o(�U�S��6�|�P�P�Q��4�{�T�U��2�|�V�jQ[��]�p �Ƃ���Ƃ��AK��Q(��) �ŁA��B�̑�����
�@�@�\���́A
{-���C���C�R���|�S��3�C�|�R���{�S��3�C�|�T���{�Q�O��3�|�P�U��5�C �T���|�Q�O��3�{�P�U��5}
�ƂȂ邱�Ƃ������B
��Q�@f[��]���V��6�|�R�T��4�{�Q�P��2�|�P �ɂ��āA��P�Ɠ��l�ɋc�_����B
��@���@��P�A��Q���K�E�X�ɂȂ炢�A���̉�B��L�����ŕ\������B
�@�K�E�X���@���ɂ��Ė`���̂S���������̑��̉�B��L�����ŕ\�������̂��A�@���ɂ���
���o���ꂽ�̂��A���L���茳�ɂȂ������킯�ɂ������Ȃ����D�D�D�B�i�����Q�R�N�W���W���t���j
�@���̓K�E�X�搶�̗L��������M���āA�g�c�P�`�����̔@���A���̉���Q(�āj�łȂ��AQ[��]
�̌��Ƃ��ă�2[��]�i�R�����j��\�����m���l�܂����B(f[��2[��]]���O�@���͂��܂������܂��j
��@���@�c��̃K�E�X�搶�̗L��������Q[��]�̌��Ƃ��ă�3[��]�A��4[��]�i�R�����ȉ��j��
�@�@�@�@�\�����ĉ������B�����āAK��Q[�w]/�if[�w]Q[�w]�j��Q�̐��K�g��̂ł��邱�Ƃ������A
�@�@�@�@��4�E��3���A��ϕ\���쐬���A�e��j �̈ʐ������߂ăK���A�Q�̍\���𖾂炩�ɂ���
�@�@�@�@�������B�܂���K �̑S�Ă̒��ԑ̂��L�ڂ��Ă��������B
�@�_�ˑ�w������ł́Ag(��)��Q[��](�Q���ȉ��̑�����)�̓��o���@�≽�̂��̂悤�ɑ���
�����\���\�Ȃ̂��ɂ��āA�܂������G��Ă��Ȃ��B���̂��Ƃ𑼂̍����ɂ��Ă�����
�ĉ������B�i���@�Q�l�j�`���̖���_�ˑ�ɂȂ炢�����ĉ������B���Ȃ킿�A
��@���@(�P)�@�S���������̑��̉����AQ�W���̂R���ȉ��̑������Ƃ��ĕ\������B
�@�@�@�@�@(�Q)�@�i�P�j��p���āA�K�E�X�̔@���A�L�����\�������߂�B
�@Lagrange�̕�Ԍ������g���A�g�c�P�`�����́@Q[X]/f[X]*Q[X] �̃K���A�Q�̌������߂�
�ƁA�Ⴆ�A-�X��3/�S�|�S�U�T��2/�S�{�R�W�X��/�S�|�Q�R/�S�@���B���ꂪ�����ł��邱�Ƃ́A
f[-�X��3/�S�|�S�U�T��2/�S�{�R�W�X��/�S�|�Q�R/�S]���e�ՂɈ��������ł��邱�Ƃ���m�F�\�B
�@����ɂ��āAf[��] ����3�{�����{�� ���߁A�K���A�Q�� S3 �ł��邱�Ƃ������A��2-6-3 ��
�m�F���ĉ������B�i���@�Q�l�F�u���ʎ��i�p��Łj�v�A�u���ʎ��i�ƌ�Łj�v�j
�@��2-6-3 �̂T����F[��]�ɂ��āA�����̒Ⴂ�g�c�P�`�����̔@�����̕\�����\�Ȃ�A
�肢�܂��B
�@�g�c�P�`������K���A���_��ǂ����Ǝ��݁A�V�� �ŗ����~�܂�A�^���ɑF�������^���ł��B
�K�E�X�̂P�V�X�V�N�̓��L�̍s�Ԃ߂�w�͂́@�������s�ׂł��傤�B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�R�N�W���X���t���j
�@���ꂩ��Q�N��́A�P�V�X�X�N�̃K�E�X�̓��L����A�l�@�P���l�@�Q���������������B
�@�L���ȍ��ؒ厡�搶�̋��ȏ��w��͊T�_�x�̑�P�́u��{�I�ȊT�O�v�͖̏����K����
1�ԁA���Ȃ킿�A���̋��ȏ��̂�����ŏ��̗��K���F�A
�@��1����1���O�@�A�������i����-1�{����-1�j/�Q�@�A �@�Ƃ���A���� �����A���� ��
�@�Ƃ���A���� �����A���� ��
����̋Ɍ��l�Ɏ�������B���̋Ɍ��l���A��1�A��1 �̎Z�p���ςƂ����B�i�f���������j
�́A�u�������ςƑ��敽�ρv�Ƃ����A���Z���̂₳�������K���̂悤�ȏ����Ȏ�������A�s
��Ȑ��E���L�����Ă��܂��B�������A���w�ɂ͂��������Ⴊ�����ɂ����āA��L�͂ق�̈�
��ɂ����܂���B�Ƃ���ŁA�������ς̕��ɑs��Ȑ��E���݂�߂��ł��D�D�D�B�i����j
�i�ʐ��̔�r�I�������m���̗L���QG�ʼn��d���ςɒ�����D�D�D�@���@�Q�l)
�@�g�c�P�`�����̖��ŁA�c��̉����AQ[��]�̌��Ƃ��āi�R�����ȉ��j�\�����ĉ������B
�@�g�Ă�Q��㐔�I �� Q[��] = Q(��)�h�@�ł��BQ(��) �̌��� Q[��] �̌��Ƃ��ĕ\���ł����
�͖��炩�ł��傤�B�ł��A�U�l���̐��w�҂��o�ꂷ�����̐��s���悭���ǂ݂��������B�@����
���傤���H�U�l�̐��w�ҁi���ɁA�K�E�X�i���{����j�A�A�[�x���j���N�\��NjL���l�@�����
�`�͂���̂ł͂Ȃ����낤���B
�@�~���̓����Ɋւ�� Q[X]/�o(X4�{X3�{X2�{X�{1)Q[X]�p��Q(��)��Q[��] �͉�B��Q[��]
�̌��Ƃ��ĕ\�����邱�Ƃ͗e�Ղ��낤�B
�@���ۂɁA�@{���C ��2�C ��3�C �|��3�|��2�|���|�P}�@ �� ����悢�B
�@�܂��A ��4[��]���|��3�|��2�|���|�P�@���Ƃ��A���̈ʐ������e�Ղɋ��߂���B
�i���@�Q�l�F�u�~���̂T�����_�̍�}�v�j
��@��@�@���i���j��X4�{X3�{X2�{X�{1���O�@�̉��̈�����Ƃ����Ƃ��A
�@�@�@�@�@���i�|��3�|��2�|���|�P�j�@�̒l�����߂�B
�i���j�@��4�{��3�{��2�{���{1���O�@���A�@��4���|��3�|��2�|���|�P�@�A�@��5���P
�@�@�@���̂Ƃ��A�@���i�|��3�|��2�|���|�P�j�����i��4�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@����16�{��12�{��8�{��4�{1
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�����{��2�{��3�{��4�{1���O�@�@�i�I�j
����Ȃ�A�����������Əグ�āA�Ⴆ�A
Q[X]/�o�iX14+X13+X12+X11+X10+X9+X8+X7+X6+X5+X4+X3+X2+X+1�jQ[X]�p=Q(��)=Q[��]
�̉�B���AQ[��]�̌��Ƃ��āi13�����ȉ��Ɂj�\�����邱�Ƃ͗e�Ղ��낤�B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�R�N�W���P�O���t���j
���ۂɁA
�@�@�@{���C��2�C��3�C��4�C��5�C��6�C��7�C-��5-1�C-��6-���C-��7-��2�C-��7+��5-��4-��+1�C
�@�@�@�@�@�@�@�@�@�@-��7+��6-��4+��3-��2+1�C��7-��5+��4-��3+��-1�C��7-��6-��3+��2-1}
�Ƃ���悢�B ��14+��13+��12+��11+��10+��9+��8+��7+��6+��5+��4+��3+��2+��+1���O
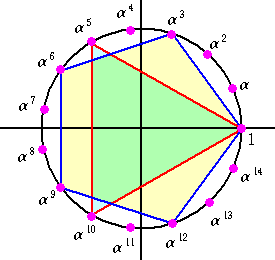 |
��15��1�A��10+��5+1���O�A
�@�@�@�@�@�@�@�@�@�@��12+��9+��6+��3+1���O �@���A
��10��-��5-1�A��11��-��6-���A��12��-��7-��2�A
�@-��7-��2+��9+��6+��3+1���O�@���A
�@�@�@�@�@�@�@�@�@�@�@�@�@��9����7-��6-��3+��2-1
���̂Ƃ��A��10����8-��7-��4+��3-����-��5-1
���A�@��8����7+��4-��3+��-��5-1
�@�@�@�@�@�@ ����7-��5+��4-��3+��-1
��13��-��10-��7-��4-��
�@�@�@����5+1-��7-��4-��
�@�@�@��-��7+��5-��4-��+1 |
��14��-��8+��6-��5-��2+��
�@�@ ��-��7+��5-��4+��3-��+1+��6-��5-��2+����-��7+��6-��4+��3-��2+1
�@�Ƃ���ŁA�������������ꍇ�ɁA�~�� �_ �搶�i����E���������Ȋw��U�����j������
�Ă���R���������̖��͂ǂ����낤���H
�@�@f[X]��X3�{�UX2�|�W�@�ɂ��āA�@f[X]���O �̉������Ƃ���Ƃ��A���̉�B�����
�@�@���Q���ȉ��̑������ŕ\���B
�@�i���@�Q�l�F�@�Q���������̏ꍇ�i�g�c�P�`�����̂U�ł� X2�|�UX�{�V �̍l�@�j)
�@�~�� �_ �搶�ɂȂ炢�A
�@�@f[X]��X3�|�UX�{A�@�Ƃ��āA���ʎ�D�����߁A��D ����b��Q�ɑ����Ȃ��悤��A��I��
�@���A���̂Q���ȉ��̑������\�����s���āA�~�� �_ �搶�̂��̂Ƃ̈Ⴂ��_���ĉ������B
�i���@�Q�l�F�u���炫���������̎G�L���@���ʎ��v�A�uDiscriminant�v�j
�@�U�l���̐��w�҂��o�ꂷ�鐔�s���A�悭�ڂ��Â炵�Č��ĉ������B�g�c�P�`�����̂��̂�
�l�@����Ӌ`�͔@���H
�i���@�Q�l�F�@�u��P�v�@�u��Q�v�@�u��R�v�@�u��S�v�@�@�K���A���_���g�c�P�`�����j
��@���@f[��]����3�{�R�S�T���|�P�Q�@�̂Ƃ��@�ŏ��̂W���Ƃ͈قȂ�_���݂邱�ƂL���A
�@�@�@�@�@f[��]���O �̉������Ƃ���Ƃ��A���̉����@K[��]�̌��Ƃ��ĕ\������B
�@�@�@�@�@�@�܂��A�K�E�X�ɕ킢�L�����\�������B
�@�u�I�����v�ɑ����̖���B���݂�܂����A�uCox 4.4 �㐔�g��Ɋւ���藝�B�̏ؖ��v�A�u�i
�c�@�̘_�@�藝2.14 �n2.15(68p �藝2.12.1)�B�̏ؖ��v����������@�Ƃ��āA�W�ŋߖT��
��@Q(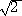 �{
�{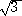 )�A ���R�Ȋg���Ƃ��āA�i�c�̘_�@74�ł�Q(
)�A ���R�Ȋg���Ƃ��āA�i�c�̘_�@74�ł�Q(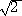 �C
�C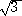 �C
�C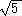 )�@���A���ɂ͗L��
)�@���A���ɂ͗L��
��ł��B�i�����Q�R�N�W���P�Q���t���j
�i�ؖ������N��͌É߂��ċL����Ă��Ȃ��āA�I������p���Ă̋��__�N�Ɓ@��^�����l�̋L�^�݂��j
�i�R�����g�j�@�u�I�����v�̂S�Ł`�X�ł́A��̗���L�x�ŕ�����₷���ł��ˁI
�@�~�� �_ �搶������Ă���R���������̖��Ɋ֘A���āA
(1)�@�Q�������� ��2�{���{�P���O �̉��� �� �Ƃ���Ƃ��A �a��+����Q��㐔�I���͖��炩��
�@�@���A�u�I�����v��Proposition 2 [Loos 1982b]�́u�I�����v��p���āA��+�� ��Q��̍ŏ�
�@�@������ f[X] �����߂�B
(2)�@f[X]���O �̉� �Ɓ����{�� �̂T���ȉ��̑������i��Q[��]�j�ő��̉���\������B
(3)�@��2[��]��(-36��5 - 551��4 - 2630��3 - 3135��2 + 1326�� - 9291)/2166�@����`���A
�@�@�e��j�̍����i�p�j�����A��jn �����߂� ��j��[��]=�ƂȂ� �� �����߂�B
(4)�@f[X]���AQ(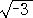 )[X]����������B
)[X]����������B
(5)�@f[X]���O�@�̉�B�́AGauss���ʏ�@���ɕ��z���Ă��邩�A�}������B
�@�@����ƂƂ���ƁA��2[��]�͂ǂ�ł���? ��22[��]�͂ǂ�ł���? �D�D�D��
�@�uFast Computation With�@Two Algebraic Numbers�v�ɂ��āA�σ�����Q��㐔�I���͖�
�炩�����A��L�̖₢�Ɠ��l�ɂ��āA���� ��Q��̍ŏ������� f[X] �����߂�
�B�����āA���
(2)�ȍ~�̔@���l�@������B
�@���̂悤�Ȗ�肪����B�i�����Q�R�N�W���P�R���t���j
�@�@f[��]����3�|�R���{�P�@�ɂ��āA�@f[��]���O �̉������Ƃ���Ƃ��A
�@���̉�B����̔@���Q���ȉ��̑������ŕ\���B
�@f[��]���O ���������߂ɁA�@�������{�P/���@�Ƃ����ƁA�@�i���{�P/���j3�|�R�i���{�P/���j�{�P���O
�@����āA�@��3�{�P/��3�{�P���O�@���Ȃ킿�A�@��6�{��3�{�P���O
�@���̂Ƃ��A��3 �́A�P�̂R�捪 �� ��p���āA�@��3���ց@�܂��́@��3����2
�@�� �̂R�捪�� �Á��������i�Q��/�X�j �Ƃ���ƁA�@�ց���3�@�ŁA�����ÁA�ÃցA�Ã�2
�@�@�@���Ȃ킿�A�@�����ÁA��4�A��7�@�ƂȂ�B
�@�����ŁA�@��9����3���P�@���A�@�P/�Á���8�@�A�P/��4����5�@�A�P/��7����2�@�Ȃ̂ŁA
�@f[��]���O �̂R�̉��́A�@�����Á{��8�@�A������2�{��7�@�A������4�{��5
�@���Ȃ킿�A�@�����Q�������i�Q��/�X�j�@�A�����Q�������i�S��/�X�j�@�A�����Q�������i�W��/�X�j
�@�����ŁA�@�����Q�������i�S��/�X�j���S������2�i�Q��/�X�j�|�Q����2�|�Q
�@�@�@�@�@�@�@�����Q�������i�W��/�X�j���S������2�i�S��/�X�j�|�Q����2�|�Q
�@�@�@��3���R���|�P�@�ɒ��ӂ��āA
�@������2�|�Q���i��2�|�Q�j2�|�Q����4�|�S��2�{�Q���R��2�|���|�S��2�{�Q���|��2�|���{�Q
�@�ȏォ��A�@f[��]���O �̈�̉��� �� �Ƃ���ƁA���̉�B�́A
�@�@�@�@�@������2�|�Q�@�@�A�@�@�����|��2�|���{�Q
�ƕ\�����B�i���@�Q�l�j
�@�R����������ʏ�Ȃ獢��ȁA��荂���̂U���������ɕϊ��������Ă��邪�A�Ȃ��A�u��
�i�������{�P/���j�������̂��낤���H
�@�R�������� ��3�|�R���{�P���O�@�̉������Ƃ���B
(1)�@�Q�������� ��2�{���{�P���O �̉��� �� �Ƃ���Ƃ��A �a��+����Q��㐔�I���͖��炩��
�@�@���A�u�I�����v��Proposition 2 [Loos 1982b]�́u�I�����v��p���āA��+�� ��Q��̍ŏ�
�@�@������ f[X] �����߂�B
(2)�@f[X]���O �̉� �Ɓ����{�� �̂T���ȉ��̑������i��Q[��]�j�ő��̉���\������B
(3)�@f[X]���O�@�̉�B�́AGauss���ʏ�@���ɕ��z���Ă��邩�A�Q�l�̔@���}������B
(4) ���ʎ�D �̕���������b��Q�ɑ���@��3�{����2�{�����{�����O�@����̓I�ɒ�� �Q�l
�@�@�̒u�� �������{�P/�� �ɕ���āA�@���Ȃ�j�]���邩���L�ڂ��ĉ������B
(5) ���̔��z�ŁA�������Ƃ��A�Q���ȉ��̑������ő��̉���\�����ĉ������B
�@�@�g�m�u�y�M�̎q�v�����u�����v����ɒ��킳��܂����B�i�����Q�T�N�P�Q���Q�U���t���j
�@�@S(H)���������̈�������Ă݂܂����B�������肵�܂����B�ȑO���܂��܂g�o�Ō������A
�@�����͐��w�҂̗��Ƃ��ڂ������̉������ɏK���Ă��܂��B
�@�@�uMathematica8�v�������Ă���̂ŁA�������̓W�J��A��]�͏u���ɂł��܂��B�l�b�g
�@��́uWolfwarm�v�ł��ł���Ǝv���܂��B�o�Ȑ��W�̖��́A���܂��肪�o�܂��A
�@�K���A�̂̂�����̘b�́A�����킩���Ă��܂����B�Q�A�A�̂��ЂƂ̃n�[�h���̂悤��
�@���B
�@�@�@��3�|�P�Q���{�W���O�@�̈�̉������Ƃ��āA���̉������̑������ŕ\���B
�@�i���j�@���ƌW���̊W����A�@���{���{�����O�A�����{�����{�������|�P�Q�A���������|�W
�@�@�@���ʎ��F��2���|�S�i�|�P�Q�j3�|�Q�V�E�W2���T�P�W�S���Q6�E�R4���i�Q3�E�R2�j2���V�Q2�@���A
�@�@�@�@�����i���\���j�i���\���j�i���\���j���V�Q�A�|�V�Q
�@�@�@�i���\���j�i���\���j�i���\���j���V�Q�E�E�E�i�P�j�@�Ƃ��Ă݂�B
�@�@�@�i���\���j�i���\���j���\��2�{�����{�����{�����\�Q�������|��2�|�P�Q�{�P�U/���E�E�E�i�Q�j
�@�@�@���Ȃ킿�A�@�i���\���j�i���\���j���i�|��3�|�P�Q���{�P�U�j/��
�@�@�@�����ŁA��3���P�Q���\�W�@���A�i���\���j�i���\���j���Q�S�i���\�P�j/��
�@�@�@��������炽�߂āA�i�P�j�Ƃ̊W������ƁA
�@�@�@���\�����V�Q/�o�i���\���j�i���\���j�p���V�Q/�o�Q�S�i���\�P�j/���p���R��/�i���\�P�j�E�E�E�i�R�j
�@�@�@����A�@��3�|�P�Q���{�W���i���\�P�j�i��2�{���\�P�P�j�|�R���O�@���A
�@�@�@���\�������i��2�{���\�P�P�j����3�{��2�\�P�P������2�{���|�W
�@�@�@���{�����|���@�Ƒg�ݍ��킹�āA�@�����i1/2�j��2�|�S�@�A�����|�i1/2�j��2�|���{�S�@�i�I�j
���@�u�I�����v�̂P�R�łɂ���Hadamard's inequality [1893; Mignotte, 1982]�@�藝�́A
�@�u�u���ܘY ���@���w�������Ɏg�����i�}�����[�j�v�̂Q�U�łɍ݂�܂��B�i���Q�l�u�g���������������v�j
�@�ő�l�����߂�����iX��Hom[R3�CR3]�ƍl����j���퓅��i�i���O�����W���̖���搔�@�j
�ʼn����ĉ������B���É���w�@���w���@�����Ȋw�Ȃ�����͖������̂ł����D�D�D�B
�@�퓅��i�i���O�����W���̖���搔�@�j�̗�Q�@����8��2 - 12���� + 17��2�@�ɂ����āA
8��2 - 12���� + 17��2��17 �͗L���Ȑ��ł��B�L���Ȑ������A�����̖��������Ă��������B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�R�N�W���P�S���t���j
�@�܂��A��19-3 �ɂȂ炢�A
�@f(Y)��8��2 - 12��Y + 17Y2�@-�@17��K[Y]�@�̍� y �� K���p(��) �ɓY�������Ƃ��A�k���j(��) �́A
�p�㏃���z�g��A���Ȃ킿�A�k���p(��) �ƂȂ� �����k �����݂���Bx�Ay��Q(t)�@�Ƃ��At
�𑽗l��
���z�ŏ����肢�܂��B
�@�����C���[�W����ƁA�����ł͂Ȃ��ł��傤���H���`�㐔�a�A���`�㐔�b�̋�̗�ł��m�F
�͗e�ՁB�u���w�������Ɏg�����i�u�� �ܘY ���j�v�@�Q�V�łł́A�u����Â��{�ɁAHilbert
������
���ϐ��̏����t���ő�ŏ����̉��Ƃ��ė^�����ؖ����݂�A��ɂ���ā����ꂪ�悢�Ƃ�
�v���Ȃ� �̂ŁD�D�D���Ɓv�B
�@��͊T�_�́m�� 2�n�s�̍ő�l�mHadamard �̒藝�n�̏ؖ��́AHilbert �ɋ���̂ł�
�ˁI(���́A���ؒ厡���́A�uHilbert �ɋ���v�Ɩ��L����Ȃ������̂ł��傤���H)
�@�����ł́A��͊T�_�̏��� (7) �̓Ɨ��ϐ��̌����C�ɂȂ�܂��B��͊T�_/��2��/��
��ɏ� �̂��̏ؖ��́A�������ō��f�������͑��݂��Ȃ��̂ł��傤���D�D�D�B
�@���T�S���A���̉ʂ����Ȃ��ۑ�ł��B�i�����Q�R�N�W���P�T���t���j
�@�_���̒藝1.3 �ߖT�̗�������������B �� �͒��z���̉���ł����A�^�C���p�����^-
t��C
�ƌ��At ���������Ď��ĉ������B�䑐����̌������A
�@�@�u�ŏI�u�` - �ˉe�Ɍ��ƋA�[�Ɍ� (2007) �~���_�v
�ɑ������܂����B���{�̐V�����㐔�w�̒a���ł��B
�@R3�ɉ�����Q�̋Ȗʁ@S1�F ��2 - ���� - ��2 + ��2���O �CS2�F ��2 - ��2 + ��2 - �����O �ɂ��āA
(1)�@S1��S2�@�� �������ʂɐ��ˉe��(S1��S2)���ē�����S���̑㐔�Ȑ������߂�ƁA
�@�@�@�@��2�E��2 + ��2 - ���� - ��2���O �������邱�Ƃ����߂ĉ������B
�@�@�i �Ⴆ�A�u�I�����v�́@Sylvester's matrix�@��p���āA�� ���������ĉ������B)
(2)�@�����S���̑㐔�Ȑ��ƂQ���Ȑ��̑��F ���� + ���� - (�� + 1)�����O �̌�_�����߂ĉ������B
�@�Ⴆ�A�u�I�����v�́@Sylvester's matrix�@��p���āA�� ���������ē��� �� �̕������������A
�@�@�@�@����(-��2 + �� + 1)/(��2 + 1)��Q(t)�@��������ł��傤�B�� �����߂ĉ������B
�@�ȏ�ɂ��A�S���̑㐔�Ȑ���(S1��S2)���A�L���Ȑ��@(���C��)��Q(��)2 �ł��邱�Ƃ��ؖ���
�ꂽ�B
�@R3�ɉ�����Q�̋Ȗ� S1�CS2 ����Ă��������B�i�������A(���C��)��Q(��)2�j
���� S1��S2 �́AR3�ɉ�����L���Ȑ��ł��邱�Ƃ������ĉ������B
�@��19-3 �ɂȂ炢�A��19-7 �̖͕��v���܂��B�F ��(S1��S2) �F ��2�E��2 + ��2 - ���� - ��2���O
�@f(Y)��Y2�E��2 + ��2 - Y�� - Y2��K[Y]�@�̍� y ��K�ɓY�������Ƃ��A�����ɕ킢�A��
���肢�v���܂��B�i�����Q�R�N�W���P�U���t���j
�@�э��@�ΐ搶���A���r���[�L�ڂ́u�L���̐�㉐}�@�i�u���ܘY�@���j�v��246�`251�łɁA�~
�͉~�����Łu��Ӊ��v�ł��邪�D�D�D�ƍ݂�܂��B���T�S�ɕ킢�A�����^
Q[���C��]--��-->Q[t]�@���A��(��)��2t2 - 1�A��(��)��16t5 - 20t3 + 5t�@�@�����Ƃ��A
(1)�@Ker�Ӂ�<f[���C��]> �Ȃ� f[���C��] �́Af[���C��]��16��5 - 20��3 + 5�� - 2��2 + 1�@�ł����H
(2) ���o�����㐔�Ȑ��@f[���C��]���O �̔}��ϐ��\�������āA���̂����ĉ������B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�R�N�W���P�V���t���j
�@��2 + ��2 = 1�@�̗�̗L�������̑ł��}��ϐ��\���̓��o�͗e�ՂŁA�������e�Ղł��B
��@�����^�@Q[���C��]--��-->Q[t]�@���A��(��)��2t2 - 1�A��(��)��64t7 - 112t5 + 56t3 - 7t
�@�@�����Ƃ��A
(1)�@Ker�Ӂ�<f[���C��]> �Ȃ� f[���C��]�@�����߂�B
(2) �㐔�Ȑ��@f[���C��]���O �̔}��ϐ� �� �\�������āA����
�@�@����2t2 - 1�@�A����64t7 - 112t5 + 56t3 - 7t�@�����ĉ������B
�@Proposition�T�i�����[���[�j�AProposition�V�i�N���C���j���͋C�ɂȂ�܂��H
k(t)
|
E=K=k((t12 - 33t8 - 33t4 + 1)/(t4(t4-1)4))
|
k�@�@�@�@���q��t12 - 33t8 - 33t4 + 1�@�́AQ���ŁA
�@�it2 - 2t - 1�j�it2 + 2t - 1�j�it4 + 1�j�it4 + 6t2 + 1�j
�@���̈����́@f[t]��t4 + 6t2 + 1�@���l�@�Bf[��]���O�@�Ȃ�A�Ⴆ�A�@f[��3[��]]���O�@�������A
���̂悤�ȑ��̃��̂R���ȉ��̑������B��j[��] �����߂�ƁA
�@��1[��]�����@�A��2[��]��-���@�A��3[��]��-��3 - 6���@�A��4[��]����3 + 6��
�@�ej �ɂ��āA��jn[��](n��N)�����߁A�ȒP�ɂ��Ă��������B
�@�ej �Ci �ɂ��āA��jn�E��j��[��]�@(n�Am��N)�@�����߁A�ȒP�ɂ��Ă��������B
�@�K���A�Q Gal(Q(��1[��]�C��2[��]�C�E�E�E�C��4[��])/Q) �� ���߂Ă��������B
�@Corollar��14.13�ɕ킢�A���̘_�i�i�c�j77p�A���W�� K[X1�Cx2�C�E�E�E�CXn]/�fideal�@110p�A
117p�A127p ���Ɋւ���ł����D�D�D�B�i�����Q�R�N�W���P�W���t���j
�@���̂����ɂ��āA�����@Wolfram|Alpha�P�AWolfram|Alpha�Q�@�̂悤�ɁA�㐔�Ȑ�
x4 + 4yx3 - 4x3 + 6y2x2 - 16yx2 + 12x2
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@+ 4y3x - 8y2x - 4yx + 11x + y4 - 4y3 + 8y2 - 11y + 7���O
��`���At �������o���邩���D�D�D�B
�@���̂悤�ȃO���t�ɂȂ�܂��B
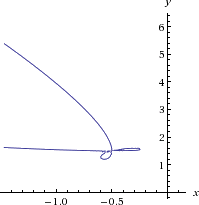 �@�@�ȑO�ɍl�@�ς݂��u�����Q�Ƃ��A���̊e��������u��
�@�@�ȑO�ɍl�@�ς݂��u�����Q�Ƃ��A���̊e��������u��
�@�@x��t + 1/t �ɂ������ĉ������B
�@�i�����͏オ�邪�A�Ղ����������ɊҌ������j
�@�i�������Ɓ@�������{�P/���@���� �� ����������Ί����B������
�@�]���A�V���x�X�^�[�s��!�j
�@�@��5 - 5��3 + 5�� - 2 = 0
�@�@��10 - 10��8 + 35��6 - 50��4 + 25��2 - 4 = 0
�i���̂悤�ȕ��������R�Y��ł��������j
�@�g�̃C�f�A���̐������̂Ƃ���͈�ӓI�ł͂Ȃ��̂ŁA��ʂ�o�肢�܂��B
�@�p���̐g��(2) �͗e�Ղł��B�i�����Q�R�N�W���P�X���t���j
�i�Q�l�����j�@���� ���@���@�u���̑̌n�̍L����A�����ϕ�
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�����Đ����_-�㐔�ƊƉ�͂̌���鐢�E-
�@�@�@�@�@�@�@�@ �����j�X�P�[�g�Ȑ�
�@Galois theory�iDavid A. Cox�j�ɍ݂�y�㐔�I�]������z�肢�v���܂��B���̊���
�^�̊j�S�����߂���́A���K������ɍ����ł��B
�@�����͈Ղ����P�[�X�ł��傤�B������������i�O�O��j�́A(2)�̂S���Ȑ����L���Ȑ��ł�
�邱�Ƃ̏ؖ��͂��b�オ�݂肻���ł��B��19-3�ɕ킢�A�₢���������z�ŏؖ����A�L��
�Ȑ���p���āA�����̖ʐς����߂ĉ������B
�@���C���́ACorollar��14.13�ɕ킢�A���W�FR[���C��]/��4��4 - 4��2 + ��2�� �̔����́i��`��
�i�c�@110p)�̍l�@�ɍ݂�܂��B
�@��������i�O�O��j���͈Ղ����A�Q���̖���������������BHilbert 90 �Ƃ̗��݂͑z���
�͈͊O�ł��傤���H
�@�э��搶���A�����Q�R�N�W���S���t���ŃA�h�o�C�X���܂����B
�@�@�@�u���搶�̂��{�̂��P�R�W�C�P�R�X�Ƀ����[���[�g�̒藝�Ɉ�ʉ��̘b�����グ����
�@�@���܂��B���̊��z���P�q�ׂ܂��B
�@�@�@��b�̂��W��0�ŕ̂̏ꍇ�ł����A���z�����P�̕�����K�̃��f���ł���Ȑ����l
�@�@����Ƃ��̎퐔g ��n�����ˉe���l�̂̕�������q=0 ��� g=0�B������L���Ȑ��ɂȂ�
�@�@����K �͗L�����̑́B�������Ċw�I�Ӗ���������B
�@�@�@���ɑ������̕����� A �����K�ł��̗L�����̂��P�����Ƃ���B�����
A=F[u] ��
�@�@������B����́A�ΐ��I�퐔�ƁA�ΐ��I�s���������l��������o��B
�@�@�@�������āA�w������Ƒ㐔�̖��̈Ӗ������m�ɂȂ�A���ׂĂ������ɂȂ�B
�i�Q�l�����j�@�uAlgebraic geometry�v�@�A�uGeometria algebrica�v
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�R�N�W���Q�O���t���j
�@�r�i�g�j����z�[�`�~���^�Ɩ������ꂽ����B�������āA�����u�㐔�I�ȊW�v�����߂�
�̂��Ȃ��Ɩ|�Ă���������Ɗ������ł��B�m�F�͗e�Ղł��B
�@�@g3-3g=(t + 1/t)3 - 3(t + 1/t)=1/t3 + t3=f �ƐԈ݂͂��������W�����߂Ă��邱�Ƃ���
����܂��B
�@�Ԉ݂͂̔@���A���A�� �́u�Ɨ��v�ł͂Ȃ��A�u�㐔�I�ȊW�v���݂邱�Ƃ͍��Z�������o�Bn=2
�̏ꍇ�� ���A���A�� �́u�㐔�I�ȊW�v�� ���o�肢�܂��B
�@�㐔�I�]��������ŁA�W�������͂œ��o���ĉ������B���K�����K�U�A���T�S�ɍ����B
�i�Q�l�����j�@�uDivision�@of�@the�@lemniscate�v
�@Galois theory�iDavid A. Cox�j�̂P�T�́D�D�D���� 29p-37p(137p-159p)
�@�g�c�P�`�����̖��ŁA ������4 �ƒu������B
�@�@��4�{�T�Q��3�|�Q�U��2�|�P�Q���{�P���O�@���A�@��16�{�T�Q��12�|�Q�U��8�|�P�Q��4�{�P���O
����������ہA�퓅��i�ɕ킢(������+���E��)�A�����A�����ɕ����A�㐔�Ȑ��B�F����=0�A����=0
�́A���R�A��������B��_�́A�uWolfram|Alpha�v�𗘗p���������B�i���@�Q�l�j
�@����=0�A����=0�@�������ہA�퓅��i�ɂ��Ay �������i�Ɖ]���V���x�X�^�[�s��j����
�������B
�@Cox �搶�͍��܂ŏ��Џ�ł������搶�̓������Ƃ��D���Ȑ搶�ł����A���K�U�͏�������
�I�z��������Ȃ��D�D�D�B�i�Ђ���Ƃ���ƁA�ǎ҂͌������đ呹�Q���邩��)�B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�R�N�W���Q�Q���t���j
�@����A16�������������ʎ��v�Z�ɐ��������B�i�}�C�R�~�W���[�i���@6��27���z�M�j
(�`)�@��[u] = �� + ���@�A��[v] = �����@�A��[w] = ��(�� - ��)2 �ƒ�`�����Ƃ��A���K�U�̂悤��
�@�@h[u�Cv�Cw]��k[u�Cv�Cw] �����߂ĉ������B�i���̌� u = b/a�Av = c/a �Ƃ��āD�D�D�j
�i�a)�@��[u] = �� + �� + ���@�A��[u] = ���� + ���� + �����@�A��[w] = �������@�A
�@�@��[D] = ���o(�� - ��)(�� - ��)(�� - ��)�p2 �ƒ�`�����Ƃ��A���K�U�̂悤��
�@�@h[u�Cv�Cw, D]��k[u�Cv�Cw, D]�@�����߂ĉ������B�i���̌� u = b/a�Av =
-c/a�Aw = d/a �Ƃ��āj
�@(���܂肫�ꂢ�Ȏ��Ƃ͂����Ȃ��ł��ˁB16���̏ꍇ���Y��Ɖ]�����w�҂����݁j
�@�u�I�����v�� Sylvester's matrix ��p�����@�ŁA���(�`)�i�a)�̌��_�y���m�z�o���ĉ�
�����B�i����̎�@���@���C�ɓ���@�ł��傤���H�j
�i�b)�ɊY��������n��A��l�̎�@�Ō��_�y���m�z�o���ĉ������B
�@�S���̏ꍇ�͂����ƕ��G�ŁA�����Ȃ�v�Z���n�߂�Ƒ�ςł����A������Ƃ����H�v�ŁA�R��
�̏ꍇ�ɋA�������邱�Ƃ��ł��܂��B
�@�uSingular point of an algebraic variety�v��k[X�CY]/��Y2-(X2(X-1)> �ɂ��āA
�@�@�@�@��[��] = t2 - 1�@�A��[��] = t3 - t�@�F�@��[���C��]-----��k[t]
���K�U�̂悤�ȍl�@���ǂ����B
(1)�@�㐔�Ȑ� C�F (-1 + ��2 + ��2)3 - ��2��3 = 0�@�̓��ٓ_�߂ĉ������B
(2) �@��̓��ٓ_�͎����ł����A���̏o��������ٓ_�ɋ^��_�������锤�ł��B�@����
�@�@�^��_�������Ȃ����܂����H
(3)�@����^�ʑ� F �F R2----------��R2 �� F[���C��]=[�� + ���C��2] �ɂ��C�̑�F(C)�����߂�
�@�@�������B�i���@�Q�l�}�j
(4) �@�܂��AF(F(C))�����߁AF(C)�AF(F(C))�̓��ٓ_�����߂ĉ������B
(5) �@C�AF(C)�AF(F(C)�̑o�Ȑ��B�����߂Ă��������B
(6) �@�e�o�Ȑ��ɔ@���Ȃ���ٓ_���o�����܂�����?
�@���C���̖��ł��B
�@��[��] = ��2 +
��2�@�A��[��] = ��3�� -
����3�@�A��[��] = ��2��2�@�ƒ�`�����Ƃ��A���K�U�̂悤��
�@h[u�Cv�Cw]��k[u�Cv�Cw]�����߂ĉ������B�i�p����(�@�@�@�@)���𒍎��Ȃ����ĉ������j
�@�������̂���A R3�ɉ����āAh[u�Cv�Cw]���O�@��`���ĉ������B
�@�@ ���W�i���̏��̂��́j�́A�i�c 110p�@�F�@ k[u�Cv�Cw]/��h[u�Cv�Cw]��
�@�@R[���C��]/(��2 +
��2 - 1)R[���C��] �݂�G�i�^�C�v�~�X�݂�j
(�k�C����w�E���E��)�@�E�K�E�X�ʑ��̐��w(�w���_�S�E�w�u�`�W) ����̉�
�@�@�@�@�@�@�@�@�@�@�@�@�@ �E�㐔�̏�̑������ƃA�t�B���㐔���l���@
�@�u���`�]���Ɛ��`�Ɨ��̔���]�v�ɂ��āi�����Q�R�N�W���Q�R���t���j
�@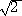 +
+ 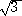 �@��Q��̍ŏ��������́A��4 - 10��2 + 1�B
�@��Q��̍ŏ��������́A��4 - 10��2 + 1�B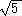 �@��Q��̍ŏ��������́A��2 - 5
�@��Q��̍ŏ��������́A��2 - 5
�@�u�I������p���āv�̔��z�ɕ킢�A
�@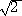 +
+ 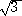 +
+ 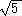 �@��Q��̍ŏ������������߂āA��8 - 40��6 + 352��4 - 960��2 + 576�@�ƂȂ�
�@��Q��̍ŏ������������߂āA��8 - 40��6 + 352��4 - 960��2 + 576�@�ƂȂ�
�܂����H�i���@�Q�l�F�@�i�c�@74p)
�@�ȉ��A�u�X�O�N�x������w�O�����n�v�̖͕�ł��B
�@��8 - 40��6 + 352��4 - 960��2 + 576 = 0�@�̉������Ƃ���ƁA���̉��́A����7���ȉ��̑�
�����ŕ\�����͖̂��炩�Ɖ]���A��͂Ȃ���Ȃ��������̒��ɑ��݂���i�ߖT�̕���
���肢���Ă݂ĉ������j�B
�@������݂�ƁA�@�@{���C-���C-5��7/288 + 97��5/144 - 95��3/18 + 59��/6�C�E�E�E}
�c��̂T������ĉ������B
�@������A��j[��]�@�Ƃ��A�Q�\���쐬���A�����Q�����߁A�e�����Q�ɑΉ�����
�@�@�@�́@Q[��]/<��8 - 40��6 + 352��4 - 960��2 + 576>
�@�@�@�@|
�@�@�@�@Q�@�@�@�̒��ԑ̂�S�ċ��߂Ă��������B
�@���K�����(a)�ɂ��āA���߂����ӂ� f[��]��Q[��] �Ƃ���Bf[��]=0 �̉������Ƃ���Ƃ��A
{-2��3/7 - 16��2/7 - 29��/7 - 9/7�C2��3/7 + 2��2/7 - 13��/7 - 12/7�C
-4��3/7 - 18��2/7 - 9��/7 + 3/7�C -�� - 3�C���C4��3/7 + 18��2/7 + 9��/7 - 24/7}
�B�����ł����H
(b)�ɂ��āA���߂����ӂ� f[��]��Q[��] �Ƃ���Bf[��]=0 �̉������Ƃ���Ƃ��A���̉����܂߂āA
�@Sol={2 - ���C���C -��3 + 3��2 - 2�� + 1�C ��3 - 3��2 + 2�� + 1}
�Ős������邱�Ƃo���ĉ������B��́A�u�X�O�N�x������w�O�����n�v�̖͕�ł��B
�@���K����̉��F�g���Q�Ƃ��āA���̖�������Ă��������B
��11 - (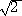 +
+ 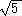 )��5 + (1 + 3��)�� +
)��5 + (1 + 3��)�� +  =0 ���� f[x]��Q[x] ���� ���ĉ������B
=0 ���� f[x]��Q[x] ���� ���ĉ������B
�@Garrett Birkhoff�ASaunders Mac Lane�@���Ꭶ�� w=u2-u �����������j�b�N�Ȋ��������
�����߂铱�o�@�͉���x���Ǝv���܂��H�i�����Q�R�N�W���Q�S���t���j
Q[x]/<��3-2x+2>=Q(u)��w=u2-u (��)
�@�@�@|
�@�@�@Q
�@Q(u)�@�i�������A��3-2��+2=0 �j
�ɂ����āA�@w=u2-u�@���������ׂ������������߂����B
���̂��߂ɁA�@w2=u4-2u3+u2�@�Aw3=u6-3u5+3u4-u3�@�ƓW�J���A��3=2��-2�@��������ƁA
�@�@�@�@�@w=u2-u�@�Aw2=3u2-6��+4�@�Aw3=16u2-28��+18
�ƂȂ�B������A�A���������@u2-u=w�@�A3u2-6��+4=w2�@�Ƃ݂ĉ����ƁA
�@�@�@3u2-4=6w-w2�@�A3��-4=3w-w2�@����A�@u2=-w2/3+2w+4/3�@�A��=-w2/3+w+4/3
�@�������Aw3=16u2-28��+18�@�ɑ�����āA
�@�@�@w3=16(-w2/3+2w+4/3)-28(-w2/3+w+4/3)+18=4w2+4w+2�@���A
�@w ���������ׂ��������́A�@w3-4w2-4w-2=0�@�ƂȂ�B
�@��L�̌v�Z�ł͂Ȃ��A�u���ɁAg[w]=w3-4w2-4w-2 �锭�z�����肢�v���܂��B
�@��L�̌v�Z�Ƃ͈قȂ锭�z�i�I�����𗘗p�j�ʼn����Ă݂܂����B
w=u2-u
���A�@u2-u-��=0�@�ŁA����ɁA�@u3-2u+2=0�@�@�Q�����A���� �� ���������āA
�@w3
- 4w2 - 4w - 2 = 0�@�ƂȂ�B
�@�ug[w] �̔��ʎ� D ��Sqrt[D]��Q �ł͂Ȃ��v ���Ƃ��m���߁Ag[w]=0�@�̗�_�� �� �Ƃ����
���A���̗�_��Q�ł͂Ȃ��AQ(Sqrt[D])�W���̂Q���ȉ��̑������ŕ\���\�Ȃ��Ƃ͎�����
�Еt�����A��肢�܂��B��́A�u�X�O�N�x������w�O�����n�v�̖͕�̖͕�ł����H
�@�u�g�c�P�`�����v�� �f���������̓��L�̂S���������̉��� u �Ƃ���Ƃ��Aw=u3 +
7u2 + 5u + 3
�������� ���j�b�N�Ȋ�������������߂铱�o�@��
(�C�j�uGarrett Birkhoff�ASaunders Mac Lane�v�ɕ키���@
(��) �u�I�����v��Sylvester's
matrix�@���@�g�����@
(�n�j�f���������̓��L�̂S���������̉��͋��߂���B�i�����A�����j�X�P�[�g�́Q�Q������
�@�@����K�ƃR���p�X�ʼn\�j
�@�@���ۂɁA���߁A�e�����@u3
+ 7u2 + 5u + 3 �ɑ�����������̂��A��j
�Ƃ��A
(w-z1)(w-z2)(w-z3)(w-z4)
�����߂āA(�C)(��) �ƈ�v����܂ŁA�撣���ĉ������B
(�j)(�z)
�Ƒ��̔��z�B���Ă��A����ĉ������B
�Ƃ��肢���܂������A
Q[X]/<�f���������̂S����>��Q(u)���p[u]�@
�@�@�@|�@ �@�@�@�@�@�@�@(�i�c�@41p�@�藝 2.1.6�ACox�AAbel����L�����߂ė��������l�������j
�@�@�@Q
���AQ(u) �̔C�ӂ̌����AAu3 + Bu2 + Cu + D��Q[u]�@�ƈ�ӓI�ɕ\�������̂ŁA�f��������
�̓��L�̂S���������̉��� u �Ƃ���Ƃ��Aw=Au3 + Bu2 + Cu + D �����������j�b�N�Ȋ���
����������C�ɋ��߂ĉ������B�@u4+(-144628A + 2756B -
52C + 4D)u3+...................=0
�����āA{A �� 1, B ��
7, C �� 5, D �� 3}�@�Ɠ��ꉻ���A�O�̂������邱�Ƃ��m�F���ĉ������B
���́AQ[u]=Q(u)�@�ɂ��ẮAReid ��Corollary 2.29(Cf�F2.28)�ɃY�o���݂�܂��B
����ȑO�́A33p ��15�ŁiLet a denote the image of x
in�@��f����椂�ʼn�����!!�j
�����Ɖ]�킸�A�Ղ�������B���i�@���l�Ȕ��z�j�ʼn����āA�ƍ݂�܂��̂łǂ����I
�@g[w]=0 �̉������Ƃ���Ƃ��A�g�c�P�`����̂��̂�^�����A�����A�L�����\���̕��łȂ��A
���̉��̂R���ȉ��̑������\�������݂Ė�����ʼn������B
��1[��]=���@�A��2[��]�@�A�E�E�E�@�A��4[��]
����́A�u�X�O�N�x������w�O�����n�v�̖͕�ł��B
��ɂ���āAG��{��1�C��2�C�E�E�E�C��4}�@�̕����Q�ɑΉ�����́G
Q[X]/<g[X]>
�@�@�@|
�@�@�@Q�@�@�@�̒��ԑ̂�S�ċ��߂ĉ������B
�@���́A�r�i�g�j����z�[�`�~���^�Ɩ������ꂽ����̌^�̂��̂ł��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�R�N�W���Q�T���t���j
�@�_���̋ɁA��������^�ӁFk[F�CG�CH]----------->k[���C��]�@���`���A���K�U�̂�
���ȁ@h[F�CG�CH]��k[F�CG�CH]�@�����߂ĉ������B���߂��@h[F�CG�CH]�@�́A�E�̑��F�g�ɂ�
��܂������H�����㐔�Ȗ� k[F�CG�CH]/<h[F�CG�CH]>�@���������ꍇ�́A�����W�����AH
�ɂ��ĉ����A�uWolfram|Alpha�v�𗘗p���ĉ������B
�@Galois theory�iDavid A. Cox�j����Q�D�Q�D�U�@���K�S�@�ɂ����āA�Ȃ��ACox �搶�́A
�uShow carefully�v�Ɖ]����̂ł��傤���H�i�����Q�R�N�W���Q�U���t���j
�T�d�ɂ��Ȃ���A�@���Ȃ�듚�������Ă��܂��̂��A�듚��B�L�肢�܂��B
�@��z�[�E�`�E�~���^�̖���ɂ�����W�̓��o�����肢���܂��B�i�����Q�R�N�W���Q�V���t���j
�@���g�̐���Ԙg�� X�AY�AZ �̊W(syzgy�@idesl)�o�肢�܂��B���̌�A�㐔�Ȗ�
R[X�CY�CZ]/<h[X�CY�CZ]> ������`���Ċӏ܊肢�܂��B���̍ہA�ȉ������l���肢�܂��B
�@Galois theory�iDavid A. Cox�j�ɍ݂�y�㐔�I�]�����z�F���K�U
�@�r�i�g�j����̃q���g�ɕ킢�A�����v�Z���Ă݂��B
�x���o���i�R�{��2�j�i�P�|��2�j�{�Q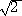 ���p/�i�P�{��2�j�@�A�y���o�|�Q�����i�R�{��2�j�{
���p/�i�P�{��2�j�@�A�y���o�|�Q�����i�R�{��2�j�{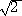 �i�P�|��2�j�p/�i�P�{��2�j
�i�P�|��2�j�p/�i�P�{��2�j
�ɂ����āA�@�i�P�|��2�j/�i�P�{��2�j���������Ɓ@�A�Q��/�i�P�{��2�j���������Ɓ@�Ƃ����ƁA
�@ �x�����i�R�{��2�j�������Ɓ{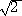 �������Ɓ@�A�y���|���i�R�{��2�j�������Ɓ{
�������Ɓ@�A�y���|���i�R�{��2�j�������Ɓ{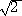 ��������
��������
�Ȃ̂ŁA�@�x2�{�y2����2�i�R�{��2�j2�{�Q�@�ƂȂ�B
�@�����ŁA�@�w���Q�{��2�@���A�@�x2�{�y2���i�w�|�Q�j�i�w�{�P�j2�{�Q���w3�|�R�w�@�ƂȂ�B
�@���̋Ȗʂ��A�u�f�����������R�c�v��p���ĕ`���Ă݂�ƁA�摜�����̉~�����艜�̕��ɂ���
��傫���Ȃ��Ă����悤�ȕ��͋C�B�ł��A�w���Q�ŁA�~ �x2�{�y2���q2�ɂ����āA�q2���w3�|�R�w��
�P�������Ƃ������Ƃ��l����Γ��R���ȁB
�@���F�݂͂����z�́A�ȉ�����ŁA�����z�g��Ɖ~�������C�҂͔c�����Ă�������̂�
���傤���H�i�����Q�R�N�W���R�O���t���j
�@Galois theory�iDavid A. Cox�j�ɍ݂�y�㐔�I�]������z���Q�Ƃ��Ak[X�CY�CZ]--��-->k[T]
��Ker[��]�����߁A��A�̖�B�������ĉ������B�܂��AV(Ker[��])�̂Q�Ȗʂ̌���肪�悭��
����悤�ɐ}�������肢���܂��B
�@����̐̉ӏ��́A�u�X�O�N�x������w�O�����n�v�̖͕�ł��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�R�N�W���R�P���t���j
�@�N�ł��o���������������܂��B�e������(j��{1�C2}) �ɂ��āA�lj�������B�̍l�@������
�����܂��B�������������A��13���A�� �̑������Ŏ����ł�����A��13��Q[��]
���ؖ��D�D�D�B
������2�ɍ����������݂�܂��B�������̂��AQ���ł��錻�ۂ͑z��͈͓̔��̗��R
���q�ׂĉ������B
�@�����Q������肢�v���܂��B���ɁA��� 31�� f[��]��K(X) �̏o���̔�b�����肢���܂��B
�@��������āA(a)�̋�͌o���ς݁B��19-3 �ɂȂ炢�A����̖͕�1�A2 �������ĉ������B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�R�N�X���P���t���j
�i�����A�㐔�Ȑ����Q�Ƃ��A
�@�@�@V(��3 - 3�� - ��2 +
2)�A V(-��7 + 7��5 - 14��3 + 7�� + ��5 -
5��3 + 5��)
���L���Ȑ��ł��邱�Ƃ�����At ���������A���̊m�F���B)
�@������ Deutsch
��(wikipedia.org/wiki/Kurve_(algebraische_Geometrie))�ɂ́ADuale
Kurve
���L�������B
�@C1��V(��3 - 3�� - ��2 +
2) �A C2��V(-��7 + 7��5 - 14��3 + 7�� +
��5 - 5��3 + 5��)
�� Duale Kurve
C1* �AC2* �����߂ėL���Ȑ��ł��邱�Ƃ�����A�� ���������A���̊m�F���B
�@���̘g���̖�����肢�v���܂��B
�@�܂��A������������Q������n��A������������Ƃ̖����݂�������ĉ������B
�i (�� - ��[-4 + ��2])n + �E�E�E�@�̂悤�Ȃ��̂��o�����锤�B�j
�@����́A�����Ԉ͂��̔@���A�e�Ղ����A�d�v�炵���B���̍����́A������152p�̕��4.20
�ŁA�ȍ~�̕łɗ��ށE�E�E
�@���g�̂Q�̗���Q�Ƃ��A�i�����Q�R�N�X���Q���t���j
�@(1) ���g�̃C�f�A���̐������@f(x�Cy�Cz)�@�����߂ĉ������B
�i���H��́Af(x�Cy�Cz) ���A�Ȃ�Ɩ��L���A
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���̂Ƃ��Af(x�Cy�Cz)���Ȃ�ׂ��ȒP�ɂ���Əo�肳��Ă���D�D�D���T)
�@(2) ���g�� f=f3 �ɕ킢�Af5=t5 + 1/t5 �Ƃ���Ƃ��A�Ԙg�̂悤�� g �̑������\�������ĉ�
�@�@�@�����B
�@(3) g �� T �Ƃ��A��=f3�A��=f5 ����AT ���������A�㐔�Ȑ��@F(���C��)=0 �����߁A�}�����ĉ���
�@�@�@���B�iF(���C��)=��5 -�Q��3 + 5�� - ��2 +�Q �̂悤�ɂȂ锤�j
�@�@�}�����ꂽ�㐔�Ȑ��@F(���C��)=0 �����āA���ꂪ�L���Ȑ����Ɣ��芐���܂����H
�@�@�L���_�� 117117 �� ��肢�܂��B(7�ł������ł��D�D�D�B�j
�@�t�������ŁAWolfram|Alpha�@�̋ɑ}������A�㐔�Ȑ����`����B
�@�p�����^�[���������A�X�ɁA�Ď�������������ƁA��4 + (2��2 - ��2)�E��2 + ��4 + ��2��2 �������
��A���̖و���Ő����ł��B
�@�ڂŌ��Ċm���߂�ɂ́A�u((1-t^2)/(1+t^2),(2*t)/(1+t^2))�v�� Wolfram|Alpha�@�̋ɑ}
�������������B
�@�b �F ��4 + (2��2 - ��2)�E��2 + ��4 + ��2��2=0 �̑o�Ȑ��@�b* �����߁A���ꂪ�L���Ȑ��ł��邱
�Ƃ͎����ł��p�����^�[�\������ �b* �̗L���_�B��17���߂ĉ������B(7�ł������ł��B�j
�@�o�Ȑ��@�b* �̒�`�Ǝ���́A�u�f�J���g�̐��_�Ƒ㐔���v�̑�1�� �㐔�Ȑ��̊�
�w(�����Ȑ��_�j�ɍ݂�܂��B�i���@�Q�l�F��19-3�@�A�������j
�@�u�͕�P�A�Q�v�́A�ȑO�ɂ��肢���܂������A����̃��C���F�͕�R �̃C�f�A�� I = <4��> ��
V(I) �́A�p�����^�[�\������ƁA�D�D�D�B�i�����Q�R�N�X���R���t���j
�@�͕�S �� t��K(x,y).�o�肢�܂��B�͕�S�̂S���̑㐔�Ȑ��@�b �F ��2��2 + ��2 - ���� - ��2=0
�̑o�Ȑ��@�b* �����߁A�p�����^�[�\�������A�b* �̗L���_�B��117���߂ĉ������B
�i17�ł������ł��B�j
(0) �@Cox ���p���̎��g�̖͕�ł��鉩�F�g�� h[x,y] �����߂ĉ������B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�R�N�X���S���t���j
����h[���C��]�́A�� ���邢�́A�� �ɂ��ĉ����ł����H
�@���l�ɁACox ���p���̎��g�̖͕�ł���e���F�g�� h[���C���C��] �����߂ĉ������B
�@�c��̖���̉��ʁA�ϋȓ_�ɊS���A
(1) �@t �𑽗l�Ȕ��z�ŏ������A�㐔�Ȑ� �b�FF[���C��]=0 �����߂ĉ������B
�@�u�I�����v��Sylvester's matrix ��p�����@�͏퓅��i�ł��B
(2) �@C �̕ϋȓ_�����߂�ׁAC�̑o�Ȑ��@C* �F F*[���C��]=0 �����߂ĉ������B
(3)�@�o�Ȑ��@C*�@�̓��ٓ_�̐�_�����߂āA�}�̂悤�ɂȂ邱�Ƃ������ĉ������B
(4)�@�L���ʑ��i��`�́u�f�J���g�̐��_�Ƒ㐔���v��27p�j�@C-----��------>C*�@�����
�@�@�I�ɖ��L���ĉ������B
(5)�@�L���ʑ��̑��݂ɂ��AC* ���L���Ȑ��ł��邱�Ƃ͖����ł����A�����Ēm��ʂӂ��
�@�@���āAF*[���C��]=0 �݂̂����āA�L���Ȑ��ł��邱�Ƃ�����ĉ������B
(6) �@F[���C��]=0 �͉����Ȑ��H�@F*[���C��]=0 �͉����Ȑ��H (���ꂪ�Ղ����ł��傤���H)
(7) �@C* �̑o�Ȑ��@(C*)* �����߁A���� C �ƂȂ邱�Ƃ��A�����ł������ĉ������B
�@�@���߂Đ}�������@C*�F F*[���C��]=0 �ɂ́A�������_���݂�܂����AC �̂ǂ̓_�ɑΉ�
�@���܂����H
�i�R�����g�j�@�����P�ɁA�c��`�m�̖������������������玟�̂悤�ɂ���悢�B
�@�@�@������3�{�P�@�A�����|��2�{���@�ɂ����āA�@�����O�@���Ȃ킿�A�@�����|�P�@�̂Ƃ��A�����|�Q�@��
�@�@�Ȃ�A�Ȑ� �������i���j �́A�_�i�O�C�|�Q�j��ʂ�B�܂��A�@����/�������R��2�@�A����/�������|�Q���{�P
�@�@���A�����P/�Q�@�̂Ƃ��A�� �͍ő�A���Ȃ킿�A�@�����X/�W�@�̂Ƃ��A�ő�l �P/�S ���Ƃ�B
�@�@�@����ɁA��2��/����2���Q���i���|�P�j/�i�X��6�j���O�@���A�@�O�������P�A���Ȃ킿�A�@�P�������Q�@��
�@�@�����āA��ɏ�ɓʂ̃O���t�ƂȂ�B���߂�ʐς́A
�@�@�@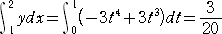
�@�c��̔}��ϐ��\���̖͕�����܂��B
����@�@�� = (2t - 1)/(t4 - 2t3 - 2t + 1)�@�A���@= (3t2)/(t4 - 2t3 - 2t + 1)�@�ɂ���
(8) t �𑽗l�Ȕ��z�ŏ������A�㐔�Ȑ��@C�F G[���C��]=0 �����߂ĉ������B
(9)�@�����@G[���C��]=0 �@�̓��ٓ_�����߁A�}�������肢���܂��B
(10) �㐔�Ȑ��@C�F G[���C��]=0 �̑o�Ȑ��@C* �F�@G*[���C��]=0 ��̗L���_���A13���߂�
�@�@�������B
�@��L�̖����A�ق�̏���������A�u���̘_�@�i�։ؖ[�j�v��122�ł̖�
�@����2 + ����2 = ����2 ���W���Q�łȂ���K�Ŏ����łȂ�����K�Łi���ɑf��K=Q)����
�߂̕K�v�\�������́AK(���C��)=K(t) �Ȃ錳 t ���݂�Ƃ�
����\�Ȃ̂ŁA���肢�v���܂��B�i�����Q�R�N�X���T���t���j
�^�� �F �e�ՂɎ�����̂ɁA���́u K(���C��)=K(t) �Ȃ錳 t ���݂�v�Ɠ���ȕ\�����Ȃ���H
| �@�p |
�@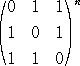 |
��Hom[K3�CK3]�@���l����B |
��@�����R�@�̂Ƃ�
| �@�i���C���C���j��ʂ�Q�̋O�� |
�@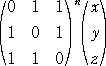 |
��K3�@���l����B |
��@�����Q�̂Ƃ�
�@�����Q �̂Ƃ��� Result ��p���A��[X]�A��[Y]�A��[Z]�@���`����B
��[X] = 2�� + �� + ���@�A��[Y] = �� + 2�� + ���@�A��[Z] = �� + �� + 2���@�A��[W]
= ��3 + ��3 + ��3 -
3������
���K�U�̔@���Ah[X�CY�CZ�CW] �����o���ƁAh[X�CY�CZ�CW] = �w3 + �x3 + �y3 - 3�x�y�w - 4�v ��
�Ȃ�܂����H�i���o�ł͂Ȃ��A�m�F�Ȃ�A�ƂĂ��e��)
�@�����P �̂Ƃ��� Result ��p���A��[X]�A��[Y]�A��[Z]�@���`����B
��[X]= y + z, ��[Y]=x + z, ��[Z]=x + y ,��[W]= ��3 + ��3 +
��3 - 3������
���K�U�̔@���Ah[X�CY�CZ�CW] �����瓱�o���ĉ������B
�@�����R �̂Ƃ��� Result ��p���A��[X]�A��[Y]�A��[Z]�@���`����B
��[X]�A��[Y]�A��[Z]�A��[W]= ��3 + ��3 + ��3 -
3������
���K�U�̔@���Ah[X,Y,Z,W] ���@����@���o���ĉ������B
�@�����S �̂Ƃ��� Result ��p���A��[X]�A ��[Y]�A ��[Z]�@���`����B
��[X]�A��[Y]�A��[Z]�A��[W]= ��3 + ��3 + ��3 -
3������
���K�U�̔@���Ah[X,Y,Z,W] ���@����@���o���ĉ������B
�����T �̂Ƃ�,�@h[X�CY�CZ�CW]=�Q�Q�i�\�z���ǂ����j
�C�ӂ́@n��N�@�̂Ƃ��Ah[X�CY�CZ�CW]=�Q�Q�i�ؖ����肢�܂��j
��[X]�A��[Y]�A��[Z]�A��[W]�@���`����B
��[X] = ��2 + 2yz�@�A��[Y] = ��2 +
2�����@�A��[Z] = 2���� + ��2�@�A��[W] = ��3 + ��3 +
��3 - 3������
���K�U�̔@���Ah[X�CY�CZ�CW] �����瓱�o���ĉ������B
�@�����́A���_ C �Ŋ���ł͂Ȃ���B�� C ��ň����������肢�܂��B
�@�c��̖���̖͕�����܂��B
����@�@�� = (1 - 3��2)/(-1 + t2)2�@�A���@= (2t)/(-1 + t2)2�@�ɂ���
(1) t �𑽗l�Ȕ��z�ŏ������A�㐔�Ȑ��@C�F �e[���C��]=0 �����߂ĉ������B
(2)�@�����㐔�Ȑ��@C�F �e[���C��]=0 �̑o�Ȑ��@C* �F�@�e*[���C��]=0�@�����߂Ă��������B
(3) �o�Ȑ��@C* �̊T�`��`���ĉ������B
(4)�@��19-3�ɕ킢�A�e*[���C��]=0�@�ɂ��āA(���C��)��Q(t)2 �\���肢�v���܂��B
(5) �@���̑o�Ȑ� C* �ɂ���Ĉ͂܂�镔���̖ʐς��A1�ɕ킢���߂ĉ������B
�@����́A���锭�z�œ��o�ς݂̂��̂����Ƃ������ɐ^���ɐԗ��X�Ɍ������L�ڒv���܂�
���B�i�����Q�R�N�X���U���t���j
(1)�@C�F 3125��6 + 108��8 + 900��6�� + 4500��4��2 + 216��6��2 + 1316��4��3
�@�@�@�@�@�@�@�@�@�@�@�@�@+ 432��2��4 + 108��4��4 - 46656��5 - 1472��2��5 - 13824��6 - 1024��7 = 0
�� �o�Ȑ� C* �́A��6 - ��2��3 - ��5 = 0�@�ł��邱�Ƃo���A�o����}�����ĉ������B
(2)�@���ꂼ��̎����̈Ⴂ��T�`���悭���āA���z���L�ڊ肢�܂��B
(3)�@�� = -(2t5(3 + 2t2))/(1 + t2)2�A y = t6(5 + 3t2))/(1 + t2)2�@���� t �𑽗l�Ȕ��z�ŏ���
�@�@���AC �ɂȂ邩�m�F���ĉ������B
(4) �o�L���ʑ��FC--��-->C* ������ĉ������B
(5) ���ɂ�鑜�@�iX�CY)=��(-(2t5(3 + 2t2))/(1 + t2)2�Ct6(5 + 3t2))/(1 + t2)2)�@�����߂āAt ��
�@���l�Ȕ��z�ŏ������AC* �ɂȂ邩�m�F���ĉ������B
(6) �Ȑ��@C* �ɂ��āA��19-3�̔@���l�@���肢�܂��B
(7) (3)�̃p�����^-�\���́A�����ȏ��ЂɌf�ڂ���Ă���̂ɍ������Ă��܂��B�����ȏ���
�@�@�Ƃ́H
�@�ȉ��́A�^���ɂ��b�オ���݂��ׂ��AX=____���Ԑ��Ȃ��������ł��B���̐}�� C �Ɛ悸
���锭�z�ɂ�邻�̑o�Ή� C* �̋���A�ӏ܂Ȃ����āABefore-After�̃O���t�B������
�ĉ������B�i�����Q�R�N�X���W���t���j
�i���_�@C ��̊e�_�ɉ�����ڐ�����O��Before�}�ɕ`���A�o�Ȑ� C* ��̔@���Ȃ�_
�Ɏʑ�����Ă��邩�{���Ɋӏ܂��D�D�D�B�j
�@�w�_��C* �Ɛڐ��x�����Z���ɕ킢����{���ɋ
��v�Z�Ŋ����ׂ��A�����̒Ⴂ�������̑� (p1[t]�Cp2[t]) ��K[t]2 ���`����B
p1[t] = 4t2 - 2�@�A�@p2[t] = 8t3 - 12t
�@����
pj[t] �B�́y�m��l���m��z�������ł��B���i���́j��__________________
(p2[t]
�̖{���̔ԍ��́HHint �F ���V�A�̐��w�ҁI)
(�C)�@X=p1[t]�AY=p2[t] ���� t �𑽗l�Ȕ��z�ŏ������ĉ������B�������Q�Ƃ��A
(��)�@p1[X]��p2[Y]�@�����Ap1[X]�|p2[Y]=0
�Ə�̌��_������ׂĉ������B
�@(�C)=(��) �Ȃ�y�F��z���K��܂������H
(�n)�@(�C)�œ����㐔�Ȑ� C �̑o�Ȑ� C* �����߂ĉ������B�i����`�j
(�j)�@�o�L���ϊ��@C--��--> C* �߂ĉ������B
(�z)�@[X�CY] = ��[4t2 - 2�C8t3 - 12t]�@�����߂�ƁA(3 - 6t2)/(6 + 8t4)�C t/(3 + 4t4))
�@�@�ƂȂ�܂����H [X�CY] = ��[4t2 - 2�C8t3 - 12t] ���� t �𑽗l�Ȕ��z�ŏ������ĉ������B
(�w)�@(�n)�ŋ��߂��o�Ȑ� C* ��(�z)�̏�����̑㐔�Ȑ�������ׂĉ������B
(�g)�@�o�Ȑ� C* �͗L���Ȑ��ł��邱�Ƃ͎����ł����A�{���ɗL���_�B�����߂Đ}����
�@�@���̂��A�A�t�^�[����}��̐ԓ_�B�ł��B�ԓ_�ȊO�̗L���_���T���߂ĉ������B
(�`)�@(�C)�ŋ��߂� C �̎����́A____���B(�n)�ŋ��߂� C* �̎����́A____���B
(��) �Ȑ��@t -----> (p1[t]�Cp2[t])�@�ɉ����鈽��_�B�ɉ�����ڐ��B���R���߁A�Ή���
�@�@�� C* ��̂R�_�����߂Ă��������B
�@���@�藝�����x���J��Ԃ��p����ƁAcos���Ƃ́Acos�Ƃ� �� ���������ŕ\�����
�@�iChebyshev�������̓��V�A�̐��w��Chebyshev(1821�`1894)�������������̂ŁA����
�@�����̉��p������ƂĂ��d�v�ȑ������ŁA��w�����ł������Ώo�肳��܂��B�j
�@��S�̒�`�F Chebyshev�������Ƃ́AChebyshev�̔����������������𑽍����ŁA
�@�@�@�@�@�@�@��P���Chebyshev�������Ƒ�Q���Chebyshev���������悭�m���Ă��܂��B
�@�X�ɁA��R��̑������Ƒ�S��̑�����������A���ꂼ����������������܂��B
(2)�@Chebyshev�������̂R�l�̒�`���݂�܂��B���ꂪ���C�ɓ���ł��傤���H
�@�uLegendre_polynomials�v���Q�Ƃ��A�� (Chebyshev�������CLegendre polynomial) ��
�l�@���܂��B�i��ʐ���,�y�ʋʁ@ChLe�����^�Ȑ��z�Ɩ����j
�@�Ⴆ�A(Chbyshev2[t]�CLegendre5[t])=(2t2
- 1�C 63t5/8 - 35t3/4 + 15t/8)��K[t]2 ���
�`����B
(�C)�@X=Chbyshev2[t]�@�AY=Legendre5[t]�@���� t �𑽗l�Ȕ��z�ŏ������ĉ������B������
�@�@�@�Ȃ�܂������H
�@(���j�@����ꂽ�㐔�Ȑ� C �� �o�Ȑ� C*
���߂āA���}�� R2 �ɕ\�����ĉ������B
�@�@�@�����ɂȂ�܂������H
�@(�n)�@�o�L���ϊ��@C-- �� -->C* �����߂Ă��������B
�@(�j�j (X�CY)=��(2t2 - 1�C
63t5/8 - 35t3/4 + 15t/8) ���� t
�𑽗l�Ȕ��z�ŏ������ĉ������B
�@�@(��)�Ɠ���̕������������܂������H
�@(�z�j�@C�ɂ͍��Z�����b��ɂ����d�ڐ����݂�̂ŋ��߂ĉ������B�ЂƂ́A�������F
�@�@�@Tp(C) �ɂȂ�܂������H
�@�@��(Tp(C))
�����߂Ă��������B���̓_�́A�o�Ȑ� C* �̓��ٓ_�ɂȂ��Ă��邱�Ƃ�����
�@�@�ĉ������B���̓��ٓ_�̖��̂́H�@���̓��ٓ_�̖��̂́H
�@(�w) �o�Ȑ� C*
���L���Ȑ��ł��邱�Ƃ͎����ł����A�L���_��
10���߂ĉ������B
(���E�̒N���l�@�����`�Ղ��Ȃ������D�D�D�Ɛ\���܂������A�l�@���Ė��ʂł������H)
�@���ٓ_�ɂ��ẮA�ȑO�ɂ��肢�����ȉ��肢�v���܂��B
(1)�㐔�Ȑ�
C�F (-1 + ��2 + ��2)3 - ��2��3
= 0�@�̓��ٓ_�����߂ĉ������B
(2) ��̓��ٓ_�͎����ł����A���̏o��������ٓ_�ɋ^��_�������锤�ł��B�@����
�@�@�@�^��_�������Ȃ����܂����H
�@����^�ʑ��@F�FR2�@���@R2
���A F[���C��]=[���{���C��2] �ɂ��C����F(C)�ɂ��āA���F�̏�
�������݂̂������A�� �� ���Chebyshev polynomial��K[x]�Ɩ������܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�R�N�X���X���t���j
�i���̒�`�Ȃ琢�E�̒N�����L�����Ղ��I)
��1���Chebyshev
polynomial�@��Q����ŋ��߂�ƁA�����ƂȂ�܂���?
��2���Chebyshev polynomial�@��Q����ŋ��߂�ƁA�����ƂȂ�܂���?
�@��(��m���Chebyshev polynomial�C��n���Chebyshev polynomial)���l�@����i�l������
���܂������j
�Ⴆ�A(��1���Chebyshev
polynomial��3�ԖځC��2���Chebyshev polynomial��5�Ԗ�)
�@�������Q�Ƃ��A�ȉ��̒Z����B�������Ă��������B
(��1���Chebyshev
polynomial��3�ԖځC��2���Chebyshev polynomial��5�Ԗ�)
=(4t3 - 3t�C
32t5 - 32t3 + 6t)
(�C)�@X=4t3 -
3t�@�AY=32t5 - 32t3 + 6t�@���� t
�𑽗l�Ȕ��z�ŏ������ĉ������B
(���j�@����ꂽ�㐔�Ȑ� C �̑o�Ȑ� C* �����߂āA���}��
R2 �ɕ\�����ĉ������B
�@�@�����ƂȂ�܂������H
(�n)�@�o�L���ϊ��@C-- �� -->C* �����߂Ă��������B��(���C��)��K(���C��)
(�j�j (X�CY)=��(4t3 -
3t�C 32t5 - 32t3 + 6t) ���� t
�𑽗l�Ȕ��z�Ő���������ĉ������B
(�z�j�@C�ɂ͍��Z�����b��ɂ����d�ڐ�Tp(C)
���݂�̂ŋ��߂ĉ������B��(Tp(C)) ����
�@�@�@�߂Ă��������B
�@�@���̓_�͑o�Ȑ� C*
�̓��ٓ_�ɂȂ��Ă��邱�Ƃ������ĉ������B
�@ ���̓��ٓ_�̖��̂�? ���̓��ٓ_�̖��̂́H
(�w) �o�Ȑ� C*
���L���Ȑ��ł��邱�Ƃ͎����ł����A�L���_��10���߂ĉ������B
(���E�̒N���l�@�����`�Ղ��Ȃ������D�D�D�Ɛ\���܂������A�l�@���Ė��ʂł������H)
(�z�j�@C�ɂ́A���Z�����b��ɂ����d�ڐ�Tp(C)���݂�̂ŋ��߂ĉ������B��(Tp(C)) ����
�@�@�@�߂Ă��������B���̓_�͑o�Ȑ� C* �̓��ٓ_�ɂȂ��Ă��邱�Ƃ������ĉ������B���̓�
�@�@�@�ٓ_�̖��̂�? ���̓��ٓ_�̖��̂́H
(�w) �o�Ȑ� C*
���L���Ȑ��ł��邱�Ƃ͎����ł����A�L���_��5���߂ĉ������B
(���E�̒N���l�@�����`�Ղ��Ȃ������D�D�D�Ɛ\���܂������A�l�@���Ė��ʂł������H)
�@�э��搶���A�u�f�J���g�̐��_�Ƒ㐔���v�Ɂu��d�ڐ��ɑ̂̌����t�������v�ƖY����
�Ȃ���ۍ��݂̗��_���݂�܂��B
�@���F�̏��������݂̂������A��m���Chebyshev
polynomial��K[x]�Ɩ������܂��B
�i���̒�`�Ȃ琢�E�̒N�����L�����Ղ��I)�O�g���l�@����B�Ⴆ�A
(��1���Chebyshev polynomial��7�ԖځC��2���Chebyshev polynomial��5�ԖځC
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@��1���Chebyshev
polynomial��7�Ԗ�)
=(64t7 - 112t5 + 56t3 - 7t�C
32t5 - 32t3 + 6t�C 64t7 - 112t5 +
56t3 - 7t) �Ɓ@757 ��
(��1���Chebyshev polynomial��7�ԖځC��2���Chebyshev polynomial��5�ԖځC
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@��1���Chebyshev
polynomial��3�Ԗ�)
=(4t7 -
112t5 + 56t3 - 7t�C 32t5 - 32t3 +
6t�C 4t3 - 3t)�@�Ɓ@753 �ł���B
�@753 �ł́A�ȉ��̂悤�ɈՂ����Ȃ����Ƃ��m�F���ĉ������j
(1)
��=64t7 - 112t5 + 56t3 - 7t�C y=32t5 -
32t3 + 6t�C z=64t7 - 112t5 + 56t3 - 7t�@���� t ��
�@�@���l�Ȕ��z�ŏ������ĉ������B
�@�@�@R��t---f---->(64t7 -
112t5 + 56t3 - 7t�C 32t5 - 32t3 + 6t�C
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@64t7 - 112t5 + 56t3 - 7t)��R3
�@�@�Ȃ�Ȑ��́AR3 �ɉ�����㐔�ȖʒB�̌����ƕ\���\�B
(2) ���ɁA�����ʁ@H �F
�����{�����{�����{��=0�@��
�@�@�@�@�@�@�㐔�Ȗʁ@S �F -��7 + 21��5 +
70����4 + 140��2��3 - 35��3
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@+ 168��3��2 - 84����2 +
112��4�� - 84��2�� + 7�� + 32��5 - 32��3 +
6��=0
�@�̌����ƂȂ�悤H���߂ĉ������B
(3)��̋�ԋȐ� f
�̋ȗ��A�������A�����{�I�l�@�����āA(2)�ƏƂ炵���킹�ĉ������B
(4) <�����{�����{�����{���C-��7 +
21��5 + 70����4 + 140��2��3 -
35��3
�@�@�@�@�@�@�@�@�@�@�@�@+ 168��3��2 -
84����2 + 112��4�� - 84��2�� + 7�� + 32��5 -
32��3 + 6��>��C3
�@�́AC[���C���C��] �̑f�C�f�A���ł��邱�Ƃ������Ă��������B
�@�㐔�Ȑ� C �F 4��2 - 4���� + ��2 - 15�� + 7�� + 13 = 0
�̐��̂͗e�ՂŁA�ŗL�l�B�ƌŗL�x
�N�g���B����e�Ղ� C ���`�ʊ����A���������悭���āA�����ɕ킢�A��=___________��K(���C��) ��
���߂ĉ������B
�@�э��搶���������Ɋւ����̗�ł��B�i���@�Q�l�}������Ηe�Ձj
�@��ŋ��߂��@��=___�@�� C �̌�_�����߁A������ C �̗L���Ȑ��\���F t--->(���C��)=(___�C___)
�����߂ĉ������B
�b �F 4��2 - 4���� + ��2 - 15�� + 7�� + 13 = 0 �̑o�Ȑ� C*
�����߂ĉ������B
����͖��_�Q���Ȑ��ƂȂ�B�i���̂́H)�@�厲���������AC* �Ǝ厲��}���肢�܂��B
�@�o�L���ϊ��F C--��-->C*�@�ŁAC* ���L���Ȑ��ł��邱�Ƃ���肢�܂��B
�����p���ā@C*��̗L���_��69���߂ĉ������B�i9�ł����܂��܂���j
�܂��A���ꂩ��@t �𑽗l�Ȕ��z�ŏ������ĉ������B
�@��L�̖�B�́A���́A���� t �����������v���Z�X�ɗU������āi�ǂ̉ӏ��ɒ���?)�n�삵
�����̂ł��B�i���肢�F��������܂ł͉������Ȃ��ł��������B)
�@�э��搶���o�����ꂽ���̂Q���Ȑ� C�i�o�Ȑ��j�̑o�Ȑ� C* �́A���R�A�Ȑ��ł��B
�@C*�@�����߁A�iC��̊���̓_p �ɉ�����ڒ�����Tp(C)�����߂�A�\�z�������A�
�������j�厲���������AC*�@�Ǝ厲��}���肢�܂��B
�@�o�L���ϊ� C�F(��+5)�� - �� = 0 --��-->C*�@�ŁAC*�@���L���Ȑ��ł��邱�Ƃ���肢�܂��B
�����p���ā@C*��̗L���_��69���߂ĉ������B�i6�ł����܂��܂���j�܂��A���ꂩ��@t
�𑽗l�Ȕ��z�ŏ������ĉ������B
�b���������������� 14�D13 �ɕ킢�A�э��搶���o�肳�ꂽ�Q���Ȑ� C�F(��+5)�� - �� = 0 �ɂ��āA
����K(���C��) �����߂ĉ������B
�@�@(5/t2�C -(t + 5)2/t2)��K(t)2�@���l�@���܂��B (���C��)=(5/t2�C -(t + 5)2/t2)
���ꂩ�� t �𑽗l�Ȕ��z�ŏ������ĉ������B g[���C��]=0�A�@g[���C��]=_____
�b���������������� 14�D13 �ɕ킢�A����K(���C��) �����߂ĉ������B
�@�э��搶���������Ɋւ����̗�ł��B�����㐔�Ȑ� C�F g[���C��]=0 �́A�Q���Ȑ��ł���
���B�ŗL�l���������A�厲 �� C ��}�����ĉ������B
�@�㐔�Ȑ��@C�F g[���C��]=0 �̑o�Ȑ��@C* �F____________________=0 ���@���߂ĉ������B
�@�o�L���ϊ��@C-----�@�� ------>C* �����߁A(���C��)=��(5/t2�C -(t + 5)2/t2) ���� t ����
������ƁA�э��搶���o�����ꂽ�Q���Ȑ� C�F(��+5)�� - �� = 0 �ɂȂ�܂����H
�@�э��搶�ɕ킢�A(�����Ƃ��Ղ����j����������₩����^���܂��B
(�����Ė�����ʼn������j
(1)�@��2 + ��2 = 1 ��@(��-5)2 + ��2 = 1 �̑o�Ȑ� C* �����߂Ȃ����B
(2)�@��2 - ��2 = 1 ��@(��-2)2 - (��-1)2 = 1 �̑o�Ȑ� C* �����߂Ȃ����B
(3)�@��2 - 2�� = 0 ��@(��-2)2 - 2(��-1) = 0 �̑o�Ȑ� C* �����߂Ȃ����B
(��������A�z��͈͓̔��ł������H�ޕ��������s�ړ����o�Ȑ���\�z���ĉ������j
�@�e�₢�ŁA�ǂ̕��s�ړ��ňَ�̓Ȑ� C* ���o������̂����E�����ĉ������B
�ȉ��́A�uVan der Waerden�fs�@Modern Algebra�v�̓ƈ��ł�161�ł̋�̗�̖͕�ŁA
�l�@������������܂����B�i�����Q�R�N�X���P�P���t���j
�@���g�͌���Ȃ��Ղ����iCox �搶�̔z���͊��������A����ɗނ��鑼�̖��Q�����݂���
���D�D�D�͎̂c�O�Ȃ̂ō��j
���F�g�̐B�́u�R���N�V�����v�𒍎����������B���F�g��h(X�CY�CZ)
���A�m��Ȃ��ӂ������
(���o�����̌��Ȃ�Ah(X�CY�CZ)��m���ł��ׂ�����тɐk����ł��傤�j
(1)�@�Ⴆ�@�I�������R�x�p���ē��o���ėV�Ԃ̂��������̂Ő������B
�u�R���N�V�����v(�ɂ��ẮA���l���Q��)
�����F�g�ł͘ǂ����Ȃ�A
(2)�@{X�CY�CZ}={��2 - ��2�C 2�����C ��3 + ��3}�ɂ����āAh(X�CY�CZ)�o���ĉ������B
(3)�@�oX�CY�CZ�CW}={��2 - ��2�C 2�����C ��3 + ��3�C ��4 + ��4} �ɂ����āAh(X�CY�CZ�CW)�o���ĉ�
�@�@�����B
�@����́A�g��̂����߂�b��ɂ��āi�����Q�R�N�X���P�Q���t���j
�@�R���ȏ�̈��������A���������̊�{�����A���������̌v�Z��r�˂��A�Θg�Ŏ~�߂��A
�g�܂ň����������������B
(�P)�@���̊e f[���C��]��Q[���C��]
��g�܂łɕ킢�A���������肢�܂��B
�@�@��2 - ��2�@�A��3 -
3����2�@�A��4 - 6��2��2 +
��4�@�A��5 - 10��3��2 +
5����4
�@�i�����܂ŗ���A�@��5 - 10��3��2 +
5����4 = 0�@�̐}���͈Ղ��߂���B�j
�@�@��6 -
15��4��2 + 15��2��4 -
��6�@�A��7 - 21��5��2 +
35��3��4 - 7����6�@�A
�@�@��8 -
28��6��2 + 70��4��4 -
28��2��6 + ��8�@�A��9 -
36��7��2 + 126��5��4 -
84��3��6 + 9����8
�@Wolfram|Alpha�@�̋Ɋe f[���C��] ��}�����āA���Ă��������B
(�Q)�@(�P)���ׂ����Ȃ�A���w���̒m���ŁAf[���C��]=0 �� R2 �ōl�@�i�����B�Ōy���`���锤�j���A
�@�@�Ⴆ�A������̑㐔�Ȑ� C1 �F ��2 + ��2�@=�@1�@�i�~)�@�Ə�̊e f[���C��]=0 �̌�_��
�@�@�i������C1�́A�e�ՂɁj���߂���̂ŁA���߂Ă��������B
�@�@�~����Y��ɕ���ł��܂������H��_��{���ɋ��߂āA�u�Y��v�����f�肢�܂��B
(�R)�@(�P)���ׂ����Ȃ�A���w���̒m���ŁAf[���C��]=0
�� R2 �ōl�@�i�����B�Ōy���`���锤�j���A
�@�@�Ⴆ�A������̑㐔�Ȑ� C2 �F ��4
+ 3��2�� + 2��2��2 - ��3 +
��4�@=�@0 �Ə�̊e f[���C��]=0
�@�@�̌�_�́i������C2�́A�e�ՂɁj���߂���̂ŁA���߂Ă��������B
�@�@C2 ���L���Ȑ��Ȃ�A�}��ϐ� t
�\�����āA���̋O�Ղ�`�ʊ肢�܂��B
�@�u�A���������̉���v����T
�@�� ������4�|�R��2�{�Q���@�̃O���t��̈قȂ�Q�_�Őڂ���ڐ��̕����������߂�B
�ɂ��āA�u�قȂ�Q�_�Őڂ���ڐ��v�����߂�ۂ́A���Ɂu�o�Ȑ��v�̏o�Ԃł��B
�u�o�Ȑ��̉���v�͂��Ȃ��ŁA�K�������A���z���L�ڊ肢�܂��B
(�P)�@��
= ��4 - 3��2 + 2�� ���ˉe�Ȑ�������Ɓ@-�w4 +
3�y2�w2 - 2�y3�w + �x�y3 = 0
�ł����H
(�Q)�@���F�g��u���K�S�D�U�D�P�P�v(�Q���ɍS���݂�j�̒�`�Ɋ�Â��A�o�Ȑ������߂ĉ�
�@�@�����B
(�R)�@���߂��o�Ȑ����A�t�B�������āA�Ԑ��@C�A���@C*�@��}������ƁA
�@�@�u�قȂ�Q�_�Őڂ���ڐ��v�ƂȂ�܂����HC�̈قȂ�_������_�Ɏʂ���Ă��܂��l�I
�@�@�i�u���K�S�D�U�D�P�P�v�̖�(�@)�̗�)�@�L���ʑ� C------��------->C*
�L���ĉ������B
(�S)�@C* �̓��ٓ_�B�����߂ĉ������B���F�̓��ٓ_�̖��̂�______�ŁA�L���ʑ����ɂ��
�@�@�Q�d�ڐ��̑������ꂩ���m�F���ĉ������B�ԐF�̓��ٓ_�̖��̂�______�ŁA���̓��ٓ_
�@�@�ɑΉ�����C�̐ڐ������߁A�}���肢�܂��B
(�T)�@C
�ƂQ�d�ڐ��ň͂܂�镔���̖ʐ� S1 �� ���߂ĉ������BC* �ň͂܂�镔���̖ʐ�
�@�@S2
�����߂ĉ������BS1/S2 �����߂čl�@�肢�܂��B
(�U)�@�悸�AC �̕ϋȓ_�����߁A�_P�i���w�j��C�̕ϋȓ_����ϋȓ_�܂œ����Ƃ��A�ׂ����
�@�@���܂܂ɘA�����ē�����(P)�i�E�w�j�̋O�Ղ����F�ŕ\���肢�܂��B
�@�э��搶�́A�u��
= ��4 - ��2�v���u�f�J���g�̐��_�Ƒ㐔���v�� 19p �ň����A�o�Α�������
���߂邱�Ƃ����ɓ���ƁB����ɂ��āA(�P)�`(�U)�����s���ĉ������B
�@�o�Ȑ������߂���B�̓��A��ԊȒP�Ȃ̂��Q���Ȑ��ŁA����焈Ղ����m��܂��A
�lj����܂����B�i�����Q�R�N�X���P�R���t���j
�@�o�Ȑ������߂�Ȍ��ɂ܂��@���݂�܂��B�����ɕ킢�A�Ⴆ�A�����o�Ȑ��̑o��
�Ȑ������߂Ă��������B
(�C)�@�悸�AA non-homogeneous polynomial (�� + 5)�� - �� ��Homogenization���āAf(���C���C��)
�@�@���瓾��ꂽ F(X�CY�CZ) ��Homogenization�@�̋t���ׂ��Ă��������B
�@�@(�@���ł������H �o�Ȑ������߂�ہA���̎�@�ŁD�D�D�B)
(��) ���̔��z�ŁA�Ⴆ�A�ڂ���ƒ����Β������ʎ���p���锭�z�łǂ����B
�@���l�ɂ��āA�����������̑o�Ȑ����A��� (�C)(��)�ŋ��߂Ă��������B
(�@���ł������H �o�Ȑ������߂�ہA���̎�@�ŁD�D�D�B)
�@�����������Ă��邩�A���� C* �̑o�Ȑ� (C*)* ���A(�C)(��)�ŕK�����߂Ċm�F�肢�܂��B
�@Devil's_curve �F�@-��4 + 2��2 + ��4 - ��2 = 0�@�̑o�Ȑ��������@�ŋ��߂Ă��������B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�R�N�X���P�S���t���j
(0)�@�悸�A�ׂ��ׂ�����(������)���ׂ��A-��4 + 2��2��2 + ��4 - ��2��2 = 0�@����A�����@�ŁI
�@�@C* �̑o�Ȑ������߁AC �ɖ߂�܂Ŋ撣���ĉ������B
�@C �ɂ́A���炩�ɁA�Q�d�ڐ������݂���B������A C* ���悭���āA���߂āA�V��ʼn������B
�@�����@�̗̉������𒍎����Ă��������B
�@Devil's_curve �F�@-��4 + 2��2 + ��4 - ��2 = 0�@����ёo�Ȑ��̓��ٓ_�B�����߂ĉ������B
�@C--��-->C*�@�̓��o�Ɓ@C* --��-->C �@�̓��o�͉������e�Ղł����H
�@C�FDevil's_curve �F�@-��4 + 2��2 + ��4 - ��2 = 0�@�̕��͒Z���̂ŁAWolfram|Alpha�@�̋�
�u-x^4+2*x^2+y^4-y^2=0�v��}���Ŋ����܂��BC*�@�̂ق��͒��߂���̂ŁA�H�v���v��܂��B
�@�Ȑ��̕����� ��3+��3-2��2+��2+��=0 ���܂��ˉe�Ȑ������A���̖₢�ɓ�����B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�R�N�X���P�T���t���j
(1)�@�o�Ȑ� �b* �����߂Ă��������B
(2)�@�������ē����o�Ȑ��@C* �̓��ٓ_�B�����߁AC* �Ƌ��ɐ}���肢�܂��B
(3)�@���߂��o�Ȑ��@C* �̓��ٓ_�B�� C �̔@���Ȃ�_�ɑΉ����Ă��܂����H
(4)�@(1) �̔��z�͊Ȍ��ł����A�L���ʑ��@C----��------>C*�@�͓����܂���̂ŁA�ʓr
�@�@���߂ĉ������B�����āA(3)���čl�肢�܂��B
(1)�@����t����(a) (b)�𖡓ǂ��A���z���L�ڊ肢�܂��B�A���A��`�̂܂܂Ŗ��NJ肢�܂��B
�@�Ⴆ�A(���C��)�́A���W�̓��ʂȏ�]�ނł��邱�Ƃ�Y�ꂸ�ɁB
(2)�@K(��)[Y]�� Y3 +(-��4 + ��2)=0 �Ȃ�Y�Ɋւ���������͉����Ă��܂��B���ہA�������Ƃɂ��A
�@�@�R�̂��ꂼ��̉��ɂ��A(a) (b) �������ĉ������B
�@���W�̂悤�ȏ��⑼�̑㐔�n�̏���Ԃɂ��āA26�N�Ԃ����w���Ŋ��ݍӂ���u
�`���ꂽ�ł��������݂�܂��B�ēx����̗ނ̑@(���C��)�@�����A
(3)�@(a)�A(b) �̓_�� f �������ŐV���ɒ�`�������Ă��������B
(4)�@�X�ɁA���� C �̑o�Ȑ��@C* �����߁A(a)�A(b) �̔@�����n��A����肢�܂��B
�@�@(���_�@K[X�CY]/(C*���`����C�f�A��) �Ȃ���W���߁A�ނ̑� (���C��) ���l����)
�@�u�f�J���g�̐��_�Ƒ㐔���v��15p �ɁA���ۓI�ɁA�u��=X+I�A��=Y+I (�ށj���`�v�ɂ��āA
9�s�����̉�������̂ł��傤��?���_�A���@�ŗނ̐� (Y+I)3 ��(X+I)3�@�́i��@�A�p�j��
�����Ɍv�Z����B
(��������@�ŁA���A�� ��^���āA ��3-��4+��2 ���̕����v�Z�͈Ղ����̂Ɣ�r��)
�@(a)�̉�����A�{���͗ނ̑������̏��ł��邱�Ƃ͕Ў������Y��Ȃ��B
�@���x�����p���܂����A�������ŗL���Ȑ��\�����������B
�@K[X�CY]/ <Y2 - X2(X + 1)>�ɂ��āA t = -((-�� - ��2)/y)��K(t)=K(���C��)
�i�����́@t=y/x��K(t)=K(���C��)�̓��o�͗e��)
�ŁA�������łȂ��A�Ȑ����Fty - (�� + ��2) = 0 �ł��L���Ȑ��\���������B
�@t = -((-�� - ��2)/��)��K(t)=K(���C��)�@�͔@���ɂ��Č��o���ꂽ���H
�@����K[X�CY]/ <Y2 - X2(X + 1)>�ɂ��Ă��A�����(a) (b) �̔@���l�@��_�� f �������߁A
����肢�܂��B
�@���_ �� �͏�]�ނŁAX+<Y2 - X2(X + 1)>�ŏ��@K[X�CY]/ <Y2 - X2(X + 1)>�̌��B �� �͏�
�]�ނŁAY+<Y2 - X2(X + 1)>�ŁA���@K[X�CY]/ <Y2 - X2(X + 1)>�̌��Bf=( )/( )��K(C) (��
���Ȑ� C �̔�����)
�@�㐔�Ȑ� C �̑o�Ȑ� C* �����߁AK(C*) ���l���A��Ɠ��l�̍l�@���肢�܂��B
�@�u���̘_�@�i�։ؖ[�j�v�́@3�@���z�g��́@�@3.10�@�㐔���l�� �ɍ��W�̒�` (110p)
���݂�܂��B���̏��̂�㐔���l��V��K��̔����̂ƁD�D�D�B
�@����𖡓ǂ��A���̊e���W������肢�܂��B
�uWolfram|Alpha�v�ɁA�Ⴆ�A��=��2-3�A����=1 ��}�����A�e���W���v���肢�܂��B��������
��ƁA�㐔�{���āA�Ղ������Ƃ����\������{�₩�Ɖ]���l�����݂��܂����H
�ߖT�̕��ɁA���̌����ߎ��������A���������������肢�܂��B
�@���̍��W���l�@���A���̏��̂����l�@�肢�܂��B�i�����Q�R�N�X���P�U���t���j
K[X�CY]/<-4X3 - 15X2 - 12X - 27Y2 + 4>
�@���W�@ K[X�CY]/<-4X3 - 15X2 - 12X - 27Y2 + 4>�@�ɂ��āA��������������
�@t = -((-�� - ��2)/��)��K(t)=K(���C��)�@�ŁA�������łȂ��Ȑ����F�� = t(-2 + 7�� + 4��2)/9�@�ŗL
���Ȑ��\���������B
�@���ہA -4X3 - 15X2 - 12X - 27Y2 + 4=0 �ƋȐ����F�� = t(-2 + 7�� + 4��2)/9 �̌�_������
�āAC ��L���p�����^-�\�����@�@(���C��)=( �C )��Q(t)2 ���肢�܂��B
�@(���C��)=(��1(t)�C��2(t))=( �C )��Q(t)2 �ɂ��āAt �f���� C �̂ɒ��z�I�Ȍ��Ƃ��A
�тɂ��Ă̘A�������� ��1(��)=��1(t)�A��2(��)=��2(t) �������āA���̌�����������
�������B�i����Ȗ���������Ƃ��݂�A���̏��Ж����D�D�D�B
�@C(t)�̕�����C(��1(t)�C��2(t)) �� �� �Ƃ���Ƃ��A�̂̊g�原���@[C(t)�C��]�����߂ĉ������B
t = -((-�� - ��2)/��)�@�͔@���ɂ��ē��o���ꂽ�̂ł��傤���H
�@�ȏ�́A�э��搶�����Ɋւ�����Ƃ��Ēv���܂����B�@���ł��傤���H
�i����������̃��C���ł��j
-4X3 - 15X2 - 12X - 27Y2 + 4=0�@�̑o�Ȑ������߂�O�ɁA�o�Ȑ��ɓ�d�ڐ�����
�݂��锤�Ɖ��̑z�芐�������R���L���ĉ������B
��1(��)=��1(t)�A��2(��)=��2(t) �����������Ƃ���A��d�ڐ�����̓I�ɋ��߂ĉ������B
�@�o�Ȑ������߁A���Ƃ̋Ȑ� -4X3 - 15X2 - 12X - 27Y2 + 4=0�@��m��ʂӂ�����A
f*[���C��]=0 �݂̂��g���A��d�ڐ������߂Ă��������B
�@�L���ϊ��@f[���C��]=0--��-->f*[���C��]=0�@�����߁A(���C��)= ��[��1(t)�C��2(t)]�@���� t ������
����Af*[���C��]=0�@�ɒH�蒅�����ł��B��肢�܂��B
�@f*[���C��]=0�@�̓��ٓ_ (x0�Cy0)�@�����߁A���̖��̂��L���A��[���C��]=(x0�Cy0) �Ȃ�(���C��)��
���� ���Ȃ����Ƃ��m���߁A�����������i���L�ڊ肢�܂��B
f[���C��]=0 ���͂ޖʐς����߂ėV��ʼn������Bf*[���C��]=0 ���͂ޖʐς����߂ėV��ʼn������B
�@���W�@ K[X�CY]/<X3 - XY + Y3>�@�ɂ��āA��������������
�@t =-(��2 - ��)/��2 ��K(t)=K(���C��)�@�ł��悢�ł����H�i�����Q�R�N�X���P�V���t���j
�@�������łȂ��Ȑ����F t =-(��2 - ��)/��2�@�ŗL���Ȑ��\���������܂����H
�@���ہA ��3 - ���� + ��3=0 �ƋȐ��� ��2 - �� + t��2=0�@�̌�_�����߂āAC ��L���p�����^-�\
����(���C��)=( , )��Q(t)2 ���肢�܂��B
�@(���C��)=(��1(t)�C��2(t))=( �C )��Q(t)2 �ɂ��āAt �f���� C �̂ɒ��z�I�Ȍ��Ƃ��A
�тɂ��Ă̘A�������� ��1(��)=��1(t)�A��2(��)=��2(t) �������āA���̌����������ĉ�
�����B�i���̖�͔э��搶�̏��Ђ̖͕�ł��j
�@C(t)�̕�����C(��1(t)�C��2(t))�� �� �Ƃ���Ƃ��A�̂̊g�原��[C(t)�C��]�����߂ĉ������B
�@t =-(��2 - ��)/��2 �͔@���ɂ��ē��o���ꂽ�̂ł��傤���H
�@�ȏ�́A�э��搶�����Ɋւ�����Ƃ��Ēv���܂����B�@���ł��傤���H
�i����������̃��C���ł��j
�������̂悤�Ɂ@��3 - ���� + ��3=0�@�̑o�Ȑ������߁A���ٓ_�ɂ��čl�@�����^�����L
�ډ������B
�@Sylvester�@�ɂ��I�����̔��z�ɁA�S�ꂩ��ӎ����q�ׂ�l�B�����E�ɐ������݂���
�ł��傤�B�u�I�����v�̂X�ŕӂ�Ɏ��Ⴊ�݂�܂��B
�@�ȉ��̂悤�ȃp�����^�[�̏����̍ۂ����g���A�ӎ����q�ׂ��o�����݂�܂����H
���́u����̂Ȃ��q��technique�i�Ɩ����j�v�ɂ��A
(0) ���̐��� t ���������ĉ������B��������ƁA���Č��ʂӂ������ ���A�� �̊W���ɂȂ�
�@�@�܂��ˁB���s�����Sylvester�@matrix ���g���܂������H
�@�㐔�Ȑ��B�@fj(���C��)=0 �ꕽ�� R2 �ɕ`���A�@���Ȃ�W�����邩�ӏ܂��A��������
�͕\�����ĉ������B
�@�������̂悤�ɁAf1(���C��)=0�@�Af2(���C��)=0 �̑o�Ȑ� f1*(���C��)=0�@�Af2*(���C��)=0 �����߁A
���W�@K[���C��]/<fj(���C��)> ���l���A�����̂悤�ȍl�@�肢�v���܂��B(j=1�A2)
�@�L���ʑ��@Cj--��j--->Cj* �����߁A
�@�@ (���C��)=��1(t(17 + 2��2 + ��4)/(2(1 + ��2)2)�C (16 + 49��2 + 2��4 + ��6)/(4(1 + ��2)2))
����u����̂Ȃ��q��technique�v�ɂ�� t ���������ĉ������B��2 �ɂ��Ă����肢���܂��B
�@�э��搶�����e��q�ǂ���X�͊撣���đ��̂Q���Ȑ��̑o�Ȑ������߂��B�i����ŏI
���H)�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�R�N�X���P�W���t���j
�@����ł͔��e���ς�炸�~���s���Ȃ̂ŁA2+1 ���Ȑ����o�Ȑ��ɒ��݁A�������
�肢�v���܂��B
�@reference ��211���݂�߂��̘_�q�̒��ɁA�u�~���i�[�v�Ɖ]���G�N�T�T�C�Y���琂����B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�R�N�X���P�X���t���j
�@�Ԑ��̎w�肳�ꂽ��̗��T��ׁA���Ԃ������A�o�Ȑ��������߁A�����B�m�F��
���肢�v���܂��B
�@����ꂽ�o�Ȑ��̕������̎��̓��ٓ_�́A�Ԑ��̕ϋȓ_�ɑΉ�����_�Ƒz��B�z��
�O�łȂ���AHessian_matrix�@���\����ɓo�ꂵ�Ȃ���Ȃ�Ȃ����B�O���t�̐Ԑ��ň�
�܂��L�̊z�قǂ̖ʐς𑽗l�Ȕ��z�ŋ��߂ĉ������B
�@�}�P�́A�}�Q�̈�ł��BC ��悸�ׂ��ׂ��Ď����iHomogenize �����j����ƁA
�@�@�@�@F[���C���C��]=��3 + 2������ + ��3 + 6����2
�@���ɁAHessian curve �����߁A����� F[���C���C��]=0 �̋��ʗ�_���݂�̂ŋ��߂ĉ������B
�S���ʼn��݂�܂����H�i���_�@P2(C) �Łj�S�ĕϋȓ_�ł����H���_�AHessian matrix����
�߁A���̍s��=0 �� Hessian curve�B
�@�o�Ȑ� C* ���A��`�Ɋ�Â����߂āArational map �Ă����߁AHomogenize �̋t���ׂ��A
C���}������ƁA�Ԑ��ɂȂ�A�o�@�Ȑ��͐�6���������̗�_�ŁA���ɂȂ邱�Ƃ��m
�F���ĉ������B
�@�}�Q�I���̕�����l�@�������R�����݂��邱�Ƃ����C�Â��ł��傤���H
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�R�N�X���Q�O���t���j
�@�ŏ��̂́A��3 + ��3 + �� + �� = 0 �Ȃ�㐔�Ȑ� C �ō��܂Œʂ�ɁAC ��悸�ׂ��ׂ��Ď�
���iHomogenize �����j����ƁA F[���C���C��]=________________���Ƃ��A�o�Ȑ������߂čl�@�Ȃ�
���ĉ�����ƍ���ɒ��ʂ���锤�ł��B�i�K������ĉ������j
�@�����Ȃ�A�ŏ��̖����㐔�Ȑ��@z13 +
z23 + z1+ z2 = 0
�Ɖ]���ė~�����B
(�ǂ����㐔�Ȗʂ�ɍl�@����̂ł��낤����A
f[z1�Cz2�Cz3]=0
)
�@�����āA�����ɁAzj=xj+yj�Ei �Ƃ��āA���������=0�A���������=0�A���������́A�l�@
�i4-���������=__�������l�́j�ƉB�������]���ė~�����B
( ���悵�� a+b�Ei
�ɂȂ�������߂�ہA��2=a+b�Ei �͏����h�A��2=(��+���Ei)2=a+b�Ei ��������A
�������l�@�������������h�j
�����ɁA�㐔�Ȑ���̈Ղ����_����̓I�ɖ��L���ĂƎ��₵�Az1=2 + 3�EI�@�̂Ƃ��A
z13 + z23 + z1+
z3 = 0�@���� z2
�B�����߂đ��̑��L���Ȃ����B
�@�u���̘_�@�i�։ؖ[�j�v��110p�ŋ�̑������ϓI�ɂ͎����ɂ����i�ƁA�i�c��X�搶����
�����j
�@�ŏ��� ��3 + ��3 + �� + �� = 0 �Ȃ�㐔�Ȑ� C �̓��ٓ_��o�Ȑ����ɂ��āA���ۓ�
�o���A����ꂽ���z���L�ڊ肢�܂��B
�@���͂��̉E����㐔�Ȗʂ̍��W�A�㐔�Ȑ��̍��W�ƁA�u���̘_�@�i�։ؖ[�j�v��
110p �ɒ�`���Ă���܂��B�ʁA���Ƃ���A�_�́AK[��]/<f(��)> ��㐔�ȓ_�̍��W�Ɩ���
���܂��B
�@�㐔�ȓ_�̍��W�ɂ��ẮA��R�l�@���܂����B
�Ⴆ�A����Q[X]/<�S���̑�����>=Q[��]�@��`����̂͗e�Ղł����A�㐔�Ȑ��̍��W
�ɂ��āA��̗�B�ŔY�o�����݂�L�q�肢�܂��B
�@�u���̘_�@�i�։ؖ[�j�v��107p�ɁA�u�㐔���l�̘̂b�͗��_��͎ˉe��ԓ��ň�������
�������肷��v�Ƃ���܂��BHessian_matrix�@���ˉe��Ԃ�O�ʂɉ����o���A�ϋȓ_��������
�������B
���F�̑ȉ~�Ȑ��@-��3 - �� + ��2=0 ��
(0)�@�悸�ׂ��ׂ��Ď����iHomogenize �����j����ƁA F[���C���C��]=-��3 - ��2�� + ��2�� �ƂȂ�
(1)�@���ɁAHessian curve �����߂�ƁA-8��3 + 24��2�� + 24����2 �ƂȂ邱�Ƃ������ĉ������B
(2)�@����ƁA F[���C���C��]=0 �̋��ʗ�_�����߂ĉ������B���A�ϋȓ_���݂�܂������H
(3)�@(0�F���F0)��P3(C)�Ȃ�_���݂�܂������H�݂�A-��3 - �� + ��2=0 �Ƃ̊ւ��Ɍ��y����
�@�@�������B
�@�ȉ~�Ȑ��@-��3 - �� + ��2=0 �̑o�Ȑ������߁A���ٓ_�����߁A�}�����Ă݂܂����B
�э��搶���A���́@-��3 - �� + ��2=0 �̕ϋȓ_���P�P�s�ɘj��_���Ă����A8+1 �݂�ƁB
����̉�����肢�܂��B
�i�X�^-�g�� -��3 - �� + ��2=0�@�Ɓ@��=����+�� ���� �� ���������A���ꂪ�R�d�������ł��B���_
�@���A�� �͕��f���ł��B)
�@���W�̒�`�́A�u���̘_�@�i�։ؖ[�j�v�ɍ݂�܂��B�nj㊴���L�ڊ肢�܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�R�N�X���Q�P���t���j
�����炭�A����قǍ�₪�e�ՂȖ������琂����o���͖����ł��傤�B
�@�����A�C�f�A�� I=<_____�C______>��K����------�Ɍ��߁AV(I)�������ɕ�������B
�@�u���̘_�@�i�։ؖ[�j�v��107p�ɁA�u�㐔���l�̘̂b�́A���_��͎ˉe��ԓ��ň�������
�������肷��v�Ƃ���܂��B
�@������Ǝˉe��Ԃ�O�ʂɉ����o�����A�o�Ȑ�����`�𖡓ǂ��ĉ������B
�i�����Ɍf���Ă���Walker �́A�o�Ȑ��̒�`��@���Ɉׂ��Ă��܂����H���Ⴊ�݂�܂�
���H)
�@��`�Ɋ�Â��A����(a) (b)�i�L���Ȑ��ɂ����ӂ���j�̑o�Ȑ������߂ĉ������B
�o�L���ϊ��@C--��--> C* �����߂ĉ������B
�@�悸�ׂ��ׂ��Ď����iHomogenize �����j�͂��Ă���܂��B���_�A���ٓ_�B�̑Ή��ɂ���
�y�Ȃ����ĉ������B
�@(b)�̌�A����������A�l�@���ꂽAlgebraic group �ɂ��Ċ��z���L�q�肢�܂��B
�@�u����A�P�U���������̔��ʎ��v�Z�ɐ����v�͎��m�B�i�����Q�R�N�X���Q�Q���t���j
�Ɖ]�����A���̂��ꂪ��j���[�X�Ȃ̂ƁB
�@��̂R���������̔��ʎ�
D ���撣���ċ��߂āA��D ����b�̂ɑ���i��Q�j���ۂ�
���f���A�y�������^�̖���z�����͂����������i�����̕������������đ��͍݂�܂�
��̂Ő���I�j
�@����́u���F�g�̐Ԙg�̂ǂ�ȑf��
�� ���y�������z���瓯�������ꂽ f[���C��] ��p���āA
f[���C��]=��
�\���������v�̙����Ɏ�Ⴊ�݂�܂��B�l�@�肢�܂��B
�@���݂ɁA�f���̗�B
{2�C 3�C 5�C 7�C 11�C 13�C
17�C�E�E�E�C17483�C 17489�C
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@17491�C 17497�C 17509�C 17519�C
17539�C�E�E�E}
�@f[���C��]=17539 �\�������ł��傤���H���_�A���W�@Q[���C��]/<f[���C��]-��>
���l�@���A�Y�݂�
���Ȃ�ł��傤�B
�@�㐔�I�]���̖��B��v���܂����B�@���P�@���Q�@���R�@���S�@���T
(1)�@�����Q�̕s�ώ� F�AG�AH �̊Ԃ�(�㐔�I�]��)�W���o�肢�܂��B
�@�@�i���h��ɂ����̂́A���̘_���Ɍ�肪�������̂Œv���܂����B���̘_���Ƃ́H)
(2)�@���o���ꂽ�㐔�Ȗ� S�F________________=0 �̑o�Ȗ� S* �����߂ĉ������B���_�A�悸��
�@�@�����iHomogenize�j����X�^�[�g���܂��B
�@�o�Ȗ� S* �͏��̌��ł����H
�����łȂ���A�o���k���L�ڊ肢�܂��B
�@�㐔�Ȑ��̑o�Ȑ��ɂ��ẮA�u�f�J���g�̐��_�Ƒ㐔���v�Ɏ��Ⴊ�݂�܂����A��
���Ȗʂ̑o�Ȗʂɂ��Ắ@��`����݂�܂���B
(3) ���̂ł��傤���H
�@�������������Ȃ��ŋȐ��ƕϋȓ_�ipoint of inflection�Cinflection point�j�̒�`���q�ׂ�
�������B�i�����Q�R�N�X���R�O���t���j
�@�����̒�`�ƈقȂ�܂������H�ϋȓ_���`����ہA���ʂɂ��Č��y�Ȃ����܂������H
�݂͂̉��̖�B�������ĉ������B
�@�܂��A�ˉe�Ȑ��@{(���F���F��)��P2(C)| ��2�� - ��3 + ��2�� - ��3 = 0 } �iP2(C)=�iC3-{(0�C0�C0})/R�j
�Ȃ����قR���Ȑ��ɂ��Ă��A���l�Ȗ�B�������ĉ������B
�@�X�ɁA���̎ˉe�Ȑ��̑o�Ύˉe�Ȑ������߁A���l�Ȗ�B�������ĉ������B
�@���W�� C[X�CY�CZ]/<�x2�y - �w3 + �y2�w - �y3> ��A���̏���
Q(C[X�CY�CZ]/<�x2�y - �w3 + �y2�w - �y3>�j�͉������l�@����܂����H
�@���̋Ȑ����ˉe�Ȑ������AHessian ��O�ʂɉ����o���A�X�̕ϋȓ_�����āA�e�ϋ�
�_�ɉ�����ڐ��L���ĉ������B
�@�͂��̉��̖�B�ɒNjL���܂��B�i�����Q�R�N�P�O���P���t���j
Hessian ��O�ʂɏo���A�����肢�܂��B
�@{(���F���F��)��P2(C) | -��4 + ��3�� + 3��2��2 - 5����3 + ����3 + 2��4 = 0 } �Ȃ�S���ˉe�Ȑ��ɂ���
���A���l�Ȗ�B�������ĉ������B
(�����A�@C�F 2 - 5�� + 3��2 + ��3 - ��4 + �� = 0 �̋ȗ������߁A�D�D�D�]�X)
�@�ϋȓ_�͉��݂�܂������H�e�ϋȓ_�ɉ�����ڐ��L���ĉ������B�X�ɁA���̎ˉe
�Ȑ��̑o�Ύˉe�Ȑ������߁A���l�Ȗ�B�������ĉ������B
�@���o�Ύˉe�Ȑ������߂��̔��z
�@AX + BY + CZ = 0�@�A-X4 + X3Z + 3X2Z2 - 5XZ3 + YZ3 + 2Z4 = 0 ����X���������AZ�Ɋ�
���锻�ʎ������߂�
�݂ĉ������B
�@�э��搶�o��̖�u ��=��/(��+5) �̂������� ���������������߂Ȃ����B�v����̔��z�Ŏ��݂ĉ������B
�@�@���Ȃ���ٓ_������܂������H���̊e���ٓ_�̏o���͑z��͈͓̔��ł������H
�@��̂S���Ȑ��̖��́A���Z�������Ƃ��l�����܂��B���̏��ȁi�k���R�l�A�k�����l�j�́H
�@���W�� C[X�CY�CZ]/<-X4 + ZX3 + 3Z2X2 - 5Z3X + 2Z4 + YZ3> ��A���̏���
Q(C[X�CY�CZ]/<-X4 + ZX3 + 3Z2X2 - 5Z3X + 2Z4 + YZ3>�j�͉������l�@����܂����H
�@�ˉe�Ȑ� ��2��2 + 4����3 - 4��4 + 4��3�� + 18��2���� - 18����2�� + 4��3�� - 27��2��2
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@+ 72������2 - 27��2��2 - 54����3 + 54����3 - 27��4 = 0
�̑o�Ȑ����A�Ⴆ����́A���̔��z�ŋ��߂ĉ������B�i�����Q�R�N�P�O���Q���t���j
(1)�@{D[f[���C���C��]�C��]�C D[f[���C���C��]�C y]�C D[f[���C���C��]�C ��]}
�����߁A
(2) {X�C Y�C Z} = �ɁE{D[f[���C���C��]�C ��]�C D[f[���C���C��]�C
��]�C D[f[���C���C��]�C ��]} �ɉ����āA
�@�@{�� -> ���C �� -> ���C �� -> ��} �Ƒ�����A
(3) �㎮���� ���A���A�� ���������A________________=0
(4) ��œ���________________=0 �ɉ����āAZ=1 �Ƃ��A________________=0 �̓��ٓ_�����߂�ƁA�Ǘ�
�@�@���ٓ_���o�����܂����H
�@�э��搶�o��̖���A����̏�̔��z�Ŏ��݂ĉ������B
(0) �悸�A�ˉe�Ȑ������A_____=0
(1)�@ {D[f[���C���C��]�C��]�C D[f[���C���C��]�C y]�C D[f[���C���C��]�C
��]} �����߁A
(2) {X�C Y�C Z} = �ɁE{D[f[���C���C��]�C ��]�C D[f[���C���C��]�C ��]�C D[f[���C���C��]�C ��]} �ɉ����āA
�@�@{�� -> ���C �� -> ���C �� -> ��} �Ƒ�����A
(3) �㎮���� ���A���A�� ���������A________________=0
(4) ��œ���________________=0 �ɉ����āAZ=1 �Ƃ��A(���_�@�����͕s�ς̑o�Ȑ��łȂ��������j
�������̎厲�����������ĉ������B
(5)�@��=��/(��+5) �̂��C�ɓ���̂V�_���߁A�e�_�ɉ�����ڐ������߁A�������� ���������� �̂ǂ�
�@�@�_�ɑΉ����Ă��邩�����ĉ������B
K[X�CY�CZ]��F[X�CY�CZ]=-X6 - 108Y6 - 36X3Y2Z - 216Y4Z2 - 4X3Z3 -108Y2Z4
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�R�N�P�O���R���t���j
(1)�@���̎ˉe�Ȑ��@{(X�FY�FZ)��P2(K)|F(X�CY�CZ)=0} �̑o�Ύˉe�Ȑ��𑽗l�Ȕ��z�ŋ��߂�
�@�@�������B���̎ˉe�Ȑ��@{(X�FY�FZ)��P2(K)|F(X�CY�CZ)=0} �̓��ٓ_�����߂ĉ������B
(2)�@�o�Ύˉe�Ȑ��@{(X�FY�FZ)��P2(K)|F*(X�CY�CZ)=0} �̕ϋȓ_�����߂ĉ������B
�@�@���_�@Hessian ����`�̔@���O�ʂɉ����o�������肢�܂��B�ϋȓ_�͉��݂�܂������H
�@�@�e�ϋȓ_�ɉ�����ڐ��L���ĉ������B
�@��̕ϋȓ_��ʂ钼���̏�ɁA�u��R�̕ϋȓ_���݂�v�Ȃ�A��̓I�ɖ��L�肢�܂��B
(3)�@{(X�FY�FZ)��P2(K)|F(X�CY�CZ)=0}�A{(X�FY�FZ)��P2(K)|F*(X�CY�CZ)=0}��������AC�AC*
�@�@�Ƃ���BK=R�@�ŁAC* �̋ȗ������߁AC*��̓_�ŁA�ȗ���0�ƂȂ�_�����߁A���̓_�ɉ�
�@�@����ڐ������߂Ă��������B
�i C*�̏k���́A�^�]�ҁA�m���Ńn���h�������薳���̉^�]�D�D�D�k�������߁AC* ��
�@�@�@�}�Ɠ��� Rn (n=2) �ɐ}���肢�܂�)
�@���g�o�́u����v�ɂ����āA
�@�u���̌��ɂ��āA�����Q�P�N�P���Q�V���t���ŁA���g�o�����������b�ɂȂ��Ă���A�炷
�@���邳��́A�u�ڂ��Ȃ��悤�� �� �̒l�����O���āA�� �̒�`������肵�āw����x�ƌĂׂ�
�@���Ȃ��v�Əq�ׂĂ�����B
���Ȃ��ɏo������u��͊T�_�E�ē��v�͝ɛ{�҂ɂȂ�ꂽ���ǎ҂��������݁B
���ؒ厡�搶�Ɍ��y�Ґ����݂�B�@�u�L���̐�㉐}�v�A�u�Q�l�}�v
(4) K=���f�ɑ̂Ƃ����Ƃ��A{(X�FY�FZ)��P2(K)|F*(X�CY�CZ)=0}����� ����C* �̕ϋȓ_��
�@���߂ĉ������B���݂�܂������H��̕ϋȓ_��ʂ钼���̏�ɑ�R�̕ϋȓ_���݂�
�@�Ȃ�A��̓I�ɖ��L�肢�܂��B�i�����Q�R�N�P�O���S���t���j
�Ⴆ�A����(�����ʁj H �F - +
+ ��+
��+ ��=0�@�ɂ͕ϋȓ_ (���C��)=(�P�|���E
��=0�@�ɂ͕ϋȓ_ (���C��)=(�P�|���E �C���E
�C���E )��C2
)��C2
���̂��Ă��铙���L�ڂȂ���ł��傤�B
�@�э��搶�@�H���F�㐔�Ȑ��̕��ڐ���ϋȓ_����������Ƃ��i���̌����e�[�}���R��j�A��
����ˉe�Ȑ��Ƃ��đ����A���A�̂�㐔�I�̂ɂƂ��Ă������Ƃ��]�܂����B�b���ȒP�ɂ�
��ׂɁAR[X]/<X2+1>�Ƃ��邱�Ƃ������B
�@���W�� K[X�CY�CZ]/<8X6 - 4Z3X3 + 72Y2ZX3 - 108Y6 - 27Y2Z4 + 108Y4Z2>�₻�̏���
�͏�ɍl�@�Ȃ����܂����H�ۂȂ�A�@���Ȃ�ꍇ�Ȃ���W�����l�@�Ȃ����܂����H
�@�э��搶�̍u�`��u�������f�p�ɁA�e�Ղɉ������z�͂Ȃ����̂��H�ƍl���A���E�̎��F
�̐l�i���Z�����j�����Ă��܂����z(0) �܂����B�O�Ղ����߂�e�ՂȔ��z(0)�ł��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�R�N�P�O���T���t���j
(�C)
�t�s���p���Ȃ����̗e�ՂȔ��z(0)
�ʼn��������̂Ɣэ��搶���������s���A��r����
�@�@�������B
(��) ��œ����o�Ȑ��̑o�Ȑ����A���̔��z(0)�ʼn��������̂Ɣэ��搶���������s���A
�@�@��r���ĉ������B
�@�i�Ώ̍s���̋t�s������߂āA�o�Ȑ��锭�z���э��搶�����Ɩ����j
�@�э��搶�����́A��=2
���Ȑ��i�ȖʁC.....)�݂̂ɂ����ʗp���Ȃ��̂��������ł��傤�B
��=2 ���Ȑ��ɂ��āA���Ƃ��A�F�{��w��w���i�����Q�R�N�x�O���j
�@(�n)
�� canonical form �ȉ~�̑o�Ȑ����A���̔��z(0)�ʼn��������̂Ɣэ��搶������
���s���A��r���ĉ������B
�@�����t���ő�ŏ����
�@(��)
�� canonical form �ł͂Ȃ���������̑ȉ~ C �̑o�Ȑ� C*�@���A���̔��z(0)
��
���������̂Ɣэ��搶���������s���A��r���ĉ������B�i�Q�l�}�j
�@(�z)
�� canonical form ��2=4�E1�E�� �� C �̑o�Ȑ� C*
���A���̔��z(0)�ʼn��������̂Ɣ�
���搶���������s���A��r���ĉ������B
�@�@���Ȃ�Q���Ȑ��̑o�Ȑ������߂邱�Ƃ��A�����e�Ղł��傤�I�����̐}����������^��
��
F �ɂ�� F(C) �̑o�Ȑ��𑽗l�Ȕ��z�ŋ��߁A�}���肢�܂��B
�@���z(0)�ɂ́A�u�悸�A�ˉe�����āv�ƍ݂�܂��B����ɕ킢��̊e�Ȑ����ˉe�����āA����
�o�Ύˉe�Ȑ������߂ĉ������B
(1)�@�}�̐��̔����̎厲��肪������Ă���o�Ȑ��̑o�Ȑ���(* *)�̔��z�ŋ���
�@�@�����B�i�����Q�R�N�P�O���U���t���j
�@�悸�A 1/9(�� - 7/2)2 - 1/4(�� - 1)2 = 1 ���ˉe������Ɓu���v���m�F���A���z�̓�s�����s
����A�u�v�̕������邱�Ƃ��m�F���ĉ������B
�@�u�v�̎厲���������A�}������A�}�̔@���Ȃ邱�Ƃ��m�F���ĉ������B�R���̑Ώ̍s��
�̋t�s������߂�э��搶�̕��������s���ĉ������B�Ꭶ�����y���ʎ��@���@�p����@���z�z
�Ȃ璆����������Ă��܂����B
(2)�@�u�v�̑o�́u�ԁv�́A�����ł��傤���A������y���ʎ���p���锭�z�z�œ��o���ĉ������B
�悸�A13��2 + 28���� + 28�� + 20��2 + 8�� + 4=0 ��э��搶�ɕ킢�ˉe������B
��̗Ꭶ�����o�Ȑ��̑o�Ȑ��͑ȉ~�ƈَ�̋Ȑ��ƂȂ�܂������A�z��͈͓̔��ł����H
(3)�@1/9(�� -��0)2 - 1/4(�� - ��0)2 = 1�@���̑o�Ȑ��̑o�Ȑ����َ�̕������ƂȂ�悤��
�@�@��0�A��0 �������߁A�������̎厲���������A�}�����ĉ������B�����������Ă��邩�́A
�@�َ�̕������̑o�Ȑ����A���C�ɓ���̈��锭�z�œ��o���A���̑o�Ȑ��ɂȂ�A����
�@�ł��B
�@(* *)�̔��z�ŁA��X�́A���ԂɕՂ��m��킽���Ă��锻�ʎ�D��p���āA�i�悸�AC����
�e�Ȑ�����)�㐔�Ȑ� C={(���C��}��K2| f[���C��]=0 } �̑o�Ȑ� C*={(���C��)��K2| f*[���C��]=0 }��
���Ă��܂����B�i�����Q�R�N�P�O���V���t���j
�@�㐔�Ȗʁ@S={(���C���C��)��K3| f[���C���C��]=0 }�̑o�Ȗ� S*={(���C���C��)��K3| f*[���C���C��]=0 }
�����߂��ɂ͂����Ȃ��ł��傤�B���ԂɕՂ��m��킽���Ă��鍂����m���̔��ʎ�D���A
�Q�x�p���āA�i�悸�@C �́@�ˉe�Ȗʉ���)�厲���������K�v�̂Ȃ�
(�� - 3)2 + (�� + 1)2 + (�� - 1)2 =22 �̑o�Ȗ� S* �����߂ĉ������B
�@���S�����낢�낸�炵�A���َ̈�̂Q���ȖʂɂȂ�悤���ݕ肢�܂��B
�@�э��搶��(* *)�̔��z�ɕ킢�A�S���̑Ώ̍s��̋t�s������߂锭�z����ςł��傤
���A�K�����s�肢�܂��B
�⒍�F���肦�Ȃ����Ƃł����A�o�Ȗʂ̒�`���B���Ȃ�A�����������A�Q�l�}����u�x��
���܂��B(��`����l�ɍ݂�A�v���ӁB������D�݂܂����H)
�@�ڋ�� Tp(M) �� L �ƒ��� ��=����+�� ---->(X�CY)=(���C��)�@�őo�Ȑ����`��������h��
���݁B
�@�i���̉p���̒��҂͒N�ł��傤���H�j�i�����Q�R�N�P�O���W���t���j
�@�iHint�F�m��l���m���I���l�F�@�Q�l�����P�@�@�@�Q�l�����Q�@�j
�@���̑o�Ȑ��̒�`���A�u���w(b�Cm)�^�o�Ȑ�C@�v�Ɩ������܂��B���܂ł� C* �́A�ڒ�
����H�ƔF�����A�`��+�a��+1=0----->(X�CY)=(A�CB) �ł������B
�@���D��=��3 �́u���w(b�Cm)�^�o�Ȑ�C@�v�o���A�o���̑㐔�Ȑ���`���܂����B
�@���D��=��2 �́u���w(b�Cm)�^�o�Ȑ�C@�v�o���ĉ������B
�@�����āA(C@)@�A((C@)@)@�A(((C@)@)@)@ ��K�����߂Ċ��z�i�u�o�炵���v���ɓ���j��
�L�ڊ肢�܂��B
�@�э��搶�́A�u�f�J���g�̐��_�Ƒ㐔�v�F��1�� �㐔�Ȑ��̊w(�����Ȑ��_�A�A�t
�B���㐔�Ȑ��A�ˉe�㐔�Ȑ��A�����^���̗��_�A�Ȑ��̎퐔�ƃ��C�G���V���g���X���q)
�v
23p �ŁA�u�ˉe�Q���Ȑ��ɂ��āA�T�s�ŕЕt���A�����ɂ��o�ΓI�ł���B�v�ƁAC* ��`�̔�
�����^������Ă����܂��B(��`C@�ɂ͂܂��������y���点��)
�@�э��搶���AC�F ��2=��3+x �� �ϋȓ_���X�ƁA���s�ɘj��v�Z�ŋ��߂Ă����܂��B����
�����ȋȐ��́u���w(b�Cm)�^�o�Ȑ�C@�v�o���AC@ �̓��ٓ_�����߂锭�z�ŕϋȓ_
���X �݂邩�m�F�肢�܂��B
�@�u���̘_�@�i�։ؖ[�j�v��107p�ɁA�u�㐔���l�̘̂b�͗��_��͎ˉe��ԓ��ň�������
�������肷��v�Ƃ���܂��BHessian_matrix�@���ˉe��Ԃ�O�ʂɉ����o���A�ϋȓ_����������
�����B
�@�ȉ��́A�ȑO�ɏq�ׂ܂����B�F�����܂ł̑o�Ȑ�C* �ŁA (C*)*=C �ł��B
�@�э��搶���A�u�f�J���g�̐��_�Ƒ㐔�v�F��1�� �㐔�Ȑ��̊w(�����Ȑ��_�A�A�t
�B���㐔�Ȑ��A�ˉe�㐔�Ȑ��A�����^���̗��_�A�Ȑ��̎퐔�ƃ��C�G���V���g���X���q) �v
�ŁA���� -��3 - �� + ��2=0 �̕ϋȓ_���P�P�s�ɘj��_���Ă����A8+1 �݂�ƁB����̉��
���肢�܂��B
�i�X�^�[�g�� -��3 - �� + ��2=0�@�Ɓ@��=����+�� ���� �� ���������A���ꂪ�R�d�������ł��B���_
�@���A�� �͕��f���ł��B)
(�C)�@�э��搶 ���AC�F �� - (��4 - ��2)=0 �ɁA��d�ڐ��i���Z���ɂ��j�����炩�ɑ��݂��邱��
�@�@���A�o�Ȑ� C* �����߁A���̓��ٓ_�����߂邱�Ƃɂ�莦���悤������Ă���B(19p)��
�@�@���肢�܂��B�iC�̈��������m�錠����L���̂ŁAC* �����߂��I�j
(��)�@���������A�t�ɕ킢�A���x�́A�u���w(b�Cm)�^�o�Ȑ�C@�v�o���āA���̓��ٓ_
�@�@�����߂邱�Ƃɂ���肢�܂��B���̕��́A(C@)@�����߂Ă݂ĉ������B(C@)@=C �ƂȂ�
�@�@�ʂ̂ŁA���o���ꂽC@�������Ă��邩���̊m�F��i�ł��肢�v���܂��B
�@����������Ƃ���A C@�F 27��4 - 144����2 - 4��2 + K��3 + 128��2 + 16�� = 0�@�i�ƂȂ�܂����B
�A���A��ӏ��B���j ����C�Ɖ��ꂪ�e�Ղł����HC@��m�錠����L���̂ŁA(C@)@������
���ɂ͂����Ȃ��ł��傤�I����B
�@C�����炩�ŁA�ʂȂ�u���w(���C���j�^�o�Ȑ� C@ �v���܂����炩�Ƃ���܂����A�Ⴆ�A
C�F ��4+��4=1 �̂Ƃ��A�u���w(���C���j�^�o�Ȑ� C@ �v�����߁A���ٓ_�̗L�������ĉ���
���BFig. 65�ɁA�u�ϋȓ_------>��t�̐�_�v���Ꭶ����Ă���B
�@�э��搶���AC�F ��2=��3+�� �̕ϋȓ_���X�ƁA���s�ɘj��v�Z�ŋ��߂Ă����܂��B����
�����ȋȐ��́u���w(���C���j�^�o�Ȑ� C@ �v�o���AC@ �̓��ٓ_�����߂锭�z�ŕϋ�
�_���X �݂邩�m�F�肢�܂��A�ƑO�ɂ��肢���܂����B
�@�э��搶�͍X�ɁA�ϋȓ_�̍l�@��Ƃ��Ĉȉ�������Ă�����B���̊e C �ɂ��āA
�u���w(���C���j�^�o�Ȑ� C@ �v�o���A C@ �̓��ٓ_�����߂锭�z�ŕϋȓ_�L����
�������B
�@�@C�F����-(��3+1)=0�@�@�@C�F(��2+1)y-1=0�@�@�@C�F(��2+1)y-��=0
�@�@C�F��-��4=0�@ �@�@C�F��-(��4+��2)=0�@�E�E�E�@(�ϋȓ_������̂Ɖ]���l�����邩��)
�@��̊e��������O�ɁA�O���t�߂āA���߂����C@ �̃O���t���ӏ܂��Ȃ���l�@�肢
�܂��B
�@�@C�F��-(��4+��2)=0 --->C@ �ɂ��ẮA(���C��)---�ϊ�--->(-4��4 - 2��2 + ���C 2��(2��2 + 1))
�����o���AC@ �̓��ٓ_�̕ϊ��ɂ�錴����K2 (K�͑�R[X]/<X2+1>�j�L���Ă��������B
�����āAC �̕ϋȓ_�ɉ�����ڐ������Ay=____��+____��K[x] (�����̌X���ł��傤�j�B
�@�Q�l�}�̐Ԑ�=C �̑o�Ȑ� C*=�� �̗�ɂ��Ă��u���w(���C���j�^�o�Ȑ� C@ �v
�o���AC@ �̓��ٓ_�����߂锭�z�ŕϋȓ_�L���ĉ������B
(�C)�@�э��搶 ���AC�F �� - (��4 - ��2)=0
�ɁA��d�ڐ��i���Z���ɂ��j�����炩�ɑ��݂��邱��
�@�@���A�o�Ȑ� C*
�����߁A���̓��ٓ_�����߂邱�Ƃɂ�莦���悤������Ă���B(19p)��
�@�@���肢�܂��B�iC�̈��������m�錠����L���̂ŁAC*
�����߂��I�j
(��)�@���������A�t�ɕ킢�A���x�́A�u���w(b�Cm)�^�o�Ȑ�C@�v�o���āA���̓��ٓ_
�@�@�����߂邱�Ƃɂ���肢�܂��B
�@�����u�c�������@�b�����������v�͎Q�l�ɂȂ邩�ȁD�D�D�B�i�����Q�R�N�P�O���X���t���j
�@C* �̋Ր��ɐG����`�i�P�@�Q�j�ɑ������܂����B���ȍ݂�āA�H�L�ł��傤���A�����ЂƂ�
�o�Ȑ�����`���݂�܂��B���̑o�Ȑ��̒�`���u���w(b�Cm)�^�o�Ȑ�C@�v�Ɩ�����
�܂����B�i�@�Q�l�����P�@�@�Q�l�����Q�@�j
�@��d�ڐ��̘b��ɁA���Z�������ނ̐V�N���ɑ̂̌������t�����ꂽ�э��搶�̒Ǒ�
�����������B
�@f[���C��]=-82��4 - 100����3 + 3��3 - 78��2��2 - 11����2 + 20��3�� + 8��2�� - 17��4 + 4��3
�Ƃ��Af[���C��]=0�@�ɓ�d�ڐ����݂邩�ۂ��A�э��搶�ɕ킢�A�݂�Γ�d�ڐ���
��=����+�� ��
���Čv�Z���A���߂ĉ������B
�i20p�ŁA�э��搶���Ꭶ����Ă���̂�������₂��܂����B������₂��ē�d�ڐ������߂�
���ƍl����̂����R�̐����ł��낤�i�Ǝt�̐^���j�j
�@�o�Ȑ��̓��ٓ_�����߂ē�d�ڐ����߂锭�z���M������Ă�����э��搶�ɕ킢
(�C)�@�悸�@f[���C��]=0 ���ˉe�����A��`�ɏ]���A�o�Ȑ� C* �����߁A�A�t�C�������A���̓�
�@�@�ٓ_�����߂邱�Ƃɂ���d�ڐ��̑��݂������Ă��������B
(��)�@���������A�t�ɕ킢�A���x�́u���w(b�Cm)�^�o�Ȑ�C@�v�o���āA���̓��ٓ_��
�@�@���߂邱�Ƃɂ���肢�܂��B
�@��X�́A�o�i�ˉe�j�Ȑ��̒�`�ɂQ���琂����BC* �̋Ր��ɐG�����`�B�����āA�o��
�Ȑ�����`���A�u���w(���C��)�^�o�Ȑ� C@ �v�Ɩ������܂����B�i�Q�l�����P�@�Q�l�����Q�j
�@���Z���������A�Ղ��� C�F-��4 + 3��3 - 2�� + ���@=�@0�@�ŁA�э��搶�ɕ킢�A����C=�Ԑ���
�͓�d�ڐ����ϋȓ_�B������̂͒m�������A�o�i�ˉe�j�Ȑ��̓��ٓ_�B�����߁AC �̈�
������𑨂������B
(1)�@C* ����ѓ��ٓ_�������}������ƁA�E�̐��̔@���Ȃ邱�Ƃ������ӏ܂��ĉ������B
�@�@�i���̈͂ޖʐς����߂ėV��ł��������j
(2) �@�u���w(���C��)�^�o�Ȑ� C@ �v����ѓ��ٓ_�������}������ƁA���̑����̔@���Ȃ�
�@�@���Ƃ������A�ӏ܂��ĉ������B
�@�@�i�����̈͂ޖʐς����߂ėV��ł��������j
�@�ȏ�ӏ܂���Ĕ@���������ł��傤���HC@�ɂ́A1+2�̓��ٓ_���p��I��ɂ��A�P��
��d�ڐ��A�Q�̕ϋȓ_�i�ɉ�����ڋ�� Tpj(C) )���Ή����Ă��錻���������܂��B
�@�Ƃ��낪�AC*�ɂ́A1+1�̓��ٓ_�݂̂�I��ɂ��A�P�̓�d�ڐ��A�P�̕ϋȓ_�i�ɉ�
����ڋ�� Tp1(C) )���Ή����Ă���ꕔ�̌����������������܂���B�i�B�����Ă������
�_���݂�A������]���ے肳��܂��j
�@C�F -��4 - 4����3 + 3��3 - 6��2��2 + 9����2 - 4��3�� + 9��2�� - ��4 + 3��3 - 3��=0
�ɂ��āA(1)(2) ��������AC@�AC* ���ꂼ��̒�`�̌��߂��L�ڊ肢�܂��B
�@�э��搶�@�H���F�u�������_�����A�ˉe�Ȑ���P2(K)�@ (K=R[X]/<X2+1>)�@�Ƃ��čl����
���Ɩ{�����𖾂ł��Ȃ��B�����A���_�����S�ɂȂ�v
�@�t�ɕ킢�A��̓�� C ��悸�ˉe�Ȑ������邱�Ƃɂ��A�o�Ύˉe�Ȑ������߁AC
��
���̂�S�Ė\�I���Ă��������B���ׂĂ̕ϋȓ_�L���铙���肢�v���܂��B
�@�㐔�Ȑ��B�̑o�Ȑ��B�̑��l�Ȕ��z�ɂ��i���E�̒N�����j����ɓw�߂Ă܂���
�܂������D�D�D��㐔�Ȑ��B�iTranscendental function�j�̑o�Ȑ����̌��͏��߂Ăł���
�����H�i�����Q�R�N�P�O���P�O���t���j�@���@����
�@��������O�ɋ���肢�܂��B��������Ȃ玟�ցB���ƂȂ�܂������H
�i���_�A����͍��܂ł̐����̗�Ƃ͈قȂ�A���Z�������ӂ̔��ʎ��͎g���Ȃ�)
�@�M�������o���ꂽC* �������Ă��邩�́A�K���A(C*)* �����߂Ď��Ȕ���肢�܂��B(C*)*
�̓��o�ߒ������L�肢�܂��B��`�̔@���A�ϋȓ_�́A�ȗ������߁A���ꂪZERO�Ȃ�_��
���z���݂�܂��B�i���@Coubure�j
�@����̋[�����K�Ȑ��@��=��(-��2) �̋ȗ������߁A�e�_�ɉ�����ڐ��̓�����`�ʂ��A��
�u�Ԃ�Ȃ��_�ŋȗ���ZERO�������ĉ������B
�@�w�Ǔ��鏊�Ԃ�܂����Ă���l���`���v���܂����B
�i�ڐ����Ԃ�܂����Ă���l�𑱂��ĕ`�ʂ��ĉ������j
�@�オ���C���ŁA���͎��̋�Y�T�O�ł��B����A��ʁD�D�D�B
�@�ڐ�������Ō�������ƁA
�@�u�Ȑ� C �̂��ׂĂ̐ڐ��̕���͂��Ȃ킿�Ȑ� C ���g�ł���v�i���Q�l�F����j
�@���{�̊T�O�̒�`�ɂ́A�u���͑̂������v���D�ɗ���������̂��݂邪�A����A��ʁA
�E�E�E�������̊������炻�̔��e���������ȃP�[�X�ɑ������A���m������A��ʂ̒�`
��WEB ��ł��������Ȃ��D�D�D�B
�@���X�э��搶��HP ��K�₳��鐢�E�̝ɛ{�ҏ����ɂ��肢�F���m�ȕ���A��ʂ�
��`�������ĉ������B
�@���_�A�э��搶�ɂ����肢���Ă���܂��B�i���ؒ厡�搶�̒�`�ł͕s�����́j
�@�Ԃ�Ă��܂��܂������A���C���͗e�Չ߂���ł��傤���A�Ԑ��̑o�̐��̕������̖�
�L���B
�@���K�̂��Ƃ��Q�ƂȂ����āA��㐔�Ȑ��Ȃ�@���H���l�@�肢�܂��B
�@�э��搶�̍u�`��u�җl�F���N�x�ɂ́A��㐔�Ȑ��̑o�Ȑ��������ɏo�܂���I��
���搶�͑O��̎��s���݂�A��������Ă݂ā@�����Ă��܂�����o�肳���ł��悤�B
�@�O��̎��s�F��=1/�� �̑o�͂����킩�邩��A�]�X�B
(�����{���ɏo�肵�����ɂ��āA�����܂Ő����Ɍ����L���ɑ����͋H�L�j
�u�L���̐�㉐}�@�i�u���ܘY�@���j�v��142p �ߖT�ɂ��Ղ��߂���F��=1/�� �̑o�ɗނ���i�H�j
�L�ڍ݂�B
�@�㐔�Ȑ� C={(���C��)��K2| f[���C��]=0 }=�Ԑ��̑o�Ȑ� C*={(���C��)��K2| f*[���C��]=0 }�ɂ�
�āA���z����A�Ⴆ�A�y���ԂɕՂ��m��킽���Ă��锻�ʎ�D�z��p���āA�i�悸�AC���ˉe
�Ȑ�����)�@C*=���Ă��܂����B�i�����Q�R�N�P�O���P�P���t���j
�@���l�ɁA�㐔�Ȗʁ@S={(���C���C��)��K3| f[���C���C��]=0 } �̑o�ȖʁF
S*={(���C���C��)��K3| f*[���C���C��]=0 } �����߂��ɂ͂����Ȃ��ł��傤�B
�@�un=2���Ȗʂ̑o�Ȗʂ͎����s�ρv�͑̌��ς݂Ȃ̂ŁAn=3���Ȗʂ̑o�Ȗʂɒ���
�ł݂܂����B�i���@�Q�l�}�j
�@S*={(���C���C��)��K3| f*[���C���C��]=0 } �����߂锭�z�Ƃ��āA�Ⴆ�A
(1)�@�y���ԂɕՂ��m��킽���Ă��锻�ʎ�D�z��p���ē��o�肢�܂��B
�@�э��搶�ɕ킢�A���_�A�悸 S ���ˉe�Ȑ������A -X3 - ZX2 + Y2X + WZX + Y2Z=0 ����
�ꕔ�B�� K=���F�A f*[���C���C��]=0 ��������܂������A.K���߂ĉ������B
(2) ����S* ��(S*)*=S �͎����ł��傤���A���ہA(S*)*�𑽗l�Ȕ��z�œ��o�肢�܂��B
(3) ����S*�������Ă��邩�m�F����p���A��ɋL�ڂ��܂������A�f�p�ɁAS�̈�_�A�Ⴆ�A
�@�@��=(1�C 2�C -3/4)��S �ɉ�����ڋ�� Tp(S) �̕����������߁ATp(S) �ɑΉ�����o��
�@�Ԃ̓_�����߂�S* �ɑ������A������������܂��B������s���ĉ������B
(4) �L���ʑ��@S------��------>S* ����������AS������������Ƃ��A�A������S*�����(p)
�@���@���ɓ������A�ώ@���ꂽ�^�����L�ڊ肢�܂��B
�@�u�f�J���g�̐��_�Ƒ㐔�v�ɑo�Ȑ��̒�`�Ƌ͂��̗� ���݂�܂����A�o�Ȗʂ�
��`������݂�܂���B�ȉ��̓��e��m�肽���Ă��܂�܂���B
�@�@��4�� ����
�@�@�@3�����㐔���l�̂̑o�L���w
�@�@�@���������w�Ƒ㐔�w
�@�@�@���wC�̃j���[�t�F�[�X
�i����́A���Z�̎w���҂⍂�Z�����߂�������Ɋ{�ɒ��ވׂ̋L���ł��傤���H)
�@���㑝�₳���ۂ́A����A�L���ʑ��@S---��--->S* �̗���R�ڂ��Ă��������B
�@�ŋ߂̑㐔�w�͒��ۉ����ɓx�ɐi��ł��āA���w�҂ɂ͍ŏ��̃n�[�h���������B
���ɁA�㐔�̍ŏ��̒i�K�ŁA�X�L�[���A�ʑ���ԏ�̑w�A�P�˓I�����𗘗p�����w
�W���R�z�����W�[���w�K����͍̂���ŁA�㐔���l�̂̒�`�ɂ��ǂ���O�ɍ��܂��Ă�
�܂��w�������Ȃ��Ȃ��B
�������ŁA���������ڍ��������ł����炷��Ƃ��āA���₳���ۂ͐���A�L���ʑ�
S---��--->S* �̗���R�ڂ��Ă��������B
�i���ۓI�ȋc�_�̑O�ɋ�̗�B��ؖ]�������͏��Ȃ��炸���݂��锤�́j
�@���̓x�̍��W�� K[X�CY�CZ]/<f[X�CY�CZ]>�AK[X�CY�CZ]/<f*[X�CY�CZ]> �⑴�̏��͉̂���
���l�@�Ȃ����܂����H�����łȂ���A�@���Ȃ�ꍇ�l�@�Ȃ���̂ł��傤���H
�@��X�́A���퐶���ɉ����āA�Ȑ����y���ɑ����Ȗʂ�ڂɂ��邪�A�Ȑ��A�ȖʁA�E�E�E��
�������t�A���������͖w�NjȖʂ�����Ă�������Ȃ��D�D�D�B�i�����Q�R�N�P�O���P�Q���t���j
�@�э��搶�ɕ킢
(1)�@�㐔�Ȗʂ̑o�Ȗʂ����߂ĉ������B�i���@�Q�l�}�j
�@�O����}�Ƃ͈قȂ�A����͓����L���Ă���܂���B���̑���ɁA
�@�@��=((153 - ��13601)/2452�C -1/18�C1/-17)��S �ɉ�����ڒ�����Tp(S) ��S�Ƌ��ɐ}��
�@���܂����B
(2)�@Tp(S)�̕����������ߑΉ�����S* �̓_�����߂邱�Ƃɂ�蓱�o���ꂽS*�F f*[���C���C��]=0
�@�����������Ƃ��m�F���ĉ������B
(3)�@�m�F�̕��@�Ƃ��āA(S*)* �����߂Č��̖و�����݂�̂ōs���ĉ������B
(4)�@S* ��}�����A�L���ʑ��FS---��--->S* �����L���AS*�̓��ٓ_�Ɏʂ����S�̓_������
�@�ĉ������B
�@����́A2+1���㐔�Ȗ� S�F��3 + ���� - ��3 + ��2��=0 �Ȃ��u��͔��vS�ɂ��Ă̂��肢�ł��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�R�N�P�O���P�R���t���j
(1)�@���l�Ȕ��z�œ��o����A�����Ă��邩�ۂ������l�Ȕ��z�Ŋm�F�����܂��B�����S�Ă�
�@�@���z���L�ڊ肢�܂��B
�@�P�W�S�X�N�A�P�[���[�͊��炩�ȂR���Ȗʂ͂��ׂĂ����萔�̒������܂ނ��ƁA�T�[����
�͂��̐��͂Q�V�ł��邱�Ƃ��ؖ������B���Ȃ킿�A�R���Ȗ�f(���C���C��)=0�ɂ͖����ɑ����̒���
���̂��Ă��邩�i���̏ꍇ�ɂ͐��D�ʂƌĂ��j�A�����łȂ���A���X�Q�V�{�̒�������
�܂܂Ȃ����Ƃ��ؖ�����Ă���i�T�[�����@�P�W�W�S�N�j�B
�Əq�ׂ��Ă���̂��������V�������L�ڊ肢�܂��B
(2)�@�����Ȃ�A�ؖ��肢�܂��B
(3)�@����̂�픧�FK[���C���C��]/<��3 + ���� - ��3 + ��2��> (K�͖��_�A�㐔�I�́@R[X]/<X-2+1>)
�@�@�ɂ��čڂ��Ă���S�Ă̒�����肢�܂��B
�@������p�����̂́A�u�����Ȋw�@�Ȗʂ̐_��v�̔э��搶�̂�=1�C2�C3�C...�Ȑ�...���f���l
�̂�7p�ł��B�i���@�Q�l�F�u�A�[�x�����l�̂��ꂱ�� (�Ȗʂ̐_��(���W))�v�A
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�u5���Ȗ� ��ʌ^�㐔�Ȗʂ�example (�Ȗʂ̐_��(���W))�v
�@���^�����^�ʑ��FKn---F--->Kn�@�ɂ�钴�Ȗʂ̑�F(���Ȗ�) �̋��ߕ����u�Ǖ��ɂ�
�Ēm��Ȃ��v�Ȃ�\��������A���Ȗʂ̔���^�ʑ��ɂ�鑜F(���Ȗ�) �̋��ߕ���_������
���V�����Ƃ�����܂���B�i�����Q�R�N�P�O���P�S���t���j
�@�Ⴆ�A��{�̍u�`�̐��^�ʑ��̋t�ʑ������߁AF(���Ȗ�)�����߂�A�Ɖ]���퓅��i�́A
����^�ʑ��ɂ͒ʗp����̂ŁA�t�ʑ��@�����߂��A���Ȗʂ̑�F(���Ȗ�)�����߂����B
�@�悸�A�Ղ������É���w�u�`���K�̑ȉ~�̑������߂�ہA�t�ʑ������߂��������߂����B
(1)�@��2/4 + ��2 - 1=0�@�AX - �� + ��=0�@�AY - �� - ��=0 ���� ���C�� ���������AX�CY �̊W����
�@�@�ĉ������B
�@�����̍ہA�L�͂ȁuSylvester's matrix �v�Ȃ��퓅��i���݂�܂��̂Ŏ��݂ĉ������B
�@�ȉ~�̑������߂�ہA�t�ʑ������߂��������߂�A��̏����ɂ�锭�z�́A�t�ʑ�F-1
�����ߓ����^�ʑ�F�FR2��(���C��)---F--->(X�CY)=F(���C��)=(��3-��2�C2����)��R2�@�ɂ��ʗp
����B����F�ɂ��ȉ~�̑�F(�ȉ~)��\���Ȑ��̕��������A
(2)�@��2/2 + ��2 - 1=0�@�AX -��3 + ��2=0�@�A Y - 2����=0 ���� ���C�� ���������AX�CY �̊W����
�@�@���ĉ������B
�@�����̍ہA�L�͂ȁuSylvester's matrix �v�Ȃ��퓅��i���݂�܂��̂Ŏ��݂ĉ������B
�@�~�@(��-1)2+��2=1 �̑������߂�ہA�t�ʑ������߂��������߂�A��̏����ɂ�锭�z�́A
�t�ʑ�F-1�����ߓ����^�ʑ�F�FR2��(���C��)---F--->(X�CY)=F(���C��)=(��2-��2�C2����)��R2
�ɂ��ʗp����B
�@����F�ɂ��~�̑�F(�~)��\���Ȑ�(�������̃n�[�g)�̕��������A
(3)�@(��-1)2+��2-1=0�@�AX -��2 + ��2=0, Y - 2����=0 ���� ���C�� ���������AX�CY �̊W����
�@�������B
(����͔����_�̉~�F|��-1|=1 ��C����-f-->��2��C �̑�f(�~�j�̈��鋁�ߕ��̕ʉ��ł��j
�@�����̍ہA�L�͂ȁuSylvester's matrix �v�Ȃ��퓅��i���݂�܂��̂Ŏ��݂ĉ������B
�@����X�AY �̊W�����A �uWolfram|Alpha�v�Ő}�����A
(4) ���̋Ȑ��̑o�Ȑ������߁A�X�ɓ��ٓ_���l�@�肢�܂��B
�@����^�ʑ�F�FR4---F--->R3 ���A
�@�@�@(��1�C��1�C��2�C��2)--->(X�CY�CZ)=F(��1�C��1�C��2�C��2)=(��1(��2 + 2)�C(��2 + 2)��1�C��2)
�Œ�`����B�i�����Q�R�N�P�O���P�T���t���j
(�C)�@F�ɂ��D={(��1�C��1�C��2�C��2)|��12 + ��12=1�@�A��22 + ��22 =1}�@�̑� F(D)���@���Ȃ�R3 ��
�@�@������㐔�ȖʂɊ܂܂�邩���A��ɕ킢�A
�@�@X - ��1(��2 + 2)=0�@�AY - (��2 + 2)��1=0�@�AZ - ��2=0�@�A��22 + ��22 - 1=0�@�A��12 + ��12 - 1=0
�@����A��1�A��1�A��2�A��2 ���������AX�AY�AZ �̊W�� f(X�CY�CZ)=0 �o�肢�܂��B
(��)�@�����㐔�ȖʁF f(X�CY�CZ)=0 ���A�Q�l�}�̔@���}���肢�܂��B
�@�@�i�}�����ꂽ�Ȗʂ͌������s�������Ȗʂł����H)
(�n)�@S�F f(X�CY�CZ)=0 ��̂T�_��j ���炢����̓I�ɒ�߁A�e�ڒ�����T��j(S)�̕���������
�@�@�߂āA�o�Ȗ� S*�̕�����f*(X�CY�CZ)=0 �����o�����ٓ_���l�@�肢�܂��B
�@����^�ʑ�F�FR2---F--->R2 ���l�@����B�i�����Q�R�N�P�O���P�U���t���j
�@�@�iX�CY)=F(���C��)=(8��3 - 4��2 - 24��2�� - 4�� + 4��2 + 1�C-8��3 + 24��2�� - 8���� - 4��)
�@���𓂓˂ɖ��̌��̔���^�̎ʑ����I�ƕ���ꂻ���ł����A�����A���͍��Z�����m��
�̎ʑ����ƁA�ȉ����������ɂȂ�ł��傤�B
(0)�@F �̐��̂́A�uJacobian matrix and determinant�v�����߂�Ɣ����̉��ɂ��炳����
�@�@�ŕK�����߂ĉ������B
�@Jacobian matrix �͓������݂�߂��A���O�����s��ł����ł��傤�B���̎ʑ��̐��͍̂�
�ؒ厡�搶���Ȃ���u��͊T�_/��2���v�i�Q�l�j����H��锤�B
�@�u��͊T�_/��5��/��͔����v�ŁA�u�����\�Ƃ����A���ȒP�ł��邪�A�ܒ~�͑���
�ł���v
(1)�@(���C��)--->determinant(Jacobian matrix)(������) �̃O���t��`���ĉ������B��O�_��
�@�����Đ��ł������Hdeterminant(Jacobian matrix)=k (k=,..3.2.1..)�Ȃ铙�������`���ĉ���
�@���B
�@�ȏォ��AF �́A��=��+���Ei --f--> f(z) �̎����A�����ō\�����ꂽ���̂��Ƃ��C�Â��ł��傤�B
�����ɁAf(��)=__��3+___��2+___��+___(<--�߂ĉ������B�j
�@���āAF�̑㐔�Ȑ��̑����A�t�ʑ������߂��@�ׂ͈���̂ŁA�����@�ŋ�������B
(�C�j�@f(��)��ZERO�_���l���A�Ⴆ�A���S=(0�C0)�A���a���F�X�̉~Cr �̑�f(Cr) �̕�������
�@�@������Ƌ��߂����B
�@f(Cr) ���A(0�C0)�̂܂��� 0 ��A���悤�A�� �������߁Af(Cr)�̕�������������Ƌ��߂�
�������B
�@f(Cr) ���A(0�C0)�̂܂��� 1 ��A���悤�A�� �������߁Af(Cr)�̕�������������Ƌ��߂�
�������B
�@f(Cr) ���A(0�C0)�̂܂��� 2 ��A���悤�A�� �������߁Af(Cr)�̕�������������Ƌ��߂�
�������B
�@f(C1)�͊����ɁA(0�C0)�̂܂��� 3��A���ł��傤�B f(C1)�̕������́A
X6 - 6X5 + 3Y2X4 - 225X4 - 12Y2X3 + 300X3 + 3Y4X2 - 462Y2X2
�@�@�@�@�@�@�@�@�@+ 15855X2 - 6Y4X + 308Y2X + 42042X + Y6 - 237Y4 + 13475Y2 - 57967=0
�ƂȂ�܂����H��̊ef(Cr)=0 �̑o�Ȑ������߁A���ٓ_���l�@�肢�܂��B
�@f(��)=________(<--�߂ĉ������B�j
�ɂ��Ă͗e�ՂɁAf(��)=8��3 - 4��2 - 4�� + 1 �o���ꂽ�ł��傤�B
�i��)�@�ȉ��́A�K���A�Q�ɗ��ނ̂ŁA�K������đ��͂���܂���B�g�c�P�`����ɕ킢�A
�@�@f(��)=0 �̉������Ƃ��鎞�A���̉������̗L������(��)��Q(��) �ŕ\���\�͎����ł��A
�@�@���̉\�Ȃ̂��̍������L�q�肢�܂��B�����āA���������A��j(��)=____ �Ə�ϕ\
�@�@��i�E��j���������ĉ������B
�@�t�ʑ�F-1�����߁AF�ɂ�钴�Ȗʂ̑� F(���Ȗ�) �����߂�ʏ�̔��z���݂�B
(���w���K,�E�E�E���É���w���w��������p���܂����j
�w�����������Ɏw������Ă����{���j�ȊO�ɂ��F(���Ȗ�)�̕������̓��o�ɍS�肽���x
�@R2 �ɉ����锽�]�FF(���C��)=(��/(��2 + ��2)�C ��/(��2 + ��2)) �ɂ��
(1)�@C�F ��2/2 - ��2 =1 �̑� F(C) ���t�ʑ�F-1�����߂��A
�@�@X= ��/(��2 + ��2)�@�A Y = ��/(��2 + ��2)�@�A -1 + ��2/2 - ��2 = 0
�@����A���A�� ���������AX�AY �̊W���o���锭�z�ł��肢���܂��BC��F(C)�̑o�Ȑ�
�@�����߁A�l�@�肢�܂��B
(2)�@C�F (�� - 1/3)4 + ��4 = 1 �̑� F(C) ���t�ʑ�F-1�����߂��A
�@�@X= ��/(��2 + ��2)�@�A Y = ��/(��2 + ��2)�@�A (�� - 1/3)4 + ��4 -1 = 0
�@����A���A�� ���������AX�AY �̊W���o���锭�z�ł��肢���܂��BC��F(C)�̑o�Ȑ�
�@�����߁A�l�@�肢�܂��B
�@R3 �ɉ����锽�]�FF(���C���C��)=(��/(��2 + ��2 + ��2)�C ��/(��2 + ��2 + ��2)�C��/(��2 + ��2 + ��2)) �ɂ��
(3)�@�Ȗ�S�F(�� - 1/2)2 + ��2 + ��2/9 = 1 �̑� F(S) ���t�ʑ�F-1�����߂��A
�@�@(�� - 1/2)2 + ��2 + ��2/9 - 1=0�@�AX = ��/(��2 + ��2 + ��2)�@�AY = ��/(��2 + ��2 + ��2)�@�A
�@�@Z = ��/(��2 + ��2 + ��2)
�@����A���A���A�� ���������AX�AY�A�y �̊W���o���锭�z�ł��肢���܂��B�r��F(�r)�̑o
�@�Ȑ������߁A�l�@�肢�܂��B
�@�� F(���Ȗ�) ���t�ʑ�F-1�����߂��A���A���A���A....���������AX�AY�AZ�A... �̊W���o��
�锭�z�̋�̊��z���L�ڊ肢�܂��B
(���w���K,�E�E�E���É���w���w��������p���܂����j�i�����Q�R�N�P�O���P�V���t���j
�@����𑽗l�Ȕ��z�ʼn����ĉ������B(���_�A�C�f�A���̊ϓ_����j
�@�t�ʑ�F-1�����߁AF�ɂ�钴�Ȗʂ̑� F(���Ȗ�) �����߂�ʏ�̔��z���݂�B
(���w���K,�E�E�E���É���w���w��������p���܂����j
�@�����̐��^�ʑ��ɂ�鑜A(S1)�AA(S2)���w�����������Ɏw������Ă����{���j�ɏ]��
�ɂȂ�AA-1�����߂锭�z�œ��o���x�A�~�Ƃ͒������Ȑ�C=A(S1)��A(S2) �ɂ��āA(1)(2)��
�悤������n�삵�A�����Ă��������B
�@S1��A(S1)�̑o�Ȗʂ����߁A�l�@�肢�܂��B
�@S2��A(S2)�̑o�Ȗʂ����߁A�l�@�肢�܂��B
�@���� n=2���Ȗʂ̑o�ɂ��ẮA�э��搶�����z�i�悸�ˉe����)���܂߁A���l�Ȕ��z
�ŋ��߂ĉ������B
A(S1)*��A(S2)* �ɂ��āA(1)(2)�̂悤�Ȗ��n�삵�����Ă��������B
�� A(S1) �� �t�s�� A-1�����߂��A���A���A���A....���������AX�AY�AZ�A... �̊W���o���锭
�z�Ő��߂ĉ������B
�� A(S2) �� �t�s�� A-1�����߂��A���A���A���A....���������AX�AY�AZ�A... �̊W���o���锭
�z�Ő��߂ĉ������B
�@R3 �ɉ����锽�]�FF(���C���C��)=(��/(��2 + ��2+��2)�C ��/(��2 + ��2+��2)�C��/(��2 + ��2+��2)) �ɂ���
��S1�̑� F(S1) ���t�ʑ� F-1�����߂��AS1�̕�����
�@�@�@X = ��/(��2 + ��2 + ��2)�@�AY = ��/(��2 + ��2 + ��2)�@�AZ = ��/(��2 + ��2 + ��2)
����A���A���A�� ���������AX�AY�AZ �̊W���o���锭�z�ł��肢���܂��B
�@F(S1)�̑o�Ȗʂ߁A�l�@�肢�܂��BF(S2)�̑o�Ȗʂ߁A�l�@�肢��
���B
F(S1)*��F(S2)* �ɂ��āA(1)(2)�̂悤�Ȗ��n�삵�A�����Ă��������B
�ȏ�A���Ȃ�̖��B��������A�����݂�ꂽ�ł��傤�B�����z��I
�@�X�ɁA���������Rn(n=4�A5�A�E�E�E�A19�A�E�E�E)�ɉ����钴���ʒB���߁A��̖��Q�̂悤
�Ȗ�B��n�삵�A���������ĉ������B
���F�g�Ɍ݂��ɑo�Ɩ��L���Ă���̂��琂��܂����B
(1)�@�U���㐔�Ȑ�����A���̑o�Ȑ��𑽗l�Ȕ��z�œ��o���A�S���㐔�Ȑ��ĉ������B
�@�@�o���̑㐔�Ȑ���}�����āA�ǂ���ɓ���݂����邩�A���P�[�g���Ƃ��Ă��������B
(2)�@�U���㐔�Ȑ����AK=R[X]/<X2+1> �ōl�@�����Ƃ��A���ٓ_�����v���A�Q�d�_����瓙
�@�@���L����Ă��܂��B���ꓙ���ؖ����A�Q�d�_�ɑΉ�����o�Ȑ��̕��f�ڐ��L�肢
�@�@�܂��B��_�ɑΉ�����o�Ȑ��̐ڐ��L�肢�܂��B
�@R2 �ɉ����锽�]�FF(���C��)=(��/(��2 + ��2)�C ��/(��2 + ��2)) �ɂ��
(3)�@C �̋t�ʑ�F-1�����߂��AX= ��/(��2 + ��2)�@�A Y = ��/(��2 + ��2)�@�A�U���㐔�Ȑ� = 0
�@����A���A�� ���������AX�AY �̊W���o���锭�z�ł��肢���܂��B�� F(C)���͂ޕ���
�@�̖ʐςƌʒ������߂Ă��������B
(4)�@C* �̑� F(C*) ���t�ʑ�F-1�����߂��A
�@�@�@X= ��/(��2 + ��2)�@�A Y = ��/(��2 + ��2)�@�A�S���㐔�Ȑ� = 0
�@����A���A�� ���������AX�AY �̊W���o���锭�z�ł��肢���܂��B�� F(C*)���͂ޕ���
�@�̖ʐςƌʒ������߂Ă��������B
(5)�@F(C)�̑o�Ȑ����A���l�Ȕ��z�œ��o�肢�܂��B
(6)�@F(C*)�̑o�Ȑ��𑽗l�Ȕ��z�œ��o�肢�܂��B
(7)�@G(���C��)=(��3 - 3����2�C 3��2�� - ��3)�Ȃ����^�ʑ����߂�B�� G(C)�A�� G(C*) �����߁A
�@�@���ꂼ��̑o�Ȑ� G(C)*�A G(C*)* �B�����߂ĉ������B
(8)�@���g�̈�s�ڂ��ؖ��肢�܂��B
�@�u�V���썂�Z�r�r�g�����v�̂悤�Ȍ��ɑ��������̂ŁA���F�g�̋Ȑ�C�Ƃ��̑o��C* �̐�
���Ȑ��B�����߂����Ȃ�܂����B
(1)�@C*�̐����Ȑ� �́A���݂�ƁA
�@X8 + 4Y2X6 - 3X6 + 6Y4X4 - 9Y2X4 + 3X4 + 4Y6X2
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@- 9Y4X2 - 21Y2X2 - X2 + Y8 - 3Y6 + 3Y4 - Y2=0
�ƂȂ�܂����B��肪�݂�A���𐳂��āA���̓��ٓ_�����߂ĉ������B
(2) C�̐����Ȑ������߁A���̓��ٓ_�����߂ĉ������B
�@�Ȑ��Ƃ��̐����Ȑ��� R2 �ɕ`���A���R�ɂ����_������������܂��B�i���̃A�j����
�L���B���R�ɂ����_���Ɋ�O�ɒj�@�i���@�Q�l�}�j�[���������邽�߂��Q�l�}
�@O�Ɋւ���C�̐����Ȑ���Pedal(O�GC)�ŕ\���B��(O�GC)�ł͗��z�������ɂȂ��D�D�D�B
�@�܂��A�ȉ~C=���F ��2/22 + ��2 = 1 �@O=(1�C1)����AC--->Pedal(O�GC)�̑㐔�Ȑ�������
�ĉ������B�������݂�ƐԐ��Ŏ�����
�@�@�@X4 - 2X3 + 2Y2X2 - 2YX2 - 3X2 - 2Y2X + 2YX + 8X + Y4 - 2Y3 + 2Y - 5=0
�ƂȂ�܂����B��肪�݂�ΏC���肢�܂��B
�@Pedal(O�GC)--->Pedal(O�GPedal(O�GC))�̑㐔�Ȑ������߂ĉ������BC--*-->C�̑o��
��C*�����߂ĉ������B
�@C����=2���Ȑ��Ȃ̂ŁA�э��搶�ɕ킢�A�悸�ˉe�����A�Ώ̍s��̋t�����݂ĉ������B
�@Pedal(O�GC)--*-->Pedal(O�GC)*�����߂ĉ������B
�i�����Q���Ȑ��ł͂Ȃ��̂ŏ�̎�@�͒ʂ��܂���j
�@Pedal(O�GPedal(O�GC))------->Pedal(O�GPedal(O�GC))*�����߂ĉ������B
�@��2+��+1 = ��2+��-��2+1+I�E(2����+��) �@�����`��������^�ʑ�F��
�@�@R2---F--->F(���C��)=(��2+��-��2+1�C2����+��)��R2�@�ɂ���߂�B
��F(C)�����߂ĉ������B��F(C) �� Pedal(O�GF(C))�����߂ĉ������B
��F(C*)�����߂ĉ������B Pedal(O�GF(C))* �����߂ĉ������B
�@��̖�B�́AO=(1�C1) �Ƃ��܂������AO ���߂�͎̂��R�ł��B�����ɁAO=(1�C9)
�Ƃ��ď�
�̑S�Ă̖�B��{���ɉ����ĉ������B
�@�u�܂��A�ȉ~C=���F ��2/22 + ��2 = 1 �@O=(1�C1)����v�Ə�ɋL���܂������A���́A�o�Ȑ�
�ɂ��āA��̖�B�̂悤�Ȗ�B��n�삵�A�����Ė�����ʼn������B���_�A���{�����{����
�����i�厲���f���łȂ�����ɂ��Ă��j�ɂ��Ă��D�D�D�B
�@�o�Ȑ������߂��p���́i�Q���Ȑ��̂̍s��\���ɂ��j���z�́A�э��搶�����j�̒�
��ł��B�i�����Q�R�N�P�O���P�W���t���j
�@�搶����ς��Ɖ]���邵�An=2���Ȑ��A�Ȗ�....�ɂ݂̂����ʗp���Ȃ��̂ŁA���݂܂ő�
�̑��l�Ȕ��z�݂̂őo�Ή����܂����B�@�������A�A���_�[���C���̎����ׂ�����A�y�_���Ȑ�
�����ꂩ��Q�b�g�Ƃ���̂ňׂ��܂����B�i���Q�l�j
�@�����o�Ȑ��@5��2 + 2���� + ��2/5 - 2���� + (2����)/5 + ��2/5=0
�@�@�@�@�@�@�@�@�@�@25��2 + 10���� + ��2 - 10���� + 2���� + ��2=0
�@���ꂩ��A(���Ӂj�ɂ����āA�@�� -> ��/(��2 + ��2)�@�A�� -> ��/(��2 + ��2)�@�A�� -> -���@����
applying the inversion transform ���s���A
�@25��2 + 10��3 + ��4 + 10���� - 2��2�� + ��2 + 10����2 + 2��2��2 - 2��3 + ��4=0
�Ȃ�y�_���Ȑ����Q�b�g�o���܂����ˁB
�i�o�Ȑ����o�ăy�_���Ȑ��Q�b�g�͏��̌��ł����ł��傤�j
(1) �э��搶���AC�F ����=1 �̑o�͂����킩��A�Ɖ]����̂ŁA���̑o�Ȑ������߁A
�@��̔@���Aapplying the inversion transform ���s���A�y�_���Ȑ� Pedal(O�GC)
(O=(0�C0))
�@�����߂ĉ������B
(2)�@�܂��A�o�Ȑ��ȂǁA�m��ʑ����ʃt�������āA���ɑ��̔��z�ŁAC�F ����=1
�̃y�_����
�@�� Pedal(O�GC) (O=(0�C0)) �����߂ĉ������B
�@�Q�l�}�̈�ԍ��̂悤�ȁA�W�̎��Ȑ�������ꂽ���ł��B�}�����ĉ������B
�@��4 - 4���� + 2��2��2 + ��4=0 �� �uWolfram|Alpha�v�Ő}���������̂ƈ�v���܂������H
(3) �����y�_���Ȑ� Pedal(O�GC) �̑o�Ȑ������߂ĉ������B�A���_�[���C���̎��́A
�@�@�y�_���Ȑ� Pedal(O�GC)���Q���Ȑ��łȂ��̂Œʂ��܂���!
�@�F�X�� C�AO=(��0�C��0)�@�ɂ��āA�y�_���Ȑ� Pedal(O�GC)�B�i�̓��ٓ_�j���������\����
�A�ȉ�����\������邩������܂���B�i���Q�l�j
�i�o�Ȑ����o�āA�y�_���Ȑ��Q�b�g�j������̃��C���ł��B�������ē�����A���z��L
�ڊ肢�܂��B
�o�Ȑ��ƃy�_���Ȑ����݂Ȃ�_���ɁA2011/10/18 �̒��A�琂��A�����A�C�����͖���
�₽���͂Ȃ��A�V�j���Ȃ���l�������Ԃ��܂߂āA�ȏ��___���ԗv���܂����B
�@�o�Ȑ��ƃy�_���Ȑ��̘_�������āA�َ��ȗ��ݍ����Ƌ����܂����B
�@�_�� �̑S�e��m�肽���ł����H�i�����Q�R�N�P�O���P�X���t���j
�@�uA Grand Tour of Pedals of Conics�v���AGoogle �Ō�������A�f�G�ȑS�e���������
���傤�B
���ǂ���A�����̊��z��K���L�ڊ肢�܂��B
�@�o�Ȑ��ƃy�_���Ȑ��̘_���̑S�e���Q�b�g���A�K�����Ă��������B
�@�k�Ђ⍋�J�i�m�߂ł̓^�C���j�Ŏ��ȊO�ɂ����ꂽ�S�i�S�̒ɂݕ\���j�̎����傪���݂�
�邩�ۂ���������Ǝ������Ȃ����@�݂�B
�@���̐S�̝������A�E���Ԑ��Ō��������ȏ�̐S�̝�����AO=(��0�C��0)��I��ŁA�y
�_���Ȑ�������A���̑㐔�Ȑ��L���A�o�Ȑ����K�����L�肢�܂��B
�uO=(��0�C��0)��I��ŁA�y�_���Ȑ����v�ŁAO �̑I�����͖����ɍ݂�A����ɉ��������̑�
���Ȑ��̃y�_���Ȑ����Y�o����A���̑o�Ȑ��̋�ŁA�����i�������߂܂��B
�@�Ⴆ�AO=(19�C4) �Ńy�_���Ȑ��F________________�@���̑o�Ȑ��F_____________________
�@�k�Г��ŁAkardioeides ���c�ވȏ�̕ό`F(kardioeides) �̔N�ł��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�R�N�P�O���Q�O���t���j
�@�@�J�[�W�I�C�h�i�Q�l�P�A�Q�l�Q�j�@kardioeides =�ukardia�i�S���j�v + �ueidos�i�`�j�v�j
�@C�F-��2 - ��2 + (��2 + �� + ��2)2=0 ���p���╺�ɋ����w�́u�~�Ɋւ��锽�]F�v�ɂ���
(1)�@F(C) �𑽗l�Ȕ��z�ŋ��߂ĉ������B(F(F(C))=C �͎����ł��傤���A���)�����āA��
�@�@���A�~�̊O��C �̊e�_���~���̂ǂ̓_�Ɏʂ���邩�A���w�ƉE�w�ŘA�����ē����l
�@�@�q�����������������B
(2)�@O=(-1�C1)�Ɋւ���F(C)�̐����Ȑ�Pedal(O�GF(C)) �����߂ĉ������B�Q�l�}�̐^��
�@�@�悤�ȋȐ��ƂȂ�܂������H
(3)�@F(C)�̑o�Ȑ��𑽗l�Ȕ��z�ŋ��߂ĉ������BF(C)���Q���Ȑ��Ȃ�o���ς݂̔э���
�@�@�������z�������̂ŁA��ςł�����ĉ������B�����āA�A���_�[���C���̎���pedal �Ȑ�
�@�@���A���̎ˉe�o�Ȑ����Q�b�g�����Ɖ]���̂ŋ���ĉ������B
(4)�@���_O=(0�C0)�Ɋւ���F(C)�̐����Ȑ�Pedal(O�GF(C)) �𑽗l�Ȕ��z�ŋ��߂ĉ������B
�@Pedal(O�GF(C))�͔@���Ȃ鑼�̋Ȑ������ȒP�ȋȐ��ƂȂ�܂������H
�@O=(-3�C1)�Ɋւ���F(C)�̐����Ȑ�Pedal(O�GF(C)) �𑽗l�Ȕ��z�ŋ��߁A���ꂪ�͂ޕ���
�̖ʐς����߂���APedal(O�GF(C))* �����߂��肵�ėV��ʼn������B
�@O=(5�C10)�Ɋւ���F(C)�̐����Ȑ�Pedal(O�GF(C)) �𑽗l�Ȕ��z�ŋ��߁A���ꂪ�͂ޕ���
�̖ʐς����߂���APedal(O�GF(C))* �����߂��肵�ėV��ʼn������B
�@n=2���Ȗʂ͗c�����猩�����Đ������An=2���Ȑ��͒����ł���Ɗw�сA�ڐ����w�Ԃ̂ŁA
�����Ȑ������ނƂ��č��������Ȃ��Ɖ��B���Ă����� ���A�����ꂽ�Ȃ�A�{���͋ӊ쐝��
���A�w���҂ɋt������p�����ɓ��������A�w���҂������ɋ�����^�ɖ]�܂����f�G�ȏ�
�ʂ�����̏�ɉ��삷��̂ł͂���܂��܂����B
�i������K�₳��鋳�猻��̏��搶�́A�Z���␢�Ԃ������Ă������Ȃ����ĉ�
�����j
����(�w����)�������ɋ�����^�ɖ]�܂����f�G�ȏ�ʂ𐢊E����������B
�u�搶�͂��̗��_�ɂ��ĉ����������ĂȂ��I�v�ƋC�t������ł��B����Ȃ��Ƃ������āA
�@���w�͎����ŕ�������̂ȂƂ����l�������������܂����B���傤�ǂ��̎���̓Z�[���A
�@�O���^���f�B�[�N�Ƃ������l�������A�㐔�w�̒��ۉ��Ɏ��g�����ɂ�����܂��āA
�@�X�L�[�����_���o�Ă��Ă��܂����B�����ŁA���̃X�L�[���ɂ��ĕ����Ă��̂ł����A��
�@�{�ł́A�܂��N�����g��ł��Ȃ��悤�ȕ���ł�������A�����Ă邾���Ńp�C�I�j�A�Ƃ�
�@�������ł����B
�@����E�̑Đ��ɗ����ꂸ�A�Ⴆ�A�m���̑ȉ~C�ƔC�ӂɓ_O=(��0�C��0) ��{���Ɏw�肵�A
�����Ȑ��B�����߁A���m�Ƃ̑����̑㐔�Ȑ��B�Ƃ̐����ȑ�����{���⎩��ɐ^���ɖ�
���B�X�ɁA���m�̂Ƃ̑����̑㐔�Ȑ� f(���C��)=0 �B���ɍ��W�@K[X�CY]/<f[X�CY]>
�Ƃ���
���̂��l�@�B
�@�ȉ~C�Ƃ��āA�Ⴆ�A�卂�Z�i�Q�O�P�O�j�� ���C�� �̊W���i���ɂ̓_(0�C-1)�����e�j�Ȃ��
�~�i�厲���������j
�@�@{4/(1 + 2�� + 2��2)�@�C -((1 + 6�� + 2��2)/(1 + 2�� + 2��2))}
���A �uWolfram|Alpha�v�ɑ}�����Ă��������B
�@���܂ŁA�э��搶�̖���Fn=2���Ȑ�C�̎ˉe�o�Ȑ��o���A�����p���A�Ԃ̃A
���_�[���C���̕��@�ŁAC�̌��_O�Ɋւ��鐂���Ȑ����I�ċ��߂��B
�@�Ԃ̃A���_�[�@���C���ɂ����@�́A�����R�C�S�C...���㐔�Ȑ��ɂ��ʂ���i�s��͕s�j�B��
���A�S���̑㐔�Ȑ�C�ɂ���
(1)�@���_O�Ɋւ��鐂���Ȑ���悸C�̎ˉe�o�Ȑ��o���ĉ������B
(2)�@�����p���A�Ԃ̃A���_�[���C���̕��@��C�̌��_O�Ɋւ��鐂���Ȑ����I�ċ���
�@�@�ĉ������B
�@��C�̏�ŋ��߂������Ȑ���}������ƁA�Q�l�}�̐Ԑ��ɂȂ�܂������H
(3)�@�I�Ȃ��ŁA���ɑ��l�Ȕ��z�Łi�����C�͗L���Ȑ��̒ǐՂ��\)�AC�̌��_O��
�@�@�ւ��鐂���Ȑ������߂ĉ������B
�@����^�ʑ�F(���C��)=(��2 + �� - ��2 +1�C2���� + ��) �ɂ��āA�i�̐��̂́AJacobian matrix����
�߂Ė\�����j�w��2 + �� - ��2 + 1 �̑f�G�ȑ��_�x���A2���� + ���@�Ɍ��܂�B
(4)�@��F(C)��\������㐔�Ȑ������߁A���̌��_O�Ɋւ��鐂���Ȑ������߂ĉ������B
(5)�@Pedal(O�GC)��F�ɂ�鑜F(Pedal(O�GC))��\������㐔�Ȑ������߁A���̌��_O�Ɋւ�
�@�@�鐂���Ȑ������߂ĉ������B
�@Ahlfors Complex Analysis 25p conjugate ���b harmonic function�@�́w���_�x���Q���F
�@���F�̑��_C1�AC2�̌��_�Ɋւ��鐂���Ȑ��B Pedal(O�GC1)�APedal(O�GC2)��o�Ȑ���
���߂āA�I�ċ��߂铙�̔��z�ŋ��߂ĉ������B
�@���F�̑��_C3�AC4�̌��_�Ɋւ��鐂���Ȑ��B Pedal(O�GC3)�APedal(O�GC4)��o�Ȑ���
���߂āA�I�ċ��߂铙�̔��z�ŋ��߂ĉ������B
�@�o�Ȑ������߂ĉI�ċ��߂锭�z�́A�@�Q�l�P�@�@�Q�l�Q
�̂悤�ȂQ���Ȑ�C��Pedal((��0�C��0)�GC)�ł͂Ȃ��̂ōs��͕s�ł��B
�@��̓I���ւ̔M���z�����N�ɓ`�������\�\���ꂪ���̖{���o���[���ɂȂ��炦�����
���R�ł���B�u��̓I�ȌX�̊��̖ʔ��������⋓����Έ�����v...���f��
�O���� ��
�����B
�@Ahlfors Complex Analysis �ɂ́@Algebraic curve ���@297p�ł悤�₭���ڌ���.�x����.....�B
�B��̋�̓I��Exercise�F
Determine the position and nature of the singularites of the algebraic function defined by
�@��3-3����+2��3=0
(1p����296p�܂ŗ������Ȃ��ƁA���̗Ⴊ�Έ��s�\�Ȃ̂ł���܂��傤���H)
�@��3-3��+��+2��3=0 �Ƃ��Ȃ��ŁA(z�Cw)��C2 �ŕ\���������ƂɈӖ����݂�悤�Ȃ̂ŁA
Algebraic curve���Af(z�Cw)=0 �ƕ\�����ė~�����B
�@�����A�����ɕ���(��=��+���Ei�@�A��=��+���Ei)�A��3-3����+2��3=0�@<---->
�@S1={(���C���C���C��)��R4| ��3 - 3��2�� - 3���� + 2��3 - 6����2 + 3����=0}
�@S2={(���C���C���C��)��R4|-��3 + 3��2�� - 3���� - 2��3 + 6��2�� - 3����=0}
�Ȃ�R4�ɉ�����Q�̒��Ȗʂ̌����S1��S2�Ȃ��̗��Έ�����ɂ́A�ǂ�����悢
�̂ł��傤���H��������Q�ł�����Ǝ�����������A4-(1+1)=2 �����̔����\���l��
�Ȃ�ؖ����肢�܂��B
�e�Ȗʂ������i�́AS1�Ȃ�A��3 - 3��2�� - 3���� + 2��3 - 6����2 + 3����=0�@�ŁA��=...-3�A-2�A-1�A
0�A1�A2�A3...��R3�Ɏˉe���A����A�z������ȊO����܂���i���ɂ́j�B
�@��(���C��)=��3-3����+2��3�@�ɂ��āA���W�@K[Z�CW]/<p(Z�CW)>�@�̏��̂��l�@�肢�܂��B
�@�A���������FD[��(���C��)�C��]=0�@�A��(���C��)=0 �̉���S�ċ��߂āA(��j�C��j)�Ƃ��A�����ʂ���
{��1�C��2�C...}�������A�C�ӂ́@z��C-{��1�C��2�C...} �ɉ����āA��(���C��)���������v�f��=f0(��)
�͂R���݂���B
���A���m�Ɂi����Ahlfors�̗B��̋�̗��Έ����j��������肢�v���܂��B
�@100p�ɂ́A��3+��3-����=0�@(��=�����Ńp�����[�^�[��) �Ȃ��̗Ⴊ�݂�B�Έ��肢�܂��B
Ahlfors �́A��2=���@�������̂ł���A�����Ƌ����ɕ����A�㐔�Ȑ��B ��2-��2=Re[��]�A2����=Im[��]
�̌����Ƒ����A3p-4p �ɒ��X�Ɖ��.....�BR[��]/<��2+1>�ɂ́A6p �ŐG���̂�.....�B
�@�������e�ɍ݂��A������������肢�v���܂��B�i�����Q�R�N�P�O���Q�P���t���j
�u�H�w�������Ȃ��v�₪�݂�܂����H1.35 �Ɉ�ԋ����ÁX�ł͂���܂��܂����H
�@����ɍS��A�u��̓I�ȌX�̔����̖ʔ��������⋓����Έ�����v�ɕ킢�����̂ŁA��
��2�Ƌ�̉����A�㐔�Ȑ�C�FY2 - (X - 2)(X - 1)X=0 ��Έ����Ă݂������A�n�ɑ���������
���́AC�̌��_�Ɋւ���C �������Ȑ��@Pedal(O,C)�ɂłȂ��AC�̑o�Ȑ��Ɋ�蓹��
���A�D���ȓ������A�Q�b�g�����Ɖ]���B
�@�Q�l�}���@C�FY2 - (X - 2)(X - 1)X=0�@�̋�̗�ŋ�������B����ɂ́A�悸�AC �̎ˉe
�o�Ȑ������߂˂Ȃ�ʁB
(1)�@�ˉe�o�Ȑ��𑽗l�Ȕ��z�ŋ��߂ĉ������i�Ȑ��ł͂Ȃ��̂Ŕэ��搶�̍s���
�@�@�@�͕s�ł��j
(2)�@�����ˉe�o�Ȑ��ɂ��āA�Ԃ��A���_-���C���̕ϊ�������A�����Ȑ�Pedal(O�GC)
�@�@�Đ}�������肢�܂��B
�@�o�Ȑ������߉I�A�����Ȑ�Pedal(O�GC) ������݂����X�ł͂���܂��܂����A
(3)�@���ɋ��߂����ł��傤�B���l�Ȕ��z�ŋ���ĉ������B
�@���肢���A�����Q�����邱�ƂɈӋ`���݂�̂ŁA���݂�ƁA
�@�@-27Y10 - 108X2Y8 + 108XY8 - 162X4Y6 +328X3Y6 - 132X2Y6 - 24XY6 + 4Y6
�@�@�@�@�@ -108X6Y4 + 336X5Y4 - 276X4Y4 + 24X3Y4 +24X2Y4 - 27X8Y2 + 120X7Y2
�@�@�@�@�@�@�@�@�@- 156X6Y2 +56X5Y2 + 4X4Y2 + 4X9 - 12X8 + 8X7 = 0
�@�Ȃ鐂���Ȑ�Pedal(O�GC)�܂����B�߂����݂�ΏC�����ĉ������B
(4) �ɂ�2�Ƌ�̉����A�㐔�Ȑ�C�FY2 - (X - 2)(X - 1)X=0�@��Έ����Ă݂����ƒv���܂���
�@�@���A���̂��C�ɓ���́A�Ⴆ�A��=19+69�Ei�����f�ɑ́@�Ƃ��A�����Ȑ�Pedal(O�GC)��
�@�@���o�肢�v���܂��B
�@�@�@�ŏ��̖���œ���������Ă���܂��B���̈�A�̖��̉����肢�v���܂��B
�@�㐔�I�̂łƂ���̂ŁAY2 - (X - 2)(X - 1)X=0�@�ł͂Ȃ��AAhlfors �ɕ킢�A
�v2 - (�y - 2)(�y - 1)�y=0�@�Ƃ��A�X�ɁAZ=X+Y�Ei�@�AW=U+V�Ei �Ƃ��č��̋�̗��Έ����Ēm
��s�����Ă݂���...�B
�@�Q�l�}�̉E�̐�=C��kardioeides�F�@(��2 + �� + ��2)2 - ��2 - ��2 = 0�@�i�v�Z�j�̓_O=(0�C0)
�Ɋւ��鐂���Ȑ� Pedal(O�GC)���A�p���̎ˉe�o�Ȑ������߂āA������o�ċ������
�]���̂ŋ�������B
(�C)�@�悸�A�э��搶�ɕ킢�AC�̎ˉe�Ȑ������ׂ��ƁA
�@(0)�@X4 + 2ZX3 + 2Y2X2 + 2Y2ZX + Y4 - Y2Z2=0�@�ƂȂ邱�Ƃ��m�F���A
�@(1)�@���l�Ȕ��z�ŁA�ˉe�o�Ȑ������߂ĉ������B
�@C��n=2���Ȑ��ł͂Ȃ��A�э��搶�̍s���@�͌����ʂ̂ŁA�������锭�z�ŋ��߂���A
�@�@�@�@2X3 + 15ZX2 + 24Z2X - 16Z3 + 27Y2Z = 0
�@�ƂȂ�܂����B�ԈႢ������Ύw�E���Ă��������B
�@(2)�@�����Ď��������ɉ����āA�p���̃A���_�[���C���Ȃ�ϊ����s���ĉ������B
�@�����s���ƁAC=����荂���̑㐔�Ȑ��܂����B�i�ԈႢ������Ύw�E���Ă��������j
�@�@16X6 + 24X5 + 48Y2X4 - 15X4 + 48Y2X3 + 2X3
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@+ 48Y4X2 - 42Y2X2 + 24Y4X + 16Y6 - 27Y4 =0
�@�`���Ă݂�ƁA�Ԑ��ɂȂ�܂����i����̐����_�����߁A�}�������܂����j�B���ꂪ�A�{��
�ɐ���kardioeides �̓_O=(0�C0)�Ɋւ��鐂���Ȑ����Ɖ��^���邱�Ƃ��d�v���Ǝv���܂��B
�@�Ⴆ�A���� p=(1/4�C /4�j�̓_�ɉ�����ڐ�Tp(C) �����߁AO���琂���̑���Tp(C)
/4�j�̓_�ɉ�����ڐ�Tp(C) �����߁AO���琂���̑���Tp(C)
�ɉ����A���̍��W���A
�@�@16X6 + 24X5 + 48Y2X4 - 15X4 + 48Y2X3 + 2X3
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@+ 48Y4X2 - 42Y2X2 + 24Y4X + 16Y6 - 27Y4 =0
�������ۂ��i�͍��Z���ɂ��e�Ձj�Ŕ��f���ĉ������B
�@�p���̎ˉe�o�Ȑ������߂āA�_O=(0�C0)�Ɋւ��鐂���Ȑ������߂邱�Ƃ́A���ɂ�
��Ǝ��͍l���܂����@���H
(��) ��Ƃ͈قȂ锭�z�B�ŁA�����Ȑ� Pedal(O�GC)�ɋ��߂ĉ������B
�@����^�ʑ�
R2��(���C��)--F-->F(���C��)=(��2 + 3��/2 - ��2 - y/2 + 1/2�C2���� + ��/2 + 3��/2 + 3/2) ��R2
�ɂ��C�̑�F(C)�����߁A�ώ@���APedal(O�GF(C)) ���A��� (�C) (���j�̔��z�ŋ��߂ĉ������B
�i��̗�B��Έ����ꂽ�@���z���@�L�ځ@�肢�܂��j
�@n=2���Ȑ��A�ȖʁA......�̑o�Ȑ��A�o�ȖʁA... �́A�s���p���A�u���ɋ�����Ƃ��A
�����\�ŁA�ׂ��ׂ��Ȃɂ��̂��Ȃ��̂ōl����ɒl���Ȃ��A�� n=3�A4�A...�A2011���Ȗʂ�
�o�Η��_�\�z�ҍ݂肩��..)�@�i�����Q�R�N�P�O���Q�Q���t���j
�@�э��搶�̑I�тʂ��ꂽ�����̎�u�҂������ł��������グ�A���Ȃ̎p���𐽎��ɕ\
����`�����X�����B
(n=2�������Ȗʂ̑o�Ȗʂ́A�s��łł���Ɛ��E�̂�������m���ł��傤���j
�@���
(0)�@��0=��0=��0�@�ƑS�R���s�ړ����Ă��Ȃ�n=2���Ȗʂ̑o�Ȗʂ͗e�Ղł��傤�B
�@���D�݂őS�R�\��Ȃ��̂ł����A�@��0=1�A��0=2�A��0=3�@�Ƃ����Ƃ��An=2���Ȗʂ̑o�Ȗ�
���A��ςł��t�ɕ킢���߁A���͂������肢���܂��B
�@�d�v�Ȕ��l�F���_�A��̂��肢�́A�э��搶�����Ȃ̕�����U�����ꂽ��B�ł��B
�@���̌����̖͕�G�@��0=��0=��0=0 �Ȃ牽�������킩���Ă��܂�����A��0=1�A��0=2�A��0=3
�@�@�@�@�@�@�@�@�@�@�@�@�@�@���e�Ղ��낤�ƍu�`�A����x�e�X�g�ɏo�肵�����A�o�����悭�Ȃ�.....�B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�P����ɍčl������A4���̑Ώ̍s��̋t������������Ƃ͏u��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�ɂ킩�邪�A�����̂͑�ς��ƁB
�@����A��ςȍs��Ɉˑ����Ȃ����z�����肢���܂��B�����āA���É���w�̍u�`�ɕ킢�A
S ��S* �̒f�ʒB��`���A���̐��̂�\���ĉ������B
�@��0�A��0�A��0�@�̑I���͎��R�ł��B���炠���������s�ړ����A��̔@���l�@���B���s�ړ���
�͕s���ł��傤�B���̔���^�ʑ��ɂ��ϊ��ɁAF�ɂ�鑜F(C) �̑o�Ȗʂ�����B
�@�u��̓I�ȌX�̔����̖ʔ��������⋓����Έ�����(��g��)�v�ɕ킢�����̂ŁA���x
�́A(4)��Έ��������B�i�����Q�R�N�P�O���Q�Q���t���j
(n=2�������Ȗʂ̑o�Ȗʂ́A�s��łł���Ɛ��E�̂�������m���ł��傤���j
�@��0=��0=��0=0�@�ƑS�R���s�ړ����Ă��Ȃ�n=2���Ȗʂ̑o�Ȗʂ͗e�Ղł��傤�B�i������
�����}���ł��傤�j
�@��0=-2�A��0=-1�A��0=2�@ (�Ə����l���āA���s�ړ��ʂ�I�т܂����j�@����n=2���Ȗʂ̑o��
�Ȗ�S*���A��ςł��э��搶�ɕ킢���߁A���͂������肢���܂��B
�@�܂��A���̑��l�Ȕ��z�ŁAS*�����߂Ă��������B�i�Ⴆ�A���ʎ������߂āj
�@�o�Ȗ�S*�����߂āA���É���̍u�`�ɕ킢�A��=�� �ŁA�X���C�X����ƁA
{3��2 + 4���� + 12�� + 2��2 + 6�� + 13 = 0�C3��2 + 4���� + 4�� + 2��2 + 2�� + 2 = 0�C
3��2 + 4���� - 4�� + 2��2 - 2�� + 1 = 0�C3��2 + 4���� - 12�� + 2��2 - 6��y + 10 = 0�C
3��2 + 4���� - 20�� + 2��2 - 10�� + 29 = 0}
�B�������܂����H��f�ʁ@3��2 + 4���� - 12�� + 2��2 - 6��y + 10 = 0�@���ς�����A
�uWolfram|Alpha�v�ɂ��肢���������A���_�u�l�̈�ʂ��������� �S�e�i�l�i�A�i���Aetc)��
�f�v���鐶�����̓}�Y�C.....�B���̒f�ʒB�����`���A�z���͂����A�o�Ȗ�S*�̌`��`��
�������B
�@�X�ɁA�ْf���钴���ʂ� H(k)�F7��+5��+3��=�� �Ƃ��AS*��H(��)���炚���������AR2�ւ̎ˉe��
���A�����A-7����7�܂ł����ċȐ��B��`���A�z���͂����A�o�Ȗʂ̌`��`�ʉ������B
�@�X�ɁA���m�������ׁA�o�Ȗʂ́An=2���ȖʂȂ̂ŁA�厲���������ɉ����āA���̖�
�̂��L���Ă��������B���̌ŗL�l�A���̌ŗL�l�����߂Ă��������B(�Ȗ�S�̖��̂��AS*�ł�
��������܂������H�z��O�ł������H)
�@�X�ɁA�Έ��������̂ŁA(4)��S�F(�� + 2)2 - (�� + 1)2 - (�� - 2)2 = 1 ��̊���̓_pj ��I
�сA���̓_pj �ɉ�����S�̐ڒ�����Tpj(S) (�̕�����������)�ɑΉ�����S* ��̓_�����߁A
��œ���S*�̕����������Ă��邩�m�F�肢�܂��B
�@�X�ɁA�L���ʑ��@S��(���C���C��)---��--->��(���C���C��)��S* �L���AS��S*��F�X�F������
�������B
�@�L���ʑ��́A�э��搶�́u�s������߂�S*��v���z�ł͓����Ȃ��ł��傤�B
�i�⒍�j�@�����̗L���ʑ��́A�������ЂƂ����グ�����̂ł��B
�Q�l�����F(�����������̈�{�Ɍg���Ă�������́Amathematica ����p���ł��傤)
�@�@��p�摜�����@�@�A���\�h�̐V���Ȏ��_�FMathematica ���g���������Ȑf�f
�@�@���茟�f
�@�u��̓I�ȌX�̔����̖ʔ��������⋓����Έ�����(��g��)�v�ɕ킢�����̂ŁA���x
�́A(6)��Έ��������B�i�����Q�R�N�P�O���Q�R���t���j
�@(3)(4)�ɂ��āA�o�Ȗ��𑽗l�Ȕ��z�ŋ��߂��̂Ɠ��l�ȍl�@��(6)�ŁD�D�D�B
�@�Ȗʁ@��=��2-��2�@�̑o�Ȗʂ𑽗l�Ȕ��z�ŋ��߂āA�o����}���肢�܂��B
�@�Ȗʁ@S�F ��=(�� + 2)2 - (�� + 1)2�@�̑o�Ȗ�S*�𑽗l�Ȕ��z�ŋ��߂āA�o����}���肢
�܂��B
�@���É���w�u�`�ْ̍f���钴���ʂ������AH(��)�F7��+5��+3��=�� �Ƃ��AS*��H(��)���炚������
���AR2�ւ̎ˉe�����A����-7����7�܂ł����ċȐ��B��`���A�z���͂����A�o�Ȗʂ̌`
��`�ʉ������B
�@�X�ɁA���m�������ׁA�o�Ȗʂ́An=2���ȖʂȂ̂ŁA�厲���������ɉ����āA���̖�
�̂��L���Ă��������B���̌ŗL�l�A���̌ŗL�l�����߂Ă��������B(�Ȗ�S�̖��̂��AS*�ł�
��������܂������H�z��O�ł������H)
�@�X�ɁA�Έ��������̂ŁA
�Ȗʁ@S�F ��=(�� + 2)2 - (�� + 1)2�@��̊���̓_pj ��I�сA���̓_pj �ɉ�����S�̐ڒ���
��Tpj(S) (�̕�����������)�ɑΉ�����S* ��̓_�����߁A��œ���S*�̕�����������
���邩�m�F�肢�܂��B
�@�X�ɁA�L���ʑ��@S��(���C���C��)---��--->��(���C���C��)��S* �L���AS��S*��F�X�F������
�������B
�@�L���ʑ��́A�э��搶�́u�s������߂�S*��v���z�ł͓����Ȃ��ł��傤�B
�i�⒍�j�@�����̗L���ʑ��́A�������ЂƂ����グ�����̂ł��B
�ȏ�A�ޔ�Ȗ�B�������A����焈Ղł��傤���H
�@�ȉ��̐����Ȗʂ́w���̌��x�ł��傤���H(���̎�́w���̌��x�k��WEB ��ł͍����҂�
���݂��Ȃ��͉̂��́H�H)
�@WEB��ɐ����Ȗʂ̒�`��������Ȃ��Ȃ��B�i�ЂƂ������݂�܂���;)����ŁA��`�ɕ킢
�����`���A�Ȗʁ@��=��2-��2 ��(0�C0�C0)�Ɋւ��鐂���Ȗʂ𑽗l�Ȕ��z�ŋ��߂Đ}������
���܂��B
�@�Ȗ�S�F ��=(�� + 2)2 - (�� + 1)2�@��O=(0�C0�C0)�Ɋւ��鐂���Ȗ�Pedal(O�GS)�𑽗l�Ȕ��z
�ŋ��߂āA�}�����肢�܂��B(S�͈Ղ����Q���Ȗʂł����APedal(O�GS)�͉����Ȗʂł����H)
�@�Ȗ�S�F ��=(�� + 2)2 - (�� + 1)2�@��ɁA�Ⴆ�Ap=(1/2�C 1�C 9/4)���̂��Ă���B
Tp(S)��(0�C0�C0)���琂���������A���̑��̍��W�����߂ĉ������B���̂悤�ȒP����Ƃ��A�T
�_��߁A�s���ĉ������B
�@�ȏ��(6)��Έ����A�����Ȗʁw�̌��x�̊��z���L�ڊ肢�܂��B(�Ƃ���ŁA�R���ȏ�̑o��
�Ȗʂ͊��x����ꂽ�̂ł��傤���H���B���L�ڊ肢�܂��B�j
�@�����������Ȃ���]�F
�@���������Km�ɉ����钴�Ȗ�S�̓_O=(��10�C��20�C.....�C��m0)�Ɋւ���Pedal(O�GS) ���`
���A��̗���f���A�����̑����e�ڒ����ʂɑ��𒅂��APedal(O�GS)��Έ��������D�D�D�B
�@��=3�A4�̏ꍇ�̖��B�����������B
�@���F�g���́A�����łȂ��Ă͐��^�ʑ�L��Hom(Kn�CKm)�̖��ɒp����̂Ŏ����ł��̂ŁA
��������^�ʑ�F��Έ��������B
(1)�@���̋Ȑ�C�F��2-��2=�P �̑�F(C) �𑽗l�Ȕ��z�ŋ��߁A���̕�������}������ƁA��
�@�@���ɂȂ邱�Ƃ������ĉ������B���R�r�s�� Jf (p) ���މ����Ă���i�K����������j�Ƃ����
�@�@�}������ƁA�ł����F�̋Ȑ��ƂȂ�A�����C�Ƃ̋��ʓ_�����߁AF �Ŏʑ�����ƁA�F��
�@�@�������_�B�ɂȂ邱�Ƃ��ؖ����ĉ������B��F(C)�͕Ȑ��̂悤�ŁA���̈͂ޕ����̖�
�@�@�ς�F(C)�̌ʒ������߂ĉ������B
(2)�@���̋Ȑ��ɍ����̋Ȑ�C�F ��2/4 - ��2/4=1 �̓�������^�ʑ�F�ɂ�鑜F(C)�ɂ�
�@�@�āA��̂悤�ȍl�@�B�����ĉ������B
(3) �@C�F -��4 - 2��2��2 + ��2 - ��4 - ��2 = 0 �Ƃ����Ƃ��A��������^�ʑ�F�ɂ�鑜F(C) �ɂ�
�@�@�āA��̂悤�ȍl�@�B�����ĉ������B
�@�@�@F�̏o�����������܂��B���̈�ԍ���n=2���Ȑ�C�F��2-��2=�P �̈���_O=(��0�C��0)�Ɋ�
�@�@����C�������Ȑ��@Pedal(O�GC) �o����ߒ��ŁA���̔���^�ʑ�F�܂����B����
�@�@�_�����߂ĉ������B
�@�@�@�܂��A��ԍ���n=2���Ȑ�C�F��2-��2=�P �̈���_�Ɋւ��鐂���Ȑ�Pedal(O�GC) ���A�p
�@�@���̂W�̎��̂悤�ɂȂ�_O�������߁AC------F----->F(C)=�@Pedal(O�GC)
�ƂȂ��
�@�@���^�ʑ�F�����߁A��̔@���l�@�����ĉ������B
�@�����w�肵���_O �ł́A�W�̎��̂悤�Ɉ͂܂ꂽ�������Q�łȂ��A��ł��B�i���Q�l�}�j
�@Pedal(O�GC)�������j�X�P�[�g(�A��`lemniscate)�ƂȂ�悤�_O=(��0�C��0)��I�сA����^��
��F�����߂ĉ������B�܂��AC�̎ˉe�o�Ȑ������߁A���ꂩ��Pedal(O�GC)�����߂锭�z��
�Ȃ����ĉ������B
�@lemniscate�Ɖ]���A�e�_�ɉ�����ȗ��~�����A�Q�l�P�@�A�Q�l�Q �̂[������
�Ɂ@........ �u���w�������Ɏg�����@�u���ܘY�@���v�� 094p �ɁAt---->(Cos[t]�CD[Cos[t],t])�Ƃ�
�������L�ڍ݂�.....�B�i�Q�l�}�j
(1)�@�Q�̕s�ώ� F�AG�AH�̊Ԃ�(�㐔�I�]��) �W���o�肢�܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�R�N�P�O���Q�S���t���j
�i���h��ɂ����̂́A���̘_���Ɍ�肪�������̂Œv���܂����B���̘_���Ƃ́H)
�@�W���@4G4 - F2G + H2=0�@�������܂������H�����������A4��4 - ��2�� + ��2=0 �Ƃ��܂��B
�@���o���ꂽ�㐔�Ȗʂr�F4��4 - ��2�� + ��2=0�@�̑o�Ȗ� S* �����߂ĉ������B����n=2�ł�
�Ȃ� n=4 ���Ȗʂ̑o�ɂ��Ă��A�э��搶�����z�F
�@���z(�C�j�@�悸�A�ˉe���@�Ď����iHomogenize)
�@�@�ˉe�����A4Y4 - WX2Y + W2Z2 ����X�^�[�g���A�D�D�D�B
�@���́A�э��搶�̔��z(�C�j�ȊO�̔��z�B�őo�Ȗ� S* �܂����B���̔��z������
�݂ĉ������B
�@���z(���j�A���z(�n�j
�@�������_�������������Ă��Ȃ����ۂ��̔��f�́A(S*)*�����߂�Ύ����Ŋ����B
�@�X�ɁA�L���ʑ��@S��(���C���C��)---��--->��(���C���C��)��S* �L���AS��S*��F�X�F����
�ĉ������B
�@�㐔�Ȗʂr�F4��4 - ��2�� + ��2=0�@�̓_O=(0�C0�C0)�Ɋւ��鐂���Ȗ�Pedal(O�GS)�z��
���z�ŋ��߁A�������_�������������Ă��Ȃ����ۂ��̔��f�̍������L�ڊ肢�܂��B
�@ �u���w�̎��E�v�͏������Ă���܂���B���ہA��k (k=0�A1�A2�A3�A4�A5�A6)�A ��j�A��j����k
�����߁A�m�F���i�Q�l�})�B�@�i�}�ŁAF(C) �͒��J�Ɍv�Z���`�ʂ��܂����j
�@���̐̔���^�ʑ�F�ɂ��āA
(1)�@F(C)�����߂�ƁA�}�̂悤�ɂȂ邱�Ƃ������ĉ������B
(2)�@F(R2)�J�ɋ��߁A�}�������ĉ������B
(3)�@F({z| |z|<1})�J�ɋ��߁A�}�������ĉ������B(�P�ʉ~����______�Ɏʂ����)�B
(4)�@F({z| 1<|z|})�J�ɋ��߁A�}�������ĉ�����(�P�ʉ~�O��______�Ɏʂ����)�B
�@���̌�A(1)���ڂ����čl�肢�܂��B
�iC=�Ԑ��ɂ͒P�ʉ~�����ƊO���̕������݂�܂��̂Łj
�@�㔼���ʁiupper half plane�j��Upper Half-Disk�ɕ킢�A{(X�CY�CZ)��R3|1��X2+Y2+Z2}����
�����ʂƌĂԁA�����āA��ƁB
�@Ahalfors Complex Analysis�@29p ��stereographic projection �̐}���ς�ƁA
�@�@�u��͊O={z| 1<|z|}�v�@�A�u���͓�{z| |z|<1}�v
�ƒ�������Bstereographic projection ��N=north pole �ƕ���S�ƕ��ʂ̗l�X�ȑg�ݍ��킹
�̗��V���݂�B
�@Ahalfors Complex Analysis�@29p ��stereographic projection ��N H�GZ=0
�}�������B
(5)�@����^�ʑ�F�̏o���̔�b�������A���o�ߒ����L�q�肢�܂��B
�Ɖ]���Ȃ���A���ɘI�悵�܂����B����\���܂ŁA�Q�l�}�����Ȃ��ʼn������B�i�z����ł�����
���傤�j����^�ʑ�F�̓��o�́A�Q�l�����ƍ������Ă��܂��B�i��������グ�����́j
�@�Q�l�}�Ȃ钊�ۓI�ȗ��_�łȂ���̓I�Ȕ���^�ʑ�F�̑����ł��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�R�N�P�O���Q�T���t���j
�@�Q�l�����̒P�ʋ��ʏ�̓_�������J���ċ��߂Ă݂܂����B
(1)�i�O�̒����j�㔼����{(X�CY�CZ)��R3|1=X2+Y2+Z2�A���A0��X�A0��Y�A0��Z}�ɍ݂�_��
�@�����łȂ��_�ɕ��ނ��ĉ������B
(2) �e�_�̑������߁A{z| 1=|z| ���A0��x ���A 0��y}�v�ɍ݂�_ �� �����łȂ��_�ɕ��ނ�
�@�ĉ������B
�@�P�ʋ��ʏ�̗����_�B����A�R�_A�AB�AC��I�сA���ʎO�p�`ABC ��}�����A�e�p
�x�����߁A�����Z���ĉ������BPrj(A)�APrj(B)�APrj(C)�����߂ĉ������B
�@�O�p�`Prj(A)Prj(B)Prj(C)�̊e�p�x�����߁A�����Z����͈̂Ղ��߂���́A���ɂ��C����
�����B�P�ʋ��ʏ�̉~En(i)����̓I�ɘA���������̉��W���Ƃ��Ċ����߂ĉ������B
�@�Q�l�}�̈�ԉ��̂Q�̎���ɍ����̗�� 2011�� �쐬�肢�܂��B�l�i�_�̑��j������
�܂��B�i���@���ۑ㐔�@���c�����Y�@���ۑ㐔�ւ̓����j
�@�Q�l������ �P�ʋ��ʏ�̓_�������J���ċ��߂Ă݂܂����B
�@X�AY�������Ăɒ�߁A�A���������@{X2+Y2+Z2= 1�AX = (2��19)/39�AY = (2��19)/39}����
���AZ = -37/39�AZ= 37/39 �āAZ= 37/39�@��I�����A�Ō�̋��ʏ�̓_��Q���Q�b�g�B
�@�u���ɁA�P�ʋ��ʏ�̓_��2011�ȏ㋁�߁A�}�����肢�܂��B
�@R3 �ɗ^����ꂽ�Ȑ��̊e�_�ƁAP0=(��0�C��0�C��0)�Ƃ����Ԓ����̘a�W���𐍖ʁA��_����
�̒��_�A���ʂ������Ă��钼���@�����Ɖ]���B�i�����Q�R�N�P�O���Q�U���t���j
�i��_____�Ȃ�T�O�̎���B�������āA��̗���L�ڊ肢�܂��B�Ⴆ�Εꔟ�� �j
�@��L�̒�`���D�ɗ��������A�`�u�A�C�X�N���[���R�[���v�Ȃ�A���F�̐l���G�߂���
�����킢�s�����Ă��āA���̑㐔�Ȗʂ̕������́A__________________=0�i�ŁA���̑o�Ȗʂ̕�
�����́A_____________________=0)�ł����A�Ⴆ�AR3 �ɗ^����ꂽ�Ȑ��F (��-2)2+(��-3)2=��2�A��=0
�̊e�_��P0=(7�C5�C3)�Ƃ����Ԓ����̘a�W���Ȃ鐍�ʂ̑㐔�Ȗʂ̕���������ꂽ��
�Ƃ͂���܂����H�����āA����ƈՂ������ʁF��2+��2+��2=R2 �̌�������߂ĉ������B
�@�ȏ�A�u��̓I�ȌX�̔����̖ʔ��������⋓����Έ�����(��g��)�v���A�u��̓I��
�X�̎����Έ�����v�ɕ킢�܂����B
�@���C�Â��ł��傤���A��̂��肢�́A�uStereographic Projection�v�����Ă��琶���܂����B
�iComplex Analysis Ahlfors 19p �����j
�@�ȉ��A����ɂ��ċL�q���܂����BComplex Analysis�i��19p�����_�A����)�A�l�����B
�@���͂��̐��ʂ̒�`�́A�N�ł��ׂ��AR3�ɔ@���Ȃ�Ȑ��Ɠ_���^�����Ă��N�ł��
�����B���ɁAice cream cone �̑㐔�Ȗʕ\���͗e�ՁB
�@��������́A�Ԃ̉~=�ԓ��O�̈Ղ����~�F(X - 1)2 + (Y - 1)2 = (1/5)2 �ł���B
�i�~�F(X - 1)2 + (Y - 1)2 = (1/5)2 ��ȉ~�ɂ����A�ȉ��̍l�@�����肢�܂��j
(1)�@���̉~��N=(0�C0�C1)���琍�ʂ̒�`�ɏ]���A���̑㐔�Ȗʕ\�����ׂ��ĉ������B
�@���ʂ͗e�ՂɒN�ł��`���邪�A���̑㐔�Ȗʂ̕���������ꂽ���Ƃ�������܂�
���H�w�o���҂͌��I�x �w���o���҂͌�肽���䖝�ł��������J�n�I�x �i�����l����������
���K���j������B�㐔�Ȗ� S�G_______________=0
(2) �����āA����S�ƈՂ������ʁF��2+��2+��2=12 �̌��S�����ʂ����߂ĉ������B
(3) �����āA���S�����ʂ� �������ʂɐ��ˉe���āA���_�@n=2���Ȑ����Ԃ̉~�O�łȂ��~��
�@�@�ɓ�����ł��傤���A�L�`���Ƌ��߁A�厲���������A�͂ޖʐρA�ʒ������߂ĉ������B
(4) ����2���Ȑ���㐔�Ȗ�S�̑o�Ȑ��A�o�Ȗʂ����߂ĉ������B
�@���ʂ̒�`�ɏ]���A���ɈՂ����~�Ɠ_(0�C0�C1) �Ő��ʂ̑㐔�Ȗʕ\�����������݂��Ƃ�
��A���_�A�Q���Ȗ�S�ŁA���̂悤�ɂȂ�܂����i�ꕔ�B�����܂�)
�@-25X2 - 50ZX + �B���EX - 25Y2 - 49Z2 + 50Y - 50YZ + 98Z - 49=0
�@�u���ʋȐ��̊��v�ɂ͖����̑㐔�Ȑ�Cj ���݂�܂��B(���A�㐔�Ȑ��Ɖ]���Ȃ���A�p
�����^-�\���Ɏ~�߁A�㐔�Ȑ��\�����ׂ���Ă��Ȃ��̂ŁA�ׂ������݂��݂�܂��j
�@�����Cj��I�сA�㐔�Ȑ��\�����Ȃ��A���̊e�Ȑ�Cj�Ɠ_(0�C0�C1) �Ő��ʂ�����A��
�ʂ̑㐔�Ȗʕ\����K���ׂ��ĉ������B
�@�����@�����Q���{�T �Ɠ_(0�C0�C1) �Ő��ʂ�����A���ʂ̑㐔�Ȗʕ\���͗e�Ղ����Ă��ׂ�
�ĉ������B
�@��ŋ���ꂽ�e�ŁA���ہA�㐔�Ȗʂɍڂ��Ă����Ԃ̒��������ꂼ��10�{���x�͔}
��ϐ��\�������Ă��������B�i�悸�A�����̌����Ȓ�`���A�ƂȂ�ĉ]���܂���j
�@�ȏ�A�u��̓I�ȌX�̔����̖ʔ��������⋓����Έ�����(��g��)�v���A�u��̓I��
�X�̎����Έ�����v�ɕ킢�܂����B
�@ice cream cone ���㐔�Ȗʕ\���̛{�K���ׂ����߂܂����B
�@����x�ɁAR3 �̖����̑㐔�Ȑ��Ǝw�肵���_����A�����̐��ʂ̑㐔�Ȗʕ\���B����
���A�㐔�Ȗʂ̛{�K�����ʂ܂ő��s�����ɂ́@�����Ȃ��ł��傤�B
�@���F�͂������肢���܂��B�i�����Q�R�N�P�O���Q�V���t���j
�@S�ɍڂ��Ă���ȉ~��20�}���肢�܂��B
�@���D���͋Ȗʂ̍\���v�f(���)�������ł���B�Ȗʂ̒��ɒ��������݂���Ƃ����s���R
���������Ƃɂ���āA���D�ʂ͑��̋Ȗʂɖ��������������� ;
�@Stereographic projection �̋�ł��B�i�����Q�R�N�P�O���Q�W���t���j
�@�ԓ��ʂ̒P�ʉ~���ɁA�Ղ�����=�ȉ~�F 900X2 + 900X + 3600Y2 - 2400Y + 589=0 ���
�߁A���{���̍H��ɕ킢�A�i�j���ʂ`�@���܂����B
�i���ʂ�Z=k �Őؒf�����ȉ~�����E����2�Ԗڂ��}�����܂����j
�i�ȉ~��̋�̓I�ȓ_��17 �� �����߁A�P�ʋ���̑Ή�����_�B�����߁A�}�����ׂ���
�������j
�@�g�̖�B���Čf���܂��̂ŁA���肢���܂��B
�@�i�j����S�̑㐔�Ȗʕ\�����ׂ��ĉ������B_______________=0 ( ����f(X�CY�CZ)��Q[X�CY�CZ]
)
�P�ʋ��ʁ�S �̔}��ϐ��\���i������ƁA������������A 3-(1+1)���������\���l�̂�
�Ȃ锤�j���肢�܂��B�X�ɁA�����R2�ɐ��ˉe�����㐔�Ȑ��́A���F�ɂȂ锤�ł����A����
�㐔�Ȑ��� ___________________=0 ( ���Ӂ@F(X�CY)��Q[X�CY]) )
(���łɁA���F�̈͂ޖʐςƌʒ������߂����Ȃ�ł��傤�j
�ȏ�ɏo�������F�̑ȉ~�A���ʁFf(X�CY�CZ)=0�AF(X�CY)=0 �̑o�Ȑ��A�o�ȖʁA�o��
�Ȑ������߂ĉ������B
�@�ȏ�A�����܂ő㐔�Ȗʕ\���B���ׂ��l�͋H�L�ł͂Ȃ��ł��傤���H
�@�F�̑ȉ~�A���ʁFf(X�CY�CZ)=0 �́@n=2���Ȑ��A�Ȗʂł�����A�э��搶�����z�����
�����܂��̂ŋ���I
�@�uSfera di Riemann�v��F�����A�������������uStereographic projection on the circle�v��
�琂��܂����G
�@����́A�u��P�X�D�R�v�A�u�������v�Ɋ��Ɍ��y�ς݂Ɗւ��܂��B�@���ł����ł��傤���H��
���肢�܂��B
�@��ɂ�ʂ鐅���ʏ�ɁA�~�݂̂ł͘ǂ����B�Ⴆ�A���̏��Ђ���`�F�r�V�F�t�Ȑ���
����I�сA�����N���琍�ʂ̑㐔�Ȗʕ\�������A����Ƌ��ʂƂ̌���������o������
�łȂ��A���ʂɍڂ��Ă���1���������\���l�̂��F�X�T�����ė~�����B
�i���@���ʋȐ��̊��j
�@�Έ͂��̓_�� R1��� 1�A2�A...�@�Ɠ������AS=C���� ��ɁA�Ⴆ�A�����j�X�P�[�g���o��
�邾���ƑË����������A���m�ɏڍׂ�S=C���� ��ɕ`�����㐔�Ȑ����A�㐔�ȖʒB��
����ZERO�_�ƃC�f�A����p���ĕ\���@�肢�܂��B�i�����Q�R�N�P�O���Q�X���t���j
�@���ɁA��� n=2 �̋Ȑ����P�[�X�͂��肢�ς݂ł��B���F�����Ȃ�A���������E�ɐ����B
����Ȏ���́A���̐�݂�B�i�����f�͊w�n�����j
�@���ʂɂ��āA�������ʏ�̔C�ӂ̑㐔�Ȑ��ƁA�Ⴆ�A�_N=(0�C0�C1) ����Y�܂��ΐ�
�ʂ̑㐔�Ȗʂ̕��������~�����̂ŁA�Љ�肢�܂��B
�@�u�~���ʂƉ~���ʂ̕������v�ɒH�蒅���A�����ۂ�A�S���@��2 + ��2 + (�� - 2)2 = 1�@�����[
����Ă�����8�̗��̐}�����āA���ʁi�S���j�Łu��ԎR�������v��z�N���܂����B
�@���́A�ΐ��ʂɂ��ʗp����A���̔��z�����C�ɓ���ł��B�i���݂Ē���Ă����@�B
�Ɣ�r���ĉ������B�j
{(���C���C��)��R3|��2+��2=��2�C��=0}�̔C�ӂ̓_(���C���C0)�� (0�C0�C5)�����Ԓ����B�ŐD��ꂽ����
�̑㐔�Ȗ� S(�̕������j�����߁A�����ۂ�@�S�� ��2 + ��2 + (�� - 2)2 = 1 �����[�����悤
�� ���߂�B�܂��AS�̑o�Ȗ�S*�����߂ėV��ʼn������B
�@�~�����̖͕������B��=��Ԃɉ����钆�S(3�C4�C0)�A���a1�̉~�𐅕��ʂɕ`�����B
���̏�̔C�ӂ̓_��(0�C0�C5)���Ō��сA���{���̍H����ׂ��A����ꂽ�Ή~���̑�
���Ȗʂ����ߕ`�ʂ���ƁA�}���B
(1)�@�Ή~���̑㐔�Ȗ� S ��\�������������߂ĉ������B���̑o�Ȗ�S* �����߂�
�@�@�������B(����ŁA�o�Ȗʂ����狁�߂��͉̂���ڂł����H�j
�@�o�Ȑ��ɂ��ẮA���x���]���܂���(�o�Ȗʂ����̂�����...)�u�f�J���g�̐��_�Ƒ�
�����v�� ����@�݂�܂��B�o�ȖʒB���~�����ƊF��Ȃŗv�]���܂��傤�B
(2)�@S�ƒ��S(3�C4�C0)�A���a1�̋��ʂ̌����}���Q�Ƃ����߂ĉ������B
�@�ŏ��̖��̒��~���̐}������ƁA���a1�̓S�������̊J��������}������ƁA���S
(0�C0�C2)�̈ʒu�ŁA�����Ă���B���̎��̐ڂ��Ă��镔���̋Ȑ��̕����������߂ĉ���
���B
(3)�@���a1�̓S����}�������Ή~���̊J��������}������Ƃ��A�͂ݏo�������A���a1/7
�@�@�̓S����}�������Ή~���̊J��������}������Ƃ��A�������ł����锤�B���̈ʒu
�@�@�����߂ĉ������B
�@�Ȗʂ��`����m�肽���Ƃ��AZ=k �Őؒf���A���ɁA���ʂׂ�̂́A���̂悤�ɏ퓅��
�i�ňׂ��ʓ��͍݂�܂���B�i�����Q�R�N�P�O���R�O���t���j
�@���� ��P(C)2 �ɉ����� n=4���㐔�Ȑ� f(���C���C��)=0 �ɂ��āA
(1)�@�ϋȓ_�����߂ĉ������B��d�ڐ������߂ĉ������B
(2)�@�o�Ȑ�(���̎������ׂ��O�ɑz�肵�j�����߁A���̓��ٓ_��(1)�̊ւ����q�ׂĉ���
�@�@���B
(3)�@���W�@K[X�CY�CZ]/<f(X�CY�CZ)>�̏��̂��l�@�肢�܂��B�i��R=k[���C��]/(��2-��3-1) �̌�
�@�@�����ȉ~�Ȑ��̌����j
�@�����̂悤�ɖ����J���ł��傤���@?
�@���́w���̕ϓN���Ȃ��悤�Ɏ�����P(C)2 �ɉ����� n=4���̑㐔�Ȑ��ɂ��āA���N�Ԃ�
�_�q�ł��܂���?�x
MSRI Publications -- Volume 35
The Eightfold Way�F The Beauty of Klein's Quartic Curve�@�@Edited by Silvio
Levy
�@Felix Klein discovered in the 1870's that the simple and elegant equation
��3y + ��3�� + ��3��
(in complex projective coordinates) describes a surface having many remarkable
properties,
including 336-fold symmetry -- the maximum possible for any surface of this genus. Since
then this object has come up in different guises in several areas of mathematics.
�@The mathematical sculptor Helaman Ferguson has tried to distill some
of the beauty and
remarkable properties of this surface in the form of a sculpture that he
entitled
The Eightfold Way, permanently installed at the Mathematical Sciences Research
Institute
in Berkeley.
�@This volume seeks to explore the rich tangle of properties and theories surrounding this
object, as well as its esthetic aspects. It contains:The text written by
William Thurston to
explain the sculpture to a wide public at the time of its inauguration.A
broad overview of
the position of the Klein quartic in mathematics, with articles by Hermann
Karcher and
Matthias Weber (geometry), Noam Elkies (number theory), and Murray Macbeath
(Riemann
surfaces).
�@A historical overview by Jeremy Gray (reprinted).A richly illustrated
essay by the sculptor,
Helaman Ferguson.An exploration of related curves by Allan Adler, with
new results and
exposition of old ones.The first English translation of Klein's seminal article,�hOn the order-
seven transformation of elliptic functions�h.
�@�uKlein quartic�v��Quaternion algebra construction�@�ɂ���3��������g(��)=0 �̉��� ��
�Ƃ���Ƃ��A�Q�l�����̔@���A���̉������̗L������Q(��)�ŕ\�����A�K���A�Q���l�@����
�������B
�@�o�ڐ��ɂ��āA�����P�A�����Q
�@�@���̖���ŋ��߂�F[X�CY�CZ]��Q[X�CY�CZ] �Œ�܂�Ɖ]���㐔�Ȗ�S�ɂ���
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�R�N�P�P���P���t���j
(1)�@�o�Ȗ�S*��S���A�Ⴆ�A(2�C3�C5)�������s�ړ�����T(S)�̑o�Ȗʂ����߁A���̖�
�@�@�̂��]���ĉ������B���z�ł́A�Ȑ��Ƃ��̑o�Ȑ��̖��̂��u�K���b�ƕς�����v�B
(2)�@���̂悤�Ɉ��镽�s�ړ� ����T(S)�̑o�Ȗ�T(S)*�̖��̂�����邱�Ƃ��݂�Ζ��L
�@�@�����������B
(3)�@�@���̖��ŁAt��R �Ƃ��邪�A�������At��[-3�C3] ��̊J���������甼�a
��[36/25]
�@�@�̓S����}������ƁA�E���̐}�̈ʒu�Ŏ~�܂����B���̓S����S�Ƃ̌���͍��Z�����e
�@�@�Ղɋ��߂܂����A���肢���܂��B
(4�j�@���x�́A��r�ɂȂ�ʒ��傫�����a 3 �̓S��S3��S �̉E������S�ɂԂ�������A��
�@�@�݂͂̐}�̈ʒu�� �u���܂荞��Łv�~�܂����B�i���܂荞��ł���l�q�̐}���B�����݂��j
�@�@���܂荞��ł��镔���̑̐ς́H �Ȃ�āA�D���Ȗ�ł͂���܂����܂荞��ł���
�@�@�����̕\�ʐς́H�Ȃ�āA�P�X�A�D���Ȗ�ł͂���܂��D�D�D�B
�@S3��S�̌�� S3��S �́A���Z���ɂ͗e�Ղł͂���܂��A��Ԃ̉����Ȑ��ł����H
�y���S�������l�̂̒�`�z���q�ׁAS3��S �������Ȃ�ؖ����ĉ������B
(5) S3��S�� �������ʂɐ��ˉe����R2 ���̑㐔�Ȑ� prj(S3��S)�̕����������߁A���̑o��
�@�@�Ȑ� prj(S3��S)*���K������(12���ł����H)�A���̓��ٓ_�����߁A (��_���d�_����
�@�@��܂����H)�A�z��͈͓̔��̓��ٓ_�ł��邱�Ƃ�Ή����錳�̋Ȑ��̓�������F�m��
�@�@���܂��B
�@prj(S3��S)�������i�ȋʂƂ��\�L�j�̂悤��...�Ȑ��ł��Bprj(S3��S) �ɂ͓�d�ڐ������肻
���ł��B���l�Ȕ��z�ŋ��߂ĉ������Bprj(S3��S) �ɂ͕ϋȓ_�����肻���ł��B���l�Ȕ��z��
���߂ĉ������B�u�f�J���g�̐��_�Ƒ㐔�v�ɏq�ׂ��Ă��锭�z�����B
�@�����ɁAM.���[�h�� �F ��ь���, ��g���X�@�@���Z���̂��߂̑㐔�� �i�c��X��
�@�㐔�́A�A���������̉��̏W���̊w�I�����ׂ�w��ł��B�{���̓��e�́A
�㐔�̖{�i�I���ɓK���邱�Ƃ����A���Z���̒m���ŁA�㐔�ɂ��Ă̗�����
���������ނ��Ƃ�ڕW�ɂ��đI�т܂����B
�@�㐔�Ȑ��̊w�@�@��g����
5 �ؗ�ȓȐ��̎ˉe�@�Ƃ���܂����A�ؗ�łȂ��̂ł��傤���H�O���ȏ�̑㐔
�Ȑ��A�ʁA ...�@�́B
�@��̓I���ւ̔M���z�����N�ɓ`�������\�\���ꂪ���̖{���o���[���ɂȂ��炦������
�ȗ��R�ł���B�u��̓I�ȌX�̊��̖ʔ��������⋓����Έ�����v...���f�� �O����
�炵���B
�̒��҂ł��B (������������Ă��Ȃ�..)�@�@���@Manifold
�@Figure 1�F The four charts each map part of the circle to an open interval,
and together
cover the whole circle
�@�u�����\���l���v�́u�P�ʉ~�́A���̂S�̊J�ߖT�ŕ������Ƃ��ł���B�v�Ȃ�͔͉A
������āA
(6) �@����f([-�C��)�~R) �� R3 �̓��������l�̂̏ؖ��́A�ǂ̂悤�ȉ�v
�@�@�@�����Ă���Ƃ��l���ł����H
�@�������ʁ��f�����������ʏ�̒m����n=2���łȂ�n=__���̐̑㐔�Ȑ�C��R3�ɖ��ߍ��݁A
N=(0�C0�C1)�Ƃ̑g�ݍ��킹���珬�{�����H�삷�鐍�ʂ�����܂����B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�R�N�P�P���Q���t���j
�@�Q�l�}�����āA�₢�����ɑΛ��Ȃ����ĉ������B�z��͈͓̔��̏����ł��傤���A����
��肢�܂��B
�@R3�ɗ^����ꂽ�C�ӂ̋Ȑ��̊e�_�ƁAP0=(X0�CY0�CZ0)�Ƃ����Ԓ����̘a�W���𐍖ʁA��
�_�����̒��_�A���ʂ������Ă��钼�������Ɖ]���B�i�����Q�R�N�P�P���R���t���j
�@lemniscate�����Ȃ郌���j�X�P�[�g�ilemniscate�j�s�ړ����A�������ʂ�R3���̋Ȑ�=��
���Ƃ��đI�сA����N=(0�C0�C1)����Y�o���ꂽ�������l�@���܂��B
(1) ���̐��ʂ̑㐔�Ȗʁ@f(���C���C��)=0�@(f(X�CY�CZ)��Q[X�CY�CZ])�o���ĉ������B
(2) �������ʂ̑㐔�Ȗ�S�ƒP�ʋ��ʂƂ̌�������ŕ`�����B������A�������ʂɐ��ˉe����
�@�@�Ȑ��@prj(S���P�ʋ��ʁj(�ɒ����j�����ŕ`�����B�Ȑ��@prj(S���P�ʋ��ʁj�̑㐔�Ȑ�
�@�@g(���C��)=0�@(g(X�CY)��Q[X�CY])�o���ĉ������B
(3) ���̌�A�����o�Ȑ��A�o�ȖʁA�o�Ȑ��B�߂ĉ������B
(4) ���g�̏������ׂ��ĉ������B�ׂ����Ȃ�A���̐A�^�̎��A�E�̍��̋Ȑ��͂��ׂ�
�@�@�L���Ȑ��ł��邱�Ƃ���������B
�@�@�u�Q�܂��͂R�����ɂ�����ȗ��Ɲ����̌����i���s�����w�@���ƌ����j�v�Œ��J�ɘ_��
�@���Ă���ȗ����̊T�O�̋�̗�Ƃ��āA
(5) �A���A���̔����{�I�l�@�� ��������Ɗ肢�܂��B
�@���̗L��pdf �̈�ԍŌ�̖��̕ʉ��Ƃ��āA�C�f�A���ōl�@���ׂ��A
I=<Y2 + 2ZY - 2Y + Z2 - Z�C aX +bY +cZ +d>�@�́i���ʁjZERO�_�Ƃ��āA���̋Ȑ����Q�b
�g�\�� ���A���A���A�� ���߁A�����ʂɂ��̋Ȑ����ڂ��Ă���Ɛ}���肢�܂��B
�@�Ȗʁ@Y2 + 2ZY - 2Y + Z2 - Z=0�@�����_�`���Ă��������B�܂��A����pdf�̗��_����A�Q�l
�}�̂悤�ȋȗ����S�̋O�Փ��������邱�Ƃ��ؖ��肢�܂��B�܂��A�ȗ����S�̋O�Ղ̑o
�Ȑ������߁A�}�������A�����{�I�l�@���� ��������Ɗ肢�܂��B
�@�Q�l�}���ς��܂܂ł����A���߂�t�����܂��B
�@�悸�AR3�̂������ʏ�ɁA��n=2���ł͂Ȃ�6���̑㐔�Ȑ�
�@�@X6 - 6X5 + 3Y2X4 + 12YX4 + 27X4 - 12Y2X3 - 48YX3 - 68X3 + 3Y4X2 + 24Y3X2
�@�@�@�@+ 86Y2X2 + 152YX2 + 119X2 - 6Y4X - 48Y3X - 148Y2X - 208YX - 118X + Y6
�@�@�@�@�@�@+ 12Y5 + 63Y4 + 184Y3 + 311Y2 + 284Y + 109 = 0
���߁A���̋�ԋȐ��Ɠ_N=(0�C0�C1)���琍�ʂ��H�삷��B�i���B�Ńs���ƒ��邾��.....)
�@�uQuadric�v��n=6���ł͂Ȃ�n=2�����ʁuConical surface�v�Ȃ�w�ǂ̐l����ς�...�B
(1)�@���炭���̌��ł��傤�B���ʂ�\���㐔�Ȗ� S �̕\���o�肢�܂��B���o��̊��z
�@�@�@������肢�܂��B
(2) S�ƒP�ʋ��ʁFX2+Y2+Z2=1�̌��=���́A3-(1+1) ���������\���l�̂Ȃ�ؖ��肢
�@�@�@�܂��B
(3) ������A�������ʂɐ��ˉe�������̑㐔�Ȑ��̕\�������߂ĉ������B
(4)�@�̋Ȑ��̑o�Ȑ��AS�̑o�ȖʁA���̑o�Ȑ������߁A���ٓ_�B�����߁A�l�@
�@�@�@�肢�܂��B
�@�X�^�[�g�̐�n=2���ł͂Ȃ��A6���̑㐔�Ȑ��Ȑ� �́A����̉��ɗ��݁A���ꂪ���
���(�s�����Łj�����������ӏ��ł��B
�@�̋Ȑ����L���Ȑ��ł��邱�Ƃ�^�ɋ���A�u�����P�v�u�����Q�v�̔@���At=____��Q(���C���j
��^�ɋ��߁A�̑㐔�Ȑ��̗L���Ȑ��\����肢�܂��B
�@Bertini �̒藝�iEugenio Bertini�@1846�`1933 �Q���j�Ȃ镶�����ŁAdual variety ���`��
�Ă���̂ɕY��(2011 11 4) ���A�^���Ɂu�� ���Ă��܂��v�B�i�����Q�R�N�P�P���T���t���j
(�������ł́Adual variety�@�琏���Ŋ����Ȃ����܂����H)
�@�����āA���o�@�͐ԗ��X�ɂ����A���ʂ̂ݖ��L����Ă����܂��B�i���_�A�ˉe��Ԃɉ�
����n=2��荂����4���Ȑ�����X�^�[�g���j���̓^���}�B�����Ă��܂����ł��傤���A�݂�
���������Ƃɂ��A���}�ȊO�������ŕ����đo�Ȑ��̊T������ŕ`���Ă��������B
�@���_�A���}�ɂ͔э��搶���G���𗧂��ǂ݂���A�����F
�u���́���d�ڐ��Ȃ��ނ̐V�N���ɑ̂̌����t�������i�̂ōđ̌����������q�j�v��ϋ�
�_�����݂��邱�Ƃ͒N�����Ă��^���̗]�n�͂Ȃ��B����́A�o�Ȑ��ɑ��̓�������`
���Ȃ��ł͂����Ȃ��̂ŁA�o�Ȑ��̊T���͎�ŕ`���āA���̌�A�̓^���}�B��S
�Ď��āA�z��͈͓̔��ł���܂��傤�B
�@�э��搶�����z�ɂ́A�悸�ˉe�Ȑ����Ƃ���܂����A���ɂ��Ă���i�����āA�t�s��̎�
�@�͌����ʁj�̂ŁA��ŕ`�����萫�I�ȍl�@�ɖ��������A���������������L����Ă����
���鐔���̃v���Z�X���݉B�����L�q���A���L����Ă��铚���̎ˉe�Ȑ��̃A�t�B���������A
���̓��ٓ_�����߂Ă��������B
�@���L����Ă��铚���������Ă��邩�A����12���̎ˉe�Ȑ��̑o�Ȑ���K�����߂ĉ���
���B�i���̖؈���͎�����ƈׂ����l���ׂ����F�߂ʕ������݂��܂��傤���A���l�Ȕ��z��
�����A���鏈��ŁA�ׂ��ʂōς܂��Ȃ����Ă悩�����Ɗ�������ł��傤�B�j
�@�u�Q�܂��͂R�����ɂ�����ȗ��Ɲ����̌����@�i���s�����w�@���ƌ����j�v�Œ��J�ɘ_��
���Ă���ȗ����̊T�O�̋�̗�Ƃ��āA�����̃A�t�B�������ׂ����Ȑ��̋ȗ�����̓I
�ɋ��߁A�z��͈͓̔��̕ϋȓ_�̏o���邾�����m�Ȉʒu���߂Ă��������B
�@���́u�ł��邾���v�Ȃ�ĉ]�����R�͖��炩�Ŏ֑��ł��傤���A�t�L���܂��B
�@�ϋȓ_�����߂�ׂ̘A���������L���A���ꂪ���܂�ɍ����́A�l�ނ����m�ȉ�����
�߂邱�Ƃ̕����𔗂�ꂽ�B
�@�i���Z�����m���́j�ϋȓ_�����߂�ׂ̘A����������K�����L���ĉ������I�i���_���`
�����݂�j
�@�ȉ����A�{���̓��C���ł��B
�@Bertini �̒藝�Ȃ镶�����ŁAdual variety ���`���Ă���̂ɕY�����u�� ���Ă��܂��v�i��
�\���܂����j�B�藝�ɉ]���O��X�̋�̗��10 ���L�����݂��]���Ă���U�L�肢�܂��B
�@Bertini �̒藝�Ȃ镶�����ŁAdual variety ���`���Ă���̂ɕY��(2011 11 4) ���A�^��
�Ɂu�� ���Ă��܂��v(�������ł�dual variety�琏���Ŋ����Ȃ����܂����H)�ƁA�\���܂���
���A�܂����Ă��A����ȕ����i�����P�A�����Q�̒��ɁD�D�D�B�i�����Q�R�N�P�P���U���t���j
�@�ڍׂ��A�����ɂ���܂��B
�@R[X�CY�CZ�CW]/(X2+Y2+Z2+W2-1)R[X�CY�CZ�CW]��x=X+(X2+Y2+Z2+W2-1)R[X�CY�CZ�CW]
�ȍ~���C�ɂȂ�....�B�����ɂ��A�����ɂ��D�D�D�B
�@�ŏ��́udual variety�v�̏ؖ�QED �̍s�Ɂudesire�v�ƍ݂�܂��B����́A�ؖ�QED �̍s�ɁA
�udesire�v�͉ʂ����ꂽ�I�ƋL�����D�D�D�B
�@Bertini �̒藝�ŁA������H��A�X�Ɂu�� ���v���ԂɊׂ�܂����B
�@Bertini �̒藝�Ȃ镶�����ŁA�udual variety�v���`���āA�ŏ��̓����t�����Q�l�}�̐�
�݂͂͗e�Չ߂��āA��d�ڐ���ϋȓ_�i�ȗ��Ɋւ��j���w�ǂȂɂ��ׂ����������邪�A
(1)�@ ���ɁA���l�Ȕ��z�ŋ��߂���
(2)�@�����āAdual variety�𑽗l�Ȕ��z�ŋ��߁A���̓��ٓ_�B���瑴�ꓙ�����߂�
�̂��������̂ŁA����Ȃ����ĉ������B
�@Bertini �̒藝�Ȃ镶�����ŁAdual variety ������������݂�i�Čf�j�A�ǂ�������o��
���͋L����Ă��܂���B
�i�Q�l�j�@����w�@�m���������g�o
�@�@�@�@�i���̑o�ȖʒB���������Ăق�������....�B�����āA���̓��ٓ_�����j
�@�m������i����23�N5��2���A�R�x���̂̂��ߐ����B���N57�B���͑㐔�w�j��
�����ŞH���B�i�����Q�R�N�P�P���U���t���j
�@�Ⴆ�A�~ {(���C��)��C2|��2+��2-1=0} �i���Ȃ킿�AC[���C��]/(��2+��2-1)C[���C��]�j�ɂ����āA��
�͂f�����������ʏ���A�����ʂ̂f�����������ʏ���A�W�@��2+��2-1=0�@�����B
�@�~�ɍڂ��Ă��̗���A���ɕ킢�A10�������ĉ������B
�@�@(-1- I/(2 )�C 1/2 - I/
)�C 1/2 - I/ )�@�A(-1353/1105 - 96I/1105�C164/1105 - 792I/1105)
)�@�A(-1353/1105 - 96I/1105�C164/1105 - 792I/1105)
�@�u���̘_�v�i3.10�@�㐔���l�� �@110p �̂T�s�̒��Ӂj�ŁA�i�c��X���H���B
�@�u�����Ȋw�@�Ȗʂ̐_��v�̔э��搶��n=1�A2�A3�A....�@�Ȑ�...�@���f���l�̂�6p�ŞH���B
�@��2+��2=1 (���_�A��=��+���EI�A��=��+���EI��)��R4�ōl�@���A�C�f�A��
�@�@{u2 - v2 + ��2 - ��2 - 1�C 2���� + 2����} �̋���ZERO�_
{-��4 + u2y2 - v2y2 - y2 + u2v2�C y3 - u2y + v2y + y + uv���C uv + �����Cu2 - v2 + x2 - y2 - 1}
�� ����ZERO�_�ł�����i���Ƃ̏ؖ����I�j
�@z�Aw�Ŋ������o�邪.....�@���̗L�������W���Ƃ���w��n��������
�@�@�@�@P(z�Cw)=wn+a1(z)�Ewn-1+�E�E�E+an(z)��C(z)[w]
�𐳒��ɋL���AP(��+��I�Cu+vI)=0�@���������v�f��n���݂���ƂȂ�ƁA�Õ��ɓ˂���
�Ƃ����͎̂������ł��傤���H�i���@�uAlgebraic function�v�j
�@�������Ap(���C��)=0 �łȂ��A�э��搶�����ɐԗ��X�ɁAp(z�Cw)=0�@�Ap(��+��I�Cu+vI)=0
�ƋL��
�ė~�����B
�@�Ⴆ�A���̈Ղ���������@y-(��4-��2)=0 ���э��搶�����ɐԗ��X�ɁAw-(z4-z2)=0 ��
�L���A�C�f�A��{-��4 + 6��2��2 + ��2 - ��4 - ��2 + u�C -4����3 + 4��3�� + 2���� + ��}�̋���ZERO�_��
�L���ׂ��ł����B
�@�㐔�Ȑ��@f(���C��)=0 ��C2�ōl�@����ہA�����ɁA f(z�Cw)=0 �@f(��+��I�Cu+vI)=0 �ƋL���A��
���Ƌ����ɕ�����̂��P�ɏ��]�ł��傤���H
�@Lars AhlforsDied �i October 1996(1996-10-11) (aged 89)�j������291p�ȍ~�ŁAP(w�Cz)=0
�ƋL���ċc�_�B���T�A����D�D�D�B
�u�����Ȋw�@�Ȗʂ̐_��v�̔э��搶�� n=1�A2�A3�A�E�E�E�@�Ȑ��A���f���l�̂�6p�ŞH���B
�@��2+��2=1�@ (���_�A��=��+��I�Cw=u+vI�@��)�AR4�ōl�@���A�C�f�A��
�@�@�@{u2 - v2 + ��2 - ��2 - 1�C 2���� + 2����} �̋���ZERO�_�i�ȏ�Čf�j
�̉��K���Ȃ����Ɯf�r���A�͔͉�H��̂��h���A���ɐ�قǑ������܂����B
�@ real part=0�@�A imaginary part=0�@���A
��4- 6��2��2 - ��2 + 12���� + ��4 + ��2 = 0�A 4����3 - 6��2 - 4��3�� - 2���� + 6��2 + 6 = 0�@��
(1) �e�S���Ȑ��̑o�Ȑ����A���l�Ȕ��z�ŋ��߂ĉ������B�i�����Ƒz��Ȃ����܂����H)
�@�݂͂����́A���Z�����ׂ���ŁA�o�Ȑ����S���Łi�e�ՁH��) ����܂����B
�@�u�f�J���g�̐��_�Ƒ㐔�v��37p-39p�Ɂi���ٓ_�ɒ��Ⴕ�Ă̋����́j���ޕ\���݂��
���B�i�ǂ̂��炢���ޕ\�̍쐬�ɔN����v�����̂��͋L����Ă��Ȃ��B�w�ǎ҂ŁA����
�m�F��Ƃ��ׂ��ꂽ�������E�ɑ��݂���ł��낤���H)
�@�]����āG �i��̊m�F��Ƃ����ʂ܂ł��Ă� ���ł͏I���Ȃ���....)
�@�E���W�[�~���E�A�[�m���h(Vladimir I. Arnold)��������6��3���������ꂽ�B���N72�B
���A���w�҂͒����̕��������悤�ȋC�����܂����A�����Ɛ����Ȃ��炦�Ċ��ݍӂ������_��
������c���Ăق��������B
(2) �����real part=0�A imaginary part=0�@�͂ǂ̃^�C�v�ł����H
�@�U����V���Ȑ��̕��ނ́A�܂��Ȃ���Ă��Ȃ��ƁA39p�ɁB
�@�����real part=0�A imaginary part=0�@�o�Ȑ��̎����͑���ȏ�ł��B�e�o�Ȑ���
���ٓ_�����߂ĉ������B���Ƃ̂͒�Ȃ̂ŁA
�@�@4����3 - 6��2 - 4��3�� - 2���� + 6��2 + 6 = 0
�� �uWolfram|Alpha�v�Ő}�����Ď���ƁA
(3) ��d�ڐ���ϋȓ_�͂��肻���ȋC�z�A�́A�o�Ȑ��̓��ٓ_�����ߐ������邩�A����
�@�ȗ������߂Ċm�F����Ƃ��V��Ł@�������B
(4) ���_�A�r���œ���ꂽ�L���ʑ��F Cj---��--->Cj* (��=1�A2) ���Ȃ����ĉ������B
(5) �o�Ȑ��A�o�ȖʁA..... �����߂�ߒ��ŁA�Q�b�g�������^�ʑ����ł����A�o�Ή���
�@�O�̑��̏�ʂŔ���^�ʑ��ɑ������������ꂽ�o����������܂����H
�@��{�����K����A�����Ɉ��܂��������Ƃ����l�ђv���܂��B�Ɠ����ɁA�����Ɉ�����A
�{�эb�オ���݂��܂����̂ŁA��⁕�͔͉L�ڎ҂Ɏӎ����q�ׂ܂��B
(6) �����Ɉ�����A�{�эb�オ���݂ɂ��āA���l�Ȍo���k�B�� �L�ڊ肢�܂��B
�@�uCHALLENGE�@PROBLEMS�v�ɂ͍��Z�������̖�B�������t���Œ���Ă���
�����A�udual variety�v �����g�ނƑ�{���������ÁX�̖₪�݂锤�B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�R�N�P�P���W���t���j
�@2�Ԃ̖�i�̂݉������悤�j�́A���ɂ���ŁA�㐔�Ȑ��@C1�Fy - (��3 - 3�� + 4)=0 �A
C2�F y - 3(��2 - ��)=0 �ɂ��āAdual variety�B�����߂Ė����݂����B
(1)�@C1�AC2 �̑o�Ȑ� C1*�A,C2* �𑽗l�Ȕ��z�Ő��߂ĉ������B�����āA���_�A�L��
�@�@�ʑ��B�����L���āA���ٓ_�̗L�����v�Z�ɂ�蒲�����ĉ������B
�@C1----��1--->C1* �@�A�@�@C2----��2--->C2*
C1�AC2�AC1*�AC2*��R2�ɐ}�����āA��1�A��2 ���݂Ŋӏ܂��ĉ������B
�@���̑o�Ȑ������߂��p���́i�Q���Ȑ��̂̍s��\���ɂ��j���z�́A�э��搶�����j
�̒ʂ�ł��B�i�搶����ς��Ɖ]���邵�An=2���Ȑ��A�Ȗ�....�ɂ݂̂����ʗp���܂���j
�@����́AC2�ɂ̂݉\�ł��̂ŁA�э��搶�̔��z�ŁAC2*�����߂ĉ������B
(2)�@C1*��C2*�����߁A2�Ԃ̖�ŗv������Ă��邱�Ƃ�S�čs���ĉ������B
�@���dual variety�����߂ĉ������z���A�H����琂����{���Ɋ��߂ĉ������B
(3)�@2�Ԃ̖�́A���Z�������̖�̂悤�Ȃ̂ŁA���Z���ɕ킢�A�����Ă��������B
�@���(1)(2)�Ɣ�r���āA���z���L�ڊ肢�܂��B
�@���Z�����������������āA�㐔�Ȑ��@C1�F��-��2=0 �AC2�F ��-��3=0 �ɂ��āAdual variety�B
�����߂Ė����݂����B
(1)�@C1�AC2 �̑o�Ȑ� C1*�AC2*�𑽗l�Ȕ��z�ŁA���߂ĉ������B�����āA���_�A�L��
�@�@�ʑ��B�����L���āA���ٓ_�̗L�����v�Z�ɂ�蒲�����ĉ������B
�@C1----��1--->C1* �@�A�@�@C2----��2--->C2*
C1�AC2�AC1*�AC2*��R2�ɐ}�����āA��1�A��2 ���݂Ŋӏ܂��ĉ������B
�@���̑o�Ȑ������߂��p���́i�Q���Ȑ��̂̍s��\���ɂ��j���z�́A�э��搶�����j
�̒ʂ�ł��B�i�搶����ς��Ɖ]���邵�An=2���Ȑ��A�Ȗ�....�ɂ݂̂����ʗp���܂���j
�@����́AC1�ɂ̂݉\�ł��̂ŁA�э��搶�̔��z�ŁAC1*�����߂ĉ������B
(2)�@C1*��C2*�����߁A2�Ԃ̖�ŗv������Ă��邱�Ƃ�S�čs���ĉ������B
�@��� dual variety�@�����߂ĉ������z���A�H����琂����{���Ɋ��߂ĉ������B
(3)�@���̖�́A���Z�������̖�̂悤�Ȃ̂ŁA���Z���ɕ킢�A���l�Ȕ��z�ʼn����A���(1)
�@�@(2)�Ɣ�r���āA���z���L�ڊ肢�܂��B
�@���̍��Z�������̖₩�m��ʂ��A�r�����Ȃ��킢�����Ȃ�����ɐ�ق��� ���܂����B��
����ƌ��āA�v�Z�̉���͕��������Ȃ��A�����Ɂ@����̕ʉ�����炸�ɂ͂���ꂸ�ׂ��܂�
���B���̒��ł����Ƃ����肢���A�����Ă��������āA��{�������͂Ȃ��I
�@�udual variety�v �ɂ���@���A���肢���܂��Bdual variety �����g�ނƁA��{����������
�X�ŁA�K���ׂ����B
�@����́A�o����n=2���̑㐔�Ȑ��@C1�F��2 + ��2 - 8�� = 0 �A C2�F ��2/9 - ��2/4 - 1 = 0�@��
���āAdual variety�B�����߂Ė����݂����B
(1)�@C1�AC2 �̑o�Ȑ� C1*�AC2* �𑽗l�Ȕ��z�Ő��߂ĉ������B�����āA���_�A�L��
�@�@�ʑ��B�����L���ē��ٓ_�̗L�����v�Z�ɂ�蒲�����ĉ������B
�@C1----��1--->C1* �@�A�@�@C2----��2--->C2*
C1�AC2�AC1*�AC2*��R2�ɐ}�����āA��1�A��2 ���݂Ŋӏ܂��ĉ������B
�@���̑o�Ȑ������߂��p���́i�Q���Ȑ��̂̍s��\���ɂ��j���z�́A�э��搶�����j
�̒ʂ�ł��B�i�搶����ς��Ɖ]���邵�An=2���Ȑ��A�Ȗ�....�ɂ݂̂����ʗp���܂���j
�@����́A�Ȃ�Ƒo���Ƃ�n=2���Ȑ��Ȃ̂ŁA�э��搶�̔��z�ŁAC1*�AC2*�����߂ĉ������B
���_�A�э��搶�ɕ킢�A�悸�A�o���Ƃ��ˉe�����A
(2)�@C1*��C2*�����߁A�������̉���̍Ō�̌��_���u���ɁA�e�ՂɁA����ꂽ���Ƃ��m
�@�@�F�肢�܂��B
�@���dual variety�����߂ĉ������z���A�H����琂����{���Ɋ��߂ĉ������B
(3)�@���̉������̐��E�ɔ��������́A���Z�������̖�̂悤�Ȃ̂ŁA���Z���ɕ킢�A��
�@�@�l�Ȕ��z�ʼn����A���(1)(2)�Ɣ�r���Ċ��z���L�ڊ肢�܂��B
�@�udual variety�B�����߂Ė����݂����v�̖ړI�͉ʂ��������ł����A���킸�����Ȃ̂��Ƃ�
�]��Ȃ��ł͂����Ȃ��̂ŁA�]���܂��B
�@dual variety�Ȃ�o���`���ꂽ�Â̝ɛ{�҂́A���̂悤�ȓ��������u���ɉ����ׂ�
dual variety�Ȃ�i�v�ɕs�łȊT�O���㐢�Ɏc���ꂽ�̂Ƃ͈Ⴄ�I���������쐬�Ȃ���
�搶���́A�������̉���̂悤�ȗU�����ɂ��ق����ނ��Ƃ́A�������֍ۈׂ��炸�A
dual variety���̂��̂ɓ��{����A��{���ƔF����Ă��܂�������̂Ă������A�i�v�ɕs
�ł̊T�O�ւ̗U����艻�ɉb�q���X���A���ʂ܂ŋꓬ���ׂ��A�ݖ�ɂ��g���������B
�@�y�����́A���̑o���ɐڂ������ł��B
�@�udual variety�v �����g�ނƁA��{���������ÁX�ŕK���A2���ʂɂ��Ă��l�@�����ɂ�
�����Ȃ�����c�̈Ղ������ɑ������܂����B�o�Ή����āA�����ĉ������B
�@����� �o����n=2���̑㐔�Ȑ�
�@�@�@C1�F (�� - 5 )2 + y2 - 52=0�@�AC2�F(�� + 4
)2 + y2 - 52=0�@�AC2�F(�� + 4 )2 + y2 - 42=0
)2 + y2 - 42=0
�ɂ��āAdual variety�B�����߂Ė����݂����B
(1)�@C1�AC2 �̑o�Ȑ� C1*�AC2* �𑽗l�Ȕ��z�Ő��߂ĉ������B�����āA���_�A�L��
�@�@�ʑ��B�����L���ē��ٓ_�̗L�����v�Z�ɂ�蒲�����ĉ������B
�@C1----��1--->C1* �@�A�@�@C2----��2--->C2*
C1�AC2�AC1*�AC2*��R2�ɐ}�����āA��1�A��2 ���݂Ŋӏ܂��ĉ������B
�@���̑o�Ȑ������߂��p���́i�Q���Ȑ��̂̍s��\���ɂ��j���z�́A�э��搶�����j
�̒ʂ�ł��B�i�搶����ς��Ɖ]���邵�An=2���Ȑ��A�Ȗ�....�ɂ݂̂����ʗp���܂���j
�@����͂Ȃ�Ƒo���Ƃ�n=2���Ȑ��Ȃ̂ŁA�э��搶�̔��z�ŁAC1*�AC2*�����߂ĉ������B
���_�A�э��搶�ɕ킢�A�悸�A�o���Ƃ��ˉe�����A
(2) C1*��C2*�����߁A 4�{�݂���̂Q�{���u���ɓ����邱�Ƃ��m�F�肢�܂��B
�@���āA���Ƃ̂Q�{�ł����AC1* �̎ˉe�������Ȑ����@50X2 - 25Y2 + 10 XZ + Z2=0 �Ƃ�
XZ + Z2=0 �Ƃ�
�锤�ŁAC2*������ˉe�����A���̂Q�{�������邱�Ƃ������ĉ������B
�@����c�̂Q�~�̈ʒu��������B�@�@(�� - 8)2 + ��2 - 52=0�@�A (�� + 4)2 + ��2 - 42=0
�Ƃ����Ƃ��́AC1*��C2*����u���ɂS�{�S�Ă����߂��邱�Ƃ��m�F�肢�܂��B
�@���dual variety�����߂ĉ������z���A�H����琂����{���Ɋ��߂ĉ������B
(3)�@���̉���́A���Z�������̂悤�Ȃ̂ŁA���߂āi��̑ȉ~�ɂ�������@�����邩���l
�@�@���j�A���(1)(2)�Ɣ�r���āA���z���L�ڊ肢�܂��B
�@�udual variety�v �����g�ނƁA��{���������ÁX�ŕK���Q���ʂɂ��Ă��l�@�����ɂ�
�����Ȃ�����c�̈Ղ������ɑ������܂����B
�@���̋��ʐڐ��̂S�{��o�Ή����ċ��߂ĉ������Ƃ��肢�����B����c�̂Q�~���Q�ȉ~�ɑ�
���A����́A�o����n=2�����㐔�Ȑ�C1�F�ԑ��AC2�F�ԍׂɂ��āAdual variety�B������
�Ė����݂����B
(1)�@C1�AC2 �̐}�������o�Ȑ�C1*�AC2*�𑽗l�Ȕ��z�Ő��߂ĉ������B�����āA��
�@�@�_�A�L���ʑ��B�����L���ĉ������B
�@C1----��1--->C1* �@�A�@�@C2----��2--->C2*
C1�AC2�AC1*�AC2*��R2�ɐ}�����āA��1�A��2 ���݂Ŋӏ܂��ĉ������B
�@���̑o�Ȑ������߂��p���́i�Q���Ȑ��̂̍s��\���ɂ��j���z�́A�э��搶�����j
�̒ʂ�ł��B�i�搶����ς��Ɖ]���邵�An=2���Ȑ��A�Ȗ�....�ɂ݂̂����ʗp���܂���j
�@����͂Ȃ�Ƒo���Ƃ�n=2���Ȑ��Ȃ̂ŁA�э��搶�̔��z�ŁAC1*�AC2*�����߂ĉ������B
���_�A�э��搶�ɕ킢�A�悸�A�o���Ƃ��ˉe�����A
(2)�@C1*��C2*= �o�Ȑ��Ƒȉ~�̌�_�����߁A���ʐڐ��̂S�{�����ł��傤�B
�@�@�i����c�̖��Ȃ�@�u���ɓ���ꂽ�j
���A����̑o�Ȑ��B�͐��̂Q���Ȑ��A�o�Ȑ��Ƒȉ~�ł����@���H
�@C1*��C2*���� �� ���������ē�����S�����������ώ@�肢�܂��B
�}���������F�̋��ʐڐ��FAj��+Bj��+1=0 �@(j=1�A2�A3�A4) ���ߎ��łȂ����m�ɋ��߂邱�Ƃ���
�\�Ȑl�����̒��ɑ��݂��܂����H
�@�Q���Ȑ��A�ȖʁA...�@�̑o���肪�ƁA����焈ՂƂ̐������݂������Ȃ̂ŁA���l�сB
�i���@�f�����A�Q�l�j
�@�O�̕��̉҂́A�o�Ȑ������߂āA���o�Ȃǂ����тɂ��o���Ȃ��ʼnB�����A����I�z
�������A�����̂݁B�uI get y = 2x +5�@�A tangent at (1,7) and (4,13) �ƁB�v
�@�Q���ł͂Ȃ��S���̑㐔�Ȑ� K[���C��]/<��-( ��4 - 10��3 + 33��2 - 38�� + 21)> �̑o�Ȑ����A
���锭�z�Ŏ������߂���A
�@K[���C��]/<27��4 - 2164����3 - 39576��2��2 - 4152����2 -211872��3�� - 42288��2��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@- 1920���� - 347584��4 -100128��3 - 8976��2 - 256�� >
�ƂȂ�A�������������オ��Ȃ������B�i��肪�݂�ΏC���肢�܂��j
�@�э��搶�@___�N�O�Ɂu�f�J���g�̐��_�Ƒ㐔�v�@19p �Ɂ@�H���A
�uK[X�CY]/<(Y-(X4-X2)>�̎��A�o�Ȑ������߂邱�Ƃ����ɓ���v
�i�����̂��Ƃł�����A���_�A��������v�Z�ŋ��߂悤�Ƌꓬ��̖��O�̐����ȋL�q�ɈႢ
�Ȃ��B���锭�z�łȂ�A��v�Z�ō���ł��Ȃ����Ƃ�m�锤�B����ĉ������B�j
�@�Ⴆ�A{x �� 2/5�C y �� -(1/5)}����A�iBest Answer - Chosen by Voters�@ get y = 2x +5�j
�������邱�Ƃ��m�F���A���g���A���̏�ɖ��L�������ٓ_�B����_�ł��邱�Ƃ��ؖ����A
���ꓙ�����Ƃ̗e�Ղ� ��=��4 - 10��3 + 33��2 - 38�� + 21 �̕ϋȓ_�ɉ�����ڐ��ł��邱��
���A�����ł��ȗ��̍l�@��s�����Ċ��\�����z���L�q�肢�܂��B
�@���_�AK�͕��f��铂����e����̂œ��ٓ_�B�͂܂������݂�܂��B���߂čl�@�肢�܂��B
�Q�l�i�R�����g�͏��F����������ƕ\������܂��j�ɂ��Ă��A�o�Ȑ������߁A��̂悤��
�l�@�B��Ȃ����ċL�q�肢�܂��B
�i���b��Q�֑����j


 �@�@�ȑO�ɍl�@�ς݂�
�@�@�ȑO�ɍl�@�ς݂�