新学習指導要領で、中学校での連立方程式の扱いが軽減されて以来、高校に入ってか
ら苦労する人が絶えない。数学の高校程度の問題は、最後は連立方程式の問題に帰着
されることが多いので、簡単な2元1次連立方程式しか練習してきていない場合は、その
連立方程式の多様さに圧倒されて計算が進まず、高校での学習内容の習得に支障をき
たす場合が多い。
連立方程式の解法があやしい人は、より簡単な1元1次方程式(例 2x=1/2)の解法
そのものがあやしい場合が多い。連立方程式は、1元の方程式の積み重ねとして存在し
ているので、連立方程式の解法を確かなものとするためには、基本となる1次方程式、2
次方程式の習熟が急務だろう。連立方程式は、ある一定時期に集中して学習すると効果
が出ると思われるが、最近の指導要領では、「現地調達方式」ということで、新しい概念を
学びながらの学習となるので、定着率は芳しくない。
そこで、このページでは、普通は連立方程式を用いて解かれる問題を連立方程式を回
避して解く方法など、学習者の負担が軽減できるような話題について整理しようと思う。
例1 ・・・ 部分分数分解
部分分数分解それ自体は、単純な計算であるが、数列における和の計算や分数関数の
積分などで大活躍するように、習得すべき必須の技法と言えるだろう。
教科書等では、部分分数分解は次のように解かれている。
とおき、分母を払って整理すると、 2(A+B)x−A+B=1
よって、 A+B=0 、 −A+B=1 より、 A=−1/2 、 B=1/2
したがって、
と部分分数分解される。
これに対して、次のような解法はどうであろうか?
1=(1/2){(2x+1)−(2x−1)} なので、両辺を (2x+1)(2x−1) で割って、
を得る。
(コメント) この別解のポイントは、部分分数分解される分数の分子を、分母の因数を用い
て如何に表せるかを見いだすことである。そこに気がつけば、わざわざ連立方程
式を持ち込むまでもなく答えは暗算で求められる。
当HPがいつもお世話になっているHN「攻略法」さんが例1について考察された。
(平成23年9月9日付け)
部分分数分解について
※へヴィサイドの方法
の両辺に 2x+1 をかけると、 1/(2x-1)=A+B(2x+1)/(2x-1)
x=-1/2 を代入すると、 -1/2=A+B・0/(-2) より、 A=-1/2
同様に、両辺に 2x-1 をかけると、 1/(2x+1)=A(2x-1)/(2x+1)+B
x=1/2 を代入すると、 1/2=A・0/2+B より、 B=1/2
(コメント) う〜む、上手い!
練習問題 次の式が、xについての恒等式であるとき、定数A、B、Cの値を求めよ。
x2/{(x+1)(x+2)(x+3)}=A/(x+1)+B/(x+2)+C/(x+3)
(解) 与式の両辺に x+1 をかけると、 x2/{(x+2)(x+3)}=A+B(x+1)/(x+2)+C(x+1)/(x+3)
x=-1 を代入すると、 (-1)2/{((-1)+2)((-1)+3)}=A+B・0/1+C・0/2 より、 A=1/2
同様に、両辺に x+2 をかけると、 x2/{(x+1)(x+3)}=A(x+2)/(x+1)+B+C(x+2)/(x+3)
x=-2 を代入すると、 (-2)2/{((-2)+1)((-2)+3)}=A・0/(-1)+B+C・0/1 より、 B=-4
同様に、両辺に x+3 をかけると、 x2/{(x+1)(x+2)}=A(x+3)/(x+1)+B(x+3)/(x+2)+C
x=-3 を代入すると、 (-3)2/{((-3)+1)((-3)+2)}=A・0/(-2)+B・0/(-1)+C より、 C=9/2 (終)
攻略法さんからの続報です。(平成23年9月24日付け)
上記の練習問題について、ラグランジュの補間公式より、
f(x)=f(-1)(x+2)(x+3)/{((-1)+2)((-1)+3)}+f(-2)(x+1)(x+3)/{((-2)+1)((-2)+3)}
+f(-3)(x+1)(x+2)/{((-3)+1)((-3)+2)}
=f(-1)(x+2)(x+3)/2 -f(-2)(x+1)(x+3) +f(-3)(x+1)(x+2)/2
両辺を、(x+1)(x+2)(x+3) で割ると、
f(x)/{(x+1)(x+2)(x+3)} = {f(-1)/2}(x+1) +{-f(-2)}/(x+2) +{f(-3)/2}/(x+3)
f(x)=x2 なので、f(-1)=1、f(-2)=4、f(-3)=9 より、
x2/{(x+1)(x+2)(x+3)} = (1/2)/(x+1) +(-4)/(x+2) +(9/2)/(x+3)
(コメント) ラグランジュの補間公式の斬新な使い方ですね!感動しました。
FNさんからのコメントです。(平成23年9月24日付け)
なるほど!ラグランジュの補間公式は、このタイプの問題に使えますね。逆に言えば、こ
のようにしてラグランジュの補間公式が作られたということでもあります。
f(a)=A、f(b)=B、f(c)=C を満たす2次関数を求めよ。
(解) f(x)=p(x-b)(x-c)+q(x-c)(x-a)+r(x-a)(x-b) とおく。
f(a)=A より、 A=p(a-b)(a-c) なので、 p=A/((a-b)(a-c))
同様にして、q=B/((b-c)(b-a)) 、r=C/((c-a)(c-b))
これでラグランジュの補間公式が得られた。 (終)
f(x)=p(x-b)(x-c)+q(x-c)(x-a)+r(x-a)(x-b) より、
f(x)/((x-a)(x-b)(x-c))=p/(x-a)+q/(x-b)+r/(x-c)
となり、上の練習問題と同じになります。
攻略法さんからの続報です。(平成23年9月25日付け)
問題(オイラーの分数式)
分数式 a/{(a-b)(a-c)}+b/{(b-a)(b-c)}+c/{(c-a)(c-b)} の値を求めよ。
(解) 3点 (a,A)、(b,B)、(c,C) を通る2次関数は、ラグランジュの補間公式より、
f(x)={A/((a-b)(a-c))}(x-b)(x-c) +{B/((b-a)(b-c))}(x-a)(x-c) +{C/((c-a)(c-b))}(x-a)(x-b)
f(x)を 1、x、x2 とすると、Aは、1、a、a2、Bは、1、b、b2、Cは、1、c、c2 となる。
両辺の x2 の係数を比較すると、
1/{(a-b)(a-c)}+1/{(b-a)(b-c)}+1/{(c-a)(c-b)} = 0
a/{(a-b)(a-c)}+b/{(b-a)(b-c)}+c/{(c-a)(c-b)} = 0
a2/{(a-b)(a-c)}+b2/{(b-a)(b-c)}+c2/{(c-a)(c-b)} = 1
を得る。 (終)
一般に、g(x)=xn とすると、 g(a)=an、g(b)=bn、g(c)=cn となる。
f(x)=(x-a)(x-b)(x-c) として、g(x)をf(x)で割ったときの商をQ(x)、余りをR(x)とすると、
g(x)=f(x)Q(x)+R(x) と書ける。
よって、 R(x)=g(x)-f(x)Q(x)=xn-(x-a)(x-b)(x-c)Q(x)
このR(x)は、R(a)=an、R(b)=bn、R(c)=cn を満たす2次式以下の多項式になる。
R(x)に、f(x)=(x-a)(x-b)(x-c) として、ラグランジュの補間公式を適用すると、
R(x)=an(x-b)(x-c)/{(a-b)(a-c)}+bn(x-a)(x-c)/{(b-a)(b-c)}+cn(x-a)(x-b)/{(c-a)(c-b)}
両辺の x2 の係数を比較すると、
an/{(a-b)(a-c)}+bn/{(b-a)(b-c)}+cn/{(c-a)(c-b)}
の値が得られる。
練習問題 (n=3の場合)
a3/{(a-b)(a-c)}+b3/{(b-a)(b-c)}+c3/{(c-a)(c-b)} の値を求めよ。
(解) g(x)=x3 を、f(x)=(x-a)(x-b)(x-c) で割ると、
商が 1、余りが (a+b+c)x2-(ab+bc+ca)x+abc なので、
R(x)=(a+b+c)x2-(ab+bc+ca)x+abc よって、求める値は、a+b+c (終)
(コメント) 私が高校1年のときに経験した問題です。因数分解と約分が大変でした!攻略
法さんの別解に感動しました。
攻略法さんからの続報です。(平成23年9月27日付け)
類題
(1) bc/{(a-b)(a-c)}+ca/{(b-c)(b-a)}+ab/{(c-a)(c-b)} の値を求めよ。
(2) (b+c)/{(a-b)(a-c)}+(c+a)/{(b-c)(b-a)}+(a+b)/{(c-a)(c-b)} の値を求めよ。
(解) f(x)=1として、
1=(x-b)(x-c)/{(a-b)(a-c)} +(x-c)(x-a)/{(b-c)(b-a)} +(x-a)(x-b)/{(c-a)(c-b)}
定数項を比較すると、1=bc/{(a-b)(a-c)}+ca/{(b-c)(b-a)}+ab/{(c-a)(c-b)}
x の係数を比較すると、
0=(b+c)/{(a-b)(a-c)}+(c+a)/{(b-c)(b-a)}+(a+b)/{(c-a)(c-b)} (終)
類題
(1) abc/{(a-b)(a-c)}+abc/{(b-c)(b-a)}+abc/{(c-a)(c-b)} の値を求めよ。
(2) a(b+c)/{(a-b)(a-c)}+b(c+a)/{(b-c)(b-a)}+c(a+b)/{(c-a)(c-b)} の値を求めよ。
(解) f(x)=x として、
x=a(x-b)(x-c)/{(a-b)(a-c)} +b(x-c)(x-a)/{(b-c)(b-a)} +c(x-a)(x-b)/{(c-a)(c-b)}
定数項を比較すると、0=abc/{(a-b)(a-c)}+abc/{(b-c)(b-a)}+abc/{(c-a)(c-b)}
x の係数を比較すると、
-1=a(b+c)/{(a-b)(a-c)}+b(c+a)/{(b-c)(b-a)}+c(a+b)/{(c-a)(c-b)} (終)
FNさんからのコメントです。(平成23年9月25日付け)
上記の一般の場合、即ち、次の形のオイラーの分数式を求めることを考えてみました。
E(n)=an/{(a-b)(a-c)}+bn/{(b-a)(b-c)}+cn/{(c-a)(c-b)} を求めよ。
既に、E(0)=E(1)=0、E(2)=1、E(3)=a+b+c は求められています。
まず、E(n)は、a、b、c の対称式である。実際に、aとbを交換すると、
bn/{(b-a)(b-c)}+an/{(a-b)(a-c)}+cn/{(c-b)(c-a)} となって、E(n)に等しい。
bとc、cとa の交換も同様。
次に、E(n)は、a、b、c の多項式である。
即ち、E(n)の分母を(a-b)(b-c)(c-a)として通分したときの分子Aは、(a-b)(b-c)(c-a)で割
り切れる。
実際に、A=-an(b-c)-bn(c-a)-cn(a-b)で、これを、a の多項式とみて、A(a)とおくと、
A(b)=-bn(b-c)-bn(c-b)-cn(b-b)=0 となって、Aは、a-bで割り切れる。
同様にして、b-c、c-a でも割り切れて、(a-b)(b-c)(c-a) で割り切れ、E(n)は、a、b、c の
多項式である。
E(n)の次数は、n−2 である。ただし、n=0、1のときは、E(n)=0
E(n)の分母を(a-b)(b-c)(c-a)として通分したとき、分母の次数は3で、分子の次数は n+1
従って、E(n)の次数は、n+1-3=n-2 となる。ただし、n=0、1 のときは、分母が3次で、分子
が2次以下。それで分子が分母で割り切れるのは、分子=0 しかない。
E(0)=E(1)=0 は求まった。E(2)は0次式、即ち、定数である。分母・分子のa2 の係数をみ
るとどちらも c-b。従って、E(2)=1。
E(3)は1次式。a、b、c の対称式で1次のものは、a+b+c の定数倍しかない。分母の a2
の係数は c-b、分子の a3 の係数も同じ。従って、E(3)=a+b+c
さて、問題はここから先です。E(4)は2次です。abがあれば、bc、ca も同じだけあります。
a2、b2、c2 についても同じです。そして、これら以外はありません。だから、abとa2の係数
が決まれば終わりです。c=0 とおいてみます。分子は、ab(b3-a3)で、分母は、ab(b-a) と
なる。従って、a2+ab+b2 となって、a2、ab とも係数は1
以上から、 E(4)=a2+b2+c2+ab+bc+ca である。
では、E(5)はどうなるでしょうか?
FNさんからの続報です。(平成23年9月26日付け)
n=4のときに使った c=0 と置く方法を、最初から使えば、n=2、3 のあたりも簡単になりま
す。一般のnについても、ある程度までわかります。
n≧2のとき、E(n)が、a、b、c に関して n-2次の対称式であることは証明しました。しかも、
n-2次の同次式です。即ち、n-2次の項しかありません。
分子が、n+1次の同次式で、分母が3次の同次式であることからわかります。
E(n)に現れる項は、apbqcr(p+q+r=n、p、q、rは負でない整数)の形ですが、a、b、c に
関する対称式だから、p、q、r を入れ替えたものの係数は同じです。
例えば、 a3・bc、b3・ca、c3・ab の係数は同じです。だから文字が2つ以下であるものに
ついては、c=0 とおいて調べることができます。
c=0のとき、
E(n)=an-1/(a-b)+bn-1/(b-a)=(an-1−bn-1)/(a-b)=an-2+an-3・b+・・・・+bn-2
従って、文字が2個以下である項の係数はすべて1であることがわかります。これより、
E(2)=1 、E(3)=a+b+c 、E(4)=a2+b2+c2+ab+bc+ca となります。E(5)ではじめて文字が
3個の項 abc が現れます。この項を除けば係数は、すべて1ですから、
E(5)=a3+b3+c3+a2b+ab2+b2c+bc2+c2a+ca2+kabc
となります。abcの項の係数は別の方法で求めるしかありません。どうすればいいのかわか
りません。
当HPの読者のHN「空舟」さんからのコメントです。(平成23年9月26日付け)
E(n)を c について k 回微分したものに、c=0 を代入することを考えます。第一項と第二
項は容易です。第三項は分子にcnがあるので、k<n では、c=0 のとき、0となります。そ
の結果、 k!{an-1-k-bn-1-k}/(a-b) のような形になります。E(n)のうち ck がつく項の係
数がすべて1になることがわかります。
3次方程式については、1つの解をαとした時に、他の解をαの2次式で表す手順がある
ようです。(この掲示板のどこかで見ました)それについて、4次方程式の場合に同じことを
試みて、うまくいきませんでした。「S(H)さんからの話題」というページには4次方程式どころ
か、8次方程式について、同様な7次式を求めている結果が書いてあって、大変衝撃を受
けました。いったいどのように計算したのか興味があります...。
FNさんからのコメントです。(平成23年9月26日付け)
確かに証明できているようですね。私は証明としてきちんと書かないと理解できないので、
きちんと書いてみようと思います。有難うございました。
FNさんからの続報です。(平成23年9月27日付け)
E(n)=bn/{(b-a)(b-c)}+an/{(a-b)(a-c)}+cn/{(c-b)(c-a)} を求めよ。
について、n≧2 のとき、E(n)=Σap・bq・cr
(ただし、Σは、p+q+r=n-2 を満たす負でない整数の組 (p,q,r)すべてについての和)
空舟さんが書かれたことで十分とも言えますが、高校生にもわかるような形で証明を書き
ます。前に書いたことも含めて書きます。n=0、1は省略します。
(解) E(n)のcをxに変えたものを f(x) とおく。
即ち、 f(x)=xn/{(x-a)(x-b)}-an/(a-b)・1/(x-a)-bn/(b-a)・1/(x-b)
まず、f(x)は、n-2次の多項式である。(これは前に証明していますが...。)
g(x)=(x-a)(x-b)f(x)とおくと、g(x)=xn-an/(a-b)・(x-b)-bn/(b-a)・1/(x-a)
g(a)=g(b)=0 より、g(x)は、(x-a)(x-b)で割り切れ、g(x)は、n次式だから、
f(x)は、n-2次の多項式
0≦k≦n-2 である k について、f(x)のxkの係数が、
Σap・bq (Σは、p+q=n-k-2 を満たす非負整数の組(p,q)すべての和)
であることを示せばよい。このΣは、n-k-2=m とおけば、am+am-1b+・・・・+bmであり、これは
(am+1-bm+1)/(a-b) 即ち、(an-k-1-bn-k-1)/(a-b)
である。f(x)をk回微分して、x=0 とおくと、f(x)の xk の係数に、k!をかけたものになる。
従って、証明すべきことは、f(x)を k 回微分して、x=0 とおいたものが、
k!(an-k-1-bn-k-1)/(a-b)
となることである。
xn/{(x-a)(x-b)}を商の微分の公式を使って、k回微分すると、
分母={(x-a)(x-b)}2k で、分子=xn-k・(xの整式)となる。(きちんとするなら数学的帰納法)
k≦n-2 であるから、x=0 を代入すると、0 になる。-an/(a-b)・1/(x-a)を k 回微分すると、
-an/(a-b)・(-1)k・k!(x-a)-k-1
x=0 を代入すると、 k!an-k-1/(a-b) で、-bn/(b-a)・1/(x-b)を k 回微分すると、
-bn/(b-a)・(-1)k・k!(x-b)-k-1
x=0 を代入すると、 k!bn-k-1/(b-a)
従って、f(x)を k 回微分して、x=0 とおくと、k!(an-k-1-bn-k-1)/(a-b) となる。 (終)
FNさんからの続報です。(平成23年9月27日付け)
E(n)=bn/{(b-a)(b-c)}+an/{(a-b)(a-c)}+cn/{(c-b)(c-a)} を求めよ。
昨日の朝、書きこんだ時点では、一般の n について、E(n)を求めるのは無理だろうと思っ
ていました。E(5)やE(6)ぐらいはなんとかなるかなと思っていました。空舟さんによって完全
解決したのでもう意味はないのですが、昨日考えてE(5)やE(6)を求めることはできたので、
一応書いておきます。
E(n)の a、b、c を 1 にしたいのですが、直接では、分母が0になります。(a=b=c=1とする
と、すべての項が1になるのでE(5)のkabcのkはわかる。E(6)も文字が3つの項は、a2bc
のタイプだけだから求めることができる)
そこで、a=1+h、b=1-h、c=1 とおいて、h→0 の極限を求めるという方針にしました。このと
き、E(n)は、 {(1+h)n+(1-h)n-2}/(2h2) となります。
これの、h→0 のときの極限を求めるのは、高校生の手頃な練習問題です。結果は、
n(n-1)/2=nC2
となります。
a、b、c のn-2次の単項式(係数が1のもの)の数は異なる3個の文字 a、b、c から重複を
許してn-2個とる重複組合せの数 3Hn-2=3+n-2-1Cn-2=nCn-2=nC2 です。上の結果 nC2 と
一致します。このことは、E(n)に現れるすべての単項式の係数が1である可能性を示唆します。
もちろん、弱い状況証拠程度で、証明には程遠いです。
E(5)とE(6)の結果を書いておきます。3次、4次の単項式をすべて書くだけですが...。
E(5)=a3+b3+c3+a2b+ab2+b2c+bc2+c2a+ca2+abc
E(6)=a4+b4+c4+a3b+ab3+b3c+bc3+c3a+ca3+a2b2+b2c2+c2a2+a2bc+b2ca+c2ab
上の高校生向きの練習問題を一般化します。分母の2は消しています。
f(x) は2回微分可能とする。{f(a+h)+f(a-h)-2f(a)}/h2 の h→0 のときの極限を求
めよ。
これを高校数学の範囲でやってください。ロピタルの定理は使用禁止です。
FNさんが上記の問題の解を与えられました。(平成23年10月3日付け)
普通はロピタルの定理の真似をして、従って、コーシーの平均値の定理の真似をして証
明すると思います。あるいはテーラー展開の2階微分の項までの式を真似をしながら作っ
てもいいでしょう。それでいいのですが、そして、その方がいいのですが、ラグランジュの補
間公式を使った証明が載っていたので書いておきます。ちょっと面白いと思いました。
ただし、f"(x)の存在の他に連続性も必要なので、本当は上の問題の解答としては不十分
です。
(解) a<b<c に対して、P(a)=f(a)、P(b)=f(b)、P(c)=f(c) を満たす2次以下の整式P(x)
が一意的に存在する。ラグランジュの補間公式として具体的に与えられる。
g(x)=f(x)-P(x)とおく。g(x)は2回微分可能で、g(a)=g(b)=g(c)=0 であるから、ロルの定理に
より、g’(s)=0、g’(t)=0 (a<s<b<t<c) を満たす s、t が存在する。
従って、再びロルの定理により、g”(u)=0 (s<u<t) を満たす u が存在する。
このとき、f”(u)=P”(u)
ラグランジュの補間公式の形から容易にわかるように、
P”(u)=2f(a)/{(a-b)(a-c)}+2f(b)/{(b-c)(b-a)}+2f(c)/{(c-a)(c-b)}
である。(P(x)は2次式だから、P”(x)は定数で、uを含まない) また、a<u<c
ここで、a,b,c を、a-h、a、a+h として適用すると、a-h<u<a+h で、
f”(u)=P”(u)=2f(a-h)/{(-h)(-2h)}+2f(a)/{h(-h)}+2f(a+h)/(2hh)={f(a+h)+f(a-h)-2f(a)}/(h2)
h→0 とすると、u→a だから、{f(a+h)+f(a-h)-2f(a)}/(h2)→f”(a) (終)
(※最後のところで、f”(x)の連続性を使っている。)
練習問題 次の式が、xについての恒等式であるとき、定数A、B、Cの値を求めよ。
4(x+2)/{(x+1)2(x+3)}=A/(x+1)2+B/(x+1)+C/(x+3)
(解) 与式の両辺に (x+1)2 をかけると、 4(x+2)/(x+3)=A+B(x+1)+C(x+1)2/(x+3)
x=-1 を代入すると、 4・((-1)+2)/((-1)+3)=A+B・0+C・02/2 より、 A=2
同様に、両辺に x+3 をかけると、 4(x+2)/(x+1)2=A(x+3)/(x+1)2+B(x+3)/(x+1)+C
x=-3 を代入すると、 4・((-3)+2)/((-3)+1)2=A・0/(-2)2+B・0/(-2)+C より、 C=-1
同様に、両辺に x+1 をかけると、 4(x+2)/{(x+1)(x+3)}=A/(x+1)+B+C/(x+3)
x=0 を代入すると、 4・(0+2)/{(0+1)(0+3)}=A/1+B+C/3 より、A+B+C/3=8/38/3=A+B+C/3
A=2、C=-1 を代入すると、 8/3=2+B-1/3 より、 B=1 (終)
当HPがいつもお世話になっているHN「FN」さんが、例1について考察された。
(平成23年9月14日付け)
上記で、1/((2x+1)(2x-1))の部分分数分解が取り上げられている。教科書では連立方程式
にするのが普通かもしれないが、分母の2つの因数の差が定数で分子も定数なら、ある程度
慣れれば暗算でいきなり結果を書くでしょう。
連立方程式にしたなら、分母を払った式 1=A(2x-1)+B(2x+1) に、x=1/2、-1/2 を代入し
て、事実上連立方程式でない形にして、A、Bを求めるのが普通だと思います。
ただ、このやりかたは、分母を 0 にする値を代入するので、幾分気持ちの悪さがあります。
当然教科書には書けません。もちろん正当化はできます。きちんと正当化できる用意は必要
です。答案に書く必要はありません。代入する値は、普通は分母を 0 にする値ですが、やや
こしい分数や無理数、さらには、虚数であっても、何が何でも分母を 0 にする値を代入するか
どうかです。
1/(x3-1) を部分分数の和で表せ。
1/(x3-1)=A/(x-1)+(Bx+C)/(x2+x+1) とおく。分母を払って、
1=A(x2+x+1)+(Bx+C)(x-1)
x=1 を代入して、 1=3A より、 A=1/3
(ここまでは誰がやっても同じです。)このあと、x=0、-1 あたりを代入すれば、無難です。
そして、多分その方が早い。しかし、意地でも、x2+x+1=0 の解、即ち、1の虚数立方根 ω
を代入したいという考え方もある。 1=(Bω+C)(ω-1) において、右辺を展開するようでは、
ωを代入する意味はありません。Bω+C=1/(ω-1) として、1/(ω-1) の計算にはいらなけ
ればいけません。
1/(ω-1)=(ω2-1)/{(ω-1)(ω2-1)}=(-ω-2)/(ω3-ω2-ω+1)=(-2-ω)/3=-2/3-(1/3)ω
よって、係数比較して、 C=-2/3 、 B=-1/3 となる。
やっぱり、x=0、-1 あたりを代入した方が早そうです。しかし、事実上連立方程式を回避し
たという意味で一定の意味はあるでしょう
攻略法さんからのコメントです。(平成23年9月14日付け)
1/(ω-1) の有理化について
共役なものがわかる場合 conj(ω)=ω2 より、(ω-1)(conj(ω)-1)=(ω-1)(ω2-1)
共役なものがわからない場合
x2+x+1=(x-1)Q(x)+R とすると、 1=(x2+x+1)/R-(x-1)Q(x)/R となる。
x2+x+1=0 の1つの解を ω とすると、 1=-(ω-1)Q(ω)/R
よって、 1/(ω-1)=-Q(ω)/R
このことから、 (x2+x+1)÷(x-1) の商 x+2 余り 3 なので、 1/(ω-1)=-(ω+2)/3
FNさんからのコメントです。(平成23年9月15日付け)
攻略法さんの用いられた手法は、Euclidの互除法のようですね。次の例で考えます。
1/((x2+x+2)(x2-2x-1))を部分分数に分けよ。
与式=(Ax+B)/(x2+x+2)+(Cx+D)/(x2-2x-1)とおく。分母を払って、
(Ax+B)(x2-2x-1)+(Cx+D)(x2+x+2)=1
x2-2x-1=0 の解αと x2+x+2=0 の解βを代入すればできますが、かなりの計算です。
x=0、1、-1、2 とかを代入してもできますが、やはり、かなりの計算です。両方やってみま
したが、どちらが楽かは何とも言えません。
数値代入をしないで、Euclidの互除法で直接やれば、もう少し簡単なようです。
x2-2x-1 を A(x)、x2+x+2 を B(x)、Ax+B を P(x)、Cx+D を Q(x) とおけば、
A(x)P(x)+B(x)Q(x)=1
を満たす P(x)、Q(x) を求めよという問題です。
(P(x)、Q(x)は1次以下とする。1つ見つかればよい。)
「5x+8y=1 を満たす整数 x、y を(1つ)求めよ」という問題と同じです。これは、Euclidの互除
法でできることは知られています。係数が5と8ぐらいなら適当に捜せばできますが、もっと大
きい係数になれば、手順を踏むべきでしょう。手順に従ってやります。
A(x)をB(x)で割ると、商は、1で、余りは、-3x-3=-3(x+1)
A(x)=B(x)-3(x+1) これより、 x+1=(-1/3)A(x)+(1/3)B(x)・・・(*)
B(x)をx+1で割ると、商は、xで、余りは、2
B(x)=(x+1)x+2 これより、1=(1/2)B(x)-(x/2)(x+1)
(*)を代入して、 1=(1/2)B(x)-(x/2)((-1/3)A(x)+(1/3)B(x)) より、
1=A(x)(x/6)+B(x)(-x/6+1/2)
よって、 P(x)=x/6 、 Q(x)=-x/6+1/2 より、
1/((x2+x+2)(x2-2x-1))=(x/6)/(x2+x+2)+(-x/6+1/2)/(x2-2x-1)
当HPがいつもお世話になっているHN「らすかる」さんからのコメントです。
(平成23年9月15日付け)
1/((x2+x+2)(x2-2x-1))を部分分数に分けよ。
について、
与式=(Ax+B)/(x2+x+2)+(Cx+D)/(x2-2x-1) の分母の2次の項の係数が、1:1なので、
A:C=1:-1 である。
x/(x2+x+2)+(-x)/(x2-2x-1)=(-3x2-3x)/((x2+x+2)(x2-2x-1)) ・・・(1)
3x2+3x+6=3(x2+x+2) だから、(1)を
x/(x2+x+2)+(-x+3)/(x2-2x-1) とすれば、定数項以外が消えて定数 6 が残る。
よって、答えは、
与式={x/(x2+x+2)+(-x+3)/(x2-2x-1)}/6=(x/6)/(x2+x+2)-(x/6-1/2)/(x2-2x-1)
FNさんからのコメントです。(平成23年9月16日付け)
なるほど、C=-A はすぐわかりますね。さらに、B、Dを 0 にすれば、分子の定数項を除い
たものが一方の分母の定数項を除いたものの定数倍になるということで簡単にできますね。
多項式 f(x)とg(x)が公約数をもたないとき、f(x)P(x)+g(x)Q(x)=1 を満たす P(x)、Q(x)が存
在することはよく知られていますが、具体的に、f(x)、g(x)が与えられたとき、P(x)、Q(x)を求
めるのはかなり面倒と思われます。
Euclidの互除法が普通だと思ったのですが、具体的な式でやれば、余りの係数が大きくな
って、分数がたくさんでてきて諦めました。やはり個々のケースでいろいろ考えた方がいいの
かもしれません。
3次式にしてみました。
f(x)=x3-3x+1、g(x)=x3+x2+6 のとき、f(x)P(x)+g(x)Q(x)=1 を満たす2次以下の整
式P(x)、Q(x)を(1つ)求めよ。
今までの流れからすれば、上のような問題になりますが、分数係数であまりきれいじゃな
いので次の形にします。
(1) f(x)=x3-3x+1、g(x)=x3+x2+6 のとき、f(x)P(x)+g(x)Q(x) が自然数となるような
整数係数の2次以下の整式P(x)、Q(x)を(1つ)求めよ。
Euclidの互除法でもいいし、違う方法でもいいです。やってみてください。
前の2次式の場合は、 f(x)=x2+x+2、g(x)=x2-2x-1で、P(x)=-x+3、Q(x)=x のとき、
f(x)P(x)+g(x)Q(x)=(x2+x+2)(-x+3)+(x2-2x-1)x=6 でした。この「6」は最小であると思われま
す。これは証明できるでしょうか。即ち、
(2) f(x)=x2+x+2、g(x)=x2-2x-1 とする。整数係数の整式P(x)、Q(x)に対して、
f(x)P(x)+g(x)Q(x)=n (nは自然数) になれば、nは6の倍数である。
私は証明できてませんが成り立ちそうな気がします。
(連立方程式の回避という話からは脱線してしまっていますが...。)
例2 ・・・ 2点を通る直線の方程式
直線の方程式というと、生徒は直ぐに「y=ax+b」の形を思い出すくらい馴染みが十分あ
るらしい。直線の方程式で「ax+by+c=0」の形を思いつく生徒はそう多くはいない。
2点を通る直線の場合は、y 軸に平行かどうかさえ注意すれば、「y=ax+b」の形は結構
有効である。傾き a を求めれば、後は1次方程式に帰着される。ところが、生徒にとっては
傾きの計算がとても苦手らしい。そもそも比の計算が出来ない人が最近多いように感じる。
この傾きの計算が十分習得されていないので、微分積分の基礎の部分「平均変化率から
微分係数の計算」が思うように出来ないようだ。かなりな進学校の生徒でさえ、定義による
微分係数の計算が出来ないと聞く。
結局は、小学校で学ぶ「比の概念」に習熟しないまま数学を学んでいるのが実状なわけ
で、学習に支障をきたしている生徒の割合は以前よりも大幅に増加しているように感じる。
これから述べることは、これらの改善策である。
2点A(1,2)、B(4,6)を通る直線の方程式は、中学生・高校生的には普通次のよ
うに解かれるであろう。
求める直線の方程式を、 y=ax+b とおく。2点A(1,2)、B(4,6)を通るので、
a+b=2 、 4a+b=6 これらを解いて、 a=4/3 、 b=2/3 となるので、
求める直線の方程式は、 y=(4/3)x+(2/3) となる。
もっとも、この問題は、傾きを最初に計算した方が、本当は易しい。
2点A(1,2)、B(4,6)を結ぶ線分の傾きは、 (6−2)/(4−1)=4/3
よって、求める直線の方程式は、 y=(4/3)x+b とおける。
点A(1,2)を通ることから、 2=(4/3)+b より、 b=2/3
ゆえに、 求める直線の方程式は、 y=(4/3)x+(2/3) となる。
このような解法に対して、私自身の方策としてはベクトル方程式の活用を是非推奨したい。
2点A(1,2)、B(4,6)を通る直線のベクトル方程式は、実数を t として、
(x,y)−(1,2)=t{(4,6)−(1,2)}
と書ける。 よって、 x−1=3t 、 y−2=4t となる。
これより、 t=(x−1)/3 、 t=(y−2)/4 なので、
求める直線の方程式は、 (x−1)/3=(y−2)/4 となる。
(コメント) このベクトルを用いた解法は、連立方程式の回避になっていないのではと、い
ろいろ意見を醸し出すかもしれない。
当HPがいつもお世話になっているHN「攻略法」さんから別解を頂きました。
(平成23年9月12日付け)
公式に数値を当てはめてみました。
2点(x1,y1)、(x2,y2) を通る直線の方程式は、行列式
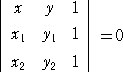
で表される。2点(1,2)、(4,6)を代入して、
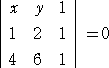
より、 -4x + 3y - 2 = 0
例3 ・・・ 3点を通る放物線の決定
現在の学習指導要領では、3元1次連立方程式は、数学 I の「2次関数」で学ぶ。しかし、
そこで学ぶものは、一般の3元1次連立方程式と言えるようなものではない。2次関数の一
般形の特殊性から、どうしても定数項が浮いてしまって、結局は、2元1次の連立方程式の
域を出ていないように感じる。
3点A(1,−3)、B(−2,0)、C(3,15)を通る放物線の方程式を求める問題は、
通常、次のように解かれている。
求める放物線の方程式を、 y=ax2+bx+c とおくと、3点A、B、Cを通ることから、
a+b+c=−3 ・・・ (1)、 4a−2b+c=0 ・・・ (2)、 9a+3b+c=15 ・・・(3)
(2)−(1) より、 3a−3b=3 すなわち、 a−b=1 ・・・ (4)
(3)−(2) より、 5a+5b=15 すなわち、 a+b=3 ・・・ (5)
よって、 (4)+(5) より、 2a=4 すなわち、 a=2 、 b=1 、 c=−6
以上から、求める放物線の方程式は、 y=2x2+x−6 となる。
(コメント) 連立方程式が苦手な生徒は、まず、方程式の多さに圧倒され、どうしてよいか
分からなくなるようだ。
その意味で、定数項を引き算で消して中学校で学んだ2元1次の連立方程式の形に誘導す
る現行の教え方は一見理にかなっているように見える。しかし、2次関数を離れた単元で、一
般の3元1次連立方程式が現れた場合によく見受けられることだが、加減法をよく理解しない
まま、式同士を闇雲に引き算して収拾がつかなくなってしまうことが度々ある。これも、3元1次
連立方程式を特殊な場合のみに限定して教えている一種の功罪といえると思う。
このような問題に対して、次のようなエレガントな解法が知られている。
2点A(1,−3)、B(−2,0)を通る直線の方程式は、 y=−x−2 なので、
求める放物線の方程式は、 y=a(x−1)(x+2)−x−2 とおける。
この放物線が、点C(3,15)を通るので、 10a−5=15 より、 a=2
したがって、求める放物線の方程式は、 y=2(x−1)(x+2)−x−2=2x2+x−6
(コメント) この解法だと、暗算でも求められるような予感...。
(補足) 平成18年12月7日付けで、「magata」様より、「具体的に詳しい解法を教えてい
ただけないか」というメールを頂いた。ただ、メールの送信日が、平成18年1月23日
で、ちょっと怪しさを感じたので、メールでの返信はせず、HP上で回答することにした。
上記のエレガントな解法のポイントは、x 軸と2点(1,0)、(−2,0)で交わる放物線の方
程式が、y=a(x−1)(x+2) と書けることだろう。あとは、この放物線を平行移動して、2点
A(1,−3)、B(−2,0)を通るようにすればよい。
その部分が、 y=a(x−1)(x+2) に −x−2 を加えたところである。
(コメント) 一つの幾何的現象を代数的に数式化できるところがおもしろいですね!
当HPがいつもお世話になっているHN「FN」さんが、例3に関連する話題を考察された。
(平成23年9月13日付け)
3次関数の場合を考えてみよう。
f(-1)=-12 、f(1)=-2 、f(2)=3 、f(3)=16 を満たす3次関数を求めよ。
2次関数の場合を一般の形で書くと、
x1、x2、x3 を相異なる数とする。f(x1)=y1 、f(x2)=y2 、f(x3)=y3 を満たす2次以
下の関数 f(x) を求めよ。
上記は、次のように解いたことになります。
g(x1)=y1 、g(x2)=y2 を満たす2次以下の関数を1つ求める。2次関数でもいいが、普通
は、1次関数で求める。即ち、2点を通る直線である。
h(x1)=0 、h(x2)=0 を満たす2次関数を1つ求める。h(x)=(x-x1)(x-x2) でいい。
そこで、 f(x)=g(x)+k・h(x) とおく。これは、f(x1)=y1 、f(x2)=y2 を満たす2次以下の関数
である。しかも、f(x1)=y1 、f(x2)=y2 を満たす2次以下の関数はすべてこの形で得られる。
(f(x)-g(x)を考えればすぐわかる)
あとは、f(x3)=y3 を満たすように、k を決めればよい。(kは一意的に存在する。)
3次関数の場合を、2次関数の場合と全く同じように解くなら次のようになります。
まず、3次関数の場合を一般の形で書くと、
x1、x2、x3、x4 を相異なる数とする。f(x1)=y1 、f(x2)=y2 、f(x3)=y3 、f(x4)=y4
を満たす3次以下の関数 f(x) を求めよ。
g(x1)=y1 、g(x2)=y2 、g(x3)=y3 を満たす3次以下の関数を1つ求める。普通は、2次関
数で求めるでしょうが、これは2次関数の場合を解くことになります。
(だから、それなりに一人前の問題です)
h(x1)=0 、h(x2)=0 、h(x3)=0 を満たす3次関数を1つ求める。h(x)=(x-x1)(x-x2)(x-x3)
でいい。そこで、 f(x)=g(x)+k・h(x) とおく。以下同様である。
この解法で、g(x) が求まったあとは問題ないですが、g(x) を求めるのが面倒です。だから、
2次関数のときの方法を忠実にまねるより中途半端にまねたほうがいいようです。
g(x1)=y1 、g(x2)=y2 を満たす2次以下の関数を1つ求める。もちろん1次関数でよい。
h(x1)=0 、h(x2)=0 を満たす2次関数を1つ求める。h(x)=(x-x1)(x-x2) でいい。
(ここまで、2次関数の場合と全く同じです。従って、この方が2次関数のときの方法の忠実
な真似だとも言えます。ただし本質的な真似ではなく表面的な真似ですが。)
f(x)=g(x)+k・h(x) とおいたのでは2次関数にしかならないので、定数 k の代わりに、1次
関数をとって、 f(x)=g(x)+(ax+b)h(x) とおく。
これが、f(x3)=y3 、f(x4)=y4 を満たすように、a、b を定める。
理論的には前者の方がいいでしょうが、実際に解くなら、後者の方がいいと思います。た
だし、前者は連立方程式の回避になりますが、後者はなりません。後者で解いておきます。
多少表現は変えます。
g(-1)=-12 、g(1)=-2 を満たす1次関数を求めると、 g(x)=5x-7
P(x)=f(x)-g(x) は、P(-1)=0 、P(1)=0 を満たす3次関数であるから
P(x)=(ax+b)(x+1)(x-1) とかける。 すなわち、 f(x)=(ax+b)(x+1)(x-1)+5x-7
ここで、 f(2)=3 、f(3)=16 より、 (2a+b)・3+3=3 、(3a+b)・8+8=16 なので、
2a+b=0 、3a+b=1
これを解いて、 a=1 、b=-2 より、 f(x)=(x-2)(x2-1)+5x-7=x3-2x2+4x-5
一般に、連立方程式の回避にはあまりこだわらない方がいいようです。
(コメント) f(-1)=-12 、f(1)=-2 、f(2)=3 、f(3)=16 を満たす3次関数を求めよ。
とのFNさんの問題設定ですが、2次関数であれ、3次関数であれ、ラグランジュの補間公式
を用いれば、関数は一気に求められます。「ちょっと、銀行に行ってから〜」と思って、午後か
ら続きをやろうと考えていたら、攻略法さんに「ニュートンの多項式補間公式」で先を越され
てしまいました!(→ 参考:「関数の補間」)
攻略法さんが例3について考察されました。(平成23年9月13日付け)
3点A(1,−3)、B(−2,0)、C(3,15)を通る放物線の方程式を求めよ。
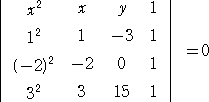
より、 -60x2 - 30x + 30y + 180 = 0 なので、 2x2 + x - y - 6 = 0
f(-1)=-12 、f(1)=-2 、f(2)=3 、f(3)=16 を満たす3次関数を求めよ。
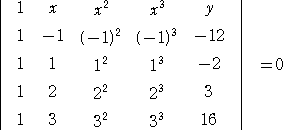
を展開すれば求まると思います。
(コメント) 攻略法さんは、上記の行列式の計算を「厳しいですね。」と仰っていますが、実
際にやってみると、そんなでもないです...f(^_^;)
行列式の基本公式を用いて、 4(x - 1) - (2(x2 - 1) + y + 2 - (x3 - 1)) = 0
すなわち、 y=x3-2x2+4x-5 となる。
攻略法さんは、上記の行列式の計算を回避するために、ニュートンの多項式補間公式を
使って解かれました。この考え方は、FNさんの解法の基本でもある。
題意より、 y0=f(x0)=f(-1)=-12 y1=f(x1)=f(1)=-2 y2=f(x2)=f(2)=3 y3=f(x3)=f(3)=16
これより、 f0(x)=c0=f(-1)=-12
f1(x)=f0(x)+c1(x-x0)=(-12)+c1(x+1)
(-12)+c1(x1+1)=y1 より、c1=5 なので、 f1(x)=-12+5(x+1)=5x-7
f2(x)=f1(x)+c2(x-x0)(x-x1)=(5x-7) + c2(x+1)(x-1)
(5x2-7) + c2(x2+1)(x2-1)=y2 より、c2=0 なので、 f2(x)=5x-7
f3(x)=f2(x)+c3(x-x0)(x-x1)(x-x2)=(5x-7) + c3(x+1)(x-1)(x-2)
(5x3-7) + c3(x3+1)(x3-1)(x3-2)=y3 より、c3=1 なので、
f3(x)=x3-2x2+4x-5 ←求める3次関数
※数値計算としては、次のような表をつくって計算します。
-1 -12 ← c0
(-2-(-12))/(1-(-1))=5 ← c1
1 -2 (5-5)/(2-(-1))=0 ← c2
(3-(-2))/(2-1)=5 (4-0)/(3-(-1))=1 ← c3
2 3 (13-5)/(3-1)=4
(16-3)/(3-2)=13
3 16
上記の計算を補足すると、
f(x)=c0+c1(x-x0)+c2(x-x0)(x-x1)+c3(x-x0)(x-x1)(x-x2)+・・・ において、
c0=c0[x0]=f(x0)=-12
c1=c1[x0,x1]=(c0[x1]-c0[x0])/(x1-x0)={f(x1)-f(x0)}/(x1-x0) なので、
c1=(-2+12)/(1-(-1))=5
c2=c2[x0,x1,x2]=(c1[x1,x2]-c1[x0,x1])/(x2-x0) において、
c1[x1,x2]=(3-(-2))/(2-1)=5 c1[x0,x1])=5 より、 c2=(5-5)/(2-(-1))=0
c3=c3[x0,x1,x2,x3]=(c2[x1,x2,x3]-c2[x0,x1,x2])/(x3-x0) において、
c2[x1,x2,x3]=(c1[x2,x3]-c1[x1,x2])/(x3-x1)={(16-3)/(3-2)-(3-(-2))/(2-1)}/(3-1)=4
c2[x0,x1,x2]=0 より、 c3=(4-0)/(3-(-1))=1
以上から、 f(x)=-12+5(x+1)+(x+1)(x-1)(x-2)=x3-2x2+4x-5 となる。
FNさんからのコメントです。(平成23年9月13日付け)
攻略法さんがされていることは、連立方程式の回避をさらに進めて、方程式の回避ですね。
方程式を解くことすらやめていきなり答えを出そうということのようです。確かに問題によって
は、公式に代入して直接答えを出すのが適切です。しかし、問題が複雑になれば、当然に複
雑になります。行列式とかを使って一応書けたとして、それを具体的に書き下すとなると、か
なりの計算です。
ニュートンの多項式補間公式というのは役に立ちそうですね。私が忠実な真似として書いた
のが、f2(x)を求めにいくやり方で、中途半端な真似として書いたのが、f1(x)を求めにいくやり
かたのようです。問題を適当に書いたので、f1(x)=f2(x)となってしまいました。
ラグランジュの補間公式は、一発で答えをとりあえず書けますが、実際に手計算をやる気
力のある人はあまりいないのではないかと思います。少なくとも、私はやる気力はありませ
ん。ニュートンの多項式補間公式ならできそうです。これは方程式は避けてません。やはり
ある程度以上の問題で方程式を完全に避けると、計算が大変なことになるようです。
FNさんからの続報です。(平成23年9月24日付け)
f(-1)=-12 、f(1)=-2 、f(2)=3 、f(3)=16 を満たす3次関数を求めよ。
これを、ラグランジュの補間公式でやってみました。
(解) (x-1)(x-2)(x-3)/(-24)・(-12)+(x-2)(x-3)(x+1)/4・(-2)
+(x-3)(x+1)(x-1)/(-3)・3+(x+1)(x-1)(x-2)/8・16
=(x3-6x2+11x-6)/2-(x3-4x2+x+6)/2-(x3-3x2-x+3)+2(x3-2x2-x+2)
=x3-2x2+4x-5 (終)
私が適当に作った問題ですが、不思議に簡単な係数になって、以外と簡単にできました。
上のf(x)に1だけ足した次の問題だったら、かなり面倒だったでしょう。
f(-1)=-11 、f(1)=-1 、f(2)=4 、f(3)=17 を満たす3次関数を求めよ。
これなら、2行目の式は次のようになります。
=(11/24)(x3-6x2+11x-6)-(1/4)(x3-4x2+x+6)-(3/4)(x3-3x2-x+3)+(17/8)(x3-2x2-x+2)
あまりやりたくない式ですが、できないことはありません。ラグランジュの補間公式を具体
的な問題で使うことは一生に一度で十分です。以後使うことはないでしょう。もちろんラグ
ランジュの補間公式の理論的面白さを否定するものでは全くありません。
未知数 0 個とか、f(x)=ax3+bx2+cx+d とおく未知数4個とかの両極端はあまりよくありま
せん。やはり中庸が妥当でしょう。
(コメント) 「過ぎたるは及ばざるが如し」ですかね...。
例4 ・・・ 多項式の整除問題(1)
現行の学習指導要領では「数学II 」で学ぶ多項式の整除問題であるが、以前に比べて
その内容は相当に軽減されている。これからの学習の計算の基礎になる部分なのに、こ
んな軽い扱いでいいのかな?といつも疑問に思う。計算力をしっかり身につけるチャンス
なのに、教科書等の問題の絶対量は少なく、プリント等でいくつかを補充して、次の単元
に行かなければならないのが気にかかる。学習指導要領全体が「学習者の負担の軽減」
という流れになっており、複雑な計算を忌避する傾向になっていることは否めない。
「整式」という言葉は最近使われなくなりつつある。「多項式」という言葉で統一すること
にしよう。
多項式 P(x) を、x+1 で割った余りは −3、(x−1)2 で割った余りは 2x+3
であるという。このとき、多項式 P(x) を、(x+1)(x−1)2 で割った余りを求めよ。
教科書的には通常、次のように解かれる。
多項式 P(x) を、(x+1)(x−1)2 で割った余りは高々2次式なので、ax2+bx+c と
おかれる。即ち、商を Q(x) とおくと、P(x)=(x+1)(x−1)2Q(x)+ax2+bx+c
問題の条件から、 a−b+c=−3 、 2a+b=2 、 −a+c=3
これらを解いて、 a=−1 、b=4 、c=2 となるので、求める余りは、−x2+4x+2
このような解法に対して、次のような鮮やかな別解が知られている。
多項式 P(x) を、(x−1)2 で割った商をQ(x) とおくと、問題の条件より、
P(x)=(x−1)2Q(x)+2x+3
と書ける。 商Q(x) を、x+1 で割った商をQ’(x)、余りを k とおくと、
Q(x)=(x+1)Q’(x)+k
と書ける。 これを上式に代入して、P(x)=(x+1)(x−1)2Q’(x)+k(x−1)2+2x+3
剰余の定理から、 P(−1)=−3 であるので、 4k+1=−3 より、k=−1
よって、求める余りは、 −(x−1)2+2x+3=−x2+4x+2
(コメント) 私自身、この別解を高校1年のときに知って非常に感動したことを今でも覚え
ている。ただ、「商を割る」という発想が馴染めず苦労する人がいるかもしれない。
「商を割る」という発想は、微分法における有名な公式 :
多項式 P(x) を (x−α)2 で割った余りは、 P’(α)(x−α)+P(α)
特に、多項式 P(x) が (x−α)2 で割りきれるための必要十分条件は、
P’(α)=0 、 P(α)=0
に相通じるものがある。
すなわち、 P(x)=(x+1)(x−1)2Q(x)+ax2+bx+c を (x−1)2 で割った余りは、
ax2+bx+c を (x−1)2 で割った余りに等しい。
よって、ax2+bx+c−(2x+3)=ax2+(b−2)x+c−3 が (x−1)2 で割りきれるの
で、 a+b+c−5=0 、 2a+b−2=0
これより、 b=2−2a 、 c=a+3 なので、
ax2+bx+c=ax2+(2−2a)x+a+3=a(x−1)2+2x+3
となる。
(コメント) このような面倒な計算と対比すれば、「商を割る」という発想がいかに素晴らしい
ものであるかが実感できるだろう。
当HPがいつもお世話になっているHN「FN」さんが、例4に関連する話題を考察された。
(平成23年9月18日付け)
多項式 P(x) を、x+1 で割った余りは −3、(x−1)2 で割った余りは 2x+3
であるという。このとき、多項式 P(x) を、(x+1)(x−1)2 で割った余りを求めよ。
・・・・・・・・・(A)
整数における同じタイプの問題と対比させながら考えてみよう。
整数Pを5で割ると余りは2、7で割ると余りは3であるという。このとき、整数Pを35
で割った余りを求めよ。・・・・・・・・・(B)
まず、(B)を考える。「整数Pを5で割ると余りは2」を式で書くと、 P=5Q+2
求めたいのは、Pを35で割った余りだから、 P=35X+Y の形の式が欲しい。
そこで、Qを7で割った余りをRとして、 Q=7S+R とおく。これを代入して、
P=5(7S+R)+2=35S+5R+2
ここで、Pを7で割ると、余りは3だから、5R+2を7で割ると余りは3、即ち、5Rを7で割
ると余りは1となる。Rは、0、1、2、3、4、5、6 のどれかだから、順に調べると、R=3
よって、求める余りは、 5R+2=17 である。
「5で割ると余りは2」と「7で割ると余りは3」は、ほぼ対等であるが、(前者が1/5に絞るの
に対し後者は1/7に絞る。一般にきつい条件を使って式を書く方がいいので、後者から出発
する方が少し良かった)
「x+1で割ると余りは、-3」と「(x-1)2で割ると余りは、2x+3」は対等ではない。当然、後者が
重要でこちらを使って式を書く。
P(x)=(x-1)2Q(x)+2x+3 において、(x+1)(x-1)2 で割った余りを求めるから、Q(x)を x+1
で割った余りが必要になる。そこで、 Q(x)=(x+1)S(x)+R とおく。
これを代入して、 P(x)=(x-1)2(x+1)S(x)+(x-1)2R+2x+3
「x+1で割ると余りは、-3」は、P(-1)=-3 だから、上の式に、x=-1 を代入して...。
(以下、例4の解答と同じです。)
数値代入という手があるから、こちらの方が易しいような気もするが、整数の方は有限個
を調べればいいので、この方が楽なのかもしれない。似たようなものなのでしょう。
整数環に比べて、多項式環は取り扱い安い印象がある。余りを ax2+bx+c と置くなどと
いう安易な手があるから、下手なやりかたでもできてしまう。これが幸せなことか不幸せなこ
とかはわかりません。
類題として次の問題を考えます。
整式 P(x) を (x-1)(x+2) で割った余りは -x-2、P(x) を x-3 で割った余りは 15
である。このとき、P(x) を (x-1)(x+2)(x-3) で割った余りを求めよ。
もちろん全く同じやり方でできます。では、次の問題を考えます。
整式 P(x) を x-1 で割った余りは -3、x+2 で割った余りは 0、x-3 で割った余りは
15 である。このとき、P(x) を (x-1)(x+2)(x-3) で割った余りを求めよ。
これが、上の問題とほぼ同じであることは容易に確認できるでしょう。(整式P(x)を x-1で割
った余りが-3、x+2 で割った余りが 0 のとき、P(x)を (x-1)(x+2) で割った余りを求めよ、とい
う問題が間にある)
これが、次の問題とほぼ同じであることもすぐにわかるでしょう。
f(1)=-3、f(-2)=0、f(3)=15 を満たす2次以下の整式 f(x) を求めよ。
そして、これは例3と同じです。だから、例3と例4は親戚です。遠い親戚と考えるか、近い
親戚と考えるか、それが問題です。
当HPがいつもお世話になっているHN「攻略法」さんからのコメントです。
(平成23年9月22日付け)
問題 多項式 f(x) を、x−α で割った余りは f(α)、x−β で割った余りは f(β) と
するとき、多項式 f(x) を、(x−α)(x−β) で割った余り ax+b を求めよ。
(解) f(x)を x-α で割った余りは、f(α) より、f(x)=(x-α)Q(x)+f(α) とおける。
Q(x) を x-β で割ったとき、商を S(x)、余りを R とすると、Q(x)=(x-β)S(x)+R とおける。
よって、f(x)=(x-α){(x-β)S(x)+R}+f(α)=(x-α)(x-β)S(x)+(x-α)R+f(α)
f(x) を x-β で割った余りは、f(β) より、 f(β)=(β-α)R+f(α)
よって、 R=(f(β)-f(α))/(β-α) なので、余りは、{(f(β)-f(α))/(β-α)}(x-α)+f(α)
となる。 (終)
(参考) これは、2点(α,f(α))、(β,f(β)) を通る直線の方程式に対応する。
(余談) 連立方程式なら、f(x)=(x-α)(x-β)Q(x)+ax+b とおいて、
f(x) を x-α で割った余りは、f(α) より、 f(α)=aα+b
f(x) を x-β で割った余りは、f(β) より、 f(β)=aβ+b
から、a、bを求めればよい。
ところで、求めた余りの式(直線の方程式)は、
{(x-α)/(β-α)}f(β) + {(x-β)/(α-β)}f(α) ←式1
と変形できる。同様にして、
問題 多項式 f(x) を、x−α で割った余りは f(α)、x−β で割った余りは f(β)、
x−γ で割った余りは f(γ) とするとき、多項式 f(x) を、
(x−α)(x−β)(x−γ) で割った余り ax2+bx+c を求めよ。
は、3点(α,f(α))、(β,f(β))、(γ,f(γ)) を通る放物線の方程式に対応する。
具体的に、a、b、c を求めてみる。
(解) f(x) を x-α で割った余りは、f(α)、f(x) を x-β で割った余りは、f(β) なので、
f(x) を (x-α)(x-β) で割った余りは、上記の問題より、
f(x)=(x-α)(x-β)Q(x)+{(f(β)-f(α))/(β-α)}(x-α)+f(α)
Q(x) を x-γ で割ったとき、商を S(x)、余りを R とすると、Q(x)=(x-γ)S(x)+Rとおける。
よって、 f(x)=(x-α)(x-β){(x-γ)S(x)+R}+{(f(β)-f(α))/(β-α)}(x-α)+f(α) より、
f(x)=(x-α)(x-β)(x-γ)S(x)+(x-α)(x-β)R+{(f(β)-f(α))/(β-α)}(x-α)+f(α)
f(x) を x-γ で割った余りは、f(γ) より、
f(γ)=(γ-α)(γ-β)R+{(f(β)-f(α))/(β-α)}(γ-α)+f(α)
よって、 R=f(α)/{(α-β)(α-γ)} +f(β)/{(β-α)(β-γ)} +f(γ)/{(γ-α)(γ-β)}
これより、放物線の方程式が求まる。ところで、求めた余りの式(放物線の方程式)は、
{ (x-γ)(x-α)/{(β-γ)(β-α)} }f(β)+{ (x-β)(x-γ)/{(α-β)(α-γ)} }f(α)
+{ (x-α)(x-β)/{(γ-α)(γ-β)} }f(γ) ←式2
と変形できる。式1、式2は、ラグランジュの補間公式である。
FNさんからのコメントです。(平成23年9月23日付け)
「 {(f(β)-f(α))/(β-α)}(x-α)+f(α) は、2点(α,f(α))、(β,f(β)) を通る直線の方程
式に対応する。」
について、例4のタイプで1番簡単な上記の問題と例2は同じになりますね。
(1) 2点 (1,3)、(2,5) を通る直線の方程式を求めよ。
(2) 整式 P(x) を x-1 で割ると余りは 3、x-2 で割ると余りは 5 である。
整式 P(x) を (x-1)(x-2) で割ったときの余りを求めよ。
(1)を連立方程式で解くのは中学生で、高校生以上なら邪道です。(2)は余りを ax+b とお
いて、連立方程式を解くのが普通です。だから、親戚ではあるけど、それほど近い親戚でも
ないようです。(2)を(1)に還元させることにより、方程式なしで解いてみます。
(解) まず、2点 (1,3)、(2,5) を通る直線の方程式を求める。
傾きが2で、 (1,3)を通るから、 y-3=2(x-1) より、 y=2x+1
だから、 f(x)=2x+1 とおくと、 f(1)=3 、f(2)=5
また、剰余定理より、 P(1)=3 、P(2)=5 従って、 g(x)=P(x)-f(x) とおくと
g(1)=P(1)-f(1)=3-3=0 、g(2)=P(2)-f(2)=5-5=0
因数定理より、g(x)は、x-1、x-2 で割り切れるから、(x-1)(x-2)で割り切れる。
g(x)=(x-1)(x-2)Q(x)とかける。P(x)=g(x)+f(x)であるから、P(x)=(x-1)(x-2)Q(x)+2x+1
よって、求める余りは、2x+1 (終)
普通に解くよりはるかに長くなっています。従って、実用性はありません。f(x)が求まったあ
との5行が、(1)と(2)の距離をあらわします。これはちょっと丁寧に書きすぎで、5行は3行ぐら
いになるでしょう。今は1次式ですが、次数が上がっても、(1)と(2)の距離は変わりません。
次数があがれば、近い親戚と言えそうです。
例5 ・・・ 多項式の整除問題(2)
例1から例4まで、連立方程式からの回避策をいろいろ見てきたが、いつもそのような考
え方で上手くいくわけではないことを指摘しておかなければならない。
このことを理解するには、次の問題を考えてみればよいだろう。
関数 y=x4−3x2+2x のグラフ上の異なる2点で接する接線の方程式を求めよ。
この問題に対して、「連立方程式の回避」を念頭に置くと次のような解になる。
接点( t ,t4−3t2+2t )における接線の方程式は、
y=(4t3−6t+2)(x−t)+t4−3t2+2t=(4t3−6t+2)x−3t4+3t2
よって、 x4−3x2+2x=(4t3−6t+2)x−3t4+3t2 すなわち、
x4−3x2−(4t3−6t)x+3t4−3t2=0
この方程式は、x=t を重解として持つので、(x−t)2(x2+2tx+3t2−3)=0
問題の条件から、 2次方程式 x2+2tx+3t2−3=0 は重解を持つ。
よって、判別式をDとおくと、 D/4=t2−(3t2−3)=−2t2+3=0 より、t2=3/2
これを接線の式に代入して、 y=2x−9/4 となる。
このような問題に対して上記のように解くよりも、次のように解く方が断然楽だろう!
求める接線の方程式を、 y=mx+n とおくと、
x4−3x2+2x=mx+n すなわち、 x4−3x2+(2−m)x−n=0
は重解を2つ持つ。 それを、α、β とおくと、
x4−3x2+(2−m)x−n=(x−α)2(x−β)2
と書ける。
右辺=(x2−(α+β)x+αβ)2
=x4−2(α+β)x3+(α+β+2αβ)x2−2αβ(α+β)x+α2β2
なので、両辺の係数を比較して、
α+β=0 、 α+β+2αβ=−3 、 −2αβ(α+β)=2−m 、 α2β2=−n
よって、 αβ=−3/2 より、 m=2 、 n=−9/4 より、
求める接線の方程式は、 y=2x−9/4 となる。
(コメント) 「どちらかの解法を選べ!」と言われたら、迷うことなく後者でしょう...ネ!
当HPがいつもお世話になっているHN「FN」さんが、例5について考察された。
(平成23年9月11日付け)
例5の2番目の解で、x4−3x2+(2−m)x−n=(x−α)2(x−β)2 としたあとについて
です。4次方程式の解と係数の関係は普通は扱わないですが、解の和と解の積については
すぐわかるので、2α+2β=0 即ち、β=−α がでます。
「解と係数の関係より」とも書きにくいので、「x3 の係数を比較して」と書くでしょうが...。
これで、 x4−3x2+(2−m)x−n=(x−α)2(x−β)2=(x2−α2)2=x4−2α2x2+α4
となり、 3=2α2 、2−m=0 、−n=α4
これは、事実上、連立方程式ではなくなっています。これで、一応連立方程式の回避はで
きたと言ってもいいでしょう。
4次関数の複接線の問題では、計算量に対する配慮から、x3 の項をなしにしてくれる場合
が多いように思います。そのときは、β=−α を出してから展開するほうがいいと思います。
(→ 関連話題)
(追記) 令和2年8月3日付け
小金澤 貴弘 著 「複接線定理」 数研通信 No.97(数研出版)において、次の定理が
紹介されている。
複接線定理 複接線を持つ4次関数 y=F(x) において、F'''(x)=0 となる値を
x=γとすると、複接線の傾きは、F’(γ)である。
(証明) 複接線の方程式を y=mx+n とすると、題意より、
F(x)=k(x−α)2(x−β)2+mx+n (k≠0) とおける。
このとき、
F’(x)=k{2(x−α)(x−β)2+2(x−α)2(x−β)}+m
=2k(x−α)(x−β)(2x−α−β)+m
F”(x)=2k{(x−β)(2x−α−β)+(x−α)(2x−α−β)+2(x−α)(x−β)}
F'''(x)=2k{(2x−α−β)+2(x−β)+(2x−α−β)+2(x−α)+2(x−α)+2(x−β)}
=12k(2x−α−β)
よって、 F'''(x)=0 から、 γ=(α+β)/2 なので、 m=F’(γ) (証終)
この定理を、
関数 y=x4−3x2+2x のグラフ上の異なる2点で接する接線の方程式を求めよ。
の複接線の問題に適用してみよう。
(解) y’=4x3−6x+2 、y”=12x2−6 、y'''=24x=0 から、 x=0
よって、複接線の方程式 y=mx+n において、 m=2 であることが分かる。
このとき、 x4−3x2+2x=2x+n すなわち、x4−3x2−n=0 は、異なる2つの2重解
を持ち、完全平方式となる。 x2=t とおくと、 t2−3t−n=0 は重解を持つ。
よって、 判別式 D=9+4n=0 から、 n=−9/4
以上から、複接線の方程式は、 y=2x−9/4 となる。 (終)
例6 ・・・ 三角形の外接円
三角形の外接円を求める問題は、同一直線上にない3点から等距離にある点の計算な
ど、その応用は幅広い。
平面上の3点A(1,0)、B(3,2)、C(−1,6)において、△ABCの外接円の方程
式を求めよ。また、△ABCの外心の座標を求めよ。
教科書の場面場面でその解法は異なると思うが、だいたい次の2種類にまとめられるだ
ろう。
(円の方程式の利用) 求める外接円の方程式を、 x2+y2+ax+by+c=0 とおく。
3点A、B、C を通ることから、
1+a+c=0 、 13+3a+2b+c=0 、 37−a+6b+c=0
これらより、まず c を消去して、 6+a+b=0 、 18−a+3b=0
よって、 a=0 、b=−6 、c=−1 となり、外接円の方程式は、x2+y2−6y−1=0
ここで、 x2+(y−3)2=10 より、 外心の座標は、(0,3) である。
(距離の公式の利用) 求める外心の座標を、 (a,b) とすると、3点A、B、C から等
距離にあるので、(a−1)2+(b−0)2=(a−3)2+(b−2)2=(a+1)2+(b−6)2
よって、2式同士を組み合わせて、 a+b=3 、a−b=−3
これを解いて、 a=0 、 b=3 なので、外心の座標は、(0,3) となる。
このとき、外接円の半径の平方は、 (0−1)2+(3−0)2=10
よって、求める外接円の方程式は、 x2+y2−6y−1=0 である。
上記では、3元、2元の違いはあるものの、結局はその解法を連立方程式の解法に帰着
させている。
これに対して、次のような解法は如何だろうか?
線分ABの垂直2等分線は、 y=−x+3 で、線分BCの垂直2等分線は、 y=x+3
この2直線の交点が外心であるので、その座標は、(0,3) となる。
このとき、外接円の半径の平方は、 (0−1)2+(3−0)2=10
よって、求める外接円の方程式は、 x2+y2−6y−1=0 である。
(コメント) この別解も結局は連立方程式であるが、計算の負担は軽くなっていると思う。
当HPがいつもお世話になっているHN「FN」さんが、例6について考察された。
(平成23年9月10日付け)
例6において、
解1(円の方程式の利用) 、解2(距離の公式の利用) 、解3(垂直2等分線の利用)
の3通りの解が示してあります。解1が円の方程式を x2 + y2 + ax + by + c = 0 (A) と置
くのに対して、解2、解3は、(x-a)2+(y-b)2=r2 (B) と置くのに相当します。解2でも、r は置
いてないし、解3は、a、bも置いてませんが...。
(A)と(B)とどちらがいいかは状況によるので一概には言えませんが、一般に計算だけでや
るなら(A)、図形的な性質も使うなら(B)かなと思います。この問題なら(A)でいいように思いま
す。
解1、2、3 ともに連立方程式の回避にはなってません。例3と似たような考え方で連立方
程式の回避ができます。そのためには、2点を通る円の方程式が必要です。
そのために、まず、2点を通る円を1つ求めます。2点を直径の両端とする円が一番求め
やすいでしょう。
ABを直径とする円は、中心がABの中点(2,1)で、半径は
即ち、x2+y2-4x-2y+3=0 次に、直線ABの方程式を求めます。y=x-1 即ち、x-y-1=0
(これは、2点A、Bを通る半径∞の円と考えることもできます。とすれば、2つの特殊解を求
めたと言えます)
x2+y2-4x-2y+3+k(x-y-1)=0 が、2点A、Bを通る円であることはすぐにわかります。
また、2点A、Bを通る円がすべてこの形で得られることも容易にわかります。あとは、これ
が、Cを通ることから、k を決めれば終わりです。ただし、k がきれいな数にならなかったら
残務処理がやや面倒ですが...。
C(-1,6) を通ることより、1+36+4-12+3+k(-1-6-1)=0 なので、 32=8k よって、 k=4
このとき、 x2+y2-4x-2y+3+4x-4y-4=0 より、 x2+y2-6y-1=0 即ち、x2+(y-3)2=10
これは、連立方程式の回避にはなっています。解1でいいと思いますが...。
(コメント) 確かに、解1、2、3 ともに連立方程式の回避にはなってませんね!問題の特
殊性に胡座をかいていました。FNさんの解は見事に連立方程式の回避にはなっ
ています。FNさんに感謝します。
FNさんからの続報です。(平成23年9月12日付け)
連立方程式の回避にはなりませんが、2点を通る円ではなく、1点を通る円を使う方法も
あります。この方がいいような気もします。
曲線 ( x - 1 )( x - a ) + y( y - b ) = 0 は円であり、かつ、点Aを通る。
これがBを通ることより、 2( 3 - a ) + 2( 2 - b ) = 0 より、 6 - 2a + 4 - 2b = 0
すなわち、 a + b = 5
Cを通ることより、 -2( -1 - a ) + 6( 6 - b ) = 0 より、 2 + 2a + 36 - 6b = 0
すなわち、 a - 3b = -19
これを解いて、 a = -1 、b = 6 なので、 ( x - 1 )( x + 1 ) + y( y - 6 ) = 0
すなわち、 x2 + y2 - 6y - 1 = 0
本当は、
点Aを通る円がすべて ( x - 1 )( x - a ) + y( y - b ) = 0 の形で書ける
ことも示しておく方がいいでしょう。
x2 + y2 + px + qy + r = 0 において、x2 + px を x - 1で割ったときの商を x - a とし、
y2 + qy を y で割ったときの商を y - b とおいたということです。あとは定数の処理だけで
すが、点Aを通ることから定数は、0 になります。
図形的には、Aを一方の端とする直径のもう一方の端を D(a,b) と置いたということです。
それで、APとDPが垂直、即ち、内積=0 を式に書いたものです。
この考え方で、上記に書いた2点を通る円を使う方法も少し変えることができます。
平面上の3点A(1,0)、B(3,2)、C(−1,6)において、△ABCの外接円の方程
式を求めよ。また、△ABCの外心の座標を求めよ。
曲線 (x-1)(x-3)+y(y-2)=0 は円であり、かつ、2点A、Bを通る。これはもちろん、ABを直
径とする円ですが、そのことは不要です。単に、2点A、Bを通る1つの円であることだけで
十分です。あとは、直線ABの方程式を求めて以下同様にします。
これは連立方程式の回避になっています。
当HPがいつもお世話になっているHN「攻略法」さんから別解を頂きました。
(平成23年9月12日付け)
公式に数値を当てはめてみました。
3点を通る円の方程式は、行列式
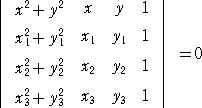
で表される。3点A(1,0)、B(3,2)、C(−1,6)を代入して、
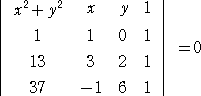
より、 x2 + y2 - 6y - 1 = 0
当HPがいつもお世話になっているHN「よおすけ」さんから別解を頂きました。
(平成24年12月13日付け)
座標平面上の3点A(1,0)、B(3,2)、C(−1,6)は、複素数平面上ではそれぞれ、
A(1)、B(3+2i)、C(-1+6i) に対応する。異なる3点A(α)、B(β)、C(γ)から等距離にある点を
zとすると、
α×conjgα(β-γ)+β×conjgβ(γ-α)+γ×conjgγ(α-β)
z=--------------------------------------------------------
conjgα(β-γ)+conjgβ(γ-α)+conjgγ(α-β)
※ 上式は、|z-α|2=|z-β|2、|z-α|2=|z-γ|2 を連立して解き、conjgzを消去して、zについ
ての式に整理すれば得られます。
ここで、1、3+2i 、-1+6i の共役複素数はそれぞれ 1、3-2i、-1-6i だから、それぞれ z の式
に代入して計算すれば、3点A、B、Cから等距離の点は、z=3i
これは、座標平面では、点(0,3)に対応する。また、点(1)と中心点(3i)との距離は√10より、
半径は√10
まとめて、外接円の方程式は、x2+(y-3)2=10 で、3点A、B、Cから等距離の点(外心)は、
(0,3)である。
よおすけさんから、例6の話題について、練習問題を頂きました。
(平成24年3月28日付け)
3点A(-3,3)、B(2,-2)、C(-3,-7)を通る円の方程式を求めよ。
とりあえず、自分の略解です。例6に倣えば、
円の方程式 x2+y2+ax+by+c=0 が、点A、B、Cをそれぞれ通ることから、
9+9-3a+3b+c=0 より、 -3a+3b+c=-18
4+4+2a-2b+c=0 より、 2a-2b+c=-8
9+49-3a-7b+c=0 より、 -3a-7b+c=-58
これらを解けば、a=6、b=4、c=-12 となり、求める式は、 x2+y2+6x+4y-12=0
となります。実をいうと、この3点は・・・おっと、これは見ておられる方の練習問題とします。
らすかるさんからのコメントです。(平成24年3月28日付け)
ACの中点Mは、(-3,-2)で、AM=BM=CM=5 だから、 (x+3)2+(y+2)2=52
よおすけさんからのコメントです。(平成24年3月28日付け)
らすかるさん、ありがとうございます。先程言いかけたのは、この3点で作られる三角形は、
AB=BC、∠B=90°の直角二等辺三角形で、ACがそのまま円の直径になります。
(コメント) まさに、数学は「図が命!」の典型例ですね。図を描くことにより、連立方程式の
回避が瞬時に解決します。
例7 ・・・ 2直線の交点
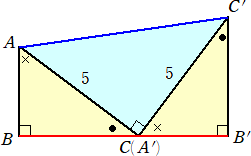
図形問題におけるベクトルの有効性は確かであるが、やはり、その解法にもいくつかの
分かれ目が存在する。
例えば、大学入試センター試験にも頻出の次のような問題について検討してみよう。
△ABCの辺ABを2:1の比に内分する点をD、辺ACを3:2に内分する点をEとし、
線分CDとBEの交点をPとする。直線APと辺BCの交点をFとするとき、
(1) AP : PF (2) BF : FC
をそれぞれ求めよ。
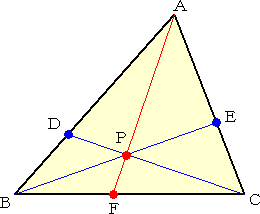
教科書を始めとして、通常は次のように解かれる。これは、ベクトルの一次独立を利用
する解法である。
(学習指導要領において「ベクトルの一次独立」は学習内容には含まれず、教科書等でも参考・発展の扱いに
なっている。したがって、教科書本文で堂々と「一次独立」という言葉は用いられず、「2つのベクトルは平行で
ないから」という物言いになっている。)
以下の解答において、ベクトルを太字で表すことにする。
AB=3a 、AC=5b とおく。 BP : PE = s : 1−s 、CP : PD = t : 1−t と
おくと、 AP=(1−s)AB+sAE=3(1−s)a+3sb
同様にして、 AP=tAD+(1−t)AC=2ta+5(1−t)b
ここで、a 、b は、零ベクトルでなく平行でもないので、3(1−s)=2t 、3s=5(1−t)
2式を辺々加えて、 3=5−3t より、 t=2/3 よって、 s=5/9
以上から、
AP=(4/9)AB+(5/9)AE=(4/9)AB+(5/9)×(3/5)AC=(4/9)AB+(1/3)AC
=(7/9){(4/7)AB+(3/7)AC)}=(7/9)AF
よって、(1) AP : PF = 7 : 2 (2) BF : FC = 3 : 4
一次独立を用いた上記の解法では、2変数 s,t に関する連立方程式が関わっている。
これに対して、共線条件や直線のベクトル方程式を用いると、連立方程式が回避できる
ことが知られている。
BP : PE = s : 1−s とすると、
AP=(1−s)AB+sAE=(1−s)×(3/2)AD+s×(3/5)AC
3点 C、P、D は同一直線上にあるので、 (1−s)×(3/2)+s×(3/5)=1
よって、 s=5/9 なので、
AP=(4/9)AB+(5/9)AE=(4/9)AB+(5/9)×(3/5)AC
=(4/9)AB+(1/3)AC=(7/9){(4/7)AB+(3/7)AC)}=(7/9)AF
よって、(1) AP : PF = 7 : 2 (2) BF : FC = 3 : 4
何れの解法も後半部分は同じであるが、前半部分のような式変形もあり得ることは是非
注目したいところである。
(コメント) チェバの定理、メネラウスの定理を用いれば、上記の比の計算は、もちろん暗
算で求められる。
チェバの定理から、 (2/1)(BF/FC)(2/3)=1 より、 BF/FC=3/4 ・・・ (2)
メネラウスの定理から、 (AP/PF)(4/7)(1/2)=1 より、 AP/PF=7/2 ・・・ (1)
また、「ギブスの三角形」における重心の概念を利用すれば、次のように鮮やかに解くこ
とができる。