ギブスの三角形　　　　　　　　　　　　　　　　　　　　　戻る

　数学・物理等において、重心の果たす役割は大きい。物体は、重心でつりあい、剛体の
運動は、全質量が重心にあるものとして論ずることができる。

　重心の概念は、紀元前３世紀ごろ、ギリシャのアルキメデスによって初めて研究されたと
いう。重心は力学で最も重要なものの一つであるが、それだけにとどまらない。

　アルキメデス自身、放物線と直線で囲まれる部分の面積や球の体積を計算するのに、重
心の概念を用いている。

　重心の概念を用いると、難しい幾何学の問題が比較的簡単に直観的に解かれるという話、
いくつかの不等式が簡単に得られるという話を聞くと、この重心の話題を追究し、その応用
例を極めたいという衝動に駆られるのは何も私だけではないだろう。

　化学においても、いくつかの溶液の混合溶液を作る場合、実は、重心の計算と同じよう
な計算が存在する。さらに、ある組成（３種類の金属でできている）をもつ、いくつかの合金
を溶融するとき、まるで図形の重心を求めるかのように、できるであろう合金の組成を求め
ることもできる。このとき利用されるのが、ギブスの三角形である。

　このページでは、重心の概念の様々な応用例を堪能することにしよう。

　位置を表す幾何学的な点Ａと質量ｍの対により、質点（Ａ，ｍ）を表す。質点とは、大きさ
が無視できる質量ｍの小さい球状の物体のことをいう。

　２つの質点（Ａ，ｍ）と（Ｂ，ｎ）の重心（Ｇ，ｇ）とは、線分ＡＢ上にあり、つり合う点をいう。

このことを、　　（Ｇ，ｇ）＝（Ａ，ｍ）＋（Ｂ，ｎ）　　と表す。

　すなわち、　（ｍ＋ｎ）Ｇ＝ｍ・Ａ＋ｎ・Ｂ　、　ｇ＝ｍ＋ｎ　である。

　特に、ｇ＝１ のとき、Ｇ＝ｍ・Ａ＋ｎ・Ｂ である。

　このような計算を、質点の合成という。

例　長さが １０ の線分の両端に、２つの質点（０，３）と（１０，２）がある。

　このとき、重心（Ｇ，５）は、

　（３＋２）Ｇ＝３・０＋２・１０＝２０　より、　５Ｇ＝２０　　よって、　Ｇ＝４

　このことは、数直線上で座標がそれぞれ ０、１０ である２点を結ぶ線分を、２ ： ３　に内分
する点であることを意味する。


　３つの質点（Ａ，ｍ）、（Ｂ，ｎ）、（Ｃ，ｋ）で定まる三角形を、メビウスの座標三角形という。

　この重心を（Ｇ，ｇ）とすると、（Ｇ，ｇ）は次のように表される。

　（Ｇ，ｇ）＝（Ａ，ｍ）＋（Ｂ，ｎ）＋（Ｃ，ｋ）　　ただし、　ｇ＝ｍ＋ｎ＋ｋ

　このことは、イメージ的に次のように考えれば理解できるだろう。

（今までの幾何的イメージ）

　

　　（質量を負荷したイメージ）

　

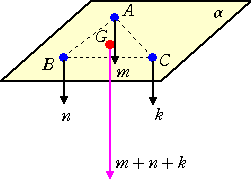
　実際に上記を計算する場合、

　（Ａ，ｍ）＋（Ｂ，ｎ）＝（Ｇ’，ｇ’）　の後、　（Ｇ’，ｇ’）＋（Ｃ，ｋ）を計算

　（Ｂ，ｎ）＋（Ｃ，ｋ）＝（Ｇ’，ｇ’）　の後、　（Ｇ”，ｇ”）＋（Ａ，ｍ）を計算

の両者は相等しい。（これを、重心の一意性という。）

　また、３つの質点（Ａ，ｍ）、（Ｂ，ｎ）、（Ｃ，ｋ）の重心が（Ｇ，ｇ）であるとき、２つの質点（Ａ，ｍ）、
（Ｂ，ｎ）を、その合成　（Ａ，ｍ）＋（Ｂ，ｎ）＝（Ｇ’，ｇ’）　で置き換えても重心は不変である。
（これを、質点系の組み分け可能の定理という。）


（追記）　カルピスさんから面白い数学の授業のサイトをご紹介いただきました。
　（平成２９年２月１３日付け）

　私はチェバとかメネラウスの定理、習った記憶まるで無し。（覚えようとも思わないけど）
上記サイト、いいな。「天秤が釣り合う原理」って重さだけでなく、いろいろな所で使えるんで
すね。


（コメント）　上記サイトの方法は、このページの話題に関連しますね。つりあいの考えで、比
　　　　　　がすべて求められる説明が上手いです。


　ますた〜さんからのコメントです。（平成２９年２月１４日付け）

　これは初めて知りました。僕は、「ほのぼの数学頑張ろう〜」で主にやっていてこちらは記
述でも大丈夫ですし数学的にも自然な一般化のような気がします(メネラウスの)。しかしその
構図を含むものに限っては答えを出すだけならそちらの方がぐっと楽になりそうですね。しか
もチェバまで含んでいるのに加えて物理的直感にもフィットしているのはただの偶然なのだろ
うか．．．？


　カルピスさんからのコメントです。（平成２９年２月１４日付け）

　「数学」も難しい言い方をしなければ『数楽』になるのに。「〜の定理」とかいうのも本当は
「自然の摂理」なのでしょうね。


　さて、上記の重心の計算を、化学に応用してみよう。

例　アルコール（Ａ）１００ｇと水（Ｂ）３００ｇの溶液がある。このとき、

　　アルコール（Ａ）の濃度は、１００％（＝１）で、水の濃度は、０％である。

このとき、混合溶液Ｋは、下図のような数直線で表される。Ｋは線分ＡＢの重心である。

　

記号で表せば、（Ｋ，４００）＝（Ａ，１００）＋（Ｂ，３００） となる。

このとき、　４００Ｋ＝１００×１＋３００×０＝１００　より、　Ｋ＝１/４＝０．２５　である。

　一般的に、次の定理が成り立つ。

定理　２つの混合物が質点（Ｋ1，ｍ1）、（Ｋ2，ｍ2）で表されるとき、これらを混ぜて作った
　　　混合物（Ｋ，ｍ）について、

　（Ｋ，ｍ）＝（Ｋ1，ｍ1）＋（Ｋ2，ｍ2）　　ただし、　ｍ＝ｍ1＋ｍ2

が成り立つ。

例　アルコールの水溶液が２つある。それらを、Ａ、Ｂとする。

　Ａは、重さ２００ｇで、１０％のアルコールを含み、
　Ｂは、重さ３００ｇで、６０％のアルコールを含む。

　これらの溶液を混ぜて、１つの溶液を作るとき、その中のアルコールは何％になるか。

（通常の計算）　Ａに含まれるアルコール量は、２００×０．１＝２０ｇ

　Ｂに含まれるアルコール量は、３００×０．６＝１８０ｇ

よって、アルコールの総量は、２００ｇだから、濃度は、　２００/５００＝０．４＝４０％

（重心を利用した場合）

　

このとき、　（Ｋ，５００）＝（０．１，２００）＋（０．６，３００）　なので、

　５００Ｋ＝２００×０．１＋３００×０．６＝２０＋１８０＝２００

よって、　Ｋ＝２００/５００＝０．４　すなわち、　Ｋの濃度は、４０％

例　２５％の食塩水６００ｇに５％の食塩水を何ｇ加えたら、２０％の食塩水になるか。

　Ｘｇ加えるとすると、　（０．２，６００＋Ｘ）＝（０．２５，６００）＋（０．０５，Ｘ）　なので、

　（６００＋Ｘ）・０．２＝６００・０．２５＋Ｘ・０．０５

　１２０＋０．２Ｘ＝１５０＋０．０５Ｘ　より、　０．１５Ｘ＝３０　よって、　Ｘ＝２００（ｇ）


　今までの計算では、アルコールと水、食塩と水のように組成物が２種類だったので、直線
上に表現することができた。

　それでは、３種類の組成物の場合は、どう表現するのであろうか。このとき用いられる図
形が、標題のギブスの三角形である。

　　

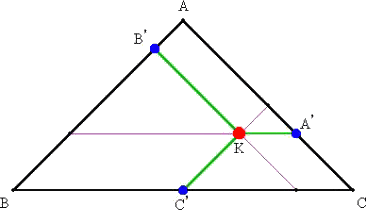
　上図の△ＡＢＣで、　Ａ→B　、　B→C　、　C→A　の向きに目盛がふられている。

　Ｋから各辺に平行線を引き、その交点を上図のようにおく。

このとき、比　A’C/AC　の値が、Ｋ に含まれる Ａ の組成比率を表す。

　Ｂ、Ｃ についても同様である。（参考：アメリカの学者　Ｊ．Ｗ．Gibbs　が１８７６年に提唱）

　一般に、次の定理が成り立つ。

定理　２つの３成分混合物が質点（Ｋ1，ｍ1）、（Ｋ2，ｍ2）で表されるとき、これらを混ぜて
　　　作った混合物（Ｋ，ｍ）について、

　（Ｋ，ｍ）＝（Ｋ1，ｍ1）＋（Ｋ2，ｍ2）　　ただし、　ｍ＝ｍ1＋ｍ2

が成り立つ。

例　次のような２種類の銀の合金がある。

　Ａ ： 銀３０％　銅５０％　亜鉛２０％ 　　Ｂ： 銀６０％　銅２０％　亜鉛２０％

　Ａ ２０ｇ と Ｂ １０ｇ から得られる合金 Ｋ の組成はどうなるだろうか。

　上記の定理を適用してみよう。
　まず、銀の組成について、

　３０銀＝２０・０．３＋１０・０．６＝１２

　　よって、　銀＝０．４

同様に、銅の組成について、

　３０銅＝２０・０．５＋１０・０．２＝１２

　　よって、　銅＝０．４

　亜鉛の組成について、

　３０亜鉛＝２０・０．２＋１０・０．２＝６

　　よって、　亜鉛＝０．２
 　
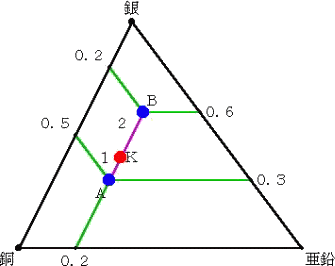　従って、新しくできる合金の組成比率は、　銀　４０％　銅　４０％　亜鉛　２０％　である。

　上記の計算は、右上図のギブスの三角形において、　ＫA ： ＫＢ ＝ １０ ： ２０ ＝ １ ： ２
となるように、線分ＡＢの内分点Ｋを求めていることに等しい。

　実際に、上図の三角形の各辺上において、

　銀　（０．３×２＋０．６×１）/３＝１．２/３＝０．４

　銅　（０．５×２＋０．２×１）/３＝１．２/３＝０．４

　亜鉛　（０．２×２＋０．２×１）/３＝０．６/３＝０．２

である。

　次に、重心の概念を利用して、幾何学の問題に応用してみよう。

問　題　　任意の△ＡＢＣにおいて、３中線は１点で交わり、各中線はこの点により、２ ： １
　　　　　の比に分けられることを示せ。

　この問題は、よく知られた重心の性質であるが、通常は、座標幾何的に、もしくは純粋に
中点連結の定理を用いる幾何的な解法で示される。

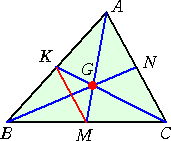　（参考：幾何的な証明）

　　　左図の△ＡＢＣにおいて、３中線をＡＭ、ＢＮ、ＣＫ　とする。

　　いま、２つの中線ＡＭとＣＫの交点をＧ’とする。

　　このとき、中点連結の定理により、

　　　　ＫＭ‖ＡＣ　　、　　２ＫＭ＝ＡＣ
　

　よって、　△Ｇ’ＭＫ∽△Ｇ’ＡＣ　で、　ＡＧ’ ： Ｇ’Ｍ＝ＡＣ ： ＫＭ＝２ ： １

同様にして、２つの中線ＡＭとＢＮの交点をＧ”とすると、

　△Ｇ”ＭＮ∽△Ｇ”ＡＢ　で、　ＡＧ” ： Ｇ”Ｍ＝ＡＢ ： ＮＭ＝２ ： １

以上から、　Ｇ’＝Ｇ”　で、３中線は１点で交わり、各中線はこの点により、２ ： １　の比に

分けられる。　（証終）


　重心の概念を用いると、その斬新な解法に心打たれそう．．．。

（解）　３つの質点（Ａ，１）、（Ｂ，１）、（Ｃ，１）の重心を（Ｇ，３）とする。

　このとき、　（Ｇ，３）＝（Ａ，１）＋（Ｂ，１）＋（Ｃ，１）　である。

　１つの中線を ＡＭ とすると、　（Ｍ，２）＝（Ａ，１）＋（Ｂ，１）　である。

よって、　（Ｇ，３）＝（Ｍ，２）＋（Ｃ，１）　から、　Ｇは中線 ＡＭ 上の点である。

同様にして、　Ｇは中線 ＢＮ　、ＣＫ 上の点である。

よって、３中線は、１点Ｇで交わる。

　また、　３Ｇ＝２Ｍ＋Ｃ　から、　ＣＧ ： ＧＭ＝ ２ ： １　となり、各中線は、重心Ｇにより、

２ ： １　の比に分けられる。　（終）

　四面体において、次の事実が成り立つことは周知のことだろう。

　四面体において、各頂点とそれに対する面の３中線の交点を結ぶ。このとき、４つ
の線分は同じ点で交わり、しかも、この点で各線分は ３ ： １ の比に分けられる。

　上記と同様に、重心の概念を用いれば、証明は明らかだろう。

　４つの質点（Ａ，１）、（Ｂ，１）、（Ｃ，１）、（Ｄ，１）の重心を（Ｇ，４）とすると、

　（Ｇ，４）＝（Ａ，１）＋（Ｂ，１）＋（Ｃ，１）＋（Ｄ，１）

の成り立つことが肝要である。

　この式を、　（Ｇ，４）＝（Ａ，１）＋｛（Ｂ，１）＋（Ｃ，１）＋（Ｄ，１）｝　と考えれば上記のような
表現になるが、

　（Ｇ，４）＝｛（Ａ，１）＋（Ｂ，１）｝＋｛（Ｃ，１）＋（Ｄ，１）｝

と考えれば、次のような表現にも変換できることが分かる。

　このことが直ぐ理解できるところが、重心の概念のよさなのだろう。

　四面体において、頂点を共有しない対辺同士の中点を結ぶ３本の線分は同じ点で
交わり、しかも、この点で各線分は １ ： １ の比に分けられる。

　次の問題は一見すると重心の概念とは無関係のような気がするが、重心の概念を利用
すると鮮やかに解かれうる。

問　題　　任意の△ＡＢＣにおいて、３つの頂角の２等分線は１点で交わり、各２等分線は、
　　　　　この点により、

　　　底辺の長さ ： 他の２辺の長さの和

の比に分けられることを示せ。

（解）　各頂点に適当に質量を与え、２等分線の交点が重心となるようにすればよい。
　（　→　この発想は凄いですね！感動的です．．．。）

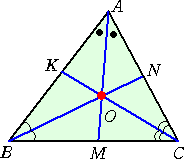　頂点 （Ｂ，ｎ） に対して、（Ｍ，ｎ＋ｋ）が線分ＢＣの重心となる
ように、頂点（Ｃ，ｋ） の質量を定めることができる。

　（ｎ＋ｋ）Ｍ＝ｎＢ＋ｋＣ　より、　ＢＭ ： ＭＣ＝ ｋ ： ｎ

　一方、角の２等分線の性質から、　ＢＭ ： ＭＣ＝ ｃ ： ｂ

　よって、　ｋ＝（ｃ/ｂ）ｎ　と定めればよい。
　

　同様にして、　ｍ＝（ａ/ｃ）ｋ　と定めるとき、頂点（Ａ，ｍ）と（Ｃ，ｋ）の重心が、（Ｎ，ｍ＋ｋ）
となる。

　このとき、　ｍ＝（ａ/ｃ）ｋ＝（ａ/ｃ）（ｃ/ｂ）ｎ＝（ａ/ｂ）ｎ　となり、

　ＡＫ ： ＫＢ＝ ｂ ： ａ ＝ ｎ ： ｍ 　が成り立つことから、　（ｍ＋ｎ）Ｋ＝ｍＡ＋ｎＢ　である。

すなわち、　（Ｋ，ｍ＋ｎ）は、頂点（Ａ，ｍ）と（Ｂ，ｎ）の重心となる。

　３頂点（Ａ，ｍ）、（Ｂ，ｎ）、（Ｃ，ｋ）の重心を（Ｇ，ｍ＋ｎ＋ｋ）とすると、

　（Ｇ，ｍ＋ｎ＋ｋ）＝（Ａ，ｍ）＋（Ｂ，ｎ）＋（Ｃ，ｋ）

　この式より、重心Ｇは、線分ＡＭ、ＢＮ、ＣＫ上にあり、３本の２等分線の交点Ｏと一致する。

このとき、　（Ｏ，ｍ＋ｎ＋ｋ）＝（Ａ，ｍ）＋（Ｍ，ｎ＋ｋ）　より、

　ＯＡ ： ＯＭ ＝ ｎ＋ｋ ： ｍ ＝ ｎ＋（ｃ/ｂ）ｎ ： （ａ/ｂ）ｎ ＝ ｂ＋ｃ ： ａ　　（終）


（コメント）　重心の概念を用いると、ごく当たり前の事実のように感じられますね！

　３つの頂角の２等分線が１点で交わることは通常次のように証明される。（中学２年程度）

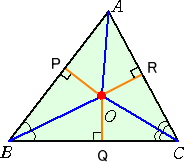（証明）　頂角Ｂ、Ｃの２等分線の交点をＯとする。

　　　　このとき、　△ＯＰＢ≡△ＯＱＢ　、　△ＯＱＣ≡△ＯＲＣ

　　　より、　ＯＰ＝OQ＝ＯＲ　となる。

　　　よって、　△ＯＰＡ≡△ＯＲＡ　より、線分ＯＡは頂角Ａの

　　２等分線となる。

　　以上から、頂角の２等分線は１点で交わる。　（証終）

（コメント）　重心の概念を用いると、たった１行の式

　（Ｇ，ｍ＋ｎ＋ｋ）＝（Ａ，ｍ）＋（Ｂ，ｎ）＋（Ｃ，ｋ）

で自明なのに、幾何的な証明だと、６行もかかるんですね！

　次の性質は、オイラーが発見した美しい幾何の定理の一つである。

問　題　　任意の△ＡＢＣにおいて、３中線の交点Ｇは、外接円の中心Ｏと３垂線の交点Ｈ
　　　　を結ぶ線分ＯＨ上にあって、ＯＨを１：２の比に分けることを示せ。

　（３点Ｏ、Ｇ、Ｈを通る直線は、オイラー線と言われる。）

（ → 参考：「九点円について」、「オイラーの定理」、「垂心の証明」）

（解）　△ＡＢＣが∠Ａ＝∠Ｒの直角三角形のとき、Ｏは辺ＢＣの中点で、Ｈは頂点Ａと一致す

る。このとき、Ｇは、中線ＯＨ上にあり、ＯＨを１：２の比に分けることは明らかである。

∠Ｂ＝∠Ｒ、∠Ｃ＝∠Ｒとしても同様である。

よって、以下では、△ＡＢＣは直角三角形ではないものと仮定してよい。

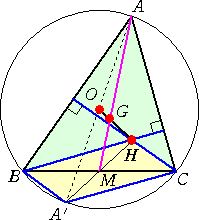　　　点Ｏに関して点Ａと対称な点をＡ’とする。このとき、

　　Ａ’Ｂ⊥ＡＢ、Ａ’Ｃ⊥ＡＣなので、四角形Ａ’ＣＨＢは平行四

　　辺形である。

　　　よって、辺ＢＣの中点Ｍは、Ａ’Ｈの中点となる。

　　いま、△ＡＡ’Ｈにおいて、３つの頂点を、

　　　　（Ａ，１）　、（Ａ’，１）　、（Ｈ，１）

　　とし、その重心を（Ｇ’，３）とする。

　すなわち、　（Ｇ’，３）＝（Ａ，１）＋（Ａ’，１）＋（Ｈ，１）　である。

　点Ｇ’は、線分ＯＨと線分ＡＭの交点である。

このとき、　（Ｍ，２）＝（Ａ’，１）＋（Ｈ，１）　で、　（Ｇ’，３）＝（Ａ，１）＋（Ｍ，２）

そこで、　（Ｂ，１）　、（Ｃ，１）　とすれば、　（Ｍ，２）＝（Ｂ，１）＋（Ｃ，１）　で、

　（Ｇ’，３）＝（Ａ，１）＋（Ｂ，１）＋（Ｃ，１）

よって、　（Ｇ’，３）は、３点 （Ａ，１）、（Ｂ，１）、（Ｃ，１） の重心となり、　Ｇ’＝Ｇ

すなわち、点Ｇは、線分ＯＨと線分ＡＭの交点である。

ところで、　（Ｇ，３）＝（Ａ，１）＋（Ａ’，１）＋（Ｈ，１）＝（Ｏ，２）＋（Ｈ，１）　なので、

ＯＧ ： ＧＨ ＝ １ ： ２　が成り立つ。　　（終）

　次のような面積の比の計算にも重心の概念が生かされることには驚かされる。

問　題　　任意の△ＡＢＣにおいて、３辺ＢＣ、ＣＡ、ＡＢをそれぞれ ２ ： １ に内分する点を、
　　　　　Ａ’、Ｂ’、Ｃ’とする。このとき、３つの線分ＡＡ’、ＢＢ’、ＣＣ’で囲まれた△ＰＱＲの
　　　　　面積は、△ＡＢＣの面積の １/７ であることを示せ。

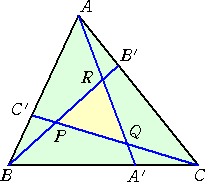（解）　左図において、（Ｂ，１）、（Ｃ，２）とすると、

　　　（Ａ’，３）＝（Ｂ，１）＋（Ｃ，２）

　　さらに、（Ａ，４）に対して、

　　　（Ｂ’，６）＝（Ｃ，２）＋（Ａ，４）

　　このとき、　（Ｒ，７）＝（Ａ，４）＋（Ｂ，１）＋（Ｃ，２）

が成り立ち、　（Ｒ，７）＝（Ｂ，１）＋（Ｂ’，６）　より、　ＢＲ ： ＲＢ’ ＝ ６ ： １

　よって、　△ＡＢＲ＝（６/７）△ＡＢＢ’＝（６/７）・（１/３）△ＡＢＣ＝（２/７）△ＡＢＣ

同様にして、　△ＢＣＰ＝（２/７）△ＡＢＣ　、△ＣＡＱ＝（２/７）△ＡＢＣ　なので、

　△ＰＱＲ＝（１−２/７−２/７−２/７）△ＡＢＣ＝（１/７）△ＡＢＣ　　（終）　


（コメント）　もちろん、メネラウスの定理を用いれば、もっと簡単に　ＢＲ ： ＲＢ’が求められる。

　△Ｂ’ＢＣ において、３点Ａ、Ｒ、Ａ’が一直線上にあるので、メネラウスの定理より、

　（ＢＡ’/Ａ’Ｃ）（ＣＡ/ＡＢ’）（Ｂ’Ｒ/ＲＢ）＝（２/１）（３/１）（Ｂ’Ｒ/ＲＢ）＝１

すなわち、　　Ｂ’Ｒ/ＲＢ＝１/６　より、　ＢＲ ： ＲＢ’ ＝ ６ ： １　である。

　しかし、両者の解法を比べて、重心の概念を用いた解法もだんだん味があっていいように
感じてくるから不思議ですね。

　上記の問題をもっと一般の場合に拡張しよう。

問　題　　任意の△ＡＢＣにおいて、

　辺ＢＣを ｋａ ： １ 　（ ただし、ｋａ＞０ ）に内分する点を Ａ’、
　辺ＣＡを ｋｂ ： １ 　（ ただし、ｋｂ＞０ ）に内分する点を Ｂ’、
　辺ＡＢを ｋｃ ： １ 　（ ただし、ｋｃ＞０ ）に内分する点を Ｃ’

とする。このとき、３つの線分ＡＡ’、ＢＢ’、ＣＣ’で囲まれた△ＰＱＲの面積は、△ＡＢＣの面
積の何倍になるか。

（解）　考え方は上記の問題と同様である。

　（Ｂ，１）、（Ｃ，ｍｃ）に対して、　（Ａ’，１＋ｍｃ）＝（Ｂ，１）＋（Ｃ，ｍｃ）　となるためには、

　ＢＡ’ ： Ａ’Ｃ ＝ ｍｃ ： １ ＝ ｋａ ： １　から、　ｍｃ＝ｋａ　とすればよい。

　同様に、　（Ｃ，ｋａ）、（Ａ，ｍａ）に対して、　（Ｂ’，ｋａ＋ｍａ）＝（Ｃ，ｋａ）＋（Ａ，ｍａ）　となる

ためには、　ＣＢ’ ： Ｂ’Ａ ＝ ｍａ ： ｋａ ＝ ｋｂ ： １　から、　ｍａ＝ｋａｋｂ　とすればよい。

　このとき、　（Ｒ，ｋａｋｂ＋ｋａ＋１）＝（Ａ，ｋａｋｂ）＋（Ｂ，１）＋（Ｃ，ｋａ）　が成り立つ。

　よって、　（Ｒ，ｋａｋｂ＋ｋａ＋１）＝（Ｂ，１）＋（Ｂ’，ｋａｋｂ＋ｋａ）　より、

　　ＢＲ ： ＲＢ’ ＝ ｋａｋｂ＋ｋａ ： １

となる。

　よって、

△ＡＢＲ＝｛（ｋａｋｂ＋ｋａ）/（ｋａｋｂ＋ｋａ＋１）｝△ＡＢＢ’

　＝｛（ｋａｋｂ＋ｋａ）/（ｋａｋｂ＋ｋａ＋１）｝・｛１/（ｋｂ＋１）｝△ＡＢＣ

　＝｛ｋａ/（ｋａｋｂ＋ｋａ＋１）｝△ＡＢＣ

同様にして、

△ＢＣＰ＝｛ｋｂ/（ｋｂｋｃ＋ｋｂ＋１）｝△ＡＢＣ

△ＣＡＱ＝｛ｋｃ/（ｋｃｋａ＋ｋｃ＋１）｝△ＡＢＣ

　したがって、

　１−ｋａ/（ｋａｋｂ＋ｋａ＋１）−ｋｂ/（ｋｂｋｃ＋ｋｂ＋１）−ｋｃ/（ｋｃｋａ＋ｋｃ＋１）

＝１−１/（ｋｂ＋１/ｋａ＋１）−１/（ｋｃ＋１/ｋｂ＋１）−１/（ｋａ＋１/ｋｃ＋１）

　ここで、　ｘ＝ｋｂ＋１/ｋａ　、ｙ＝ｋｃ＋１/ｋｂ　、ｚ＝ｋａ＋１/ｋｃ　とおくと、

与式＝１−１/（ｘ＋１）−１/（ｙ＋１）−１/（ｚ＋１）

＝｛（ｘ＋１）（ｙ＋１）（ｚ＋１）−（ｙ＋１）（ｚ＋１）−（ｚ＋１）（ｘ＋１）
　−（ｘ＋１）（ｙ＋１）｝/（ｘ＋１）（ｙ＋１）（ｚ＋１）

＝（ｘｙｚ−ｘ−ｙ−ｚ−２）/（ｘ＋１）（ｙ＋１）（ｚ＋１）

＝ｋａｋｂｋｃ（ｘｙｚ−ｘ−ｙ−ｚ−２）/｛ｋａｋｂｋｃ（ｘ＋１）（ｙ＋１）（ｚ＋１）｝

＝（ｋａ2ｋｂ2ｋｃ2−２ｋａｋｂｋｃ＋１）/｛（ｋａｋｂ＋ｋａ＋１）（ｋｂｋｃ＋ｋｂ＋１）（ｋｃｋａ＋ｋｃ＋１）｝

＝（ｋａｋｂｋｃ−１）2/｛（ｋａｋｂ＋ｋａ＋１）（ｋｂｋｃ＋ｋｂ＋１）（ｋｃｋａ＋ｋｃ＋１）｝

　したがって、△ＰＱＲは、△ＡＢＣの

　　（ｋａｋｂｋｃ−１）2/｛（ｋａｋｂ＋ｋａ＋１）（ｋｂｋｃ＋ｋｂ＋１）（ｋｃｋａ＋ｋｃ＋１）｝ 倍

となる。　（終）

（コメント）　一般の場合も予想に反して意外に美しい結果ですね！
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（．．．でも、計算は大変．．．ｆ(^^;) でした。）

例　　ＢＡ’ ： Ａ’Ｃ ＝ ３ ： ２　、ＣＢ’ ： Ｂ’Ａ ＝ ２ ： １　、ＡＣ’ ： Ｃ’Ｂ ＝ ４ ： １　とすると、

　△ＰＱＲ＝（２/１１）△ＡＢＣ

かな．．．。　倍数がきれいな数になる組合せ（ ｋａ ， ｋｂ ， ｋｃ ）が見つかると、いい問題が
作れそうですね！


（追記）　当ＨＰがいつもお世話になっているＳ（Ｈ）さんから、

　（ｋａｋｂｋｃ−１）2/｛（ｋａｋｂ＋ｋａ＋１）（ｋｂｋｃ＋ｋｂ＋１）（ｋｃｋａ＋ｋｃ＋１）｝

において、　ｋａ＝ｋｂ＝ｋｃ （＝ｋ　とする）の場合について、もう少し調べてみたらというご助
言をいただいた。（平成２１年７月３１日付け）

　Ｆ（ｋ）＝（ｋ3−１）2/（ｋ2＋ｋ＋１）3

　関数 Ｆ（ｋ） が、ｋ＞０ において、どのような振る舞いをするのか、まず、そのグラフを観察
してみよう。

　

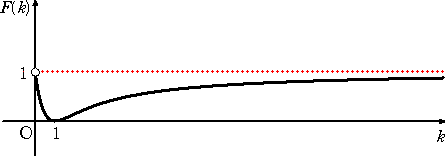
　上図において、ｋ→１ のとき、△ＰＱＲは、△ＡＢＣの重心に収束し、ｋ→０　や ｋ→∞　の
ときは、△ＰＱＲは、△ＡＢＣに収束する。


　これまでの展開で気がついた方がいらっしゃると思うが、例えば、△ＡＢＣにおいて、ある
点が重心となるように、各頂点に負荷する質量を題意に応じて調整している点である。

　一般に、次の事実が成り立つ。

定　理

　　　　△ＡＢＣ内の任意の点をＧとする。

　　　このとき、質量 ｍ 、ｎ 、ｋ を適当に選んで、

　　　　　　（Ｇ，ｍ＋ｎ＋ｋ）＝（Ａ，ｍ）＋（Ｂ，ｎ）＋（Ｃ，ｋ）

　　　が成り立つように必ず出来る。
　　

　今までの推論を整理すれば、その証明は容易だろう。

（証明）　頂点 （Ｂ，ｎ） に対して、（Ｍ，ｎ＋ｋ）が線分ＢＣの重心となるように、頂点（Ｃ，ｋ）

　の質量を定めることができる。実際に、

　（ｎ＋ｋ）Ｍ＝ｎＢ＋ｋＣ　より、　ＢＭ ： ＭＣ＝ ｋ ： ｎ

より、　ｋ＝（ＢＭ/ＭＣ）ｎ　と定めればよい。

　次に、点（Ｍ，ｎ＋ｋ）に対して、（Ｇ，ｍ＋ｎ＋ｋ）が線分ＡＭの重心となるように、頂点（Ａ，ｍ）
の質量を定めることができる。実際に、

　（ｍ＋ｎ＋ｋ）Ｇ＝ｍＡ＋（ｎ＋ｋ）Ｍ　より、　ＡＧ ： ＧＭ＝ ｎ＋ｋ ： ｍ

より、　ｍ＝（ＧＭ/ＡＧ）（ｎ＋ｋ）　と定めればよい。

以上から、　（Ｇ，ｍ＋ｎ＋ｋ）＝（Ａ，ｍ）＋（Ｂ，ｎ）＋（Ｃ，ｋ）　が成り立ち、点Ｇは、

３頂点　（Ａ，ｍ）、（Ｂ，ｎ）、（Ｃ，ｋ）　の重心となる。　　（証終）


　上記の計算で、　ｋ＝（ＢＭ/ＭＣ）ｎ　と同様にして、　ｍ＝（ＣＮ/ＮＡ）ｋ　と定めるとき、

頂点（Ａ，ｍ）と（Ｃ，ｋ）の重心が、（Ｎ，ｍ＋ｋ）となる。

　このとき、　ｍ＝（ＣＮ/ＮＡ）ｋ＝（ＣＮ/ＮＡ）（ＢＭ/ＭＣ）ｎ　である。

また、（Ａ，ｍ）、（Ｂ，ｎ）の重心が、（Ｋ，ｍ＋ｎ）であることを考えると、

　ＡＫ ： ＫＢ＝ ｎ ： ｍ 　が成り立つことから、　ｍ＝（ＫＢ/ＡＫ）ｎ　が成り立つ。

このとき、　ｍ＝（ＣＮ/ＮＡ）（ＢＭ/ＭＣ）ｎ　、ｍ＝（ＫＢ/ＡＫ）ｎ　から、

　（ＣＮ/ＮＡ）（ＢＭ/ＭＣ）＝ＫＢ/ＡＫ　が成り立つ。

すなわち、　（ＡＫ/ＫＢ）（ＢＭ/ＭＣ）（ＣＮ/ＮＡ）＝１　が成り立つ。

＃これって、チェバの定理かな？

（コメント）　これまで学校教育で学んだいろいろな幾何の定理達が、重心の概念と密接に
　　　　　結びついている様子が伺えますね！

　ところで、上記で各頂点に負荷する質量を線分の長さを用いて与えたが、もちろん次のよ
うに考えてもよい。

　　　左図において、

　　　　　ＢＭ/ＭＣ＝△ＡＢＧ/△ＣＡＧ

　　　　　ＣＮ/ＮＡ＝△ＢＣＧ/△ＡＢＧ

　　　　　ＫＢ/ＡＫ＝△ＢＣＧ/△ＣＡＧ

　そこで、　Ｂに負荷する質量を、　ｎ＝△ＣＡＧ　とすれば、他の頂点に負荷する質量は、

　ｋ＝（△ＡＢＧ/△ＣＡＧ）ｎ＝△ＡＢＧ　、　ｍ＝（△ＢＣＧ/△ＣＡＧ）ｎ＝△ＢＣＧ

となる。

　このことを用いると、△ＡＢＣの各頂角の２等分線の交点（内心）について、次のように各
頂点に質量を負荷すればよいことが分かる。

　　　左図において、各頂点 Ａ、Ｂ、Ｃ には、それぞれ

　　　　△ＢＣＯ＝ｒ・ａ　　（ ｒ は内接円の半径）

　　　　△ＣＡＯ＝ｒ・ｂ

　　　　△ＡＢＯ＝ｒ・ｃ　　　と書けるので、

　　３質点として、　（Ａ，ａ）、（Ｂ，ｂ）、（Ｃ，ｃ）　とおけばよい。

このとき、内心を Ｉ とすれば、（ Ｉ ，ａ＋ｂ＋ｃ）＝（Ａ，ａ）＋（Ｂ，ｂ）＋（Ｃ，ｃ）　となる。

この式と、ベクトルを用いた公式（この公式は何次元でも可）

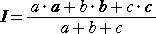　　　（→　参考：「加重平均の底力」）

に類似性があって面白い。（内心の計算も結局は重心と同じ範疇なんですね！）

　すなわち、　（ Ｉ ，ａ＋ｂ＋ｃ）＝（Ａ，ａ）＋（Ｂ，ｂ）＋（Ｃ，ｃ）＝（Ａ，ａ）＋（Ｍ，ｂ＋ｃ）

なので、　（ａ＋ｂ＋ｃ）Ｉ＝ａA＋（ｂ＋ｃ）Ｍ　　において、　（ｂ＋ｃ）Ｍ＝ｂＢ＋ｃＣ　である。

　このことを用いれば、平成２１年８月３日付けのＳ（Ｈ）さんからの問いかけ

　Ｒ3 内の３点 Ａ（３，３，４）、Ｂ（−３，０，０）、Ｃ（１，−２，−３）に如何ほどの負荷をかけれ
ば内心でつり合うか

についても答えは容易だろう。

　３辺の長さ ＡＢ、ＢＣ、ＣＡ に比例する質量を負荷すればよい。


　次の問題もベクトルを用いれば容易だろうが、純粋に幾何的に解こうと思ったら少し難し
い問題かもしれない。

問　題　　左下図のような台形ＡＢＣＤにおいて、

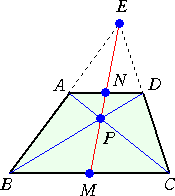　　　　　辺ＡＢとＣＤの延長線の交点を Ｅ

　　　　　辺ＢＣ、ＡＤの中点をそれぞれ Ｍ、Ｎ

　　　　　対角線ＡＣとＢＣの交点を Ｐ

　　　　とするとき、

　　　　　４点 Ｅ、Ｍ、Ｎ、Ｐ　は一直線上にある

　　　　ことを示せ。

（ベクトルを用いた解法）

　ＥＡ＝２ａ　、ＡＤ＝２ｂ　とおくと、実数 ｋ を用いて、　ＥＢ＝２ｋａ　、ＢＣ＝２ｋｂ

このとき、　ＥＭ＝２ｋａ＋ｋｂ＝ｋ（２ａ＋ｂ）　、ＥＮ＝２ａ＋ｂ

　また、△ＥＢＤにおいて、３点Ａ、Ｐ、Ｃが一直線上にあるので、メネラウスの定理より、

　（ＥＡ/ＡＢ）（ＢＰ/ＰＤ）（ＤＣ/ＣＥ）＝１

すなわち、　｛１/（ｋ−１）｝（ＢＰ/ＰＤ）｛（ｋ−１）/ｋ｝＝１　より、　ＢＰ/ＰＤ＝ｋ　なので、

　ＥＰ＝｛２ｋａ＋ｋ（２ａ＋２ｂ）｝/（ｋ＋１）＝｛２ｋ/（ｋ＋１）｝（２ａ＋ｂ）

　以上から、　（ｋ＋１）ＥＰ＝２ＥＭ＝２ｋＥＮ　が成り立つので、４点 Ｅ、Ｍ、Ｎ、Ｐ　は一直線

上にある。　（終）

　この問題を重心の概念を用いて解けば次のようになる。多分その解法の鮮烈さは感動に
値するだろう。

（解）　ＡＤ‖ＢＣ　より、　ＥＡ ： ＡＢ ＝ ＥＤ ： ＤＣ　なので、（Ｅ，１）に対して、

　（Ｂ，ｎ）、（Ｃ，ｎ）の質量 ｎ を適当に選んで、

　（Ａ，ｎ＋１）＝（Ｅ，１）＋（Ｂ，ｎ）　、　（Ｄ，ｎ＋１）＝（Ｅ，１）＋（Ｃ，ｎ）

であるように出来る。このとき、３頂点 （Ｅ，１）、（Ｂ，ｎ）、（Ｃ，ｎ） の重心を、Ｐ’とおくと、

　（Ｐ’，２ｎ＋１）＝（Ｅ，１）＋（Ｂ，ｎ）＋（Ｃ，ｎ）

よって、　（Ｐ’，２ｎ＋１）＝（Ａ，ｎ＋１）＋（Ｃ，ｎ）　より、　Ｐ’は、線分ＡＣ上にある。

　同様にして、（Ｐ’，２ｎ＋１）＝（Ｂ，ｎ）＋（Ｄ，ｎ＋１）　より、　Ｐ’は、線分ＢＤ上にある。

したがって、　Ｐ’＝Ｐ　で、Ｐは、３点 （Ｅ，１）、（Ｂ，ｎ）、（Ｃ，ｎ） の重心となる。

　また、（Ｂ，ｎ）、（Ｃ，ｎ）を結ぶ線分の中点Ｍは、（Ｂ，ｎ）、（Ｃ，ｎ）の重心であり、

　（Ｍ，２ｎ）＝（Ｂ，ｎ）＋（Ｃ，ｎ）　より、　（Ｐ，２ｎ＋１）＝（Ｅ，１）＋（Ｍ，２ｎ）

よって、　Ｐは直線ＥＭ上にある。

　上記と同様の議論を、今度は、３頂点 （Ｅ，１）、（Ａ，ｍ）、（Ｄ，ｍ） に対して行えば、Ｐが直
線ＥＮ上にあることが示される。

　以上から、　４点 Ｅ、Ｍ、Ｎ、Ｐ　は一直線上にある。　（終）


　２つの質点（Ａ，ｍ）と（Ｂ，ｎ）の重心（Ｇ，ｇ）は、線分ＡＢ上にあり、つり合う点であった。

このとき、　ＡＧ ： ＧＢ＝ ｎ ： ｍ　　すなわち、　　ｍ・ＡＧ＝ｎ・ＧＢ　　が成り立つわけだが、

これは、物理でいうところの「モーメントが等しい」ということである。ちょうど重心の周りの

モーメントを求めていることになる。

　点 Ａ の点 Ｇ の周りのモーメントを　μＧ（Ａ）　と表すことにすれば、

　Ｇ が２点 Ａ、Ｂ の重心　⇔　μＧ（Ａ）＝μＧ（Ｂ）

となる。

　一般に、Ｏ を端点とする一つの半直線上に、いくつかの質点

　（Ａ，ｍ）　、（Ｂ，ｎ）　、・・・　、（Ｃ，ｋ）

がある質点系を考える。

　このとき、この質点系のモーメント μ とは、

　μ＝μＯ（Ａ）＋μＯ（Ｂ）＋・・・＋μＯ（Ｃ）

であるものとする。

　このとき、２つの質点（Ａ，ｍ）と（Ｂ，ｎ）の重心（Ｇ，ｇ）について

　（Ｇ，ｇ）＝（Ａ，ｍ）＋（Ｂ，ｎ）

すなわち、　（ｍ＋ｎ）Ｇ＝ｍ・Ａ＋ｎ・Ｂ　、　ｇ＝ｍ＋ｎ　が成り立つということは、

　μＯ（Ｇ）＝μＯ（Ａ）＋μＯ（Ｂ）

が成り立つことを意味する。

　（μＧ（Ａ）＝μＧ（Ｂ）　と　μＧ（Ａ）＋μＧ（Ｂ）＝０　が両立するためには、線分の長さに符号を付加す
　　るか、または質量に符号を付加しなければならないだろう。）

　特に、ある直線上の質点系

　｛（Ａ，ｍ）、（Ｂ，ｎ）、・・・、（Ｃ，ｋ）、（Ａ’，ｍ’）、（Ｂ’，ｎ’）、・・・、（Ｃ’，ｋ’）｝

について、その重心をＧとし、Ｇより左側にある質点系を

　｛（Ａ，ｍ）　、（Ｂ，ｎ）　、・・・　、（Ｃ，ｋ）｝

Ｇより右側にある質点系を

　｛（Ａ’，ｍ’）、（Ｂ’，ｎ’）、・・・、（Ｃ’，ｋ’）｝

とするとき、

　μＧ（Ａ）＋μＧ（Ｂ）＋・・・＋μＧ（Ｃ）＝μＧ（Ａ’）＋μＧ（Ｂ’）＋・・・＋μＧ（Ｃ’）

が成り立つ。

実際に、　μＧ（Ｇ’）＝μＧ（Ａ）＋μＧ（Ｂ）＋・・・＋μＧ（Ｃ）

　μＧ（Ｇ”）＝μＧ（Ａ’）＋μＧ（Ｂ’）＋・・・＋μＧ（Ｃ’）

について、Ｇは、２つの質点Ｇ’、Ｇ”の重心であるので、　μＧ（Ｇ’）＝μＧ（Ｇ”）　だからであ
る。

　このことを利用すると、端点が原点Ｏである半直線上の２点Ａ（ａ）、Ｂ（ｂ）の重心の座標
Ｇ（ｘ）が求められる。Ａ、Ｂには、それぞれ質量 ｍ、ｎ が負荷されているものとする。
（→　参考：「重心の位置」）

　

　このとき、Ｇより左側にある質点は、（Ａ，ｍ） で、Ｇより右側にある質点は、 （Ｂ，ｎ） なの
で、

　μＧ（Ａ）＝μＧ（Ｂ）　　すなわち、　ｍ・（ｘ−ａ）＝ｎ・（ｂ−ｘ）　より、

　

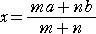
が成り立つ。今まで意識して座標との関わりを避けてきたが、この公式が最初の座標との
関わりを示すものである。

（コメント）　これは、（ｍ＋ｎ）ｘ＝ｍａ＋ｎｂ　と考えれば、μＯ（Ｇ）＝μＯ（Ａ）＋μＯ（Ｂ）　とい
　　　　うわけで、これは正に、（Ｇ，ｇ）＝（Ａ，ｍ）＋（Ｂ，ｎ）　と類似していますね！


　上記の公式は、もっと一般の質点系の場合に拡張できる。

　端点が原点Ｏである半直線上の ｎ 個の点　Ａ1（ａ1）、Ａ2（ａ2）、・・・、Ａｎ（ａｎ）には、それ
ぞれ質量 ｍ1、ｍ2、・・・、ｍｎ が負荷されているものとする。

　このとき、　μＯ（Ｇ’）＝μＯ（Ａ）＋μＯ（Ｂ）　という公式を繰り返し用いることにより、

　μＯ（Ｇ）＝μＯ（Ａ1）＋μＯ（Ａ2）＋・・・＋μＯ（Ａｎ）

　（ｍ1＋ｍ2＋・・・＋ｍｎ）ｘ＝ ｍ1・ａ1＋ｍ2・ａ2＋・・・＋ｍｎ・ａｎ

　したがって、

　

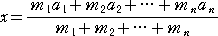
が成り立つ。

　この重心の位置を求める公式は、自然数の平方の和を求める方法に応用される。

　数直線の原点Ｏを端点とする半直線上に、ｎ 個の点

　Ａ1（ａ）　、Ａ2（ａ＋１）　、・・・　、Ａｎ（ａ＋ｎ−１）

を考える。このとき、Ａ1Ａｎを高さとする正三角形Ａ1ＢｎＣｎを作り、各点 Ａ2、・・・、Ａｎ-1 にお

ける線分Ａ1Ａｎの垂線が辺Ａ1Ｂｎ、辺Ａ1Ｃｎと交わる点をそれぞれ

　　　Ｂ2　、Ｂ3　、・・・　、Ｂｎ-1　、Ｃ2　、Ｃ3　、・・・　、Ｃｎ-1

とする。さらに、各分点を通って各辺に平行線を引いて、下図を得る。

　

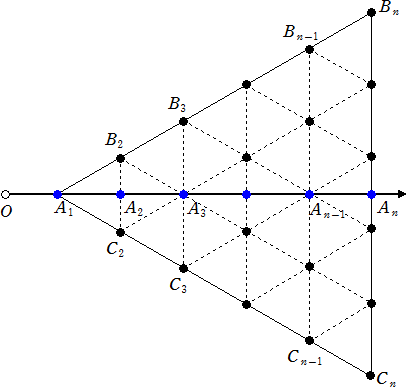
　上図には、高さ １ の正三角形Ａ1Ｂ2Ｃ2 と合同な正三角形が並ぶ。正三角形の頂点にな

りうる点には、質量 １ を負荷するものとする。

　このとき、△Ａ1ＢｎＣｎ の重心をＧとすると、Ｇの座標は、ａ＋２（ｎ−１）/３　である。

　正三角形の頂点の総数は、　１＋２＋・・・＋ｎ＝ｎ（ｎ＋１）/２　個なので、上図の質点系

の質量合計は、ｎ（ｎ＋１）/２　となる。

　ところで、各線分 Ｂ2Ｃ2 、Ｂ3Ｃ3 、・・・、ＢｎＣｎ 上にある重心を、Ａ’2 、Ａ’3 、・・・、Ａ’ｎ と

すると、これらの点は、線分Ａ1Ａｎ上の点 Ａ2、・・・、Ａｎ と重なる。

　このとき、（Ａ’2，２）＝（Ｂ2，１）＋（Ｃ2，１）

　（Ａ’3，３）＝（Ｂ3，１）＋（Ａ3，１）＋（Ｃ3，１）

　（Ａ’4，４）＝（Ｂ4，１）＋・・・＋（Ｃ4，１）

　　・・・・・・・・・・・・・・・・・・・・・・

　（Ａ’ｎ，ｎ）＝（Ｂｎ，１）＋・・・＋（Ｃｎ，１）

したがって、モーメントの計算から、

　｛ｎ（ｎ＋１）/２｝・｛ａ＋２（ｎ−１）/３｝＝１・ａ＋２・（ａ＋１）＋・・・＋ｎ・（ａ＋ｎ−１）

が成り立つ。　特に、ａ＝１　とすると、

　｛ｎ（ｎ＋１）/２｝・（２ｎ＋１）/３＝１2＋２2＋・・・＋ｎ2

すなわち、　　１2＋２2＋・・・＋ｎ2＝ｎ（ｎ＋１）（２ｎ＋１）/６　が成り立つ。

　これは、よく知られた自然数の平方の和の公式である。

　また、ａ＝０　とすると、

　｛ｎ（ｎ＋１）/２｝・｛２（ｎ−１）/３｝＝１・０＋２・１＋・・・＋ｎ・（ｎ−１）

すなわち、１・２＋２・３＋・・・＋（ｎ−１）・ｎ＝（ｎ−１）ｎ（ｎ＋１）/３　という美しい公式も同時
に得られる。


（コメント）　Σの計算公式を用いず、Σ（ｋ−１）ｋ の公式が瞬時に得られるとは．．．！

　同様にして、数直線の原点Ｏを端点とする半直線上に、ｎ 個の点

　　　　　Ａｎ（ａ）　、Ａｎ-1（ａ＋１）　、・・・　、Ａ1（ａ＋ｎ−１）

を考え、Ａ1Ａｎを高さとする正三角形Ａ1ＢｎＣｎを作ることにより、明らかに、

　ｎ・ａ＋（ｎ−１）・（ａ＋１）＋・・・＋１・（ａ＋ｎ−１）＝｛ｎ（ｎ＋１）/２｝・｛ａ＋（ｎ−１）/３｝

が成り立つ。　特に、ａ＝１　とすると、

　ｎ・１＋（ｎ−１）・２＋・・・＋１・ｎ＝｛ｎ（ｎ＋１）/２｝・（ｎ＋２）/３＝ｎ（ｎ＋１）（ｎ＋２）/６

が成り立つ。これもお馴染みの公式だろう。

　同様にして、数直線の原点Ｏを端点とする半直線上に、ｎ 個の点

　Ａ1（１）　、Ａ2（２）　、・・・　、Ａn（ｎ）

を考え、各点に、それぞれ、

　１・ｎ　、２・（ｎ−１）　、・・・　、ｎ・１

の質量を負荷すれば、重心は、Ｇ（（ｎ＋１）/２）であり、モーメントの計算から、

｛１・ｎ＋２・（ｎ−１）＋・・・＋ｎ・１｝・（ｎ＋１）/２＝１2・ｎ＋２2・（ｎ−１）＋・・・＋ｎ2・１

である。

　よって、　１2・ｎ＋２2・（ｎ−１）＋・・・＋ｎ2・１＝｛ｎ（ｎ＋１）（ｎ＋２）/６｝・（ｎ＋１）/２

すなわち、　１2・ｎ＋２2・（ｎ−１）＋・・・＋ｎ2・１＝ｎ（ｎ＋１）2（ｎ＋２）/１２

　以上の２つの公式

　　Σｋ2＝ｎ（ｎ＋１）（２ｎ＋１）/６　　、　Σｋ2（ｎ＋１−ｋ）＝ｎ（ｎ＋１）2（ｎ＋２）/１２

を用いて、　ｋ3＝ｋ3＋（ｎ＋１）ｋ2−（ｎ＋１）ｋ2＝（ｎ＋１）ｋ2−ｋ2（ｎ＋１−ｋ）　から、

Σｋ3＝（ｎ＋１）・ｎ（ｎ＋１）（２ｎ＋１）/６−ｎ（ｎ＋１）2（ｎ＋２）/１２

　＝ｎ（ｎ＋１）2（４ｎ＋２−ｎ−２）/１２＝ｎ2（ｎ＋１）2/４＝｛ｎ（ｎ＋１）/２｝2

が得られる。


（コメント）　通常の求め方とは一風変わっていて新鮮ですね！（　→　参考：「数列の和」）


（追記）　当ＨＰがいつもお世話になっているＨＮ「Ｋ．Ｓ．」が三角形の中心のベクトル表示に
　　　　ついてまとめられた。（平成２７年１月１６日付け）

重心Ｇの位置ベクトルは、　ＯＧ＝（ＯＡ＋ＯＢ＋ＯＣ）/３

内心Ｉの位置ベクトルは、　ＯＩ＝（ａＯＡ＋ｂＯＢ＋ｃＯＣ）/（ａ＋ｂ＋ｃ）

垂心Ｈの位置ベクトルは、

　　ＯＨ＝（ΔｂΔｃＯＡ＋ΔｃΔａＯＢ＋ΔａΔｂＯＣ）/（ΔａΔｂ＋ΔｂΔｃ＋ΔｃΔａ）

　ここで、　Δａ＝ｂ2＋ｃ2−ａ2　、Δｂ＝ｃ2＋ａ2−ｂ2　、Δｃ＝ａ2＋ｂ2−ｃ2

外心Ｊの位置ベクトルは、

　ＯＪ＝（（ΔａΔｂ＋ΔａΔｃ）ＯＡ＋（ΔｂΔａ＋ΔｂΔｃ）ＯＢ＋（ΔｃΔａ＋ΔｃΔｂ）ＯＣ）/２（ΔａΔｂ＋ΔｂΔｃ＋ΔｃΔａ）

フェルマー点Ｆの位置ベクトルは、

ＯＦ＝（ａ√（ａ2＋ｃ2＋ａｃ）ＯＡ＋ｂ√（ｂ2＋ａ2＋ａｂ）ＯＢ＋ｃ√（ｂ2＋ｃ2＋ｂｃ）ＯＣ）/（ａ√（ａ2＋ｃ2＋ａｃ）＋ｂ√（ｂ2＋ａ2＋ａｂ）＋ｃ√（ｂ2＋ｃ2＋ｂｃ））


　当ＨＰ読者のＡ．Ｉ．さんからメールで質問を頂いた。（平成２７年３月２０日付け）

　初めまして、予備校で数学を教えています。上記のモーメントを利用してΣ公式を証明する
部分、大変面白く感じ興味を持たせていただきました。その部分について質問がありますの
で、もしよろしければお教えいただけると幸いです。

　上記では、質点を正三角形の形に配置して、重心を利用してΣk2の公式を証明しています。
逆に、Σ公式を利用して重心の位置を計算すると、重心は、Σk2 /Σk を計算することにより、
当然重心の座標 (2n+1)/3が得られます。

　私は正三角形の重心の座標は質点が離散的に置かれているのではなく、重さが一様に分
布している状態で得られるものではないか？との疑問を抱きました。そこで、積分を利用した
重心の座標を求める公式

∫1n xf(x)dx / ∫f(x)dx　　（正三角形なので、f(x)=(1/)(x-1) としました。傾きは正の値で
　　　　　　　　　　　　　　　　　あれば、いくつでも同様の結果が得られるようです）

を計算してみたところ、同じく（2n+1）/3が得られたので、離散の状態にある質点全体の重心
が一様に分布している状態で得られる重心と一致するのだなと納得をしました。

　そこで、同じようにして、Σk3についても調べてみました。まずは、質点を境界線が２次関
数のグラフになるように配置すると考え、Σk3 /Σk2 を計算すると、重心の座標は、
3n(n+1) / 2(2n+1)となるはずです。

　ところが、積分を利用して重心の座標を求めると、3(n+1)2 / 4(n+2)となり、上記のものと
一致しませんでした。
（積分区間は1からnまでで、f(x)=1/2(x2-1) 。対称性からｘ軸の上側の部分のみ考える）

　そこで、以下の２点について、ご意見を頂ければと思います。

（１）　連続量と離散量によって計算した重心が一致したのは、正三角形の形に質点を配置し
　　　たのがたまたまであり、境界線が曲線になったりすると一般的には一致しないものであ
　　　るのか？

もしくは、

（２）　正三角形の形で配置した時に重さが一様に分布しているとみなせる何か確たる根拠の
　　ようなものが存在するのか？


（コメント）　Ａ．Ｉ．さん、メールを頂きありがとうございます。

　このページで取り扱っている重心は、あくまでも質点系の重心で、剛体の重心は考えていま
せん。なので、「連続量と離散量によって計算した重心が一致」はたまたまだと思います。

　例えば、円の面積πｒ2を微分すると、円周の長さ ２πｒ が得られるが、正方形の面積 ｘ2
を微分しても、正方形の周の長さ ４ｘ は得られない、・・・みたいな感じですかね？

　（２）については、上記の定理が参考になると思います。


（追記）　令和４年６月２６日付け

　上記では、重心の考え方を利用して、いろいろな濃度等の計算を行ってきた。このような
計算は天秤算と言われる。

問　題　　３％の食塩水２００ｇと９％の食塩水１００ｇに、１２％の食塩水を何ｇか混ぜて、
　　　　　１０％の食塩水を作りたい。何ｇ混ぜたらよいか？

（通常の計算）　ｍ ｇ 混ぜるとすると、食塩の量に着目して、

　　０．０３×２００＋０．０９×１００＋０．１２×ｍ＝０．１（２００＋１００＋ｍ）

　よって、　６＋９＋０．１２ｍ＝３０＋０．１ｍ　より、　０．０２ｍ＝１５　なので、　ｍ＝７５０

　以上から、１２％の食塩水を７５０ｇ混ぜればよい。　　（終）

（重心を利用した場合）　ｍ ｇ 混ぜるとすると、

　（０．１，３００＋ｍ）＝（０．０３，２００）＋（０．０９，１００）＋（０．１２，ｍ）

なので、　（３００＋ｍ）・０．１＝２００・０．０３＋１００・０．０９＋ｍ・０．１２

　３０＋０．１ｍ＝１５＋０．１２ｍ　より、　０．０２ｍ＝１５　なので、　ｍ＝７５０

　以上から、１２％の食塩水を７５０ｇ混ぜればよい。　　（終）


（コメント）　この問題の場合、天秤図は次のようになる。

　

　Ｋの周りのモーメントを考えれば、次のようにも計算できる。

　　２００×（１０−３）＋１００×（１０−９）＝ｍ×（１２−１０）

すなわち、　１４００＋１００＝２ｍ　より、　ｍ＝７５０（ｇ）


（追記）　令和４年６月２７日付け

　重心を利用した解法は、濃度以外に次のような問題に対しても有効である。

問　題　　１００ｇ７００円のお茶（Ａ）２００ｇと１００ｇ１０００円のお茶（Ｂ）と１００ｇ２０００円の
　　　　　お茶（Ｃ）２００ｇを混ぜて、１００ｇ１２００円のお茶（Ｄ）を作りたい。お茶（Ｂ）を何ｇ
　　　　　混ぜればいいだろうか？

（通常の計算）　ｍ ｇ 混ぜるとすると、

　　（７００/１００）×２００＋（１０００/１００）×ｍ＋（２０００/１００）×２００
　＝（１２００/１００）（２００＋ｍ＋２００）

すなわち、　１４００＋１０ｍ＋４０００＝１２ｍ＋４８００　より、２ｍ＝６００　から、ｍ＝３００

　以上から、１００ｇ１０００円のお茶（Ｂ）を３００ｇ混ぜればよい。　　（終）

（重心を利用した場合）　ｍ ｇ 混ぜるとする。次のような天秤図を考える。

　

　　　　　　　　（※）　線分の上側の数字は、お茶１ｇあたりの値段

　Ｋの周りのモーメントを考えれば、

　　２００×（１２−７）＋ｍ×（１２−１０）＝２００×（２０−１２）

　すなわち、　１０００＋２ｍ＝１６００　より、　ｍ＝３００（ｇ）　　（終）

（参考文献：バルク　著　鳥居一雄・宮本敏雄　訳　重心の概念の幾何への応用（東京図書））



　　　以下、工事中！