垂心の証明　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　三角形には、五心（重心、外心、内心、垂心、傍心）がある。現在の高校１年生の多くが
学ぶであろう「数学Ａ」では、残念ながら、垂心、傍心に関して、教科書の本文での説明は
割愛されている。旧課程では、五心の説明がしっかり書かれていたことを思うと、非常に
残念である。

　重心は「つりあい」、外心は「外接円」、内心は「内接円」と比較的扱いやすい題材が豊
富なのと、分かりやすさから多分生き残ったのだろう。

　それに対して、垂心とか傍心は応用もままならず、扱いにくい題材がゆえに省略された
のではないだろうか。

　しかしながら、傍心はまだしも、美しい性質を持つ垂心を生徒の目から遠ざけるというの
は、私個人的には賛成できない。ところで、垂心とは、三角形の３つの頂点から、それぞ
れの対辺に下ろした３つの垂線の交点のことをいう。

例　△ＡＢＣ の外心を Ｏ 、垂心を Ｈ 、重心を Ｇ とおくと、

　　　

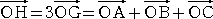
が成り立つ。すなわち、

オイラーの定理（１７６５年）

　△ＡＢＣ の外心 Ｏ 、重心 Ｇ 、垂心 Ｈ は一直線上にあり、

　ＯＧ ： ＧＨ ＝ １ ： ２　である

（注）　３点 Ｏ 、Ｈ 、Ｇ を通る直線を、オイラー線（Ｅｕｌｅｒ Ｌｉｎｅ）という。

　この事実に関連して、次の事実も有名だろう。

　三角形の内心、外心、重心、垂心の４つのうちの２つが一致するならば、その三角
形は正三角形である

（証明）　△ＡＢＣ の内心を Ｉ 、外心を Ｏ 、重心を Ｇ 、垂心を Ｈ とおく。

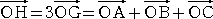　　より、

　Ｏ＝Ｈ　ならば、　Ｏ＝Ｇ　となり、このとき、　△ＯＡＢ、△ＯＢＣ、△ＯＣＡ がすべて合同に
なることから、△ＡＢＣ は正三角形となる。

　同様に、

　Ｏ＝Ｇ　ならば、　Ｏ＝Ｈ　となり、このとき、　△ＯＡＢ、△ＯＢＣ、△ＯＣＡ がすべて合同に
なることから、△ＡＢＣ は正三角形となる。

　Ｏ＝Ｉ　ならば、　△ＯＡＢ、△ＯＢＣ、△ＯＣＡ がすべて合同になることから、△ＡＢＣ は正
三角形となる。

　Ｇ＝Ｈ　ならば、　Ｇ＝Ｏ　となり、このとき、　△ＯＡＢ、△ＯＢＣ、△ＯＣＡ がすべて合同に
なることから、△ＡＢＣ は正三角形となる。

　Ｇ＝Ｉ　とする。このとき、　３ＡＧ＝ＡＢ＋ＡＣ　である。いま、ＡＢ＝ａ 、ＡＣ＝ｂ とおくと、
　　　ｋ（ａ＋ｂ）ＡＩ＝ｂＡＢ＋ａＡＣ
となる。ＡＢ、ＡＣ は一次独立なので、　３ｋａ＝ａ＋ｂ　、３ｋｂ＝ａ＋ｂ　より、　ａ＝ｂ
同様にして、ＡＢ＝ＢＣ＝ＣＡ　が示される。よって、△ＡＢＣ は正三角形となる。

　Ｈ＝Ｉ　ならば、　Ｇ＝Ｈ　となり、このとき、　△ＡＢＣ は正三角形となる。　　（証終）

（コメント）　上記の証明では、「Ｇ＝Ｉの場合」が少し不本意ですね。もっと幾何的な証明が
　　　　　　ないのかな？

　オイラーの定理の証明は、ベクトルの内積を用いると味気ないが、平行四辺形の性質を
巧妙に用いた証明には、思わず引き込まれてしまうほどの美しいものがある。

（証明）○ ベクトルの内積を用いる場合

　重心の性質から、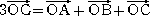　であることは明らか。　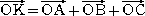と
おくと、　
　よって、ＡＫ⊥ＢＣ　となる。同様にして、ＢＫ⊥ＣＡ、ＣＫ⊥ＡＢ　が示される。
　したがって、Ｋは垂心となり、Ｋ＝Ｈ　である。よって、定理は成り立つ。

　　　　○ 平行四辺形の性質を用いる場合

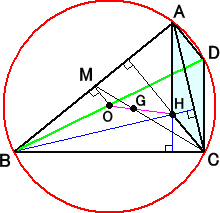△ＡＢＣにおいて、辺ＡＢの中点をＭ、外心Ｏを通る 　　直径を ＢＤ とする。 　　　また、ＣＭ と ＯＨ の交点を Ｇ とする。 　　このとき、四角形ＡＨＣＤ は平行四辺形。 　　中点連結の定理により、ＡＤ＝２ＯＭ 　　よって、ＣＨ＝ＡＤ　より、ＣＨ：ＯＭ＝ ２ ： １ 　　△ＣＨＧ ∽ △ＭＯＧ　より、ＣＧ ： ＧＭ ＝ ２ ： １ 　　よって、Ｇ は △ＡＢＣ の重心。 　　したがって、３点 Ｏ、Ｇ、Ｈ は一直線上にあり 　　ＯＧ ： ＧＨ ＝ １ ： ２　が成り立つ。

　「３つの垂線が１点で交わる」ことの証明としては、いろいろあるが、私自身としては、座
標幾何を用いて、直接的に証明するのが一番分かりやすいと、ずっと思っていた。

　ところが、あるセミナーで横浜国立大学教育人間科学部の橋本吉彦先生から、このこと
に関してお話を伺う機会があり、興味を持って、教科書等にあたると、もっと分かりやすい
証明がなされていることを知った。

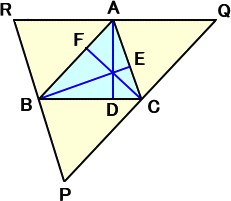	左図の△ＡＢＣにおいて、各頂点を通り、対辺に 　　平行な線分を引き、△ＰＱＲを作る。 　　　このとき、Ａは辺ＱＲの中点で、ＡＤは辺ＱＲの垂 　　線である。 　　　同様に、Ｂは辺ＰＲの中点で、ＢＥは辺ＰＲの垂 　　線である。 　　　よって、垂線ＡＤ、ＢＥの交点Ｈは、△ＰＱＲの外 　　接円の中心である。 　　　したがって、辺ＰＱの垂直二等分線ＣＦは、点Ｈ 　　を通る。
（注意）　３つの垂線が１点で交わることを、３つの垂直二等分線が１点で交わるという話 　　　　に置き換えているわけで、とても巧妙なテクニックですね！

（追記）　令和６年７月６日付け

　将棋の王位戦が７月６日〜７日に名古屋・徳川園で行われる。隣接する徳川美術館では、
尾張徳川家ゆかりの将棋盤が９月８日まで特別公開されるという。おやつ候補として提供さ
れる予定の「竹千代」も１２月１５日まで販売されるらしい。

　垂心に関する問題が、東北大学　文理共通（１９６６）で出題されている。

第２問　　２定点Ｂ（−１，０）、Ｃ（１，０）に対して、点Ａが直線 ｙ＝ａ （ａ＞０） 上を動くとき、
　　次の各問いに答えよ。

（１）　△ＡＢＣの垂心Ｈの描く図形の方程式を求めよ。
（２）　原点ＯとＨの距離の最小値を求めよ。

（解）（１）　Ａ（ｔ，ａ） とおくと、直線ＡＨの方程式は、ｘ＝ｔ

　直線ＢＣの傾きは、　ａ/（ｔ−１）　なので、直線ＢＨの方程式は、

　ｙ＝−｛（ｔ−１）/ａ｝（ｘ＋１）　なので、　ｘ＝ｔ　を代入して、ｙ＝（１−ｔ²）/ａ

よって、垂心Ｈの描く図形の方程式は、　ｙ＝（１−ｘ²）/ａ

（２）　ＯＨ²＝ｔ²＋（１−ｔ²）²/ａ²＝（１/ａ²）ｔ⁴＋（１−２/ａ²）ｔ²＋１/ａ²

ここで、ｔ²＝ｘ　とおくと、ｘ≧０　で、　ＯＨ²＝（１/ａ²）ｘ²＋（１−２/ａ²）ｘ＋１/ａ²

よって、

ＯＨ²＝（１/ａ²）（ｘ＋（ａ²/２−１））²＋１/ａ²−（１/ａ²）（ａ²/２−１）²

　＝（１/ａ²）（ｘ＋（ａ²/２−１））²＋１−ａ²/４

　軸の方程式　ｘ＝１−ａ²/２　なので、

　１−ａ²/２≦０　すなわち、ａ≧　のとき、ＯＨ²の最小値は、ｘ＝０　のときで、１/ａ²

　すなわち、ａ≧　のとき、ＯＨの最小値は、１/ａ

　１−ａ²/２＞０　すなわち、０＜ａ＜　のとき、ＯＨ²の最小値は、

　ｘ＝１−ａ²/２　のときで、１−ａ²/４

　すなわち、０＜ａ＜　のとき、ＯＨの最小値は、√（１−ａ²/４）　　（終）


（コメント）　「複素数の底力」の「三角形の垂心」で、次の公式が示されている。

　ガウス平面上の３点Ａ（α）、Ｂ（β）、Ｃ（０）に対して、△ＡＢＣの垂心Ｈ（ｚ）は、

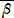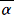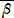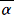　　ｚ＝（α−β）（α＋β）/（α−β）

である。

　この公式を用いてみよう。

　Ａ（ｔ，ａ）、Ｂ（−１，０）、Ｃ（１，０）　に対して、ｘ 軸方向に１だけ平行移動すると、

　Ａ（（ｔ＋１，ａ）、Ｂ’（０，０）、Ｃ’（２，０）　となる。

そこで、　α＝ｔ＋１＋ａ・ｉ　、β＝２　として、公式に代入すると、ｚ＝ｔ＋１＋｛（１−ｔ²）/ａ｝ｉ

　ｘ＝ｔ＋１　、ｙ＝（１−ｔ²）/ａ　とおいて、ｔ を消去すると、　ｙ＝（１−（ｘ−１）²）/ａ

ｘ 軸方向に−１だけ平行移動すると、　ｙ＝（１−ｘ²）/ａ　となり、先の結果と一致する。


　　以下、工事中！