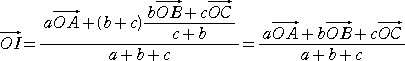オイラーの定理 
世の中に、あの数学界の巨星 Euler の偉大さを物語るように、定理に「オイラーの」と冠
されるものは数多い。例えば、
● 立体図形におけるオイラーの多面体定理
(頂点の個数)−(辺の個数)+(面の個数)=2
● 関数論におけるオイラーの定理
eX+iY=eX(cosY+isinY)
● 整数論におけるオイラーの定理
aφ(n)≡1 (mod n)
ただし、n は正の整数で、1 から n までの自然数のうち、n と互いに素となるものの個数
を φ(n) (オイラー関数)、a は n と互いに素な整数とする。
● ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
ここで、またオイラーの定理というものを紹介するのは、少し気が引けるが、とても興味あ
る事実なので、あえて取り上げたいと思う。
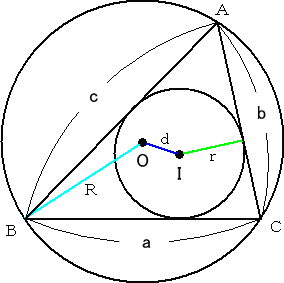
オイラーの定理 三角形の内接円の中心 I と外接円の中心 O との距離 d は、
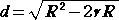
で与えられる。 ただし、R は、外接円の半径、 r は、内接円の半径 である。
 |
三角形の外心O、重心G、垂心Hには、
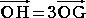
という美しい関係が成り立つことは、よく
知られている。(→証明は、こちら)
しかし、それに劣らず、
外心 O と内心 I の中心間の距離が、
両者の半径のみによって表される
という事実も、とても興味深い。
(流石!オイラーですね...。) |
(証明) よく知られた公式により、
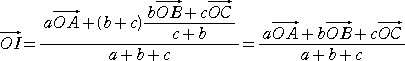
が成り立つ。このとき、
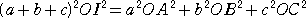
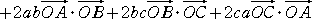
において、
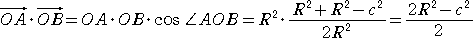
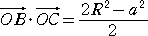 、
、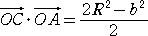
であるので、
(a+b+c)2OI2
=a2R2+b2R2+c2R2+2abR2−abc2+2bcR2−a2bc+2caR2−ab2c
=(a+b+c)2R2−abc(a+b+c)
ここで、△ABC の面積を S とおくと、2S=r(a+b+c) 、4RS=abc が成り立つので、
abc=2rR(a+b+c) である。
よって、 (a+b+c)2OI2=(a+b+c)2R2−2rR(a+b+c)2 より、
OI2=R2−2rR すなわち、 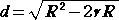
が成り立つ。 (証終)
このオイラーの定理により、 R−2r ≧0 なので、
三角形の外接円の半径は、内接円の直径以上である
ことが分かる。もちろん、正三角形においては、R=2r が成り立つ。
上記では、三角形の外心と内心の距離に注目した公式であったが、外心と傍心の距離
についても同様の公式が成り立つ。(→ 参考:「傍接円の話題」)
定理 三角形の一つの傍接円の中心 I’ と外接円の中心 O との距離 d は、
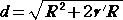
で与えられる。 ただし、R は外接円の半径、 r’ は傍接円の半径 である。
(証明) △ABC において、BC=a、CA=b、AB=c とし、2s=a+b+c とおく。
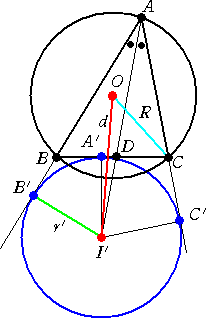 |
BA : BD = b+c : a で、BI’ は∠ABCの外角の
2等分線なので、 I’ は線分ADを、b+c : a に外分
する点である。 よって、
(−a+b+c)OI’=−aOA+bOB+cOC
が成り立つ。 このとき、
(−a+b+c)2OI’2
=a2OA2+b2OB2+c2OC2
−2abOA・OB+2bcOB・OC−2caOC・OA
において、 |
OA・OB=OA・OB・cos∠AOB=R2(R2+R2−c2)/(2R2)=(2R2−c2)/2
OB・OC=(2R2−a2)/2 、OC・OA=(2R2−b2)/2
であるので、
(−a+b+c)2OI’2
=a2R2+b2R2+c2R2−2abR2+abc2+2bcR2−a2bc−2caR2+ab2c
=(−a+b+c)2R2+abc(−a+b+c)
ここで、△ABC の面積を S とおくと、 4RS=abc で、さらに、
S=△AB’I’+△AC’I’−△BB’I’−△BA’I’−△CC’I’−CA’I’
=sr’−(s−c)r’−(s−b)r’=(−a+b+c)r’/2
が成り立つので、 abc=2r’R(−a+b+c) である。
よって、 (−a+b+c)2OI’2=(−a+b+c)2R2+2r’R(−a+b+c)2 より、
OI’2=R2+2r’R すなわち、 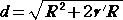
が成り立つ。 (証終)
(コメント) 2円の中心間の距離が半径のみで得られるのは、とても美しい結果ですね!
ちょっと証明が大変かな?と思ったのですが、今日の出張先での空き時間にチョ
コチョコっと計算したらあっさり証明が出来てしまいました!
(追記) 令和元年9月29日付け
最近、正三角形の内接円、外接円、傍接円の半径の比が、1:2:3 という美しい比になる
ことを知り、確認してみた。
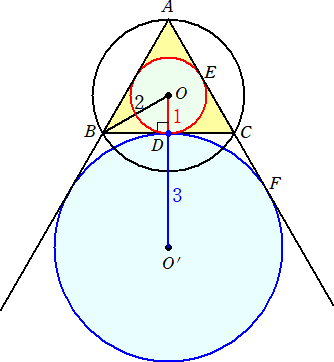 |
左図において、正三角形の内接円の半
径を1とすると、
外接円の半径は2、傍接円の半径は3
となることは明らかだろう。
こんな美しい比に出会えて幸せです!
また、CDを介して、CE=CF となる
ことも興味深い性質ですね。
これを、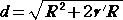 に代入す に代入す
ると、確かに、d=4 となりますね。 |